Mechanistic insight into phase transfer agent assisted ultrasonic desulfurization†
Abstract
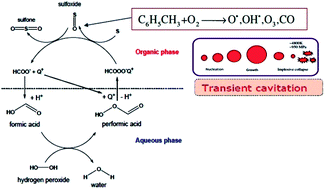
This paper attempts to gain physical insight into the phase transfer agent (PTA) assisted ultrasonic oxidative desulfurization process. Essentially, the synergistic links between mechanisms of PTA and ultrasound/cavitation have been identified by coupling experimental results with simulations of cavitation bubble dynamics and Arrhenius & thermodynamic analysis of reaction kinetics. It is revealed that ultrasonic oxidative desulfurization has a radical-based mechanism with a low activation energy. However, due to the high instability of radicals, the frequency factor is small leading to low dibenzothiophene (DBT) oxidation. PTA-assisted oxidative desulfurization has an ionic mechanism with a much higher activation energy. The synergistic effect of fine emulsification generated by micro-convection due to ultrasound and cavitation, and PTA-assisted interphase transport of oxidant results in almost complete oxidation of DBT. It is thus established that synergy between the mechanisms of ultrasound/cavitation and PTA is predominantly of a physical nature. Moreover, the effect of PTA is more marked for an ultrasonic system than a mechanically agitated system.

 Please wait while we load your content...
Please wait while we load your content...