Open Access Article
Open Access ArticleAn in-depth assessment into simultaneous monitoring of dissolved reactive phosphorus (DRP) and low-molecular-weight organic phosphorus (LMWOP) in aquatic environments using diffusive gradients in thin films (DGT)
Christian Wilhelm
Mohr
*a,
Rolf David
Vogt
a,
Oddvar
Røyset
b,
Tom
Andersen
c and
Neha Amit
Parekh
a
aDepartment of Chemistry, University of Oslo, Norway. E-mail: c.w.mohr@kjemi.uio.no
bNorwegian Institute for Water Research (NIVA), Oslo, Norway
cDepartment of Bioscience, University of Oslo, Norway
First published on 5th March 2015
Abstract
Long-term laborious and thus costly monitoring of phosphorus (P) fractions is required in order to provide reasonable estimates of the levels of bioavailable phosphorus for eutrophication studies. A practical solution to this problem is the application of passive samplers, known as Diffusive Gradient in Thin films (DGTs), providing time-average concentrations. DGT, with the phosphate adsorbent Fe-oxide based binding gel, is capable of collecting both orthophosphate and low molecular weight organic phosphorus (LMWOP) compounds, such as adenosine monophosphate (AMP) and myo-inositol hexakisphosphate (IP6). The diffusion coefficient (D) is a key parameter relating the amount of analyte determined from the DGT to a time averaged ambient concentration. D at 20 °C for AMP and IP6 were experimentally determined to be 2.9 × 10−6 cm2 s−1 and 1.0 × 10−6 cm2 s−1, respectively. Estimations by conceptual models of LMWOP uptake by DGTs indicated that this fraction constituted more than 75% of the dissolved organic phosphorus (DOP) accumulated. Since there is no one D for LMWOP, a D range was estimated through assessment of D models. The models tested for estimating D for a variety of common LMWOP molecules proved to be still too uncertain for practical use. The experimentally determined D for AMP and IP6 were therefore used as upper and lower D, respectively, in order to estimate minimum and maximum ambient concentrations of LMWOP. Validation of the DGT data was performed by comparing concentrations of P fractions determined in natural water samples with concentration of P fractions determined using DGT. Stream water draining three catchments with different land-use (forest, mixed and agriculture) showed clear differences in relative and absolute concentrations of dissolved reactive phosphorus (DRP) and dissolved organic P (DOP). There was no significant difference between water sample and DGT DRP (p > 0.05). Moreover, the upper and lower limit D for LMWOP proved reasonable as water sample determined DOP was found to lie in-between the limits of DGT LMWOP concentrations, indicating that on average DOP consists mainly of LMWOP. “Best fit” D was determined for each stream in order to practically use the DGTs for estimating time average DOP. Applying DGT in a eutrophic lake provided insight into P cycling in the water column.
Environmental impactIt is well known that eutrophication is a continuous growing environmental problem, as the increase in human activity associated with urbanization and agricultural practices results in nutrient pollution in the aquatic and marine environment from point and non-point sources. However, a less known issue is the possible impact climate change and acid rain reduction may have on eutrophication in many Nordic countries with marine clay soil becoming phosphorus rich (due to the rising of land from the sea during the post-glacial period). This paper focuses on the monitoring of dissolved reactive phosphorus (DRP) and dissolved organic phosphorus (DOP), and especially the DOP subfraction low-molecular-weight organic phosphorus (LMWOP), which are known to be bioavailable. The method chosen for monitoring is passive sampling by using Diffusive Gradients in Thin-films (DGTs). |
1 Introduction
1.1. The role of background P flux in eutrophication
Deterioration of water resources due to the increased rate of eutrophication has been a large and increasing environmental problem in most parts of the world. The problem is related to excessive input of nutrients (mainly phosphorus (P) and nitrogen (N)) from human activities: agriculture, industry, and sewage disposal. Abatement actions used in order to reduce the anthropogenic nutrient loading to water bodies have been shown to counter eutrophication.1,2 However, the progression in resolving the eutrophication problems is generally very slow, such as in the lake Vansjø, south-eastern Norway. Despite numerous and costly abatement actions, such as redirecting sewage wastewater and reducing the P input from agricultural sites in the catchment, the water quality remains poor. This has brought attention to the role of the background flux of P.3 The main natural transport mechanism of P from forested watersheds to surface waters is associated with Dissolved Natural Organic Matter (DNOM). With 85% of the Vansjø catchment being forested, and approx. 90% of the land being below the marine limit, it is found that this background flux accounts for 39% of the total P flux to the lake.4 The contribution of P to DNOM is thus a considerable portion of the total P flux to the lake. Moreover, the concentrations of DNOM in streams have increased significantly in the southern parts of the Nordic countries since the 1980's.5–7 It is hypothesized that this has caused an increased flux of P bound to the DNOM, and that this partly compensates for the decreased anthropogenic P loading – thereby disguising the effect of abatement actions.3 It is furthermore likely that a considerable fraction of the P associated with DNOM is bioavailable low-molecular-weight (molecular weight <1 kDa)8 organic phosphorus (LMWOP) compounds. Nucleic acid derivatives, phospholipids, sugar phosphates and inositol polyphosphates are all bioavailable LMWOP species commonly found in the soil and water.9–16 The concentrations of these molecules, as well as the inorganic orthophosphate species, fluctuate, but are generally held low even in eutrophic freshwaters. This is due to rapid fixation by algae and other microorganisms as well as precipitation/co-precipitation with aluminium, iron, calcium and manganese. The fluctuating and very low concentrations of these compounds present major challenges in the monitoring of the bioavailable P fraction by standard methods.1.2. Diffusive gradients in thin films
The use of Diffusive Gradient in Thin films (DGTs), a passive sampler based on diffusive uptake, represents a major break-through in environmental water-chemistry monitoring for a number of chemical species commonly present in concentrations close to the limit of detection. The DGTs' ability to accumulate specific chemical species linearly over time (within limits) makes it possible to determine the time average concentrations of specific species. Furthermore, because DGTs accumulate the analyte, even species with concentrations near the detection limit can be determined with good precision and accuracy.17The DGTs' linear uptake of an analyte is based on Fick's law for steady-state diffusion in dilute solutions.18 The diffusion flux (J) over the permeable thin-film membrane of the DGT is dependent on the area of cross-section (A), the diffusion coefficient (D) and the concentration gradients across the membrane and diffusive boundary layer combined (dc/dx) (eqn (1)).
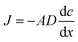 | (1) |
The analyte that has diffused across the membrane is rapidly and completely bound to the binding gel. The concentration of dissolved analyte in the binding gel is thus practically zero, simplifying the flux equation (eqn (2)).
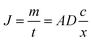 | (2) |
DGTs fitted with Fe-oxide binding gel have been shown to adsorb phosphate, arsenate and selenate.19,20 The strong affinity of Fe-oxide for phosphate makes it a suitable adsorbent also for many LMWOP compounds. Fe-oxide binding gel has been tested in regards to some organic and condensed phosphates that are commonly encountered in the aquatic environment.21 These findings are strongly supported by a review of organic P sorption studies by Celi and Barberis.22 In this study LMWOP compounds were shown to adsorb to ferric oxide surfaces in the soil. Moreover, the sorption properties were linked to the phosphate functional group. Similar sorption–desorption properties were found to be common with the well-studied orthophosphate.
Other DGT phosphate binding gel materials, such as titanium dioxide23 and amorphous zirconium oxide,24 have been assessed. Both produced promising results regarding dissolved reactive phosphorus (DRP) in terms of sorption capacity and binding gel stability over time. Zirconium oxide has also been shown to adsorb LMWOP.25 It is therefore likely that titanium dioxide also adsorbs LMWOP, due to its similar properties to zirconium oxide in binding to orthophosphate. However, a minimum elution strength of 1 M NaOH is required in order to efficiently extract phosphate from both titanium dioxide and zirconium oxide.23,24 In the case of zirconium oxide this has been shown to increase the risk of hydrolysis for some P compounds.25 In this study only the Fe-oxide binding gel has been studied, based on its well-established record as a phosphate adsorbent and commercial availability (DGT Research Ltd).
Employing DGTs to sample LMWOP is not novel in itself, as both Moorlegham et al.21 and Sun et al.25 have studied the adsorption of LMWOP by the DGTs. However, the question how to use the amount of analyte determined from the DGTs to predict the ambient concentration of LMWOP is yet unresolved. In the study by Dougherth et al.26 it was shown that total dissolved phosphorus (TDP) runoff from peat soil could be empirically estimated from time average measured DRP in soil pore water using soil deployment DGT with Fe-oxide binding gel. However the application of this study in a real world scenario is limited to risk assessment of runoff from peat soil, and not actual monitoring of water bodies for a variety of land-use. Furthermore in the study only an inorganic fertilizer was applied to the peat soil, which makes it highly likely that the relationship found between TDP in the runoff and DRP from the DGTs is actually fundamentally a relationship between DRP in the runoff and DRP from the DGTs, since TDP in this case is likely approx. equal to DRP. This is not always the case, since different land-uses will have different DRP to dissolved organic P (DOP = TDP − DRP) ratios as will be presented in the field studies in Chapter. 4.7.
Operationally defined, LMWOP is the fraction of organic molecules containing P that are small enough to diffuse through the APA-gel of the DGT and accumulate in the Fe-oxide binding gel. LMWOP is operationally determined as the difference between the TDP and the DRP, based on the amounts extracted from the DGT binding gels, see Chapter 2.4. The average ambient concentration of a phosphorus species (c) is calculated by solving eqn (2) in regards to c (eqn (3)), using the D determined for the specific molecular compound.
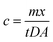 | (3) |
LMWOP constitutes a continuum of a poorly defined group of compounds that exhibit large spatial variation.11 This represents a challenge when converting the amount of LMWOP measured in the binding gel to the ambient concentration of the LMWOP fraction. A single diffusion coefficient for the LMWOP fraction cannot be applied since diffusion coefficients are species specific. A more accurate perspective would be to view the concentration of LMWOP (cLMWOP) as the sum of the concentration of the individual LMWOP species (ci; eqn (4)).
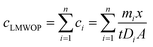 | (4) |
Using a LMWOP D range is to some degree impractical for the application of monitoring water bodies by DGT, as it only results in giving a possible LMWOP concentration range. However for the sake of practicality it is possible to estimate a “best fit” D for the entire DOP fraction by testing different D values until the bulk temporal distribution of monitored DGT LMWOP matches the bulk temporal distribution of monitored water sample DOP. This makes it possible to “tailor” the LMWOP D for a specific water body, i.e. a form of calibrating the D for time average determination of DOP. In this study the Wilcoxon rank-sum statistical test was used to search for a “best fit” D. The test was also used for the validation of DGT DRP data, discussed in depth in Chapter 4.7.
2 Materials and methods
All DGTs used in this study were solution deployment style DGTs purchased from DGT Research Ltd. Each unit consisted of a piston-cap with a 2.0 cm diameter sampling window fitted with 0.12 mm thick cellulose nitrate membranes and 0.8 mm thick agarose polyacrylamide (APA) diffusive gel situated over the Fe-oxide binding gel.17 All data were processed using R statistical software.272.1. Experimental determination of the range of LMWOP diffusion coefficients
Adenosine monophosphate (AMP) and inositol hexakisphosphate (IP6; or phytic acid) were selected as model compounds since the sizes of these two compounds span most of the molecular weight range of LMWOP. Moreover, they represent nucleoside polyphosphates and inositol polyphosphates, two LMWOP compounds commonly encountered in the environment.11The diffusion coefficients (D) for these model compounds were experimentally determined by placing the DGTs in a 40–45 L solution containing the model compounds. The DGTs were mounted on 3 central rotating disks in the container and submerged face down into the solution. The rotor was set to a fixed rotating speed of 6 rpm (equivalent speed of 5–10 cm s−1 depending on the mounting distance from the center point) to ensure a low laminar diffusive boundary layer (<0.1 mm) during the experiments.28
The DGTs were collected from the AMP solution over a period of 19 days at intervals of approx. 2 days (2 replicates). The sampling scheme for the DGTs in the IP6 solution was daily samples for 8 days (1 replicate). Aliquots of 30 mL test solution were sampled along with the DGTs for determining the concentration of P fractions in the test solution. Temperature was measured during DGT and test solution sample collection and was shown to remain relatively constant (22.4 ± 0.6 and 23.6 ± 0.5 °C for the AMP and IP6 solution respectively). Collected DGTs and water samples were refrigerated at 4 °C and kept in the dark until extraction and analysis of P fractions. Non-exposed DGTs were used as DGT blanks for background correction and determination of the limit of detection (n = 4).
The 45 L test solution containing 25 μg P/L AMP was prepared by dissolving disodium adenosine-5′-monophosphate salt (C10H12N5Na2O7P, brand: Merck, purity: ≥99%) in deionized water. In order to match natural water pH and ionic strength (IS), the pH was adjusted to 5.0 by adding 0.1 M ammonium acetate (CH3COONH4) and IS was increased by adding NaCl to a final concentration of 1 mM.
In a similar manner the 40 L test solution containing 32 μg P/L IP6 was prepared by dissolving phytic acid dipotassium salt (C6H16O24P6K2, brand: Sigma-Aldrich, purity: ≥95%) in deionized water. The pH in the tank was buffered to 5.5 by adding 1 M sodium acetate/acetic acid buffer (CH3COO−/CH3COOH). The IS was increased by adding NaCl to a final concentration of 1 mM. Both solutions were left to stabilize for 24 h prior to the experiment.
2.2. Monitoring of P fractions in stream and lake water with DGTs
The concentration of dissolved reactive phosphorus (DRP; i.e. mainly orthophosphate) and LMWOP in streams was measured using DGTs. The DGTs were placed in three 1st order streams draining catchments which differ in land-use; Dalen is a boreal forested catchment (Forest), Huggenes is a mixed catchment (Mixed), comprised of approx. 32% forest, 59% agriculture and 9% other land-use, while Støa is an agricultural catchment (Agricultural).29 The streams drain into the eutrophic western basin of Vansjø, a lake located south of Oslo, Norway. The concentrations of P fractions in the stream water were monitored as a part of the Eutropia research project.3 The streams were therefore known to differ in the level and composition of P fractions. All DGTs were deployed in the streams for 1 to 2 week intervals over a period of approx. 3 months from June to September, 2011. Water temperature was measured at the time of deployment and collection to correct diffusion coefficients for temperature differences. Water samples for the determination of P fractions were collected along with the deployment and collection of DGTs, and occasionally more frequently during increased runoff periods. Evaluation of compliance between the DGT measured DRP and grab sample DRP was performed using the Wilcoxon rank-sum test.A practical performance study using DGTs was performed in Grepperødfjorden, a shallow sub-basin of lake Vansjø. DGTs were placed at depths ∼0 m (i.e. just below the surface), 2.5 m, 3.75 m and in the sediment at ∼4 m (DGT window faced down into the sediment under buoy anchor). The DGTs were deployed in replicates of 3 at each depth, except in the sediment in which only a single DGT was used. All DGTs placed in the lake water were fitted with a nylon net mesh coated with an antifouling agent (Seajet 034 spray, Sola Shipping AS) situated a few mm from the DGT window. The purpose of the net was to reduce algae growth on the DGT window. The DGTs were placed in the lake for 13 days during mid-August, 2012. Water samples at 2.5 m depth were collected and water temperature profiles were measured during deployment and collection of the DGTs. Differences in P fractionation between depths were analyzed by one-way ANOVAs on log-transformed variables. Log-transformation was necessary to stabilize variances.
2.3. Elution of P from the DGT binding gel
DGTs were dissembled and the Fe-oxide binding gels were placed in polypropylene tubes. 0.7 mL deionized water was added to the tube, followed by 0.3 mL of 4 M H2SO4, giving an initial concentration of 1.2 M H2SO4. The binding gels were left for 24 h ensuring a complete dissolution of the Fe-oxides in the binding gel. The final acid concentration was adjusted to 0.04 M H2SO4 by dilution with deionized water, matching the acid concentration of the standards used for the phosphate determination.2.4. Phosphorus fractionation and analysis
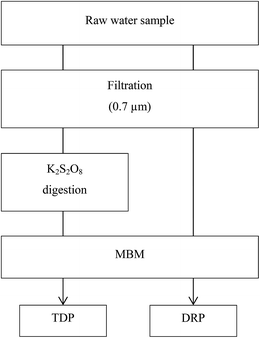
The two P fractions, Total Dissolved P (TDP) and Dissolved Reactive P (DRP), were determined in the water samples by combining potassium peroxodisulfate (K2S2O8) digestion30 and non-digestion of filtered (0.7 μm Whatman® glass microfiber filters, Grade GF/F) samples as pre-treatment steps prior to the determination of DRP by the molybdate blue method (MBM)31 (see Fig. 1). 0.7 μm Whatman® glass microfiber filters (Grade GF/F) were employed as this was required for the concurrent monitoring within the Eutropia research project for studying the characteristics of particulate matter. TDP and DRP fractions in the DGT extracts were analyzed in a similar manner, though without the filtration step. Still, only dissolved P compounds are sampled by DGTs as only molecules smaller than 5–10 nm pass through the APA diffusive gel of the DGTs. Discrepancies are expected between TDP determined in the water samples and DGTs due to the smaller pore-sizes of the DGT membranes (700 nm versus 5–10 nm), causing size exclusion of the fraction of large dissolved molecules by the DGT.MBM is considered a wet chemical selective method for the determination of orthophosphate. However studies have shown that the reagents added in the MBM method alter the natural equilibrium in the water sample, resulting in an overestimation of the orthophosphate.32 It is nevertheless assumed here that the DRP fraction is approximately equal to the free aqueous orthophosphate concentration in solution.
The concentrations of TDP and DRP in the water and DGT samples were determined using a customized continuous flow auto-analyzer (SKALAR San++ Automated Wet Chemistry Analyser), with online digestion prior to analysis of TDP. pH was measured and dissolved organic carbon (DOC) was determined in all water samples. DOC was determined using a Shimadzu TOC-5000A total organic carbon analyzer after 0.7 μm filtration. pH measurements were used to determine the protonated distribution of orthophosphates, and correct the orthophosphate diffusion coefficients for this distribution.
3 Modelling
3.1. Relating range in size, mass and charge of P fractions to DGT diffusion coefficients
The Stokes–Einstein equation (eqn (5a)) can be used to theoretically predict diffusion coefficients of organic molecules in liquid media: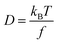 | (5a) |
| f = 6πηr0 | (5b) |
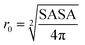 | (6) |
This theoretical approach is explored in order to estimate the D for a number of LMWOP molecules lacking experimentally derived D, and thereby help assess the upper and lower diffusion coefficient values for the LMWOP molecules.
3.2. Assessing humic substance uptake by DGT
The main DNOM fraction in water is humic substances (HS), constituting approx. 60% of the total organic carbon (TOC) in freshwater.37 The molecular size of HS are generally on average larger than the low molecular weight (LMW) compounds,38 comprising LMWOP, and thereby considered as a high molecular weight fraction (HMW). HS are also assumed to contain P, though the mass percentage of P in HS is relatively low compared to LMWOP compounds (e.g. nucleoside phosphates, inositol phosphates, some phospholipids, etc., see Table 1). Still, the abundance of HS implies that this fraction constitutes not only a significant amount of the high molecular weight organic P (HMWOP), but also the total DOP in surface waters. It is therefore necessary to assess to what degree HS may be adsorbed by the DGTs. Depending on the size, some of the HS may be able to pass through the APA membrane owing to the molecular cut-off of 5–10 nm.39 If successful in passing the membrane they are assumed to be efficiently adsorbed by the Fe-oxide binding gel, as HS and phosphate strongly compete for adsorption sites on Fe-oxide.40 A theoretical solute radius for HS cannot be determined using eqn (6) as there is no specific chemical structure. Therefore, it is not possible to determine a theoretical diffusion coefficient for the HS using the Stokes–Einstein equation (eqn (5)). The diffusion coefficient can instead be semi-empirically estimated using eqn (7), developed by Buffle,41 providing a relationship between molecular weight (M) and D in water at 20 °C (eqn (7)).42 The coefficient in this equation is based on a study of a number of organic molecules in the molecular weight range of 200–105 Da. The friction coefficient, ϕ/ϕ0, is ideally equal to one, however it has been shown to increase with molecular size. For HS a friction coefficient of 1.16 was found to give the best fit,43 and has thus been used in this study for the calculation of diffusion coefficients for HS.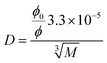 | (7) |
| Substance | M (Da) | P content (w/w%) | P/C mass ratio |
|---|---|---|---|
| a ATP, adenosine tri-phosphate; G6P, glucose 6-phosphate; DLPA, 1,2-dilauroylphosphatidic acid. b Perdue and Ritchie.37 c IHSS: Suwannee River FA and HA fractions.44 | |||
| G6P | 260 | 12 | 0.431 |
| AMP | 347 | 9 | 0.258 |
| ATP | 507 | 18 | 0.775 |
| DLPA | 536 | 5.8 | 0.095 |
| IP6 | 660 | 28 | 2.584 |
| FA (average) | 500–2800b | ∼0.004c | ∼7.6 × 10−5c |
| HA (average) | 1300–6500b | ∼0.013c | ∼2.5 × 10−4c |
HS in freshwater consists of mainly fulvic acids (FA) and humic acids (HA). Their number- and weight-average molecular weights (Mn and Mw respectively) given in the literature vary greatly, mainly due to variations in sampling sites and the operationally defined analytical techniques used for their determination. In a comprehensive review by Perdue and Ritchie37 the combined range of Mn and Mw for FA and HA was found to range from approx. 500 to 2800 and 1300 to 6500 Da, respectively.
The smaller molecular weight FA fraction will have a higher diffusion coefficient, and can therefore accumulate at a higher rate than the larger molecular weight HA fractions. It is therefore necessary to assess both the ambient concentration of both FA and HA bound P and the molecular weight distribution of these two humic fractions in order to calculate the total amount of accumulated HS bound P.
The concentrations of FA and HA bound P (cFA-P and cHA-P) are calculated using eqn (8a) and (8b), based on dissolved organic carbon (DOC) concentration in the collected water samples, weighted by the relative fractions of HA and FA (fFA-C = 46 and fHA-C = 13% from Perdue and Ritchie37) and their P to C ratio (P/C) for FA and HA (Table 1).
| cFA-P = DOC × fFA-C × P/C | (8a) |
| cHA-P = DOC × fHA-C × P/C | (8b) |
It has been shown that the molecular weight distributions of FA follows a log-normal distribution. A log-normal Gaussian distribution of the molecular weight can be calculated only if Mn and Mw45 are known (eqn (9a)):
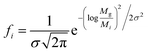 | (9a) |
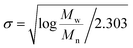 | (9b) |
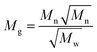 | (9c) |
Due to the polydisperse nature of HS it is presumed that HA, like FA, also follows a log-normal distribution. On the basis of this assumption the molecular weight distribution of freshwater FA and HA can be calculated by taking the mean Mn and Mw for a number of observations derived from different analytical methods (vapour pressure osmometry (VPO), cryoscopy (CRY), size exclusion chromatography (SEC), UV scanning ultracentrifugation (UV-UCGN) and flow field-flow fractionation (FFF)) from the review paper of Perdue and Ritchie.37 The mean Mn and Mw are weighted for the number of observations for each analytical method. A probability density plot for the molecular weight is then created based on the determined molar frequency (Fig. 2).
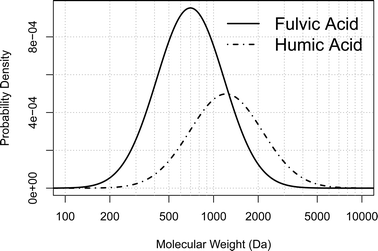 | ||
| Fig. 2 Probability density plot of the molecular weight distribution of FA and HA calculated from a log-normal model (eqn (9)) based on the mean Mn and Mw data from Perdue and Ritchie.37 | ||
Using the probability density data the probability of every molecular weight fraction, p(xi), from 100 to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da can be calculated for both FA and HA by multiplying p(xi) with the calculated concentration of FA and HA bound P (cFA-P and cHA-P, respectively), with the assumption that the P content in FA and HA is constant for the molecular weight distribution within each fraction (eqn (10a) and (10b)).
000 Da can be calculated for both FA and HA by multiplying p(xi) with the calculated concentration of FA and HA bound P (cFA-P and cHA-P, respectively), with the assumption that the P content in FA and HA is constant for the molecular weight distribution within each fraction (eqn (10a) and (10b)).
| FA-Pi = p(xi) × cHA-P | (10a) |
| HA-Pi = p(xi) × cHA-P | (10b) |
The total flux of FA-P and HA-P across the DGT membrane is then calculated using eqn (11):
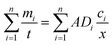 | (11) |
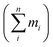 of each molecular weight fraction divided by time (t).
of each molecular weight fraction divided by time (t).
3.3. Accounting for diffusion retention by the DGT APA membrane
Zhang et al.20 measured a 29% lower diffusion coefficient (D) for H2PO4− using DGT compared to D measured in water. This was explained by phosphate retention due to positively charged sites on the APA diffusive gel.20 Similar reduced diffusion in DGTs is thus likely to be a factor for all negatively charged compounds. Furthermore, as the molecular size increases there is likely to be an increase in friction as the molecular size approaches the pore size (5–10 nm) of the APA membrane. It is therefore important that the free-diffusion in water, as calculated by the Stokes–Einstein (eqn (5)) or Buffle's equation (eqn (7)), is corrected for the reduced diffusion caused by the APA membrane. Three empirical regression fit models, y = αx + β, y = αxβ and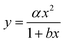 , were tested on experimentally determined free and DGT restricted D in order to assess the best model for D correction.
, were tested on experimentally determined free and DGT restricted D in order to assess the best model for D correction.
3.4. Theoretical determination of diffusion coefficients for LMWOP molecules
The molecular composition of the LMWOP fraction (Mw < 1 kDa) in any specific surface water is generally unknown as it varies in time and space. A single averaged diffusion coefficient can therefore not be theoretically calculated or directly derived from experimental data for the LMWOP fraction. Instead the adopted approach is to determine the upper and lower diffusion coefficients, covering the range of LMWOP compounds expected to be encountered in surface waters. As introduced in Chapter 1.1 the most dominant group of LMWOP compounds are nucleic acids, phospholipids, sugar phosphates and inositol polyphosphates. Some of the most common as well as most studied LMWOP compounds in soil and water are presented in Table 1.11 The exception is DLPA (1,2-dilauroylphosphatidic acid), which only serves as a representative of a small phospholipid, of which there are numerous varieties.Three conceptually based models were used for theoretically estimating the upper and lower diffusion coefficients:
• Buffle's model: estimation by Buffle's semi-empirical equation (eqn (7)), where molecular weight is the only variable and the friction coefficient (ϕ/ϕ0) is set by default to 1.
• ChemAxon-Stokes–Einstein model: estimation using the Stokes–Einstein equation (eqn (5)), based on the friction coefficient (f) achieved using the solute radius (r0), which was based on the computational model for determining SASA from the chemical structure, pH and the radius of the solute water molecule (radius = 1.4 Å). pH was used to calculate the dominant molecular species. SASA was calculated at pH 5 since the pH in the experimental determination of diffusion coefficients for AMP and IP6 was 5.0 and 5.5, respectively (Chapter 2.1).
• ChemAxon-Wilke–Chang model: estimation by the Wilke–Chang correlation46 (eqn (12a)):
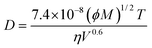 | (12a) |
| V = 4πr03N/3 | (12b) |
Evaluation of the three models was done by comparing the modelled D of AMP and IP6 with the experimentally derived D.
4 Results and discussion
4.1. Experimental determination of diffusion coefficients
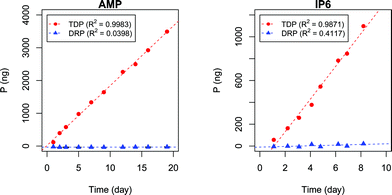
In Fig. 3 the accumulated amounts of TDP and DRP by DGTs are plotted against their deployment time in the test solutions.The results presented in Fig. 3 show a clear linear uptake of AMP and IP6 with time, where all TDP measurements are above LOD (1.7 μg P L−1). Based on correlation slopes the uptake rates for AMP and IP6 were found to be 182 ± 2.7 ng P day−1 (p < 10−11) and 150 ± 7.0 ng P day−1 (p < 10−6), respectively.
In the AMP experiment the amount of DRP found in the extract remained below LOD (1.2 μg P L−1), with no clear increasing trend with time (0.15 ± 0.27 ng P day−1, p = 0.58). This indicates that there was negligible or no AMP degradation in the tank or when bound to the DGT binding gel, or during the extraction step. The IP6 experiment, on the other hand, showed a slight indication of an increase in DRP concentration with time (3.0 ± 1.5, p = 0.086). This may be due to degradation. However, this is conceptually unlikely since IP6 had a shorter experiment time than AMP. A possible explanation may instead lie in the relatively lower purity of the IP6 chemical reagent compared to the AMP chemical reagent (≥95% vs. ≥99% purity, respectively). Nevertheless DRP measurements for IP6 experiment were below LOD.
Uptake flux rates for the two experiments cannot be directly compared due to different concentrations of analyte and temperatures. In order to compare the uptake of AMP with IP6 the diffusion coefficient (D) for each TDP measurement presented in Fig. 3 must therefore first be calculated by eqn (13), derived by rearranging eqn (3).
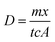 | (13) |
Moreover, the concentration of analytes (measured as TDP) in the tanks decreased over time during both experiments. Interpolation through linear regression was therefore used to estimate the time average concentration (c). D needs to be corrected for different ambient temperatures. The correction is calculated by eqn (14) (derived from the Stokes–Einstein equation, eqn (5)), in which DT1 is the diffusion coefficient for temperature T1, η1 is the viscosity of water at temperature T1, DT2 is the diffusion coefficient for temperature T2, and η2 is the viscosity of water at temperature T2, where temperature is given in Kelvin and viscosity in kg m−1 s−1.
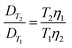 | (14) |
The water viscosity is calculated using a quadratic empirically based equation (eqn (15)), where T is the temperature given in Kelvin. The constants a = 5.53 × 10−7, b = −3.51 × 10−4 and c = 5.65 × 10−2 were determined using a second degree regression model (R2 = 0.998) to fit the equation to measured viscosities for water at different temperatures (0 to 40 °C in 5 °C increments) taken from Zwolinski and Eicher.47Eqn (15) is only applicable for temperatures between 0 and 40 °C.
| η = aT2 + bT + c | (15) |
From these equations the diffusion coefficient at 20 °C was calculated. The average D for AMP and IP6 were found to be 2.9 ± 0.4 × 10−6 cm2 s−1 and 1.0 ± 0.3 × 10−6 cm2 s−1, respectively.
4.2. Elution efficiency from DGT
The elution of AMP and IP6 from the Fe-oxide binding gel was conducted using 1.2 M H2SO4. This acid concentration is far stronger than the 0.25 M H2SO4 recommended by Zhang et al.20 The higher acidity was used to ensure a total recovery of orthophosphate, which has been shown to increase with increased acid concentration.20 Since organic phosphates and orthophosphate have similar adsorption/desorption chemistry (Chapter 1.2) it is fair to assume complete elusion. On the other hand, a high sulphuric acid strength increases the risk of hydrolysis (i.e. of the ester-bonds linking phosphate to the adenosine or inositol molecule) decomposing the organic compounds. As addressed in Chapter 4.1 the DRP concentration remained low in the test solution (Fig. 3), which documents that AMP and IP6 were not significantly hydrolysed. However, the study by Moorlegham et al.21 suggests that a few LMWOP compounds are susceptible to hydrolysis under strong acidic conditions (pH ≤ 0). It is therefore perceivable that some LMWOP compounds accumulated by the DGT from the natural aquatic environment may have hydrolysed during elusion.4.3. DGT APA membrane resistance
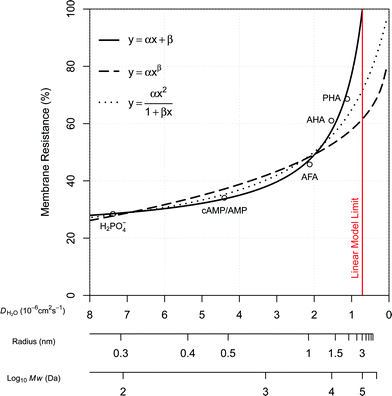
The plots presented in Fig. 4 show the relationship between the determined D for water (DH2O) with the determined D for DGTs with APA diffusive gel (DDGT). Out of the three models presented, the linear regression fit model, y = αx + β (left plot), shows the strongest correlation with the D data (R2 = 0.9997), with the estimated values for parameters, α and β, highly significant for explaining the variations (p < 0.001). It should be noted that the linear empirical model is not applicable for correcting all DH2O, as it intersects the x-axis at DH2O = 0.71. The non-linear model, y = αxβ (centre plot), also shows a strong correlation with the data (R2 = 0.9967). However it remains the weakest correlation of the three plots. The advantage of the equation y = αxβ is that as DH2O decreases towards 0, DDGT also decreases towards 0, making the model applicable for all DH2O. The third model,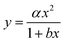 (right plot), is a combination of a quadratic and linear equation (R2 = 0.9989). The choice of this equation is because it supports the linear trend as DH2O increases
(right plot), is a combination of a quadratic and linear equation (R2 = 0.9989). The choice of this equation is because it supports the linear trend as DH2O increases 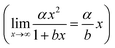 , while allowing a non-linear trend towards 0 as DH2O decreases
, while allowing a non-linear trend towards 0 as DH2O decreases 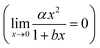 , thereby making the model applicable for all DH2O.
, thereby making the model applicable for all DH2O.
 | ||
Fig. 4 Three regression models fitted to diffusion coefficients in water and DGT data for H2PO4− (Zhang et al.20), aquatic derived FA and HA (AFA and AHA respectively), peat derived HA (PHA) (Zhang and Davison39) and cAMP in water (Dworkin and Keller48) with AMP for DGTs, all corrected for 20 °C. Water diffusion coefficients for AFA, AHA and PHA are calculated using Buffle's equation (eqn (7), with friction coefficient = 1.16) based on the Mw for the fractions (2400, 6300 and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 Da respectively).49 500 Da respectively).49 | ||
The main difference between the linear model and the two non-linear models is the conceptual understanding of the relationship between DH2O and DDGT as a result of membrane resistance. Presented in Fig. 5, where membrane resistance (MR) can be calculated from DH2O and DDGT (eqn (16)), the linear model presents the cut-off point (100% retention) for DH2O = 0.71, while the non-linear models show a continuous increase in retention only reaching 100% once DH2O = 0.
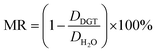 | (16) |
Using the Stokes–Einstein equation (eqn (5)) the molecular radius can be calculated to be approx. 3 nm for DH2O = 0.71. This is a diameter of approx. 6 nm, which is within the range of the pore size, 5–10 nm, for the APA membrane. It seems therefore likely that molecules larger than ∼6 nm in diameter are unable to diffuse through the APA membrane. This is a molecular weight of approx. 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–100
000–100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Da calculated by Buffle's equation (eqn (7)) for a friction coefficient = 1.16–1, respectively. On the basis of this concept and the good fit with the data, the linear model (eqn (17)) is chosen for correcting the free D for MR.
000 Da calculated by Buffle's equation (eqn (7)) for a friction coefficient = 1.16–1, respectively. On the basis of this concept and the good fit with the data, the linear model (eqn (17)) is chosen for correcting the free D for MR.
| DDGT = 0.7907DH2O − 0.5621 | (17) |
4.4. Assessment of the amount of adsorbed humic substance P and HMWOP by DGT
Based on the model approach presented in Chapter 3.2 followed by MR correction, an assessment was made to estimate the amount of phosphorus associated with HS accumulated by the DGT. Mean concentrations of DOC in the water samples (Table 2) were used in eqn (8a) and (8b) to determine the amount of FA and HA bound P (FA-P and HA-P) for each of the three studied sites (Table 2).| Location | Dissolved Organic Carbon (DOC) | |||
|---|---|---|---|---|
| Mean (mg C L−1) | Stdev (mg C L−1) | RSD (%) | n | |
| Forest | 38 | 2.5 | 6.7 | 26 |
| Mixed | 17 | 3.3 | 20.2 | 8 |
| Agricultural | 12 | 1.4 | 11.5 | 12 |
The mean total flux of DOP was calculated by taking the accumulated amounts of DOP (TDP–DRP) adsorbed and dividing by the field deployment time of the DGTs. The mean HA-P and FA-P flux could then be calculated, in accordance with eqn (7)–(11), (14) and (17), as a fraction of the mean total DOP flux for each study site. The non-HS DOP, which is presumed to be accounted for by the LMWOP, was calculated by subtracting the HA-P and FA-P flux from the total DOP flux. The results given in Table 3 show that the amounts of HA-P and FA-P (i.e. comprising HMWOP) accumulated by the DGTs are negligible compared to the LMWOP fraction.
| Site | HA-P (%) | FA-P (%) | LMWOP (%) |
|---|---|---|---|
| Forest | 0.21 | 0.31 | 99.46 |
| Mixed | 0.03 | 0.05 | 99.91 |
| Agricultural | 0.02 | 0.04 | 99.94 |
The negligible contribution is mainly attributed to the extremely low P/C ratio reported for the FA-P and HA-P fractions (Table 1). These data are based on HS that were isolated using the XAD solid phase column extraction method and fractionated by precipitation of FA at pH < 1 (IHSS Suwannee River FA and HA fractions44). It is possible that the XAD alters the natural equilibrium of phosphate bound to Al and Fe complexed by HS. The low pH (1–2) and high pH (13) used in the XAD extraction method may desorb phosphate bound to the Al and Fe (ref. 50 and 51) on the HS. In the review by Copper et al.,52 it was shown that even after isolating HMW organic matter (>1 kDa) from natural waters, the large majority of organic phosphorus species determined for this fraction by mass spectrometry techniques were below 1 kDa. The confounding result was assumed to be a result of disruption of ionic interaction between large humic-like substances and LMWOP species, due to the electrospray ionization step, i.e. they were separated before analysis, despite being naturally found to be weakly linked together in natural waters. A study of freshwater from the Everglades, by Ged and Boyer8 showed that approx. 40% of their DOP was associated with compounds larger than 10 kDa. That being said the study also showed that approx. 44% of the DOP was associated with low molecular weight species (<1 kDa), leaving only ∼16% DOP in the molecular weight fraction between 1 and 10 Da. Based on these DOP data a rough estimated calculation of DOP uptake by the DGTs can be conducted in which the flux is calculated using the concentration of DOP for each fraction (c) and D of the middle molecular weight of each molecular weight fraction. Unfortunately, no middle molecular weight can be estimated for >10 kDa, so a “worst case scenario” is used in which the average molecular weight for the >10 kDa fraction is assumed to be equal to 10 kDa. The results presented in Table 4 show that despite the relatively high concentration of DOP associated with HMW compounds, the relative flux of >10 kDa DOP into the DGT is only 16% vs. approx. 75% being associated with <1 kDa. However unlike the first assessment made from Table 3, where HS are shown to be negligible, these data show that >1 kDa or HMWOP may account for approx. 25% of the accumulated DOP fraction. Since much of DNOM larger than 1 kDa is HS, it cannot be exactly concluded to what degree HS contributes to the fraction of DOP adsorbed by the DGT. Instead it can be concluded that more than 75% of the DOP accumulated by the DGT is associated with LMWOP.
| Molecular weight fraction (kDa) | Middle molecular weight (kDa) | Relative DOP concentration (%) | DOP fluxb (%) |
|---|---|---|---|
| a Worst case scenario of 10 kDa is chosen. b Diffusion coefficients for the flux were calculated using Buffle's eqn with a friction coefficient = 1. | |||
| <1 | 0.5 | 44 | 74.9 |
| 1–3 | 2 | 2 | 1.9 |
| 3–5 | 4 | 4 | 2.7 |
| 5–10 | 7.5 | 10 | 4.7 |
| >10 | 10a | 40 | 15.9 |
4.5. Assessment of ambient LMWOP from adsorbed DOP by the DGT
Diffusion coefficients at 20 °C for five LMWOP compounds (Table 5) were calculated using the three theoretically based methods discussed in Chapter 3.4, and corrected for MR using the linear empirical model derived in Chapter 4.3 (eqn (17)).| Substance | M (Da) | Solute radius (Å) | Estimated DDGT (10−6 cm2 s−1) | ||
|---|---|---|---|---|---|
| Buffle | ChemAxon-Stokes–Einstein | ChemAxon-Wilke–Chang | |||
| G6P | 260 | 5.3 | 3.5 | 2.6 | 4.7 |
| AMP | 346 | 6.1 | 3.2 | 2.2 | 3.5 |
| ATP | 507 | 7.1 | 2.7 | 1.8 | 2.5 |
| DLPA | 535 | 9.7 | 2.7 | 1.2 | 1.2 |
| IP6 | 656 | 7.1 | 2.4 | 1.8 | 2.5 |
The estimated lower and upper D ranges were found to be 2.4–3.5, 1.2–2.6 and 1.2–4.7 for Buffle, ChemAxon-Stokes–Einstein and ChemAxon-Wilke–Chang models, respectively. ChemAxon-Wilke–Chang gave a much larger range, with a difference of 3.5 from the lowest to the highest D, compared to the spans of Buffle and ChemAxon-Einstein–Stokes (1.1 and 1.4, respectively). Overall, Buffle produced slightly higher D values than ChemAxon-Einstein–Stokes. All three models show G6P to have the highest D. The lowest D, however, varies among the Buffle and ChemAxon models. The Buffle equation indicates that IP6 is the slowest molecule, because it has the largest mass of the five compounds. However based on the molecular structure the largest r0 is DLPA, which is why the ChemAxon model indicates that this compound has the lowest D. This reflects the weakness of using Buffle's equation for LMWOP. Buffle's semi-empirical equation is based on that the organic molecules have a mole fraction dominated by the atoms 12C, 1H, 16O and small amounts of 14N. This generates rather similar molecular densities for the organic molecules. However, molecules dense in 31P, such as IP6, have considerably higher molecular density. However, the phosphate groups cause the compound to have a relatively high net negative charge, producing a large hydrodynamic radius (possibly not accounted for by the ChemAxon model) and retention by the DGT APA membrane. IP6 has a strong negative charge of −6 to −8 at the pH range of 5–7 (Chapter 3.1), encountered in the studied water bodies. This results in a high absolute charge to mass/size ratio, explaining the relatively lower diffusion coefficient than what might be expected considering mass and size based on structure.
Deviations between experimentally measured diffusion coefficients for AMP and IP6 (Chapter 4.1) and their three theoretically derived constants are given in Table 6. The diffusion coefficients of AMP and IP6 are assumed to cover the range of D values encountered by LMWOP. Estimated D based on Buffle's equation deviates only 9% from the observed value for AMP, while both the ChemAxon models have an absolute error of 23%. Moreover, all models perform extremely poorly in estimating D for IP6. The estimated values using the ChemAxon-Stokes–Einstein model is slightly closer, with only 81% deviation, though still too high to be useful for any meaningful prediction of D. Apparently, retardation of the charged IP6 by the slightly positively charged APA gel (Chapter 3.3) considerably reduces the diffusion of the molecule causing the experimentally observed D value to be significantly lower than the modelled D estimates.
| Compound | Observed DDGT (10−6 cm2 s−1) | Estimated DDGT (10−6 cm2 s−1) | Deviation (%) | ||||
|---|---|---|---|---|---|---|---|
| Buffle | C.A.-Stokes–Einstein | C.A.-Wilke–Chang | Buffle | C.A.-Stokes–Einstein | C.A.-Wilke–Chang | ||
| a C.A.: abbreviation for ChemAxon. | |||||||
| AMP | 2.9 | 3.2 | 2.2 | 3.5 | 8.8 | −23 | 23 |
| IP6 | 1.0 | 2.4 | 1.8 | 2.5 | 144 | 81 | 152 |
ChemAxon-Wilke–Chang appeared to be the poorest model in this test. The other two models performed slightly better, but were also poor predictors for lower and upper D of LMWOP. However, the combined D range of Buffle and ChemAxon-Stokes–Einstein models for the five studied compounds (1.2–3.5; Table 5) does not deviate much from the experimental D range of 1.0–2.9, captured by measuring IP6 and AMP.
The experimentally derived values of D for AMP and IP6 will be used for determining the ambient LMWOP concentration in the catchment study (Chapter 4.7) since they span the theoretically derived D values based on a set of LMWOP with large differences in physiochemical characteristics.
4.6. pH correction of dissolved reactive phosphate (DRP)
The common D constant used for determining ambient DRP from DGT measurements is 5.28 × 10−6 cm2 s−1 for H2PO4− (Zhang et al.20). The problem however is that H2PO4− is not the dominant species at all pH commonly encountered in the environment. E.g., the median pH during the monitoring period for the Forest, Mixed and Agricultural catchment streams was 4.4, 6.9 and 7.8, respectively. Within this range the dominant species of orthophosphate differ between H2PO4− and HPO42−. As each of these species has its own D the distribution of H2PO4− and HPO42− with pH needs to be accounted for. The distribution (α) for each species can be calculated from eqn (18) and (19), where the pKa values for H3PO4, H2PO4− and HPO42− are 2.16, 7.21 and 12.3, respectively.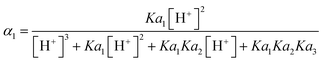 | (18) |
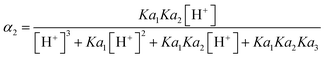 | (19) |
In the forest catchment stream, with pH 4.4, 99.3% (α1) is in the form of H2PO4− and 0.2% (α2) is HPO42−. In the mixed catchment stream, having pH 6.9, 63.2% is in the form of H2PO4− and 36.8% is HPO42−, while for the agricultural catchment stream, with pH 7.8, only 34.9% is in the form of H2PO4− and 65.1% is HPO42−. The challenge is that there exists no experimentally DGT determined D value for HPO42−. There is however a water determined D for HPO42− (6.40 × 10−6 cm2 s−1 at 20 °C),53 which after correction for DGT retardation due to MR (eqn (17)) is calculated to be 4.50 × 10−6 cm2 s−1. One can then calculate a pH adjusted D for DRP at any given pH by multiplying the fractional contribution of the two species, with their corresponding D and adding the two products (eqn (20)).
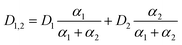 | (20) |
It should be noted that the reason eqn (20) does not use the fractions directly is due to the fact that the forest catchment stream, with a median pH of 4.4, also contains the H3PO4 species (0.5%). There is however a lack of available data on D for H3PO4, making it difficult to employ for this special case.
4.7. Field study of DGTs in stream water
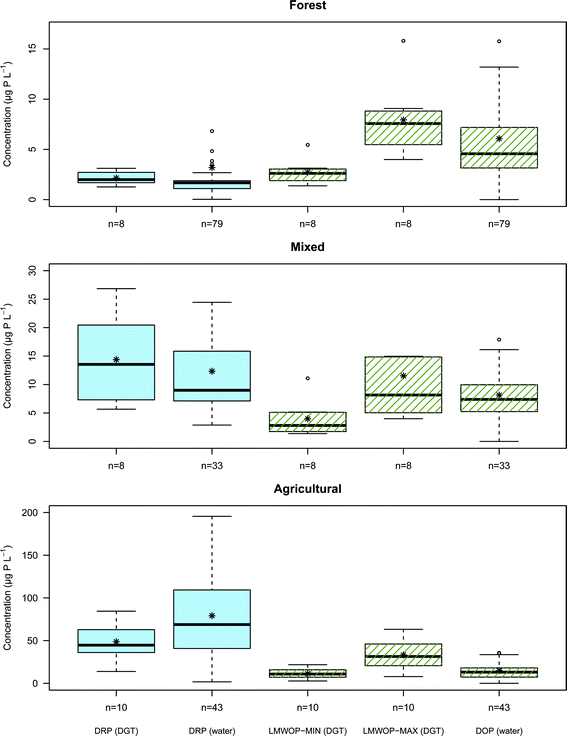
Median, mean, variation and range in DRP and DOP concentration, derived from DGTs and water samples collected from the streams draining Forest, Mixed and Agricultural catchments, are shown in Fig. 6. As expected the drainage from agricultural catchment shows a considerably higher concentration of DRP compared to the mixed and forested catchment. The agricultural stream shows also a greater concentration of DRP compared to DOP, while the opposite is the case for the forest stream. The reason is without doubt the large amount of inorganic phosphate fertilizer used in the cultivation of the agriculture sites, governing the higher DRP to DOP ratio. In forest catchments the DRP is kept low as it is efficiently consumed by the perennial forest vegetation. It is the leaching of DNOM from the forest soil which contributes most to the DOP found in the Forest stream. The stream water from the Mixed catchment has inherently a DRP to DOP ratio that lies between the ratios found for the Forest and Agricultural streams.Validation of the DGT's ability to measure time average concentrations of DRP was performed by comparing the DRP concentrations derived from DGTs with the DRP measured directly in water samples collected from the streams during the DGT deployment period. The Wilcoxon rank-sum statistical test (also known as the Mann–Whitney U test) is a nonparametric test for the null hypothesis of two sample groups originating from the same population. The main advantage of the Wilcoxon test is its efficiency and robustness in comparing populations, which are not necessarily normally distributed and vary in the number of observations, i.e. non-paired test. This is practical, considering that DGTs are time average measurements, while grab samples are only momentary measurements. For good comparison more grab samples than DGT measurements are required. The test does not require an interval dataset, only that the data is ordinal, which is necessary since sampling intervals varied during the period (Chapter 2.2). The statistical test found no significant difference (p < 0.05) between DRP from DGTs and water samples for the Forest, Mixed and Agricultural catchment streams (p = 0.053, p = 0.39 and p = 0.078, respectively). However it should be noted that both the Forest and Agricultural catchments were borderline to failing the null hypothesis. It is important also to note that without pH correction (Chapter 4.6) the Wilcoxon rank-sum test would have predicted a significant difference (p = 0.032) for the Agricultural catchment stream. From the boxplots in Fig. 6 it can be seen that the median values of the forest DRP values for DGT and water sample are close (2.0 μg P L−1 and 1.7 μg P L−1 respectively), but that the bulk distribution of measurements overlap poorly. The DGT time average measurements show an overall slightly higher DRP concentration than the water samples. For the stream draining the Agricultural catchment there is good agreement between the two distributions of DGT and water sample DRP measurements. However, the DGT show a far narrower spread in measurements as these are time averaged values. All the water sample DRP measurements from the median to the 3rd quartile are higher than the main bulk distribution of DGT DRP measurements. It is possible that this larger DRP concentration in the water sample is a result of over-estimation, possibly contributed by P lightly adsorbed to colloid-particles bypassing the 0.7 μm filter (see Chapter 2.4).
Overall there is clearly far less difference between the two methods of DRP determination (i.e. DGT and water sample), relative to the difference in DRP concentration between the three catchment streams.
Validation of DOP by comparing significant deviations between DGT determined LMWOP and water samples determined DOP is not sound for the following two reasons:
(1) DOP in the water sample may also contain a significant fraction of HMWOP (Chapter 4.4).
(2) Only minimum and maximum concentrations of LMWOP can be determined. The actual amount remains unknown until further information is acquired regarding the relative distribution of DOP molecular species for the streams draining the different catchments. It can however be assumed, based on the findings in Chapter 4.4, that the large majority of the DGT accumulated DOP is LMWOP (>75%).
For all streams the maximum LMWOP concentration determined is higher than the DOP concentration determined from the water sample. This simply reflects that on average not all of the DOP molecular compounds in the water samples are as large or have a D as low as IP6. The minimum LMWOP concentration has to be smaller than or equal to the DOP in the water samples, since LMWOP is a fraction of the DOP fraction. Based on the good match between DOP in the water sample and the minimum LMWOP concentration in the Agricultural stream it appears that the average size of the DOP molecules in the agricultural runoff is of the size of AMP. The mixed catchment shows closer match with the larger molecular compounds, such as IP6. For the forest stream the DOP on average consists of a medium sized LMWOP. The results clearly show that streams draining from catchments with different land-use have different distributions of LMWOP.
For the practical application of using DGTs to monitor time average DOP we need to determine a “best fit” D, which results in the best match between DGT determined LMWOP and water determined DOP. Using the same Wilcoxon rank-sum test, which was used to validate the DRP data, we can compare the DGT LMWOP with the water sample DOP data for different D from 1.0 to 2.9 in 0.05 increments. The D resulting in the highest p-value for the test will indicate minimum significant difference between the two datasets (Table 7). It should however be noted that this serves only as a practical means of using the DGTs to determine time average DOP, because there is an assumption that the relative distribution of LMWOP/DOP compounds remains constant within each stream, despite changes in the overall LMWOP/DOP concentration. However even if the assumption of constant relative distribution is likely correct, the D determined by this stream calibration method is likely smaller than the true unattainable number average D for LMWOP, because the DOP concentration in water samples (also containing HMWOP) is always larger than LMWOP.
| Location | D (10−6 cm2 s−1) | p-value |
|---|---|---|
| Forest | 1.6 | 0.959 |
| Mixed | 1.15 | 0.936 |
| Agricultural | 2.45 | 0.973 |
4.8. Field study of lake water DRP and LMWOP using DGT
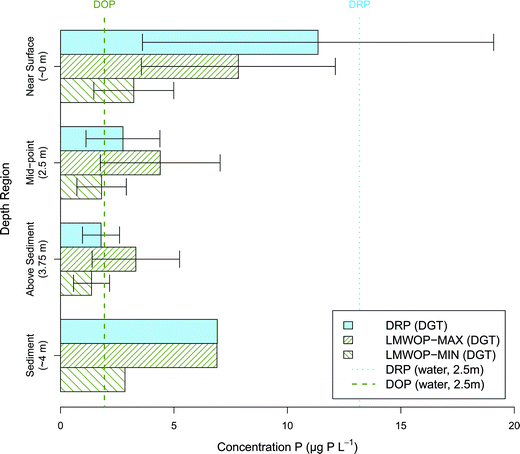
The DGT study at the lake basin Grepperødfjorden provides some insight into the dynamics of P bioavailability through the water column (Fig. 7). Temperature showed a fairly minor and constant decline with depth, from 21.3 to 18.7 °C. The lake basin is shallow and was non-stratified due to mixing by water turbulence. This is however not always the case, as the lake basin occasionally experiences stratification and hypoxia in the hypolimnion. During the summer and early autumn periods (the warmest months) the lake experiences algae blooms, dominated mainly by Gonyostomum semen (phytoplankton fraction approx. 60–80%).54 This phytoplankton species is typically found in humic lakes and is capable of diel vertical movement (DVM). This means it is able to migrate towards the surface for enough light for photosynthesis during the day and migrate towards the sediments for a source of P, typically during the night.55,56 It would be expected that the DVM of phytoplankton and lack of stratification would result in a fairly even distribution of DRP and LMWOP concentration through the water column. The DGT results presented in Fig. 7 show however that DRP decreased significantly with depth (p < 0.05), while there was no significant difference between depths for LMWOP (p > 0.05). The highest concentrations of both DRP and LMWOP were found near the surface. Based on conventional grab samples the levels of bioavailable P species in the photic zone are commonly found to be close to the detection limit even in eutrophic lakes, due to efficient phosphorus assimilation by phytoplankton during the day. On the other hand, DGTs capture the time average concentration, and thus integrate out diurnal variation, while grab samples are usually only taken during the day. This may mean that biochemical processes that may give the net production of DRP and LMWOP during the night are not detected by the conventional sampling method. For instance, it is known that macrozooplankton migrate towards the sediments during the day to avoid predation due to reduced visibility in deeper, darker waters. During the night however they are safe to migrate back towards the surface where they can feed on phytoplankton in the warmer epilimnion.57 As a result of sufficient food and warmer temperatures, their metabolic rate increases, which results in the release of DRP and LMWOP through excretion.14 The second explanation for the high DRP and LMWOP near the surface is cell death, which is common near the surface due to the intense solar radiation. Phytoplankton are dependent on getting sufficient photosynthetically active radiation (PAR, ∼380–710 nm), which declines exponentially with depth, known as vertical light attenuation. Furthermore UV-radiation, but also wavelengths (WL) in the blue spectrum of PAR, decline exponentially with increase in DNOM.58 In humic water bodies, such as Grepperødfjorden, this results in a thin euphotic zone at the surface of the water. Minimal change in distance from the surface results in large changes in the amount of available PAR. A little too far below the surface results in insufficient photosynthesis to balance their energy demand for metabolic activity.59 A little too near the surface and the high intensity of light, in particular UV-radiation, result in DNA damage and cell death, not to mention that photo-degradation of DNOM results in reactive oxygen species toxic to biota.58,60 Cell death is followed by lysis, which results in the release of DOP to the water. In addition many of the enzymes capable of hydrolysing phosphate from DOP are also released as a result of cell lysis, which may explain the high DRP concentration in the surface waters.14At the deeper depths of the water column it appears that P uptake keeps the P concentration low, and the reduced UV-radiation keeps the phytoplankton safe from harmful exposure. Finally the DGT placed in the sediment measures high concentrations of both P fractions, as would be expected due to internal loading from the sediments.
It remains unclear why DRP measured from the water sample collected at 2.5 m is far greater than the DGT determined DRP at 2.5 m. DOP from the water sample remains near the LMWOP determined concentrations.
5 Conclusion
The solution type DGTs fitted with Fe-oxide binding gel proved to be successful in the linear uptake of AMP and IP6, and will therefore most likely capture other LMWOP, and thus bioavailable, compounds in a similar manner. Modelling of HA-P and FA-P uptake indicated that the DGTs only collect negligible amounts of P associated with HS. Even using higher P/C ratios reported by Ged and Boyer,8 less than approx. 25% of the DOP that was accumulated could be over >1 kDa. It should be noted that a negligible amount of this is associated with HS as this is the largest DNOM fraction. More studies are needed to better quantify the distribution of DOP with molecular weight for a variety of catchments with different land-use. Nonetheless, the results remain fairly conclusive that more than 75% of the DOP accumulated by the DGT is LMWOP.Both the Buffle and the ChemAxon-Stokes–Einstein models are still in their infancy in regards to predicting DGT diffusion coefficients (D) of LMWOP molecules. This is partly because there is currently insufficient observed/experimental data available to develop good models. More LMWOP molecules need to have their D determined experimentally so that better calibration and validation can be performed. There is little doubt that charge plays an important role in the diffusion of molecules through the DGT APA membrane. It is therefore inherent that the D needs to be determined at different pH, in order to compensate for the changes in negative charge as a result of protonation and de-protonation of phosphate and other weak acid functional groups.
The catchment study indicates that there is a reasonable match between the dissolved P fractions determined from water samples and by DGTs, and that molecular weight distribution of LMWOP/DOP is different for the three study sites. However, accurate determination of the concentration of the LMWOP fraction remains infeasible without knowing the distribution of LMWOP molecules in the streams. The application of DGTs will not be practical for the determination of the time average LMWOP fraction if one needs to determine the relative distribution of the LMWOP molecules each time the DGT is used. A practical compromise was however found by determining a “best fit” D for each study site that results in the least significant difference between the two datasets, DGT LMWOP and the water sample DOP. In this way “tailored” D for the individual water bodies can be determined as a means to roughly assess the time average DOP.
The lake study clearly shows the strengths of the DGT as a better means of capturing the spatial variation of DRP and LMWOP in the lake. Further studies are still required to better explain P cycling in the lake. Nevertheless, the use of DGTs provides a far better ambient approach to monitoring bioavailable P concentrations than the conventional grab sample, which often fails to capture long-term diel, seasonal and spatial variations due to the practical restraints of sampling.
Funding
Department of Chemistry, University of Oslo and RCN project no. 190028-S30 and 209687-E40.Acknowledgements
Per-Johan Færovig, Alexander Engebretsen, Grethe Wibetoe, Tomas Alder Blakseth, Jan Roots, Claus Jørgen Nielsen.References
- S. R. Carpenter, N. F. Caraco, D. L. Correll, R. W. Howarth, A. N. Sharpley and V. H. Smith, Nonpoint Pollution of Surface Waters with Phosphorus and Nitrogen, Ecol. Appl., 1998, 8, 559–568 CrossRef.
- M. F. Chslock, E. Doster, R. A. Zitomer and A. E. Wilson, Eutrophication: Causes, Consequences, and Controls in Aquatic Ecosystems, Nat. Educ. Knowl., 2013, 4, 10 Search PubMed.
- R. D. Vogt, Water Quality in a Changing Environment, Public Serv. Rev. Eur. Union, 2012, 23, 386–387 Search PubMed.
- A. Blankenberg, S. Turtumøygard, A. Pengerud, H. Borch, E. Skarbøvik, L. Øyegarden, M. Bechmann, N. Syversen and N. Vagstad, Tiltaksanalyse for Morsa: "Effekter av Fosforreduserende Tiltak i Morsa 2000–2006; Bioforsk, Jord og Miljø, Ås, Norway, 2008, p. 54.
- D. Hongve, G. Riise and J. F. Kristiansen, Increased Colour and Organic Acid Concentrations in Norwegian Forest Lakes and Drinking Water – a Result of Increased Precipitation?, Aquat. Sci., 2004, 66, 231–238 CrossRef CAS PubMed.
- NORDTEST, Increase in Colour and Amount of Organic Matter in Surface Waters, The Nordic Council of Ministers, 2003, pp. 1–12 Search PubMed.
- B. L. Skjelkvåle, Overvåkning av Langtransporterte Forurensninger 2009; Klima- og Forurensningsdirektoratet (Eng. Climate and Pollution Agency), 2010, p. 87.
- E. C. Ged and T. H. Boyer, Molecular Weight Distribution of Phosphorus Fraction of Aquatic Dissolved Organic Matter, Chemosphere, 2013, 91, 921–927 CrossRef CAS PubMed.
- S. Hino, Fluctuation of Algal Alkaline Phosphatase Activity and the Possible Mechanisms of Hydrolysis of Dissolved Organic Phosphorus in Lake Barato, Hydrobiologia, 1988, 157, 77–84 CrossRef CAS.
- R. C. Dalal, Soil Organic Phosphorus, Adv. Agron., 1977, 29, 83–117 CAS.
- B. L. Turner, E. Frossard and D. S. Baldwin, Organic Phosphorus in the Environment, ed. B. Turner, E. Frossard and D. Baldwin; CABI Publishing, 1st edn, 2005 Search PubMed.
- B. A. Whitton, S. L. Grainger, G. R. Hawley and J. W. Simon, Cell-Bound and Extracellular Phosphatase Activities of Cyanobacterial Isolates, Microb. Ecol., 1991, 21, 85–98 CrossRef CAS PubMed.
- I. D. McKelvie, B. T. Hart, T. J. Cardwell and R. W. Cattrall, Use of Immobilized 3-Phytase and Flow Injection for the Determination of Phosphorus Species in Natural Waters, Anal. Chim. Acta, 1995, 316, 277–289 CrossRef CAS.
- A. D. Cembella, N. J. Antia and P. J. Harrison, The Utilization of Inorganic and Organic Phosphorous Compounds as Nutrients by Eukaryotic Microalgae: A Multidisciplinary Perspective: Part 1, CRC Crit. Rev. Microbiol., 1984, 10, 317–391 CrossRef CAS.
- A. D. Cembella, N. J. Antia, P. J. Harrison and A. D. Cernbella, The Utilization of Inorganic and Organic Phosphorous Compounds as Nutrients by Eukaryotic Microalgae: A Mulitdiciplinary Perspective: Part 2, CRC Crit. Rev. Microbiol., 1984, 11, 13–81 CrossRef CAS PubMed.
- P. J. Worsfold, P. Monbet, A. D. Tappin, M. F. Fitzsimons, D. A. Stiles and I. D. McKelvie, Characterisation and Quantification of Organic Phosphorus and Organic Nitrogen Components in Aquatic Systems: A Review, Anal. Chim. Acta, 2008, 624, 37–58 CrossRef CAS PubMed.
- H. Zhang, DGT - for Measurements in Water, Soil and Sediments, DGT Research Ltd, Lancaster, 2005, pp. 1–58 Search PubMed.
- E. L. Cussler, Diffusion: Mass Transfer in Fluids Systems, Cambridge University Press, 3rd edn, 2009 Search PubMed.
- O. Røyset, S. Eich-Greatorex, T. A. Sogn, Å. R. Almås and E. Bjerke, Simultaneous Sampling of Phosphate, Arsenate, and Selenate in Water by Diffusive Gradients in Thin Films (DGT), Oslo, 2004, p. 17.
- H. Zhang, W. Davidson, R. Gadi and T. Kobayashi, In Situ Measurement of Dissolved Phosphorus in Natural Waters Using DGT, Anal. Chim. Acta, 1998, 340, 29–38 CrossRef.
- C. Van Moorleghem, L. Six, F. Degryse, E. Smolders and R. Merckx, Effect of Organic P Forms and P Present in Inorganic Colloids on the Determination of Dissolved P in Environmental Samples by the Diffusive Gradient in Thin Films Technique, Ion Chromatography, and Colorimetry, Anal. Chem., 2011, 83, 5317–5323 CrossRef CAS PubMed.
- L. Celi and E. Barberis, Abiotic Stabilization of Organic Phosphorus in Environmet, in Organic Phosphorus in the Environment, ed. B. Turner, E. Frossard and D. S. Baldwin, CABI Publishing, Wallinford, 2005, pp. 113–132 Search PubMed.
- J. G. Panther, P. R. Teasdale, W. W. Bennett, D. T. Welsh and H. Zhao, Titanium Dioxide-Based DGT Technique for in Situ Measurement of Dissolved Reactive Phosphorus in Fresh and Marine Waters, Environ. Sci. Technol., 2010, 44, 9419–9424 CrossRef CAS PubMed.
- S. Ding, D. Xu, Q. Sun, H. Yin and C. Zhang, Measurement of Dissolved Reactive Phosphorus Using the Diffusive Gradients in Thin Films Technique with a High-Capacity Binding Phase, Environ. Sci. Technol., 2010, 44, 8169–8174 CrossRef CAS PubMed.
- Q. Sun, Y. Chen, D. Xu, Y. Wang and S. Ding, Investigation of Potential Interferences on the Measurement of Dissolved Reactive Phosphate Using Zirconium Oxide-Based DGT Technique, J. Environ. Sci., 2013, 25, 1592–1600 CrossRef CAS.
- W. J. Dougherty, S. D. Mason, L. L. Burkitt and P. J. Milham, Relationship between Phosphorus Concentration in Surface Runoff and a Novel Soil Phosphorus Test Procedure (DGT) under Simulated Rainfall, Soil Res., 2011, 49, 523 CrossRef.
- R Core Team, R: A Language and Environment for Statistical Computing, Vienna, Austria, http://www.R-project.org/, 2013 Search PubMed.
- O. A. Garmo, K. R. Naqvi, O. Røyset and E. Steinnes, Estimation of Diffusive Boundary Layer Thickness in Studies Involving Diffusive Gradients in Thin Films (DGT), Anal. Bioanal. Chem., 2006, 386, 2233–2237 CrossRef CAS PubMed.
- E. Skarbøvik, M. Bechmann, T. Rohrlack and S. Haande, Overvåking Vansjø/Morsa 2008, 2009, vol. 4, p. 108.
- D. S. Jeffres, F. P. Dieken and D. E. Jones, Performance Of The Autoclave Digestion Method For Total Phosphorus Analysis, Water Reasearch Pergamon Press, 1979, 13, 275–279 Search PubMed.
- J. Murphy and J. P. Riley, A Modified Single Solution Method for the Determination of Phosphate in Natural Waters, Anal. Chim. Acta, 1962, 27, 31–36 CrossRef CAS.
- F. H. A. Rigler, Dynamic View of the Phosphorus Cycle in Lakes, in Environmental Phosphorus Handbook, ed. E. J. Griffith, A. Beeton, J. M. Spencer and D. T. Mitchell, John Wiley and Sons., New York, 1973, pp. 539–572 Search PubMed.
- P. W. Atkins and J. De Paula, Molecules in Motion, in Atkin's Physical Chemistry, Oxford University Press, 2006, pp. 747–783 Search PubMed.
- L. Heighton, W. F. Schmidt and R. L. Siefert, Kinetic and Equilibrium Constants of Phytic Acid and Ferric and Ferrous Phytate Derived from Nuclear Magnetic Resonance Spectroscopy, J. Agric. Food Chem., 2008, 56, 9543–9547 CrossRef CAS PubMed.
- ChemAxon, Marvin 6.1.2, http://www.chemaxon.com/, 2013 Search PubMed.
- P. Ferrara, J. Apostolakis and A. Caflisch, Evaluation of a Fast Implicit Solvent Model for Molecular Dynamics Simulations, Proteins: Struct., Funct., Bioinf., 2002, 46, 24–33 CrossRef CAS PubMed.
- E. Perdue and J. Ritchie, Dissolved Organic Matter in Freshwaters, in Treatise on Geochemistry, Vol. 5: Surface and Ground Water, Weathering, and Soils, ed. J. I. Drever, H. D. Holland and K. K. Turekian, Elsevier Ltd, Oxford, 2003, pp. 273–318 Search PubMed.
- S. A. Huber, A. Balz, M. Abert and W. Pronk, Characterisation of Aquatic Humic and Non-Humic Matter with Size-Exclusion Chromatography - Organic Carbon Detection - Organic Nitrogen Detection (LC-OCD-OND), Water Res., 2011, 45, 879–885 CrossRef CAS PubMed.
- H. Zhang and W. Davison, Diffusional Characteristics of Hydrogels Used in DGT and DET Techniques, Anal. Chim. Acta, 1999, 398, 329–340 CrossRef CAS.
- E. Tipping, The Adsorption of Aquatic Humic Substances by Iron Oxides, Geochim. Cosmochim. Acta, 1981, 45, 191–199 CrossRef CAS.
- J. Buffle, Complexation Properties of Homologous Complexants and Choice of Measuring Methods, in Complexation Reactions in Aquatic Systems an Anlytical Approach, ed. R. A. Chalmers and M. R. Masson, Ellis Horwood Limited, Chichester, 1988, pp. 359–363 Search PubMed.
- J. Buffle, Complexation Reactions in Aquatic Systems an Analytical Approach, ed. J. Buffle, Ellis Horwood Limited, Chichester, 1988, p. 673 Search PubMed.
- J. Buffle, Z. Zhang and K. Startchev, Metal Flux and Dynamic Speciation at (bio)interfaces. Part I: Critical Evaluation and Compilation of Physicochemical Parameters for Complexes with Simple Ligands and Fulvic/humic Substances, Environ. Sci. Technol., 2007, 41, 7609–7620 CrossRef CAS.
- International Humic Substances Society, Elemental Compositions and Stable Isotopic Ratios of IHSS Samples, http://www.humicsubstances.org/elements.html/, accessed Jan 30, 2014 Search PubMed.
- S. E. Cabaniss, Q. Zhou, P. A. Maurice, Y.-P. Chin and G. R. Aiken, A Log-Normal Distribution Model for the Molecular Weight of Aquatic Fulvic Acids, Environ. Sci. Technol., 2000, 34, 1103–1109 CrossRef CAS.
- C. R. Wilke and P. Chang, Correlation of Diffusion Coefficients in Dilute Solutions, AIChE J., 1955, 1, 264–270 CrossRef CAS.
- B. J. Zwolinski and L. D. Eicher, High-Precision Viscosity of Supercooled Water and Analysis of the Extended Range Temperature Coefficient, J. Phys. Chem., 1971, 75, 2016–2024 CrossRef CAS.
- M. Dworkin and K. H. Keller, Solubility and Diffusion Coefficient of Adenosine 3′:5′-Monophosphate, J. Biol. Chem., 1977, 252, 864–865 CAS.
- J. R. Lead, J. Hamilton-Taylor, N. Hesketh, M. N. Jones, A. E. Wilkinson and E. Tipping, A Comparative Study of Proton and Alkaline Earth Metal Binding by Humic Substances, Anal. Chim. Acta, 1994, 294, 319–327 CrossRef CAS.
- M. Petrovic and M. Kastelan-Macan, The Uptake of Inorganic Phosphorus by Insoluble Metal-Humic Complexes, Water Sci. Technol., 1996, 34, 253–258 CrossRef CAS.
- E. M. Thurman and R. L. Malcolm, Preparative Isolation of Aquatic Humic Substances, Environ. Sci. Technol., 1981, 15, 463–466 CrossRef CAS PubMed.
- W. T. Cooper, J. M. Llewelyn, G. L. Bennett, A. C. Stenson and V. J. M. Salters, Organic Phosphorus Speciation in Natural Waters by Mass Spectrometry, in Organic Phosphorus in the Environment, ed. B. L. Turner, E. Frossard and D. S. Baldwin, CABI Publishing, 2005, pp. 45–74 Search PubMed.
- L. Yuan-Hui and S. Gregory, Diffusion of Ions in Sea Water and in Deep-Sea Sediments, Geochim. Cosmochim. Acta, 1974, 38, 703–714 CrossRef.
- E. Skarbøvik, M. Bechmann, T. Rohrlack and S. Haande, Overvåking Vansjø/Morsa 2009–2010, Bioforsk, 2011, vol. 6, p. 121.
- G. Cronberg, The Life Cycle of Gonyostomum Semen (Raphidophyceae), Phycologia, 2005, 44, 285–293 CrossRef.
- K. Salonen, Advantages from Diel Vertical Migration Can Explain the Dominance of Gonyostomum Semen (Raphidophyceae) in a Small, Steeply-Stratified Humic Lake, J. Plankton Res., 2000, 22, 1841–1853 CrossRef PubMed.
- J. Kalff, Zooplankton, in Limnology: Inland Water Ecosystems, ed. T. Ryu and J. Hakim, Prentice-Hall, Inc., Upper Saddle River, NJ, 2002, pp. 376–407 Search PubMed.
- J. Kalff, Light, in Limnology: Inland Water Ecosystems, ed. T. Ryu and J. Hakim, Prentice-Hall, Inc., Upper Saddle River, NJ, 2002, pp. 136–153 Search PubMed.
- S. I. Dodson, Setting the Stage: Water as an Environment, in Introduction to Limnology, McGraw-Hill Higher Education, 2005, pp. 39–56 Search PubMed.
- D.-P. Häder, H. D. Kumar, R. C. Smith and R. C. Worrest, Effects of Solar UV Radiation on Aquatic Ecosystems and Interactions with Climate Change, Photochem. Photobiol. Sci., 2007, 6, 267–285 Search PubMed.
| This journal is © The Royal Society of Chemistry 2015 |