Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The first example of a mixed valence ternary compound of silver with random distribution of Ag(I) and Ag(II) cations†
Zoran
Mazej
*a,
Tomasz
Michałowski
bc,
Evgeny A.
Goreshnik
a,
Zvonko
Jagličić
d,
Iztok
Arčon
ef,
Jadwiga
Szydłowska
c and
Wojciech
Grochala
*b
aDepartment of Inorganic Chemistry and Technology, Jožef Stefan Institute, Jamova 39, SI–1000 Ljubljana, Slovenia. E-mail: zoran.mazej@ijs.si
bCENT, University of Warsaw, Żwirki i Wigury 93, 02–089 Warsaw, Poland. E-mail: w.grochala@cent.uw.edu.pl
cFaculty of Chemistry, University of Warsaw, Pasteur 1, 02–093, Warsaw, Poland
dUniversity of Ljubljana, Faculty of Civil and Geodetic Engineering, and Institute of Mathematics, Physics and Mechanics, Jadranska 19, SI–1000 Ljubljana, Slovenia
eUniversity of Nova Gorica, Vipavska 13, SI–5000 Nova Gorica, Slovenia
fDepartment of Low and Medium Energy Physics, Jožef Stefan Institute, Jamova 39, SI–1000 Ljubljana, Slovenia
First published on 27th March 2015
Abstract
The reaction between colourless AgSbF6 and sky-blue Ag(SbF6)2 (molar ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) in gaseous HF at 323 K yields green Ag3(SbF6)4, a new mixed-valence ternary fluoride of silver. Unlike in all other Ag(I)/Ag(II) systems known to date, the Ag+ and Ag2+ cations are randomly distributed on a single 12b Wyckoff position at the
1) in gaseous HF at 323 K yields green Ag3(SbF6)4, a new mixed-valence ternary fluoride of silver. Unlike in all other Ag(I)/Ag(II) systems known to date, the Ag+ and Ag2+ cations are randomly distributed on a single 12b Wyckoff position at the ![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) axis of the I
axis of the I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d cell. Each silver forms four short (4 × 2.316(7) Å) and four long (4 × 2.764(6) Å) contacts with the neighbouring fluorine atoms. The valence bond sum analysis suggests that such coordination would correspond to a severely overbonded Ag(I) and strongly underbonded Ag(II). Thorough inspection of thermal ellipsoids of the fluorine atoms closest to Ag centres reveals their unusual shape, indicating that silver atoms must in fact have different local coordination spheres; this is not immediately apparent from the crystal structure due to static disorder of fluorine atoms. The Ag K-edge XANES analysis confirmed that the average oxidation state of silver is indeed close to +1⅓. The optical absorption spectra lack features typical of a metal thus pointing out to the semiconducting nature of Ag3(SbF6)4. Ag3(SbF6)4 is magnetically diluted and paramagnetic (μeff = 1.9 μB) down to 20 K with a very weak temperature independent paramagnetism. Below 20 K weak antiferromagnetism is observed (Θ = −4.1 K). Replacement of Ag(I) with potassium gives K(I)2Ag(II)(SbF6)4 which is isostructural to Ag(I)2Ag(II)(SbF6)4. Ag3(SbF6)4 is a genuine mixed-valence Ag(I)/Ag(II) compound, i.e. Robin and Day Class I system (localized valences), despite Ag(I) and Ag(II) adopting the same crystallographic position.
3d cell. Each silver forms four short (4 × 2.316(7) Å) and four long (4 × 2.764(6) Å) contacts with the neighbouring fluorine atoms. The valence bond sum analysis suggests that such coordination would correspond to a severely overbonded Ag(I) and strongly underbonded Ag(II). Thorough inspection of thermal ellipsoids of the fluorine atoms closest to Ag centres reveals their unusual shape, indicating that silver atoms must in fact have different local coordination spheres; this is not immediately apparent from the crystal structure due to static disorder of fluorine atoms. The Ag K-edge XANES analysis confirmed that the average oxidation state of silver is indeed close to +1⅓. The optical absorption spectra lack features typical of a metal thus pointing out to the semiconducting nature of Ag3(SbF6)4. Ag3(SbF6)4 is magnetically diluted and paramagnetic (μeff = 1.9 μB) down to 20 K with a very weak temperature independent paramagnetism. Below 20 K weak antiferromagnetism is observed (Θ = −4.1 K). Replacement of Ag(I) with potassium gives K(I)2Ag(II)(SbF6)4 which is isostructural to Ag(I)2Ag(II)(SbF6)4. Ag3(SbF6)4 is a genuine mixed-valence Ag(I)/Ag(II) compound, i.e. Robin and Day Class I system (localized valences), despite Ag(I) and Ag(II) adopting the same crystallographic position.
Introduction
Chemical compounds with an element in more than one oxidation state have been labelled as “mixed-valence” systems, although the expression “mixed oxidation state compounds” perhaps conveys a clearer idea about what is signified.1–3 One striking feature about many mixed-valence compounds is their intense colour; some – such as minium (Pb(II)2Pb(IV)O4), or magnetite (Fe(II)Fe(III)2O4) – have been used since antiquity as pigments. Prussian blue, Fe(III)4[Fe(II)(CN)6]3·nH2O, first prepared over three centuries ago well before the organic chemists joined the dye business, was the first mixed-valence inorganic compound synthesized by men for use in paints and inks.4 In 1967 Robin and Day5 (almost simultaneously with Allen and Hush6) published an extensive survey of mixed-valence systems. Their classification, which remains widely utilized today, is based upon the local symmetry and strength of the ligand fields around metal cations. In Class I systems, cations are found in sites of different symmetry and/or ligand field strength (valences are firmly trapped, i.e. localized; such compounds adopt mixed valence). On the other hand, in Class III the electron density is delocalized over cationic sites and two distinct oxidation states cannot be distinguished (“intermediate valence”) – such systems often exhibit metallic conductivity. In some cases it is not possible to make a clear demarcation between Class I and Class III behaviour. Class II compounds represent such a rare intermediate case in which some degree of delocalization is observed although the cationic sites remain distinguishable. One of the most famous examples of Class II systems is the so called Creutz–Taube Ru(II)/Ru(III) complex,7 which reveals Class I or Class III characteristics depending on the energy/time scale of experiments (“dynamic delocalization”).Mixed-valence compounds exhibit a broad range of fascinating physicochemical properties which are related to electron transfer between distinct oxidation states (i.e. inter-valence charge transfer).8 The most striking of those is high-temperature superconductivity which results from either hole or electron doping to layered Cu(II) oxides9,10 to an appropriate degree;11,12 doping may be realized either via chemical substitutions or charge injection13,14 formally leading to introduction of Cu(III) or Cu(I) to the parent Cu(II) systems. Chemically doped copper oxides are now the best crystallographically researched group of inorganic compounds, with over eight thousand distinct structures available in databases.15 In majority of cases (except for YBCO-like systems) these are Class III systems, where doped charge is equally distributed over all copper sites.
Silver is a heavier sibling of copper and it is natural to search for superconductivity in doped compounds of Ag(II). Many such attempts were made in the early days of oxocuprate superconductivity16 (late 1980s–early 1990s) but without success – in each case only Ag(I) could be introduced into the oxide matrix, which was detrimental to superconducting properties. Only later it was realized that the oxide environment is not appropriate for hosting paramagnetic Ag(II) since the latter species is an enormously strong oxidizer (thus it cannot be obtained by the action of O2, and it is readily reduced to Ag(I)17) and it also tends to disproportionate to Ag(I) and Ag(III) in the oxide environment.18,19 Instead, Ag(II) systems with fluoride anions were suggested as being analogous to Cu(II) oxides as evidenced by many similarities between the two families of compounds. Moreover, the quantum mechanical calculations have revealed that layered Ag(II) fluorides would have a strikingly similar electronic structure to that of undoped oxocuprates,20,21 thus supporting the surmise that superconductivity could be generated upon doping to the former type of material just like it is observed for the latter.22
Regretfully, mixed-valence compounds of silver are quite rare, with about 20 documented stoichiometries (cf. Table 1 in ref. 23). The Ag(II)/Ag(I) system – relevant to electron doping to the parent Ag(II) compound – is limited to two complex compounds with organic ligands,24–26 and two inorganic systems: Ag3(SO3F)4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27,28 and a recently prepared Ag9(PO2F2)14.29,30 The first coordination spheres of Ag(I) and Ag(II) in these systems are quite different: in organic systems both types of silver cations are coordinated by different ligands, while in homoleptic inorganic systems Ag(II) and Ag(I) sit on different crystallographic sites and the local geometries around them differ markedly, thus leading in all cases to the Class I behaviour.
27,28 and a recently prepared Ag9(PO2F2)14.29,30 The first coordination spheres of Ag(I) and Ag(II) in these systems are quite different: in organic systems both types of silver cations are coordinated by different ligands, while in homoleptic inorganic systems Ag(II) and Ag(I) sit on different crystallographic sites and the local geometries around them differ markedly, thus leading in all cases to the Class I behaviour.
In the present work, we describe the results of detailed examination of green Ag3(SbF6)4 (Fig. 1) and of a related K2Ag(SbF6)4. We show that Ag3(SbF6)4 – unlike its predecessors – is an example of a mixed valence ternary compound of silver (Ag(I)2Ag(II)(SbF6)4) with random distribution of Ag(I) and Ag(II) cations on the same crystallographic site in the crystal lattice – which nevertheless preserves a localized-valence character – and we discuss possible consequences of this finding.
 | ||
| Fig. 1 A sample of extremely moisture-sensitive green Ag(I)2Ag(II)(SbF6)4 enclosed in a prefluorinated 0.3 mm quartz capillary. | ||
Experimental
Caution: anhydrous HF (aHF) and some fluorides are highly toxic and must be handled using appropriate apparatus and protective gear. Organic matter may ignite upon contact with compounds of Ag(II).31Materials and methods
Synthetic procedures
There are two crucial factors which may impact the fate of this reaction. The first one is the amount of aHF; if it is too large and sufficient that aHF will start to liquefy when the reactor is cooled down to ambient temperature, aHF(l) will inevitably solvolize part of the Ag3(SbF6)4 product back to AgSbF6 and Ag(SbF6)2 which is detected as blue staining of the liquid phase. The second important thing is to avoid the diffusion of traces of water and even oxygen through the walls of the FEP tube which could lead to reduction of Ag(II).
Crystallography
KSbF6 (0.34 mmol) and Ag(SbF6)2 (0.17 mmol) were loaded into the 19 mm o.d. arm of the crystallization vessel inside a dry-box. The reagent mixture was then transferred to a metal/Teflon manifold where aHF (5 ml) was condensed onto the starting material at −196 °C. The crystallization mixture was warmed to ambient temperature and the resulting clear, blue solution was decanted into the 6 mm o.d. side arm. Evaporation of the solvent from this solution was carried out by maintaining a temperature gradient of ca. 10 °C between the 6 mm o.d. tube and the 19 mm o.d. tube for one day. Slow distillation of aHF from the 6 mm o.d. tube into the 19 mm o.d. tube resulted in crystal growth inside the 6 mm o.d. tube. Selected green single crystals were transferred to 0.3 mm quartz capillaries inside the dry box. In addition, some colorless crystals were observed; their Raman spectra correspond to KSbF6.
The corresponding crystal data and refinement results are summarized in Table 1.
| Chemical formula | Ag3(SbF6)4 | K2Ag(SbF6)4 |
|---|---|---|
a
R
1 is defined as ∑||Fo| − |Fc||∑|Fo| for I > 2σ(I).
b wR2 is defined as [∑[w(Fo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 − Fc 2 − Fc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2)2]/∑w(Fo 2)2]/∑w(Fo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2)2]1/2 for I > 2σ(I). 2)2]1/2 for I > 2σ(I).
|
||
| F w (g mol−1) | 2533.3 | 2258.1 |
| Space group |
I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d 3d |
I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d 3d |
| a (Å) | 12.3613(4) | 12.498(1) |
| V (Å3) | 1888.83(18) | 1952.3(4) |
| Z | 4 | 4 |
| D calc (g cm−3) | 4.454 | 3.841 |
| T (K) | 150 | 200 |
R
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
0.0297 | 0.0836 |
wR2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
0.0642 | 0.2055 |
Instrumental methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 514 eV. Harmonics were effectively eliminated by using a flat silicon mirror. The three 30 cm long ionisation chamber was filled with Kr, the first at the pressure of 120 mbar, the second and third at the pressure of 420 mbar.
514 eV. Harmonics were effectively eliminated by using a flat silicon mirror. The three 30 cm long ionisation chamber was filled with Kr, the first at the pressure of 120 mbar, the second and third at the pressure of 420 mbar.
The absorption spectra were obtained within the −250 eV/+250 eV interval relative to the Ag K-edge. In the XANES region equidistant energy steps of 0.5 eV were used with an integration time of 1 s per step. In all experiments the exact energy calibration was established with simultaneous absorption measurements on a 25 μm thick Ag metal foil placed between the second and the third ionization chamber. The first maximum of the derivative of the Ag foil spectrum was assigned to 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 514.0 eV.
514.0 eV.
The compounds in the form of fine powder were pressed into self-supported homogeneous pellets (diameter 6 mm, thickness less than 1 mm) in a dry-box to prevent hydrolysis and sealed under an inert atmosphere into a thin-walled FEP tube (cf. ESI, Fig. S3†). The FEP tube containing the pellet was mounted on a sample holder in a vacuum chamber of the beam-line. The sealed sample was perfectly stable for several hours of the experiment: no sign of hydrolysis was observed after demounting.
The analysis of Ag K-edge XANES spectra was performed with the IFEFFIT program package ATHENA.41 The relative Ag K shell contribution in the absorption spectra of the samples was obtained by removing the extrapolated best-fit linear function determined in the pre-edge region (−150 eV to −50 eV). By conventional normalization, extrapolating the post-edge spline background, determined in the range of 50 to 250 eV, the Ag K-edge jump is set to 1.42–44
Theoretical methods
Results and discussion
Towards Ag3(SbF6)4 through serendipity and via many failures
Solid Ag(SbF6)2 and its aHF solution have characteristic sky-blue colour typical of the presence of solvated Ag(II) (Fig. S1, ESI†). During the investigations of the Ag(I)/Ag(II)/SbF5/aHF system in 2003,33 one of us (ZM) has observed that addition of hydrogen into a clear blue solution of Ag(SbF6)2 dissolved in aHF–SbF5, results in the change of colour. The colour of the blue solution first turned to green and with time to colourless with precipitation of AgSbF6 and AgSb2F11. In addition, during routine preparations of Ag(SbF6)2 in the last ten years for different purposes,32,46,47 many times it happened that the isolated dry Ag(SbF6)2 was not completely sky-blue but its colour varied from greenish-blue to green. It was also observed that, when dry sky-blue Ag(SbF6)2 was stored for a few months’ time in a glovebox (where the temperature might increase up to 303 K) its colour changed to green-blue. The presence of Ag(SbF6)2 as a major phase in these samples could (beside by its typical colour) be unambiguously determined from its characteristic Raman spectrum.48 However, all samples, where a shade of green colour was observed, gave Raman spectra with an additional very intense band at 664 cm−1 (Fig. S2, ESI†). Analysis of single crystals of this phase solved the mystery showing that the green phase corresponds to a new intermediate compound in the AgSbF6/Ag(SbF6)2 system, i.e. Ag3(SbF6)4.Moreover, crystallizations of Ag(SbF6)2 from its aHF solutions resulted sometimes in green crystals of Ag3(SbF6)4 and a colorless solid (instead of sky-blue crystals of Ag(SbF6)2). The Raman spectra of the colorless solid showed a very narrow intense band at 1864 cm−1 which is typical of O2+ stretching mode of O2SbF6.49 Cationic Ag(II) solvated in aHF is known to be one of the strongest oxidizers known. In aHF acidified with AsF5, solvated Ag(II) is capable of oxidizing molecular oxygen at 195 K, but at 213 K the products (O2AsF6/AgAsF6) re-establish the reactants (Ag(II)(sol)/O2(g)/AsF5(sol)).50 It seems that in the case of Ag(SbF6)2, dissolved in aHF, the silver(II) salt is only partly reduced, forming Ag(I)2Ag(II)(SbF6)4 and O2SbF6 as a by-product. Therefore crystals of Ag3(SbF6)4 may also be formed in situ during the slow reaction of Ag(SbF6)2 with traces of water or oxygen penetrating through the walls of crystallization vessels (cf. the Experimental part).
Since the chemical identity of the green phase has been established, many attempts were made to synthesize larger quantities of Ag3(SbF6)4 as a high-purity product suitable for physicochemical characterization. The most obvious path – by direct reaction between the corresponding amounts of AgSbF6 and Ag(SbF6)2 in liquid aHF (eqn (1)) – has failed
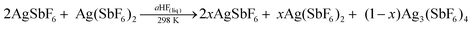 | (1) |
(i) 2AgSbF6 + Ag(SbF6)2 in liquid SbF5 → no reaction;
(ii) 2AgBF4 + AgF2 in liquid SbF5 and gaseous aHF → AgSb2F11 and Ag3(SbF6)4;
(iii) 2AgSb2F11 + AgF2 in gaseous aHF → AgSbF6, Ag(SbF6)2 and Ag3(SbF6)4;
(iv) Ag(SbF6)2 + H2 in liquid aHF → AgSbF6 and AgSb2F11;
(v) Ag(SbF6)2 + H2O in liquid aHF → AgSbF6 and Ag(SbF6)2.
Finally, it was established that the solid state reaction between 2AgSbF6 and Ag(SbF6)2 at 318 K in the presence of traces of the aHF mediator in the gas phase provides the optimum way to prepare high-purity Ag3(SbF6)4 (eqn (2))
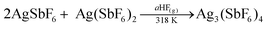 | (2) |
According to quantitative phase analysis based on powder X-ray diffraction, the so-obtained product contains 96.6 wt% Ag3(SbF6)4 and 3.4 wt% AgSbF6; Ag(SbF6)2 could not be detected in the powder pattern. This sample has also proven to be suitable for ESR characterization and hence magnetic measurements were performed since Ag(SbF6)2 could not be detected in the spectra/magnetization curves (recall AgSbF6 is diamagnetic).
Crystal structures of Ag3(SbF6)4 and related K2Ag(SbF6)4
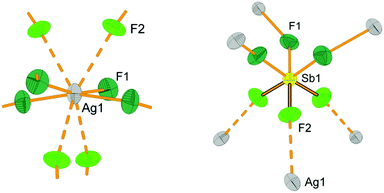
The title compound has been found to crystallize in the body-centered cubic cell (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d), with a = 12.3613(4) Å (Table 1). The related potassium compound, green K(I)2Ag(II)(SbF6)4, is isomorphic, albeit with a larger unit cell vector of a = 12.498(1) Å, consistent with the larger ionic radius of K(I) than that of Ag(I). There are four formula units inside the unit cell. There is only one Ag atom, one Sb atom and two crystallographically independent F atoms inside the irreducible cell (Fig. 2).
3d), with a = 12.3613(4) Å (Table 1). The related potassium compound, green K(I)2Ag(II)(SbF6)4, is isomorphic, albeit with a larger unit cell vector of a = 12.498(1) Å, consistent with the larger ionic radius of K(I) than that of Ag(I). There are four formula units inside the unit cell. There is only one Ag atom, one Sb atom and two crystallographically independent F atoms inside the irreducible cell (Fig. 2).
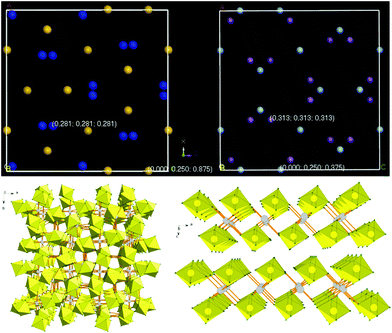 | ||
Fig. 2 Top: comparson of the unit cells of the I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d polytype of Si3N4 and51 that of the Ag & Sb sublattice of Ag(I)2Ag(II)(SbF6)4. Note the similarity of the N & Sb sublattices. Bottom: the packing diagrams of Ag(I)2Ag(II)(SbF6)4 (left) and Ag(SbF6)2 (right) (grey circles: silver atoms; yellow octahedra: SbF6 units), two projections were shown. 3d polytype of Si3N4 and51 that of the Ag & Sb sublattice of Ag(I)2Ag(II)(SbF6)4. Note the similarity of the N & Sb sublattices. Bottom: the packing diagrams of Ag(I)2Ag(II)(SbF6)4 (left) and Ag(SbF6)2 (right) (grey circles: silver atoms; yellow octahedra: SbF6 units), two projections were shown. | ||
Inspection of the Medea database15 returns over 500 crystal structures of inorganic compounds containing at least one metal atom, which adopt the I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d space group (no. 220). However, despite their A3B4 stoichiometry for many of these compounds, none of them is isostructural to Ag3(SbF6)4.52 In particular, none of the very few quasi-binary A(I)A(II)2B4 compounds of elements, which are known to exhibit both the first and second oxidation state (Cu, Ag, Au, Hg), adopt the I
3d space group (no. 220). However, despite their A3B4 stoichiometry for many of these compounds, none of them is isostructural to Ag3(SbF6)4.52 In particular, none of the very few quasi-binary A(I)A(II)2B4 compounds of elements, which are known to exhibit both the first and second oxidation state (Cu, Ag, Au, Hg), adopt the I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d polytype; for example, Cu3Cl4 is isomorphic to magnetite (Fe3O4, spinel). Similarly, we could not find good structural analogies for A(II)A(IV)2B4 compounds where B is a divalent anion, such as Pt3O4 or Pb3O4. However, it turns out that the crystal structure of Ag3(SbF6)4 is somewhat similar to that of a certain metastable polytype of Si3N4 (Fig. 2).51
3d polytype; for example, Cu3Cl4 is isomorphic to magnetite (Fe3O4, spinel). Similarly, we could not find good structural analogies for A(II)A(IV)2B4 compounds where B is a divalent anion, such as Pt3O4 or Pb3O4. However, it turns out that the crystal structure of Ag3(SbF6)4 is somewhat similar to that of a certain metastable polytype of Si3N4 (Fig. 2).51
The Sb/N atom in these structures occupies the (x, x, x) position where x = ½ + δ, with δ ≈ 0.03 (N) and δ ≈ 0.06 (Sb); for x = 0 the packing of anions would correspond to the ideal bcc sublattice. The major difference between both structures is that the Ag atom is found in the (0, 1/4, 3/8) position while the Si atom occupies the (0, 1/4, 7/8) one, which leads to a different bonding pattern. Each compound, however, may be viewed as a defective and severely distorted AB polytype, [A□A3]B4.
The most interesting feature of the crystal structure of Ag3(SbF6)4 of relevance to its mixed-valence character is that all silver atoms are found in a single crystallographic site (occupying a 12b Wyckoff position at the ![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) axis) thus reflecting a random distribution of the Ag(I) and Ag(II) cations (in the 2
axis) thus reflecting a random distribution of the Ag(I) and Ag(II) cations (in the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
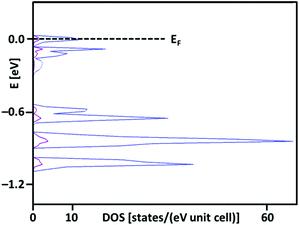
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio). Thus, irrespective of a noticeable difference in ionic radii of Ag(I) and Ag(II), all silver cations are found in an identical environment of eight fluorine atoms (Fig. 3). Such a feature would imply that Ag3(SbF6)4 is in fact an intermediate valence (Class III) system, with an average oxidation state of Ag of +1⅓, while rendering Ag3(SbF6)4 the first Ag(II)/Ag(I) system of this type. What is more, Ag3(SbF6)4 would then be analogous to a family of the long known silver clathrate salts Ag7O8X (X = NO3, HF2, HCO3, etc.) which also crystallize in cubic lattices, and they are comproportionated, metallic and superconducting, with an average oxidation state of silver of +2.43.53 Indeed, in the case of comproportionation Ag3(SbF6)4 would be metallic, with a substantial density of states at the Fermi level (Fig. 4) available for Bose–Einstein condensation, and thus likely even superconducting below a certain temperature.
1 ratio). Thus, irrespective of a noticeable difference in ionic radii of Ag(I) and Ag(II), all silver cations are found in an identical environment of eight fluorine atoms (Fig. 3). Such a feature would imply that Ag3(SbF6)4 is in fact an intermediate valence (Class III) system, with an average oxidation state of Ag of +1⅓, while rendering Ag3(SbF6)4 the first Ag(II)/Ag(I) system of this type. What is more, Ag3(SbF6)4 would then be analogous to a family of the long known silver clathrate salts Ag7O8X (X = NO3, HF2, HCO3, etc.) which also crystallize in cubic lattices, and they are comproportionated, metallic and superconducting, with an average oxidation state of silver of +2.43.53 Indeed, in the case of comproportionation Ag3(SbF6)4 would be metallic, with a substantial density of states at the Fermi level (Fig. 4) available for Bose–Einstein condensation, and thus likely even superconducting below a certain temperature.
However, it turns out that the situation for Ag3(SbF6)4 is more complex than that. The first coordination sphere of silver consists of four short bonds to fluorine (2.316(7) Å) which are arranged in a close-to square planar geometry, and four additional long contacts at 2.764(6) Å (Fig. 1). The short contacts are too long for typical Ag(II)–F bonds (in Ag(SbF6)2: 2.095(5)–2.132(4) Å;34 in [IF6][Ag(SbF6)3]: 2.11(1) Å;32 in AgFAsF6: 1.995(5)–2.004(5) Å;54 AgF2: 2.086 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55) and simultaneously too short for Ag(I)–F bonds (the shortest Ag–F bond lengths in AgBF4 are 2.561(4) Å,56 in AgSbF6 2.505(2) Å,57 in AgSb2F11 2.472(8) Å
55) and simultaneously too short for Ag(I)–F bonds (the shortest Ag–F bond lengths in AgBF4 are 2.561(4) Å,56 in AgSbF6 2.505(2) Å,57 in AgSb2F11 2.472(8) Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 and in AgF 2.55 Å
33 and in AgF 2.55 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58). Not surprisingly, the valence bond sum analysis59 suggests that such coordination corresponds to a severely overbonded Ag(I) (VBS = 1.288) and strongly underbonded Ag(II) (VBS = 1.252). This alone is a peculiar but not disqualifying factor, since a silver site should indeed have bonding characteristics typical of Ag+1⅓.60 However, closer inspection of thermal ellipsoids of fluorine atoms next to silver cations reveals an unusual flattened shape, indicating a possibility that F atoms might exhibit static disorder, and thus there might be at least two types of silver cations in the structure, each with a different coordination sphere. One site would have a markedly covalent Ag(II)–F bonding with a nearly square-planar AgF4 unit, while the other would resemble a typical Ag(I)–F site with eight ligands in a more ionic environment61 (Fig. 1). This surmise is further supported by the fact that the latter site – corresponding to Ag(I) – may be substituted with K(I) in a new distinct compound, K2Ag(SbF6)4 (Table 1).62
58). Not surprisingly, the valence bond sum analysis59 suggests that such coordination corresponds to a severely overbonded Ag(I) (VBS = 1.288) and strongly underbonded Ag(II) (VBS = 1.252). This alone is a peculiar but not disqualifying factor, since a silver site should indeed have bonding characteristics typical of Ag+1⅓.60 However, closer inspection of thermal ellipsoids of fluorine atoms next to silver cations reveals an unusual flattened shape, indicating a possibility that F atoms might exhibit static disorder, and thus there might be at least two types of silver cations in the structure, each with a different coordination sphere. One site would have a markedly covalent Ag(II)–F bonding with a nearly square-planar AgF4 unit, while the other would resemble a typical Ag(I)–F site with eight ligands in a more ionic environment61 (Fig. 1). This surmise is further supported by the fact that the latter site – corresponding to Ag(I) – may be substituted with K(I) in a new distinct compound, K2Ag(SbF6)4 (Table 1).62
Based on what was discussed above, one may suspect that – despite a single crystallographic site for Ag in Ag3(SbF6)4 – this compound is not a genuine Class III system. However, it is still unclear at this stage whether Ag3(SbF6)4 is a well-defined frozen-valence Class I or rather a Class II system. Since vibrational spectra – albeit different for Ag3(SbF6)4, Ag(SbF6)2 and AgSbF6 (cf. ESI†) – are not unequivocally indicative of oxidation states, we have further studied Ag3(SbF6)4 with a range of physicochemical methods more sensitive to the nature of silver cations present in this compound.
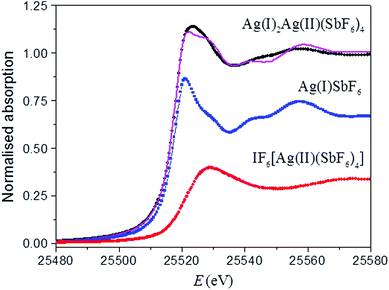
X-ray absorption near-edge structure spectroscopy (XANES) of Ag3(SbF6)4 and Ag(I)SbF6, and IF6[Ag(II)(SbF6)3] references
The average value of the Ag oxidation state in the Ag3(SbF6)4 sample was obtained by Ag K-edge XANES analysis. The binding energies of the valence orbitals and therefore the energy position of the edge and the pre-edge features in the XANES spectrum are known to be correlated with the valence state of the absorbing atom in the sample. Namely, each absorption feature in the XANES spectrum is shifted to higher energies with an increasing oxidation state of a given element; this feature is now routinely used to deduce the valence state.42,43,63,64 For example, examining the XANES spectra of two reference compounds AgSbF6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 65 and IF6[Ag(SbF6)3]32 (Fig. 5) with a known crystal structure and a Ag valence state, we found out that the Ag K-edge shifts by about 5.4 eV per valence from Ag(I) to Ag(II).
65 and IF6[Ag(SbF6)3]32 (Fig. 5) with a known crystal structure and a Ag valence state, we found out that the Ag K-edge shifts by about 5.4 eV per valence from Ag(I) to Ag(II).
If the sample contains the same element in two or more sites with a different local structure and/or valence state, the measured XANES spectrum is a linear combination of individual XANES spectra of individual sites. In such a case the relative amounts of cations at each site can be determined by the linear combination fit using XANES spectra of appropriate reference compounds, i.e. compounds that contain the element with the same valence state and the same or very similar local structure to the element on each site in the sample.43,63,64 We applied this procedure to the Ag XANES spectrum measured for the Ag3(SbF6)4 sample. The spectrum may indeed be described as a linear combination of the XANES profiles of AgSbF6 (containing Ag(I) in the 8-coordinated site) and IF6[Ag(SbF6)3] (containing Ag(II) in a close-to square-planar site) (Fig. 5). The fit yields the relative amounts of Ag(I) and Ag(II) of, respectively, 68% and 32%, with an uncertainty of about 2%; obtained values are in excellent agreement with the expected ones of 66.6% and 33.3% for the proposed structure of the sample.
Thus, XANES results have nicely confirmed not only the average oxidation state of silver (+1⅓) in Ag3(SbF6)4, but also that the Ag cations in the structure are present in two valence states Ag(I) and Ag(II) in a relative ratio of 2 to 1.
ESR spectra and magnetochemistry of Ag3(SbF6)4 and Ag(SbF6)2
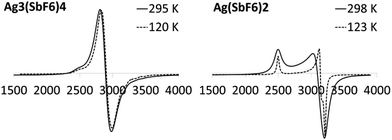
One of the key features which distinguish Ag(II) from Ag(I) – apart from voracious oxidizing properties of Ag(II) – is the presence of one unpaired electron in the former species (4d9), while the latter is diamagnetic (4d10). This allows easy detection of the presence of paramagnetic Ag(II) in the samples by applying electron spin spectroscopy and magnetometry.The ESR spectrum of the Ag(II)(SbF6)2 reference sample taken at room temperature (Fig. 6) shows the presence of a familiar two-constituent signal with the following components of the g tensor: g‖ = 2.699 and g⊥ = 2.161. When the temperature is decreased to 120 K, the higher-field signal is split into two, with g‖ = 2.702, g⊥1 = 2.149, and g⊥2 = 2.103. Such components of the rhombic g tensor with g‖ ≫ g⊥1 ≈ g⊥2 suggest that the local environment of Ag(II) takes the slightly distorted square-planar form (i.e. a strongly elongated octahedron)66–68 consistent with the previously determined crystal structure of this compound (Fig. 2).34 The absolute values of the g tensor components are larger than the corresponding values for AgZrF6 (g‖ = 2.58, g⊥ = 2.11) and AgSnF6 (g‖ = 2.65, g⊥ = 2.12)66 in agreement with the weaker ligand field66,69 exerted by weakly coordinating SbF6− anions than those of the more electron-rich MF6−2 ones (M = Zr, Sn).
On the other hand, the ESR spectrum of Ag3(SbF6)4 recorded at room temperature (Fig. 6) shows the presence of a broad signal at g = 2.333, with some weak additional features. When the temperature is decreased to 120 K, the signal shifts slightly to g = 2.324 but without splitting. The measured g value is similar to the arithmetic average of g‖, g⊥1, and g⊥2 obtained for Ag(SbF6)2, i.e. 2.318 (at 120 K). This result clearly suggests that (i) distinct paramagnetic Ag(II) cations are present in the crystal structure of Ag3(SbF6)4 while (ii) the local environment of Ag(II) possibly takes the form of a square plane albeit either substantial local disorder or/and fast relaxation, which broadens the signal and prevents the separation of g components.
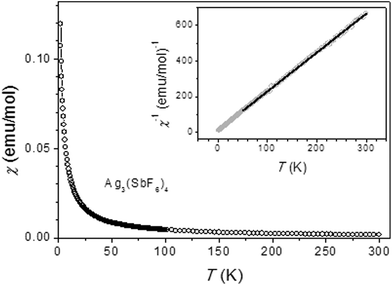
The magnetic susceptibility of Ag3(SbF6)4 has been investigated between 2 K and 300 K in a constant magnetic field H = 1000 Oe. The molar magnetic susceptibility free from diamagnetic core contribution70 as a function of temperature of Ag3(SbF6)4 is plotted in Fig. 7. The susceptibility monotonically increases with decreasing temperature and obeys a Curie–Weiss law as can be observed from linear χ−1vs. T dependence (inset in Fig. 7). In the 50–300 K temperature range the data were fitted to the Curie–Weiss law with the Curie constant C = 0.46 emu K mol−1 (μeff = 1.9 B.M.) and θp = −4.0 K. The value of the Curie constant is consistent with the spin-only value for one Ag(II) per formula unit. This result further confirms that one out of three silver cations corresponds to paramagnetic Ag(II) while the remaining two cations are diamagnetic Ag(I). The negative value of θp is characteristic of weak antiferromagnetic interactions. Further comparison of magnetic properties of Ag3(SbF6)4 with those of parent Ag(SbF6)2 is given in ESI.†
Concluding this section we note that ESR spectroscopy as well as magnetometry have helped to unequivocally establish Ag3(SbF6)4 as a mixed-valence (Class I) compound with localized oxidation states, i.e. Ag(I)2Ag(II)(SbF6)4, and despite the same crystallographic site occupied by both types of cations.
Electronic spectra of Ag3(SbF6)4, Ag(SbF6)2, and AgSbF6 in the UV-vis-NIR range
Electronic spectra – in conjecture with the ESR spectra and quantum mechanical calculations – have proven in the past to be very useful for analysis of chemical bonding in the Ag(II) systems.66–69 Here we have studied the electronic spectra for the samples of Ag3(SbF6)4, and two reference samples (Ag(SbF6)2 and AgSbF6) in the NUV-vis-NIR range (5–50k cm−1 or ca. 0.6–6.2 eV).The reflectance spectra in the vis-NIR region are presented in Fig. 8, while the less informative NUV region is shown in ESI.†
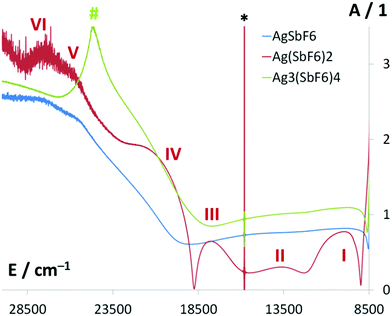
The spectrum of Ag(SbF6)2 is rich in bands (I–VI in Fig. 8). Since local geometry at the Ag(II) site in this compound is quasi-tetragonal, the assignment is based on the literature data for related compounds of Ag(II) exhibiting D4h local symmetry.66–69 The broad band centered at 9.95k cm−1 (I) is assigned to the 5a1g→3b1g transition, that at 13.64k cm−1 (II) to the 2b2g→3b1g, while the one at 17.83k cm−1 (III) to the 3eg→3b1g. From these energies of d–d transitions one may immediately derive66 the values δ1 and δ2 governing the splitting of the, respectively, 2Eg and 2T2g terms, as follows: δ1 = 2.49k cm−1 and δ2 = 1.40k cm−1, as well as the value of the ligand-field splitting energy, Δ = 11.45k cm−1. The value of Δ falls in the 9.2–12.0k cm−1 range typical of compounds of Ag(II).66
The broad absorption seen at ca. 20–21.5k cm−1 (IV) has not been assigned in the past; judging from its energy and using the previously computed orbital scheme67,69 and selection rules, we tentatively assign it to the charge-transfer (CT) transition 2eg→3b1g involving axial F atoms, Fax→Ag(II). Using the same scheme, the absorption seen at ca. 25.9–27.6k cm−1 (V–VI) may be assigned to another Fax→Ag(II) CT transition (4a1g→3b1g) which is split since local symmetry around Ag(II) is in fact slightly departing from ideal D4h (equatorial Ag–F bond lengths are 2.09 Å and 2.13 Å). The CT transitions involving equatorial F atoms, Feq.→Ag(II), have been predicted67,69 to fall in the region 35–41k cm−1 and, indeed, some absorption is seen in this part of the NUV region (ESI†).
The electronic spectrum of Ag3(SbF6)4 is rather poor in bands as compared to that of Ag(SbF6)2. The bands I–III are hard to detect, which likely originates from substantial static disorder of F atoms around Ag(II) in this compound, and thus to excessively broad absorption bands. An unstructured shoulder may be seen at ca. 21.3k cm−1 possibly corresponding to the CT transition analogous to IV seen for Ag(SbF6)2. The strong band (#) peaking at 24.67k cm−1 (3.06 eV, 405 nm) is the only preeminent feature of the absorption spectrum. Such a strong feature is absent in the spectrum of Ag(SbF6)2 and also the AgSbF6 reference. Since mixed-valence compounds often exhibit a new strong electronic absorption band due to the inter-valence charge transfer (IVCT) transition, it is tempting to assign the 405 nm absorption band to the vertical Ag(I)→Ag(II) CT process. The energy of this transition is quite large (3 times larger than that of the d–d transitions) and thus the valences are firmly localized in Ag3(SbF6)4, while the electronic conduction due to electron hopping between Ag(I) and Ag(II) sites must be difficult. Indeed, single crystals of Ag3(SbF6)4 are quite transparent to light and they do not exhibit metallic luster, typical of metals and narrow-band gap semiconductors.
Conclusions and prospect
We have prepared and studied Ag3(SbF6)4, which is one of five currently known mixed-valence compounds of Ag(II)/Ag(I). This compound crystallizes in the cubic system (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d cell) with just one crystallographic position for silver cations, which finds no precedence in the chemistry of Ag(II)/Ag(I) compounds of silver. A number of physicochemical methods applied have confirmed the mixed- (Class I) and not an intermediate-valence (Class III) character of this compound. The localized-oxidation state character, i.e. Ag(I)2Ag(II)(SbF6)4, cannot be deduced from X-ray data due to substantial static disorder of fluorine atoms of the SbF6− anions, which leads to a misleading averaged bonding picture. The strong absorption band seen at 3.05 eV in the electronic spectrum of Ag3(SbF6)4 has been tentatively assigned to the IVCT transition, Ag(I)→Ag(II). If the energy of this transition were substantially decreased due to application of a large external pressure,71 a fraction of Ag(4d) electrons should become itinerant thus resulting in metallic conductivity, like it has been observed for other prototypical mixed-valence systems.
3d cell) with just one crystallographic position for silver cations, which finds no precedence in the chemistry of Ag(II)/Ag(I) compounds of silver. A number of physicochemical methods applied have confirmed the mixed- (Class I) and not an intermediate-valence (Class III) character of this compound. The localized-oxidation state character, i.e. Ag(I)2Ag(II)(SbF6)4, cannot be deduced from X-ray data due to substantial static disorder of fluorine atoms of the SbF6− anions, which leads to a misleading averaged bonding picture. The strong absorption band seen at 3.05 eV in the electronic spectrum of Ag3(SbF6)4 has been tentatively assigned to the IVCT transition, Ag(I)→Ag(II). If the energy of this transition were substantially decreased due to application of a large external pressure,71 a fraction of Ag(4d) electrons should become itinerant thus resulting in metallic conductivity, like it has been observed for other prototypical mixed-valence systems.
Since Ag3(SbF6)4 may be obtained from 2AgSbF6 + Ag(SbF6)2 precursors, it seems the enthalpy factor is slightly in favour of the formation reaction; this process may be viewed as a Lewis acid/Lewis base reaction, with Ag(SbF6)2 playing the role of an acid, similar to the analogous case of Ag3(SO3F)4 formation. Moreover, the volume of Ag3(SbF6)4 per formula unit (∼472.21 Å3) is slightly larger than that of the reactant mixture (∼454.93 Å3) which points to an additional small entropic stabilization of Ag3(SbF6)4 (of about 9.2 kJ mol−1 in ST factor) with respect to the substrates.72 The quest for new mixed-valence compounds of Ag(II)/Ag(I) – and in particular the Class III systems – is on.
Acknowledgements
Z.M., E.G., Z.J. and I.A. gratefully acknowledge the Slovenian Research Agency (ARRS) for the financial support of the present study within the research program: P1-0045 Inorganic Chemistry and Technology, P1-0112 Studies of atoms, molecules and structures with photons and particles, and P2-0348 New imaging and analytic methods. The project ‘AgCENT: novel unique magnetic and electronic materials based on Ag(II) compounds’ is financed by the Polish National Science Centre (NCN, project UMO-2011/01/B/ST5/06673). The selected measurements were carried out by using the CePT infrastructure financed by the EU European Regional Development Fund within the Operational Programme “Innovative economy” for 2007–2013 (POIG.02.02.00-14-024/08-00). DFT calculations were carried out using ICM supercomputers (grant G29-3). Access to beamline BM23 of European Synchrotron Radiation Facility within the project LS 2209 is acknowledged. We would like to thank Gleb Parakhonskiy and Olivier Mathon of ESRF for expert advice on beamline operation.References
- P. Day, N. S. Hush and J. H. Clark, Philos. Trans. R. Soc. London, Ser. A, 2008, 366, 5–14 CrossRef CAS PubMed.
- J. P. Fackler Jr., Mixed Valence Compounds, in Encyclopedia of Inorganic Chemistry, ed. R. B. King, John Wiley & Sons, Chichester, 2005, vol. 5 Search PubMed.
- K. D. Demadis, C. M. Hartshorn and T. J. Meyer, Chem. Rev., 2001, 101, 2655–2685 CrossRef CAS PubMed.
- J. Woodward, Philos. Trans. R. Soc. London, 1724, 33, 15 CrossRef . The first synthesis, however, took place in 1704.
- M. B. Robin and P. Day, Adv. Inorg. Chem. Radiochem., 1967, 10, 248–422 Search PubMed.
- G. C. Allen and N. S. Hush, in Progress in Inorganic Chemistry, John Wiley & Sons, New York, 1967, vol. 8, pp. 357–389 Search PubMed.
- C. Creutz and H. Taube, J. Am. Chem. Soc., 1973, 95, 1086–1094 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- J. G. Bednorz and K. A. Müller, Z. Phys. B: Condens. Matter, 1986, 64, 189–193 CrossRef CAS.
- Y. Tokura, H. Takagi and S. Uchida, Nature, 1989, 337, 345–347 CrossRef CAS.
- E. Dagotto, Rev. Mod. Phys., 1994, 66, 763–840 CrossRef CAS.
- K. J. Fijałkowski and W. Grochala, Dalton Trans., 2008, 5447–5453 RSC.
- C. H. Ahn, et al. , Rev. Mod. Phys., 2006, 78, 1185–1212 CrossRef CAS.
- A. T. Bollinger, G. Dubuis, J. Yoon, D. Pavuna, J. Misewich and I. Božović, Nature, 2011, 472, 458–460 CrossRef CAS PubMed.
- The Infomatica 3.1 database of Medea package lists over 4.1 thousand structures of quaternary (4-element) copper oxides AtBxCuyOz (excluding systems such as complex sulphates, nitrates etc.), over 3.0 thousand systems built of 5 elements, over 1.3 thousand combinations of 6 and more-elements. © Materials Design (2014).
- These attempts left rather little trace in the literature, since failed experiments are less frequently reported than the successful ones. J. Wang and M. Sayer, Cryogenics, 1993, 33, 1164–1169 CrossRef CAS; A. K. Tyagi, S. Tyagi and T. P. Sharma, Mater. Sci. Eng., B, 1997, 45, 88–97 CrossRef; J. E. Rodriguez, A. Marino and J. Giraldo, Physica C, 1997, 282, 1253–1254 CrossRef.
- W. Grochala and R. Hoffmann, Angew. Chem., Int. Ed., 2001, 40, 2742–2781 CrossRef CAS.
- K. Yvon, A. Bezinge and P. Tissot, et al. , J. Solid State Chem., 1986, 65, 225–230 CrossRef CAS.
- M. Jansen and P. Fischer, J. Less-Common Met., 1988, 137, 123–131 CrossRef CAS.
- W. Grochala, Scr. Mater., 2006, 55, 811–814 CrossRef CAS.
- X. Yang and H. Su, Sci. Rep., 2014, 4, 5420 CAS.
- W. Grochala, J. Mater. Chem., 2009, 19, 6949–6968 RSC.
- W. Grochala, J. Mol. Model, 2011, 17, 2237–2248 CrossRef CAS PubMed.
- Q.-M. Wang, H. K. Lee and T. C. W. Mak, New J. Chem., 2002, 26, 513–515 RSC.
- Q.-M. Wang and T. C. W. Mak, Chem. Commun., 2001, 807–808 RSC.
- A system erroneously claimed to contain Ag(II) and Ag(I) has been later shown to be a Ag(I) system (the presence of H+ escaped the attention of the first set of researchers): D. Sun, C.-F. Yang, H.-R. Xu, H.-X. Zhao, Z.-H. Wei, N. Zhang, L.-J. Yu, R.-B. Huang and L.-S. Zheng, Chem. Commun., 2010, 8168–8170 RSC; P. J. Leszczyński, A. Budzianowski, M. Derzsi, Ł. Dobrzycki, M. K. Cyrański and W. Grochala, Dalton Trans., 2012, 41, 396–402 RSC.
- P. C. Leung and F. Aubke, Inorg. Chem., 1978, 17, 1765–1772 CrossRef CAS.
- T. Michałowski, P. Malinowski, M. Derzsi, Z. Mazej, Z. Jagličić, P. J. Leszczyński and W. Grochala, Eur. J. Inorg. Chem., 2011, 2508–2516 CrossRef.
- T. Michałowski et al. , 16th Frühjahrssymposium of the Münster Division of the German Chemical Society's Young Chemists Section, Münster 26–29.03.2014.
- P. J. Malinowski et al. , manuscript in preparation, 2015.
- D. Grzybowska, P. Malinowski, Z. Mazej and W. Grochala, Collect. Czech. Chem. Commun., 2008, 73, 1729–1746 CrossRef CAS.
- Z. Mazej, E. Goreshnik, I. Arčon, N. Zabukovec Logar and V. Kaučič, Z. Anorg. Allg. Chem., 2010, 636, 224–229 CrossRef CAS.
- Z. Mazej and P. Benkič, Inorg. Chem., 2003, 42, 8337–8343 CrossRef CAS PubMed.
- D. Gantar, I. Leban, B. Frlec and J. H. Holloway, J. Chem. Soc., Dalton Trans., 1987, 2379–2383 RSC.
- A. Altomare, M. Cascarano, C. Giacovazzo and A. Guagliardi, J. Appl. Crystallogr., 1993, 26, 343–350 CrossRef.
- Molecular Structure Corporation, teXsan for Windows. Single Crystal Structure Analysis Software. Version 1.06, MSC, 9009 New Trails Drive, The Woodlands, TX 77381, USA, 1997–1999 Search PubMed.
- L. J. Farrugia, J. Appl. Crystallogr., 1999, 32, 837–838 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- DIAMOND v3.1, Crystal Impact GbR, Bonn, Germany, 2004–2005 Search PubMed.
- Materials Studio v.8.0.0.843, © Dassault Systems, 2014 Search PubMed.
- B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541 CrossRef CAS PubMed.
- J. Wong, F. W. Lytle, R. P. Messmer and D. H. Maylotte, Phys. Rev. B: Condens. Matter, 1984, 30, 5596–5610 CrossRef CAS.
- P. Behrens, S. Assmann, U. Bilow, C. Linke and M. Jansen, Z. Anorg. Allg. Chem., 1999, 625, 111–116 CrossRef CAS.
- I. Ahmed, E. A. Abou Neel, S. P. Valappil, S. N. Nazhat, D. M. Pickup, D. Carta, D. L. Carroll, R. J. Newport, M. E. Smith and J. C. Knowles, J. Mater. Sci., 2007, 42, 9827–9835 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186 CrossRef CAS; G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter, 1999, 59, 1758–1775 CrossRef.
- P. J. Malinowski, M. Derzsi, Z. Mazej, Z. Jaglčić, B. Gaweł, W. Łasocha and W. Grochala, Angew. Chem., Int. Ed., 2010, 49, 1683–1686 CrossRef CAS PubMed.
- P. J. Malinowski, M. Derzsi, Z. Mazej, Z. Jagličić, P. J. Leszczyński, T. Michałowski and W. Grochala, Eur. J. Inorg. Chem., 2011, 2499–2507 CrossRef CAS.
- Z. Mazej, J. Fluorine Chem., 2004, 125, 1723–1733 CrossRef CAS.
- Z. Mazej, M. Ponikvar-Svet, J. F. Liebman, J. Passmore and H. D. B. Jenkins, J. Fluorine Chem., 2009, 130, 788–791 CrossRef CAS.
- G. Lucier, C. Shen, W. J. Casteel Jr., L. Chacón and N. Bartlett, J. Fluorine Chem., 1995, 72, 157–163 CrossRef CAS.
- M. Billy, J. C. Labbe, A. Selvaraj and G. Roult, Mater. Res. Bull., 1983, 18, 921–934 CrossRef CAS; P. Kroll, J. Solid State Chem., 2003, 176, 530–537 CrossRef.
- The most frequently found types are those similar to stoichiometric Th(IV)3(As3−)4 (Z = 4), Bi(III)4(SiO4)3 (Z = 4) or to (formally) mixed valence Pr(II)Pr(III)2(S2−)4 (Z = 4).
- I. Naray-Szabo, G. Argay and P. Szabo, Acta Crystallogr., 1965, 19, 180 CrossRef CAS; M. B. Robin, K. Andres, T. H. Geballe, N. A. Kuebler and D. B. McWhan, Phys. Rev. Lett., 1966, 17, 917–919 CrossRef; M. Jansen and S. Vensky, Z. Naturforsch., B: Anorg. Chem. Org. Chem., 2000, 55, 882–886 Search PubMed.
- D. Gantar, B. Frlec, D. R. Russell and J. H. Holloway, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1987, 43, 618–620 CrossRef.
- A. Jesih, K. Lutar, B. Žemva, B. Bachmann, S. Becker, B. G. Müller and R. Hoppe, Z. Anorg. Allg. Chem., 1990, 588, 77–83 CrossRef CAS.
- E. Goreshnik and Z. Mazej, Solid State Sci., 2005, 7, 1225–1229 CrossRef CAS.
- K. Matsumoto, R. Hagiwara, Y. Ito and O. Tamada, J. Fluorine Chem., 2001, 110, 117–122 CrossRef CAS.
- P. M. Halleck, J. C. Jamieson and C. W. F. T. Pistorius, J. Phys. Chem. Solids, 1972, 33, 769–773 CrossRef CAS; B. G. Müller, Angew. Chem., Int. Ed. Engl., 1987, 26, 1081–1097 CrossRef.
- Analysis performed using parameters listed in: http://www.ccp14.ac.uk/ccp/web-mirrors/i_d_brown/, i.e. RAg(I) = 1.8 Å, RAg(II) = 1.79 Å and s = 0.37.
- The Sb–F2 distances are quite short (1.839(6) Å) and in the range of typical Sb–Ft (Ft = terminal fluorine atom) distances. Since antimony atom occupies a 16c Wyckoff position at the 3 axis, according to the symmetry, each SbF6 unit has three such short Sb–F2 distances. The coordination sphere of each Sb atom is completed by additional three fluorine atoms at much longer distances (1.886(7) Å), typical of Sb–Fb contacts (Fb = bridging fluorine atom). Indeed, F1 acts as a linker atom in the Sb–F1–Ag bridges. Similar Sb–F bond lengths were observed for Ag(SbF6)2
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52 where three fluorine atoms play a bridging role, and three others are terminal.
52 where three fluorine atoms play a bridging role, and three others are terminal. - As seen e.g. for AgBF4, AgSb2F11 and the high-pressure form of AgF at p > 2.5 GPa.
- Although the quality of X-ray data collected for K2Ag(SbF6)4 is not as satisfactory as for Ag3(SbF6)4, similar features may be observed in the crystal structure of both compounds. First, there is a random distribution of the K(I) and Ag(II) cations in a 2
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio at the same crystallographic positions. Second, there are four short (4 × 2.34(2) Å) and four long K/Ag–F distances (2.82(2) Å); these K/Ag–F distances are too long for Ag(II)–F and too short for typical K–F bonds. Similar to the case of Ag3(SbF6)4, this could be explained by abnormal flattened thermal ellipsoids of fluorine atoms, indicating that potassium and silver atoms in fact do not have identical coordination spheres, which is obviously to be expected.
1 ratio at the same crystallographic positions. Second, there are four short (4 × 2.34(2) Å) and four long K/Ag–F distances (2.82(2) Å); these K/Ag–F distances are too long for Ag(II)–F and too short for typical K–F bonds. Similar to the case of Ag3(SbF6)4, this could be explained by abnormal flattened thermal ellipsoids of fluorine atoms, indicating that potassium and silver atoms in fact do not have identical coordination spheres, which is obviously to be expected. - R. Dominko, C. Sirisopanaporn, C. Masquelier, D. Hanzel, I. Arčon and M. Gaberšček, J. Electrochem. Soc., 2010, 157, A1309–A1316 CrossRef CAS.
- I. Arčon, J. Kolar, A. Kodre, D. Hanžel and M. Strlič, X-Ray Spectrom., 2007, 36, 199–205 CrossRef.
- Z. Mazej and R. Hagiwara, J. Fluorine Chem., 2007, 128, 423–437 CrossRef CAS.
- C. Friebel and D. Reinen, Z. Anorg. Allg. Chem., 1975, 413, 51–60 CrossRef CAS.
- J. A. Aramburu, M. Moreno and M. T. Barriuso, J. Phys.: Condens. Matter, 1992, 4, 9089–9112 CrossRef CAS.
- A. Monnier, A. Gerber and H. Bill, J. Chem. Phys., 1991, 94, 5891–5896 CrossRef CAS.
- R. Valiente, J. A. Aramburu, M. T. Barriuso and M. Moreno, J. Phys.: Condens. Matter, 1994, 6, 4515–4525 CrossRef CAS.
- O. Khan, Molecular Magnetism, VCH Publishers, New York, 1993 Search PubMed.
- W. Grochala, J. Feng, R. Hoffmann and N. W. Ashcroft, Angew. Chem., Int. Ed., 2007, 46, 3620–3642 CrossRef CAS PubMed.
- H. D. B. Jenkins and L. Glasser, Inorg. Chem., 2003, 42, 8702–8708 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: X-ray crystallographic files in the CIF format, a photo of a Ag(SbF6)2 solution in aHF, the Raman spectrum of impure blue-green Ag(SbF6)2, photos showing self-supported homogeneous pellets used for XANES spectroscopy, XRDP for a powder sample of Ag3(SbF6)4, Raman spectra of Ag3(SbF6)4 compared to several relevant reference samples, FIR and MIR absorption spectra for Ag3(SbF6)4, Ag(SbF6)2, and AgSbF6, comparison of magnetic properties of Ag3(SbF6)4 and Ag(SbF6)2, M vs. H curves at various temperatures for Ag(SbF6)2, and NUV absorption spectra for Ag3(SbF6)4, Ag(SbF6)2 and AgSbF6. Further details of the crystal structure determination could be found and CIF files may be obtained from Fachinformationszentrum Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany (e-mail: crysdata@fiz-karlsruhe.de; http://www.fiz-karlsruhe.de/request_for_deposited_data.html). CCDC 429207 (Ag3(SbF6)4) and 429208 (K2Ag(SbF6)4). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5dt00740b |
| This journal is © The Royal Society of Chemistry 2015 |