Open Access Article
Open Access ArticleStructure, solvent, and relativistic effects on the NMR chemical shifts in square-planar transition-metal complexes: assessment of DFT approaches†
Jan
Vícha‡
ab,
Jan
Novotný‡
a,
Michal
Straka
ac,
Michal
Repisky
d,
Kenneth
Ruud
d,
Stanislav
Komorovsky
*d and
Radek
Marek
 *ae
*ae
aCEITEC – Central European Institute of Technology, Masaryk University, Kamenice 5/A4, CZ-62500 Brno, Czech Republic. E-mail: radek.marek@ceitec.muni.cz
bCentre of Polymer Systems, University Institute, Tomas Bata University in Zlin, Trida T. Bati 5678, CZ-76001 Zlin, Czech Republic
cInstitute of Organic Chemistry and Biochemistry, Academy of Sciences of the Czech Republic, Flemingovo nám. 2, CZ-16610 Prague, Czech Republic
dCentre for Theoretical and Computational Chemistry, Department of Chemistry, UiT – The Arctic University of Norway, N-9037 Tromsø, Norway. E-mail: stanislav.komorovsky@uit.no
eDepartment of Chemistry, Faculty of Science, Masaryk University, Kamenice 5, CZ-62500 Brno, Czech Republic
First published on 25th August 2015
Abstract
The role of various factors (structure, solvent, and relativistic treatment) was evaluated for square-planar 4d and 5d transition-metal complexes. The DFT method for calculating the structures was calibrated using a cluster approach and compared to X-ray geometries, with the PBE0 functional (def2-TZVPP basis set) providing the best results, followed closely by the hybrid TPSSH and the MN12SX functionals. Calculations of the NMR chemical shifts using the two-component (2c, Zeroth-Order Regular Approximation as implemented in the ADF package) and four-component (4c, Dirac–Coulomb as implemented in the ReSpect code) relativistic approaches were performed to analyze and demonstrate the importance of solvent corrections (2c) as well as a proper treatment of relativistic effects (4c). The importance of increased exact-exchange admixture in the functional (here PBE0) for reproducing the experimental data using the current implementation of the 2c approach is partly rationalized as a compensation for the missing exchange–correlation response kernel. The kernel contribution was identified to be about 15–20% of the spin–orbit-induced NMR chemical shift, ΔδSO, which roughly corresponds to an increase in ΔδSO introduced by the artificially increased exact-exchange admixture in the functional. Finally, the role of individual effects (geometry, solvent, relativity) in the NMR chemical shift is discussed in selected complexes. Although a fully relativistic DFT approach is still awaiting the implementation of GIAOs for hybrid functionals and an implicit solvent model, it nevertheless provides reliable NMR chemical shift data at an affordable computational cost. It is expected to outperform the 2c approach, in particular for the calculation of NMR parameters in heavy-element compounds.
1. Introduction
Square-planar transition-metal complexes, molecules with ligands arranged in a square-like pattern around the central metal, are typically preferred by d8 elements such as platinum(II). Their unique chemistry is dominated by a trans effect that makes them well suited for various practical applications ranging from cancer treatment (cisplatin, oxaliplatin)1 to chemical catalysis,2 molecular switches and beyond.3 Generally, a detailed analysis of the structure and various properties is required to understand their biological effects in the human body as well as their role in catalytic processes. In addition to experimental methods (e.g., X-ray diffraction, NMR spectroscopy) theoretical methods are also frequently being employed to investigate their structure, chemistry and properties, often supplementing experimental NMR studies. The synergy between theoretical and experimental approaches allows us to combine the experimental precision with the predictive and explanatory power of theoretical methods, yielding new insight unachievable by the experimental or theoretical approaches alone.4 Relativistic effects have a significant influence on the NMR chemical shifts of light ligand atoms (LA) in the vicinity of the heavy-atom center (HA). Particular attention in NMR calculations should be paid to the spin–orbit effects, part of so-called HALA effects,5 typically propagated from the heavy element to light spectator atoms via the spin–orbit/Fermi-contact (SO/FC) mechanism.5,6 The spin–orbit contribution to the NMR chemical shift, ΔδSO, represents a relativistic correction to the NMR chemical shift that can amount from ten to hundreds of ppm.7Calculated relativistic effects in the vicinity of the heavy metal are generally very sensitive to (i) the character of metal–ligand bonding,8,9 requiring the use of correct and accurate structures, (ii) the inclusion of environmental effects (e.g., solvent),10 and (iii) reliable methods for treating the relativistic effects.11
(i) Density functional theory (DFT) is nowadays the most commonly used method for optimizing the structures and calculating various properties of molecules and molecular systems, mainly due to its favorable scaling with system size and the rather good accuracy that can be achieved. A large number of density functionals have been developed over the years for calculating the molecular structures and/or molecular properties. The performance of individual functionals differs dramatically for various properties and systems, and careful evaluation/calibration of the functional behavior must be performed before production DFT calculation can be used for interpreting any chemical problem.
Nice examples of such assessments are the calibration studies by Bühl and coworkers,8,12 which focused on the optimization of structures of transition-metal complexes, with DFT structures optimized in vacuo and referenced to structural parameters obtained in the gas phase. However, the geometries obtained in vacuo (or in an implicit solvent) are frequently inappropriately referenced to the structures determined by X-ray diffraction, neglecting any crystal effects. This approximation can lead to substantial errors and even to incorrect conclusions.13,14
To achieve the best available precision in the geometry optimizations, either molecular clusters based on experimental X-ray structures or periodic-boundary calculations should be used for calibrating the methods for solid-state structure optimization. In this work we focus on the cluster approach to assess the performance of the DFT functionals in optimizing the molecular geometry.
Recently, we applied this approach to a very limited number of complexes (mainly octahedral),10,15 but a wider selection of compounds and new functionals are required in order to draw more general conclusions. Therefore, the cluster-based comparison of ten DFT functionals (with or without D3 dispersion corrections) for structure optimization is presented in this work for seven square-planar complexes with various ligands and central metal atoms (Pt, Pd, Au, Rh, Fig. 1). These complexes were selected primarily based on the availability of high-quality X-ray structures and the availability of complete NMR data and variability of central metals.
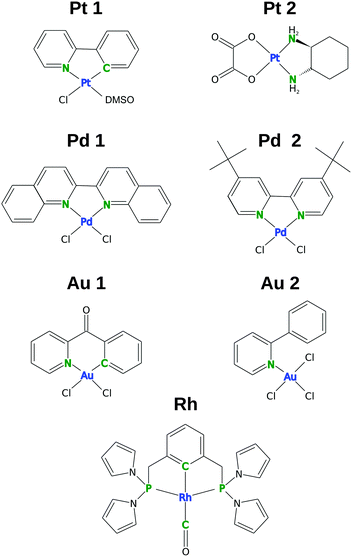 | ||
| Fig. 1 Structures of selected square-planar complexes. The transition-metal centers are shown in blue and the ligand spectator NMR atoms (LA) are shown in green. | ||
(ii) The solvent effects can be simulated using explicit solvent molecules or implicit solvent models. Whereas implicit solvent models in general are limited to accounting for electrostatic effects of the solvent environment (continuum) on the NMR parameters of the solute,16 an explicit solvent model accounts also for specific weak interactions (hydrogen bonding, stacking),17 which can significantly alter the NMR chemical shifts of atoms involved in these interactions. This applies in particular to the hydrogen atoms and the easily polarizable heavy element.18 The application of an explicit solvent model is, however, beyond the scope of everyday calculations due to its complexity. For a proper determination of the NMR chemical shifts, classical molecular dynamic (MD) or QM/MD simulations must be performed to determine the positions of the solvent molecules relative to the solute and to calculate NMR chemical shifts averaged over individual snapshots, which can be very time and resource consuming, although great advances are being made for NMR parameters of molecules containing light elements.19,20 Furthermore, computationally demanding QM/MD simulations are limited by the size of the model that can be evaluated in a reasonable period of time, whereas specialized force-field parameters for MD simulations must be developed for each structurally different molecule or non-standard solvent.21 Therefore, the explicit solvent model is used predominantly in detailed studies of individual systems, whereas the implicit solvent model is adopted more generally, being usually sufficient for calculations of many properties, including NMR chemical shifts of HALA-influenced light atoms as we demonstrate in this work.
(iii) The relativistic effects can be treated in several ways at various levels of theory. A majority of the current computational codes operate with an approximate treatment of relativity. One of the most widely used approaches is the Zeroth-Order Regular Approximation. The ZORA Hamiltonian can be defined as:22
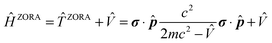 | (1) |
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) ZORA allows for the inclusion of SO contributions, yielding the two-component (2c) spin–orbit ZORA (SO-ZORA) approach.23,24
ZORA allows for the inclusion of SO contributions, yielding the two-component (2c) spin–orbit ZORA (SO-ZORA) approach.23,24
The SO-ZORA approach provides a good description of the valence-shell orbitals, often comparable with that of four-component methods.23 Because the NMR chemical shifts of the light atoms (e.g., 1H, 13C, 15N) are significantly influenced by the type of chemical bonding, determined by the valence orbitals, the performance of the SO-ZORA approach for NMR chemical shift calculations of light atoms is good.4,7,25,26 However, it has been demonstrated10,11,15,27 that increasing the admixture of exact exchange in the functional is required to obtain correct NMR chemical shifts of atoms strongly affected by HALA effects. Recently, the role of the missing self-consistent first-order response of the DFT exchange–correlation (XC) potential to the external magnetic-field perturbation, the so-called XC response kernel (fxc), has been highlighted in NMR chemical shift calculations using the SO-ZORA approach.28 The missing terms arising from fxc were found to be quite sizable for hydrogen and mercury NMR chemical shifts. However, to the best of our knowledge, these effects have not been evaluated for light, non-hydrogen NMR atoms (13C, 15N).
For a more complete inclusion of relativistic effects, the Dirac Hamiltonian must be considered:29
ĤD = cα·![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) + βmc2 + + βmc2 + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) | (2) |
Therefore, in addition to the two-component (2c) SO-ZORA approach, we employed four-component (4c) calculations in the Dirac–Coulomb framework. The fully relativistic NMR calculations (ReSpect program) use restricted magnetically balanced basis sets for the small-component wave function.32 To further improve basis-set convergence, gauge-including atomic orbitals (GIAO) are employed for the pure DFT functionals.33 In the case of the hybrid functionals, only the common gauge origin (CGO) methodology is implemented in the ReSpect program, and thus special attention must be paid to errors arising from basis-set incompleteness in these calculations. In contrast, the implementation of the state-of-the-art non-collinear DFT kernel for GGA (generalized gradient approximation) functionals is used.34
Here we evaluate the influence of structure, solvent, spin–orbit contribution, exact-exchange admixture, role of fxc, and CGO approximation for hybrid functionals on relativistic NMR chemical shift calculations (2c and 4c) of light atoms in the vicinity of a heavy element for a series of square-planar transitional-metal complexes.
2. Methods
2.1 Selection of complexes and experimental data
A set of square-planar complexes with high-quality X-ray structures, complete NMR chemical shift data, and a diversity of the central metal atom was selected. The experimental data for the selected complexes are summarized in Table 1. In addition to “regular” square-planar platinum and palladium complexes with aromatic and aliphatic ligands (Pt and Pd), also complexes with ideal square-planar geometries distorted by the shape of the ligands, namely Au1 and Rh (see Fig. 1) are investigated. In Au1, the 2-benzoylpyridine ligand is bent out of the plane by 30°, whereas for Rh, where the square-planar shape is enforced by the so-called PCP “pincer” ligand, the bond angles around the central metal are about 12° distorted from the ideal 90°.| Acronym | Formula | R-factor (%) | CSD code | NMR chemical shifta | NMR solvent | Ref. |
|---|---|---|---|---|---|---|
| a All 15N NMR chemical shifts are reported relative to liquid NH3. b This work. | ||||||
| Pt1 | trans(S,N)-[Pt(2-ppy*)(DMSO)Cl] | 1.8 | JISPAD01 | 15N 220.6 | DMSO-d6 | 35 and 36 |
| 13C 140.2 | ||||||
| Pt2 | [Pt(oxalato)(1R,2R-cyclohexanediamine)] | 1.9 | CUHKEV | 15N 9.1b | DMSO-d6 | 37 |
| Pd1 | [Pd(2,2′-biquinoline)Cl2] | 2.7 | YASPAK | 15N 224.0 | CDCl3 | 38 and 39 |
| Pd2 | [Pd(4,4-di-tert-butylbipyridine)Cl2] | 4.8 | MOYWIG01 | 15N 211.1 | DMSO-d6 | 40 and 41 |
| Au1 | [Au(2-benzoylpyridine)Cl2] | 2.9 | PUKYAV | 15N 215.2 | DMSO-d6 | 42 and 43 |
| 13C 136.7 | ||||||
| Au2 | [Au(2-phenylpyridine)Cl3] | 2.2 | YIDMAA | 15N 227.7 | CDCl3 | 44 and 45 |
| Rh | [Rh(dipyrrolylphoshinoxylene) CO] | 3.3 | SOWDUE | 31P 119.8 | THF-d8 | 46 |
| 13C 172.2 | ||||||
2.2 Geometry optimization – DFT functional and basis set
Molecular cluster models were prepared for each complex individually, with a single central molecule (color-coded in Fig. 2) completely surrounded by crystal-packing molecules (orange-coded in Fig. 2) in a way that all close-contact interactions between the central molecule and the packing ones were treated in the final cluster. As a result, the central molecule was completely surrounded in a crystal-like environment with a packing sphere up to 12 Å, depending on the size of the central and packing molecules. Subsequently, the coordinates of the packing molecules were fixed, whereas the geometry of the central molecule was optimized using different DFT functionals in the field created by packing ones. This approach is assumed to recover the majority of the crystal lattice effects10,15,47–50 allowing for a direct comparison of calculated parameters to experimental X-ray data. An example of the molecular cluster for Au1 is shown in Fig. 2.The geometries of the central molecules in the clusters were optimized using the def2-TZVPP basis set51 for all atoms, with corresponding relativistic effective core potentials (def2-ECPs)52 for the metal center (ECP substituting 60 electrons for Pt and Au and 28 electrons for Rh and Pd). The packing molecules with fixed coordinates were treated using the def2-SVP basis set51 for all atoms, with corresponding ECP for the metal center.
Each cluster was optimized using ten selected density functionals. The LYP-based53 functionals BLYP,54 B3LYP,55 and BHLYP56 were selected to map the effect of exact-exchange admixture on the structural parameters. Due to the known unbalanced performance of the B3LYP functional in calculations involving transition metals,57 the CAM-B3LYP,58 the B3LYP functional with corrected long-range exchange, was included in the test set. From the GGA family, PBE59 and BP8654,60 are present because they are known to perform reasonably well for transition-metal complexes.12 The TPSSH61,62 functional is an example of a successful meta-GGA hybrid functional, and it was shown to be a very good choice for optimizing transition-metal complexes.8,12 The PBE0,63,64 the hybrid version of the “parameter-free” PBE functional, has demonstrated superb performance for geometry optimization of heavy transition-metal compounds.10,12,15 Advanced long-range corrected hybrid functional with empirical dispersion corrections, ωB97XD,65,66 was recently tested with good results in structure optimizations of transition-metal complexes.67 Furthermore, a recent addition to the family of “Minnesota functionals”, the so-called screened-exchange density functional, MN12SX,68 which was reported to offer very good performance in calculating various properties,68 is included. The effect of the D3 dispersion correction69 on the geometry was tested in several cases, see Fig. S1 (ESI†). The observed effect was found negligible for the PBE0 functional (it even deteriorates the results by 0.2 pm for PBE and BP86), and the D3 correction is thus not further considered in this work.
A convergence of the basis set was estimated in the series def2-SVP → def2-QZVPP using the PBE0 functional, see Fig. 3. The def2-TZVPP basis provides results almost identical (difference <1 pm) to those of much larger (and computationally demanding) QZ bases, confirming our previous results.10
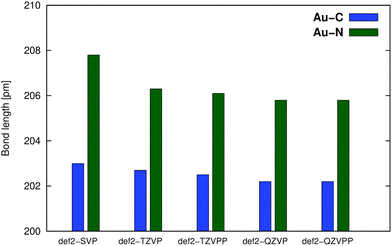 | ||
| Fig. 3 Basis-set effects on the M–L distance in the optimization of compound Au1 using the PBE0 functional with def2-ECP. | ||
Based on the performance of individual functionals (vide infra), the basis-set effects (Fig. 3), computational costs, and the marginal effects of dispersion correction, the PBE0/def2-TZVPP/ECP approach was used to optimize molecular geometries in the production calculations. For all the in-solution optimizations discussed below, the COSMO (COnductor-like Screening MOdel)16 solvent model was used, see Section 2.3.
2.3 NMR chemical shift calculations – solvent effects and method selection
To determine the importance of fxc, 4c calculations using the ReSpect code were performed also without fxc, and the corresponding correction to the NMR chemical shift, ΔδXCkernel, was obtained as a difference between the NMR chemical shift calculated with and without kernel contribution at a given level of theory. With ΔδXCkernel being unaffected by the gauge origin (GIAO vs. CGO), (tested using GIAO/CGO calculations at the 4c-PBE level, data not shown) we assume its additivity for the 2c SO-ZORA results (vide infra).
| δi = σref − σi + δref |
3. Results and discussion
3.1 Geometry optimization – estimating the structural effects on the NMR chemical shift
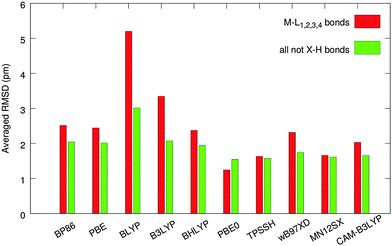
The molecular clusters were built based on X-ray diffraction geometries (for details, see Methods Section) and the central molecule of each cluster was optimized in the field created by fixed packing molecules. The performance of individual functionals was evaluated using bond distances for non-hydrogen atoms (comparison with the experimental values for 161 bonds) with special focus on 28 bonds between the central metal and the ligand atoms. Root-mean-square deviations (RMSD) between calculated and experimental values for all 161 non-hydrogen bonds (RMSD161) and for 28 bonds around the metal center (RMSD28) from all molecules of our set are summarized in Fig. 5.Poor results are obtained by using the BLYP functional, which greatly overestimates the M–L bonds (RMSD28 = 5.2 pm) and thus should not be used for structure optimizations of transition-metal complexes.10 Increasing the exact-exchange admixture in the LYP-based functionals improves the correlation with experimental data for M–L bonds [BLYP (0%, 5.2 pm) → B3LYP (20%, 3.3 pm) → BHLYP (50%, 2.4 pm)] notably. When all bond lengths are considered, both B3LYP and BHLYP are performing with the same level of accuracy (RMSD161 ∼ 2 pm), which is due to the fact that the impact of non-metal ligand bonds (mostly organics, in which B3LYP is known to perform excellently) compensates for the inaccuracy in describing the M–L bonds. The best of the LYP-based functionals, BHLYP, produced moderately accurate results (RMSD28 = 2.4 pm, RMSD161 = 1.9 pm) compared to the rest of the functionals. However, almost identical performance was observed for PBE and BP86, at notably lower computational costs. Both of these GGA functionals can be recommended for geometry optimization of transition-metal complexes in cases where the use of hybrid GGAs is inconvenient, e.g. for very large molecules or molecular clusters.
The ωB97XD functional produces good overall results (RMSD161 = 1.7 pm), whereas the description of the M–L bonding is comparable to BHLYP, BP86, and PBE.
The importance of corrected long-range exchange in the CAM-B3LYP functional to optimize the geometry of the transition-metal complexes is obvious from a comparison of the B3LYP and CAM-B3LYP results. The CAM version improves the results of B3LYP by 40% for M–L bonds (RMSD28 is 2.0 pm vs. 3.3 pm for B3LYP) and by about 20% for all non-hydrogen bonds (RMSD161 is 1.7 pm vs. 2.1), see Fig. 5.
The best results for the tested set were produced by three functionals – MN12SX (RMSD28 = 1.7 pm and RMSD161 = 1.6 pm), TPSSH (with RMSD28 = RMSD161 = 1.6 pm), and PBE0, which performs excellently in describing the M–L bonds (RMSD28 = 1.2 pm, RMSD161 = 1.5 pm). For a more detailed analysis of the results according to the atom type (Fig. S2 and S3, ESI†) and for a comparison between the cluster approach and the in vacuo results (Fig. S4), see ESI.†
To estimate the magnitude of the structural effects on the NMR chemical shifts (NMR CS) separately from all the other factors, we calculated the NMR CS of metal-bonded light atoms (highlighted in green in Fig. 1) using non-relativistic and SO-ZORA approaches at the PBE-40/TZP level in vacuo for BLYP, B3LYP, PBE0, and MN12SX geometries (def2-TZVPP/def2-ECP basis set) optimized in vacuo (see Table 2). The difference between the NMR CS calculated using BLYP and MN12SX functionals (Δδgeom, see Table 2) ranges between 5–14 ppm at the non-relativistic level, and 2–22 ppm at the 2c SO-ZORA level. Also, the deficiency of the popular B3LYP functional in describing the M–L bond length can result in a 19 ppm difference in the relativistic 13C NMR chemical shift (e.g., 13C in Au1 calculated at the 2c SO-ZORA level). We conclude that the inaccurate geometry can be reflected in the 13C and 15N NMR CS deviations, amounting easily to as much as 10–20 ppm. These deviations are more pronounced for the NMR chemical shifts calculated at the relativistic level (SO-ZORA) compared to those calculated using the non-relativistic approach (Table 2). This relativistic effect is particularly evident for the 13C NMR CS in Au1 due to the more covalent character of the M–C bond compared to that of the M–N bond (Table 2).11,82 As expected, the PBE0, TPSSH, and MN12SX functionals, producing the most reliable geometries in the test set, give very similar calculated NMR CS.
| Non-relativistic | SO-ZORA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BLYP | B3LYP | PBE0 | MN12SX | Δδgeoma | BLYP | B3LYP | PBE0 | MN12SX | Δδgeoma | |
| a Δδgeom calculated as δ(BLYP) – δ(MN12SX); note that δ(BLYP) – δ(PBE0) would result in almost identical numbers. | ||||||||||
| Pt1 | ||||||||||
| 13C | 182.8 | 179.1 | 177.0 | 177.0 | 5.8 | 141.6 | 141.1 | 143.2 | 143.4 | −1.8 |
| 15N | 270.0 | 261.6 | 257.1 | 256.6 | 13.4 | 234.8 | 229.3 | 228.8 | 228.2 | 6.6 |
| Au1 | ||||||||||
| 13C | 176.6 | 172.1 | 168.9 | 168.6 | 8.0 | 147.0 | 144.6 | 125.6 | 125.3 | 21.7 |
| 15N | 250.4 | 242.3 | 237.2 | 236.8 | 13.6 | 244.2 | 236.0 | 230.5 | 230.2 | 14.0 |
In this work, the PBE0/def2-TZVPP/def2-ECP approach was selected for all further geometry optimizations in Sections 3.2–3.5.
3.2 Relativistic calculations of NMR chemical shifts (NMR CS) – role of exact-exchange (EE) admixture
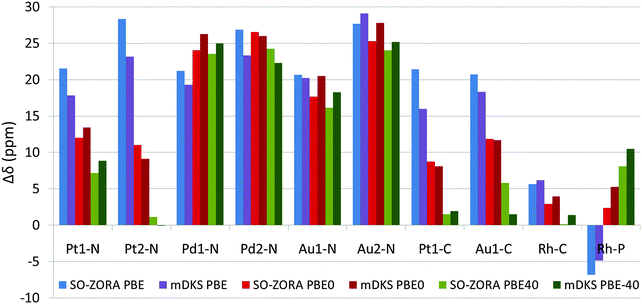
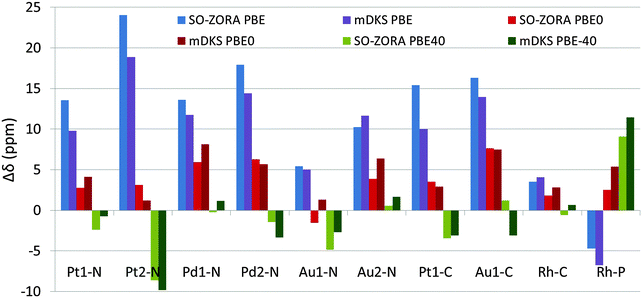
All the NMR chemical shifts were calculated for single molecules optimized using the PBE0 functional (for details, see Methods Section and Section 3.1), however, only those that require relativistic treatment, namely atoms significantly affected by the HALA effects from the metal atom (see Fig. 1 and Introduction part), are reported here for clarity. It is known that the calculated NMR CS are significantly modulated by the amount of exact-exchange admixture in the hybrid GGA functional.11,27 To analyze the role of exact-exchange admixture, we performed relativistic calculations of the light-atom NMR CS using 2c SO-ZORA and 4c mDKS with the PBE, PBE0, and PBE-40 functionals. Results (in vacuo), plotted as deviations from the experimental values (Δδ), are shown in Fig. 6 and more details are given in Tables S1 and S2 (ESI†); for the influence of the CGO correction in the 4c mDKS PBE0 and PBE-40 calculations, see Fig. S5 (ESI†).Generally, increasing the EE admixture in the functional increases the nuclear magnetic shielding of the light atoms bound to the metal center in platinum and gold compounds considerably.10,82 However, this effect is marginal for palladium and even reversed for 31P in the rhodium complex. The increased EE admixture improves the results for some cases already in vacuo, particularly for 13C NMR CS, where the solvent effects obviously play a less significant role compared to 15N NMR CS.80,83–85 For instance, the PBE functional results in Δδ(13C) = 21.4 ppm for Pt1-C, whereas PBE-40 gives Δδ(13C) = 1.5 ppm (see Fig. 6). Conversely, the improvement is small or negligible for 15N NMR CS, where solvent effects are known to play a significant role and the effects of the EE admixture are less important (see the palladium and gold complexes in Fig. 6).
3.3 Solvent correction to the NMR CS
Due to the sensitivity of the NMR CS (particularly 15N)85 to the solvent, it is necessary to include bulk environmental effects in the NMR calculations.86 In this study, we analyzed the effect of the implicit solvent model on the NMR CS of LA (13C and 15N). Solvent corrections to the NMR CS (Δδsolv), calculated at the SO-ZORA level using the PBE, PBE0, and PBE-40 functionals with the COSMO model for the solvent, are summarized in Table 3.| Δδsolv | |||
|---|---|---|---|
| Atom | PBE | PBE0 | PBE-40 |
| Pt1-N | −5.0 | −5.7 | −6.1 |
| Pt2-N | −1.3 | −4.4 | −6.3 |
| Pd1-N | −4.6 | −14.6 | −20.4 |
| Pd2-N | −6.0 | −16.8 | −22.2 |
| Au1-N | −12.3 | −15.7 | −17.5 |
| Au2-N | −14.5 | −17.9 | −20.1 |
| Pt1-C | −4.1 | −4.4 | −4.5 |
| Au1-C | −2.5 | −3.4 | −4.1 |
| Rh-C | −0.2 | −0.3 | −0.2 |
| Rh-P | +2.7 | +2.2 | +2.0 |
The implicit solvent improved the RMSDSO-ZORAPBE from 21.5 ppm in vacuo to 14 ppm with COSMO (for RMSDmDKSPBE, 18.6 ppm in vacuo and 11.4 ppm including Δδsolv). In parallel, the RMSDSO-ZORAPBE0 was reduced from 16.5 ppm to 4.4 ppm (RMSDmDKSPBE0 from 17.5 ppm to 5.1) and the RMSDSO-ZORAPBE-40 from 14.6 ppm to 4.5 ppm (RMSDmDKSPBE-40 15.1 ppm to 5.2 ppm).
Note that the magnitude of Δδsolv is increasing considerably with increasing exact-exchange admixture in the functional; the more exact exchange in the functional, the more important the solvent correction is, which is partially reflected in the decrease of the RSMD for the individual approaches. Whereas PBE results for both the 2c SO-ZORA and 4c mDKS approaches still deviate significantly from the experimental values, which is partially due to the differences in the description of ΔδSO by the individual functionals (see Table 4), PBE0 and PBE-40 results are considerably closer to the experimental data. For the differences between calculated (PBE, PBE0, or PBE-40 functional using implicit solvent) and experimental NMR CS, see Fig. 7.
| Atom | ΔδSO (ZORA) | ΔδSO (mDKS) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PBE | PBE0 | PBE-40 | ΔΔδSOa | ΔΔδtotalb | PBE | PBE0 | PBE-40 | ΔΔδSOa | ΔΔδtotalb | |
| a Calculated as ΔΔδSO = ΔδSOPBE-40 − ΔδSOPBE. b Calculated as ΔΔδtotal = ΔδtotalPBE-40 − ΔδtotalPBE. | ||||||||||
| Pt1-N | −9.3 | −15.2 | −19.1 | −9.8 | −14.4 | −10.7 | −15.7 | −19.0 | −8.3 | −9.0 |
| Pt2-N | −24.5 | −27.5 | −30.3 | −5.8 | −27.2 | −24.7 | −27.5 | −29.6 | −4.0 | −23.3 |
| Pd1-N | −5.1 | −9.3 | −12.4 | −7.3 | +2.4 | −5.6 | −9.5 | −12.6 | −7.0 | +5.7 |
| Pd2-N | −7.1 | −11.5 | −15.1 | −8.0 | −2.7 | −8.6 | −13.8 | −17.6 | −9.0 | −1.0 |
| Au1-N | −2.7 | −3.5 | −4.5 | −1.8 | −4.6 | 0.6 | −1.5 | −3.0 | −3.6 | −1.9 |
| Au2-N | 6.0 | 5.6 | 5.0 | −1.0 | −3.6 | 9.9 | 7.3 | 6.3 | −3.6 | −3.9 |
| Pt1-C | −14.0 | −23.2 | −29.1 | −15.1 | −19.9 | −18.3 | −28.1 | −29.5 | −11.2 | −14.1 |
| Au1-C | −8.0 | −12.1 | −16.2 | −8.2 | −14.9 | −9.0 | −14.3 | −18.4 | −9.4 | −16.8 |
| Rh-C | −3.1 | −4.3 | −5.9 | −2.8 | −5.5 | −2.5 | −4.5 | −5.8 | −3.3 | −4.8 |
| Rh-P | −17.0 | −22.0 | −24.9 | −7.9 | +14.9 | −5.1 | −10.3 | −12.7 | −7.6 | +15.3 |
Although at the SO-ZORA relativistic level with solvent correction, the PBE0 and PBE-40 calculations result in almost identical averaged RMSD values (RMSDSO-ZORAPBE0 = 4.4 ppm and RMSDSO-ZORAPBE-40 = 4.5 ppm), the PBE-40 provides better results in 7 out of 10 systems, which is in agreement with previous studies.10,11 The better average RMSD achieved by the PBE0 functional can be ascribed to quite poor results of the PBE-40 approach for Pt2-N, NH2 group in oxaliplatin, which is probably involved in protonation equilibria affecting its experimental 15N NMR CS, and overestimated 31P NMR chemical shift for Rh-P. When the two abovementioned problematic Pt2-N and Rh-P cases are excluded, RMSDSO-ZORAPBE-40 decreases to 2.4 ppm, whereas RMSDSO-ZORAPBE0 = 4.7 ppm.
Similar results were achieved by the 4c mDKS approach, where slightly better RMSD was obtained by using PBE0 (RMSDmDKSPBE0 = 5.1 ppm) than by PBE-40 (RMSDmDKSPBE-40 = 5.2 ppm), however, one should keep in mind that this was achieved by applying several external corrections (solvent, CGO).
Given the good results obtained for PBE0 and PBE-40 with an implicit solvent correction, the use of explicit solvent models would not bring any considerable improvement at reasonable costs for routine NMR applications; therefore, we use the COSMO implicit solvent model for calculating the NMR CS in subsequent sections.
3.4 Spin–orbit contribution to the NMR CS
It is well known that most of the HA-LA effect is due to spin–orbit coupling.86–89 Hence it is vitally important to observe and analyze the difference between calculations with and without the SO contribution (ΔδSO), i.e., the SO in ZORA as well as the difference between the full mDKS and that without SO. Analogously to Δδsolv, the shielding character of ΔδSO is increasing considerably with increasing EE admixture, see Table 4.The increase in the shielding character of ΔδSO is an important factor for explaining the differences between the values calculated at the PBE, PBE0, and PBE-40 levels (vide infra). Comparing ΔδSO calculated at these three levels of theory with total NMR chemical shift differences (in vacuo, Table S1, ESI†) indicates that ΔΔδSO (Table 4) induced by altering the exact-exchange admixture (40 → 0%) can represent a significant portion of the ΔΔδtotal.
The ΔδSO values in Table 4 calculated using the ZORA and mDKS methods are of a comparable magnitude. Generally, the ΔδSO values vary between +5 ppm for Au2 (deshielding) and −30 ppm for Pt2 (strong shielding contribution). It should be noted that the electronic factors responsible for the SO deshielding (Au2-N) or small ΔδSO (Au1-N) in the gold complexes compared to their platinum counterparts were interpreted very recently by our group as a result of the involvement of 6p orbitals in Au–N bonding82 caused by the electrostatic potential of Au3+ and large scalar-relativistic effects90 found in the gold complexes.
3.5 The effect of response exchange–correlation kernel
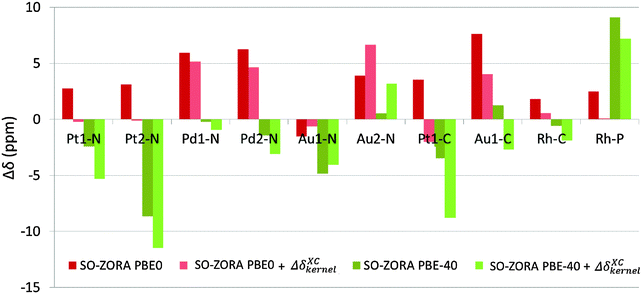
The kernel-corrected SO-ZORA approach for NMR CS calculations is currently missing from the available code (ADF 2014). Therefore, we are using the 4c mDKS approach at the PBE, PBE0, and PBE-40 levels to estimate an approximate influence of terms arising from the missing XC response kernel (fxc) to the NMR chemical shift (see Table S3 in ESI†), denoted as ΔδXCkernel. The ΔδXCkernel was found to range between +0.3 and −5.2 ppm, with an average value of about −2.1 ppm for PBE and between +2.7 and −5.3 ppm (−1.8 ppm in average) for PBE-40. Similarly to ΔδSO,82 the ΔδXCkernel values cause deshielding in Au complexes, but they have shielding character for the Pt, Pd, and Rh compounds (see Table S3, ESI†). On average, the exchange–correlation kernel corresponds to 15–20% of ΔδSO found for a given spectator atom.To illustrate the role of the missing fxc terms, appropriate ΔδXCkernel values were added to the 2c SO-ZORA NMR chemical shifts calculated at the PBE0 and PBE-40 levels, see Fig. 8.
Upon addition of ΔδXCkernel, the majority of the PBE0 results were improved, with the RMSDSO-ZORAPBE0 reduced to 3.4 ppm, whereas the PBE-40 results are uniformly deteriorated (RMSDSO-ZORAPBE-40 = 5.8 ppm). The most important fact is revealed, however, when the differences in ΔδSO caused by the increase of the EE admixture from 25% to 40% are compared with the ΔδXCkernel calculated at the PBE0 level, see Table 5. Our observations suggest that the absence of the response fxc term in the current SO-ZORA implementation (ADF2014) results in ΔδXCkernel deviations that are almost perfectly counterbalanced by the artificial ΔδSO rise introduced by increasing the EE admixture in the functional (25 → 40% in PBE0), ΔΔδSO in Table 5.
| Atom | ΔΔδSOa | ΔδXCkernelb |
|---|---|---|
| a Calculated at the SO-ZORA level as ΔΔδSO = ΔδSOPBE0 − ΔδSOPBE-40. b ΔδXCkernel estimated at the mDKS level by using the PBE0 functional. | ||
| Pt1-N | −3.9 | −3.0 |
| Pt2-N | −2.8 | −3.2 |
| Pd1-N | −3.1 | −0.8 |
| Pd2-N | −3.6 | −1.6 |
| Au1-N | −1.0 | 0.9 |
| Au2-N | −0.6 | 2.7 |
| Pt1-C | −5.9 | −5.6 |
| Au1-C | −4.1 | −3.6 |
| Rh-C | −1.6 | −1.3 |
| Rh-P | −2.9 | −2.4 |
3.6 A summary: importance of the individual effects on the total NMR CS
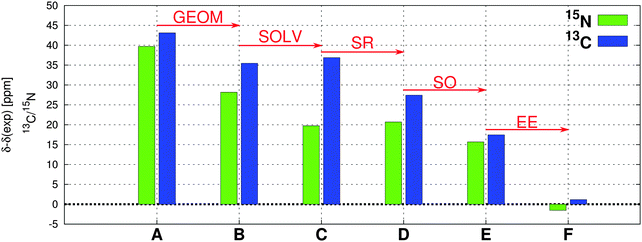
To demonstrate the importance of the individual effects on the total NMR CS, we performed a comparative stepwise analysis. This includes the evaluation of the role of geometry, solvent, scalar relativity, spin–orbit coupling, and admixture of exact exchange in the functional as discussed in detail in Sections 3.1–3.5. The case study of 13C and 15N NMR chemical shifts for compound Au1 is shown in Fig. 9 (for additional data, see ESI†).Although individual factors play different roles in 13C and 15N NMR CS of different compounds, the EE admixture seems to be crucial and one of the most important factors for reproducing the experimental NMR values. However, as demonstrated here, when the correct geometry and the treatment of solvent effects is combined with the proper description of relativity (including terms arising from fxc), standard 25% exact-exchange admixture in the PBE0 functional (instead of somewhat artificial 40%) seems to be sufficient for the NMR CS calculations in square-planar transition-metal complexes.
4. Conclusions
In this work, we evaluated the effects of molecular geometry, implicit solvent, role of the functional, and the treatment of relativistic effects on the NMR chemical shifts calculated for light atoms in the vicinity of a heavy-metal center in selected square-planar complexes. The selection of the DFT functional used for optimizing the geometry was performed by a cluster approach. The best geometries were obtained for the PBE0 functional, closely followed by TPSSH and MN12SX. The effect of geometry on the NMR chemical shifts (deviation between best and worst structure) was found to be rather large, 14 ppm for 15N and 22 ppm for 13C.The role of an implicit solvent was found to be of considerable importance for the NMR chemical shifts in the square-planar complexes, mainly for 15N, with an average 13 ppm contribution to the total NMR chemical shifts (estimated at the SO-ZORA level using the PBE0 functional).
The most important relativistic NMR CS contribution is the ΔδSO, with its size varying between +5 ppm and −30 ppm (for both 2c SO-ZORA and 4c mDKS), which was also demonstrated to be highly dependent on the amount of exact-exchange admixture in the functional.
The importance of increased exact-exchange admixture to 40% in the PBE0 functional for the 2c SO-ZORA approach was confirmed for the light spectator atoms (13C, 15N, and 31P), and rationalized as a compensation for the missing ΔδXCkernel contribution. Therefore, with the current implementation of the SO-ZORA approach used in this work, the PBE-40 functional slightly outperforms PBE0. However, accounting for the effect of the response exchange–correlation kernel, the standard PBE0 functional provides somewhat better agreement with the experiment. Undoubtedly, the effect of the XC kernel should not be neglected for systems with a large HALA effect, such as actinides.7
Finally, the relative importance of individual effects (geometry, solvent, relativistic approximation, DFT functional) to the total NMR CS is demonstrated by stepwise calculations. Currently, the use of hybrid GGA functionals (with the DFT functionals used) is mandatory for reproducing the experimental NMR data in heavy-element compounds.
In the fully relativistic mDKS approach using restricted magnetically balanced basis sets, an implementation of GIAOs for hybrid functionals as well as an implicit solvent model is still missing. However, using simple empirical corrections estimated at the 2c SO-ZORA level provides reliable NMR CS data at affordable computational costs. Undoubtedly, the four-component mDKS method would outperform 2c approaches in calculating heavy-element NMR parameters.91 Our efforts in this direction will be reported elsewhere.
Acknowledgements
This work was supported by the Czech Science Foundation (15-09381S to RM and 14-03564S to MS) and carried out at CEITEC – the Central European Institute of Technology with research infrastructure supported by the project CZ.1.05/1.1.00/02.0068 financed by the European Regional Development Fund. This work also received support from the Research Council of Norway through a Centre of Excellence Grant and project grants (Grant No. 179568, 214095 and 177558). The Czech-Norway mobility grant (NF-CZ07-MOP-3-245-2015) from Norway Funds administrated by Ministry of Education of the Czech Republic is gratefully acknowledged. The access to computing and storage facilities owned by parties and projects contributing to the National Grid Infrastructure MetaCentrum, and provided under the program “Projects of Large Infrastructure for Research, Development, and Innovations” (LM2010005), and the CERIT-SC computing and storage facilities, provided under the program Center CERIT Scientific Cloud, part of the Operational Program Research and Development for Innovations (CZ.1.05/3.2.00/08.0144), is acknowledged.References
- X. Wang and Z. Guo, Chem. Soc. Rev., 2012, 42(1), 202–224 RSC.
- D. Steinborn, Fundamentals of Organometallic Catalysis, in Translator, ed. A. Frankel, Wiley-VCH, Weinheim, 1st edn, 2011 Search PubMed.
- I. Eryazici, C. N. Moorefield and G. R. Newkome, Chem. Rev., 2008, 108(6), 1834–1895 CrossRef CAS.
- J. Vícha, G. Demo and R. Marek, Inorg. Chem., 2012, 51(3), 1371–1379 CrossRef.
- N. Nakagawa, S. Coelho and S. Obinata, 6th NMR Symp. 1967, p. 8.
- M. Kaupp, O. L. Malkina, V. G. Malkin and P. Pyykkö, Chem. – Eur. J., 1998, 4(1), 118–126 CrossRef CAS.
- P. Hrobárik, V. Hrobáriková, A. H. Greif and M. Kaupp, Angew. Chem., Int. Ed., 2012, 51(43), 10884–10888 CrossRef.
- M. Bühl and H. Kabrede, J. Chem. Theory Comput., 2006, 2(5), 1282–1290 CrossRef.
- J. Vícha, M. Straka, M. L. Munzarová and R. Marek, J. Chem. Theory Comput., 2014, 10(4), 1489–1499 CrossRef.
- J. Vícha, M. Patzschke and R. Marek, Phys. Chem. Chem. Phys., 2013, 15(20), 7740–7754 RSC.
- T. Pawlak, M. L. Munzarová, L. Pazderski and R. Marek, J. Chem. Theory Comput., 2011, 7(12), 3909–3923 CrossRef CAS.
- M. Bühl, C. Reimann, D. A. Pantazis, T. Bredow and F. Neese, J. Chem. Theory Comput., 2008, 4(9), 1449–1459 CrossRef.
- P. Comba, in Fundamental Principles of Molecular Modeling, ed. W. Gans, A. Amann and J. C. A. Boeyens, Springer, US, 1996, pp. 167–187 Search PubMed.
- P. Comba, in Intermolecular Interactions, ed. W. Gans and J. C. A. Boeyens, Springer, US, 1998, pp. 97–109 Search PubMed.
- T. Pawlak, D. Niedzielska, J. Vícha, R. Marek and L. Pazderski, J. Organomet. Chem., 2014, 759, 58–66 CrossRef CAS.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- S. Standara, P. Kulhánek, R. Marek, J. Horníček, P. Bouř and M. Straka, Theor. Chem. Acc., 2011, 129(3–5), 677–684 CrossRef CAS.
- L. A. Truflandier, K. Sutter and J. Autschbach, Inorg. Chem., 2011, 50(5), 1723–1732 CrossRef CAS.
- K. Aidas, A. Møgelhøj, C. B. Nielsen, K. V. Mikkelsen, K. Ruud, O. Christiansen and J. Kongsted, J. Phys. Chem. A, 2007, 111(20), 4199–4210 CrossRef CAS.
- M. Dračínský and P. Bouř, J. Chem. Theory Comput., 2010, 6(1), 288–299 CrossRef.
- J. M. Olsen, K. Aidas and J. Kongsted, J. Chem. Theory Comput., 2010, 6(12), 3721–3734 CrossRef CAS.
- F. Jensen, Introduction to Computational Chemistry, Wiley, 2006 Search PubMed.
- T. Saue, ChemPhysChem, 2011, 12(17), 3077–3094 CrossRef CAS.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105(15), 6505–6516 CrossRef CAS.
- L. A. Seaman, P. Hrobárik, M. F. Schettini, S. Fortier, M. Kaupp and T. W. Hayton, Angew. Chem., Int. Ed., 2013, 52(11), 3259–3263 CrossRef CAS.
- K. Sutter and J. Autschbach, J. Am. Chem. Soc., 2012, 134(32), 13374–13385 CrossRef CAS.
- M. Bühl, Chem. Phys. Lett., 1997, 267(3–4), 251–257 CrossRef.
- J. Autschbach, Mol. Phys., 2013, 111(16–17), 2544–2554 CrossRef CAS.
- K. G. Dyall and K. Faegri Jr, Introduction to Relativistic Quantum Chemistry, Oxford University Press, 2007, pp. 35–53 Search PubMed.
- S. Komorovsky, M. Repisky, K. Ruud, O. L. Malkina and V. G. Malkin, J. Phys. Chem. A, 2013, 117(51), 14209–14219 CrossRef CAS.
- L. Belpassi, L. Storchi, H. M. Quiney and F. Tarantelli, Phys. Chem. Chem. Phys., 2011, 13(27), 12368–12394 RSC.
- S. Komorovský, M. Repiský, O. L. Malkina, V. G. Malkin, I. Malkin Ondík and M. Kaupp, J. Chem. Phys., 2008, 128(10), 104101 CrossRef.
- S. Komorovský, M. Repiský, O. L. Malkina and V. G. Malkin, J. Chem. Phys., 2010, 132(15), 154101 CrossRef.
- S. Komorovsky, M. Repisky, E. Malkin, T. B. Demissie and K. Ruud, J. Chem. Theory Comput., 2015, 11(8), 3729–3739 CrossRef CAS.
- M. Kobayashi, S. Masaoka and K. Sakai, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2008, 64(10), m1325 CAS.
- L. Pazderski, T. Pawlak, J. Sitkowski, L. Kozerski and E. Szłyk, Magn. Reson. Chem., 2009, 47(11), 932–941 CrossRef CAS.
- M. A. Bruck, R. Bau, M. Noji, K. Inagaki and Y. Kidani, Inorg. Chim. Acta, 1984, 92(4), 279–284 CrossRef CAS.
- Y. Muranishi, Y. Wang, M. Odoko and N. Okabe, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2005, 61(6), m307–m310 Search PubMed.
- L. Pazderski, J. Toušek, J. Sitkowski, L. Kozerski and E. Szłyk, Magn. Reson. Chem., 2007, 45(12), 1059–1071 CrossRef CAS.
- E. J. MacLean, R. I. Robinson, S. J. Teat, C. Wilson and S. Woodward, J. Chem. Soc., Dalton Trans., 2002, 3518–3524 RSC.
- T. Pawlak, L. Pazderski, J. Sitkowski, L. Kozerski and E. Szłyk, Magn. Reson. Chem., 2011, 49(2), 59–64 CrossRef CAS.
- D. Niedzielska, T. Pawlak, T. Czubachowski and L. Pazderski, J. Spectrosc., 2012, 2013, 1–8 CrossRef.
- Y. Fuchita, H. Ieda, Y. Tsunemune, J. Kinoshita-Nagaoka and H. Kawano, J. Chem. Soc., Dalton Trans., 1998, 791–796 RSC.
- X.-P. Zhang, G. Yang, L. Wang and S. W. Ng, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2007, 63(6), m1582 CAS.
- L. Pazderski, J. Toušek, J. Sitkowski, L. Kozerski and E. Szłyk, Magn. Reson. Chem., 2009, 47(8), 658–665 CrossRef CAS.
- E. Kossoy, B. Rybtchinski, Y. Diskin-Posner, L. J. W. Shimon, G. Leitus and D. Milstein, Organometallics, 2009, 28(2), 523–533 CrossRef CAS.
- K. Maliňáková, L. Novosadová, M. Lahtinen, E. Kolehmainen, J. Brus and R. Marek, J. Phys. Chem. A, 2010, 114(4), 1985–1995 CrossRef.
- K. Maliňáková, L. Novosadová, M. Pipíška and R. Marek, ChemPhysChem, 2011, 12(2), 379–388 CrossRef.
- K. Bouzková, M. Babinský, L. Novosadová and R. Marek, J. Chem. Theory Comput., 2013, 9(6), 2629–2638 CrossRef.
- M. Babinský, K. Bouzková, M. Pipíška, L. Novosadová and R. Marek, J. Phys. Chem. A, 2013, 117(2), 497–503 CrossRef.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305 RSC.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77(2), 123–141 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37(2), 785–789 CrossRef CAS.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38(6), 3098–3100 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98(45), 11623–11627 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98(2), 1372–1377 CrossRef CAS.
- J. Paier, M. Marsman and G. Kresse, J. Chem. Phys., 2007, 127(2), 024103 CrossRef.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393(1–3), 51–57 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS; J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33(12), 8822–8824 CrossRef; J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 7406 CrossRef.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119(23), 12129–12137 CrossRef CAS.
- J. P. Perdew, J. Tao, V. N. Staroverov and G. E. Scuseria, J. Chem. Phys., 2004, 120(15), 6898–6911 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110(13), 6158–6170 CrossRef CAS.
- C. Adamo, G. E. Scuseria and V. Barone, J. Chem. Phys., 1999, 111(7), 2889–2899 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27(15), 1787–1799 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10(44), 6615–6620 RSC.
- Y. Minenkov, Å. Singstad, G. Occhipinti and V. R. Jensen, Dalton Trans., 2012, 41(18), 5526–5541 RSC.
- R. Peverati and D. G. Truhlar, Phys. Chem. Chem. Phys., 2012, 14(47), 16187–16191 RSC.
- S. Grimme, J. Comput. Chem., 2004, 25(12), 1463–1473 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101(11), 9783–9792 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99(6), 4597–4610 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112(23), 8251–8260 CrossRef CAS.
- M. Repiský, S. Komorovský, V. G. Malkin, O. L. Malkina, M. Kaupp, K. Ruud, R. Bast, U. Ekstrom, M. Kadek, S. Knecht, L. Konečný, E. Malkin and I. Malkin Ondík, Relativistic Spectroscopy DFT program ReSpect, developer version 3.4.2, 2015, http://www.respectprogram.org Search PubMed.
- F. Jensen, J. Chem. Phys., 2002, 116(8), 3502 CrossRef CAS.
- F. Jensen and T. Helgaker, J. Chem. Phys., 2004, 121(8), 3463–3470 CrossRef CAS.
- K. G. Dyall, Theor. Chem. Acc., 2004, 112(5–6), 403–409 CrossRef CAS.
- K. G. Dyall, Theor. Chem. Acc., 2006, 117(4), 483–489 CrossRef.
- K. G. Dyall and A. S. P. Gomes, Theor. Chem. Acc., 2009, 125(1–2), 97–100 Search PubMed.
- R. Marek and A. Lycka, Curr. Org. Chem., 2002, 6(1), 35–66 CrossRef CAS.
- R. Marek and A. Lyčka, Curr. Org. Chem., 2007, 11, 1154–1205 CrossRef CAS.
- A. Bruker, Bruker GmbH, Karlsruhe, Germany, 1991 Search PubMed.
- J. Vícha, C. Foroutan-Nejad, T. Pawlak, M. L. Munzarová, M. Straka and R. Marek, J. Chem. Theory Comput., 2015, 11(4), 1509–1517 CrossRef.
- J. Toušek, S. Van Miert, L. Pieters, G. Van Baelen, S. Hostyn, B. U. W. Maes, G. Lemière, R. Dommisse and R. Marek, Magn. Reson. Chem., 2008, 46(1), 42–51 CrossRef.
- R. Marek, in Encyclopedia of Spectroscopy and Spectrometry, ed. J. C. Lindon, Academic Press, Oxford, 2nd edn, 2010, pp. 1892–1898 Search PubMed.
- H. Andersson, A.-C. C. Carlsson, B. Nekoueishahraki, U. Brath and M. Erdélyi, Annual Reports on NMR Spectroscopy, Academic Press, 2015 DOI:10.1016/bs.arnmr.2015.04.002.
- S. Standara, K. Maliňáková, R. Marek, J. Marek, M. Hocek, J. Vaara and M. Straka, Phys. Chem. Chem. Phys., 2010, 12(19), 5126–5139 RSC.
- P. Manninen, P. Lantto, J. Vaara and K. Ruud, J. Chem. Phys., 2003, 119(5), 2623–2637 CrossRef CAS.
- J. Vaara, P. Manninen and P. Lantto, in Calculation of NMR and EPR Parameters, ed. M. Kaupp, M. Bühl and V. Malkin, Wiley-VCH, Verlag GmbH & Co. KGaA, 2004, pp. 209–226 Search PubMed.
- P. Manninen, K. Ruud, P. Lantto and J. Vaara, J. Chem. Phys., 2005, 122(11), 114107 CrossRef.
- P. Pyykko and J. P. Desclaux, Acc. Chem. Res., 1979, 12(8), 276–281 CrossRef CAS.
- E. Malkin, S. Komorovsky, M. Repisky, T. B. Demissie and K. Ruud, J. Phys. Chem. Lett., 2013, 4(3), 459–463 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. Fig. S1: role of dispersion (empirical D3 correction) in cluster-based geometry optimizations; Fig. S2: the RMSDs (pm) for the interatomic distances according to the type of central metal; Fig. S3: the RMSDs (pm) for the interatomic distances according to the type of the light spectator atom; Fig. S4: comparison of total RMSDs (in pm) for interatomic distances calculated in vacuo and in cluster; Fig. S5: the 4c mDKS NMR chemical shifts with and without empirical “CGO corrections”. Table S1: the Δδ (ppm), in vacuo; Table S2: the Δδ (ppm), COSMO; Table S3: the ΔδXCkernel values (ppm). See DOI: 10.1039/c5cp04214c |
| ‡ These two authors contributed equally. |
| This journal is © the Owner Societies 2015 |