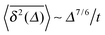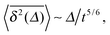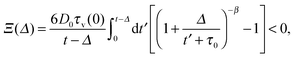DOI:
10.1039/C5CP02824H
(Communication)
Phys. Chem. Chem. Phys., 2015,
17, 21791-21798
Quantifying non-ergodic dynamics of force-free granular gases
Received
15th May 2015
, Accepted 27th July 2015
First published on 27th July 2015
Abstract
Brownian motion is ergodic in the Boltzmann–Khinchin sense that long time averages of physical observables such as the mean squared displacement provide the same information as the corresponding ensemble average, even at out-of-equilibrium conditions. This property is the fundamental prerequisite for single particle tracking and its analysis in simple liquids. We study analytically and by event-driven molecular dynamics simulations the dynamics of force-free cooling granular gases and reveal a violation of ergodicity in this Boltzmann–Khinchin sense as well as distinct ageing of the system. Such granular gases comprise materials such as dilute gases of stones, sand, various types of powders, or large molecules, and their mixtures are ubiquitous in Nature and technology, in particular in Space. We treat—depending on the physical-chemical properties of the inter-particle interaction upon their pair collisions—both a constant and a velocity-dependent (viscoelastic) restitution coefficient ε. Moreover we compare the granular gas dynamics with an effective single particle stochastic model based on an underdamped Langevin equation with time dependent diffusivity. We find that both models share the same behaviour of the ensemble mean squared displacement (MSD) and the velocity correlations in the limit of weak dissipation. Qualitatively, the reported non-ergodic behaviour is generic for granular gases with any realistic dependence of ε on the impact velocity of particles.
I. Introduction
Granular materials such as sand or different types of powders are ubiquitous in Nature and technology, for instance, in the cosmetic, food, and building industries.1 Rarefied granular systems, in which the distance between particles exceeds their size, are called granular gases.2–4 Such granular gases represent a fundamental physical system in statistical mechanics, extending the ideal gas model to include dissipation on particle collisions. Within granular matter physics granular gases represent a reference model system.5 On Earth, granular gases may be realised by placing granular matter into a container with vibrating6 or rotating7 walls, applying electrostatic8 or magnetic9 forces, etc. Granular gases are common in Space, occurring in protoplanetary discs, interstellar clouds, and planetary rings (e.g. of Saturn).10
Ergodicity is a fundamental concept of statistical mechanics. Starting with Boltzmann, the ergodic hypothesis states that long time averages  of a physical observable
of a physical observable 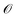 are identical to their ensemble averages
are identical to their ensemble averages 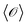 .11,12 In this sense, Brownian motion is ergodic even at out-of-equilibrium conditions, while a range of anomalous diffusion processes exhibit a distinct disparity
.11,12 In this sense, Brownian motion is ergodic even at out-of-equilibrium conditions, while a range of anomalous diffusion processes exhibit a distinct disparity 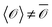 : for instance, for sufficiently long observation times the time averaged mean squared displacement (MSD) of a Brownian particle converges to the corresponding ensemble average 〈R2(t)〉13,14 calling for generalisation of the classical ergodic theories.12 In fact, similar concepts were already discussed in the context of glassy systems.15 In the wake of modern microscopic techniques, such as single particle tracking,16 in which individual trajectories of single molecules or submicron tracers are routinely measured, knowledge of the ergodic properties of the system is again pressing. While the time averages are measured in single particle assays or massive computer simulations, generally ensemble averages are more accessible theoretically. How measured time averages can be interpreted in terms of ensemble approaches and diffusion models is thus an imminent topic.13,14
: for instance, for sufficiently long observation times the time averaged mean squared displacement (MSD) of a Brownian particle converges to the corresponding ensemble average 〈R2(t)〉13,14 calling for generalisation of the classical ergodic theories.12 In fact, similar concepts were already discussed in the context of glassy systems.15 In the wake of modern microscopic techniques, such as single particle tracking,16 in which individual trajectories of single molecules or submicron tracers are routinely measured, knowledge of the ergodic properties of the system is again pressing. While the time averages are measured in single particle assays or massive computer simulations, generally ensemble averages are more accessible theoretically. How measured time averages can be interpreted in terms of ensemble approaches and diffusion models is thus an imminent topic.13,14
Here we quantify in detail from analytical derivations and extensive simulations how exactly the ergodicity is violated in simple mechanical systems such as force-free granular gases. Our results for generic granular gases are relevant both from a fundamental statistical mechanical point of view and for the practical analysis of time series of granular gas particles from observations and computer simulations. Specifically, (i) we here derive the time and ensemble averaged MSDs and show that for both constant and viscoelastic restitution coefficients the time averaged MSD is fundamentally different from the corresponding ensemble MSD. (ii) Moreover, the amplitude of the time averaged MSD is shown to be a decaying function of the length of the measured trajectory (ageing). (iii) We study an effective single particle mean field approach to the granular gas dynamics. This underdamped scaled Brownian motion (SBM) demonstrates how non-ergodicity and ageing emerge from the non-stationarity invoked by the time dependence of the granular temperature, which translates into the power-law time dependence of the diffusion coefficient of SBM. We note that systems with time dependent diffusion coefficients are in fact common in nature, ranging from mobility of proteins in cell membranes,17 motion of molecules in porous environments,18 water diffusion in brain as measured by magnetic resonance imaging,19 to snow-melt dynamics.20,21
II. Collisions in granular gases
Granular gas particles collide inelastically and a fraction of their kinetic energy is transformed into heat stored in internal degrees of freedom. The dissipative nature of granular gases effects many interesting physical properties.2 In absence of external forces the gas gradually cools down. During the first stage of its evolution, the granular gas is in the homogeneous cooling state characterised by uniform density and absence of macroscopic fluxes,2 realised e.g. in microgravity environments.22 Eventually instabilities occur and vertexes develop in the system.2,23 Hereafter, we focus on spatially uniform granular systems.
The energy dissipation in a pair-wise collision event of granular particles is quantified by the restitution coefficient
| | 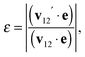 | (1) |
where
v12′ =
v2′ −
v1′ and
v12 =
v2 −
v1 are the relative velocities of two particles after and before the collision, respectively, and
e is a unit vector connecting their centres at the collision instant. The post-collision velocities are related to the pre-collision velocities
v1 and
v2 as
2| | 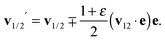 | (2) |
The case
ε = 1 denotes perfectly elastic collisions, while
ε = 0 reflects the perfectly inelastic case. In oblique collisions negative values of the restitution coefficient may be observed.
24 For 0 <
ε < 1 the granular temperature
given by the mean kinetic energy of particles with mass
m continuously decreases according to Haff's law for granular gases,
25| | | T(t) = T0/(1 + t/τ0)2. | (4) |
Here
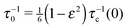
is the inverse characteristic time of the granular temperature decay, involving the initial value of the inverse mean collision time scaling as
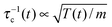
. Weak dissipation (
ε ≃ 1) thus implies
τ0 ≫
τc. Due to the temperature decrease the self-diffusion coefficient
D(
t) of the gas is time dependent,
2,26–29| | | D(t) = T(t)τv(t)/m = D0/(1 + t/τ0), | (5) |
where
τv(
t) is the velocity correlation time,
D0 =
T0τv(0)/
m (see
Fig. 1). For
ε = 1 we recover normal diffusion with the constant diffusivity.
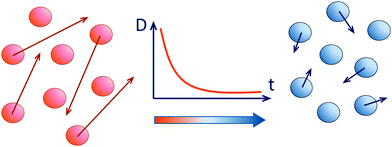 |
| | Fig. 1 Collisions in a free granular gas with a restitution coefficient ε < 1 lead to its cooling with time. Along with the reduced kinetic energy of the gas particles, the diffusion coefficient in a free cooling granular gas decreases with time. | |
Most studies of granular gases assume that ε is constant. Different approaches consider the dependence of ε on the relative collision speed of the form30,31
| | | ε(v12) ≃ 1 − C1Aκ2/5(v12·e)1/5 + C2A2κ4/5(v12·e)2/5. | (6) |
Here the numerical constants are
C1 = 1.15 and
C2 = 0.798, where
A quantifies the specific viscous material properties of particles,
κ = (3/2)
3/2Yσ1/2/[
m(1 −
ν2)] is the elastic constant,
Y is Young's modulus,
ν is the Poisson ratio, and
σ is the diameter of the particles. The granular temperature of the viscoelastic gas scales as
T(
t) ∼
t−5/3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33,34
33,34 implying
26which leads to crossover from super- to subdiffusion in granular Brownian motion.
35 We note that there exist more elaborate models for the viscoelastic restitution coefficient.
31 However, as the continuous decay of temperature is common to all these models, the properties of non-ergodicity and ageing obtained in this work are also generic to these more elaborate models.
III. Computer simulations and observables
We perform event-driven Molecular Dynamics (MD) simulations of a gas of hard-sphere granular particles of unit mass and radius, colliding with constant (see Fig. 2) and viscoelastic (Fig. 3) restitution coefficients. Our simulations code is based on the algorithm suggested in ref. 36. The particles move freely between pairwise collisions, while during the collisions the particle velocities are updated according to eqn (2). The duration time of collision is equal to zero, that is, the velocities of particles are updated instantaneously. We simulate N = 1000 particles in a three dimensional cubic box with edge length L = 40 and periodic boundary conditions. The box size is expressed in terms of the particle radius. The particle volume density is ϕ ≈ 0.065 and the initial granular temperature in the system is T0 = 1.
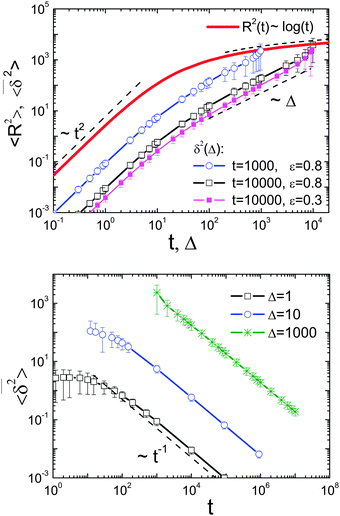 |
| | Fig. 2 Ensemble (〈R2(t)〉) and time averaged 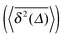 MSDs versus (lag) time (upper graph) and MSDs versus (lag) time (upper graph) and 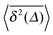 versus length t of the time series (lower graph), from event-driven MD simulations of a granular gas with two different values of the restitution coefficient, ε = 0.3 and 0.8. While the ensemble MSD crosses over from ballistic motion 〈R2(t)〉 ∼ t2 for t ≪ τ0 to the logarithmic law 〈R2(t)〉 ∼ log(t) for t ≫ τ0, the time averaged MSD starts ballistically and crosses over to the scaling versus length t of the time series (lower graph), from event-driven MD simulations of a granular gas with two different values of the restitution coefficient, ε = 0.3 and 0.8. While the ensemble MSD crosses over from ballistic motion 〈R2(t)〉 ∼ t2 for t ≪ τ0 to the logarithmic law 〈R2(t)〉 ∼ log(t) for t ≫ τ0, the time averaged MSD starts ballistically and crosses over to the scaling 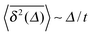 given by eqn (A10). given by eqn (A10). | |
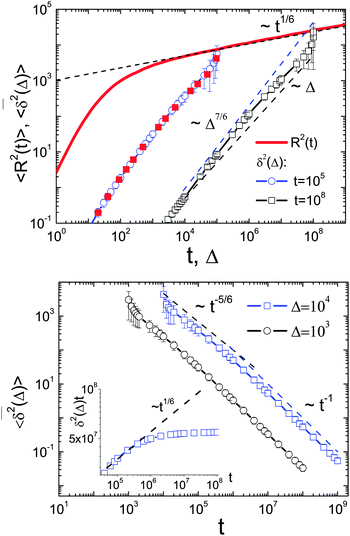 |
| | Fig. 3 MSDs 〈R2(t)〉 and 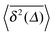 as function of (lag) time (top) and as function of (lag) time (top) and 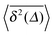 versus the measurement time t (bottom) from MD simulations (symbols) of a granular gas with viscoelastic ε(v12). We observe the scaling 〈R2(t)〉 ∼ t1/6 in the limit t ≫ τ0. The scaling of the time averaged MSD slowly changes between the indicated slopes (dashed lines). The continuous change of slope of versus the measurement time t (bottom) from MD simulations (symbols) of a granular gas with viscoelastic ε(v12). We observe the scaling 〈R2(t)〉 ∼ t1/6 in the limit t ≫ τ0. The scaling of the time averaged MSD slowly changes between the indicated slopes (dashed lines). The continuous change of slope of 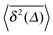 as function of the length t of time traces from slope −5/6 to −1 is seen in the inset of the bottom graph. The results for the time averaged MSD with the restitution coefficient computed according to the Padé approximation32 (see text for details) are shown as the red filled squares in the top panel. as function of the length t of time traces from slope −5/6 to −1 is seen in the inset of the bottom graph. The results for the time averaged MSD with the restitution coefficient computed according to the Padé approximation32 (see text for details) are shown as the red filled squares in the top panel. | |
We evaluate the gas dynamics in terms of the standard ensemble MSD 〈R2(t)〉, obtained from averaging over all gas particles at time t, as well as the time averaged MSD
| | 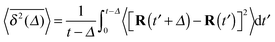 | (8) |
for a time series
R(
t) of length
t as function of the lag time
Δ.
Eqn (8) is a standard definition to evaluate time series in experiments and simulations.
13,14,37,38 Here the angular brackets denote the average
| | 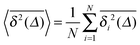 | (9) |
over all
N particle traces. For an ergodic system, such as an ideal gas with unit restitution coefficient corresponding to normal particle diffusion, the ensemble and time averaged MSDs are equivalent at any time,
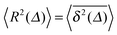
.
13,14 In contrast, several systems characterised by anomalous diffusion with power-law MSD 〈
R2(
t)〉 ≃
tα (
α ≠ 1) or a corresponding logarithmic growth of the MSD, are non-ergodic and display the disparity
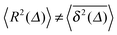
.
13–15,38–41
Fig. 2 shows the results of our computer simulations of a granular gas with constant ε = 0.8 and 0.3. The ensemble MSD shows initial ballistic particle motion, 〈R2(t)〉 ∼ t2. Eventually, the particles start to collide and gradually lose kinetic energy. The ensemble MSD of the gas in this regime follows the logarithmic law 〈R2(t)〉 ∼ log(t) (the red line in Fig. 2, top panel).2 The time averaged MSD at short lag times Δ preserves the ballistic law 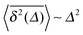 . At longer lag times, we observe the linear growth
. At longer lag times, we observe the linear growth 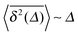 (black symbols in Fig. 2, top). In addition to this non-ergodic behaviour, the time averaged MSD decreases with increasing length t of the recorded trajectory,
(black symbols in Fig. 2, top). In addition to this non-ergodic behaviour, the time averaged MSD decreases with increasing length t of the recorded trajectory, 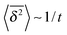 . This highly non-stationary behaviour is also referred to as ageing, the dependence of the system dynamics on its time of evolution.41 The dependence on the trace length we observe in the bottom panel of Fig. 2 implies that the system is becoming progressively slower. We observe the convergence
. This highly non-stationary behaviour is also referred to as ageing, the dependence of the system dynamics on its time of evolution.41 The dependence on the trace length we observe in the bottom panel of Fig. 2 implies that the system is becoming progressively slower. We observe the convergence 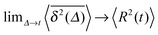 .
.
Fig. 3 depicts the results of MD simulations for a granular gas with viscoelastic restitution coefficient (6) with Aκ2/5 = 0.2. In this case the ensemble MSD scales as
for the time scale
t ≫
τ0. The time averaged MSD does not seem to follow a universal scaling law but appears to transiently change from the power-law
| | 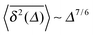 | (11) |
at intermediate lag times to
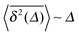
at longer
Δ. As function of the length
t of particle traces, we observe the crossover from
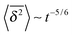
to
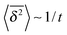
, see the bottom panel in
Fig. 3.
IV. Granular gas with constant ε
Let us explore this behaviour in more detail. The dynamics of a granular gas can be mapped to that of a molecular gas by a rescaling of time from t to τ as 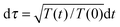 .2,28,42 Using Haff's law (4), it follows that
.2,28,42 Using Haff's law (4), it follows that| | τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(1 + t/τ0). log(1 + t/τ0). | (12) |
The correlation function for the dimensionless velocity 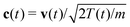 of granular particles decays exponentially in this time scale,2
of granular particles decays exponentially in this time scale,2| | | 〈c(τ1)c(τ2)〉 = (3/2)exp(−|τ2 − τ1|/τv(0)). | (13) |
In the real time t we find (t2 ≥ t1)| | 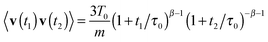 | (14) |
for the velocity correlator; here
The MSD is| | 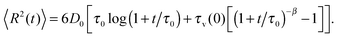 | (15) |
At short times the particles move ballistically, 〈R2(t)〉 ∼ 3D0t2/τv(0), crossing over to the logarithmic growth 〈R2(t)〉 ∼ 6D0τ0 × log(t/τ0), as seen in the top panel of Fig. 2.
From the autocorrelation function (14) we obtain the time averaged MSD (see Appendix A)
| | 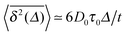 | (16) |
valid in the range
τ0 ≪
Δ ≪
t, where
τ0 is the characteristic temperature decay time in
eqn (4). This result indeed explains the behaviour observed in
Fig. 2: the time averaged MSD scales linearly with the lag time and inverse-proportionally with the trace length
t. Comparison of
eqn (15) and (16) demonstrates the non-ergodicity and ageing properties of the system of granular gas particles.
V. Viscoelastic granular gas
For a velocity-dependent restitution coefficient ε(v12) the temperature decays like T(t) ≃ T0(t/τ0)−5/3, and the time transformation reads τ = 6τ05/6t1/6. The MSD in this case exhibits the long time scaling
seen in the top panel of Fig. 3. For the time averaged MSD we analytically obtain the bounds
and
compare the details in Appendix A. These bounds are given by the dashed lines in the top panel of Fig. 3. Concurrent to this change of slopes as a function of the lag time, the bottom panel of Fig. 3 shows the change of slope of 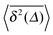 as function of the trajectory length t from the slope −5/6 to −1 at a fixed lag time Δ.
as function of the trajectory length t from the slope −5/6 to −1 at a fixed lag time Δ.
We note that a more explicit expression for the viscoelastic restitution coefficient can be obtained in terms of the Padé approximant [3/6]ε, as derived in ref. 32. In Fig. 3 we demonstrate, however, that for the range of parameters used in our simulations—corresponding to relatively slow collision velocities of granular particles (scaled thermal velocity v* < 0.3)—we obtain nearly the same results for the time averaged MSD as our previous simulations with the restitution coefficient (6), see the red filled squares in Fig. 3.
VI. Scaled Brownian motion
For the unit restitution coefficient individual gas particles at long times perform Brownian motion at a fixed temperature defined by the initial velocity distribution of the particles. For the dissipative granular gases considered herein, the granular temperature scales like T(t) ≃ 1/t2 and ≃ 1/t5/3, respectively. Single particle stochastic processes with power-law time-varying temperature or, equivalently, time dependent diffusivity D(t), are well known. Such SBM is described in terms of the overdamped Langevin equation (neglecting the inertia term) with the diffusivityfor 0 < α < 2.43,44 SBM is a highly non-stationary process and is known to be non-ergodic and ageing.14,44–46 Recently, the case of α = 0 corresponding to ultraslow SBM was considered.47
To study whether SBM provides an effective single particle description of diffusion in dissipative granular gases we extend SBM to the underdamped case. We thus take the inertial term explicitly into account when considering the dynamics,
| | 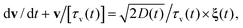 | (18) |
driven by white Gaussian noise
ξ(
t) with correlation function 〈
ξi(
t1)
ξj(
t2)〉 =
δi,jδ(
t1 −
t2) for the components.
For α = 0 the velocity correlation may be derived from the Langevin eqn (18), namely
| | 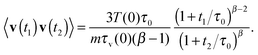 | (19) |
This result for the ultraslow SBM in the underdamped limit (see
ref. 47) formally coincides with the velocity correlation
function (14) for granular gases in the limit
β ≫ 1, in which the velocity correlation time
τv(0) is much shorter than the characteristic decay time
τ0 of the granular temperature. This is achieved for sufficiently weak dissipation in the system (
ε ≲ 1).
VII. Conclusions
The occurrence of non-ergodicity in the form of the disparity between long time and ensemble averages of physical observables and ageing, is not surprising in strongly disordered systems described by the prominent class of continuous time random walk models involving divergent time scales of the dynamics.13–15,39 Examples include diffusive motion in amorphous semiconductors, structured disordered environments, or living biological cells.14
Here, we demonstrated how non-ergodicity arises in a simple mechanistic systems such as force-free granular gases. Physically, it stems from a strong non-stationary character of this process brought about by the continuous decay of the gas temperature. Therefore, the ergodicity breaking is expected independent of the particular model of the restitution coefficient ε, while the precise behaviour of the MSD and time averaged MSD clearly depends on the specific law for ε.
For a constant restitution coefficient, the MSD of gas particles 〈R2(t)〉 grows logarithmically, while the time averaged MSD 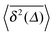 is linear in the lag time and decays inverse proportionally with the trace length (ageing). We derived the observed non-ergodicity and the ageing behaviour of granular gases from the velocity autocorrelation functions. We note that ageing in the homogeneous cooling state of granular gases was reported previously,48 however, it was not put in context with the diffusive dynamics of gas particles.
is linear in the lag time and decays inverse proportionally with the trace length (ageing). We derived the observed non-ergodicity and the ageing behaviour of granular gases from the velocity autocorrelation functions. We note that ageing in the homogeneous cooling state of granular gases was reported previously,48 however, it was not put in context with the diffusive dynamics of gas particles.
The decaying temperature of the dissipative force-free granular gas corresponds to an increase of the time span between successive collisions of gas particles, a feature directly built into the SBM model.44 As we showed here, SBM and its ultraslow extension with the logarithmic growth of the MSD indeed captures certain features of the observed motion and may serve as an effective single particle model for the granular gas. It is particularly useful when more complex situations are considered, such as the presence of external force fields. Our results shed new light on the physics of granular gases with respect to their violation of ergodicity in the Boltzmann sense. They are important for a better understanding of dissipation in free gases as well as the analysis of experimental observations and MD studies of granular gases.
It will be interesting to compare the results obtained herein—based on the two standard assumptions for the restitution coefficient—with experimental observations of granular gas systems. Similarly, it might be of interest to see to what extent the present scenario pertains to dilute gases of complex molecules with a large number of internal degrees of freedom ready to absorb a part of the collision energies.2–4
Appendix A: constant restitution coefficient
In this section and the next we present details of the derivation of the results from the main text of the manuscript as well as an additional figure.
The time averaged MSD for the granular gas with constant restitution coefficient, eqn (8) in the main text, may be written as
| | 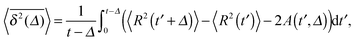 | (A1) |
where the MSD 〈
R2(
t)〉 is defined by
eqn (15) and
| | 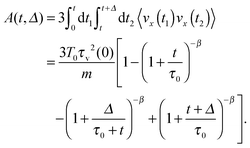 | (A2) |
This term accounts for the position correlations at different time instants
t and
t +
Δ. In the present consideration, this term is non-zero. It arises due to the fact that the normal component of the relative velocity of the colliding particles decreases while the tangential component remains unchanged in the course of collisions. Introducing
eqn (A2) and (15) into
eqn (A1), we obtain the time averaged MSD in the form
| | 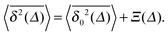 | (A3) |
The first term is the time averaged MSD for overdamped SBM,
| | 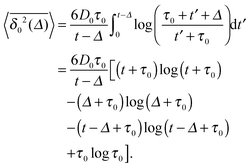 | (A4) |
For
τ0 ≪
Δ ≪
t| | 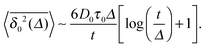 | (A5) |
The second term in
eqn (A3) has the form
where
β =
τ0/
τv(0), see the main text. Introducing the new variable
y =
Δ/
t′ we get in the limit
τ0 ≪
Δ that
| | 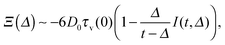 | (A6) |
where
| | 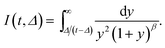 | (A7) |
This integral can be taken by parts
| | 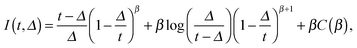 | (A8) |
where
| | 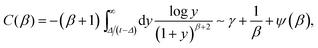 | (A9) |
γ = 0.5772… is the Euler's constant, and
ψ(
z) = d
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
log
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ
Γ(
z)/d
z is the digamma function. Finally we find in the limit
t ≫
Δ that
| | 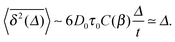 | (A10) |
This confirms the linear scaling of the time averaged MSD.
Appendix B: velocity-dependent restitution coefficient
Similarly, for the viscoelastic granular gas with ε = ε(v12) the time averaged MSD may be presented as the sum of two parts, see eqn (A3). The first term corresponds to the time averaged MSD of the SBM process, described by the overdamped Langevin equation to yield| | 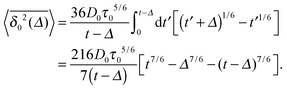 | (B1) |
The second term becomes| | 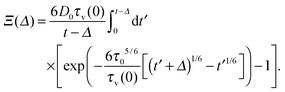 | (B2) |
This integral can be presented as a sum of three parts| | 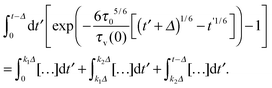 | (B3) |
We choose the coefficients k1,2 in the following ranges
and
|
τ
0Δ1/5/τv6/5(0) ≪ k2 ≪ t/Δ. |
This enables us to evaluate the first integral in
eqn (B3) as follows
| | 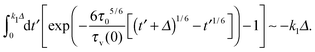 | (B4) |
The third term in
eqn (B3) can be evaluated as
| | 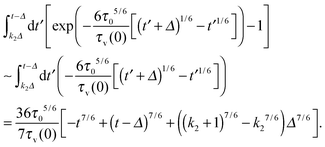 | (B5) |
For the chosen range of parameters
k1,2 the contribution
(B4) can be neglected. Finally, assuming that the second term in
eqn (B3) is small enough compared to
eqn (B5) we get to leading order
| | 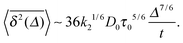 | (B6) |
For longer lag times
Δ, in the range
τv(0)
t5/6/
τ05/6 ≪
Δ ≪
t that is opposite to the condition for
k2 above, we have the upper estimate for the correction
Ξ(
Δ) to the time averaged MSD of the SBM process, namely
| | 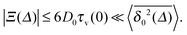 | (B7) |
Then we get in the limit
Δ ≪
t that
| | 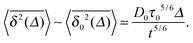 | (B8) |
In addition to these analytical estimates, we computed numerically the full
expression (A3). It agrees well with our MD simulation data, compare the curves in
Fig. 4 where we explicitly plot
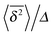
. It shows that in the range of parameters
τ0,
τv and
D0 consistent with the results of simulations presented in the main text, the transient scaling behaviour
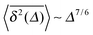
is realised in a limited range of
Δ. Note also that in this range the linear SBM scaling for
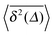
as prescribed by
eqn (B8) is no longer valid. The reason is that for large values of
Δ, when
Δ →
t for any length of the trajectory, in
eqn (B2) the evolution of the time averaged MSD with the lag time
Δ becomes inherently nonlinear.
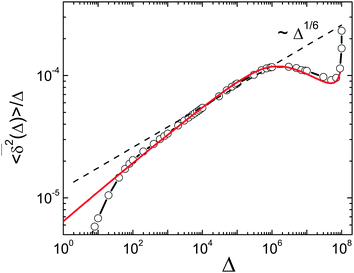 |
| | Fig. 4 Time averaged MSD 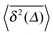 divided by lag time Δ as function of Δ from MD simulations (symbols) of a granular gas with velocity-dependent restitution coefficient. The lines connecting the symbols guide the eye. Red line corresponds to numerical calculation of divided by lag time Δ as function of Δ from MD simulations (symbols) of a granular gas with velocity-dependent restitution coefficient. The lines connecting the symbols guide the eye. Red line corresponds to numerical calculation of 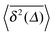 in eqn (A3) for τ0 = 25, τv = 2, D0 = 2. These values ensure the closest agreement and are consistent with the parameters of the granular gas as used in MD simulations apart from very short lag times. Dashed line shows the asymptotic in eqn (A3) for τ0 = 25, τv = 2, D0 = 2. These values ensure the closest agreement and are consistent with the parameters of the granular gas as used in MD simulations apart from very short lag times. Dashed line shows the asymptotic 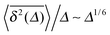 behaviour according to eqn (B8). behaviour according to eqn (B8). | |
Acknowledgements
We thank F. Spahn, I. M. Sokolov and N. V. Brilliantov for discussions. Simulations were run at Moscow State University's Chebyshev supercomputer. We acknowledge support from EU IRSES grant DCP-PhysBio N269139 (to AB), the IMU Berlin Einstein Foundation (to AVC), DFG grant CH 707/5-1 (to AGC), and the Academy of Finland (Suomen Akatemia, Finland Distinguished Professor programme, RM).
References
- H. M. Jaeger, S. R. Nagel and R. P. Behringer, Rev. Mod. Phys., 1996, 68, 1259 CrossRef;
Physics of Dry Granular Media, ed. H. J. Herrmann, J.-P. Hovi and S. Luding, NATO ASI Series, Kluwer, Dordrecht, 1998 Search PubMed.
-
N. V. Brilliantov and T. Pöschel, Kinetic theory of Granular Gases, Oxford University Press, 2004 Search PubMed.
-
Mathematics and Mechanics of Granular Materials, ed. J. M. Hill and A. P. S. Selvadurai, Springer, 2005 Search PubMed.
-
Unifying Concepts in Granular Media and Glasses, ed. A. A. Coniglio, H. J. Herrmann and M. Nicodemi, Elsevier, Amsterdam, 2004 Search PubMed.
-
A. Mehta, in Granular Physics, Cambridge University Press, 2011 Search PubMed;
Granular Matter, ed. A. Mehta, Springer, Berlin, 2011 Search PubMed.
- R. D. Wildman and D. J. Parker, Phys. Rev. Lett., 2002, 88, 064301 CrossRef CAS; A. Prevost, D. A. Egolf and J. S. Urbach, Phys. Rev. Lett., 2002, 89, 084301 CrossRef.
- O. Zik, D. Levine, S. Lipson, S. Shtrikman and J. Stavans, Phys. Rev. Lett., 1994, 73, 644 CrossRef.
- I. S. Aranson and J. S. Olafsen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 061302 CrossRef CAS.
- A. Snezhko, I. S. Aranson and W.-K. Kwok, Phys. Rev. Lett., 2005, 94, 108002 CrossRef CAS; C. C. Maaß, N. Isert, G. Maret and C. M. Aegerter, Phys. Rev. Lett., 2008, 100, 248001 CrossRef.
-
R. Greenberg and A. Brahic, Planetary Rings, University of Arizona Press, Tucson, AZ, 1984 CrossRef CAS PubMed; A. Bodrova, J. Schmidt, F. Spahn and N. V. Brilliantov, Icarus, 2012, 218, 60 CrossRef CAS PubMed; F. Spahn, U. Schwarz and J. Kurths, Phys. Rev. Lett., 1997, 78, 1596 CrossRef.
-
A. I. Khinchin, Mathematical foundations of statistical mechanics, Dover, New York, NY, 1949 Search PubMed;
M. Toda, R. Kubo and N. Saitô, Statistical Physics I, Springer, Berlin, 1992 Search PubMed.
- S. Burov, R. Metzler and E. Barkai, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13228 CrossRef CAS PubMed.
- E. Barkai, Y. Garini and R. Metzler, Phys. Today, 2012, 65(8), 29 CrossRef CAS PubMed; I. M. Sokolov, Soft Matter, 2012, 8, 9043 RSC; S. Burov, J.-H. Jeon, R. Metzler and E. Barkai, Phys. Chem. Chem. Phys., 2011, 13, 1800 RSC.
- R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Phys. Chem. Chem. Phys., 2014, 16, 24128 RSC.
- J.-P. Bouchaud, J. Phys. I, 1992, 2, 1705 CrossRef.
-
C. Bräuchle, D. C. Lamb and J. Michaelis, Single Particle Tracking and Single Molecule Energy Transfer, Wiley-VCH, Weinheim, Germany, 2012 CrossRef CAS PubMed; X. S. Xie, P. J. Choi, G.-W. Li, N. K. Lee and G. Lia, Annu. Rev. Biophys., 2008, 37, 417 CrossRef CAS PubMed.
- T. J. Feder, I. Brust-Mascher, J. P. Slattery, B. Baird and W. W. Webb, Biophys. J., 1996, 70, 2767 CrossRef CAS.
- P. N. Sen, Concepts Magn. Reson., Part A, 2004, 23, 1 CrossRef PubMed.
- D. S. Novikov, J. H. Jensen, J. A. Helpern and E. Fieremans, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 5088 CrossRef CAS PubMed.
- A. Molini, P. Talkner, G. G. Katul and A. Porporato, Physica A, 2011, 390, 1841 CrossRef CAS PubMed.
-
D. De Walle and A. Rango, Principles of Snow Hydrology, Cambridge University Press, 2008 Search PubMed.
- Y. Grasselli, G. Bossis and G. Goutallier, Europhys. Lett., 2009, 86, 60007 CrossRef.
- M. J. Ruiz-Montero and J. J. Brey, Eur. Phys. J.: Spec. Top., 2009, 179, 249 CrossRef PubMed.
- K. Saitoh, A. Bodrova, H. Hayakawa and N. V. Brilliantov, Phys. Rev. Lett., 2010, 105, 238001 CrossRef.
- P. K. Haff, J. Fluid Mech., 1983, 134, 401 CrossRef.
- N. V. Brilliantov and T. Pöschel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 1716 CrossRef CAS.
- J. J. Brey, M. J. Ruiz-Montero, D. Cubero and R. Garcia-Rojo, Phys. Fluids, 2000, 12, 876 CrossRef CAS PubMed.
- J. W. Dufty, J. J. Brey and J. Lutsko, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 051303 CrossRef; J. Lutsko, J. J. Brey and J. W. Dufty, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 051304 CrossRef.
- A. Bodrova and N. Brilliantov, Granular Matter, 2012, 14, 85 CrossRef CAS.
- R. Ramirez, T. Pöschel, N. V. Brilliantov and T. Schwager, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 4465 CrossRef CAS; D. L. Blair and A. Kudrolli, Phys. Rev. E, 2003, 67, 041301 CrossRef.
- T. Schwager and T. Pöschel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 051304 CrossRef.
- P. Müller and T. Pöschel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 021302 CrossRef.
- T. Schwager and T. Pöschel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 650 CrossRef CAS.
- N. V. Brilliantov and T. Pöschel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 5573 CrossRef CAS.
- A. Bodrova, A. K. Dubey, S. Puri and N. Brilliantov, Phys. Rev. Lett., 2012, 109, 178001 CrossRef.
-
T. Pöschel and T. Schwager, Computational Granular Dynamics, Springer, Berlin, 2005, see also http://www.mss.cbi.uni-erlangen.de/cgd/ Search PubMed.
- I. Golding and E. C. Cox, Phys. Rev. Lett., 2006, 96, 092102 CrossRef CAS PubMed; Y. M. Wang, R. H. Austin and E. C. Cox, Phys. Rev. Lett., 2006, 97, 048302 CrossRef.
- A. V. Weigel, B. Simon, M. M. Tamkun and D. Krapf, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6438 CrossRef CAS PubMed; S. M. A. Tabei, S. Burov, H. Y. Kim, A. Kuznetsov, T. Huynh, J. Jureller, L. H. Philipson, A. R. Dinner and N. F. Scherer, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4911 CrossRef PubMed; J.-H. Jeon, V. Tejedor, S. Burov, E. Barkai, C. Selhuber-Unkel, K. Berg-Sørensen, L. Oddershede and R. Metzler, Phys. Rev. Lett., 2011, 106, 048103 CrossRef.
- Y. He, S. Burov, R. Metzler and E. Barkai, Phys. Rev. Lett., 2008, 101, 058101 CrossRef CAS; A. Lubelski, I. M. Sokolov and J. Klafter, Phys. Rev. Lett., 2008, 100, 250602 CrossRef.
- A. Godec, A. V. Chechkin, H. Kantz, E. Barkai and R. Metzler, J. Phys. A: Math. Theor., 2014, 47, 492002 CrossRef.
- J. H. P. Schulz, E. Barkai and R. Metzler, Phys. Rev. Lett., 2013, 110, 020602 CrossRef; J. H. P. Schulz, E. Barkai and R. Metzler, Phys. Rev. X, 2014, 4, 011028 Search PubMed.
- T. P. C. van Noije, M. H. Ernst, R. Brito and J. A. G. Orza, Phys. Rev. Lett., 1997, 79, 411 CrossRef CAS; J. F. Lutsko, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 061211 CrossRef.
- S. C. Lim and S. V. Muniandy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 021114 CrossRef CAS; M. J. Saxton, Biophys. J., 2001, 81, 2226 CrossRef; P. P. Mitra, P. N. Sen, L. M. Schwartz and P. Le Doussal, Phys. Rev. Lett., 1992, 68, 3555 CrossRef; J. F. Lutsko and J. P. Boon, Phys. Rev. Lett., 2013, 88, 022108 Search PubMed.
- A. Fuliński, J. Chem. Phys., 2013, 138, 021101 CrossRef CAS PubMed; A. Fuliński, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 061140 CrossRef; F. Thiel and I. M. Sokolov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 012115 CrossRef; J.-H. Jeon, A. V. Chechkin and R. Metzler, Phys. Chem. Chem. Phys., 2014, 16, 15811 RSC.
-
H. Safdari, A. G. Cherstvy, A. V. Chechkin, F. Thiel, I. M. Sokolov and R. Metzler, J. Phys. A, E-print arXiv:1507.02450 Search PubMed.
- H. Safdari, A. V. Chechkin, G. R. Jafari and R. Metzler, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 042107 CrossRef.
- A. Bodrova, A. V. Chechkin, A. G. Cherstvy and R. Metzler, New J. Phys., 2015, 17, 063038 CrossRef.
- J. J. Brey, A. Prados, M. I. Garca de Soria and P. Maynar, J. Phys. A: Math. Theor., 2007, 40, 14331 CrossRef CAS.
|
| This journal is © the Owner Societies 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ae
*ae
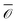 of a physical observable
of a physical observable 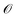 are identical to their ensemble averages
are identical to their ensemble averages 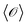 .11,12 In this sense, Brownian motion is ergodic even at out-of-equilibrium conditions, while a range of anomalous diffusion processes exhibit a distinct disparity
.11,12 In this sense, Brownian motion is ergodic even at out-of-equilibrium conditions, while a range of anomalous diffusion processes exhibit a distinct disparity 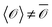 : for instance, for sufficiently long observation times the time averaged mean squared displacement (MSD) of a Brownian particle converges to the corresponding ensemble average 〈R2(t)〉13,14 calling for generalisation of the classical ergodic theories.12 In fact, similar concepts were already discussed in the context of glassy systems.15 In the wake of modern microscopic techniques, such as single particle tracking,16 in which individual trajectories of single molecules or submicron tracers are routinely measured, knowledge of the ergodic properties of the system is again pressing. While the time averages are measured in single particle assays or massive computer simulations, generally ensemble averages are more accessible theoretically. How measured time averages can be interpreted in terms of ensemble approaches and diffusion models is thus an imminent topic.13,14
: for instance, for sufficiently long observation times the time averaged mean squared displacement (MSD) of a Brownian particle converges to the corresponding ensemble average 〈R2(t)〉13,14 calling for generalisation of the classical ergodic theories.12 In fact, similar concepts were already discussed in the context of glassy systems.15 In the wake of modern microscopic techniques, such as single particle tracking,16 in which individual trajectories of single molecules or submicron tracers are routinely measured, knowledge of the ergodic properties of the system is again pressing. While the time averages are measured in single particle assays or massive computer simulations, generally ensemble averages are more accessible theoretically. How measured time averages can be interpreted in terms of ensemble approaches and diffusion models is thus an imminent topic.13,14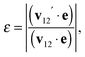
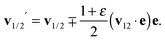
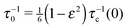 is the inverse characteristic time of the granular temperature decay, involving the initial value of the inverse mean collision time scaling as
is the inverse characteristic time of the granular temperature decay, involving the initial value of the inverse mean collision time scaling as 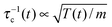 . Weak dissipation (ε ≃ 1) thus implies τ0 ≫ τc. Due to the temperature decrease the self-diffusion coefficient D(t) of the gas is time dependent,2,26–29
. Weak dissipation (ε ≃ 1) thus implies τ0 ≫ τc. Due to the temperature decrease the self-diffusion coefficient D(t) of the gas is time dependent,2,26–29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33,34 implying26
33,34 implying26
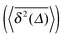 MSDs versus (lag) time (upper graph) and
MSDs versus (lag) time (upper graph) and 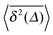 versus length t of the time series (lower graph), from event-driven MD simulations of a granular gas with two different values of the restitution coefficient, ε = 0.3 and 0.8. While the ensemble MSD crosses over from ballistic motion 〈R2(t)〉 ∼ t2 for t ≪ τ0 to the logarithmic law 〈R2(t)〉 ∼ log(t) for t ≫ τ0, the time averaged MSD starts ballistically and crosses over to the scaling
versus length t of the time series (lower graph), from event-driven MD simulations of a granular gas with two different values of the restitution coefficient, ε = 0.3 and 0.8. While the ensemble MSD crosses over from ballistic motion 〈R2(t)〉 ∼ t2 for t ≪ τ0 to the logarithmic law 〈R2(t)〉 ∼ log(t) for t ≫ τ0, the time averaged MSD starts ballistically and crosses over to the scaling 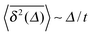 given by eqn (A10).
given by eqn (A10).
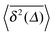 as function of (lag) time (top) and
as function of (lag) time (top) and 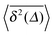 versus the measurement time t (bottom) from MD simulations (symbols) of a granular gas with viscoelastic ε(v12). We observe the scaling 〈R2(t)〉 ∼ t1/6 in the limit t ≫ τ0. The scaling of the time averaged MSD slowly changes between the indicated slopes (dashed lines). The continuous change of slope of
versus the measurement time t (bottom) from MD simulations (symbols) of a granular gas with viscoelastic ε(v12). We observe the scaling 〈R2(t)〉 ∼ t1/6 in the limit t ≫ τ0. The scaling of the time averaged MSD slowly changes between the indicated slopes (dashed lines). The continuous change of slope of 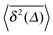 as function of the length t of time traces from slope −5/6 to −1 is seen in the inset of the bottom graph. The results for the time averaged MSD with the restitution coefficient computed according to the Padé approximation32 (see text for details) are shown as the red filled squares in the top panel.
as function of the length t of time traces from slope −5/6 to −1 is seen in the inset of the bottom graph. The results for the time averaged MSD with the restitution coefficient computed according to the Padé approximation32 (see text for details) are shown as the red filled squares in the top panel.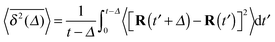
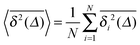
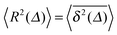 .13,14 In contrast, several systems characterised by anomalous diffusion with power-law MSD 〈R2(t)〉 ≃ tα (α ≠ 1) or a corresponding logarithmic growth of the MSD, are non-ergodic and display the disparity
.13,14 In contrast, several systems characterised by anomalous diffusion with power-law MSD 〈R2(t)〉 ≃ tα (α ≠ 1) or a corresponding logarithmic growth of the MSD, are non-ergodic and display the disparity 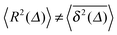 .13–15,38–41
.13–15,38–41
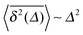 . At longer lag times, we observe the linear growth
. At longer lag times, we observe the linear growth 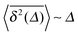 (black symbols in Fig. 2, top). In addition to this non-ergodic behaviour, the time averaged MSD decreases with increasing length t of the recorded trajectory,
(black symbols in Fig. 2, top). In addition to this non-ergodic behaviour, the time averaged MSD decreases with increasing length t of the recorded trajectory, 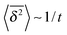 . This highly non-stationary behaviour is also referred to as ageing, the dependence of the system dynamics on its time of evolution.41 The dependence on the trace length we observe in the bottom panel of Fig. 2 implies that the system is becoming progressively slower. We observe the convergence
. This highly non-stationary behaviour is also referred to as ageing, the dependence of the system dynamics on its time of evolution.41 The dependence on the trace length we observe in the bottom panel of Fig. 2 implies that the system is becoming progressively slower. We observe the convergence 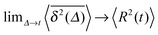 .
.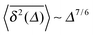
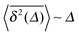 at longer Δ. As function of the length t of particle traces, we observe the crossover from
at longer Δ. As function of the length t of particle traces, we observe the crossover from 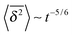 to
to 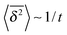 , see the bottom panel in Fig. 3.
, see the bottom panel in Fig. 3.
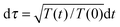 .2,28,42 Using Haff's law (4), it follows that
.2,28,42 Using Haff's law (4), it follows that![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(1 + t/τ0).
log(1 + t/τ0).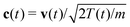 of granular particles decays exponentially in this time scale,2
of granular particles decays exponentially in this time scale,2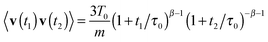
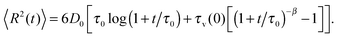
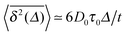
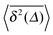 as function of the trajectory length t from the slope −5/6 to −1 at a fixed lag time Δ.
as function of the trajectory length t from the slope −5/6 to −1 at a fixed lag time Δ.
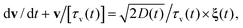
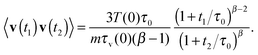
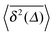 is linear in the lag time and decays inverse proportionally with the trace length (ageing). We derived the observed non-ergodicity and the ageing behaviour of granular gases from the velocity autocorrelation functions. We note that ageing in the homogeneous cooling state of granular gases was reported previously,48 however, it was not put in context with the diffusive dynamics of gas particles.
is linear in the lag time and decays inverse proportionally with the trace length (ageing). We derived the observed non-ergodicity and the ageing behaviour of granular gases from the velocity autocorrelation functions. We note that ageing in the homogeneous cooling state of granular gases was reported previously,48 however, it was not put in context with the diffusive dynamics of gas particles.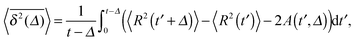
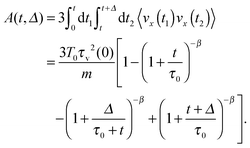
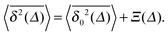
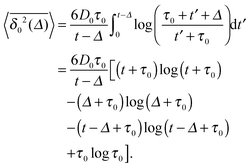
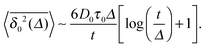
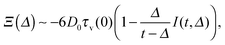
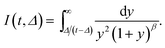
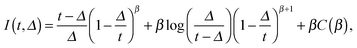
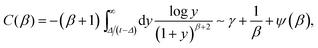
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Γ(z)/dz is the digamma function. Finally we find in the limit t ≫ Δ that
Γ(z)/dz is the digamma function. Finally we find in the limit t ≫ Δ that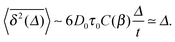
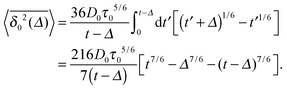
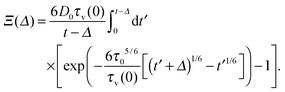
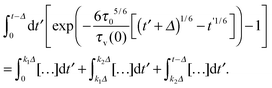
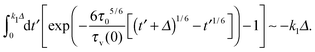
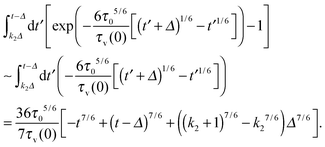
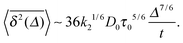
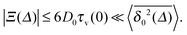
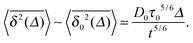
 . It shows that in the range of parameters τ0, τv and D0 consistent with the results of simulations presented in the main text, the transient scaling behaviour
. It shows that in the range of parameters τ0, τv and D0 consistent with the results of simulations presented in the main text, the transient scaling behaviour 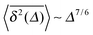 is realised in a limited range of Δ. Note also that in this range the linear SBM scaling for
is realised in a limited range of Δ. Note also that in this range the linear SBM scaling for 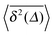 as prescribed by eqn (B8) is no longer valid. The reason is that for large values of Δ, when Δ → t for any length of the trajectory, in eqn (B2) the evolution of the time averaged MSD with the lag time Δ becomes inherently nonlinear.
as prescribed by eqn (B8) is no longer valid. The reason is that for large values of Δ, when Δ → t for any length of the trajectory, in eqn (B2) the evolution of the time averaged MSD with the lag time Δ becomes inherently nonlinear.

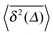 divided by lag time Δ as function of Δ from MD simulations (symbols) of a granular gas with velocity-dependent restitution coefficient. The lines connecting the symbols guide the eye. Red line corresponds to numerical calculation of
divided by lag time Δ as function of Δ from MD simulations (symbols) of a granular gas with velocity-dependent restitution coefficient. The lines connecting the symbols guide the eye. Red line corresponds to numerical calculation of 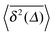 in eqn (A3) for τ0 = 25, τv = 2, D0 = 2. These values ensure the closest agreement and are consistent with the parameters of the granular gas as used in MD simulations apart from very short lag times. Dashed line shows the asymptotic
in eqn (A3) for τ0 = 25, τv = 2, D0 = 2. These values ensure the closest agreement and are consistent with the parameters of the granular gas as used in MD simulations apart from very short lag times. Dashed line shows the asymptotic 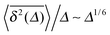 behaviour according to eqn (B8).
behaviour according to eqn (B8).