Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unusual Mn coordination and redox chemistry in the high capacity borate cathode Li7Mn(BO3)3†
Julian
Roos
ab,
Christopher
Eames
*a,
Stephen M.
Wood
a,
Alexander
Whiteside
ac and
M.
Saiful Islam
*a
aDepartment of Chemistry, University of Bath, Bath, BA2 7AY, UK. E-mail: m.s.islam@bath.ac.uk; c.eames@bath.ac.uk
bTechnical University of Munich, 85748 Garching/Munich, Germany
cDepartment of Chemistry, University of Cambridge, Cambridge, CB2 1TN, UK
First published on 29th July 2015
Abstract
The recently discovered lithium-rich cathode material Li7Mn(BO3)3 has a high theoretical capacity and an unusual tetrahedral Mn2+ coordination. Atomistic simulation and density functional theory (DFT) techniques are employed to provide insights into the defect and redox chemistry, the structural changes upon lithium extraction and the mechanisms of lithium ion diffusion. The most favourable intrinsic defects are Li/Mn anti-site pairs, where Li and Mn ions occupy interchanged positions, and Li Frenkel defects. DFT calculations reproduce the experimental cell voltage and confirm the presence of the unusually high MnV redox state, which corresponds to a theoretical capacity of nearly 288 mA h g−1. The ability to reach the high manganese oxidation state is related to both the initial tetrahedral coordination of Mn and the observed distortion/tilting of the BO3 units to accommodate the contraction of the Mn–O bonds upon oxidation. Molecular dynamics (MD) simulations indicate fast three-dimensional lithium diffusion in line with the good rate performance observed.
1. Introduction
The implementation of layered LiCoO2 as the cathode in rechargeable lithium-ion batteries heralded the revolution in portable electronics. Since then, the search for alternative cathode materials has generated considerable research activity,1–6 particularly for large-scale applications such as electric vehicles or grid storage. Significant interest has focused on materials such as olivine-structured LiFePO4,1–5,7 where the strong binding in the polyanion unit leads to a stable framework with long cycle life and high safety. Further polyanionic framework systems have been explored, and several promising candidates have been identified, including: Li2MSiO4,8,9 LiMSO4F,10–12 Li2MPO4F,13 Li2MP2O7,14 and Li2M(SO4)215,16 (M = Fe, Mn, Ni).The borate family of cathode materials LiMBO317–25 offer high capacities due to the low mass of the borate polyanion. Yamada et al.17 demonstrated capacities of about 190 mA h g−1 for the monoborate system LiFeBO3 (theoretical capacity 220 mA h g−1), which is considerable compared to LiCoO2 and LiFePO4 with theoretical capacities of 272 and 170 mA h g−1 respectively.7,26 More recently, the new borate system Li7Mn(BO3)3 with a rare tetrahedral Mn coordination environment was discovered27 (Fig. 1), which displays an extremely large theoretical capacity of ≈288 mA h g−1 upon extraction of 3 lithium ions per formula unit. After preparation of nano-composite electrodes, the material was found to deliver first charge and discharge capacities of about 280 and 154 mA h g−1 respectively, and was subsequently cycled in the range 4.7–1.7 V at 10 mA g−1 h−1 with moderate capacity losses.27 The first charge capacity corresponds to an unusually high oxidation of manganese from MnII up to MnV.
However, such redox behaviour in this system is not fully understood. Indeed, knowledge of the fundamental solid-state properties at the atomic scale is required to better understand the factors influencing the electrochemical behaviour of Li7Mn(BO3)3. In this study, well-established atomistic simulation28–30 and density functional theory31–37 (DFT) techniques are employed to examine key issues related to point defects, Mn redox chemistry and lithium diffusion. This computational study will provide useful insights into this promising manganese borate system, and may trigger renewed interest into the related class of lithium-rich electrode materials.
2. Methodology
Since this study employs well-established atomistic and DFT techniques, which are described in detail elsewhere,4,36,37 only a general outline will be given here. The interatomic potentials comprise a long-range Coulombic term and a short-range component representing Pauli repulsion and van der Waals interactions, represented by Buckingham potentials28 of the form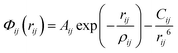 | (1) |
Lithium diffusion at finite temperature was modelled using molecular dynamics (MD) with DL_POLY40 (v4.05). An 8 × 7 × 6 supercell, containing 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939 atoms, was employed. 10% lithium vacancies were introduced at random to give a composition of Li6.3Mn(BO3)3. To maintain charge neutrality, a corresponding excess charge was distributed across all the manganese ions. The system was allowed to equilibrate for 1 ns, with the main production runs performed with a 2 fs time step for almost 1 ns. The calculations were conducted at temperatures in the range of 325–1025 K at intervals of 100 K using the NPT ensemble with a Berendsen thermostat.41 It is worth noting that such large supercells and long time-scales are not yet accessible by ab initio methods. Such potentials-based MD methods are well established in the simulation of ion diffusion in lithium battery materials.42–50
939 atoms, was employed. 10% lithium vacancies were introduced at random to give a composition of Li6.3Mn(BO3)3. To maintain charge neutrality, a corresponding excess charge was distributed across all the manganese ions. The system was allowed to equilibrate for 1 ns, with the main production runs performed with a 2 fs time step for almost 1 ns. The calculations were conducted at temperatures in the range of 325–1025 K at intervals of 100 K using the NPT ensemble with a Berendsen thermostat.41 It is worth noting that such large supercells and long time-scales are not yet accessible by ab initio methods. Such potentials-based MD methods are well established in the simulation of ion diffusion in lithium battery materials.42–50
DFT calculations used the plane wave code VASP51 (v5.3.5). The basis set was converged against the stress, instead of the forces, due to its higher sensitivity to an under-converged basis set. A cutoff energy of 800 eV with a k-point mesh density larger than 0.04 Å−1 was required to adequately converge the stress (3 × 3 × 3 grid). PAW pseudopotentials52,53 and the PBEsol exchange–correlation functional54,55 were used. Calculations of various spin configurations found the ferromagnetic state to be favourable. To account for the strong correlation effects associated with the manganese d-electrons, a DFT+U methodology was used, with an effective Hubbard Ueff = U − J = 5.1 eV (J = 1.0 eV); this value is in agreement with previous theoretical studies of Mn-based cathode materials.56
DFT-based methods are well-established in examining lithium insertion/extraction properties of electrode materials,4,32 and have been successfully applied to predict trends in cell voltages. Upon deriving the correct delithiated structure, the average open circuit voltage can be calculated using:
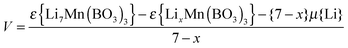 | (2) |
3. Results and discussion
3.1. Structure and intrinsic defect chemistry
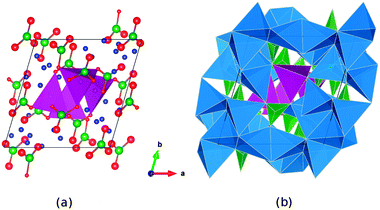
The triclinic Li7Mn(BO3)3 compound has previously been presented as a new structure type of space group![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) ,27 and contains Mn2+ species in an unusual tetrahedral coordination environment. The lithium ions sit inside a range of different LiOx polyhedra with x = 3, 4, 5. The structure (Fig. 1) comprises pillars of MnO4 tetrahedra linked via borate groups and extending along the c-axis. Around these pillars expands a complex framework of edge- and vertex-sharing lithium polyhedra, enclosing additional borate units.
,27 and contains Mn2+ species in an unusual tetrahedral coordination environment. The lithium ions sit inside a range of different LiOx polyhedra with x = 3, 4, 5. The structure (Fig. 1) comprises pillars of MnO4 tetrahedra linked via borate groups and extending along the c-axis. Around these pillars expands a complex framework of edge- and vertex-sharing lithium polyhedra, enclosing additional borate units.
The starting point of the computer modelling study was to reproduce the experimentally observed crystal structure. The interatomic potential parameters used in this work are presented in Table 1. A direct comparison of the calculated and experimental unit cell parameters is presented in Table 2, which shows deviations from experiment within 3% and in most cases much less. There were several structural complexities to be dealt with while developing the potential model. The first is a lithium split site,27 which has to be modelled explicitly in the simulation, removing the inversion centre. Another challenge was posed by the wide range of individual boron– and lithium–oxygen bond lengths (d(B–O) = 1.31–1.43 Å, d(Li–O) = 1.87–2.21 Å).27 Despite the complexity, the potentials-based and DFT simulations were able to reproduce the observed crystal structure.
| Interaction | A (eV) | ρ (Å) | C (eV Å6) |
|---|---|---|---|
| Li+–O2− | 638.712146 | 0.290560 | 0.00 |
| Mn2+–O2− | 2580.723796 | 0.277521 | 0.00 |
| B3+–O2− | 539.797394 | 0.340031 | 0.00 |
| O2−–O2− | 22764.3 | 0.149 | 46.94 |
| Expt. | Calc. (potentials) | Calc. (DFT) | |
|---|---|---|---|
| a/Å | 8.3234 | 8.2814 | 8.3015 |
| b/Å | 9.1952 | 9.4215 | 9.1935 |
| c/Å | 11.248 | 11.539 | 11.216 |
| α/° | 71.495 | 69.926 | 71.639 |
| β/° | 79.525 | 79.953 | 79.686 |
| γ/° | 71.368 | 71.193 | 71.400 |
| Li–O/Å | 1.99 | 2.03 | 1.98 |
| Mn–O/Å | 2.05 | 2.07 | 2.06 |
| B–O/Å | 1.38 | 1.31 | 1.39 |
Atomic-scale insight into the defect chemistry of cathode materials is essential to better understand their electrochemical performance. The determination of formation energies of Frenkel- and Schottky-type defects in the Li7Mn(BO3)3 compound required the calculation and subsequent combination of a series of isolated point defect (vacancy and interstitial) energies. A general Kröger–Vink representation of the relevant defect equations is given below:
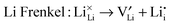 | (3) |
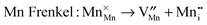 | (4) |
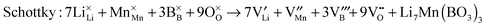 | (5) |
In addition, the Li/Mn “anti-site” pair defect was investigated, which involves a Li+ ion (radius 0.76 Å) and a Mn2+ ion (radius 0.83 Å) exchanging positions, according to:
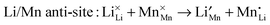 | (6) |
This type of defect is worth considering because Li/M anti-site or cation exchange effects have been observed in other polyanionic materials such as LiFePO4.28 Such disorder can inhibit long-range lithium migration in systems with low dimensional lithium-ion diffusion.
The formation energies of all these types of intrinsic defects are presented in Table 3, from which several conclusions can be drawn. First, the high energies associated with the occurrence of Mn Frenkel and Schottky defects suggest that such intrinsic disorder is not significant in this system. Second, the most favourable types of defect in Li7Mn(BO3)3 are predicted to be the Li/Mn anti-site pair and Li Frenkel disorder, with the low energy of the cation intersite exchange being in line with calculations in an earlier study of LiFePO4.28 The concentration of anti-site disorder would be temperature sensitive and consequently depend on experimental synthesis conditions. Finally, the low formation energies of lithium interstitial defects indicate a certain degree of flexibility of the lithium framework, which is an interesting property for an intercalation system.
3.2. Mn redox activity
Stable MnV oxides are relatively rare. Examples include Li3MnO4,57,58 Ba3Mn2O8,59 brownmillerite60 Ba2In2−xMnxO5−x and a number of Mn-doped apatite and spodiosite arsenates, phosphates and vanadates.61–64 In all these compounds a tetrahedral MnO43− coordination environment is observed. One rationale behind this is that the small size of the MnV ion (ionic radius 0.47 Å) makes octahedral coordination unfavourable. From ligand field theory58,63 it is known that coordination has a strong influence on the redox chemistry. The t2 and e energy levels of the d-orbitals in tetrahedral coordination are high in energy and closely spaced. Oxidation from Mn4+ to Mn5+ can occur almost as readily as oxidation from Mn3+ to Mn4+. By contrast, in octahedral coordination, the eg and t2g orbitals are lower in energy and more widely spaced. Significant energy is required to oxidise Mn4+ to form octahedrally coordinated Mn5+. For this reason there are no stable MnV oxides reported with manganese in octahedral coordination. For battery applications this suggests that to reach higher oxidation states of manganese, and hence higher capacities, the parent structure must contain tetrahedrally coordinated manganese prior to lithium extraction.Such a tetrahedral Mn coordination environment is found in Li7Mn(BO3)3 and it facilitates the oxidation of manganese from MnII up to MnV. The first charge capacity has been reported as ∼280 mA h g−1, corresponding to the removal of around three lithium ions per formula unit.27
A key issue in transition metal redox chemistry is “redox stress”: as the transition metal is oxidised the transition metal to oxygen bonds shorten and introduce stress into the structure which can cause severe distortion. It was suggested27 that in Li4Mn(BO3)3 the Mn oxidation states as high as +5 may be stabilised by the borate network compensating for redox stress. To investigate this unusual redox activity, ab initio DFT calculations were carried out on both the lithiated and delithiated structures. The calculated and experimental unit cell parameters and mean bond lengths of the lithiated structure are given in Table 2 and show good agreement with experiment, with differences within 0.8% of experiment.
Using the computed total energies of both the lithiated and the delithiated structures, it is possible to calculate the voltage for the following reaction (employing eqn (2)):
| Li7MnII(BO3)3 → Li4MnV(BO3)3 + 3Li+ | (7) |
To further understand the stabilisation of such an unusually high redox state, the DFT structural data was analysed. It has been suggested that distortions within the BO3 framework could be present to accommodate the redox stress.27 To examine this, the Baur distortion coefficient65
 | (8) |
| Compound | Mean B–O bond length/Å | Mean Mn–O bond length/Å | B–O distortion coefficient × 10−2 |
|---|---|---|---|
| Li7Mn(BO3)3 | 1.39 | 2.06 | 1.2 |
| Li4Mn(BO3)3 | 1.39 | 1.95 | 5.3 |
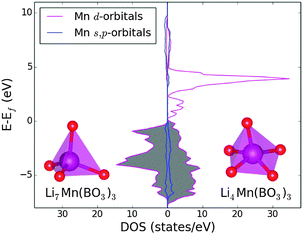
The changes in the Mn polyhedra are also important. In most polyanionic systems, oxidation of the transition metal leads to large contractions of the M–O bonds (M = Fe, Mn, Co, Ni). For example, in the Li2Mn(SO4)2 material the Mn–O mean bond length in the MnO6 octahedra decreases by ≈7% during oxidation from MnII to MnIII.33 Here, the mean bond length contracts by ≈5% during much greater oxidation, from MnII to MnV (Table 4). This suggests that less stress is introduced into the system upon oxidation of tetrahedrally coordinated Mn. However, there are major changes to the Mn coordination as lithium is removed and the BO3 units tilt and rotate. The result is that half of the Mn polyhedra become square pyramidal or trigonal bipyramidal (delithiated structure presented in Fig. 2). This has a significant effect on the electronic structure. To illustrate this, the electronic density of states (DOS) has been computed and is presented in Fig. 3. For Li7Mn(BO3)3 the DOS contains a large band gap of around 5 eV, consistent with the known insulating behaviour and as expected for a tetrahedral crystal field splitting. In Li4Mn(BO3)3, however, the band gap is not present since the unoccupied d-states are shifted up in energy. The change in coordination from tetrahedral to pyramidal thus removes the crystal field splitting. An interesting consequence of this is that Li7Mn(BO3)3 is predicted to change from electronically insulating to (semi)-metallic on delithiation to form Li4Mn(BO3)3.
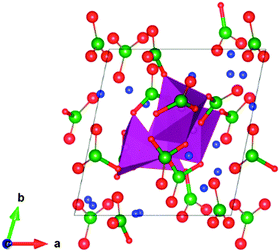 | ||
| Fig. 2 Calculated (DFT) delithiated crystal structure of Li4Mn(BO3)3 seen along [001]; key: O-red, B-green, Li-blue, Mn polyhedra-violet. | ||
These significant coordination changes in the Mn polyhedra could partly explain the capacity loss of almost 50% reported after the first cycle27 since they may prevent the structure from re-admitting all lithium ions upon discharge. A number of other factors could also cause the capacity fade, including structural disintegration, amorphisation and thermal decomposition via the release of O2. For example, recent work by Ceder et al.66 has suggested that in transition metal borates the temperature at which O2 is released drops from around 500 °C for transition metals in a +3 oxidation state to around 250 °C for transition metals in a +4 oxidation state. It seems likely that for MnV the O2 release temperature could be even lower, perhaps within the typical operating temperature of the battery, which warrants further study as well as possible disproportionation57 of MnV into other oxidation states.
To summarise, although it is difficult to isolate the impact of individual structural features upon the voltage, it would seem that the initial tetrahedral coordination of Mn together with the distortion and tilting offered by the BO3 units both act to minimise the redox stress and allow for higher Mn oxidation states to be stabilised; this allows more lithium to be extracted and higher electrode capacities to be reached. However, changes in the Mn coordination environment may inhibit subsequent lithium intercalation, in line with the dramatic capacity loss observed on first discharge.27
3.3. Lithium-ion diffusion
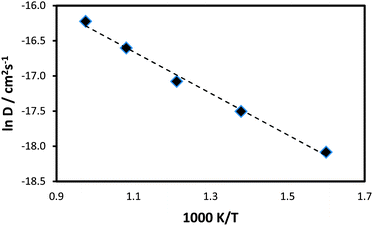
Knowledge of Li-ion transport properties is vital for a better understanding of electrode kinetics in potential cathode materials. In this study, MD calculations over long simulation time scales were performed for the Li7Mn(BO3)3 system for a range of temperatures.First, the mean squared displacements (MSDs), 〈[r(t)]2〉, of lithium ions have been calculated. Examples of these are presented in Fig. S1 (ESI†) and indicate significant lithium-ion diffusion in this system. The lithium ion diffusion coefficient (DLi) was determined from the MSD data for a number of different temperatures. There is currently no experimental conductivity data available for this system. However, the calculated DLi value, of the order of 10−9 cm2 s−1 at 325 K, is in agreement with other electrode materials, such as the conventional cathode LiCoO2 and its solid solution derivative Li(Ni,Mn,Co)O2, for which experimental lithium diffusion coefficients between 10−11 and 10−8 cm2 s−1 have been reported for comparable temperatures.67–70
The data is presented as an Arrhenius plot (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D vs. 1/T) in Fig. 4, from which an estimation of the migration activation energy (Eact) can be derived. The resulting activation energy of 0.25 eV suggests considerable Li-ion mobility in this system, which is in line with its good rate capability found by experimental investigations.27
D vs. 1/T) in Fig. 4, from which an estimation of the migration activation energy (Eact) can be derived. The resulting activation energy of 0.25 eV suggests considerable Li-ion mobility in this system, which is in line with its good rate capability found by experimental investigations.27
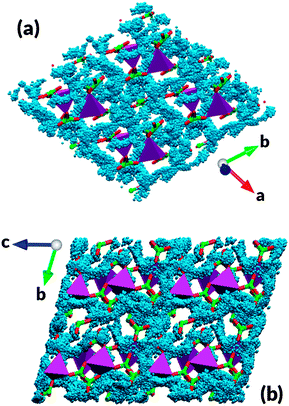
A key property of any electrode material is the dimensionality of lithium diffusion. Systems with lithium movement constrained to 1D channels often need careful control of particle morphology to reduce the influence of blocking defects on the electrode rate capability and systems with 3D lithium migration offer advantages. Scatter or density plots of the locations of Li ions during MD simulations are a powerful tool to visualize the most frequently traversed trajectories inside the lattice. Density plots of a section of the simulation cell are shown in Fig. 5. The diffuse distribution of lithium ion positions, overlapping to form a coherent network of migration paths expanding in all three dimensions, indicates the presence of 3D lithium diffusion in the Li7Mn(BO3)3 cathode material. Observation of the lithium motion in Li7Mn(BO3)3 reveals that the diffusion is cooperative whereby the motion of one lithium ion affects nearby ions causing several ions to move in each event, which might be a consequence of the high lithium density in this material. Finally, as noted, Li/Mn anti-site pairs are expected to be present in the compound. These anti-site defects are not expected to significantly inhibit long-range lithium migration since the 3D network of diffusion trajectories allows lithium ions to bypass “blocked” migration pathways and substantially diminishes the impact of such disorder on the electrode's rate capability.
4. Conclusions
This study of the Li-rich battery material Li7Mn(BO3)3 has employed well-established atomistic simulation and DFT techniques to provide deeper fundamental insight into the defect and redox chemistry, and the mechanisms of lithium diffusion. The main findings can be summarized as follows:(1) A new interatomic potential model successfully reproduces the observed complex structure of Li7Mn(BO3)3 with its unusual tetrahedral Mn2+ coordination. The most favourable intrinsic defects are Li/Mn anti-site pairs, where Li+ and Mn2+ ions exchange positions, and Li Frenkel disorder, indicating a certain degree of flexibility of the lithium framework. The degree of disorder would be sensitive to synthesis conditions and thermal history.
(2) Molecular dynamics (MD) simulations reveal a low migration activation energy (≈0.25 eV) and 3D lithium diffusion. These results are consistent with the good rate capability found by electrochemical measurements. The presence of a coherent 3D network of migration pathways reduces the influence of “channel blocking” anti-site defects.
(3) For the lithium extraction process from Li7Mn(BO3)3 to Li4Mn(BO3)3 DFT calculations derive a cell voltage of 4.1 V, in good agreement with the experimental voltage during first charge (≈4 V). The results indicate the activation of the unusual MnV redox state. On lithium extraction to form Li4Mn(BO3)3 a 5% contraction of the Mn–O bonds is found, together with distortion and tilting of the BO3 units, which relieves the redox stress and allows the higher oxidation state (and higher capacity) to be reached. However, during this lithium extraction, half of the Mn tetrahedra become square pyramidal or trigonal bipyramidal; these structural rearrangements may impede subsequent insertion of lithium back into the structure and could be the cause of the significant capacity loss observed after the first cycle.
Acknowledgements
We thank the EPSRC (programme grant EP/K016288/1), the MCC/Archer consortium (EP/L000202) and the ERASMUS scheme for supporting this work.References
- M. Armand and J. M. Tarascon, Nature, 2008, 451, 652 CrossRef CAS PubMed.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587 CrossRef CAS.
- B. L. Ellis, K. T. Lee and L. F. Nazar, Chem. Mater., 2010, 22, 691 CrossRef CAS.
- M. S. Islam and C. A. Fisher, Chem. Soc. Rev., 2014, 43, 185 RSC.
- C. Masquelier and L. Croguennec, Chem. Rev., 2013, 113, 6552 CrossRef CAS PubMed.
- V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243 CAS.
- A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, J. Electrochem. Soc., 1997, 144, 1188 CrossRef CAS PubMed.
- A. Nyten, A. Abouimrane, M. Armand, T. Gustafsson and J. O. Thomas, Electrochem. Commun., 2005, 7, 156 CrossRef CAS PubMed.
- M. S. Islam, R. Dominko, C. Masquelier, C. Sirisopanaporn, A. R. Armstrong and P. G. Bruce, J. Mater. Chem., 2011, 21, 9811 RSC.
- N. Recham, J. N. Chotard, L. Dupont, C. Delacourt, W. Walker, M. Armand and J. M. Tarascon, Nat. Mater., 2010, 9, 68 CrossRef CAS PubMed.
- R. Tripathi, T. N. Ramesh, B. L. Ellis and L. F. Nazar, Angew. Chem., Int. Ed., 2010, 49, 8738 CrossRef CAS PubMed.
- G. Rousse and J. M. Tarascon, Chem. Mater., 2014, 26, 394 CrossRef CAS.
- B. L. Ellis, W. R. M. Makahnouk, Y. Makimura, K. Toghill and L. F. Nazar, Nat. Mater., 2007, 6, 749 CrossRef CAS PubMed.
- S. Nishimura, M. Nakamura, R. Natsui and A. Yamada, J. Am. Chem. Soc., 2010, 132, 13596 CrossRef CAS PubMed.
- M. Reynaud, M. Ati, B. C. Melot, M. T. Sougrati, G. Rousse, J. N. Chotard and J. M. Tarascon, Electrochem. Commun., 2012, 21, 77 CrossRef CAS PubMed.
- J. M. Clark, C. Eames, M. Reynaud, G. Rousse, J. N. Chotard, J. M. Tarascon and M. S. Islam, J. Mater. Chem. A, 2014, 2, 7446 CAS.
- A. Yamada, N. Iwane, Y. Harada, S. Nishimura, Y. Koyama and I. Tanaka, Adv. Mater., 2010, 22, 3583 CrossRef CAS PubMed.
- V. Legagneur, Y. An, A. Mosbah, R. Portal, A. Le Gal La Salle, A. Verbaere, D. Guyomard and Y. Piffard, Solid State Ionics, 2001, 139, 37 CrossRef CAS.
- A. Abouimrane, M. Armand and N. Ravet, Proc. – Electrochem. Soc., 2003, 20, 15 Search PubMed.
- L. Chen, Y. Zhao, X. An, J. Liu, Y. Dong, Y. Chen and Q. Kuang, J. Alloys Compd., 2010, 494, 415 CrossRef CAS PubMed.
- J. C. Kim, C. J. Moore, B. Kang, G. Hautler, A. Jain and G. Ceder, J. Electrochem. Soc., 2011, 158, A309 CrossRef CAS PubMed.
- Y. Janssen, D. S. Middlemiss, S. H. Bo, C. P. Grey and P. G. Khalifah, J. Am. Chem. Soc., 2012, 134, 12516 CrossRef CAS PubMed.
- S. Afyon, D. Kundu, F. Krumeich and R. Nesper, J. Power Sources, 2013, 224, 145 CrossRef CAS PubMed.
- L. Tao, G. Rousse, J. N. Chotard, L. Dupont, S. Bruyère, D. Hanzel, G. Mali, R. Dominko, S. Levasseur and C. Masquelier, J. Mater. Chem. A, 2014, 2, 2060 CAS.
- Y. S. Lee and H. Lee, Electron. Mater. Lett., 2014, 10, 253 CrossRef CAS.
- K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, Mater. Res. Bull., 1980, 15, 783 CrossRef CAS.
- S. Afyon, M. Wörle and R. Nesper, Angew. Chem., Int. Ed., 2013, 52, 12541 CrossRef CAS PubMed.
- M. S. Islam, D. J. Driscoll, C. A. J. Fisher and P. R. Slater, Chem. Mater., 2005, 17, 5085 CrossRef CAS.
- A. R. Armstrong, N. Kuganathan, M. S. Islam and P. G. Bruce, J. Am. Chem. Soc., 2011, 133, 13031 CrossRef CAS PubMed.
- A. Whiteside, C. A. J. Fisher, S. C. Parker and M. S. Islam, Phys. Chem. Chem. Phys., 2014, 16, 21788 RSC.
- C. Eames, A. R. Armstrong, P. G. Bruce and M. S. Islam, Chem. Mater., 2012, 24, 2155 CrossRef CAS.
- F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 23 Search PubMed.
- C. Eames, J. M. Clark, G. Rousse, J.-M. Tarascon and M. S. Islam, Chem. Mater., 2014, 26, 3672 CrossRef CAS.
- A. R. Armstrong, C. Lyness, P. M. Panchmatia, M. S. Islam and P. G. Bruce, Nat. Mater., 2011, 10, 223 CrossRef CAS PubMed.
- C. Eames and M. S. Islam, J. Am. Chem. Soc., 2014, 136, 16270 CrossRef CAS PubMed.
- A. Walsh, A. A. Sokol and C. R. A. Catlow, Computational Approaches to Energy Materials, Wiley-Blackwell, 2013 Search PubMed.
- W. Koch and M. C. Holthausen, A Chemist's Guide to Density Functional Theory, Wiley-VCH Verlag GmbH, Weinheim, 2001 Search PubMed.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291 CrossRef CAS PubMed.
- C. R. A. Catlow, Computer Modelling, Inorganic Crystallography, Academic Press, San Diego, 1997 Search PubMed.
- W. Smith and T. R. Forester, J. Mol. Graphics, 1996, 14, 136 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684 CrossRef CAS PubMed.
- S. Lee and S. S. Park, J. Phys. Chem. C, 2012, 116, 6486 Search PubMed.
- C. Tealdi, C. Spreafico and P. Mustarelli, J. Mater. Chem., 2012, 22, 24870 RSC.
- S. Adams and R. P. Rao, Solid State Ionics, 2011, 184, 57 CrossRef CAS PubMed.
- M. Vijayakumar, S. Kerisit, K. M. Rosso, S. D. Burton, J. A. Sears, Z. Yang, G. L. Graff, J. Liu and J. Hu, J. Power Sources, 2011, 196, 2211 CrossRef CAS PubMed.
- S. E. Boulfelfel, G. Seifert and S. Leoni, J. Mater. Chem., 2011, 21, 16365 RSC.
- M. Salanne, M. Marrocchelli and G. W. Watson, J. Phys. Chem. C, 2012, 116, 18618 CAS.
- P. M. Panchmatia, A. R. Armstrong, P. G. Bruce and M. S. Islam, Phys. Chem. Chem. Phys., 2014, 16, 21114 RSC.
- M. Schroeder, C. Eames, D. A. Tompsett, G. Lieser and M. S. Islam, Phys. Chem. Chem. Phys., 2013, 15, 20473 RSC.
- A. Chroneos, D. Parfitt, J. A. Kilner and R. W. Grimes, J. Mater. Chem., 2010, 20, 266 RSC.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef.
- F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235121 CrossRef.
- G. Meyer and R. Hoppe, Z. Anorg. Allg. Chem., 1976, 424, 249 CrossRef CAS PubMed.
- J. A. Saint, M. M. Doeff and J. Reed, J. Power Sources, 2007, 172, 189 CrossRef CAS PubMed.
- M. T. Weller and S. J. Skinner, Acta Cryst., 1999, C55, 154 CAS.
- P. Jiang, J. Li, A. Ozarowski, A. W. Sleight and M. Subramanian, Inorg. Chem., 2013, 52, 1349 CrossRef CAS PubMed.
- D. A. Grisafe and F. A. Hummel, J. Solid State Chem., 1970, 2, 160 CrossRef CAS.
- D. Reinen and R. Allman, Z. Anorg. Allg. Chem., 1986, 542, 71 CrossRef CAS PubMed.
- H. Lachwa and D. Reinen, Inorg. Chem., 1989, 8, 1021 Search PubMed.
- M. H. Whitmore, H. R. Verdún and D. J. Singel, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 11479 CrossRef CAS.
- W. H. Baur, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 1195 CrossRef CAS.
- A. Jain, G. Hautier, S. P. Ong, S. Dacek and G. Ceder, Phys. Chem. Chem. Phys., 2015, 17, 5942 RSC.
- Q. S. Wang, J. H. Sun, C. H. Chen and X. M. Zhou, J. Therm. Anal. Calorim., 2008, 92, 563 CrossRef CAS.
- M. Park, X. Zhang, M. Chung, G. B. Less and A. M. Sastry, J. Power Sources, 2010, 195, 7904 CrossRef CAS PubMed.
- P. Jeevan-Kumar, K. Jayanth-Babu, O. M. Hussain and C. M. Julien, Solid State Ionics, 2013, 19, 47 Search PubMed.
- W. C. West, J. Soler, M. C. Smart, B. V. Ratnakumar, S. Firdosy, V. Ravi, M. S. Anderson, J. Hrbacek, E. S. Lee and A. Manthiram, J. Electrochem. Soc., 2011, 158, A883 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp02711j |
| This journal is © the Owner Societies 2015 |