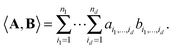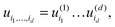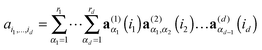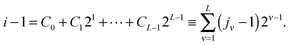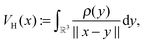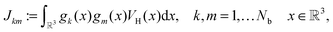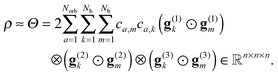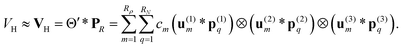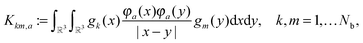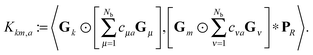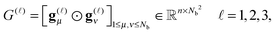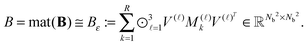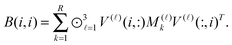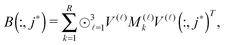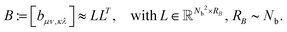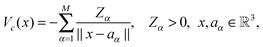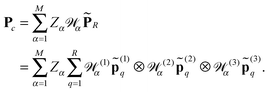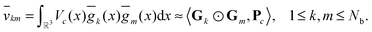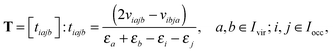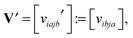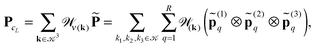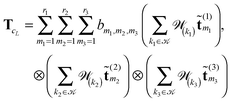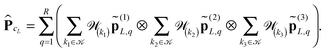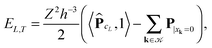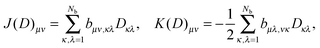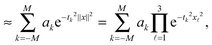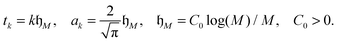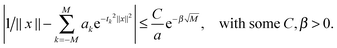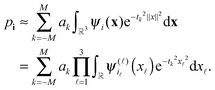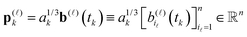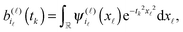Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tensor numerical methods in quantum chemistry: from Hartree–Fock to excitation energies
Venera
Khoromskaia
ab and
Boris N.
Khoromskij
b
aMax-Planck-Institute for Dynamics of Complex Systems, Magdeburg, Germany. E-mail: vekh@mis.mpg.de
bMax-Planck Institute for Mathematics in the Sciences, Inselstr. 22-26, Leipzig, Germany
First published on 28th May 2015
Abstract
We resume the recent successes of the grid-based tensor numerical methods and discuss their prospects in real-space electronic structure calculations. These methods, based on the low-rank representation of the multidimensional functions and integral operators, first appeared as an accurate tensor calculus for the 3D Hartree potential using 1D complexity operations, and have evolved to entirely grid-based tensor-structured 3D Hartree–Fock eigenvalue solver. It benefits from tensor calculation of the core Hamiltonian and two-electron integrals (TEI) in O(n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n) complexity using the rank-structured approximation of basis functions, electron densities and convolution integral operators all represented on 3D n × n × n Cartesian grids. The algorithm for calculating TEI tensor in a form of the Cholesky decomposition is based on multiple factorizations using algebraic 1D “density fitting” scheme, which yield an almost irreducible number of product basis functions involved in the 3D convolution integrals, depending on a threshold ε > 0. The basis functions are not restricted to separable Gaussians, since the analytical integration is substituted by high-precision tensor-structured numerical quadratures. The tensor approaches to post-Hartree–Fock calculations for the MP2 energy correction and for the Bethe–Salpeter excitation energies, based on using low-rank factorizations and the reduced basis method, were recently introduced. Another direction is towards the tensor-based Hartree–Fock numerical scheme for finite lattices, where one of the numerical challenges is the summation of electrostatic potentials of a large number of nuclei. The 3D grid-based tensor method for calculation of a potential sum on a L × L × L lattice manifests the linear in L computational work, O(L), instead of the usual O(L3
n) complexity using the rank-structured approximation of basis functions, electron densities and convolution integral operators all represented on 3D n × n × n Cartesian grids. The algorithm for calculating TEI tensor in a form of the Cholesky decomposition is based on multiple factorizations using algebraic 1D “density fitting” scheme, which yield an almost irreducible number of product basis functions involved in the 3D convolution integrals, depending on a threshold ε > 0. The basis functions are not restricted to separable Gaussians, since the analytical integration is substituted by high-precision tensor-structured numerical quadratures. The tensor approaches to post-Hartree–Fock calculations for the MP2 energy correction and for the Bethe–Salpeter excitation energies, based on using low-rank factorizations and the reduced basis method, were recently introduced. Another direction is towards the tensor-based Hartree–Fock numerical scheme for finite lattices, where one of the numerical challenges is the summation of electrostatic potentials of a large number of nuclei. The 3D grid-based tensor method for calculation of a potential sum on a L × L × L lattice manifests the linear in L computational work, O(L), instead of the usual O(L3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L) scaling by the Ewald-type approaches.
L) scaling by the Ewald-type approaches.
1 Introduction
The problems of numerical modeling the many-particle interactions in large molecular systems, lattice structured metallic clusters and crystals, proteins and nanomaterials are the most challenging tasks in modern computational physics and chemistry. The traditional approaches for these multidimensional problems are restricted to the concepts which have well recognized limitations for computations with higher accuracy and for larger non-periodic molecular systems, as well as for efficient calculation of excited states. Recent advances in numerical analysis for multidimensional problems and significant achievements in high performance computing suggest new creative approaches to these problems.The Hartree–Fock (HF) equation governed by the 3D integral-differential operator29,67 is one of the basic models for ab initio calculation of the ground state energy of molecular systems. It is a strongly nonlinear eigenvalue problem (EVP) in a sense, that one should solve the equation in a self-consistent way when the integral part of the governing operator depends on the solution itself. Multiple strong singularities in the electron density of a molecule due to nuclear cusps impose strong requirements on the accuracy of calculations.
Commonly used numerical methods for solution of the Hartree–Fock equation are based on the analytical computation of the arising two-electron integrals (convolution type integrals in ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3) in the problem adapted naturally separable Gaussian-type bases,1,17 by using erf-function expansions. This rigorous approach resulted in a number of efficient implementations which are widely used in computational quantum chemistry. The success of the analytical integration methods stems from the big amount of precomputed information based on the physical insight including the construction of problem adapted atomic orbitals basis sets and elaborate nonlinear optimization for calculation of density fitting basis. The known limitations of this approach appear due to a strong dependence of the numerical efficiency on the size and quality of the chosen Gaussian basis sets, that might be crucial for larger molecular clusters and heavier atoms.
3) in the problem adapted naturally separable Gaussian-type bases,1,17 by using erf-function expansions. This rigorous approach resulted in a number of efficient implementations which are widely used in computational quantum chemistry. The success of the analytical integration methods stems from the big amount of precomputed information based on the physical insight including the construction of problem adapted atomic orbitals basis sets and elaborate nonlinear optimization for calculation of density fitting basis. The known limitations of this approach appear due to a strong dependence of the numerical efficiency on the size and quality of the chosen Gaussian basis sets, that might be crucial for larger molecular clusters and heavier atoms.
The intention to replace or assist the analytical calculations for the Hartree–Fock problem by a data-sparse grid-based numerical schemes has a long history. First success was the grid-based numerical method for the diatomic molecules in ref. 66, though this approach was not feasible to compact (3D) molecules. The wavelet multiresolution schemes13 capable for the accurate representation of nuclear cusps, have been applied to electronic structure simulations,21,28,63 and recently this approach was further advanced due to achievements in high performance supercomputing.8,18,20,63 However, due to extensive computational resources, the entirely wavelet-based or sparse-grid approaches24,74 are limited so far only to rather small atomic systems with few electrons.2 Tensor hyper-contraction decompositions in density fitting schemes have been analyzed in ref. 32 and 59.
The newly developed tensor-structured numerical methods, both the name and the concept, appeared during the work on the grid-based tensor approach to the solution of the 3D Hartree–Fock problem.38,39,42 The central point is the representation of d-variate functions and integral/differential operators on large n⊗d grids and their approximation in the low-rank tensor formats, which allows numerical calculations in O(dn) complexity instead of O(nd) by conventional methods.
In this paper we summarize the main benefits of the tensor numerical methods in electronic structure calculations, and discuss further prospects of this approach in several directions, such as
(a) Algebraic directional density fitting and tensor factorization of the two-electron integrals in Hartree–Fock calculations;
(b) Tensor decompositions in the MP2 energy correction, and in calculation of excitation energies based on the Bethe–Salpeter equation;
(c) Fast tensor summation of electrostatic potentials on large 3D lattices for efficient calculation of the Fock matrix in the case of lattice-structured systems;
(d) Fast method for calculation of the interaction energy of a large number of Coulombic potentials on a 3D lattice.
Notice that basic rank-structured tensor formats such as the canonical (PARAFAC/CANDECOMP) and Tucker tensor decompositions have been since long used in the computer science for the quantitative analysis of correlations in the experimental multidimensional data arrays in data processing and chemometrics, see ref. 12, 50 and 64 and references therein. In 2006 the exceptional properties of the Tucker decomposition for the discretized multidimensional functions have been revealed in ref. 36 and 38, where it was proven that for a class of function-related tensors the approximation error of the Tucker decomposition decays exponentially with respect to the Tucker rank. This gives the opportunity to represent the discretized multidimensional functions and integral (convolution) operators in an algebraically separable form and thus reduce the numerical treatment of the multidimensional transforms to 1D operations. It was shown that the number of vectors in such a representation depends only logarithmically on the size of the d-dimensional grid, O(nd), used for discretization of multivariate functions.
The above results have led to the idea to calculate the Hartree potential and the Coulomb and exchange operators by numerical quadratures39 using Gaussian-type basis functions discretized on 3D Cartesian grids and the fast tensor-product convolution.35 In this way, the efficient low-rank canonical tensor representation to the Newton kernel was an essential contribution.7 To reduce the initial rank of the electron density, that is quadratically proportional to the number of GTO basis functions, the canonical-to-Tucker tensor transform was invented,38,39 which made computations for large tensor grids and extended molecules tractable (even in Matlab).
The initial version of tensor-structured algorithms for solving Hartree–Fock equation employed the 3D grid-based calculation of the Coulomb and exchange integral operators “on-the-fly”, thus avoiding precomputation and storage of the TEI tensor.40,42 In particular, it was shown that tensor calculus allows to reduce the 3D convolution integrals to combinations of 1D convolutions, and 1D Hadamard and scalar products. Besides, these results promoted spreading of the tensor-structured methods in the community of numerical analysis,22,27,37 and further development of the tree-tensor formats like tensor-train57 and hierarchical Tucker representations.26
Further development of tensor methods in electronic structure calculations was due to the fast algorithm for the grid-based computation of the TEI tensor44 in O(Nb3) storage in the number of basis functions Nb. The fourth order TEI tensor is calculated in a form of the Cholesky factorization by using the algebraic 1D “density fitting” scheme, which applies to the product basis functions. Imposing the low-rank tensor representation of the product basis functions and the Newton convolving kernel all discretized on n × n × n Cartesian grid, the 3D integral transforms are calculated in O(n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n) complexity. Given the factorized TEI, the update of the Column and exchange parts in the Fock matrix reduces to the cheap algebraic operations. Other steps are tensor calculation of the core Hamiltonian and the efficient MP2 energy correction scheme,45 which all together gave rise to the black-box Hartree–Fock solver.46
n) complexity. Given the factorized TEI, the update of the Column and exchange parts in the Fock matrix reduces to the cheap algebraic operations. Other steps are tensor calculation of the core Hamiltonian and the efficient MP2 energy correction scheme,45 which all together gave rise to the black-box Hartree–Fock solver.46
Due to the grid representation of basis functions basis sets are now not restricted to Gaussian-type orbitals and allowed to be any well-separable function defined on a grid. The tensor-based Hartree–Fock solver is competitive in computational time and accuracy with the standard packages based on analytical calculation of integrals. High accuracy is attained owing to easy calculations on large 3D grids up to n3 = 1018, so that the resolution with mesh size h of the order of atomic radii, 10−4 Å, is possible.
Motivated by tensor decompositions in the MP2 scheme, the new approach for calculation of the excited states in the framework of the Bethe–Salpeter equation was recently introduced,6 that employs the reduced basis method in combination with low-rank tensor approximations.
Further developments of the tensor methods in multi-particle simulations are focused on the large lattice structures in a box and nearly periodic systems, for which the tensor approach may reduce computational costs dramatically.48 One of the challenging problems in the numerical treatment of the crystalline-type molecular clusters is summation of a large number of electrostatic potentials distributed on a non-periodic (finite) lattice. The novel grid-based method for summation of the long-range potentials in the canonical and Tucker formats47,49 works on L × L × L lattices with the computational cost O(L) instead of O(L3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L) by the traditional Ewald-type methods.19 The required precision is guaranteed by employing large 3D Cartesian grids for representation of potentials. The method remains efficient for lattices with non-rectangular geometries and in the presence of multiple defects.48,49
L) by the traditional Ewald-type methods.19 The required precision is guaranteed by employing large 3D Cartesian grids for representation of potentials. The method remains efficient for lattices with non-rectangular geometries and in the presence of multiple defects.48,49
In particular, we present fast tensor method for the summation of the long-range interaction potentials on a 3D lattice by using the assembled vectors of their canonical and Tucker tensor representations. The important application of this approach to calculation of interaction energy of the Coulombic potentials on a lattice with sub-linear cost in the lattice size is described in detail.
The rest of the paper is organized as follows. In Section 2, we overview the basic tensor formats and show why the orthogonal Tucker tensor decomposition, originating from computer science and data processing, became useful for the treatment of the multidimensional functions and operators in numerical analysis. In particular, Sections 2.3 and 2.4 discuss the matrix product states (tensor train) formats and the novel quantics tensor approximation method, respectively, while Section 2.5 addresses the basic tensor-structured multilinear algebra operations. Section 3 describes tensor calculus of the multidimensional convolution transform on examples of the Hartree potential (Section 3.1) and the TEI tensor (Section 3.2), and recalls the main building blocks in the tensor-based black-box Hartree–Fock solver. Section 4 shows benefits of the tensor approach in MP2 calculations and in calculation of the lowest part of the excitation energies in the framework of the Bethe–Salpeter equation. Section 5 describes the benefits of tensor methods in applications to lattice-type molecular systems. Appendix discusses some computational details on the Canonical-to-Tucker tensor transform, the Galerkin discretization scheme for the nonlinear Hartree–Fock equation, and the basics of the low-rank canonical tensor representation for the Newton kernel.
2 Rank-structured tensor representations of discretized functions and operators
In this section we discuss shortly why the rank-structured tensors, which were traditionally used in experimental data processing, appeared to be useful for the separable representation of multivariate functions and operators represented on tensor product grids. There is a numerous literature on application of the canonical and Tucker tensor decompositions in chemometrics and data processing, see ref. 12, 31, 50, 64 and 68 and references therein. In the recent decade the class of matrix product states type tensor formats became popular in the simulations of quantum spin systems and quantum molecular dynamics. We refer to ref. 37 and 62 for recent literature surveys on commonly used tensor formats.2.1 Canonical and Tucker tensor formats
We consider a tensor of order d, as a real multidimensional array A = [ai1,…,id] ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n1×…×nd numbered by a d-tuple index set,† with multi-index notation i = (i1,…,id), i
n1×…×nd numbered by a d-tuple index set,† with multi-index notation i = (i1,…,id), i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∈ {1,…,n
∈ {1,…,n![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) },
}, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1,…,d. It is an element of the linear vector space
= 1,…,d. It is an element of the linear vector space ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n1×⋯×nd equipped with the Euclidean scalar product,
n1×⋯×nd equipped with the Euclidean scalar product,Euclidean vectors and matrices are the special case of dth order tensors. For a general tensor, the required storage scales exponentially in the dimension, n1n2…nd, (the so-called “curse of dimensionality”). To get rid of exponential scaling in the dimension, one can apply the rank-structured separable representations of multidimensional tensors. The simplest separable element is given by rank-1 canonical tensor,
U = u(1)⊗⋯⊗u(d) ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n1×⋯×nd, n1×⋯×nd, |
requiring only n1 +⋯+ nd numbers to store it.
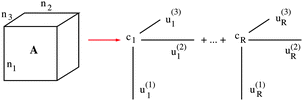
A tensor in the R-term canonical format is defined by
 | (1) |
 are normalized vectors, and R is called the canonical rank of a tensor. It is convenient to introduce the so-called side matrices
are normalized vectors, and R is called the canonical rank of a tensor. It is convenient to introduce the so-called side matrices 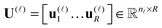 ,
, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, 2, 3, obtained by concatenation of the canonical vectors
= 1, 2, 3, obtained by concatenation of the canonical vectors 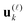 , k = 1,…,R. Now the storage cost is bounded by dRn. For d ≥ 3 computation of the canonical rank of a tensor U, i.e. the minimal number R in representation (1) and the respective decomposition, is an N–P hard problem. In the case d = 2 the representation (1) is merely a rank-R matrix.
, k = 1,…,R. Now the storage cost is bounded by dRn. For d ≥ 3 computation of the canonical rank of a tensor U, i.e. the minimal number R in representation (1) and the respective decomposition, is an N–P hard problem. In the case d = 2 the representation (1) is merely a rank-R matrix.
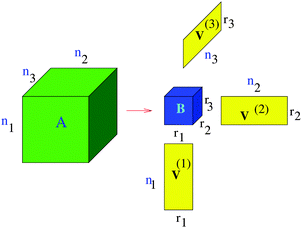
We say that a tensor A is represented in the rank-r orthogonal Tucker format with the rank parameter r = (r1,…,rd), if
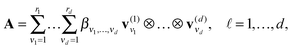 | (2) |
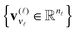 represents the set of orthonormal vectors, and β = [βν1,…,νd] ∈
represents the set of orthonormal vectors, and β = [βν1,…,νd] ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) r1×⋯×rd is the Tucker core tensor. The storage cost for the Tucker tensor is bounded by drn + rd, r = max r
r1×⋯×rd is the Tucker core tensor. The storage cost for the Tucker tensor is bounded by drn + rd, r = max r![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) . Often the equivalent notation for the Tucker tensor format is used,
. Often the equivalent notation for the Tucker tensor format is used,| A = β ×1V(1) ×2V(2) ×⋯×dV(d), | (3) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) denotes the contraction along the mode
denotes the contraction along the mode ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and orthogonal matrices V(
and orthogonal matrices V(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) incorporate the set of vectors
) incorporate the set of vectors 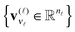 . In the case d = 2, the orthogonal Tucker decomposition is equivalent to the singular value decomposition (SVD) of a rectangular matrix. Fig. 1 and 2 visualizes the canonical and Tucker tensors in the case d = 3. Canonical tensor decomposition leads to an ill-posed problem and, up to our best knowledge, there are no robust algebraic algorithms for the canonical approximation of an arbitrary tensor. For some classes of analytic functions, the explicit low-rank approximation can be constructed in analytic form by using sinc-quadrature approximation to the Laplace transform. The robust methods for Tucker decomposition are based on the orthogonal projections using the higher order singular value decomposition16 (HOSVD) that is the generalization of the singular value decomposition (SVD) of matrices.
. In the case d = 2, the orthogonal Tucker decomposition is equivalent to the singular value decomposition (SVD) of a rectangular matrix. Fig. 1 and 2 visualizes the canonical and Tucker tensors in the case d = 3. Canonical tensor decomposition leads to an ill-posed problem and, up to our best knowledge, there are no robust algebraic algorithms for the canonical approximation of an arbitrary tensor. For some classes of analytic functions, the explicit low-rank approximation can be constructed in analytic form by using sinc-quadrature approximation to the Laplace transform. The robust methods for Tucker decomposition are based on the orthogonal projections using the higher order singular value decomposition16 (HOSVD) that is the generalization of the singular value decomposition (SVD) of matrices.
The rank-structured decomposition (approximation) of multidimensional tensors provides means for the separation of variables in the discretized representation of multivariate functions and operators, and thus the possibility to substitute multidimensional algebraic transforms by univariate operations. Notice that in the computer science community these possibilities were restricted to moderate-dimensional tensors of small mode size (with rather large rank parameters) obtained from the experimental data sets.
2.2 Tucker decomposition for function related tensors. Canonical-to-Tucker approximation
It was proven and shown in numerical simulations,36,38 that the rank of the (fixed accuracy) Tucker approximation to some function related tensors depends only logarithmically on the size of the discretization grid. In particular, it was shown that for tensors resulting from the grid discretization of physically relevant multidimensional functions one can find algebraically a reduced subspace in each mode of the 3D tensor, which lead to a separable approximation of the function by a tensor product of a small number of vectors.For a given continuous function f: Ω → ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) ,
, 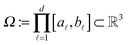 , we introduced the function related 3rd order tensor, obtained by Galerkin discretization in a volume box using n × n × n 3D Cartesian grid. In particular, the low-rank tensor approximations were calculated for functions of the Slater type f(x) = exp
, we introduced the function related 3rd order tensor, obtained by Galerkin discretization in a volume box using n × n × n 3D Cartesian grid. In particular, the low-rank tensor approximations were calculated for functions of the Slater type f(x) = exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (−α||x||), Newton kernel
(−α||x||), Newton kernel 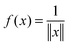 , Yukawa potential
, Yukawa potential 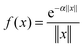 , and the Helmholtz potential
, and the Helmholtz potential 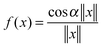 , x ∈
, x ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3.
3.
Numerical tests demonstrated that the error of the rank-r (with r = (r,r,r)) Tucker approximation applied to these third order tensors decays exponentially with respect to the Tucker rank r. Moreover, for fixed approximation error, the Tucker rank r scales as O(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n) for above mentioned functions.35
n) for above mentioned functions.35
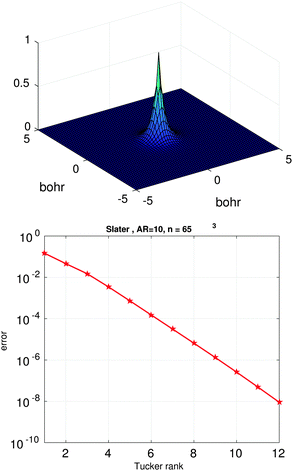
Fig. 3 (bottom) shows the exponential convergence of the Tucker tensor approximation in the Tucker rank r of the Slater function in the relative Frobenius norm, 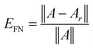 . Fig. 3 and 4 demonstrate that the exponential decay of approximation error is nearly the same for both a single potential and for a sum of the same potentials distributed in nodes of a cubic lattice. This property of the Tucker decomposition will be further gainfully applied to the fast lattice summation of interaction potentials.
. Fig. 3 and 4 demonstrate that the exponential decay of approximation error is nearly the same for both a single potential and for a sum of the same potentials distributed in nodes of a cubic lattice. This property of the Tucker decomposition will be further gainfully applied to the fast lattice summation of interaction potentials.
 | ||
| Fig. 3 The Tucker approximation error in the Frobenius norm vs. the Tucker rank r for a single Slater function. | ||
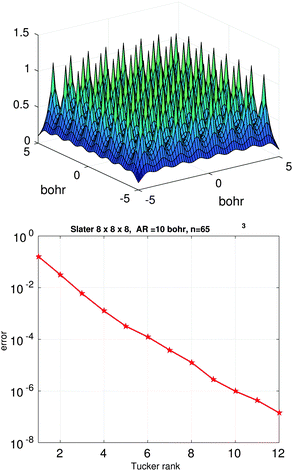 | ||
| Fig. 4 The Tucker approximation error in the Frobenius norm vs. the Tucker rank r for a sum of 512 Slater potentials over the cubic 8 × 8 × 8 lattice (right). | ||
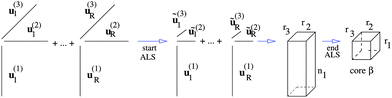
Motivated by these observations, we invented the canonical-to-Tucker (C2T) decomposition for function related tensors,38 based on the reduced higher order singular value decomposition (RHOSVD) (Theorem 2.5, ref. 39). The canonical-to-Tucker algorithm (see Appendix) combined with the Tucker-to-canonical transform serves for reducing the ranks of canonical tensors with large R. Fig. 5 in its ALS part shows the algorithmic step for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, which is repeated for every mode
= 1, which is repeated for every mode ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, 2, 3 (see Appendix). The computational work for the multigrid tensor decomposition C2T algorithm introduced in ref. 39 exhibits linear complexity scaling with respect to all input parameters, O(Rnr).
= 1, 2, 3 (see Appendix). The computational work for the multigrid tensor decomposition C2T algorithm introduced in ref. 39 exhibits linear complexity scaling with respect to all input parameters, O(Rnr).
The multigrid Tucker decomposition algorithm applied to full format tensors39 leads to the complexity scaling O(n3), whereas its standard version (commonly used HOSVD algorithm in computer science) scales as O(n4), becoming intractable even for moderate sizes of tensors.
We conclude by notice that the optimized Tucker and canonical tensor approximations can be computed by the alternating least square (ALS) iteration with initial guess obtained by HOSVD/RHOSVD approximations.
2.3 Matrix product states/tensor train format
The product-type representation of dth order tensors, which is called in the physical literature as the matrix product states (MPS) decomposition (or more generally, tensor network states models), was introduced and successfully applied in DMRG quantum computations,62,69,73 and, independently, in quantum molecular dynamics as the multilayer (ML) MCTDH methods.54,71 MPS type representations reduce the storage complexity to O(dr2N), where r is the maximal rank parameter.In the recent years the various versions of the MPS-type tensor approximations were discussed and further investigated in mathematical literature including the hierarchical dimension splitting,36 the tensor train (TT),14,57 the quantics-TT (QTT),34 as well as the hierarchical Tucker representation,26 which belongs to the class of tensor network states model.
The TT format is the particular form of MPS type factorization in the case of open boundary conditions. For a given rank parameter r = (r0,…,rd), the rank-r TT format contains all elements A = [ai1,…,id] ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n1×⋯×nd, which can be represented as the contracted products of 3-tensors, that in the index notation takes a form,
n1×⋯×nd, which can be represented as the contracted products of 3-tensors, that in the index notation takes a form,
| ≡ A(1)(i1)A(2)(i2)…A(d)(id), |
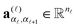 , (
, (![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1,…,d), or equivalently by the vector-valued r
= 1,…,d), or equivalently by the vector-valued r![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) × r
× r![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) +1 matrices,
+1 matrices, 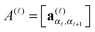 , (i.e., 3-tensors), cf.(2). The latter representation is written in the matrix product form, explaining the notion MPS, where A(
, (i.e., 3-tensors), cf.(2). The latter representation is written in the matrix product form, explaining the notion MPS, where A(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )(i
)(i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) is r
) is r![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) −1 × r
−1 × r![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) matrix.
matrix.
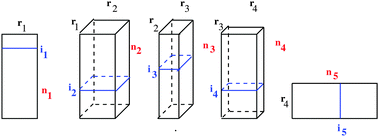
Fig. 6 illustrates the TT representation of a 5th-order tensor, where each particular entry is factorized as a product of five matrices, ai1,i2,…,i5 = A(1)(i1)A(2)(i2)…A(5)(i5), where, for example, A(2)(i2) ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) r1×r2.
r1×r2.
The rank-structured tensor formats like canonical, Tucker and MPS/TT-type decompositions also apply to matrices. For example, the d-dimensional FFT matrix over N⊗d grid can be implemented on the rank-k tensor with the linear-logarithmic cost O(dkN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log2
log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N), due to the rank-1 factorized representation
N), due to the rank-1 factorized representation
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (d)N = (F(1)N ⊗ I…⊗ I)(I ⊗ F(2)N…⊗ I)…(I ⊗ I…⊗ F(d)N) ≡ F(1)N ⊗…⊗ F(d)N, (d)N = (F(1)N ⊗ I…⊗ I)(I ⊗ F(2)N…⊗ I)…(I ⊗ I…⊗ F(d)N) ≡ F(1)N ⊗…⊗ F(d)N, |
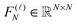 represents the univariate FFT matrix along mode
represents the univariate FFT matrix along mode ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) .
.
2.4 Quantics tensor approximation of functional vectors
In the case of large mode size, the asymptotic storage cost for a class of function related N–d tensors can be reduced to O(d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N) by using quantics-TT (QTT) tensor approximation method.34 The QTT-type approximation of an N-vector with N = 2L, L ∈
N) by using quantics-TT (QTT) tensor approximation method.34 The QTT-type approximation of an N-vector with N = 2L, L ∈ ![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) , is defined as the tensor decomposition (approximation) in the canonical, TT or more general formats applied to a tensor obtained by the dyadic folding (reshaping) of the target vector to an L-dimensional 2 ×⋯× 2 data array (tensor) that is thought as an element of the L-dimensional quantized tensor space.
, is defined as the tensor decomposition (approximation) in the canonical, TT or more general formats applied to a tensor obtained by the dyadic folding (reshaping) of the target vector to an L-dimensional 2 ×⋯× 2 data array (tensor) that is thought as an element of the L-dimensional quantized tensor space.
In the vector case, i.e. for d = 1, a vector x = [xi] ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) N, with N = 2L, is reshaped to its quantics (quantized) image in
N, with N = 2L, is reshaped to its quantics (quantized) image in 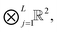 by dyadic folding,
by dyadic folding,
Next figure visualizes the QTT approximation process.
Suppose that the quantics image for an N-vector, i.e. an element of L-dimensional quantized tensor space 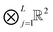 with L = log2
with L = log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N, can be represented (approximated) by the low-rank canonical or TT tensor of order L, thus introducing the QTT approximation of an N-vector. Given rank parameters {rk} (k = 1,…,L), the QTT approximation of an N-vector requires a number of representation parameters estimated by
N, can be represented (approximated) by the low-rank canonical or TT tensor of order L, thus introducing the QTT approximation of an N-vector. Given rank parameters {rk} (k = 1,…,L), the QTT approximation of an N-vector requires a number of representation parameters estimated by
2r2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log2 log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N ≪ N, where rk ≤ r, k = 1,…,L, N ≪ N, where rk ≤ r, k = 1,…,L, |
The power of QTT approximation method is explained by the theoretical substantiation of the QTT approximation properties discovered in ref. 34 and establishing the perfect rank-r decomposition for the wide class of function-related tensors obtained by sampling continuous functions over uniform (or properly refined) grid:
• r = 1 for complex exponents,
• r = 2 for trigonometric functions and plain-waves,
• r ≤ m + 1 for polynomials of degree m,
• r is a small constant for wavelet functions, Gaussians, etc. all independently on the vector size N.
Notice that the notion quantics (or quantized) tensor approximation (with a shorthand QTT) originally introduced in 2009, see ref. 34, is reminiscent of the entity “quantum of information”, that mimics the minimal possible mode size (n = 2) of the quantized image.
Concerning the matrix case, it was first found in ref. 56 by numerical tests that in some cases the dyadic reshaping of an N × N matrix with N = 2L may lead to a small TT-rank of the resultant matrix rearranged to the tensor form. The efficient low-rank QTT representation for a class of discrete multidimensional elliptic operators (matrices) and their inverse was proven in ref. 33. Moreover, based on the QTT approximation, the important algebraic matrix operations like FFT, convolution and wavelet transforms can be implemented by superfast algorithms in O(log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N)-complexity, see survey paper37 and references therein.
N)-complexity, see survey paper37 and references therein.
2.5 Rank-structured tensor operations in 1D complexity
The rank-structured tensor representation provides 1D complexity of multilinear operations with multidimensional tensors. Rank-structured tensor representation provides fast multi-linear algebra with linear complexity scaling in the dimension d.For given canonical tensors A and B as in (1), with ranks Ra and Rb, respectively, their Euclidean scalar product can be computed by univariate operations
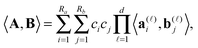 | (4) |
The Hadamard (entrywise) product of tensors A, B is defined by Y = [yi1,…,id]: = A ⊙ B, where yi1,…,id = ai1,…,idbi1,…,id. For canonical tensors A and B given in form (1), the Hadamard product is calculated in O(dnRaRb) operations by 1D entrywise products of vectors,
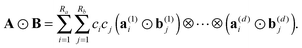 | (5) |
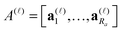 and
and 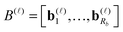 ,
,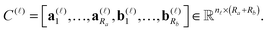 | (6) |
In electronic structure calculations, the 3D convolution transform with the Newton kernel, 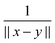 , is the most computationally expensive operation. The tensor method to compute convolution over large n × n × n Cartesian grids in O(n
, is the most computationally expensive operation. The tensor method to compute convolution over large n × n × n Cartesian grids in O(n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n) complexity was introduced in ref. 35. Given canonical tensors A, B, their convolution product is represented by the sum of tensor products of 1D convolutions,
n) complexity was introduced in ref. 35. Given canonical tensors A, B, their convolution product is represented by the sum of tensor products of 1D convolutions,
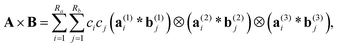 | (7) |
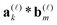 denotes the univariate convolution product of n-vectors. The cost of tensor convolution in both storage and time is estimated by O(RaRbn
denotes the univariate convolution product of n-vectors. The cost of tensor convolution in both storage and time is estimated by O(RaRbn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n). The resulting algorithm considerably outperforms the conventional 3D FFT-based approaches of complexity O(n3
n). The resulting algorithm considerably outperforms the conventional 3D FFT-based approaches of complexity O(n3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n), see numerics in ref. 39.
n), see numerics in ref. 39.
The sequences of rank-structured operations on matrices and vectors normally lead to the increase of tensor ranks, usually being multiplied or added after each operation. The necessary rank reduction in the Tucker and MPS type formats can be implemented by stable algorithms based on the higher order SVD. In the physical community the HOSVD-type algorithms are known since longer as the Schmidt decomposition.62,69,70 In the case of canonical tensors the rank reduction can be performed by the RHOSVD algorithm based on the canonical-to-Tucker and then Tucker-to-canonical transforms described and analyzed in ref. 38, 39 and 49 (see Section 2.2 and Appendix), which demonstrated the stable behavior for most of examples in the Hartree–Fock calculations we considered so far. The stability conditions for the RHOSVD have been discussed in ref. 39 and 49.
3 Tensor calculus for the Hartree–Fock equation
3.1 Calculation of multi-dimensional integrals
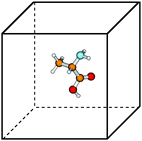
Tensor-structured calculation of the multidimensional convolution integral operators with the Newton kernel have been introduced in ref. 39, 40 and 42, where on the examples of the Hartree and exchange operators in the Hartree–Fock equation, it was shown that calculation of the 3D and 6D convolution integrals can be reduced to a combination of 1D Hadamard products, 1D convolutions and 1D scalar products.The molecule is embedded in a certain fixed computational box Ω = [−b,b]3 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3, as in Fig. 7.‡ For a given discretization parameter n ∈
3, as in Fig. 7.‡ For a given discretization parameter n ∈ ![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) , we use the equidistant n × n × n tensor grid ω3,n = {xi}, i ∈
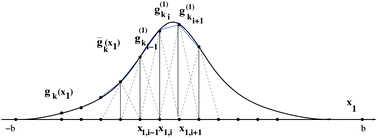
, we use the equidistant n × n × n tensor grid ω3,n = {xi}, i ∈ ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) := {1,…,n}3, with the mesh-size h = 2b/(n + 1). In calculations of integral terms, the Gaussian basis functions gk(x), x ∈
:= {1,…,n}3, with the mesh-size h = 2b/(n + 1). In calculations of integral terms, the Gaussian basis functions gk(x), x ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3, are approximated by sampling their values at the centers of discretization intervals, as in Fig. 8, using one-dimensional piecewise constant basis functions
3, are approximated by sampling their values at the centers of discretization intervals, as in Fig. 8, using one-dimensional piecewise constant basis functions 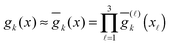 ,
, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, 2, 3, yielding their rank-1 tensor representation,
= 1, 2, 3, yielding their rank-1 tensor representation,
Gk = g(1)k ⊗ g(2)k ⊗ g(3)k ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n×n×n, k = 1,…,Nb. n×n×n, k = 1,…,Nb. | (8) |
Let us consider the tensor calculation of the Hartree potential
where the electron density,
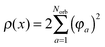 , is represented in terms of molecular orbitals
, is represented in terms of molecular orbitals 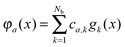 . Given the discrete tensor representation of basis functions (8), the electron density is approximated using 1D Hadamard products of rank-1 tensors (instead of product of Gaussians),
. Given the discrete tensor representation of basis functions (8), the electron density is approximated using 1D Hadamard products of rank-1 tensors (instead of product of Gaussians),Further, the representation of the Newton kernel 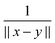 by a canonical rank-RN tensor7 is used (see Appendix for details),
by a canonical rank-RN tensor7 is used (see Appendix for details),
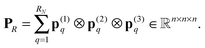 | (9) |
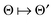 by several orders of magnitude, from Nb2/2 to Rρ ≪Nb2/2. Then the 3D tensor representation of the Hartree potential is calculated by using the 3D tensor product convolution, which is a sum of tensor products of 1D convolutions,
by several orders of magnitude, from Nb2/2 to Rρ ≪Nb2/2. Then the 3D tensor representation of the Hartree potential is calculated by using the 3D tensor product convolution, which is a sum of tensor products of 1D convolutions,The Coulomb matrix entries Jkm are obtained by 1D scalar products of VH with the Galerkin basis consisting of rank-1 tensors,
| Jkm ≈ 〈Gk ⊙ Gm,VH〉, k, m = 1,…Nb. |
The cost of 3D tensor product convolution is O(n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n) instead of O(n3
n) instead of O(n3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n) for the standard benchmark 3D convolution using the 3D FFT. Table 1 shows CPU times (s) for the Matlab computation of VH for H2O molecule39 on a SUN station using 8 Opteron Dual-Core/2600 processors (times for 3D FFT for n ≥ 1024 are obtained by extrapolation). C2T shows the time for the canonical-to-Tucker rank reduction. In a similar way, the algorithm for 3D grid-based tensor-structured calculation of 6D integrals in the exchange potential operator was introduced in ref. 40,
n) for the standard benchmark 3D convolution using the 3D FFT. Table 1 shows CPU times (s) for the Matlab computation of VH for H2O molecule39 on a SUN station using 8 Opteron Dual-Core/2600 processors (times for 3D FFT for n ≥ 1024 are obtained by extrapolation). C2T shows the time for the canonical-to-Tucker rank reduction. In a similar way, the algorithm for 3D grid-based tensor-structured calculation of 6D integrals in the exchange potential operator was introduced in ref. 40, 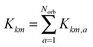 with
with
| n 3 | 10243 | 20483 | 40963 | 81923 | 163843 |
| FFT3 | ∼6000 | — | — | — | ∼2 years |
| C × C | 8.8 | 20.0 | 61.0 | 157.5 | 299.2 |
| C2T | 6.9 | 10.9 | 20.0 | 37.9 | 86.0 |
Here, the tensor product convolution is first calculated for each ath orbital, and then scalar products in canonical format yield the contributions to entries of the exchange Galerkin matrix from the a-th orbital.
These algorithms were employed in the first tensor-structured solver using 3D grid-based evaluation of the Coulomb and exchange matrices in 1D complexity at every step of SCF EVP iteration.41,42 A sequence of dyadically refined 3D Cartesian grids was used for reducing time in first iterations, with an ε convergence criterion for switching to larger grids. This is a nonstandard computational scheme avoiding calculation of the two-electron integrals. The accuracy for small molecules like H2O and CH4 was of the order of 10−4 Hartree. Though time performance of this solver was not compatible with the standard Hartree–Fock packages it was the first proof of concept for the tensor numerical methods.
3.2 3D grid-based calculation of the two-electron integrals
The basic tensor-structured Hartree–Fock solver employs the factorized 3D grid-based calculation of the two-electron integrals tensor, B = [bμνκλ], in the form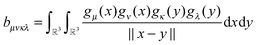 | (10) |
| = 〈Gμ ⊙ Gν,PR * (Gκ ⊙ Gλ)〉n⊗3, |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) representing on the grid the full set of canonical vectors composing the products of the Gaussian basis functions, {Gμ ⊙ Gν},
) representing on the grid the full set of canonical vectors composing the products of the Gaussian basis functions, {Gμ ⊙ Gν},where in most of our Hartree–Fock calculations grids of size n3 = 32 × 103 or n3 = 64 × 103 have been used. It was found that the large matrices G(
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) of size n × Nb2 (e.g. Nb2 = 40
) of size n × Nb2 (e.g. Nb2 = 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 for Alanine amino acid) can be approximated with high accuracy by low rank matrices with the rank parameter bounded by R
000 for Alanine amino acid) can be approximated with high accuracy by low rank matrices with the rank parameter bounded by R![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≤ Nb.44,45 The corresponding low-rank factorizations (“1D density fitting”) in the form (for
≤ Nb.44,45 The corresponding low-rank factorizations (“1D density fitting”) in the form (for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, 2, 3)
= 1, 2, 3)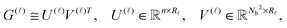 | (11) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )G(
)G(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )T (see ref. 44 and 45 for more details).
)T (see ref. 44 and 45 for more details).
Based on factorization (11), the number of convolutions in (10) is reduced dramatically from Nb2 to Nb at most (say from 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 200). In fact, using canonical factors from the rank-R canonical tensor PR representing the Newton kernel (9) (see (31) in Appendix) we, first, precompute the set of “convolution” matrices for every space variable
000 to 200). In fact, using canonical factors from the rank-R canonical tensor PR representing the Newton kernel (9) (see (31) in Appendix) we, first, precompute the set of “convolution” matrices for every space variable ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,
, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, 2, 3,
= 1, 2, 3,
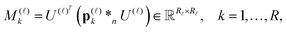 | (12) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ≤ Nb column vectors of the matrix
≤ Nb column vectors of the matrix 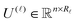 instead of Nb2/2 convolutions in the initial formulation.
instead of Nb2/2 convolutions in the initial formulation.
Given matrices 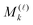 , then the resulting 4-th order TEI tensor is represented in a matrix form
, then the resulting 4-th order TEI tensor is represented in a matrix form
The above nonstandard factorization of the TEI matrix B allows to reduce dramatically the computational cost of the standard Cholesky factorization schemes3,5,30 applied to the reduced-rank symmetric positive definite matrix B. In fact, the low-rank Cholesky decomposition of B is calculated in the following sequence. First, the diagonal elements of B are calculated as
Then the selected columns of the matrix B, required for the rank-truncated Cholesky factorization scheme, are computed by the following fast tensor operations
This algorithm is much faster than the direct Cholesky decomposition of the matrix B with on-the-fly computation of the required column vectors.
Table 2 represents times (s) for 3D grid-based calculation of the directional density fitting and the TEI tensor (electron repulsion integrals) for H2O molecule in a box [−20,20]3 bohr3, performed in Matlab on a 2-Intel Xeon Hexa-Core/2677. Time for convolution integrals in (12) scales almost linearly in the 1D grid-size n as expected by theory.
| n 3 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3843 3843 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7683 7683 |
65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5363 5363 |
131![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0723 0723 |
| Mesh (bohr) | 0.0024 | 0.0012 | 6 × 10−4 | 3 × 10−4 |
| Had. prod. | 1.6 | 3.4 | 12 | 19 |
| Density fit. | 0.5 | 1.0 | 2.0 | 4.0 |
| 3D conv. time | 69 | 151 | 698 | 496 |
| Chol. time | 2.2 | 2.2 | 2.2 | 2.2 |
Note that the algorithm for fast tensor computation of TEI is described in detail for the case of rank-1 GTO basis functions in form (8). However, this approach can be also applied to basis sets with low separation rank, say, to Slater-type basis functions or some kind of agglomerated basis. The advantage of use the “more compressed” basis is the essential reduction in the number of basis functions, Nb, that enters to the size of TEI tensor in the fourth power. The payoff for such a reduction in the tensor size is the additional costs for calculation of the particular entries of TEI tensor in (10), since in that case the number of terms in tensor representation of the scalar products in (10) increases quadratically in the separation rank of basis functions. The resulting effect from implementation of the reduced basis sets (with larger separation ranks) depends on subsequent (post) Hartree–Fock calculations and it will be studied in detail in the forthcoming paper.
3.3 Core Hamiltonian
The Galerkin representation of the 3D Laplace operator in the nonlocal Gaussian basis {gk(x)}1≤k≤Nb, x ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3, leads to the fully populated matrix Ag = [akm] ∈
3, leads to the fully populated matrix Ag = [akm] ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nb×Nb. Tensor calculation of the matrix entries akm for the discrete Laplacian Ag in the separable Gaussian basis is reduced to 1D matrix operations46 involving the FEM Laplacian Δ3, defined on n × n × n grid,
Nb×Nb. Tensor calculation of the matrix entries akm for the discrete Laplacian Ag in the separable Gaussian basis is reduced to 1D matrix operations46 involving the FEM Laplacian Δ3, defined on n × n × n grid,| Δ3 = Δ1(1) ⊗ I(2) ⊗ I(3) + I(1) ⊗ Δ(2)1 ⊗ I(3) + I(1) ⊗ I(2) ⊗ Δ(3)1, |
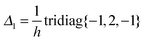 . Specifically, we have
. Specifically, we have| akm = 〈Δ3Gk,Gm〉, |
In the case of large n × n × n grids, this calculation can be implemented with logarithmic cost in n by using the low-rank QTT representation of the large matrix Δ3, see ref. 33, 43 and 46.
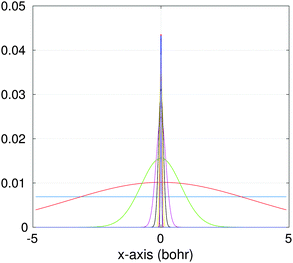 | ||
| Fig. 10 Several vectors of the canonical representation of the Newton kernel along one of variables. | ||
For tensor calculation of the nuclear potential operator
![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) α =
α = ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) (1)α ⊗
(1)α ⊗ ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) (2)α ⊗
(2)α ⊗ ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) (3)α, for shifting the reference Newton kernel
(3)α, for shifting the reference Newton kernel ![[P with combining tilde]](https://www.rsc.org/images/entities/b_char_0050_0303.gif) R ∈
R ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2n×2n×2n according to the coordinates of nuclei in a molecule (see Section 5 and Appendix). Then the resulting nuclear potential, Pc ∈ n×n×n, is obtained as a direct tensor sum of shifted potentials,46
2n×2n×2n according to the coordinates of nuclei in a molecule (see Section 5 and Appendix). Then the resulting nuclear potential, Pc ∈ n×n×n, is obtained as a direct tensor sum of shifted potentials,46This leads to the following representation of the Galerkin matrix, Vc = [![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) km], by tensor operations
km], by tensor operations
Fig. 10, shows several vectors of the canonical representation of the Coulomb kernel along one of variables. Fig. 11, represents the cross-section of the resulting nuclear potential Pc for C2H5OH molecule.
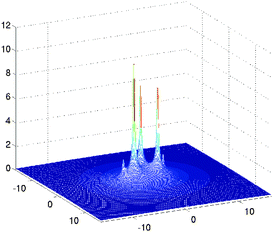 | ||
| Fig. 11 A sum of the nuclear potentials for ethanol molecule. Size of the computational box is given in bohr. | ||
3.4 Black-box tensor solver
The tensor-structured Hartree–Fock solver46 based on factorized calculation of the two-electron integrals44 includes efficient tensor implementation of the MP2 energy correction45 scheme. Though it is yet implemented in Matlab, its performance in time and accuracy is compatible with the standard packages based on analytical evaluation of the two-electron integrals. Due to 1D complexity of all calculations, it enables 3D grids of the size 1015, yielding mesh size of the order of atomic radii, 10−4 Å. That ensures high accuracy of calculations, which is controlled by the ε-ranks of tensor truncation.The solver works in a black-box way: input the grid-based basis-functions and coordinates of nuclei in a molecule and start the program. Calculation of TEI for H2O on grids 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7683 takes two minutes on a laptop. The time for TEI with n3 = 131
7683 takes two minutes on a laptop. The time for TEI with n3 = 131![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0723 for Alanine amino acid takes approximately one hour in Matlab, including incorporated density fitting.
0723 for Alanine amino acid takes approximately one hour in Matlab, including incorporated density fitting.
Next examples compare the results from benchmark Molpro program with calculations by the tensor-based solver by using the same Gaussian basis, but now discretized on 3D Cartesian grid. For all molecules we use the “cc-pVDZ” Gaussian basis set. The core Hamiltonian part in these calculations is taken from Molpro. Note that since in the tensor solver the density fitting is included in “blind” calculation of TEI, it is not easy to compare the CPU times of our calculations with those in “ab initio” procedure in the standard programs, because the density fitting step there is usually considered as off-line pre-computing.
Fig. 12, top, shows convergence to the ground state energy E0 in ab initio iterations for H2O molecule (cc-pVDZ-41), where TEI is computed on the 3D grid of size 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0723. Fig. 12, bottom presents the zoom of the last 20 iterations. The ground state energy from Molpro (E0 = 76.308 hartree) corresponding to the basis set cc-pVDZ-41 with 41 Gaussian-type basis functions is shown by the black dashed line.
0723. Fig. 12, bottom presents the zoom of the last 20 iterations. The ground state energy from Molpro (E0 = 76.308 hartree) corresponding to the basis set cc-pVDZ-41 with 41 Gaussian-type basis functions is shown by the black dashed line.
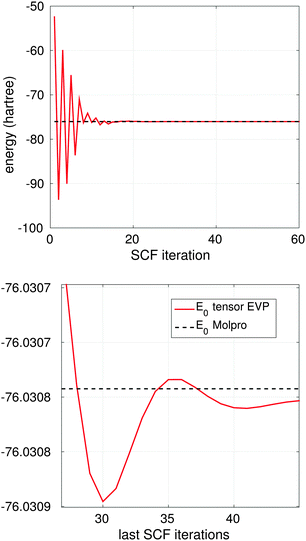 | ||
| Fig. 12 Top: convergence of the ground state energy to E0 in ab initio SCF Hartree–Fock iterations for H2O; bottom: zooming of final 20 iterations for H2O. | ||
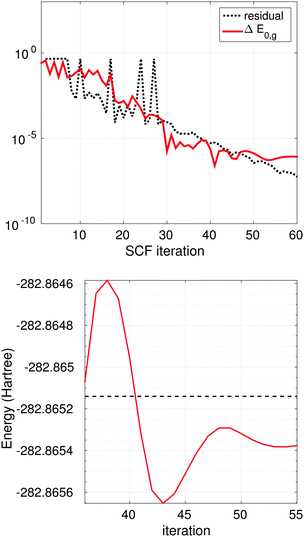
Fig. 13 (top) shows the SCF EVP iteration history for Glycine amino acid (cc-pVDZ-170), where dashed line indicates convergence of the residual and the red solid line shows convergence of the error ΔE0,g in ground state energy compared with the result from MOLPRO package72 with the same basis set,
| ΔE0,g = |E0,g − E0|/|E0|. | (13) |
Fig. 13 (bottom) illustrates the convergence of the ground state energy at final 20 iterations for Glycine, dashed line is the energy from Molpro.
The first row in Table 3 shows the number of orbitals and basis functions used in Hartree–Fock calculations for H2O (cc-pVDZ-41), H2O2 (cc-pVDZ-68), and C2H5NO2 (cc-pVDZ-170) molecules. Second row represents times (s) for one step of SCF iteration in ab initio solution of the Hartree Fock EVP. Next two rows show the relative difference in energy (13), for different grid sizes used in TEI calculations. This numerics demonstrates that in the case of fine enough spacial n × n × n-grids the accuracy in 7–8 digits (i.e. relative accuracy about 10−7–10−8) can be achieved for moderate size molecules up to small amino acids. All calculations are performed in the computational box of size [−20,20]3 bohr3. This tensor-based solver can be considered as the computational tool for trying the alternatives to Gaussian-type basis sets.
| H2O | H2O2 | C2H5NO2 | |
|---|---|---|---|
| N orb, Nb | 5; 41 | 9; 68 | 20; 170 |
| Time | 0.35 | 0.55 | 6.0 |
ΔE0,g, (65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5363) 5363) |
3.0 × 10−7 | 8.0 × 10−8 | 9.1 × 10−7 |
ΔE0,g, (131![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0723) 0723) |
1.4 × 10−7 | 3.9 × 10−8 | 8.0 × 10−7 |
4 From MP2 energy correction to excited states
4.1 MP2 correction scheme by using tensor formats
Given the set of Hartree–Fock molecular orbitals {Cp} and the corresponding energies {εp}, p = 1, 2,…,Nb, where {Ci} and {Ca} denote the occupied and virtual orbitals, respectively. First, one has to transform the TEI matrix B = [bμν,λσ], corresponding to the initial AO basis set, to those represented in the molecular orbital (MO) basis,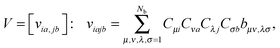 | (14) |
![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) v, i, j ∈
v, i, j ∈ ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) o, and
o, and ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) o:= {1,…,Norb},
o:= {1,…,Norb}, ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) v:= {Norb + 1,…,Nb}, with Norb denoting the number of occupied orbitals. In the following, we shall use the notation
v:= {Norb + 1,…,Nb}, with Norb denoting the number of occupied orbitals. In the following, we shall use the notation| Nv = Nb − Norb, Nov = NorbNv. |
V = LVLTV, LV ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nov×RB, Nov×RB, |
Given the tensor V = [viajb], the second order MP2 perturbation to the HF energy is calculated by
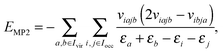 | (15) |
Introducing the so-called doubles amplitude tensor T,
| EMP2 = −〈V,T〉 = −〈V ⊙ T,1〉, |
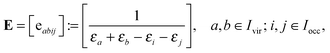 | (16) |
allows to decompose the doubles amplitude tensor T as follows
| T = T(1) + T(2) = 2V ⊙ E − V′ ⊙ E. | (17) |
Each term in the right-hand side in (17) can be treated separately by using rank-structured tensor decompositions of V and E, possibly combined with various symmetries and data sparsity. Numerical tests illustrating the tensor approach to the MP2 energy correction are presented in ref. 45.
4.2 Toward low-rank approximation of the Bethe–Salpeter equation for calculation of excitation energies
One of the commonly used approaches for calculation of the excited states in molecules and solids, along with the time-dependent DFT, is based on the solution of the Bethe–Salpeter equation (BSE), see for example.11,61 The BSE approach leads to the challenging computational task on the solution of the eigenvalue problem for determining the excitation energies ωn, governed by a large fully populated matrix of size O(Nov2) ≈ O(Nb2),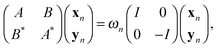 | (18) |
A = Δε + V − ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) , B = V − , B = V − ![[W with combining tilde]](https://www.rsc.org/images/entities/i_char_0057_0303.gif) , , |
Δε = [Δεia,jb] ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nov×Nov: Δεia,jb = (εa − εi)δijδab, Nov×Nov: Δεia,jb = (εa − εi)δijδab, |
![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) = [
= [![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) ia,jb] and
ia,jb] and ![[W with combining tilde]](https://www.rsc.org/images/entities/i_char_0057_0303.gif) = [
= [![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) ia,jb] are determined by permutation of the so-called static screened interaction matrix W = [wia,jb], via
ia,jb] are determined by permutation of the so-called static screened interaction matrix W = [wia,jb], via ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) ia,jb = wij,ab, and [
ia,jb = wij,ab, and [![[w with combining tilde]](https://www.rsc.org/images/entities/i_char_0077_0303.gif) ia,jb] = [wib,aj], respectively. In turn, the forth order tensor W = [wiajb] is constructed by certain linear transformations of the tensor V = [viajb], see ref. 11 and 61.
ia,jb] = [wib,aj], respectively. In turn, the forth order tensor W = [wiajb] is constructed by certain linear transformations of the tensor V = [viajb], see ref. 11 and 61.
A number of numerical methods for structured eigenvalue problems have been discussed in the literature.4,15,51,55
The tensor approach to the solution of the partial BSE eigenvalue problem for eqn (18) proposed in ref. 6 suggests to compute the reduced basis set by solving the simplified eigenvalue problem via the low-rank plus diagonal approximation to the matrix blocks A and B, and then solve spectral problem for the subsequent Galerkin projection of the initial system (18) to this reduced basis. This procedure relies entirely on multiplication of the simplified BSE matrix with vectors.
It was demonstrated on the examples of moderate size molecules6 that a small reduced basis set, obtained by separable approximation with the rank parameters of about several tens, allows to reveal several lowest excitation energies and respective excited states with the accuracy about 0.1–0.02 eV.
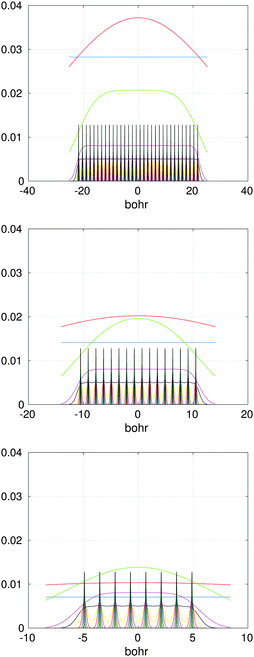
Fig. 14 illustrates the BSE energy spectrum of the NH3 molecule (based on HF calculations with cc-pDVZ-48 GTO basis) for the lowest Nred = 30 eigenvalues vs. the rank truncation parameter ε = 0.6 and 0.1, where the ranks of V and the BSE matrix block W are 4, 5 and 28, 30, respectively. For the choice ε = 0.6 and ε = 0.1, the error in the 1st (lowest) eigenvalue for the solution of the problem in reduced basis is about 0.11 eV and 0.025 eV, correspondingly. The CPU time in the laptop Matlab implementation of each example is about 5 s.
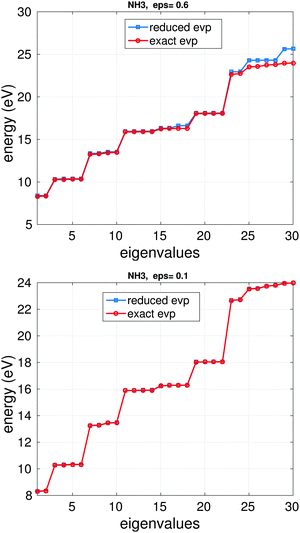 | ||
| Fig. 14 Comparison of m0 = 30 lower eigenvalues for the reduced and exact BSE systems for NH3 molecule: ε = 0.6, top; ε = 0.1, bottom. | ||
5 Tensor approach to simulation of large crystalline clusters
In this section, we briefly discuss the generalization of the tensor-based Hartree–Fock solver to the case of large lattice structured and periodic systems47,48 arising in the numerical modeling of crystalline, metallic and polymer type compounds.5.1 Fast tensor calculation of a lattice sum of interaction potentials
One of the challenges in the numerical treatment of large molecular systems is the summation of long-range potentials allocated on large 3D lattices.23,52,53,58 The conventional Ewald summation techniques based on a separate evaluation of contributions from the short- and long-range parts of the interaction potential exhibit O(L3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L) complexity scaling for a cubic L × L × L 3D lattice.
L) complexity scaling for a cubic L × L × L 3D lattice.
In the contrary, the main idea of the novel tensor summation method introduced in ref. 47 and 49 suggests to benefit from the low-rank tensor decomposition of the generating kernel approximated on the fine n × n × n representation grid in the 3D computational box ΩL. This allows to completely decouple the 3D sum into the three independent 1D summations, thus reducing drastically the numerical expenses. The resultant potential sum, which now requires only O(n) storage and O(nL) computational demands, is represented by a few assembled canonical/Tucker n-vectors of complicated shape (see Fig. 15), where n is the univariate grid size for a cubic 3D lattice.
For ease of exposition, we consider the electrostatic nuclear potential of a single hydrogen atom, 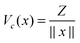 . Define the scaled unit cell, Ω0 = [0,b]3, of size b × b × b and consider a sum of a finite number of interaction potentials in a symmetric computational box
. Define the scaled unit cell, Ω0 = [0,b]3, of size b × b × b and consider a sum of a finite number of interaction potentials in a symmetric computational box
![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) 3, such that k
3, such that k![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∈
∈ ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) : =
: = ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) −∪
−∪![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) + for
+ for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, 2, 3 with
= 1, 2, 3 with 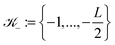 and
and 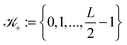 . Hence, we have ΩL = ∪k1,k2,k3 ∈
. Hence, we have ΩL = ∪k1,k2,k3 ∈ ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Ωk ∈
Ωk ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3.
3.
Recall that b = nh, where h > 0 is the fine mesh size that is the same for all spatial variables, and n is the number of grid points for each variable. We also define the accompanying domain 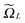 obtained by scaling of ΩL with the factor of 2,
obtained by scaling of ΩL with the factor of 2, 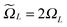 , and, similar to (31), introduce the respective rank-R reference (master) tensor
, and, similar to (31), introduce the respective rank-R reference (master) tensor
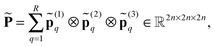 | (19) |
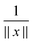 in
in 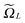 on a 2n × 2n × 2n representation grid with mesh size h.
on a 2n × 2n × 2n representation grid with mesh size h.
Let us consider a sum of single Coulomb potentials on a L × L × L lattice,
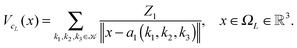 | (20) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n×n×n,
n×n×n,to the summation of directional vectors for the canonical decomposition of shifted single Newton kernels,47
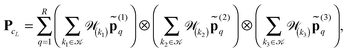 | (21) |
![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) ν(k) =
ν(k) = ![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) k1 ⊗
k1 ⊗![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) k2 ⊗
k2 ⊗![[scr W, script letter W]](https://www.rsc.org/images/entities/char_e536.gif) k3 is the shift-and-windowing (onto ΩL) separable transform along the k-grid. Remarkably that the rank of the resulting sum is the same as for the R-term canonical reference tensor (19) representing the single Newton kernel.
k3 is the shift-and-windowing (onto ΩL) separable transform along the k-grid. Remarkably that the rank of the resulting sum is the same as for the R-term canonical reference tensor (19) representing the single Newton kernel.
The numerical cost and storage size are bounded by O(RLn) and O(Rn), respectively, where n = n0L, and n0 is the grid size in the unit cell.
Fig. 15 presents the assembled canonical vectors for the cluster of 32 × 16 × 8 Hydrogen nuclei, with a distance 1.4 bohr between nuclei. The resulting potential is shown in Fig. 16. Size of the computational box is 50.4 × 28.0 × 16.8 bohr3. The corresponding 3D Cartesian grid size is 9216 × 5120 × 3072. Here the empty interval between the lattice and the boundary of the computational box equals to 3 bohr.
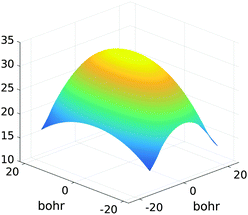 | ||
| Fig. 16 Assembled canonical sum of the Newton potentials for the cluster of 32 × 16 × 8 hydrogen atoms. | ||
The next table represents CPU times for the lattice summation of the Newton kernels over L × L × L cubic box, with very fine n × n × n representation grid.
| L3 | 4096 | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 768 768 | 262![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 144 144 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 097 097![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 152 152 |
| Time (s) | 1.8 | 0.8 | 3.1 | 15.8 |
| 3D grid size, n3 | 56323 | 97283 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9203 9203 | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3043 3043 |
where
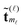 ,
, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, 2, 3, represents the Tucker vectors of the rank-r master tensor approximating the Newton kernel
= 1, 2, 3, represents the Tucker vectors of the rank-r master tensor approximating the Newton kernel 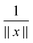 in
in 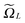 on a 2n × 2n × 2n representation grid.
on a 2n × 2n × 2n representation grid.
In the case of defected lattices the increasing rank of the final sum of Tucker tensors can be reduced by the stable ALS based algorithms applicable to the Tucker tensors (see ref. 48). The particular examples of the lattice geometries suitable for our approach are presented in Fig. 17, see ref. 48 for more detailed discussion.
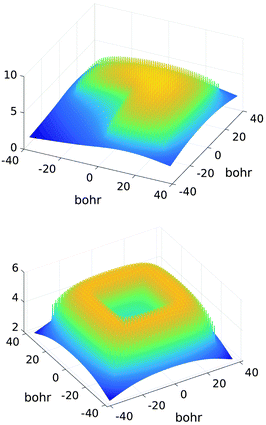 | ||
| Fig. 17 Assembled canonical sum of the Coulomb potentials on the L-shaped (top) and O-shaped (bottom) sub-lattices of a 32 × 32 × 1 lattice. | ||
For the reduced Hartree–Fock equation, where the Fock operator is confined to the core Hamiltonian, the tensor-structured block-circulant representation of the Fock matrix was introduced48 that allows the special low-rank approximation of the matrix blocks. This opens the way for the numerical treatment of large eigenvalue problems with structured matrices arising in the solution of the Hartree–Fock equation for large crystalline systems with defects.
5.2 Interaction energy of the Coulomb lattice sums
Given the nuclear charges {Zk}, centered at points xk, k ∈![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) 3, located on a finite L × L × L lattice
3, located on a finite L × L × L lattice ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) L = {xk} with the step-size b, the interaction energy of the total electrostatic potential of these charges is defined by the lattice sum
L = {xk} with the step-size b, the interaction energy of the total electrostatic potential of these charges is defined by the lattice sum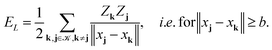 | (22) |
The tensor summation scheme (21) can be directly applied to this computational problem. In what follows we show that (22) can be treated as a particular case of the previous scheme served for calculation of (20) on a fine spacial grid. For this discussion, we assume that all charges are equal, Zk = Z.
First, notice that the rank-R reference tensor h−3![[P with combining tilde]](https://www.rsc.org/images/entities/b_char_0050_0303.gif) defined in (19) approximates with high accuracy O(h2) the (and its shifted version) Coulomb potential
defined in (19) approximates with high accuracy O(h2) the (and its shifted version) Coulomb potential 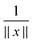 in
in  (for ||x|| ≥ b that is required for the energy expression) on the fine 2n × 2n × 2n representation grid with mesh size h. Likewise, the tensor h−3PcL approximates the potential sum VcL(x) on the same fine representation grid including the lattice points xk.
(for ||x|| ≥ b that is required for the energy expression) on the fine 2n × 2n × 2n representation grid with mesh size h. Likewise, the tensor h−3PcL approximates the potential sum VcL(x) on the same fine representation grid including the lattice points xk.
We propose to evaluate the energy expression (22) by using tensor sums as in (21), but now applied to a small sub-tensor of the rank-R canonical reference tensor ![[P with combining tilde]](https://www.rsc.org/images/entities/b_char_0050_0303.gif) , that is
, that is ![[P with combining tilde]](https://www.rsc.org/images/entities/b_char_0050_0303.gif) L: = [
L: = [![[P with combining tilde]](https://www.rsc.org/images/entities/b_char_0050_0303.gif) |xk] ∈
|xk] ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2L×2L×2L, obtained by tracing of
2L×2L×2L, obtained by tracing of ![[P with combining tilde]](https://www.rsc.org/images/entities/b_char_0050_0303.gif) at the accompanying lattice of the double size 2L × 2L × 2L, i.e.
at the accompanying lattice of the double size 2L × 2L × 2L, i.e.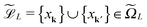 . Here
. Here ![[P with combining tilde]](https://www.rsc.org/images/entities/b_char_0050_0303.gif) |xk denotes the tensor entry corresponding to the k-th lattice point designating the atomic center xk. We are interested in the computation of the rank-R tensor
|xk denotes the tensor entry corresponding to the k-th lattice point designating the atomic center xk. We are interested in the computation of the rank-R tensor 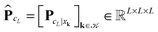 , where
, where 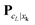 denotes the tensor entry corresponding to the k-th lattice point on
denotes the tensor entry corresponding to the k-th lattice point on ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) L. The tensor
L. The tensor 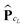 can be computed at the expense O(L2) by
can be computed at the expense O(L2) by
where the first term in brackets represents the full canonical tensor lattice sum restricted to the k-grid composing the lattice
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) L, while the second term introduces the correction at singular points xj − xk = 0. Here 1 ∈
L, while the second term introduces the correction at singular points xj − xk = 0. Here 1 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) L×L×L is the all-ones tensor. By using the rank-1 tensor P0L = P|xk=01, the correction term can be represented by a simple tensor operation
L×L×L is the all-ones tensor. By using the rank-1 tensor P0L = P|xk=01, the correction term can be represented by a simple tensor operationFinally, the interaction energy EL allows the approximate representation
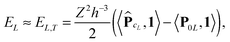 | (23) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L complexity by tensor operations with the rank-R canonical tensors in
L complexity by tensor operations with the rank-R canonical tensors in ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) L×L×L.
L×L×L.
Table 4 illustrates the performance of the algorithm described above. We compare the exact value computed by (22) with the approximate tensor representation in (23) computed on the fine representation grid with n = n0L, n0 = 128. We consider the lattice systems composed of Hydrogen atoms with interatomic distance 2.0 bohr. The geometric size of the largest 3D lattice with 2563 potentials is of the order of (2.0·256 + 6.0)3 bohr3,§ which is more than 203 cubic nanometers. Here Tfull means CPU time (sec) for direct summation of by (22) of the order of L6, where the number in brackets shows 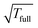 of the order of O(L3).
of the order of O(L3).
| L 3 | T full, (O(L3)) | T tens | E L,T | abs. err. |
|---|---|---|---|---|
| 243 | 37, (6.1) | 1.2 | 3.7 × 106 | 2 × 10−8 |
| 323 | 250, (15.8) | 1.5 | 1.5 × 107 | 1.5 × 10−9 |
| 483 | 3374, (58.8) | 2.8 | 1.12 × 108 | 0 |
| 643 | — | 5.7 | 5.0 × 108 | — |
| 1283 | — | 13.5 | 1.6 × 1010 | — |
| 2563 | — | 68.2 | 5.2 × 1011 | — |
The presented approach for fast calculation of the interaction energy can extended to the case of non-uniform rectangular lattices and, under certain assumptions, to the case of non-equal nuclear charges Zk. Moreover, it applies to many other types of spherically symmetric interaction potentials, for example, to shielded Coulomb interaction or van der Waals attraction sums corresponding to the distance function ||x||−2 and ||x||−6, respectively.
6 Conclusions
The goal of this paper is to attract interest of the specialists in computational quantum chemistry to recent results and open questions of the grid-based tensor approach in electronic structure calculations. Here we focus mostly on the description of main mathematical and algorithmic aspects of the tensor decomposition schemes and demonstrate their benefits in some applications.The scope of applications which can be regarded as consistent, ranges from the Hartree–Fock energy estimates for moderate size molecules, including calculation of TEI tensor with incorporated algebraic density fitting, to calculation of the excitation energies for molecules, and up to a unique superfast method for calculating the lattice potential sums and the interaction energy of long range potentials on a lattice in a finite volume. Tensor approach allows to treat above problems using moderate computational facilities. All numerics given in the paper presents implementations in Matlab.
The described numerical tools are not restricted to the applications presented here, but can be applied to various hard computational problems in (post) Hartree–Fock calculations related to accurate evaluation of multidimensional integrals, and efficient storage and manipulations with large multivariate data arrays.
The presented method for summation of long-range potentials with sub-linear computational cost does not have analogues in what is used so far in computational quantum chemistry and can have a good future. For example, it can be useful in modeling of large finite molecular structures like nanostructures or quantum dots, where the periodic approach may be inconsistent. Calculating a sum of several millions of lattice potentials on fine 3D grids takes only several seconds in Matlab on a laptop.47 This method gives also the unique possibility to present the summed 3D lattice potential in the whole computational region with very high accuracy. Integration and differentiation of this 3D potential can be easily performed on representation grid due to 1D computational costs.
Tensor approach is now being evolved for modeling the electronic structure of finite crystalline-type molecular systems. We hope that tensor numerical methods will have a good future in solving challenging multidimensional problems of computational quantum chemistry.
Appendix
Canonical-to-Tucker transform
The Canonical-to-Tucker tensor transform combined with the Tucker-to-Canonical scheme introduced in ref. 39 usually applies for the rank reduction of the function related canonical tensors with the large initial rank. Here we sketch Algorithm Canonical-to-Tucker which includes the following basic steps:Input data: side matrices 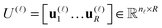 ,
, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, 2, 3, composed of vectors
= 1, 2, 3, composed of vectors 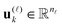 , k = 1,…R, see (1); maximal Tucker-rank parameter r; maximal number of the alternating least square (ALS) iterations mmax (usually a small number).
, k = 1,…R, see (1); maximal Tucker-rank parameter r; maximal number of the alternating least square (ALS) iterations mmax (usually a small number).
(A) Compute the singular value decomposition (SVD) of side matrices
U(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) = Z( ) = Z(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )S( )S(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )V( )V(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ), ), ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, 2, 3. = 1, 2, 3. |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) and the respective singular values up to given rank threshold, yielding the small orthogonal matrices
) and the respective singular values up to given rank threshold, yielding the small orthogonal matrices 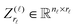 ,
, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, 2, 3.
= 1, 2, 3.
(B) Project side matrices U(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ) onto the orthogonal basis set defined by Z(
) onto the orthogonal basis set defined by Z(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )r
)r![[small script l]](https://www.rsc.org/images/entities/char_e146.gif)
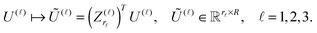 | (24) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, 2, 3 implement the following ALS iteration mmax times at most.
= 1, 2, 3 implement the following ALS iteration mmax times at most.
(D) Start ALS iteration for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, 2, 3:
= 1, 2, 3:
— For ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1: construct partially projected image of the full tensor,
= 1: construct partially projected image of the full tensor,
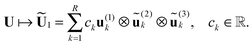 | (25) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n1 are in physical space for mode
n1 are in physical space for mode ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, while
= 1, while 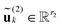 and
and 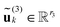 , the column vectors of
, the column vectors of 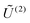 and
and 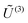 , respectively, belong to the coefficients space by means of projection.
, respectively, belong to the coefficients space by means of projection.
— Reshape the tensor 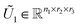 into a matrix MU1 ∈
into a matrix MU1 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n1×(r2r3), representing the span of the optimized subset of mode-1 columns in partially projected tensor Ũ1. Compute the SVD of the matrix MU1:
n1×(r2r3), representing the span of the optimized subset of mode-1 columns in partially projected tensor Ũ1. Compute the SVD of the matrix MU1:
| MU1 = Z(1)S(1)V(1), |
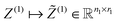 , according to the restriction on the mode-1 Tucker rank, r1.
, according to the restriction on the mode-1 Tucker rank, r1.
— Update the current approximation to the mode-1 dominating subspace 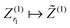 .
.
— Implement the single loop of ALS iteration for mode ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 2 and for
= 2 and for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 3.
= 3.
— End of the single ALS iteration step.
— Repeat the complete ALS iteration mmax times to obtain the optimized Tucker orthogonal side matrices ![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) (1),
(1), ![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) (2),
(2), ![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) (3), and final projected image Ũ3.
(3), and final projected image Ũ3.
(E) Project the final iterated tensor Ũ3 in (25) using the resultant basis set in ![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) (3) to obtain the core tensor, β ∈
(3) to obtain the core tensor, β ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) r1×r2×r3.
r1×r2×r3.
Output data: the Tucker core tensor β and the Tucker orthogonal side matrices ![[Z with combining tilde]](https://www.rsc.org/images/entities/char_005a_0303.gif) (
(![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ),
), ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, 2, 3.
= 1, 2, 3.
The Canonical-to-Tucker algorithm can be easily modified to the ε-truncation stopping criteria. Notice that in the case of equal Tucker ranks, r![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = r, maximal canonical rank of the core tensor β does not exceed r2, see ref. 39, which completes the Tucker-to-Canonical part of the total algorithm.¶
= r, maximal canonical rank of the core tensor β does not exceed r2, see ref. 39, which completes the Tucker-to-Canonical part of the total algorithm.¶
The Hartree–Fock equation in AO basis set
The 2N-electrons Hartree–Fock equation for pairwise L2-orthogonal electronic orbitals, ψi:![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 →
3 → ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) , ψi ∈ H1(
, ψi ∈ H1(![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3), reads as
3), reads as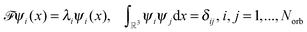 | (26) |
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) is given by
is given byHere the nuclear potential takes the form
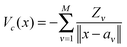 , Zν > 0, aν ∈
, Zν > 0, aν ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3, while the Hartree potential VH(x) and the nonlocal exchange operator
3, while the Hartree potential VH(x) and the nonlocal exchange operator ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) read as
read as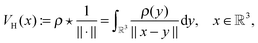 | (27) |
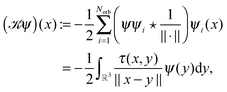 | (28) |
for the density matrix τ(x,y), and electron density ρ(x).
Usually, the Hartree–Fock equation is approximated by the standard Galerkin projection of the initial problem (26) by using the physically justified reduced basis sets (say, GTO type orbitals). For a given finite Galerkin basis set {gμ}1≤μ≤Nb, gμ ∈ H1(![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3), the occupied molecular orbitals ψi are represented (approximately) as
3), the occupied molecular orbitals ψi are represented (approximately) as 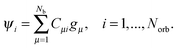 To derive an equation for the unknown coefficients matrix C = {Cμi} ∈
To derive an equation for the unknown coefficients matrix C = {Cμi} ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nb×Norb, first, we introduce the mass (overlap) matrix S = {Sμν}1≤μ,ν≤Nb, given by
Nb×Norb, first, we introduce the mass (overlap) matrix S = {Sμν}1≤μ,ν≤Nb, given by 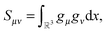 and the stiffness matrix H = {hμν} of the core Hamiltonian
and the stiffness matrix H = {hμν} of the core Hamiltonian 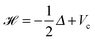 (the single-electron integrals),
(the single-electron integrals),
Given the finite basis set {gμ}1≤μ≤Nb, gμ ∈ H1(![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3), the associated fourth order two-electron integrals (TEI) tensor, B = [bμνλσ], is defined entrywise by (10), where μ, ν, λ, σ ∈ {1,…,Nb} =:
3), the associated fourth order two-electron integrals (TEI) tensor, B = [bμνλσ], is defined entrywise by (10), where μ, ν, λ, σ ∈ {1,…,Nb} =: ![[scr I, script letter I]](https://www.rsc.org/images/entities/char_e143.gif) b. In computational quantum chemistry the nonlinear terms representing the Galerkin approximation to the Hartree and exchange operators are calculated traditionally by using the low-rank Cholesky decomposition of a matrix associated with the TEI tensor B = [bμνκλ] defined in (10), that initially has the computational and storage complexity of order O(Nb4).
b. In computational quantum chemistry the nonlinear terms representing the Galerkin approximation to the Hartree and exchange operators are calculated traditionally by using the low-rank Cholesky decomposition of a matrix associated with the TEI tensor B = [bμνκλ] defined in (10), that initially has the computational and storage complexity of order O(Nb4).
Introducing the Nb × Nb matrices J(D) and K(D),
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nb×Nb is the rank-Norb symmetric density matrix, one then represents the complete Fock matrix F by
Nb×Nb is the rank-Norb symmetric density matrix, one then represents the complete Fock matrix F by| F(D) = H + J(D) + K(D). |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) Nb×Norb, and the respective eigenvalues Λ = diag(λ1,…,λNorb), reads as
Nb×Norb, and the respective eigenvalues Λ = diag(λ1,…,λNorb), reads as| F(D)C = SCΛ, CTSC = IN, |
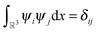 , and IN denotes the Nb × Nb identity matrix, and is usually solved by self-consistent field (SCF) DIIS iteration.60
, and IN denotes the Nb × Nb identity matrix, and is usually solved by self-consistent field (SCF) DIIS iteration.60
Tensor approximation to the Newton kernel in 3D
Methods of separable approximation to multivariate spherically symmetric functions by using the Gaussian sums have been addressed in the chemical and mathematical literature since ref. 9, 10 and 65, respectively.In this section, we discuss for the readers convenience the grid-based method for the low-rank canonical and Tucker tensor representations of a spherically symmetric functions p(||x||), x ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d in the particular case of the 3D Newton kernel
d in the particular case of the 3D Newton kernel 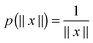 , x ∈
, x ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 by its projection onto the set of piecewise constant basis functions, see ref. 7 for more details.
3 by its projection onto the set of piecewise constant basis functions, see ref. 7 for more details.
In the computational domain Ω = [−b/2,b/2]3, let us introduce the uniform n × n × n rectangular Cartesian grid Ωn with the mesh size h = b/n (usually, n = 2k). Let {ψi} be a set of tensor-product piecewise constant basis functions, 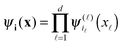 , for the 3-tuple index i = (i1, i2, i3), i
, for the 3-tuple index i = (i1, i2, i3), i![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ∈ {1,…,n},
∈ {1,…,n}, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, 2, 3. The kernel p(||x||) can be discretized by its projection onto the basis set {ψi} in the form of a third order tensor of size n × n × n, defined entrywise as
= 1, 2, 3. The kernel p(||x||) can be discretized by its projection onto the basis set {ψi} in the form of a third order tensor of size n × n × n, defined entrywise as
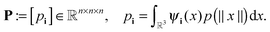 | (29) |
Given M, the low-rank canonical decomposition of the 3rd order tensor P is based on using exponentially convergent sinc-quadratures for approximation of the Laplace-Gauss transform to the analytic function p(z) = 1/z as follows,
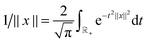 | (30) |
where the quadrature points and weights are given by
Under the assumption 0 < a ≤ ||x||<∞, x = (x1, x2, x3) ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3, this quadrature can be proven to provide the exponential convergence rate in M for a class of analytic functions including p(z) = 1/z, see ref. 10, 25 and 65,
3, this quadrature can be proven to provide the exponential convergence rate in M for a class of analytic functions including p(z) = 1/z, see ref. 10, 25 and 65,
Define the vector (recall that ak > 0)
with
then the 3rd order tensor P can be approximated by the R-term canonical representation
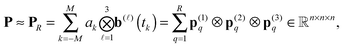 | (31) |
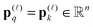 ,
, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = 1, 2, 3. For the given threshold ε > 0, M = O(|log
= 1, 2, 3. For the given threshold ε > 0, M = O(|log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε|2) is chosen as the minimal number, such that in the max-norm we have
ε|2) is chosen as the minimal number, such that in the max-norm we have| ||P − PR|| ≤ ε||P||. |
References
- J. Almlöf, in Direct methods in electronic structure theory, ed. D. R. Yarkony, Modern Electronic Structure Theory, World Scientific, Singapore, 1995, vol. II, pp. 110–151 Search PubMed.
- M. Bachmayr, Adaptive low-rank wavelet methods and applications to two-electron Schrödinger equations, PhD dissertation, RWTH Aachen, 2012 Search PubMed.
- P. Baudin, J. Marin, I. G. Cuesta and A. M. S. de Meras, Calculation of excitation energies from the CC2 linear response theory using Cholesky decomposition, J. Chem. Phys., 2014, 140, 104111 CrossRef PubMed.
- P. Benner, H. Faßbender and M. Stoll, Solving Large-Scale Quadratic Eigenvalue Problems with Hamiltonian Eigenstructure using a Structure-Preserving Krylov Subspace Method, Electronic Transactions on Numerical Analysis, 2008, 29, 212–229 Search PubMed.
- P. Benner and T. Mach, The LR Cholesky Algorithm for Symmetric Hierarchical Matrices, Linear Algebra and its Applications, 2013, 439(4), 1150–1166 CrossRef PubMed.
- P. Benner, V. Khoromskaia and B. N. Khoromskij, A reduced basis approach for calculation of the Bethe–Salpeter excitation energies using low-rank tensor factorizations, 2015, Preprint arXiv:1505.02696.
- C. Bertoglio and B. N. Khoromskij, Low-rank quadrature-based tensor approximation of the Galerkin projected Newton/Yukawa kernels, Comput. Phys. Commun., 2012, 183(4), 904–912 CrossRef CAS PubMed.
- F. A. Bischoff, R. J. Harrison and E. F. Valeev, Computing many-body wave functions with guaranteed precision: The first-order Møller-Plesset wave function for the ground state of helium atom, J. Chem. Phys., 2012, 137, 104103 CrossRef PubMed.
- S. F. Boys, G. B. Cook, C. M. Reeves and I. Shavitt, Automatic Fundamental Calculations of Molecular Structure, Nature, 1956, 178, 1207–1209 CrossRef PubMed.
- D. Braess, Asymptotics for the Approximation of Wave Functions by Exponential-Sums, J. Approx. Theory, 1995, 83, 93–103 CrossRef.
- M. E. Casida, in Recent Advances in Density Functional Methods, Part I, ed. D. P. Chong, World Scientific, Singapoure, 1995, p. 155 Search PubMed.
- A. Cichocki and Sh. Amari, Adaptive Blind Signal and Image Processing: Learning Algorithms and Applications, Wiley, 2002 Search PubMed.
- W. Dahmen, S. Proessdorf and R. Schneider, Multiscale methods for pseudo-differential equations on manifolds, Wavelet analysis and its applications, 5, Academic Press, 1995 Search PubMed.
- S. Dolgov, Tensor product methods in numerical simulation of high-dimensional dynamical problems, PhD thesis, University of Leipzig, 2014, http://nbn-resolving.de/urn:nbn:de:bsz:15-qucosa-151129 Search PubMed.
- S. Dolgov, B. N. Khoromskij, D. Savostyanov and I. Oseledets, Computation of extreme eigenvalues in higher dimensions using block tensor train format, Comput. Phys. Commun., 2014, 185(4), 1207–1216 CrossRef CAS PubMed.
- L. De Lathauwer, B. De Moor and J. Vandewalle, A multilinear singular value decomposition, SIAM J. Matrix Anal. Appl., 2000, 21, 1253–1278 CrossRef.
- T. H. Dunning Jr, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef PubMed.
- A. Durdek, S. R. Jensen, J. Juselius, P. Wind, T. Flå and L. Frediani, Adaptive order polynomial algorithm in a multi-wavelet representation scheme, Appl. Num. Math., 2014, 92, 40–53 CrossRef PubMed.
- P. P. Ewald, Die Berechnung optische und elektrostatischer Gitterpotentiale, Ann. Phys., 1921, 64, 253 CrossRef PubMed.
- L. Frediani, E. Fossgaard, T. Flå and K. Ruud, Fully adaptive algorithms for multivariate integral equations using the non-standard form and multiwavelets with applications to the Poisson and bound-state Helmholtz kernels in three dimensions, Mol. Phys., 2013, 111(9–11), 1143–1160 CrossRef CAS PubMed.
- L. Genovese, A. Neelov, S. Goedecker, T. Deutsch, S. A. Ghasemi, A. Willand, D. Caliste, O. Zilberberg, M. Rayson, A. Bergman and R. Schneider, Daubechies wavelets as a basis set for density functional pseudopotential calculations, J. Chem. Phys., 2008, 129, 014109 CrossRef PubMed.
- L. Grasedyck, D. Kressner and C. Tobler, A literature survey of low-rank tensor approximation techniques, 2013, arXiv:1302.7121v1.
- L. Greengard and V. Rochlin, A fast algorithm for particle simulations, J. Comput. Phys., 1987, 73, 325 CrossRef.
- M. Griebel and J. Hamaekers, Sparse grids for the Schroedinger equation, M2AN, 2007, 41, 215–247 CrossRef.
- W. Hackbusch and B. N. Khoromskij, Low-rank Kronecker product approximation to multi-dimensional nonlocal operators, Part I. Separable approximation of multi-variate functions, Computing, 2006, 76, 177–202 CrossRef.
- W. Hackbusch and S. Kühn, A new scheme for the tensor representation, J. Fourier Anal. Appl., 2009, 15, 706–722 CrossRef.
- W. Hackbusch and R. Schneider, in Tensor Spaces and Hierarchical Tensor Representations, ed. S. Dahlke and W. Dahmenet al., Lecture Notes in Computer Science and Engineering, 102, Springer, 2014 Search PubMed.
- R. J. Harrison, G. I. Fann, T. Yanai, Z. Gan and G. Beylkin, Multiresolution quantum chemistry: Basic theory and initial applications, J. Chem. Phys., 2004, 121(23), 11587–11598 CrossRef CAS PubMed.
- T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic-Structure Theory, Wiley, New York, 1999 Search PubMed.
- N. Higham, in Analysis of the Cholesky decomposition of a semi-definite matrix, ed. M. G. Cox and S. J. Hammarling, Reliable Numerical Computations, Oxford University Press, Oxford, 1990, pp. 161–185 Search PubMed.
- F. L. Hitchcock, The expression of a tensor or a polyadic as a sum of products, J. Math. Phys., 1927, 6, 164–189 Search PubMed.
- E. G. Hohenstein, R. M. Parrish and T. J. Martinez, Tensor hypercontraction density fitting, Quartic scaling second- and third-order Møller-Plesset perturbation theory, J. Chem. Phys., 2012, 137, 044103 CrossRef PubMed.
- V. Kazeev and B. N. Khoromskij, Explicit low-rank QTT representation of Laplace operator and its inverse, SIAM J. Matrix Anal. Appl., 2012, 33(3), 742–758 CrossRef.
- B. N. Khoromskij, O(d
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N)-Quantics Approximation of N-d Tensors in High-Dimensional Numerical Modeling, J. Const. Approx., 2011, 34(2), 257–289 CrossRef , Preprint 55/2009, MPI MiS, Leipzig 2009, http://www.mis.mpg.de/publications/preprints/2009/prepr2009-55.html.
N)-Quantics Approximation of N-d Tensors in High-Dimensional Numerical Modeling, J. Const. Approx., 2011, 34(2), 257–289 CrossRef , Preprint 55/2009, MPI MiS, Leipzig 2009, http://www.mis.mpg.de/publications/preprints/2009/prepr2009-55.html. - B. N. Khoromskij, Fast and Accurate Tensor Approximation of Multivariate Convolution with Linear Scaling in Dimension, J. Comput. Appl. Math., 2010, 234, 3122–3139 CrossRef PubMed.
- B. N. Khoromskij, Structured Rank-(r1,…,rd) Decomposition of Function-related Tensors in
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d, Comput. Method. Appl. Math., 2006, 6(2), 194–220 Search PubMed.
d, Comput. Method. Appl. Math., 2006, 6(2), 194–220 Search PubMed. - B. N. Khoromskij, in Tensor Numerical Methods for High-dimensional PDEs: Basic Theory and Initial Applications, ESAIM: Proceedings and Surveys, ed. N. Champagnat, T. Leliévre and A. Nouy, 2015, vol. 48, pp. 1–28, DOI:10.1051/proc/201448001.
- B. N. Khoromskij and V. Khoromskaia, Low Rank Tucker-Type Tensor Approximation to Classical Potentials, Cent. Eur. J. Math., 2007, 5(3), 523–550 CrossRef.
- B. N. Khoromskij and V. Khoromskaia, Multigrid Accelerated Tensor Approximation of Function Related Multi-dimensional Arrays, SIAM J. Sci. Comput., 2009, 31(4), 3002–3026 CrossRef.
- V. Khoromskaia, Computation of the Hartree–Fock Exchange in the Tensor-structured Format, Comput. Method. Appl. Math., 2010, 10(2), 1–16 Search PubMed.
- V. Khoromskaia, Numerical Solution of the Hartree–Fock Equation by Multilevel Tensor-structured methods, PhD dissertation, TU Berlin, 2010, http://opus.kobv.de/tuberlin/volltexte/2011/2948/ Search PubMed.
- B. N. Khoromskij, V. Khoromskaia and H.-J. Flad, Numerical Solution of the Hartree–Fock Equation in Multilevel Tensor-structured Format, SIAM J. Sci. Comput., 2011, 33(1), 45–65 CrossRef.
- V. Khoromskaia, D. Andrae and B. N. Khoromskij, Fast and accurate 3D tensor calculation of the Fock operator in a general basis, Comput. Phys. Commun., 2012, 183, 2392–2404 CrossRef CAS PubMed.
- V. Khoromskaia, B. N. Khoromskij and R. Schneider, Tensor-structured factorized calculation of two-electron integrals in a general basis, SIAM J. Sci. Comput., 2013, 35(2), A987–A1010 CrossRef.
- V. Khoromskaia and B. N. Khoromskij, Møller-Plesset (MP2) Energy Correction Using Tensor Factorizations of the Grid-based Two-electron Integrals, Comput. Phys. Commun., 2014, 185, 2–10 CrossRef CAS PubMed.
- V. Khoromskaia, Black Box Hartree–Fock Solver by the Tensor Numerical Methods, Comput. Method. Appl. Math., 2014, 14(1), 89–111 Search PubMed.
- V. Khoromskaia and B. N. Khoromskij, Grid-based lattice summation of electrostatic potentials by assembled canonical tensors, Comput. Phys. Commun., 2014, 185, 3162–3174 CrossRef CAS PubMed.
- V. Khoromskaia and B. N. Khoromskij, Tensor Approach to Linearized Hartree–Fock Equation for Lattice-type and Periodic Systems, 2014, Preprint 62/2014, MIS MPI, arXiv:1408.3839, submitted.
- V. Khoromskaia and B. N. Khoromskij, Tucker tensor method for fast grid-based summation of long-range potentials on 3D lattices with defects, 2014, Preprint arXiv:14.1994.
- T. G. Kolda and B. W. Bader, Tensor Decompositions and Applications, SIAM Rev., 2009, 51(3), 455–500 CrossRef.
- D. Kressner, Numerical methods and software for general and structured eigenvalue problems, PhD dissertation, TU Berlin, 2004 Search PubMed.
- K. N. Kudin and G. E. Scuseria, Revisiting infinite lattice sums with the periodic Fast Multipole Method, J. Chem. Phys., 2004, 121, 2886–2890 CrossRef CAS PubMed.
- S. A. Losilla, D. Sundholm and J. Juselius, The direct approach to gravitation and electrostatics method for periodic systems, J. Chem. Phys., 2010, 132(2), 024102 CrossRef CAS PubMed.
- Ch. Lubich, On Variational Approximations in Quantum Molecular Dynamics, Math. Comput., 2005, 74, 765–779 CrossRef.
- L. Lin, Y. Saad and C. Yang, Approximating spectral densities of large matrices, 2014, Preprint arXiv:1308.5467v2.
- I. V. Oseledets, Approximation of 2d × 2d matrices using tensor decomposition, SIAM J. Matrix Anal. Appl., 2010, 31(4), 2130–2145 CrossRef.
- I. V. Oseledets and E. E. Tyrtyshnikov, Breaking the Curse of Dimensionality, or How to Use SVD in Many Dimensions, SIAM J. Sci. Comput., 2009, 31(5), 3744–3759 CrossRef.
- C. Pisani, M. Schütz, S. Casassa, D. Usvyat, L. Maschio, M. Lorenz and A. Erba, CRYSCOR: a program for the post-Hartree–Fock treatment of periodic systems, Phys. Chem. Chem. Phys., 2012, 14, 7615–7628 RSC.
- R. Parrish, E. G. Hohenstein, T. J. Martinez and C. D. Sherrill, Discrete variable representation in electronic structure theory: Quadrature grids for least-squares tensor hypercontraction, J. Chem. Phys., 2013, 138, 194107 CrossRef PubMed.
- P. Pulay, Improved SCF convergence acceleration, J. Comput. Chem., 1982, 3, 556–560 CrossRef CAS PubMed.
- E. Ribolini, J. Toulouse and A. Savin, in Electronic excitation energies of molecular systems from the Bethe–Salpeter equation: Example of H2 molecule, ed. S. Ghosh and P. Chattaraj, Concepts and Methods in Modern Theoretical Chemistry, Electronic Structure and Reactivity, 2013, vol. 1, p. 367 Search PubMed.
- U. Schollwöck, The density-matrix renormalization group in the age of matrix product states, Ann. Phys., 2011, 326(1), 96–192 Search PubMed.
- H. Sekino, Y. Maeda, T. Yanai and R. J. Harrison, Basis set limit Hartree Fock and density functional theory response property evaluation by multiresolution multiwavelet basis, J. Chem. Phys., 2008, 129, 034111 CrossRef PubMed.
- A. Smilde, R. Bro and P. Geladi, Multi-way Analysis, Wiley, 2004 Search PubMed.
- F. Stenger, Numerical methods based on Sinc and analytic functions, Springer-Verlag, Heidelberg, 1993 Search PubMed.
- D. Sundholm, P. Pyykkö and L. Laaksonen, Two-dimensional Fully Numerical Molecular Calculations. X. Hartree–Fock Results for He2, Li12, Be2, HF, OH−, N2, CO, BF, NO+, and CN−, Mol. Phys., 1985, 56, 1411–1418 CrossRef CAS PubMed.
- A. Szabo ans N. Ostlund, Modern Quantum Chemistry, Dover Publication, New York, 1996 Search PubMed.
- L. R. Tucker, Some mathematical notes on three-mode factor analysis, Psychometrika, 1966, 31, 279–311 CrossRef CAS.
- F. Verstraete, D. Porras and J. I. Cirac, DMRG and periodic boundary conditions: A quantum information perspective, Phys. Rev. Lett., 2004, 93(22), 227205 CrossRef CAS.
- G. Vidal, Efficient classical simulation of slightly entangled quantum computations, Phys. Rev. Lett., 2003, 91(14), 147902 CrossRef.
- H. Wang and M. Thoss, Multilayer formulation of the multiconfiguration time-dependent Hartree theory, J. Chem. Phys., 2003, 119, 1289–1299 CrossRef CAS PubMed.
- H.-J. Werner and P. J. Knowleset al., MOLPRO, version 2002.10, a package of ab initio programs for electronic structure calculations Search PubMed.
- S. R. White, Density-matrix algorithms for quantum renormalization groups, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48(14), 10345–10356 CrossRef CAS.
- H. Yserentant, Regularity and Approximability of Electronic Wave Functions, Lecture Notes in Mathematics series, Springer-Verlag, 2010 Search PubMed.
Footnotes |
| † The alternative notation A = [A(i1,…,id)] can be utilized. |
| ‡ Usually for small to moderate size molecules we use the computational box of size 403 bohr3. |
| § Here 6 bohr is the chosen dummy distance. |
| ¶ Further optimization of the canonical rank in the small-size core tensor β can be implemented by applying the ALS iterative scheme in the canonical format, see e.g.ref. 50. |
| This journal is © the Owner Societies 2015 |