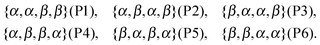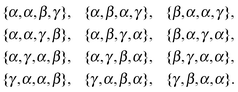Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quasi-combinatorial energy landscapes for nanoalloy structure optimisation
D.
Schebarchov
* and
D. J.
Wales
University Chemical Laboratories, Lensfield Road, Cambridge CB2 1EW, UK. E-mail: Dmitri.Schebarchov@gmail.com; dw34@cam.ac.uk
First published on 8th May 2015
Abstract
We formulate nanoalloy structure prediction as a mixed-variable optimisation problem, where the homotops can be associated with an effective, quasi-combinatorial energy landscape in permutation space. We survey this effective landscape for a representative set of binary systems modelled by the Gupta potential. In segregating systems with small lattice mismatch, we find that homotops have a relatively straightforward landscape with few local optima – a scenario well-suited for local (combinatorial) optimisation techniques that scale quadratically with system size. Combining these techniques with multiple local-neighbourhood structures yields a search for multiminima, and we demonstrate that generalised basin-hopping with a metropolis acceptance criterion in the space of multiminima can then be effective for global optimisation of binary and ternary nanoalloys.
1 Introduction
Alloy nanoparticles (nanoalloys1) exhibit structure-dependent properties with potential applications in catalysis,2 sensing,3 plasmonics,4etc.5,6 However, unlocking the full potential of this class of materials requires reliable structure prediction at the atomistic level, which, from a theoretical viewpoint, often amounts to finding the ground state (the global minimum) of a model system described by a highly nonlinear potential energy function. For homogeneous metal clusters the number of metastable states (local minima) is expected to grow exponentially with the number of atoms,7,8 but for nanoalloys the growth is significantly more rapid due to the presence of homotops9 – local minima with a similar geometric motif but a different ordering of atomic species. As a result, the exponential growth in the number of non-degenerate minima can be further multiplied by a combinatorial factor. We tackle this formidable global optimisation problem using a mixed-variable approach that targets multiminima – configurations that are local minima in more than one sense of the word “local”.While most methods currently used for nanoalloy structure prediction tend to focus on local minima in coordinate space,10–14 one could argue that it might be more effective to systematically target a smaller subspace that is somehow guaranteed to retain the global minimum. This reasoning motivated the definition of biminima15 – configurations that are local minima in two different metric domains: (i) in the usual coordinate domain, measured by the Euclidean distance metric, and (ii) in the permutation domain, measured by the interchange16 distance metric. From the viewpoint of basic topology, the two metrics induce two local neighbourhood structures: one continuous and the other discrete. It is clear that the global minimum of a model nanoalloy ought to be a local minimum with respect to both metrics/neighbourhoods and, therefore, must be a biminimum. In fact, the global minimum in a specified domain ought to be a local minimum in any subdomain that retains the global minimum and admits a definition of “locality”. Hence, one could generalise further still and define multiminima by invoking more subdomains with a different metric and/or local neighbourhood structure.
Whether incorporating another neighbourhood structure will make a global search more effective or not will depend on two competing factors: (i) the additional cost associated with multiminimisation and (ii) the consequent reduction in the number of multiminima. In the present study we show that targeting biminima15 can lead to a significant net efficiency gain, which is explained by the topography of what we call quasi-combinatorial energy landscapes. These effective landscapes may not have a well-defined global combinatorial structure, but can still be explored and (to some degree) characterised using local combinatorial constructions. For model nanoalloys with small lattice mismatch, representing a scenario where global combinatorial counting arguments are applicable, we find that the energetic preference for mixing/segregation is linked to the fraction of locally optimal homotops (with respect to the interchange distance). In strongly segregating systems this fraction is found to be minuscule, and it appears to grow with the preference for mixing – consistent with our earlier findings for binary Lennard-Jones clusters.15 Furthermore, the fraction of locally optimal homotops appears to decrease with system size for segregating nanoalloys and increase for mixing nanoalloys. We are unable to detect similarly useful trends for lattice mismatched nanoalloys, largely due to the breakdown of global combinatorial structure. However, our benchmark calculations for selected binary (CunAu38−n) and ternary (Cu13AgnAu42−n) systems clearly show that systematic multiminima-targeting provides a highly effective strategy for global optimisation.
Incidentally, the idea of using multiple definitions of “locality” in global optimisation is not new: it has been exploited by Mladenović et al. in the so-called variable neighbourhood search metaheuristic.17–20 To the best of our knowledge, this approach has been applied to either purely combinatorial17 or (to a lesser extent) purely continuous19 problems. Here we apply it within a less restrictive and relatively unexplored realm of mixed-variable optimisation, where the constituent degrees of freedom can be different: continuous, discrete, categorical, etc.
2 Framework
We formulate nanoalloy structure prediction as a mixed-variable optimisation problem, where each atom i is assigned coordinates xi ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 and a categorical label li ∈ αMα=1, with M being the number of constituent atomic species. The objective is to minimise a specified energy function E(X,L) with respect to X = {xi}Ni=1 and L = {li}Ni=1, where
3 and a categorical label li ∈ αMα=1, with M being the number of constituent atomic species. The objective is to minimise a specified energy function E(X,L) with respect to X = {xi}Ni=1 and L = {li}Ni=1, where 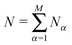 is the total number of atoms and each Nα (the population of species α) is fixed. Both X and L are treated as variables, in spite of the obvious redundancy (i.e. permuting labels has the same effect as permuting the corresponding coordinates), with L being particularly useful for exploiting (quasi-)combinatorial features of E(X,L).
is the total number of atoms and each Nα (the population of species α) is fixed. Both X and L are treated as variables, in spite of the obvious redundancy (i.e. permuting labels has the same effect as permuting the corresponding coordinates), with L being particularly useful for exploiting (quasi-)combinatorial features of E(X,L).
2.1 Multiset permutations and the interchange distance
It is helpful to think of L as an indexed multiset whose distinct permutations span the domain of nanoalloy homotops. For example, consider all distinct permutations of a multiset of N = 4 atoms, with half of the elements characterised as α-type and the other half as β-type:With this domain we can associate an interchange distance metric16 – the Hamming21 distance restricted to multiples of two – giving the minimum number of label interchanges (or swaps) required to arrive from one point in the domain to another. In the example above, the distance between permutations P1 and P2 is one interchange (“swap”), and that between P1 and P6 is two swaps (which is the maximum for N = 4). This simple metric induces a local neighbourhood structure for each permutation: it contains the permutation in question and all others that can be reached from it by a single swap. Recalling the above example again, the local neighbourhood of P1 contains all other permutations apart from P6.
For further illustration consider a (slightly) more complicated example:
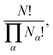 | (1) |
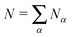 , and the size of the local neighbourhood induced by the interchange distance metric is given by
, and the size of the local neighbourhood induced by the interchange distance metric is given by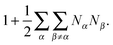 | (2) |
2.2 Quasi-combinatorial landscapes and biminima
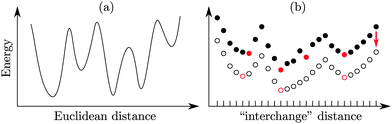
A locally optimal multiset can be defined as one with the lowest “energy” in its local neighbourhood. This definition can also be combined with the conventional notion of a local minimum (in coordinate space) to define biminima,15 which, in the context of nanoalloys, correspond to homotops that are (meta)stable with respect to both the Euclidean and the interchange distance metrics.Fig. 1 illustrates how an energy function can exhibit local minima in the two metric domains. It also illustrates how a sequence of swaps at fixed geometry may differ from a sequence where each swap is accompanied by a local geometry relaxation (i.e. a quench). Local minima in permutation space may be shifted, created or destroyed as a result of quenching (local minimisation in coordinate space), and the net effect can be difficult to track. It is even conceivable that a quenched swap may not always be a reversible operation. This potential irreversibility implies that a revisited permutation may be mapped to different energy values, and so the total number of distinct configurations that could be generated by a sequence of quenched swaps is not necessarily bounded above by the combinatorial number in (1). It is precisely for this reason that we refer to the effective energy landscape in the permutation domain as quasi-combinatorial. The term locally combinatorial may also be appropriate, because we can still rely on (2) to enumerate the local neighbourhood.
One obvious approach to biminima searching is to execute a monotonically decreasing sequence of quenched swaps15,22–24 until the sequence becomes stuck at a biminimum. That is, if we use ΔEij to denote swap gain24 – the energy change due to a quenched swap of labels between atoms i and j – the policy of accepting only swaps with ΔEij < 0 will guarantee that a sequence will converge when ΔEij ≥ 0, ∀i, j, which is precisely the definition of a biminimum.15 Note that finding a swap with ΔEij < 0 is usually easier than verifying that no such swap exists, because the verification requires an exhaustive search through the entire local neighbourhood in permutation domain. Without a reliable way of bypassing this computational bottleneck, the best case scenario for the cost of biminima searching is a linear scaling with the size of the local neighbourhood.
Finally, it is worth noting that the concepts of quasi-combinatorial landscapes and biminima are also applicable when one of the constituent species represents vacancies (quasiparticles), and so the framework of mixed-variable optimisation could subsume the approach of dynamic-lattice searching.25,26 However, since vacancies are usually not intrinsically defined in off-lattice atomistic models, they have to be generated by some additional means, and it may require introducing another, distinctly different local neighbourhood structure. In that case the term triminima would be more appropriate for describing the local optima.
3 Methods
Throughout this study, nanoalloys are modelled using the Gupta potential27 with standard parameter values.28–30 All search techniques described below have been implemented in the GMIN program.313.1 Biminimisation
We perform biminima searching (“biminimisation”) using a scheme similar to that of Lai et al.,23 which exploits correlations between ΔEij (see Section 2.2) and ΔEij* – the energy change evaluated immediately after the swap but before quenching. Systematically attempting quenched swaps within a local neighbourhood sorted by ΔEij* (from lowest to highest) is a cost-effective way of finding ΔEij < 0. The first encountered swap with ΔEij < 0 is immediately accepted, and then the local neighbourhood is reset and sorted by the new ΔEij*. The procedure terminates when a complete scan of the entire local neighbourhood fails to produce ΔEij < 0. Note that Lai et al.23 consider only the first N − 1 entries in the sorted list, which does not guarantee that our definition of biminima will necessarily be fulfilled. Also note that there are multiple ways of scanning the local neighbourhood,15 which could involve the use of point-group symmetry,32,33 though it is reasonable to expect the relative performance of these different schemes to be system specific.3.2 Generalised basin-hopping
Since biminimisation (and, more generally, multiminimisation) inherently constitutes a local search, we sample different multiminima using a generalisation of the basin-hopping (BH) global optimisation technique.10,11 While BH involves steps in the space of (conventional) minima, the new generalised variant (GBH) considers the reduced space of multiminima. In both cases one has to specify the temperature parameter for the metropolis acceptance criterion and also provide an appropriate random-move set.34 We choose to adaptively adjust the temperature to maintain the (rolling average) acceptance ratio close to 0.5, and our move set consists of just two operations: (i) random permutation of atomic labels and (ii) random Cartesian displacement of atomic coordinates. Both operations are applied at each GBH step, but for homotop optimisation the effect of random Cartesian moves can be rendered ineffectual by setting the maximum displacement to zero. Finally, when Nres GBH steps fail to produce a lower-energy multiminimum, the search is restarted from a completely random configuration/permutation. We note that such large steps in configuration space can be used, since no detailed balance condition is required.3.3 Surface refinement
Results from Lai et al.23 indicate that incorporating a surface refinement stage into a global structure search can be beneficial. Hence, when performing a global search with random Cartesian moves, we combine biminimisation with another procedure akin to a dynamic-lattice search.25,26 This procedure relies on a nearest-neighbour analysis to generate an appropriate set of vacancies (see below) for a given biminimum. These vacancies and the subset of least-coordinated atoms (irrespective of their chemical identity) define an ad hoc local neighbourhood, and we sequentially attempt quench-assisted swaps between atoms and vacancies within this neighbourhood. If a swap leads to a reduction in energy then it is immediately accepted and the local neighbourhood structure is rebuilt. By analogy with biminimsation, the surface refinement procedure terminates when an exhaustive scan of the entire neighbourhood fails to produce a lower energy structure. Note that, unlike biminimisation, the local neighbourhood structure used for surface refinement does not have a predefined size. Finally, biminimisation and surface refinement are repeated in tandem until one of them fails to produce a lower energy structure, in the end converging on a triminimum.To generate the vacancies we first identify the nearest neighbours for each atom (i) and, if its coordination number is less than twelve, we apply local inversion symmetry (about xi) on each of neighbour's coordinates to generate a local set of candidate vacancies. We discard candidates that are within δ = 0.8rNNmin from another atom, where rNNmin denotes the shortest interatomic distance in the current structure. The union of all local candidate sets is then sorted by atomic coordination number, and all but the highest coordinated vacancies are discarded. If any of the remaining candidate vacancies are separated by less than δ, they are merged and the corresponding coordinates are averaged. In the end, we proceed with the surface refinement scheme only if the coordination of remaining vacancies exceeds the lowest coordination amongst the atoms.
4 Results and discussion
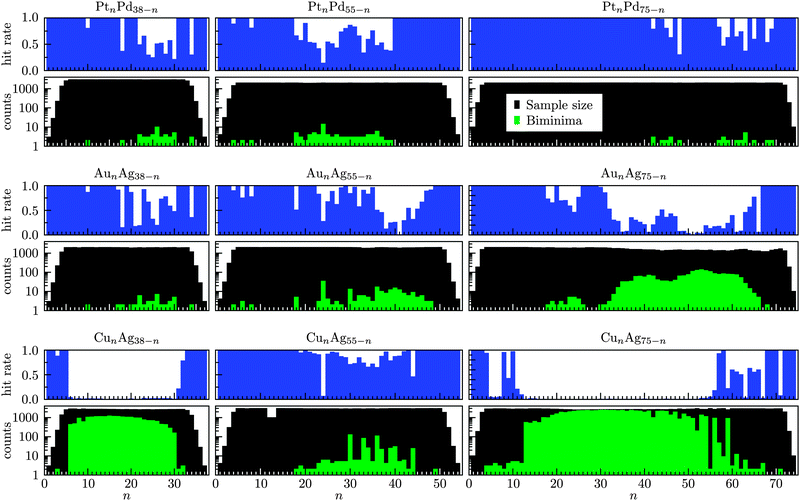
We start by attempting to characterise the quasi-combinatorial energy landscape associated with nanoalloy homotops for a representative set of binary systems: PtnPdN−n, AunAgN−n, CunAgN−n for N = 38, 55 and 75. The initial coordinates are derived from the (single-component) Lennard-Jones global minima:11,35 truncated octahedron for N = 38, Mackay icosahedron36 for N = 55, and Marks decahedron37 for N = 75. To impose appropriate nearest-neighbour separation while preserving the overall symmetry, these coordinates are multiplied by a scaling factor (ϕ) equal to the arithmetic average of the nearest-neighbour distances (rαα0) for each of the constituent metals (α), i.e.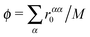 , where M is the number of species. The labels are initialised randomly but consistent with a specified stoichiometry. The resulting configurations are then used for GBH at high temperature (kBT = 1.0 eV) and without random Cartesian moves, i.e. a converged biminimum is escaped solely by virtue of randomly permuting the labels. The intention is to (i) initiate biminimisation from a uniform sample of starting points in the permutation domain, (ii) accumulate representative count statistics for energetically distinct biminima (using a threshold of 10−6 eV), and (iii) estimate the relative encounter probabilities of the (putative) lowest-lying biminimum. The results are presented in Fig. 2.
, where M is the number of species. The labels are initialised randomly but consistent with a specified stoichiometry. The resulting configurations are then used for GBH at high temperature (kBT = 1.0 eV) and without random Cartesian moves, i.e. a converged biminimum is escaped solely by virtue of randomly permuting the labels. The intention is to (i) initiate biminimisation from a uniform sample of starting points in the permutation domain, (ii) accumulate representative count statistics for energetically distinct biminima (using a threshold of 10−6 eV), and (iii) estimate the relative encounter probabilities of the (putative) lowest-lying biminimum. The results are presented in Fig. 2.
While both PtnPdN−n and AunAgN−n represent lattice-matched systems, the former favours segregation and the latter favours mixing.38 In spite of this qualitative difference, the corresponding count statistics from biminima sampling are comparable for N = 38 and 55. In both cases the number of sampled biminima is consistently orders of magnitude smaller than the number of sampled homotops, even for compositions when the size of the permutation domain is at its peak (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 stoichiometry). Furthermore, the relative occurrence (“hit rate”†) for the most elusive biminimum at a given stoichiometry often exceeds 0.5, suggesting that in many cases one or two biminimisations can be sufficient to find the lowest-lying homotop. This observation can be interpreted in terms of the effective landscape topography comprising only a few significant optima, which would make local (combinatorial) search techniques particularly effective. It is also worth noting that biminima counts for PtnPdN−n and AunAgN−n do not always peak at n = N/2, indicating that the size of the permutation domain (1) is not the only determining factor.
50 stoichiometry). Furthermore, the relative occurrence (“hit rate”†) for the most elusive biminimum at a given stoichiometry often exceeds 0.5, suggesting that in many cases one or two biminimisations can be sufficient to find the lowest-lying homotop. This observation can be interpreted in terms of the effective landscape topography comprising only a few significant optima, which would make local (combinatorial) search techniques particularly effective. It is also worth noting that biminima counts for PtnPdN−n and AunAgN−n do not always peak at n = N/2, indicating that the size of the permutation domain (1) is not the only determining factor.
Notable differences in biminima counts emerge for PtnPd75−n and AunAg75−n, and the decrease in counts for PtnPd75−n (compared to N = 55) is particularly surprising. It indicates that the effective landscape topography may become “simpler” as N increases. To corroborate this hypothesis, we applied the same homotop sampling procedure to PtnPd98−n Leary tetrahedra,39,40 in the range 43 ≤ n ≤ 55, and in each case found that a uniform random sample of about 2000 homotops was mapped onto a single biminimum. This result suggests something quite remarkable: it is possible that, out of 98!/49!49! ≈ 2.5 × 1028 homotops, only one is locally optimal with respect to the interchange distance in the permutation domain. To check if similar results can be expected for other systems, we sampled biminima for PdnAuN−n (using the “average” Gupta parameters from ref. 41) and again found biminima counts decreasing with N, similar to PtnPdN−n. We suspect that this trend is a general characteristic of segregating systems, where the number of significant optima in the permutation domain appears to diminish with system size. In contrast, the increase in biminima counts for AunAg75−n (compared to N = 55) suggests that the exact opposite may be true for systems that favour mixing, which is consistent with our previous observations for binary Lennard-Jones clusters.15
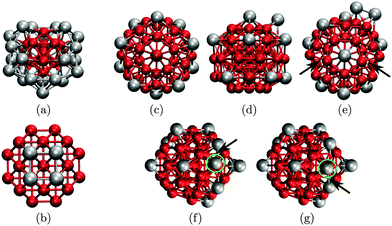
We now shift focus to CunAgN−n – a system with a relatively large degree of lattice mismatch (more than 10%). Results for N = 38 and 75 show strikingly large biminima counts, which can be attributed to our sampling procedure spanning multiple geometries that are distinctly different from the initial truncated octahedron (N = 38) or Marks decahedron (N = 75). As an illustrative example, in Fig. 3a and b we visualise the lowest-lying biminima for Cu13Ag25 (a) and Cu34Ag4 (b). In both cases the initial geometry is a truncated octahedron, which remains intact throughout biminima sampling for Cu34Ag4, but gradually changes for Cu13Ag25 solely by virtue of quenching, and eventually we find the structure illustrated in Fig. 3a. In fact, the biminimum in Fig. 3a closely resembles (but not quite matches) the putative global minimum,42 and it is noteworthy that it has been found without random Cartesian moves, especially in view of the differences between the initial and the final geometric motifs. This result implies that, for systems with large lattice mismatch, quench-assisted local combinatorial optimisation (in the permutation domain) can provide an additional and potentially significant guiding force towards the globally optimal geometry. Hence, even if the notion of nanoalloy homotops loses its global combinatorial character, the use of a local combinatorial search will still remain a viable option.
It is worth noting that CunAg55−n yields total biminima counts and hit rates that are comparable to PtnPd55−n and AunAg55−n (see Fig. 2). This congruence is possibly due to the relative robustness of closed-shell icosahedra, which evidently remain (largely) intact for all three systems. However, subtle morphological distortions still occur in CunAg55−n in the range 23 ≤ n ≤ 44. These rearrangements often involve one or two Ag atoms being dislodged from a vertex site and moved to a different position on the cluster surface, as illustrated in Fig. 3c–e. In the same system we also find configurations that look almost identical to the naked eye (and could be mistakenly regarded as the same homotop) but are actually different biminima. Snapshots in Fig. 3f and g show two such biminima, illustrating how lattice strain effects can lead to very subtle consequences that may be difficult to detect. These observations also highlight the inherent coupling of the combinatorial and the continuous sub-problems in nanoalloy structure prediction, and untangling these sub-problems in lattice mismatched systems may be particularly difficult (and perhaps unnecessary).
Due to a growing interest in trimetallic nanoalloys,43,44 we have also sampled biminima for selected PtlPdmAun and CulAumAgn Mackay icosahedra with l + m + n = 55 and the Gupta parameters taken from ref. 30 and 45. Compared with the binary counterparts, these ternary systems proved more susceptible to geometric distortion during the quasi-combinatorial sampling procedure. This complication precludes further characterisation of the effective quasi-combinatorial landscape, but it suggests that strain effects may become more pronounced as the number of species grows (at fixed total atom count).
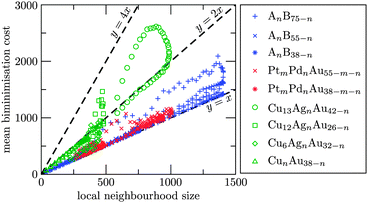
Having demonstrated the (albeit limited) utility of biminima in characterising the topography of quasi-combinatorial landscapes, we now consider the utility of bi- and multiminima for the purpose of global optimisation. Fig. 4 shows that, for all binary and ternary systems not containing both Cu and Au, the average number of quenches required to find a biminimum is only marginally larger than the local neighbourhood size. While the reasons why Cu–Au-based systems stand out are not entirely clear, the scaling for all other systems shows that most of the computational effort is spent on verifying biminima as opposed to locating them. This observation suggests that developing more efficient ways of verifying biminima will be worthwhile.
As a final demonstration, in Fig. 5 we present mean first-encounter times (MFETs) for global optimisation of CunAu38−n and Cu13AgnAu42−n, with the target energies for the putative global minima taken from ref. 29 and 30, respectively. We consider three different variants of GBH as a global search strategy, each with random displacement and permutation moves. The first variant (GBH1) includes the surface refinement scheme described in Section 3.3 and it involves complete scanning of the local neighbourhood to verify biminima each time. In the second variant (GBH2) we chose not to verify biminima and limit the sorted neighbourhood scan just to the first ten entries (recall Section 3.1). In the third variant (GBH3) we also disable the surface refinement scheme to gauge its effectiveness. Finally, the results are compared with previously reported benchmarks for the adaptive immune optimisation algorithm (AIOA).29,30
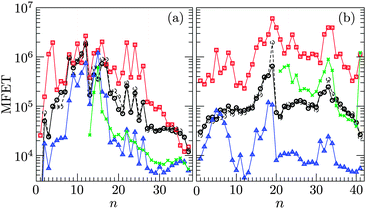 | ||
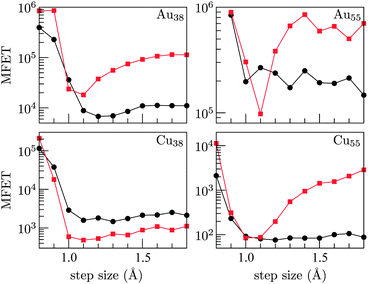
| Fig. 5 Mean first-encounter times (MFETs), quantified by the number of quenches, for (a) CunAu38−n and (b) Cu13AgnAu42−nversus n. The red squares correspond to data from (a) ref. 29 and (b) ref. 30. Black circles (GBH1), blue triangles (GBH2) and green crosses (GBH3) correspond to data sets for three different variants of generalised basin-hopping. The dashed and solid black circles represent Monte Carlo protocols with slightly different handling of the temperature parameter. | ||
Note that MFETs for GBH1 were averaged over a variable number of hits, ranging from 10 to 103. Also, the benchmarking procedure comes in two slightly different flavours: in one the temperature parameter is reset to the initial value of kBT = 0.05 eV each time the specified target energy is hit, and in the other the temperature is not reinitialised during the entire run. In both cases the random Cartesian displacement was capped at 1.5 Å, while Nres (recall Section 3.2) was set to 50 for CunAu38−n and 10 for Cu13AgnAu42−n. These minor differences in the Monte Carlo protocol are somewhat arbitrary, but the agreement between them provides some reassurance that the statistics are meaningful. Hence, from Fig. 5 we infer that GBH1 generally outperforms AIOA, by more than an order of magnitude in some cases, and is slower only in four instances: CunAu38−n with n = 11, 17, 35 and 36. For Cu13AgnAu42−n the superiority of GBH1 appears to be more convincing. In a few cases we have checked that the relative efficiency is not overly sensitive to the choice of Nres or the initial temperature, and so the superiority of GBH1 can be attributed to systematic multiminima-targeting.
It is worth reiterating that GBH1 carries a significant computational overhead due to biminima verification. This overhead is reduced in GBH2, often (but not always) yielding significantly lower MFETs. The efficiency gain varies due to variable correlation between exact (ΔEij) and approximate (ΔEij*) swap gains. Nonetheless, it is clear that reducing the local neighbourhood structure can lower the computational cost by an order of magnitude. Although the particular approximation in GBH2 (adapted from Lai et al.23) is not easily tractable and does not guarantee convergence to a biminimum, biminima candidates could be verified in a separate post-processing step if required. Alternatively, one could redefine biminima by restricting interchanges to atoms that are near-neighbours in coordinate space, which will make the size of the local neighbourhood scale roughly linearly with the number of particles (N), though it may also produce more biminima. Linear scaling with N can also be achieved by relaxing the constraint of fixed stoichiometry and using the Hamming distance,21 which measures the minimum number of substitutions (as opposed to swaps) required to obtain one multiset from another. We intend to explore these possibilities in future studies.
Finally, MFETs obtained using GBH3 show that the effectiveness of our surface refinement scheme is system-dependent. For CunAu38−n with n ≥ 13 the scheme can either increase or decrease MFET by up to an order of magnitude, while for Cu13AgnAu42−n with n ≥ 21 it consistently improves the efficiency by more than an order of magnitude. To elucidate the general utility of surface refinement we consider MFETs for single-component CuN and AuN clusters with N = 38 and 55, focusing on the effect of random step size. Fig. 6 clearly shows that, without surface refinement, choosing a random displacement step that is too small or too large can severely hamper the search performance, and there appears to be an optimal step size of around 1.1 Å for all the cases considered (and it was used in GBH3). The sweet spot exists because an overly small step decreases the probability of escape from the catchment basin of a current minimum, while an overly large step decreases the probability of reaching a low-energy minimum. Evidently, the use of surface refinement consistently reduces the penalty associated with overly large steps, which can be advantageous when an optimal step size is not known in advance and has to be chosen arbitrarily.
5 Summary
We have outlined a general strategy for global optimisation for nanoalloys based on a mixed-variable approach and systematic targeting of multiminima − configurations that are local minima with respect to multiple metrics. The strategy was incorporated into a global search method, namely generalised basin-hopping (GBH), which was used to explore and characterise the quasi-combinatorial energy landscape associated with nanoalloy homotops. The number of biminima in these effective landscapes was shown to systematically vary with the preference for mixing/segregation, whereas the computational cost of finding biminima scaled quadratically with system size in most cases. Based on these observations, we conclude that biminima targeting is likely to be more effective for model nanoalloys with a higher preference for segregation. GBH was also demonstrated to be effective for global optimisation of binary and ternary nanoalloys that feature a significant level of lattice mismatch.6 Associated content
Example input and output for generalised basin-hopping in GMIN31 can be found at http://www-wales.ch.cam.ac.uk/examples/GMIN/.Acknowledgements
This work was financially supported by EPSRC Grant No. EP/J010847/1 and the ERC.References
- R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910 CrossRef CAS PubMed.
- H.-L. Jiang and Q. Xu, J. Mater. Chem., 2011, 21, 13705–13725 RSC.
- N. Moghimi and K. Leung, Anal. Chem., 2013, 85, 5974–5980 CrossRef CAS PubMed.
- M. B. Cortie and A. M. McDonagh, Chem. Rev., 2011, 111, 3713–3735 CrossRef CAS PubMed.
- Nanoalloys: Synthesis, Structure and Properties, ed. D. Alloyeau, C. Mottet and C. Ricolleau, Springer, 2012 Search PubMed.
- Nanoalloys: from fundamentals to emergent applications, ed. F. Calvo, Elsevier, 2013 Search PubMed.
- F. H. Stillinger and T. A. Weber, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 25, 978–989 CrossRef CAS.
- D. J. Wales and J. P. K. Doye, J. Chem. Phys., 2003, 119, 12409–12416 CrossRef CAS PubMed.
- J. Jellinek and E. Krissinel, Chem. Phys. Lett., 1996, 258, 283–292 CrossRef CAS.
- Z. Li and H. A. Scheraga, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 6611–6615 CrossRef CAS.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- S. Goedecker, J. Chem. Phys., 2004, 120, 9911–9917 CrossRef CAS PubMed.
- R. L. Johnston, Dalton Trans., 2003, 4193–4207 RSC.
- A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704 CrossRef PubMed.
- D. Schebarchov and D. J. Wales, Phys. Rev. Lett., 2014, 113, 156102 CrossRef CAS.
- T. Schiavinotto and T. Sttzle, Comput. Oper. Res., 2007, 34, 3143–3153 CrossRef PubMed.
- N. Mladenović and P. Hansen, Comput. Oper. Res., 1997, 24, 1097–1100 CrossRef.
- P. Hansen and N. Mladenović, Eur. J. Oper. Res., 2001, 130, 449–467 CrossRef.
- N. Mladenović, M. Dražić, V. Kovačevic-Vujčić and M. Čangalović, Eur. J. Oper. Res., 2008, 191, 753–770 CrossRef PubMed.
- P. Hansen, N. Mladenović and J. A. Moreno Pérez, Ann. Oper. Res., 2010, 175, 367–407 CrossRef.
- R. Hamming, Bell Syst. Tech. J., 1950, 29, 147–160 CrossRef PubMed.
- T. Ye, R. Xu and W. Huang, J. Chem. Inf. Model., 2011, 51, 572–577 CrossRef CAS PubMed.
- X. Lai, R. Xu and W. Huang, J. Chem. Phys., 2011, 135, 164109 CrossRef PubMed.
- D. Schebarchov and D. J. Wales, J. Chem. Phys., 2013, 139, 221101 CrossRef CAS PubMed.
- X. Shao, L. Cheng and W. Cai, J. Comput. Chem., 2004, 25, 1693–1698 CrossRef CAS PubMed.
- X. Wu and W. Cheng, J. Chem. Phys., 2014, 141, 124110 CrossRef PubMed.
- F. Cleri and V. Rosato, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 22–33 CrossRef CAS.
- A. Rapallo, G. Rossi, R. Ferrando, A. Fortunelli, B. C. Curley, L. D. Lloyd, G. M. Tarbuck and R. L. Johnston, J. Chem. Phys., 2005, 122, 194308 CrossRef PubMed.
- X. Wu, W. Cai and X. Shao, J. Comput. Chem., 2009, 30, 1992–2000 CrossRef CAS PubMed.
- X. Wu, G. Wu, Y. Chen and Y. Qiao, J. Phys. Chem. A, 2011, 115, 13316–13323 CrossRef CAS PubMed.
- D. J. Wales, GMIN: A program for basin-hopping global optimisation, basin-sampling, and parallel tempering, URL: http://www-wales.ch.cam.ac.uk/GMIN/.
- M. T. Oakley, R. L. Johnston and D. J. Wales, Phys. Chem. Chem. Phys., 2013, 15, 3965–3976 RSC.
- G. Barcaro, L. Sementa and A. Fortunelli, Phys. Chem. Chem. Phys., 2014, 16, 24256–24265 RSC.
- G. G. Rondina and J. L. F. Da Silva, J. Chem. Inf. Model., 2013, 53, 2282–2298 CrossRef CAS PubMed.
- D. J. Wales et al., The Cambridge Cluster Database, URL http://www-wales.ch.cam.ac.uk/CCD.html, 2001.
- A. L. Mackay, Acta Crystallogr., 1962, 15, 916 CrossRef CAS.
- L. D. Marks, Philos. Mag. A, 1984, 49, 81 CrossRef CAS PubMed.
- G. Rossi, R. Ferrando, A. Rapallo, A. Fortunelli, B. C. Curley, L. D. Lloyd and R. L. Johnston, J. Chem. Phys., 2005, 122, 194309 CrossRef PubMed.
- R. H. Leary and J. P. K. Doye, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, R6320–R6322 CrossRef CAS.
- L. O. Paz-Borbon, T. V. Mortimer-Jones, R. L. Johnston, A. Posada-Amarillas, G. Barcaro and A. Fortunelli, Phys. Chem. Chem. Phys., 2007, 9, 5202–5208 RSC.
- F. Pittaway, L. O. Paz-Borbn, R. L. Johnston, H. Arslan, R. Ferrando, C. Mottet, G. Barcaro and A. Fortunelli, J. Phys. Chem. C, 2009, 113, 9141–9152 CAS.
- S. Núñez and R. L. Johnston, J. Phys. Chem. C, 2010, 114, 13255–13266 Search PubMed.
- L. Wang and Y. Yamauchi, Chem. Mater., 2011, 23, 2457–2465 CrossRef CAS.
- S. Khanal, N. Bhattarai, J. J. Velazquez-Salazar, D. Bahena, G. Soldano, A. Ponce, M. M. Mariscal, S. Mejia-Rosales and M. Jose-Yacaman, Nanoscale, 2013, 5, 12456–12463 RSC.
- G.-H. Wu, Q.-M. Liu and X. Wu, Chem. Phys. Lett., 2015, 620, 92–97 CrossRef CAS PubMed.
Footnote |
| † The hit rate, or relative encounter probability, is equal to the number of times the lowest-encountered biminimum has been hit, divided by the total number of convergences to a biminimum. |
| This journal is © the Owner Societies 2015 |