From zeolite nets to sp³ carbon allotropes: a topology-based multiscale theoretical study

Abstract

We present a comprehensive computational study of sp³-carbon allotropes based on the topologies proposed for zeolites. From ≈600 000 zeolite nets we identified six new allotropes, lying by at most 0.12 eV per atom above diamond. The analysis of cages in the allotropes has revealed close structural relations to diamond and lonsdaleite phases. Besides the energetic and mechanical stability of new allotropes, three of them show band gaps by ca. 1 eV larger than that of diamond, and therefore represent an interesting technological target as hard and transparent materials. A structural relation of new allotropes to continuous random networks is pointed out and possible engineering from diamond thin films and graphene is suggested.

---

Introduction

In the last few years there has been explosive interest in predicting novel carbon allotropes. Special attention has been paid to sp³ allotropes since most computational studies were conducted in order to elucidate the atomistic structure of the product of the graphite cold compression¹ that is different either from diamond or lonsdaleite phases of carbon. A manifold of computational techniques have been applied to address the problem of crystal structure prediction, e.g. evolutionary algorithms,² accelerated molecular dynamics (metadynamics),^2,3 graph–theoretical approaches⁴etc. Among the most stable sp³-carbon allotropes proposed so far we note W-carbon (sp. gr. Pnma, cnw‡),⁵ Z-carbon⁶ (alternatively named oC16-II^7,8 and Cco-C8,⁹ sp. gr. Cmmm, sie) and H-carbon (sp. gr. Pbam),¹⁰ the latter being energetically less stable than the diamond phase by ∼0.15 eV per atom. Quite recently, at least three novel sp³-carbons, referred to as S-S₁Z₄ (sp. gr. P2/m),¹¹oC32 (sp. gr. Cmmm)¹² and M585 (sp. gr. P2₁/m),¹³ were predicted to be even more stable, within ∼0.06–0.09 eV per atom above diamond. However, in many cases the structures generated using very sophisticated methods appeared to be topologically related to certain crystal structures (mainly silicates or zeolites) known to solid-state chemists for many years. For example, if we identify tetrahedral Si atoms in the structure of any three-dimensional silicate with a nominal composition SiO₂ and contract oxygen –O– links while keeping the structure connectivity, we end up with a 4-coordinated 3D net¹⁴ that could be considered as a hypothetical sp³-carbon allotrope (after proper rescaling of interatomic distances). Note that enumeration of silica polymorphs was shown to be beneficial for the structure prediction of ice polymorphs as well.¹⁵ Enumeration of tetrahedral nets has a long tradition in crystallography and solid-state chemistry and nowadays we have several huge catalogues^16,17 containing both experimentally observed and hypothetical structure types. Computational studies of carbon allotropes revealed quite a few phases that are topologically related either to known silicates or zeolites. We mention, for example, bct-4 carbon¹⁸ (called as such since 1999¹⁹ but firstly described in 1993 as 8-tetra(2,2)tubulane by Baughman and Galvão²⁰) that shares the same topology with zeolite BCT (crb), tP12 carbon that possesses the topology of keatite (kea)²¹ and a dense phase of carbon with the topology of quartz (qtz).²¹ More zeolite-like structures (ATO, KAN, ATN, AFI) were recently proposed by Oganov et al.,²³ although their relation to zeolites was not explicitly discussed. This motivated us to have a closer look at the databases of zeolite networks compiled by Deem¹⁶ and Treacy§¹⁷ and to perform a comprehensive study on their relevance to the chemistry of carbon allotropes.

Computational methodology and results

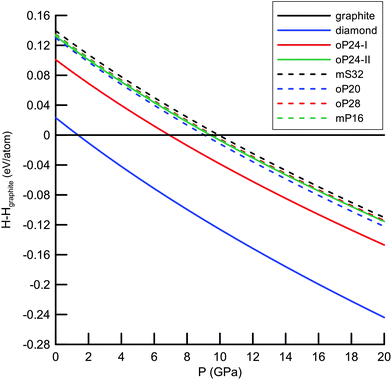
Out of databases containing 331 372 (Deem) and 274 611 (Treacy) silica polymorphs, we pre-selected only the nets without 3- and/or 4-rings (in total 5074 + 234 candidates) that would normally induce too much strain in the carbon structures. Afterwards, we performed geometrical relaxation of the nets using Systre²⁵ from the Gavrog package (http://gavrog.org/). To this end, we applied the concept of embedding of a net into 3D Euclidean space^25,26 with maximal space-group symmetry compatible with the net topology. Apart from the requirements of maximal symmetry, the nodes of the nets were placed in such a way that the distances to nearest neighbors (that correspond necessarily to the edges of the nets) should be equal, if possible, and then were finally set to 1.54 Å. However, it has long been recognized that not only the distances to nearest neighbors are important, but so are the distances to the next-nearest neighbors (normally referred to as ‘non-bonding’ distances).²⁷ For example, in the diamond structure the next-nearest neighbors are by ∼63% farther than the nearest neighbors of any atom. From the set of geometrically relaxed structures we extracted 665 nets where the distances to the next-nearest neighbours were by 40% longer than the distances to the nearest neighbors. These structures considered as being stereochemically feasible (in the sense of Öhrström and O'Keeffe)²⁷ were then optimized with the Tersoff force field²⁸ as implemented in the GULP package.²⁹ After this force-field calculation, 257 structures remained 4-coordinated and were subject to further optimizations using the density-functional-based tight-binding method (DFTB)³⁰ in its non-self-consistent version as implemented in the DFTB+ package.³¹ From the set of the DFTB-optimized structures, we selected 93 representatives that lie within a narrow energetic window (0.40 eV per atom) relative to diamond and performed structural relaxation (at the DFT-GGA (PBE) level)³² using the SIESTA package.³³ The structures that are diamond–lonsdaleite polytypes were excluded from our calculations since they had already been widely discussed in the literature.^34,35 To identify polytypes (altogether 24 structures) we used ToposPro.³⁶ Finally, we focus on the six structures being energetically the lowest, within 0.12 eV per atom (or less) relative to diamond (Fig. 1, 2 and Table 1). This threshold was chosen arbitrarily and was motivated mainly by pragmatic considerations to narrow the manifold of structures to be considered. We characterized their energetic, electronic, vibrational and mechanical properties at the DFT-GGA (PBE) level of theory (see Table 1) as implemented in the CRYSTAL14 package.^37,38 To this end, we fully optimized the structures (both unit cells and atomic coordinates) by using the conjugate-gradient method until the Hellmann–Feynman forces on the atoms became less than 0.003 eV Å⁻¹ and the stress on the cells less than 0.02 GPa. In the calculations all electrons were treated explicitly and described by the basis set of triple-ζ valence with polarization quality (TZVP) as developed by Peintinger et al.³⁹ The Monkhorst–Pack meshes for summations over Brillouin zones were chosen, as usual, based on the convergence of the total energy versus the number of k-points. The energetic stability of the allotropes was evaluated by comparing their cohesive energies (ΔE, Table 1). Additionally, we computed the enthalpies (at T = 0 K) of the allotropes relative to graphite up to 20 GPa (Fig. 1). For optimized structures we estimated elastic constants to ensure the stability against mechanical deformation (see Table S2, ESI†). This is guaranteed by the positive definiteness of the 6 × 6 matrix of the (second order) elastic constants. To qualify the dynamical stability of our allotropes, we calculated phonon band structures (at zero pressure) by applying a finite displacement method in a 2 × 2 × 2 supercell, as implemented in the CRYSTAL14 package (Fig. S2, ESI†). No imaginary frequencies were observed throughout the Brillouin zone. The DFTB-based molecular dynamics simulations in the NpT ensemble (T = 300 K, p = 1 bar) were performed using the cp2k code⁴⁰ (time step was set to 0.5 fs while the total simulation time was 10 ps) and confirmed the dynamical stability of our allotropes under ambient conditions.

Fig. 1 Enthalpies (relative to graphite) of the six novel carbon allotropes.

Fig. 2 Carbon allotropes considered in this work. To illustrate structural relations to diamond (dia) and lonsdaleite (lon), adamantane cages [6⁴] are highlighted in cyan, and the cages [6³] and [6⁵] are depicted in yellow and green, respectively.

Table 1 Structural, energetic, electronic and mechanical properties of novel carbon phases

Structure	Space group	ρ (g cm^−3)	ΔE (PBE), (eV per atom) (VASP)^a	ΔE (PBE) (eV per atom) (CRYSTAL14)	E_gap (eV) PBE/HSE	B (GPa) (PBE)	H (GPa)
a Since most computational studies on carbon allotropes were performed using the VASP code,^43,44 we also provide for comparison the energies of our allotropes relative to diamond calculated using VASP at the same level of theory (PBE functional). The numbers # correspond to the hypothetical zeolites from the Deem database.^16
Diamond	Fd3̄m	3.509	0.00	0.00	4.2/5.4	441	93.2
#8170628 (oP24-I)	Pbam	3.409	0.07	0.08	4.7/5.9	418	91.1
#8129388 (oP24-II)	Pnma	3.408	0.10	0.11	4.9/6.3	412	90.8
#8255250 (oP28)	Pnma	3.415	0.10	0.12	4.7/6.0	412	90.9
#8155755 (oP20)	Pmma	3.431	0.09	0.11	4.0/5.1	420	91.4
#8036927 (mS32)	C2/m	3.418	0.11	0.12	4.5/5.7	415	90.8
#8036926 (mP16)	P2/m	3.423	0.10	0.11	4.3/5.5	423	91.0

---

Bulk moduli (B, Table 1) were calculated by fitting the total energy as a function of volume to the third-order Birch–Murnaghan equation of state. Furthermore, we estimated the Vickers hardness (H, Table 1) of the allotropes following the empirical approach of Gao et al.⁴¹ Electronic band structures were calculated using the PBE functional (see Fig. S2, ESI†) as well as the hybrid HSE functional,⁴² the latter was chosen to more accurately estimate the band gaps.

Discussion

From the point of view of energetics, the structures found in this work are the lowest-energy (by at most 0.12 eV per atom less favourable than diamond) sp³-carbon allotropes proposed so far and compete only with the recently discovered oC32, S-S₁Z₄ and M585 carbons (all three lying within 0.08 eV per atom relative to diamond at the DFT-PBE level) illustrated in Fig. 3.¶ The calculated bulk moduli and hardness values suggest that new allotropes are slightly less hard than diamond. Furthermore, we have also computed phonon dispersion curves at the pressures of the phase transitions of graphite – predicted a new phase and also observed no imaginary frequencies, thus confirming the feasibility of the suggested phase transformations.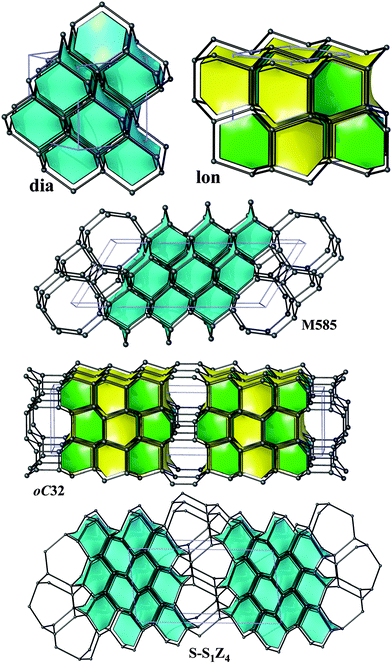

Fig. 3 Diamond (dia), lonsdaleite (lon) and the recently discovered oC32, S-S₁Z₄ and M585, illustrated in the same style as Fig. 2.

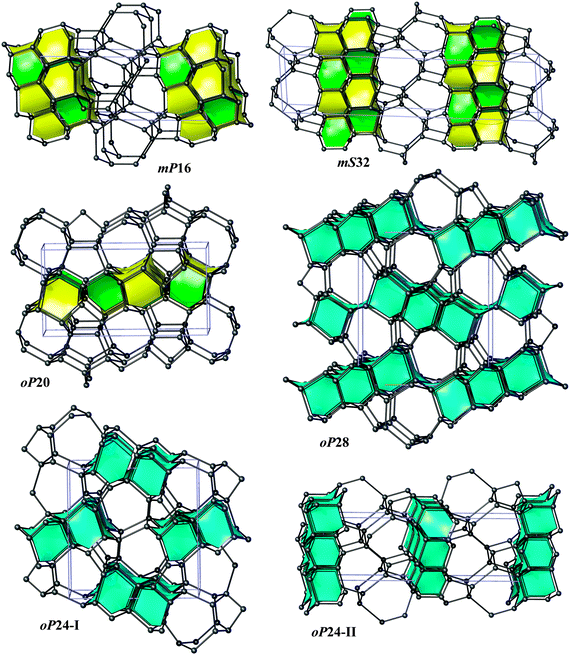
Bond lengths in the optimized structures span a relatively broad range of 1.50–1.63 Å. Bond angles are distributed in a range of 94°–128°, indicating significant deviations from the ideal tetrahedral value of 109.47° (Table S1, ESI†). However, the non-bonding distances remain quite large, by at least ∼1.38 times longer than the covalent bond lengths. To analyze the structure of allotropes in more detail, we adopted the tiling approach⁴⁵ that has been shown to be quite successful in the analysis of zeolites (both real and hypothetical)^46,47 as implemented in the ToposPro package.³⁶ In this approach, a three-periodic net is represented as a tiling of 3D space by cages that are generalized polyhedra.⁴⁵ This view provides a more detailed (and also more pictorial) structural description than e.g. ring statistics only, thus facilitating to capture structural relationships and to design new materials (especially, metal–organic frameworks, MOFs).⁴⁸ Note that three of our structures (oP24-I, oP24-II, and oP28) are closely related to diamond (dia) since adamantane cages (face symbol [6⁴])^47,49 can be easily recognized there (Fig. 2). The two structures, oP24-I and oP28, contain 1D columns of ‘fused’ adamantane cages, whereas oP24-II is built up from a monolayer of adamantane cages interconnected by corrugated graphene sheets (Fig. 4). The other three structures (oP20, mS32, and mP16) contain [6³] and [6⁵] cages that are characteristic of lonsdaleite (lon).⁵⁰ It is interesting that the [6³] and [6⁵] cages do occur in our allotropes in the same ratio 1 : 1 as it is the case for lonsdaleite itself. mP16 and mS32 are constructed from lonsdaleite bilayers interconnected by corrugated graphene sheets. In contrast, oP20 contains lonsdaleite-like monolayers linked together by ‘interstitial’ chains of isolated dumb-bells.

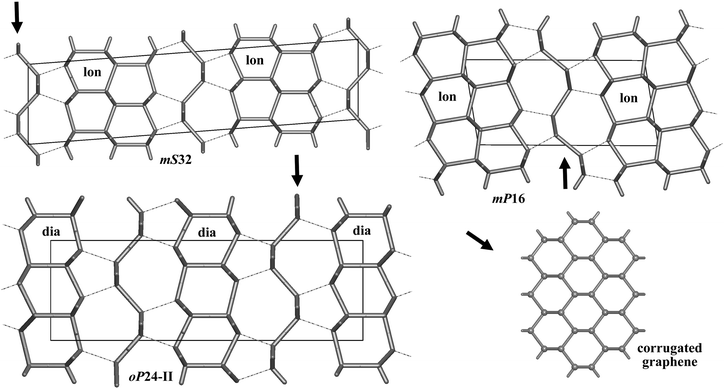Fig. 4 Three allotropes shown as built from diamond (dia) and lonsdaleite (lon) layers with intercalated corrugated graphene sheets.

In five structures there are only 5-, 6- and 7-rings, whereas oP20 contains 8-rings as well. As a result, our structures could be obtained either from diamond or lonsdaleite phases by small ‘topological flips’, for example, if two adjacent 6-rings (a ‘6 + 6’ pattern) were transformed into adjacent 5- and 7-rings (a ‘5 + 7’ pattern). In a certain sense, given also the relatively large number of symmetry-independent atoms in the unit cells (see the values of transitivity in Table 2), they resemble continuous random networks (widely used in the modeling of amorphous tetrahedral semiconductors).⁵¹ The same observation is also true for the recently proposed M585 phase¹³ that incorporates a distinctive ‘slab’ of adamantane cages and for oC32 carbon that contains a slab of lonsdaleite cages (Fig. 3). By increasing the number of atoms in the unit cell, it is thus possible to construct allotropes that will be arbitrarily close to diamond in terms of energy (at least within 0.06 eV per atom), as the example of S-S₁Z₄¹¹ demonstrates (it comprises quadruple layers of adamantane cages, Fig. 3).

Table 2 Tiling description of the carbon allotropes examined

Structure	Space group	Transitivity^a	Face symbol^b
a An important characteristic of a tiling is its transitivity [pqrs], where the integers p, q, r, and s stand for the number of inequivalent vertices, edges, faces, and tiles, respectively. b Face symbol of the form [A^a·B^b] indicates that there are a faces that are A-rings and b faces that are B-rings.^49
Diamond (dia)	Fd3̄m	[1111]	[6^4]
Lonsdaleite (lon)	P63/mmc	[1222]	[6^3] + [6^5]
M585	P21/m	[9(14)(14)8]	6[6^4] + [5^2·6^2] + [5^2·6^2·8^2]
oC32	Cmmm	[49(12)9]	6[6^3] + 6[6^5] + 2[6^2·8^2] + [4^2·6^4]
S-S1Z4	P2/m	[(12)(20)(19)(11)]	8[6^4] + [5^2·6^2] + [6^2·7^2] + [5^2·6^2·7^2]
oP24-I	Pbam	[6(10)95]	2[6^4] + [5^2·6^2] + [6^2·7^2] + [5^2·6^2·7^2]
oP24-II	Pnma	[6995]	2[6^4] + [5^2·6^2] + [6^2·7^2] + [5^2·6^2·7^2]
oP28	Pnma	[7(11)(10)6]	3[6^4] + [5^2·6^2] + [6^2·7^2] + [5^2·6^2·7^2]
oP20	Pmma	[6996]	2[6^3] + 2[6^5] + [5^2·6^2] + 2[6^2·8^2] + [5^4·6^4]
mS32	C2/m	[8(14)(12)7]	2[6^3] + 2[6^5] + [5^2·6^2] + [6^2·7^2] + [5^2·6^2·7^2]
mP16	P2/m	[8(14)(13)7]	2[6^3] + 2[6^5] + [5^2·6^2] + [6^2·7^2] + [5^2·6^2·7^2]

---

More strikingly, some of our structures (oP24-I, oP24-II, oP28) have optical band gaps that are by at most ∼1 eV higher than that of diamond (and are independent of the pressure at least up to 30 GPa). This is certainly an interesting and unexpected result since hypothetical sp³ carbon allotropes with the gaps larger than diamond are rarely found. Wide band gaps are known for some clathrate-like open frameworks, in particular, for compound VIII from ref. 24 (named ajk3 in ToposPro TTD collection)³⁶ and for the dense tP12 allotrope (kea),²¹ having the gaps of 6.4 and 6.3 eV, respectively (estimated at the HSE level),⁴² remaining the widest-gap carbon materials suggested to date. However, the structure of tP12 or clathrate-like open networks is very different either from diamond or lonsdaleite (no [6⁴], [6⁵] or [6³] cages can be found in them). The band gaps of diamond–lonsdaleite polytypes lie in between those of pure diamond (5.4 eV) and lonsdaleite (5.0 eV).^21,34,35 Our results demonstrate that wide band gaps can also be engineered in the structures closely related to diamond (e.g. upon mild amorphization). Our best candidate in this regard is the oP24-II allotrope with a gap of 6.3 eV thus representing an interesting technological target as a hard and transparent material. To engineer this material in practice, one may think of combining diamond thin films and graphene, as suggested by the structure of oP24-II (Fig. 4).

Relatively large band gaps of novel allotropes have prompted us to estimate their refractive indices (Table 3), as implemented in CRYSTAL14, at the PBE level. Since our allotropes are either orthorhombic or monoclinic, they show anisotropy of their refractive indices, although it is not so pronounced. In general, refractive indices remain close to that of diamond, despite larger band gaps. The calculation showed that the most transparent allotrope would be oP20 (competing with oP24-II) while the others appear to be ‘brilliant’ ones (i.e., as refractive as diamond at least along the z direction).

Table 3 Refractive indices for novel carbon allotropes^a

Refractive index (PBE), optical range	Diamond	oP24-II	oP20	oP28	mP16	mS32	oP24-I
a Minimal and maximal refractive indices among considered allotropes are highlighted in bold. Experimental values for diamond (300 K, λ = 589 nm)^52 are given in parentheses.
n XX	2.40 (2.42)	2.36	2.31	2.36	2.35	2.35	2.34
n YY	2.40 (2.42)	2.37	2.36	2.38	2.36	2.36	2.38
n ZZ	2.40 (2.42)	2.38	2.36	2.42	2.40	2.40	2.42

---

In conclusion, we presented a comprehensive multiscale theoretical study of sp³-carbon allotropes based on the topologies proposed for silica. We found six structures that stand out for their energetic stability, mechanical stiffness and optical properties. We showed that new allotropes are closely related to diamond and lonsdaleite. As a consequence, they could represent the structures of carbon networks upon partial, mild amorphization or otherwise point towards engineering composites to be made out of diamond thin films and graphene.

Acknowledgements

The work of D.M.P., V.A.S. and A.V.S. was financially supported by the Megagrant No. 14.25.31.0005 of the Russian Ministry of Science. I.A.B. and A.V.S. thank Prof. Dr Gotthard Seifert for fruitful discussions. The work of V.S. and A.S. was supported in part by the Russian Foundation for Basic Research under the Grant 14-03-97034.

References

1. W. L. Mao, H.-K. Mao, P. J. Eng, T. P. Trainor, M. Newville, C.-C. Kao, D. L. Heinz, J. Shu, Y. Meng and R. J. Hemley, Science, 2003, 302, 425.
2. A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704.
3. R. Marton̆ák, A. R. Oganov and C. W. Glass, Phase Transitions, 2007, 80, 277.
4. R. T. Strong, C. J. Pickard, V. Milman, G. Thimm and B. Winkler, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 045101.
5. J.-T. Wang, C. Chen and Y. Kawazoe, Phys. Rev. Lett., 2011, 106, 075501.
6. M. Amsler, J. A. Flores-Livas, L. Lehtovaara, F. Balima, S. A. Ghasemi, D. Machon, S. Pailhès, A. Willand, D. Caliste, S. Botti, A. San Miguel, S. Goedecker and M. A. L. Marques, Phys. Rev. Lett., 2012, 108, 065501.
7. D. Selli, I. A. Baburin, R. Marton̆ák and S. Leoni, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 161411.
8. S. E. Boulfelfel, D. Selli and S. Leoni, Z. Anorg. Allg. Chem., 2014, 640, 681.
9. Z. S. Zhao, B. Xu, X. F. Zhou, L. M. Wang, B. Wen, J. L. He, Z. Y. Liu, H. T. Wang and Y. J. Tian, Phys. Rev. Lett., 2011, 107, 215502.
10. C. He, L. Sun, C. Zhang, X. Peng, K. Zhang and J. Zhong, Solid State Commun., 2012, 152, 1560.
11. H. Niu, X.-Q. Chen, S. Wang, D. Li, W. L. Mao and Y. Li, Phys. Rev. Lett., 2012, 108, 135501.
12. M. Zhang, H. Liu, Y. Du, X. Zhang, Y. Wang and Q. Li, Phys. Chem. Chem. Phys., 2013, 15, 14120.
13. C. He and J. Zhong, Solid State Commun., 2014, 181, 24.
14. V. A. Blatov and D. M. Proserpio, Periodic-Graph Approaches in Crystal Structure Prediction, in Modern Methods of Crystal Structure Prediction, ed. A. R. Oganov, Wiley-VCH, Berlin, 2011, pp. 1–28.
15. G. A. Tribello, B. Slater, M. A. Zwijnenburg and R. G. Bell, Phys. Chem. Chem. Phys., 2010, 12, 8597.
16. M. W. Deem, R. Pophale, P. A. Cheeseman and D. J. Earl, J. Phys. Chem. C, 2009, 113, 21353 , http://www.hypotheticalzeolites.net/DATABASE/DEEM/DEEM_PCOD/index.php.
17. M. M. J. Treacy, K. H. Randall, S. Rao, J. A. Perry and D. J. Chadi, Z. Kristallogr., 1997, 212, 768 , http://www.hypotheticalzeolites.net/DATABASE/BRONZE_CONFIRMED/index.html.
18. K. Umemoto, R. M. Wentzcovitch, S. Saito and T. Miyake, Phys. Rev. Lett., 2010, 104, 125504.
19. P. A. Schultz, K. Leung and E. B. Stechel, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 733.
20. R. H. Baughman and D. S. Galvão, Chem. Phys. Lett., 1993, 211, 110.
21. Q. Zhu, A. R. Oganov, M. A. Salvadó, P. Pertierra and A. O. Lyakhov, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 193410.
22. M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 41, 1782.
23. M. Hu, Z. Zhao, F. Tian, A. R. Oganov, Q. Wang, M. Xiong, C. Fan, B. Wen, J. He, D. Yu, H.-T. Wang, B. Xu and Y. Tian, Sci. Rep., 2013, 3, 1331.
24. A. J. Karttunen, T. F. Fässler, M. Linnolahti and T. A. Pakkanen, Inorg. Chem., 2011, 50, 1733.
25. O. Delgado-Friedrichs and M. O'Keeffe, Acta Crystallogr., Sect. A: Found. Crystallogr., 2003, 59, 351.
26. O. Delgado-Friedrichs, M. D. Foster, M. O'Keeffe, D. M. Proserpio, M. M. J. Treacy and O. M. Yaghi, J. Solid State Chem., 2005, 178, 2533.
27. L. Öhrström and M. O'Keeffe, Z. Kristallogr., 2013, 228, 343.
28. J. Tersoff, Phys. Rev. Lett., 1988, 61, 2879.
29. J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291.
30. G. Seifert, D. Porezag and T. Frauenheim, Int. J. Quantum Chem., 1996, 58, 185.
31. B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
33. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745.
34. C. Raffy, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 075201.
35. B. Wen, J. Zhao, M. J. Bucknum, P. Yao and T. Li, Diamond Relat. Mater., 2008, 17, 356.
36. V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576.
37. R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D'Arco, Y. Noel, M. Causa, M. Rerat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287.
38. R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco, M. Llunell, M. Causà, and Y. Noël, CRYSTAL14 User's Manual, University of Torino, Torino, 2014.
39. M. F. Peintinger, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2013, 34, 451.
40. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15.
41. F. Gao, J. He, E. Wu, S. Liu, D. Yu, D. Li, S. Zhang and Y. Tian, Phys. Rev. Lett., 2003, 91, 015502.
42. J. Heyd, G. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207.
43. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
44. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
45. V. A. Blatov, O. Delgado-Friedrichs, M. O'Keeffe and D. M. Proserpio, Acta Crystallogr., Sect. A: Found. Crystallogr., 2007, 63, 418.
46. N. A. Anurova, V. A. Blatov, G. D. Ilyushin and D. M. Proserpio, J. Phys. Chem. C, 2010, 114, 10160.
47. V. A. Blatov, G. D. Ilyushin and D. M. Proserpio, Chem. Mater., 2013, 25, 412.
48. O. Delgado-Friedrichs, M. O'Keeffe and O. M. Yaghi, Phys. Chem. Chem. Phys., 2007, 9, 1035.
49. V. A. Blatov, M. O'Keeffe and D. M. Proserpio, CrystEngComm, 2009, 12, 44.
50. O. Delgado-Friedrichs, M. O'Keeffe and O. M. Yaghi, Acta Crystallogr., Sect. A: Found. Crystallogr., 2003, 59, 515.
51. F. Wooten and D. Weaire, Solid State Phys., 1987, 40, 1.
52. S. Adachi, Optical Constants of Crystalline and Amorphous Semiconductors: Numerical Data and Graphical Information, Springer Science + Business Media, 1999.

---

Footnotes

† Electronic supplementary information (ESI) available: Bond lengths and angles (Table S1), elastic constants (Table S2), electronic and phonon band structures (Fig. S1 and S2, respectively) and the coordinates (6_allotropes.cif). See DOI: 10.1039/c4cp04569f

‡ Where available, we provide bold three-letter symbols for nets as suggested by M. O’Keeffe,²² http//rcsr.net.

§ The databases of Deem and Treacy contain theoretically as well as (possibly not all) experimentally characterized zeolites. Therefore, we performed screening of carbon allotropes based on all experimentally observed zeolitic nets using the density-functional-based tight-binding method (DFTB).³⁰ We found out that the most stable allotropes (within 0.15 eV per atom above diamond) have the topologies of MTN, MEP and DOH (considered by Karttunen et al.²⁴), the next stable one being BCT/crb that is by ~0.24 eV per atom higher than diamond. Other nets give rise to even less stable sp³-carbon structures, mainly due to the large amount of 4-rings common for ‘real’ zeolites.

¶ To handle the large amount of literature on carbon allotropes and to help the researchers to avoid duplication of results, we are currently building a web-based database (SACADA – Samara Carbon Allotrope Database). A preliminary version was presented at the 14th session of the V. A. Fock Meeting on Quantum and Computational Chemistry, “Bridging the gap between solid state quantum chemistry and structural chemistry of allotropes”, 2014 Aug. 18–22, Samara, Russia (http://www.qcc.ru/~fock/meeting.en.php).

---