Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Energetics, thermal isomerisation and photochemistry of the linkage-isomer system [Ni(Et4dien)(η2-O,ON)(η1-NO2)]†
Jonathan M.
Skelton‡
,
Rachel
Crespo-Otero‡
,
Lauren E.
Hatcher
,
Stephen C.
Parker
,
Paul R.
Raithby
and
Aron
Walsh
*
Department of Chemistry, University of Bath, Claverton Down, Bath, BA1 7AY, UK. E-mail: a.walsh@bath.ac.uk
First published on 26th August 2014
Abstract
We present the results of a detailed theoretical study of the linkage isomerisation in [Ni(Et4dien)(η2-O,ON)(η1-NO2)] (Et4dien = N,N,N′,N′-tetraethyldiethylenetriamine). We probe the structure and bonding of the three experimentally-identified isomers in this system through electronic-structure calculations, and we establish possible transition pathways between them using transition-state modelling and periodic solid-state molecular-dynamics simulations. We also explore the photochemical isomerisation reaction using time-dependent density-functional theory. These results provide a thorough account of the linkage isomerisation in this compound, and add insight to ongoing experimental work on this and related systems.
Introduction
Linkage isomerisation is an interesting phenomenon whereby the binding mode of a ligand to the transition-metal centre in a coordination or organometallic complex changes in response to an external stimulus, typically thermal or photoactivation.1 Particularly in the solid state, where linkage isomerisation represents a single-crystal-to-single-crystal transition, these systems have attracted much interest. The canonical example, and one of the earliest systems studied, is perhaps sodium nitroprusside (Na[Fe(CN)5(NO)]), in which two long-lived metastable species identified spectroscopically following photoactivation2–4 were found to correspond to different binding modes of the NO ligand.5 Since this pioneering work, many more solid-state linkage-isomerisation systems have been found, with two prototypical families of compounds, viz. Ni–NO2 (ref. 6–11) and Ru–SO2,12–15 being widely studied.Solid-state linkage isomerism can be studied experimentally through single-crystal photocrystallography measurements, in which the crystal is irradiated with light in situ on the diffractometer.1 At low temperatures, the decay of the photoexcited metastable state(s) back to the stable ground state is blocked, allowing them to be characterised through single-crystal X-ray diffraction. Above a certain critical temperature, the so-called metastable limit,1 the onset of decay back to the ground-state structure occurs. Around the metastable limit, additional short-lived species may be observed in experiments where the crystal is continuously pumped with light during the data collection and thus reaches a “pseudo steady state” population of isomers.1,10
A particular challenge from a materials-design standpoint is to engineer the molecular solid so as to obtain a large photoconversion yield while maintaining the reversibility of the transition. In our recent work with linkage isomeric systems, we have chosen to employ a simple crystal-engineering approach, aiming to produce a large “reaction cavity” within which the isomerisation can take place. The reaction cavity serves both to reduce the steric barriers to the transition, and also the stress it places on the crystal.6,15 Using this design principle, several Ni–NO2 systems with reversible, 100% photoconversion yields have been synthesised.6,9,10
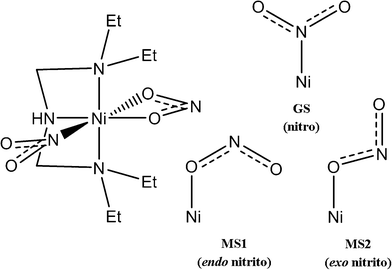
[Ni(Et4dien)(η2-O,ON)(η1-NO2)] represents a particularly interesting linkage-isomer system because the isomerisation has been shown to be thermally as well as photochemically activated.7,10 Skeletal structures of the complex and of the three binding modes of the isomerisable NO2 group are shown in Fig. 1. The octahedral Ni centre is coordinated at three sites by the tridentate Et4dien ligand, with another two sites being taken up by an η2-bound NO2 group. The sixth site is occupied by a second η1-coordinated NO2 group, the binding mode of which can be switched between three known forms. The N-bound nitro isomer is the stable ground state (GS), and is formed by cooling in the absence of illumination. The metastable O-bound endo-nitrito isomer (MS1) can be generated from the GS complex by photoactivation at 100 K and, additionally, can be generated thermally in significant population at higher temperatures.7 More recently,10 a second O-bound exo-nitrito isomer (MS2) was observed in pseudo-steady-state photocrystallographic experiments at temperatures close to the metastable limit of ~150–160 K, which indicates that this species has a lifetime that is shorter than the duration of the X-ray data collection.
While the steady-state structures of the various isomers in this system have been well characterised, little is presently known of the transition pathways which connect them. In this respect, the thermal isomerisation exhibited by this system makes it an ideal candidate for theoretical investigation. Whereas exploring excited-state potential-energy surfaces can pose a significant challenge for quantum chemistry, characterisation of ground-state properties is much less difficult. An understanding of the thermal isomerisation pathways could then, in principle, provide a basis for modelling the photochemical reaction.
In this article, we present the results of a computational study of the linkage isomerisation in [Ni(Et4dien)(η2-O,ON)(η1-NO2)], using a combination of solid-state and molecular quantum-chemistry calculations. We perform detailed electronic-structure calculations on the three species, and identify the isomerisation pathways connecting them using transition-state modelling and solid-state molecular dynamics. We also show that the crystal environment significantly influences the energetics of the isomerisation. Finally, we present some preliminary data from ongoing photochemical modelling, which provides some insight into possible excited-state isomerisation pathways. Our modelling provides important theoretical insight into the dynamics of linkage isomerisation in this system, and will support ongoing experimental work on this and related materials.
Computational methods
All computational modelling was carried out within the Kohn–Sham density-functional theory (DFT) formalism.16 Models of the ground- and metastable-state crystal structures were created from the crystallographic data published with ref. 7. For the molecular quantum-chemistry calculations, single complexes were extracted from these published structures, and an initial model of the MS2 complex was made from the MS1 structure by rotating the O-bound NO2 ligand. Separate software packages were used for the solid-state and molecular calculations, as outlined below.Periodic solid-state calculations
DFT calculations with periodic boundary conditions were carried out using the VASP code.17 The semi-local PBEsol exchange-correlation functional18 was used for the majority of the calculations, although we also tested several other functionals, viz. PBE,19 the semi-empirical dispersion-corrected PBE-D220 and PBE-D321 functionals, and the non-local vdw-DF22 and vdw-DF223 functionals. Projector-augmented wave pseudopotentials24 were used, and the Brillouin zone was sampled at the Γ point. A plane-wave cut-off of 944.5 eV was used during geometry optimisations and single-point calculations, and molecular-dynamics (MD) simulations were performed with a smaller cut-off of 755.6 eV. As described in the results section, a Hubbard U correction of 5.32 eV was applied to the Ni d bands during the MD simulations, using the scheme of Dudarev et al.25 For these calculations, non-spherical contributions to the gradient corrections within the PAW spheres were accounted for.Geometry optimisation was performed by allowing the atomic positions to relax until the magnitude of the forces on the ions was less than 10−2 eV Å−1. After convergence, we found that with PBEsol the stress on the simulation cell was less than 0.2 GPa in both models, so we opted to fix the volume and cell shape at the experimentally-determined parameters. MD simulations were carried out with the constraint that only the isomerisable NO2 ligands be allowed to move; by fixing the lighter atoms, we were then able to use a relatively long integration timestep of 5 fs. A Berendsen thermostat26 was used to fix the temperature during the dynamics simulations.
Molecular calculations
All isolated molecular calculations were performed using Gaussian09 program.27 A range of different functionals were employed for studying energetics, viz. PBE,19 the PBE0,28 B3LYP,29and TPSSH30 hybrid functionals, the M06 meta-hybrid,31 and the CAMB3LYP long-range-corrected hybrid.32 The M06 and PBE0 functionals were used for the transition-state and photochemistry modelling, due to their good general-purpose performance when describing a broad range of properties.33 Triplet and singlet states were computed using the unrestricted and restricted approaches, respectively. The LANL2DZ basis set and corresponding pseudopotential were used to treat the Ni atom, with various combinations of the split-valence 6-31G(p), 6-311G(d) and 6-311++G(d,p) basis sets being used for the lighter atoms. Polarisable continuum model (PCM) calculations, carried out to study the possible effects of the crystal environment on properties,34 were performed to mimic three different solvents with increasing dielectric constants, viz. toluene (ε = 2.4), ethanol (ε = 24.9) and water (ε = 78.4).Transition-state modelling calculations were performed in the gas phase with the 6-31G(d) and 6-311++G(d,p) basis sets and the M06 and PBE0 functionals. Calculations with water as a polarisable continuum were performed using the 6-31G(d) basis set for geometry optimisation, and the 6-311++G(d,p) basis set for single-point energy calculations. Harmonic vibrational-frequency calculations were performed to confirm the nature of all stationary points found, and Intrinsic Reaction Coordinate (IRC) calculations35 were carried out to check the connection between the reactants, transition states and products.
To study the photochemistry of the complexes, time-dependent DFT (TD-DFT) calculations on both the triplet and singlet excited states were carried out, using the corresponding triplet and singlet ground-state wavefunctions as references. Different functionals, viz. M06,31 B3LYP,29 PBE0,28 M06HF36,37 and wB97xd38 were considered in combination with the LANL2DZ pseudopotential and basis set for Ni, with a 6-311++G(d,p) basis set being used for the light atoms (this mixed basis set is referred to as LANL2DZ/6-311++G(d,p) in the text). The TD-DFT calculations were performed with water as a polarisable continuum.
Results and discussion
Energetics and ground-state magnetism
Given that the crystal structures are formed of essentially isolated complexes, one would not expect long-range magnetic interactions to occur between the Ni centres. To confirm this, we compared the relative energies of a ferromagnetic state, with all the Ni magnetic moments aligned in the same direction, and three different antiferromagnetic states with the moments on different pairs of Ni atoms oriented in opposite directions. We found no significant difference in energy between these configurations; the maximum 0.08 kJ mol−1 per molecule is well within the error of the calculations.
To compare the calculated GS–MS1 energy difference against experiment, we fitted the temperature dependence of the isomer populations reported in ref. 7 to a Boltzmann expression, which yielded an enthalpy difference of 9.69 kJ mol−1 per molecule (see ESI†). This value is less than half the difference computed in these calculations, and so we therefore opted to investigate briefly the effect of some computational parameters on the computed ΔE.
Given that the Ni centre is a central component in the isomerisation process, it is possible that the discrepancy arises from common issues which (semi-)local DFT functionals can encounter when treating strongly-correlated 3d-electrons.39 We therefore investigated the effect of applying a Hubbard U correction to the Ni d states on the energy difference between the two structures. Strikingly, we found that the difference reduced systematically with the magnitude of the U term (see ESI†), such that for a value of 5.32 eV the experimental enthalpy difference was reproduced to within 0.2 kJ mol−1. The size of this correction is reasonable, and is not too dissimilar to, for example, the typical values used in DFT + U calculations on NiO in the literature (e.g.ref. 25 and 40). We also note in passing that extrapolating the trend suggests that a larger on-site potential of around 10 eV would zero the energy difference between the isomers. Finally, it is worth mentioning that while, in the present case, the U correction was chosen to match experimental data, as is fairly common practice, an alternative, a less empirical linear-response method exists to obtain the value from first-principles;41 however, this technique is not presently implemented in VASP.
A second factor which may play an important role in the energetics is dispersion, another effect which many DFT functionals struggle to describe accurately, and which is likely to be significant in molecular crystals such as this. The PBEsol functional does not include any explicit dispersion corrections, and so to quantify the differences such corrections might make we performed additional geometry optimisations on the GS and MS1 crystals using a selection of other functionals, viz. PBE,19 PBE-D220 and PBE-D3,21 and vdw-DF22 and vdw-DF2.23 The D2/D3 functionals apply a semi-empirical correction to the PBE energies to approximately account for dispersion interactions, while the vdw-DF functionals are non-empirical and attempt to treat dispersion more accurately through a non-local electron correlation. After geometry optimization, we compared the calculated GS–MS1 energy differences, and also various bond lengths around the Ni centre, between the six functionals to experimental data (see ESI†). We found that the energy differences computed with PBE and the two vdw-DF functionals came closest to the experimental values, whereas the dispersion corrections applied by the PBE-D2/D3 methods yielded values similar to PBEsol; however, in all cases the difference was consistently overestimated. The better match of the computed energy difference with experimental data obtained with the vdw-DF functionals might be taken as an indication that dispersion forces make a significant contribution to the energetics, although this should be a tentative conclusion, since it is quite possible that the dispersion corrections in these functionals may be compensating for other issues, e.g. the aforementioned inability of standard DFT functionals to treat the correlated Ni 3d electrons.
However, bearing this caveat in mind, these two sets of tests suggest that to accurately capture the energetics of this system requires both a good description of the Ni d electrons, and also accounting for dispersion forces.
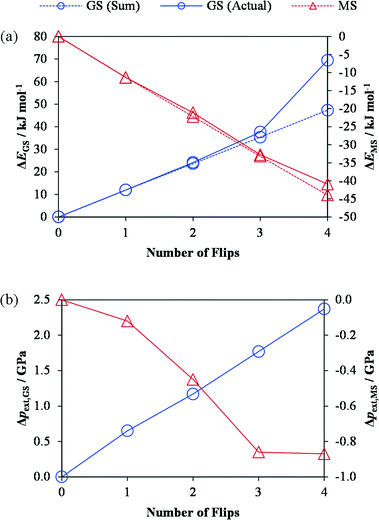
An important question about the isomerisation process is whether or not it proceeds in a concerted manner, i.e. whether one complex isomerising influences subsequent events at neighbouring sites. To investigate this, we created variants of the GS and MS1 crystal structures in which 1–4 of the η1-bound NO2 ligands were swapped with their isomers “by hand”, thereby converting 1–4 of the symmetry-equivalent molecular complexes to the other isomer. The geometries of these models were then optimized with PBEsol, and, after verifying that the isomerisation was not reversed, we compared the energy change from flipping 1–4 of the ligands in tandem against the sum of the energy required to flip the same ligands in isolation (Fig. 2a).
For the GS-to-MS1 isomerisation, up to three flips (75% conversion) leads to a change in energy which is more or less equal to the sum of those for the individual isomerisations, whereas the fourth leads to a disproportionately large relative increase in energy. We observed a linear increase in the stress on the unit cell with successive isomerisations (Fig. 2b), which is consistent with the fact that the MS1 structure has a larger unit-cell volume than the GS one. If this build-up of stress makes the final isomerisation energetically more difficult, one might infer that, during very fast (e.g. laser-induced) photoisomerisation processes, the final 25% conversion may be constrained by lattice relaxation (phonon coupling). In keeping with this picture, we found that for the reverse MS1-to-GS transition, where isomerisation leads to a negative stress, the energy required to flip all four ligands was practically identical to the sum of the individual isomerisation energies. These results thus suggest that, at equilibrium, the isomerisation is not a concerted process, in either direction, and is likely to happen randomly throughout the crystal. This is consistent with kinetic data from photocrystallographic measurements.10
The relative energy differences between the three species, calculated using various functionals and basis sets, are collected in Table 1. Corresponding energy differences between MS1 and MS2 may be found in Table 2. Interestingly, MS1 is found to be lower in energy than the GS in the gas phase for all the combinations considered, save for PBE/LANL2DZ/6-311G(d) (ΔEGS–MS1 = −13 kJ mol−1), which suggests that PBE may exhibit some favourable error compensation. To investigate this further, we created periodic molecular models of the GS and MS1 complexes, by placing the molecules in a simulation cell with a large vacuum gap to separate them from adjacent periodic images. After converging the energy as a function of the gap size and optimizing the geometry with PBEsol, we obtained an energy difference of ΔEGS–MS1 = −14.6 kJ mol−1 per molecule (see ESI†). Single-point calculations with a Hubbard U correction of 5.32 eV and with the bare PBE functional yielded energy differences of −1.4 and −9.3 kJ mol−1, respectively. The reasonably good correspondence between the latter value and the molecular calculations suggests that the 6-311G(d) basis set used in the latter is approaching the convergence limit with respect to this property.
| XC functional | Basis set | Continuum | ΔEGS–MS1/kJ mol−1 |
|---|---|---|---|
| PBE | LANL2DZ/6-31G(d) | None | 2.45 |
| PBE0 | None | 11.7 | |
| B3LYP | None | 15.70 | |
| TPSSH | None | 9.71 | |
| M06 | None | 9.33 | |
| CAMB3LYP | None | 19.70 | |
| PBE | LANL2DZ/6-311G(d) | None | −13.01 |
| PBE0 | None | 6.03 | |
| M06 | None | 1.62 | |
| M06 | 6-311G(d) | None | 2.39 |
| M06 | LANL2DZ/6-311++G(d,p) | None | 1.84 |
| M06 | PhMe | −1.81 | |
| M06 | EtOH | −6.96 | |
| M06 | H2O | −7.54 |
| XC functional | Basis set | Continuum | ΔEMS2–MS1/kJ mol−1 |
|---|---|---|---|
| M06 | LANL2DZ/6-311G++(d,p) | None | 14.31 |
| M06 | H2O | 4.83 | |
| PBE0 | None | 8.69 | |
| PBE0 | H2O | 0.86 |
For PBE, PBE0 and M06, ΔEGS–MS1 becomes more negative as the basis set size is increased, although even with the largest basis sets the latter two still predict an incorrect relative ordering. Comparing the PBE0, TPSSH and PBE functionals, which notionally have decreasing exchange-energy contributions, the energy difference is seen to decrease; this is similar to the effect of including the U correction in the periodic PBEsol calculations, and illustrates that the exchange potential makes an important contribution to the energy difference between the isomers.
To obtain the correct size of the energy difference between the isomers, we found that the basis set for the lighter elements needed to be of at least triple-zeta quality, while for the metal the use of the LANL2DZ basis set and pseudopotential did not affect significantly the results, leading to a change in ΔEMS1–GS of only 0.6 kJ mol−1 with the M06 functional. To obtain the correct sign of ΔEGS–MS1, a combination of a triple-zeta basis set for the light elements and the continuum solvent model was needed. With the M06 functional in combination with the 6-311++G(d,p) basis set, PCM simulations with the dielectric constant of toluene, ethanol and water gave ΔEGS–MS1 values of −1.81, −6.96 and −7.54 kJ mol−l, respectively.
We note that differences in vibrational zero-point energy are not expected to affect significantly the relative stabilities of the species; energy corrections estimated within the harmonic approximation at the M06/LANL2DZ/6-31G(d) level of theory change ΔEGS–MS1 by less than 1 kJ mol−1 (ΔE + ZPVE = 8.76 kJ mol−1, compared to ΔE = 9.33 kJ mol−1).
We now consider the optimised geometries of the molecular complexes. Fig. 3 shows the geometry in the plane defined by the nitro ligands and the Ni centre in the GS, MS1 and MS2 isomers. Comparing with available experimental data (see ESI†), the agreement between the bond lengths in the optimised complexes and the crystal structures is generally very good, with the only exception being a significant underestimation of the length of the O(η1-NO2)–HN distance. We note that a crystal structure containing the MS2 geometry was not available to compare this set of data against.
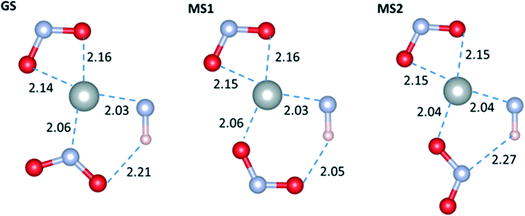 | ||
| Fig. 3 Optimised geometries of the GS, MS1 and MS2 complexes with the M06 functional and the LANL2DZ/6-311++G(d,p) basis set, with water as a dielectric continuum. | ||
The main difference between the GS and MS1 isomers lies in the relative stabilities of the Ni–N and Ni–O bonds. A Natural Bond Orbital (NBO) second-order perturbation analysis42 shows that the most important stabilisation of both bonds is through electron transfer from the ligand to the metal. The Ni–N bond is more energetically favourable by around 9 kJ mol−1 due to the better donor capacity of N (Δ2ELP(N)→Ni = 160 kJ mol−1, Δ2ELP(O)→Ni = 151 kJ mol−1 at the M06/6-311++G(d,p) level with a continuum of water).
An additional source of stabilisation is the weak hydrogen bond between the ligand O atom and the NH group on the Et4dien molecule (classified as such based on intermolecular distance criteria43). The effect of this interaction is most pronounced in the gas phase; the presence of a solvent increases the O–H–N distances, leading to a consequent weakening of the interaction due to dielectric screening. Comparing the hydrogen-bond distances between the isomers, we obtain 2.01–2.21 and 1.93–2.05 Å in the GS and MS1 complexes, respectively, depending on the level of theory.
As in MS1, the coordination of the NO2 group to Ni in the MS2 complex is through O. However, due to the geometry of the ligand, the hydrogen-bonding interaction occurs via N, and the length is comparable to the bond in the GS complex, making it weaker than the bond in the MS1 isomer. As a result of the effect of a dielectric medium on the hydrogen-bonding interaction, the energy difference between MS1 and MS2 is reduced significantly when a polarisable continuum is included in the calculations, ranging from ΔEMS2–MS1 = 18.72 kJ mol−1 in the gas phase to 4.83 kJ mol−1 in water using the M06 functional, and from 8.69 to 0.86 kJ mol−1 with PBE0.
In summary, these calculations suggest that the energy differences between the three linkage isomers is governed by a combination of the influence of the ligand on the Ni 3d states, and hydrogen-bonding interactions between the ligand and the N–H group on the Et4dien ligand. Whether modelled explicitly or implicitly, it is apparent that the crystalline environment significantly influences the relative energies of the three isomers compared to in the gas phase. However, this appears to be largely a dielectric effect, as the periodic calculations suggest a minimal interaction, if any, between complexes in the molecular crystal; this observation extends to the isomerisation process itself, as the present calculations confirm the experimental finding that the isomerization is likely to be a random, rather than a concerted, process. The pronounced effect that the crystal environment has on the isomerization energetics reinforces the idea that crystal engineering, e.g. tuning the size of the “reaction cavity”, could be used to control the switching process, as has already been discussed in relation to a number of linkage-isomer systems.6,15
| Species | Continuum | ΔEPBE0/kJ mol−1 | ΔEM06/kJ mol−1 |
|---|---|---|---|
| TS1 | None | 66.3 | 71.4 |
| H2O | 60.7 | 79.7 | |
| TS2 | None | 66.6 | 70.8 |
| H2O | 68.1 | 81.1 | |
| MTS1 | None | 31.2 | 35.9 |
| H2O | 32.2 | 33.8 | |
| MTS2 | None | 31.1 | 35.1 |
| H2O | 33.8 | 33.1 |
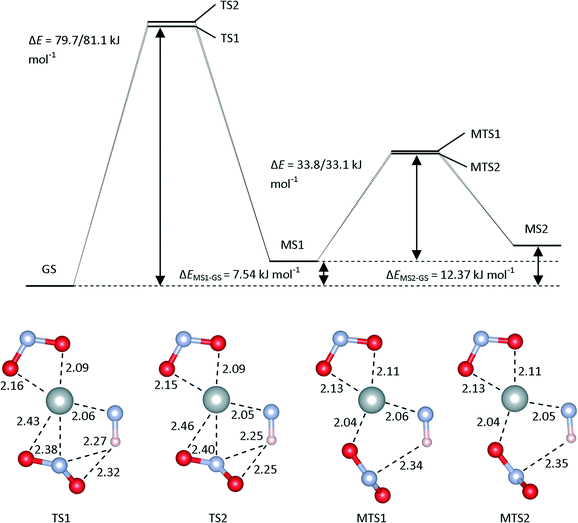
TS1 and TS2 correspond to the rotation of the NO2 group up and down with respect to the plane, respectively. The energy barriers for these processes, computed at the M06/LANL2DZ/6-311++G(d,p) level of theory, are both around 70 kJ mol−1, and the presence of water as a continuum increases both barrier heights by roughly 10 kJ mol−1. With the PBE0 functional, both barriers are reduced.
The transition states connecting MS1 and MS2, labelled MST1 and MST2, are (anti)clockwise rotations of the ligand about the Ni–O bond. In both the gas phase and continuum calculations, and for both the M06 and PBE0 functionals, the two were found to have very similar energies and geometries. While these transition states are superficially similar to TS1 and TS2, the Ni–O bond length remains constant between MS1 and MS2, indicating that this O remains bonded during the rotation; consequently, the MS1-to-MS2 isomerisation requires roughly half the energy of the GS-to-MS1 conversion.
We also explored possible direct isomerisation pathways between the GS and MS2 isomers by a relaxed scan of the Ni–O–N angle in the Ni–O2N plane. This yielded a continuous increase in energy, with no further stabilisation. When intermediate geometries were optimised as transition states, an additional transition state, TS3, was found (see ESI†), but IRC calculations indicated that this does not connect GS and MS2; rather, this transition state appears to be an in-plane rotation of the O2N ligand connecting two further high-energy metastable structures which have not been observed experimentally. Whether these structures represent transient species (e.g. detectable in ultrafast laser-excitation experiments), or are merely artifacts, is presently unclear.
The kinetic measurements reported in ref. 10 yielded an activation barrier for the decay of MS1 to the GS of 48.6 kJ mol−1, which is closer to the calculated barrier for the MS1-to-MS2 transition than to the MS1-to-GS one. In the absence of a direct GS-to-MS2 isomerisation pathway, this would suggest that the calculated barriers for the GS-to-MS1 transition have been overestimated considerably. However, if a GS-to-MS2 path did exist, and had an activation barrier lower than that for the MS1-to-MS2 transition, then the rate-limiting step in the decay would then be the MS1 → MS2 isomerisation, and the calculated barrier for this is much closer to the experimental value. With regard to the accuracy of the calculated barriers, it is worth noting that the functional, basis set and continuum were optimised to reproduce only the enthalpy differences, and not necessarily the transition barriers. Moreover, since the energetics in this system are evidently quite sensitive to the continuum, it is possible that the use of the high dielectric constant of water in the PCM model may be compensating for deficiencies in either or both of the functional or basis set.
To investigate this further requires the calculation or measurement of the macroscopic dielectric constant of the crystal, which is the subject of ongoing work.
In spite of these potential issues, the present calculations establish an intuitive isomerization pathway between the three isomers. The isomerisation between MS1 and MS2 has a (relatively) low activation energy, which would allow equilibration between them over a range of temperatures, and, as found from the energetics calculations, MS1 is the more stable of the two. This low thermal barrier to conversion between the endo and exo isomers naturally explains the observation of the latter as a transient intermediate in a narrow temperature range – when the system is heated close to the relatively low-temperature metastable limit, the MS1-to-MS2 isomerisation will be accessible, but slow (on crystallographic data-collection timescales), resulting in a small but detectable steady-state population of the MS2 state.
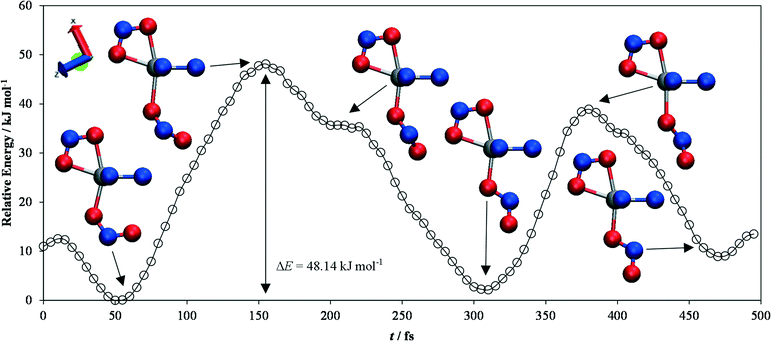 | ||
| Fig. 5 Energy profile for the endo-to-exo transition in [Ni(Et4dien)(η2-O,ON)(η1-NO2)], obtained from constrained ab initio molecular-dynamics simulations. The energies are expressed relative to the lowest-energy point on the curve. Snapshots of the geometry of the complex at various local maxima and minima on the profile are shown, with the atoms colour coded as follows: N – blue, O – red, Ni – silver. The largest energy barrier involved in the switching is 48.14 kJ mol−1, and corresponds to a clockwise rotation of the NO2 group by approximately 45° from the endo position. The snapshots were created with the VMD software.44 | ||
This analysis suggests that the largest energy barrier in the switching process is the point at which the ligand is rotated by ~45° with respect to the plane in which it sits in the endo/exo positions.
This configuration is around 12.2 kJ mol−1 higher in energy than the one with the ligand at 90°, although the latter is still a local energy maximum. Indeed, a second position with the ligand at 45° to the endo/exo plane is also an energy maximum, and in this particular trajectory appears to block the ligand from making a complete rotation when it falls from the transition state to the local exo minimum.
The overall barrier height for the endo-to-exo transition is ~48 kJ mol−1, and the energy difference between the endo and exo forms is ΔEMS2–MS1 = 2.13 kJ mol−1. The discrepancy between these results and those from the molecular calculations is most likely due in part to the use of the semi-local PBEsol functional, as opposed to the more sophisticated (meta)hybrids available for molecular calculations, plus the fact that a large part of the structure was constrained to the initial MS1 geometry, thus preventing the rest of the molecular backbone relaxing during the transition.
However, the fact that the same transition states connecting MS1 and MS2 as were observed in the molecular calculations are seem in the MD calculations – in which the system is able to explore its potential energy surface more fully – serves as a powerful validation of the mechanism established from the former.
The experimentally-reported UV-visible spectrum of the GS complex in ref. 10 shows an intense absorption band around 400 nm (3.1 eV), and we would hence expect to predict a significant absorption in this spectral region from the molecular calculations, given a suitable choice of polarisable continuum. However, the prediction of accurate absorption energies and oscillator strengths represents a significant challenge for computational chemistry,45,46 and for most of the levels of theory considered in this work the first excited state with significant intensity appears at much higher energies; only M06 and B3LYP predict bands with significant oscillator strengths (around 0.02) close to the correct spectral region (3.64 and 3.82 eV, respectively). The most important excited states, at the TD-M06/LANL2DZ/6-311++G(d,p) level of theory with water as a continuum, are listed in Table 4. We show only the excited states that could be relevant for the photoisomerisation process, but the complete TD-DFT dataset, including the transitions obtained with all the functionals tested, may be found in the ESI.†
| State | E/eV (nm) | Oscillator strength | Assignment | State | E/eV (nm) | Oscillator strength | Assignment |
|---|---|---|---|---|---|---|---|
| GS-T1 | 0.98 (1260) | 0.0002 | ML | MS1-T1 | 1.01 (1230) | 0.0000 | ML |
| GS-T2 | 1.01 (1230) | 0.0001 | ML | MS1-T2 | 1.08 (1145) | 0.0000 | ML |
| GS-T3 | 1.08 (1145) | 0.0000 | ML | MS1-T3 | 1.55 (799) | 0.0003 | ML |
| GS-T4 | 1.55 (799) | 0.0002 | ML | MS1-T4 | 1.65 (752) | 0.0000 | ML |
| GS-T5 | 1.65 (752) | 0.0000 | ML | MS1-T5 | 1.82 (682) | 0.0002 | ML |
| GS-T6 | 1.82 (682) | 0.0001 | ML | MS1-T6 | 2.73 (455) | 0.0001 | ML |
| GS-T7 | 2.73 (455) | 0.0002 | MLCT (NO2) | MS1-T7 | 2.88 (431) | 0.0000 | MLCT (NO2) |
| GS-T8 | 2.88 (431) | 0.0000 | MLCT (O2N) | MS1-T8 | 3.41 (363) | 0.0000 | MLCT (O2N) |
| GS-T9 | 3.41 (363) | 0.0073 | ML | MS1-T9 | 3.61 (343) | 0.0015 | MLCT (NO2) |
| GS-T10 | 3.61 (343) | 0.0005 | MLCT (NO2) | MS1-T10 | 3.64 (340) | 0.0197 | ML |
| GS-T11 | 3.64 (340) | 0.0376 | ML | MS1-T11 | 3.67 (338) | 0.0218 | ML |
| GS-T12 | 3.67 (338) | 0.0205 | ML | MS1-T12 | 3.73 (332) | 0.0011 | ML |
| GS-T17 | 3.98 (312) | 0.0238 | ML | MS1-T15 | 3.98 (312) | 0.0379 | ML |
| GS-T18 | 4.02 (309) | 0.1216 | ML | MS1-T16 | 4.00 (310) | 0.1044 | ML |
| GS-T19 | 4.05 (306) | 0.0272 | ML | MS1-T17 | 4.03 (308) | 0.0104 | ML |
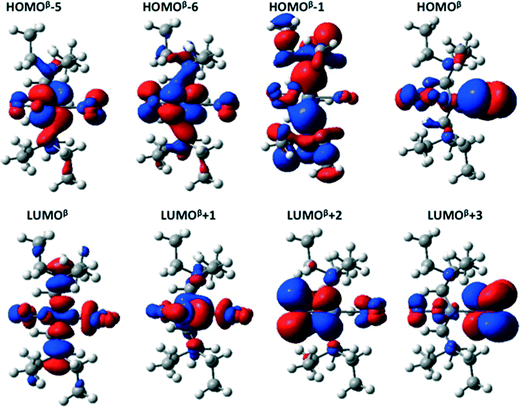
The main orbitals involved in the transitions in the GS isomer are shown in Fig. 6. The first six triplet excited states (T1 to T6) in both the GS and MS are transitions between the HOMOβ−5/HOMOβ−6 and LUMOβ/LUMOβ+1 orbitals; the orbital labelling is based on the beta spin channel (that which does not contain the two unpaired electrons) in which we found the most important calculated transitions took place. These electronic excitations all involve a redistribution of the electron density over the NO2 ligands and the metal, and as such can be assigned as delocalized metal-to-ligand (ML) transitions.
HOMOβ−5 contains an important contribution from the Ni dxz and ONO (static ligand) px orbitals, while HOMOβ−6 is made up of the Ni dxy and NO2 (isomerisable ligand) px orbitals. The LUMOβ and LUMOβ+1 orbitals have antibonding contributions between the Ni d orbitals in the yz plane and the py and pz orbitals on the nitro ligands. Consequently, the Ni–N and Ni–O bonds weaken when these excited states are populated. Although these states are not directly populated during the photoabsorption, they most likely do play a role in the deactivation process – if the molecule behaves according Kasha's rule, it is expected to persist longest in the T1 state.
For the GS molecule, the T7, T8 and T10 excited states are metal-to-ligand charge-transfer (MLCT) states, with the electron density transferred largely to the LUMOβ+2 and LUMOβ+3 orbitals, both of which are mainly localized on the NO2 and ONO groups, respectively. The equivalent excited states in the MS1 complex are T7, T8, T9 and T12.
Around 3.6 eV, there are two excited states with oscillator strengths larger than 0.02, T11 and T12, which both involve electronic transitions from the HOMOβ to LUMOβ+1 orbitals, yielding a redistribution of electron density from the orbitals in the plane to those perpendicular to it. The brightest computed excited states appear around 4 eV, and are T17–T19(GS) and T15–T17(MS1). The main electronic transitions giving rise to these states are from the HOMOβ and HOMOβ−1 to the LUMOβ and LUMOβ+1 orbitals.
The photocrystallographic experiments in ref. 10 were performed irradiating at the absorption maximum at 400 nm, and also at 500 nm to allow for better penetration of the light into the crystal. In both cases, the photoisomerisation reaction occurs with good conversion.7,10 These conditions should lead to population of excited states around T11, plus vibrationally-excited states of higher-energy electronic configurations which could contain contributions from the brightest states (e.g. T18). All these states lead to an increased antibonding interaction between the Ni and N atoms, which is consistent with their activating the GS → MS1 isomerisation.
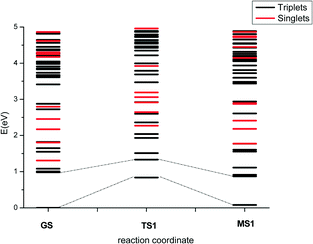
To explore this further, we computed the excited states of all the species involved in the thermal isomerisation mechanisms. Photochemical processes typically involve multiple states, and crossing between states with different spin multiplicity can also be important; therefore, singlet as well as triplet excited states were considered. The energy difference between the ground-state triplet and singlet states for the GS species is 1.31 eV, and there are three triplet excited states lower in energy than the singlet ground state.
Fig. 7 shows the energy profiles for the lowest-energy GS → MS1 photoisomerisation pathway; data for the other pathways, including for the MS1 → MS2 transition, may be found in the ESI.† The calculated isomerisation barriers in the singlet state are of the same order of magnitude or higher than the corresponding triplet barriers. Since the singlet and triplet states near in energy have different character, and the coupling between singlets and triplets requires this difference in electronic nature,47 plus a small energy difference to increase the spin–orbit coupling, crossing between singlet and triplets is a possibility which cannot be discarded; however, only a few singlet excited states are found below the corresponding triplets, which suggests crossings may not form a major part of the photochemical reaction mechanism.
Considering only the states with triplet multiplicity, three isomerisation mechanisms could potentially be important following light absorption: 1) isomerisation during the relaxation to T1; 2) isomerisation once the system is in T1; and 3) isomerisation in T0 if the excitation energy is transferred into vibrations, and the isomerisation then happens in the vibrational hot-ground state (i.e. vibronic coupling). Considering that the key experimental observations can be explained based on ground-state calculations, the third mechanism seems to be a likely candidate. Nonetheless, since photoexcitation is expected to populate states with significant antibonding character between the metal and the ligand, isomerisation in the excited state is also a strong possibility.
It is also possible that the photochemical process could occur through a combination of all these mechanisms. To distinguish between them, non-adiabatic dynamics simulations would be required. At present, such simulations are rare for organometallic compounds, due to the complexity of their potential-energy surfaces, which typically contain a high density of excited states and crossings between states of different multiplicities.45,48,49 This is an area of ongoing research that we aim to explore in our future work.
Conclusions
In summary, we have applied a combination of solid-state and molecular quantum-chemistry calculations to model the energetics and isomerisation processes in the [Ni(Et4dien)(η2-O,ON)(η1-NO2)] system.The effect of the isomerisable ligand on the Ni 3d states and weak interactions between the ligand and the Et4dien backbone appear to both be important contributors to the energy differences between the different linkage isomers. Our results suggest that the dielectric environment of the molecular crystal likewise has a significant effect on the relative stability of the isomers, and, to a lesser extent, the isomerisation barriers. However, beyond this the interactions between the molecular units in the solid are minimal, and thus polarisable-continuum model (PCM) calculations, with a suitable choice of the dielectric constant, may represent an efficient means of modelling this and, most likely, related systems.
Transition-state modelling suggests that the nitro-to-endo-nitrito and endo-to-exo-nitrito isomerisation scan both occur via rotations of the NO2 ligand out of the plane formed by the Ni–NO2 group in the (meta)stable isomers; the latter mechanism was verified by solid-state molecular dynamics, confirming the validity of this approach. There is an apparent overestimation of the activation barrier for the GS-to-MS1 transition compared to experiment, which requires further investigation; possibly in relation to this, we found no evidence of a transition path connecting the exo-nitrito and nitro forms directly, the reasons for which are not clear at present.
Modelling the photochemistry of the complex suggests that isomerisation could occur both in the electronically-excited state, and also in the vibrational hot-ground state after de-excitation. Distinguishing between these will require more involved non-adiabatic dynamics simulations, which will be a subject of further work. Furthermore, although these pathways provide a plausible mechanism for the photochemical reaction, there are additional possibilities which merit further investigation (e.g. the possible role of other transient metastable species).
Overall, this modelling study has provided a comprehensive picture of the linkage isomerisation phenomenon in this system, and we hope that the insight we have obtained will provide a sound basis both for explaining the behaviour of known, related systems, as well as for designing new materials with tunable switching behaviour and properties. Future work on this system, and on the simulation of molecular crystals in general, will benefit from exploiting more fully the synergy between solid-state and molecular modelling.
Acknowledgements
Illustrations were generated with the assistance of A. J. Jackson. The authors gratefully acknowledge financial support from an EPSRC programme grant (grant no. EP/K004956/1) and the European Research Council (grant no. 277757). We acknowledge use of the HECToR and ARCHER supercomputers through membership of the UKs HPC Materials Chemistry Consortium, which is funded by EPSRC grant no. EP/F067496, in the completion of this work. We also acknowledge use of Hartree Centre resources in this work. The STFC Hartree Centre is a research collaboratory in association with IBM providing High Performance Computing platforms funded by the UK's investment in e-Infrastructure. The Centre aims to develop and demonstrate next generation software, optimised to take advantage of the move towards exa-scale computing.Notes and references
- L. E. Hatcher and P. R. Raithby, Coord. Chem. Rev., 2014 DOI:10.1016/j.ccr.2014.02.021.
- U. Hauser, V. Oestreich and H. D. Rohrweck, Z. Phys. A: At. Nucl., 1977, 208, 17–25 CrossRef.
- H. Zöllner, T. Woike, W. Krasser and S. Haussühl, Z. Kristallogr., 1989, 188, 130–153 CrossRef PubMed.
- M. Rüdlinger, J. Schefer, G. Chevrier, N. Furer, H. U. Güdel, S. Haussühl, G. Heger, P. Schweiss, T. Vogt, T. Woike and H. Zöllner, Z. Phys. B: Condens. Matter, 1991, 83, 125–130 CrossRef.
- M. D. Carducci, M. R. Pressprich and P. Coppens, J. Am. Chem. Soc., 1997, 119, 2669–2678 CrossRef CAS.
- M. R. Warren, S. K. Brayshaw, A. L. Johnson, S. Schiffers, P. R. Raithby, T. L. Easun, M. W. George, J. E. Warren and S. J. Teat, Angew. Chem., 2009, 121, 5821–5824 CrossRef PubMed.
- L. E. Hatcher, M. R. Warren, D. R. Allan, S. K. Brayshaw, A. L. Johnson, S. Fuertes, S. Schiffers, A. J. Stevenson, S. J. Teat, C. H. Woodall and P. R. Raithby, Angew. Chem., Int. Ed., 2011, 50, 8371–8374 CrossRef CAS PubMed.
- S. K. Brayshaw, T. L. Easun, M. W. George, A. M. E. Griffin, A. L. Johnson, P. R. Raithby, T. L. Savarese, S. Schiffers, J. E. Warren, M. R. Warren and S. J. Teat, Dalton Trans., 2012, 41, 90–97 RSC.
- M. R. Warren, T. L. Easun, S. K. Brayshaw, R. J. Deeth, M. W. George, A. L. Johnson, S. Schiffers, S. J. Teat, A. J. Warren, J. E. Warren, C. C. Wilson, C. H. Woodall and P. R. Raithby, Chem. – Eur. J., 2014, 20, 5468–5477 CrossRef CAS PubMed.
- L. E. Hatcher, J. Christensen, M. L. Hamilton, J. Trincao, D. R. Allan, M. R. Warren, I. P. Clarke, M. Towrie, S. Fuertes, C. C. Wilson, C. H. Woodall and P. R. Raithby, Chem. – Eur. J., 2014, 20, 3128–3134 CrossRef CAS PubMed.
- P. Coppens, I. Novozhilova and A. Kovalevsky, Chem. Rev., 2002, 102, 861–883 CrossRef CAS PubMed.
- D. A. Johnson and V. C. Dew, Inorg. Chem., 1979, 18, 3273–3274 CrossRef CAS.
- A. Y. Kovalevsky, K. A. Bagley and P. Coppens, J. Am. Chem. Soc., 2002, 124, 9241–9248 CrossRef CAS PubMed.
- A. Y. Kovalevsky, K. A. Bagley, J. M. Cole and P. Coppens, Inorg. Chem., 2003, 42, 140–147 CrossRef CAS PubMed.
- A. E. Phillips, J. M. Cole, T. d'Almeida and K. S. Low, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 155118 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, 1133–1138 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47 Search PubMed.
- L. A. Constantin, J. M. Pitarke, J. F. Dobson, A. Garcia-Lekue and J. P. Perdew, Phys. Rev. Lett., 2008, 100 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132 Search PubMed.
- M. Dion, H. Rydberg, E. Schroder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92 Search PubMed.
- K. Lee, E. D. Murray, L. Z. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82 Search PubMed.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- H. J. C. Berendsen, J. P. M. Postma, W. F. Vangunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02. Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS PubMed.
- J. M. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- H. P. Hratchian and H. B. Schlegel, J. Chem. Phys., 2004, 120, 9918–9924 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 5121–5129 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13126–13130 CrossRef CAS PubMed.
- J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- I. A. Vladimir, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767 CrossRef.
- A. B. Shick, A. I. Liechtenstein and W. E. Pickett, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 10763–10769 CrossRef CAS.
- M. Cococcioni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71 Search PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- G. C. Pimentel and A. L. McClellan, The hydrogen bond. (Drawings by Roger Hayward.), Reinhold Publishing Corporation, New York 22, 1963 Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38 CrossRef CAS.
- R. Crespo-Otero and M. Barbatti, J. Chem. Phys., 2011, 134, 164305 CrossRef PubMed.
- D. Escudero and W. Thiel, J. Chem. Phys., 2014, 140, 194105 CrossRef PubMed.
- S. K. Lower and M. A. El-Sayed, Chem. Rev., 1966, 66, 199–241 CrossRef CAS.
- L. Freitag and L. González, Inorg. Chem., 2014, 53(13), 6415–6426 CrossRef CAS PubMed.
- I. Tavernelli, B. F. E. Curchod and U. Rothlisberger, Chem. Phys., 2011, 391, 101–109 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Includes additional calculation results, including the determination of the magnetic ground state of the GS and MS1 crystals, the GS-MS1 enthalpy differences obtained in solid-state and molecular calculations with different parameters, and complete TD-DFT datasets from calculations with several different functionals. See DOI: 10.1039/c4ce01411a |
| ‡ JMS and RCO contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2015 |