Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Role of entropic effects in controlling the polymorphism in formate ABX3 metal–organic frameworks†
Gregor
Kieslich‡
*a,
Shohei
Kumagai‡
abc,
Keith T.
Butler‡
d,
Takuro
Okamura
b,
Christopher H.
Hendon
d,
Shijing
Sun
a,
Masahiro
Yamashita
bce,
Aron
Walsh
d and
Anthony K.
Cheetham
*a
aDepartment of Materials Science and Metallurgy, University of Cambridge, Cambridge CB3 0FS, UK. E-mail: gk354@cam.ac.uk; akc30@cam.ac.uk
bDepartment of Chemistry, Graduate School of Science, Tohoku University, 6-3 Aza-Aoba, Aramaki, Aoba-ku, Sendai 980-8578, Japan
cWPI-Advanced Institute for Materials Research, Tohoku University, 2-1-1 Katahira, Aoba-ku, Sendai 980-8577, Japan
dCentre for Sustainable Chemical Technologies and Department of Chemistry, University of Bath, Claverton Down, Bath BA2 7AY, UK
eCREST, JST, 4-1-8 Honcho, Kawaguchi, Saitama 332-0012, Japan
First published on 1st September 2015
Abstract
Polymorphism in formate-based dense metal–organic frameworks with the general formula ABX3 is predicted by quantum chemical calculations and confirmed experimentally. In particular [NH3NH2]Zn(HCOO)3 crystallizes in two different polymorphs, a perovskite-like framework and a chiral structure with hexagonal channels. A detailed thermodynamic analysis reveals that both structures are very close in free energy and that entropy driven effects are responsible for stabilizing the channel structure.
Among the many fascinating properties of metal–organic frameworks (MOFs), the occurrence of polymorphism is particularly interesting in the context of materials design. A number of experimental parameters can be used to control outcomes during the synthesis of MOFs, including reaction time, temperature, solvent, pH and so on. Of these, the use of temperature is particularly important because it enables us to take advantage of entropic differences between alternative products. This is strikingly illustrated by the cobalt succinates,1 where five different phases containing varying quantities of structural and extra-framework water can be obtained from a single reaction mixture held at different temperatures. It has also been seen qualitatively in anhydrous lithium tartrates,2 where entropic differences due to hydrogen bonding are important and can be tuned with temperature. From a fundamental point of view, a knowledge of when a certain polymorph will form yields insight into the underlying thermodynamics and reveals information that is important for the design of new materials with distinct structural features. A general guideline regarding the stability of certain crystal features was given in 1929 by Pauling & Baur;3 however, due to the complex bonding interactions in hybrid materials, estimations of stabilities are often made a posteriori. From an applications point of view, the framework architecture can be used to tune electronic properties,4 and with the advent of conductive MOFs5 and hybrid photovoltaics,6 the ability to control properties such as polymorphism and crystal chemistry is becoming ever more important.
In the present work we analyse polymorphism in the ferroelectric hydrazinium formate frameworks by computational methods and experiments. In particular, we use state-of the-art density functional theory (DFT) based lattice dynamics to estimate the free energies of the two polymorphs of [NH3NH2]Zn(HCOO)3 as a function of temperature. The study reveals that polymorphism in hydrazinium formates can be understood in terms of differences in vibrational entropy between the perovskite-like modification and the alternative chiral channel structure.
The family of transition metal formates [AmH]B(HCOO)3, with [AmH]+ a protonated amine and B a divalent (transition) metal, is interesting due to the occurrence of paraelectric-to-ferroelectric phase transitions. Together with low-temperature magnetic ordering, such materials can be considered as next-generation multiferroics.7 For formate compounds with the general formula AB(HCOO)3, two different structure types have been observed:8–10 (i) a perovskite-like framework with 412·63 topology (1) and (ii) a channel structure with 49·63 topology (2). Fig. 1 shows both structures schematically with an emphasis on the location of the protonated amines. In both structures, the paraelectric-to-ferroelectric transition is related to an order–disorder transition of protonated amines in the ReO3-like cavity (1) or hexagonal channels (2), respectively.10,13 The phase transition temperature in turn is dependent on the strength of hydrogen bonds and ionic interactions between the protonated amines and the metal-formate framework of the two structures. Usually, the channel structure is observed for smaller protonated amines, such as [NH4]+ and [NH3OH]+,10,14 while the perovskite frameworks form for larger sized protonated amines.9
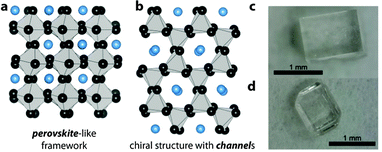 | ||
| Fig. 1 Schematics of the two structure types observed in the series [NH3NH2]B(HCOO)3 with B = Mn2+, Co2+, Zn2+ and Mg2+. The structures are simplified to emphasize the perovskite-structure motif in (a) and the hexagonal channels in (b). Grey polyhedrons are ZnO6 octahedrons, black spheres formate anions and blue spheres correspond to [NH3NH2]+ cations. (c and d) Show crystals of Zn-1 (c) and Zn-2 (d), see ESI† for more crystals. | ||
This trend is summarized by Goldschmidt's tolerance factor (TF) concept which was recently applied to organic–inorganic frameworks.12,15 Interestingly, within the series [NH3NH2]B(HCOO)3, B = Mn2+, Co2+, Zn2+ and Mg2+, both structure-types, 1 and 2, have been observed.8 In particular, the perovskite-like framework 1 is observed for M = Zn2+ and Mn2+, while use of the divalent metals Co2+ and Mg2+ leads to the channel structure 2. An overview of the metal radii, structure-types and calculated tolerance factors of the series [NH3NH2]B(HCOO)3 is given in Table 1. According to the tolerance factors, all four compounds are expected to crystallise in a perovskite-like framework; however, the intermediate size of [NH3NH2]+ seems to emphasise the role of experimental parameters (beyond simple radius arguments) on the structure formed. No study has addressed this issue hitherto, although Gao et al. suggested that polymorphism is likely to be observed in this series.8
| Compound | r M2+ (pm) | TF | Structure |
|---|---|---|---|
| [NH3NH2]Mn(HCOO)3 | 83 | 0.814 | Perovskite |
| [NH3NH2]Co(HCOO)3 | 74.5 | 0.838 | Channel |
| [NH3NH2]Zn(HCOO)3 | 74 | 0.839 | Perovskite |
| [NH3NH2]Mg(HCOO)3 | 72 | 0.845 | Channel |
In order to attain a deeper understanding of the underlying crystal chemistry and thermodynamic stabilities, first-principles calculations were performed (for details see ESI†). As representative compounds, the energies of [NH3NH2]B(HCOO)3 with B = Zn2+ and Mg2+ have been calculated. The plane-wave pseudopotential method based on density functional theory (DFT) was applied, including dispersion interactions arising from the dynamical effects of fluctuating charge distributions using the DFT-D3 method of Grimme.16 Initially, the 0 K ground state structures were calculated by fitting energy volume curves of the species to a Murnagan equation of state. The results for structure 1 and 2 are presented in Table 2 for Zn2+ and in ESI,† Table S1 for Mg2+. Note that the channel structure, Zn-2, is less dense, Table 2. In accordance with the TFs, the calculated 0 K enthalpies show that for both divalent metals the perovskite (Pna21) structure 1 is preferred to the chiral channel (P212121) structure 2. It has previously been reported, however, that the Zn compound crystallizes in the perovskite structure Zn-1 whilst the Mg species prefers to crystallize in structure 2, Mg-2. Evidently, additional factors are crucial for determining the balance of stability in these systems, which are not considered within the TF concept.
In a next step, we calculated the full Gibbs free energy by accounting for vibrational entropy. The important role of such entropic effects has been noted previously.17 Moreover, to describe the effects of thermal expansion on the free energy of the system, we have applied the quasi-harmonic approximation (QHA):
| G(T,P) = minV[U(V) + Fph(V,T) + pV], | (1) |
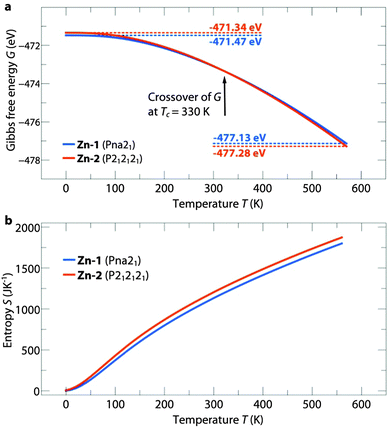
The temperature dependent free energies of Zn-1 and Zn-2 are shown in Fig. 2a. For [NH3NH2]Zn(HCOO)3 at Tc = 330 K a crossover of the free energies is observed between Zn-1 and Zn-2. The crossover is a direct result of higher vibrational entropy in the less dense structure, Zn-2, as illustrated in Fig. 2b. The transition from Zn-1 to Zn-2 is related to weaker hydrogen bonds (HBs) as reflected by the bond-lengths and, accordingly, increased vibrational entropy.20 A similar trend is observed for the Mg phase, see ESI,† Fig. S1. In [NH3NH2]Mg(HCOO)3 the crossover temperature is shifted to Tc = 300 K, which is a direct consequence of longer average HBs lengths, see ESI,† Table S2. As the bond lengths are directly related to their stiffness, the weak HBs in Mg-2 result in higher vibrational entropy which in turn accounts for the lower Tc. The DFT results show that temperature plays a significant role in determining thermodynamic stabilities in the [NH3NH2]B(HCOO)3 series and accounts for previous observations of the difference in the observed structures for Zn2+ and Mg2+, specifically Zn-1 and Mg-2. At room temperature specifically, the formation enthalpies of both structure types are very close in energy. Polymorphism is therefore expected to exist in the [NH3NH2]B(HCOO)3 family and, as will be shown in the next paragraph, is indeed accessible by varying the experimental conditions.
Looking at the experimental routes towards formate frameworks, the preparation of formate-based hybrid perovskites involves mild solution based methods or solvothermal synthesis. Following these strategies, several different compounds have been reported, e.g. [(NH2)3C]B(HCOO)3, [(CH3)2NH2]B(HCOO)3 and [NH3OH]B(HCOO)3 for many different divalent (transition) metals B.9,14,21 For the growth of single crystals of [NH3NH2]Zn(HCOO)3 in the present work, the mild solution method is the most suitable approach.8 Starting from zinc perchlorate hexahydrate, Zn(ClO4)2·6H2O, formic acid, HCOOH and hydrazinium hydrate, NH2NH2·H2O, high quality single crystals of [NH3NH2]Zn(HCOO)3 in the previously reported perovskite structure 1 can be grown within two days. Motivated by the computational results, the experimental conditions were then adjusted. Initially, we have tried to use temperature as a parameter to control polymorphism; however, such experiments only led to the perovskite structure described by Gao et al.8 A different approach towards polymorphism in solution-based crystallisation is the modification of the underlying kinetics of nucleation.22 In particular, for the zinc system, the energies of the different polymorphs are close in energy around room temperature and therefore small changes in reaction kinetics might facilitate the formation of different structures. Accordingly, the use of different solvent mixtures and templating agents was investigated. Indeed, the use of triethylamine, (C2H5)3N (TEA) and hydrazinium monochloride, N2H5Cl, as the hydrazinium source in a methanol–water mixture led to the formation of [NH3NH2]Zn(HCOO)3 in structure 2 with the hydrazinium cations in hexagonal channels (for experimental details see ESI†). Thus, as suggested by the computations, [NH3NH2]Zn(HCOO)3 indeed exists in both polymorphs, Zn-1 and Zn-2.
Fig. 1c and d show typical crystals of [NH3NH2]Zn(HCOO)3 in the perovskite arrangement, Zn-1, and in the channel structure, Zn-2. TGA/DSC measurements confirm the strong relationship of Zn-2 to the cobalt and magnesium equivalents. Zn-2 shows a phase transition at 367 K upon heating, and decomposes at 389.5 K, see ESI,† Fig. S5 and Table S4. The trend of decomposition temperatures of the polymorphs (380 K/Zn-1 and 389.5 K/Zn-2) is in good agreement with the results from our calculations, which show that at higher temperatures Zn-2 is the more stable polymorph.8,23 Detailed structural analysis of Zn-2 was conducted using single crystal X-ray diffraction at 120 K, see ESI,† Table S2. Similar to the related compounds, [NH3NH2]B(HCOO)3 with B = Co2+ and Mg2+, Zn-2 crystallizes in the chiral space-group P212121 with lattice parameters a = 7.29731(6) Å, b = 7.94804(7) Å and c = 13.82240(12) Å. The observed densities of Zn-1 and Zn-2 at 120 K are, respectively, 2.02(0) g cm−3 and 1.93(4) g cm−3 and are in reasonable agreement with densities obtained from the DFT calculations. Based on X-ray diffraction data a discussion of HBs is difficult, keeping in mind that hydrogen atoms are refined with fixed bond lengths; however, in Zn-1, all three hydrogen atoms of the NH3-group are involved in HBs, whereas the structure of Zn-2 only allows two HBs per cavity (N1–H1A–O3 and N1–H1C–O5) and one pseudo HB (N1–H1B⋯N2 bond). In addition to that, the nitrogen atom of the NH3-group has two close oxygen neighbours and therefore, in Zn-2 four oxygen atoms are involved in Coulombic interactions. In Zn-1, the geometry of the cavity favours Coulombic interactions between the positively charged nitrogen atom and the free lone pairs located at the oxygen atoms, which is reflected in 6 relatively short N–O distances (2.878–3.088 Å). This leads to a higher stiffness in Zn-1 than Zn-2. Crystals of Zn-1 seem to be indefinitely stable under ambient conditions, whereas crystals of Zn-2 transform into Zn-1 over time, see powder X-ray diffraction pattern, ESI,† Fig. S4 and S6. As Zn-2 is stable under an argon atmosphere, it is likely that transformation from Zn-2 to the perovskite Zn-1 occurs via a surface water mediated dissolution–recrystallisation mechanism.24 This is in agreement with the lower calculated energy for Zn-1 at room temperature. The trend follows the empirical Oswald rule that the less stable modification forms initially before transforming into the thermodynamically more stable polymorph.
In conclusion, a combined computational and experimental study was used to shed light on the underlying thermodynamic stabilities and polymorphism of formate-based frameworks with general formula AB(HCOO)3. Due to the intermediate size of [NH3NH2]+, entropic effects determine which polymorph is thermodynamically stable in the family of [NH3NH2]B(HCOO)3. In particular, the Gibbs free energies of the compounds Zn-1 and Zn-2, as well as Mg-1 and Mg-2, are close in energy around room temperature. By varying the experimental conditions, the preparation of both polymorphs, Zn-1 and Zn-2, is possible. The free energies as a function of temperature highlight the utility and limitations of the recently developed tolerance factor concept for hybrid materials. On the one hand, the trends of 0 K energies are predicted correctly by TFs; however, reality is much more complex, particularly for borderline compounds (TFs close to 0.8 or 1), the nature of hybrid materials emphasizes the role of entropic effects on the energies. The conclusions drawn in this work are therefore important for other types of hybrid perovskite materials. For instance, within the family of organic–inorganic lead halides, polymorphism is certainly possible, which adds a new dimension to the search for new semiconducting materials for solar cell applications.25
GK is the holder of a postdoctoral fellowship granted by the Deutsche Forschungsgemeinschaft (http://www.dfg.de/en/), KI1879. KTB, CHH and AW are supported by the EPSRC (EP/M009580/1), ERC (Grant No. 277757) and Royal Society, respectively. This work benefited from access to ARCHER, the UK's national high-performance computing service, funded by EPSRC (EP/L000202). SS is supported by Cambridge Overseas Trust and China's Scholarship council.
References
- P. M. Forster, A. R. Burbank, C. Livage, G. Férey and A. K. Cheetham, Chem. Commun., 2004, 368 RSC.
- H. H.-M. Yeung and A. K. Cheetham, Dalton Trans., 2014, 43, 95–102 RSC.
- (a) L. Pauling, J. Am. Chem. Soc., 1929, 51, 1010–1026 CrossRef CAS; (b) W. H. Baur, Trans. Am. Crystallogr. Assoc., 1970, 129–155 CAS.
- (a) K. T. Butler, C. H. Hendon and A. Walsh, J. Am. Chem. Soc., 2014, 136, 2703–2706 CrossRef CAS PubMed; (b) K. T. Butler, C. H. Hendon and A. Walsh, ACS Appl. Mater. Interfaces, 2014, 6, 22044–22050 CrossRef CAS PubMed.
- A. A. Talin, A. Centrone, A. C. Ford, M. E. Foster, V. Stavila, P. Haney, R. A. Kinney, V. Szalai, F. El Gabaly, H. P. Yoon, F. Leonard and M. D. Allendorf, Science, 2014, 343, 66–69 CrossRef CAS PubMed.
- (a) M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643–647 CrossRef CAS PubMed; (b) K. T. Butler, J. M. Frost and A. Walsh, Energy Environ. Sci., 2015, 8, 838–848 RSC.
- (a) Y. Tian, A. Stroppa, Y. Chai, L. Yan, S. Wang, P. Barone, S. Picozzi and Y. Sun, Sci. Rep., 2014, 4, 6062 CrossRef CAS PubMed; (b) P. Jain, V. Ramachandran, R. J. Clark, H. D. Zhou, B. H. Toby, N. S. Dalal, H. W. Kroto and A. K. Cheetham, J. Am. Chem. Soc., 2009, 131, 13625–13627 CrossRef CAS PubMed.
- S. Chen, R. Shang, K.-L. Hu, Z.-M. Wang and S. Gao, Inorg. Chem. Front., 2014, 1, 83–98 RSC.
- Z. Wang, B. Zhang, T. Otsuka, K. Inoue, H. Kobayashi and M. Kurmoo, Dalton Trans., 2004, 2209 RSC.
- G.-C. Xu, X.-M. Ma, L. Zhang, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2010, 132, 9588–9590 CrossRef CAS PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2015, 6, 3430–3433 RSC.
- (a) T. Asaji and K. Ashitomi, J. Phys. Chem. C, 2013, 117, 10185–10190 CrossRef CAS; (b) T. Besara, P. Jain, N. S. Dalal, P. L. Kuhns, A. P. Reyes, H. W. Kroto and A. K. Cheetham, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6828–6832 CrossRef.
- B. Liu, R. Shang, K.-L. Hu, Z.-M. Wang and S. Gao, Inorg. Chem., 2012, 51, 13363–13372 CrossRef CAS PubMed.
- G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2014, 5, 4712–4715 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- (a) L. Du Bouëssel Bourg, A. U. Ortiz, A. Boutin and F.-X. Coudert, APL Mater., 2014, 2, 124110 CrossRef PubMed; (b) G. A. Tribello and B. Slater, J. Chem. Phys., 2009, 131, 24703 CrossRef PubMed.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- W. Li, A. Thirumurugan, P. T. Barton, Z. Lin, S. Henke, H. H.-M. Yeung, M. T. Wharmby, E. G. Bithell, C. J. Howard and A. K. Cheetham, J. Am. Chem. Soc., 2014, 136, 7801–7804 CrossRef CAS PubMed.
- K.-L. Hu, M. Kurmoo, Z. Wang and S. Gao, Chem. – Eur. J., 2009, 15, 12050–12064 CrossRef CAS PubMed.
- W. Sun, S. Jayaraman, W. Chen, K. A. Persson and G. Ceder, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 3199–3204 CrossRef CAS PubMed.
- S. Chen, R. Shang, B.-W. Wang, Z.-M. Wang and S. Gao, Angew. Chem., Int. Ed., 2015 DOI:10.1002/anie.201504396.
- J. Ihli, W. C. Wong, E. H. Noel, Y.-Y. Kim, A. N. Kulak, H. K. Christenson, M. J. Duer and F. C. Meldrum, Nat. Commun., 2014, 5, 3169 Search PubMed.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1414792. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5cc06190c |
| ‡ Authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2015 |