Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Calculation of Raman optical activity spectra for vibrational analysis
Shaun T.
Mutter
*a,
François
Zielinski
b,
Paul L. A.
Popelier
b and
Ewan W.
Blanch†
*a
aManchester Institute of Biotechnology and Faculty of Life Sciences, University of Manchester, 131 Princess Street, Manchester, M1 7DN, UK. E-mail: shaun.mutter@manchester.ac.uk; ewan.blanch@rmit.edu.au
bManchester Institute of Biotechnology and School of Chemistry, University of Manchester, 131 Princess Street, Manchester, M1 7DN, UK
First published on 27th January 2015
Abstract
By looking back on the history of Raman Optical Activity (ROA), the present article shows that the success of this analytical technique was for a long time hindered, paradoxically, by the deep level of detail and wealth of structural information it can provide. Basic principles of the underlying theory are discussed, to illustrate the technique's sensitivity due to its physical origins in the delicate response of molecular vibrations to electromagnetic properties. Following a short review of significant advances in the application of ROA by UK researchers, we dedicate two extensive sections to the technical and theoretical difficulties that were overcome to eventually provide predictive power to computational simulations in terms of ROA spectral calculation. In the last sections, we focus on a new modelling strategy that has been successful in coping with the dramatic impact of solvent effects on ROA analyses. This work emphasises the role of complementarity between experiment and theory for analysing the conformations and dynamics of biomolecules, so providing new perspectives for methodological improvements and molecular modelling development. For the latter, an example of a next-generation force-field for more accurate simulations and analysis of molecular behaviour is presented. By improving the accuracy of computational modelling, the analytical capabilities of ROA spectroscopy will be further developed so generating new insights into the complex behaviour of molecules.
Introduction
Raman optical activity (ROA) spectroscopy is a powerful technique for the conformational analysis of chiral molecules. This chiroptical method measures small differences in the Raman scattering of left and right circularly polarised light of chiral systems.1,2 ROA can be instrumental in the treatment of a great many biological and chemical problems, such as structure elucidation, conformational analysis, and the assignment of absolute configuration. ROA has been shown to be particularly useful for the study of systems where traditional biological structure determination techniques are not applicable. For example, ROA can be applied to molecules that do not easily form crystals, so are difficult to study by X-ray diffraction, or have conformational motions on timescales not easily detectable by NMR.3–5 Advances in instrumentation have been of great importance for the development of ROA but this technique has also significantly benefited from the inclusion of computational modelling. With advancements in modelling it has become routine to simulate the ROA spectra of small to medium size systems. Great complementarity between experiment and theory can be realised, as comparison of simulated and experimental spectra can offer structural insights and reveal information on molecular conformations, which is not always available from experiment alone. In turn, the incredible sensitivity of ROA to molecular structure can be used as a gold standard in force field design and the modelling of solvent effects.This mutually beneficial relationship between the experimental and theoretical aspects of ROA spectroscopy creates a very powerful set of analytical tools. This offers an experimental technique with an unrivalled sensitivity to chirality,6 combined with the great amount of detail at the molecular level available through computational modelling. These computational tools aid analysis by simulating spectra that can be used to confirm structural parameters, understand the vibrational nature of observed bands, and give vital information on conformational dynamics. As ROA can be utilised as a solution structure technique it has great applicability for biomolecular systems, which have strong interactions with the aqueous environment. As such, any model needs to carefully consider the effect a solvent will have on the results of calculations. Fortunately the current state of modern computational modelling allows for the addition of a significant number of explicit solvent molecules, which has been shown to result in a significant increase in the accuracy of results.7
ROA was first predicted in 1969 in Oxford by Atkins and Barron8 and was then first observed experimentally in 1972 by Barron, Bogaard and Buckingham at Cambridge.2 The sensitivity of ROA to molecular stereochemistry was then demonstrated in a series of studies by Barron and colleagues at the University of Glasgow. It is not the purpose of this review to discuss this body of work, and interested readers are directed to a number of relevant reviews.9–11 In summary, these studies established the direct correlation between the manner in which vibrational modes sense local stereochemistry and the signs of ROA band patterns, and then showed that ROA spectra are incisive probes for complex higher order structures. For example, studies performed by spectroscopists at Manchester and the Diamond Synchrotron showed that ROA can characterise the structures adopted by glycosaminoglycans,12 complex interactions between mucin glycoproteins,13 DMSO-induced unfolding of proteins,14 as well as identified how changes in local flexibility of the protein monellin correlate with reduced sweet-taste perception.15
Basic theory of ROA
The origin of scattered light is characterised by the oscillating electric dipole, magnetic dipole, and electric quadrupole moments induced by the incident light wave. In the far from resonance approximation the electric dipole, magnetic dipole, and electric quadrupole operators are given by eqn (1)–(3), respectively;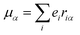 | (1) |
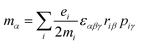 | (2) |
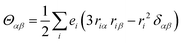 | (3) |
Molecular multipole moments and the quantum mechanical expressions for the molecular property tensors can be defined by the fields and field gradients evaluated at the molecular origin. The molecular property tensors can be extracted from time-dependent perturbation theory to give eqn (4)–(6).
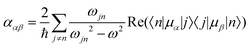 | (4) |
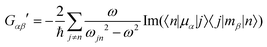 | (5) |
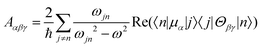 | (6) |
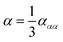 | (7) |
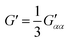 | (8) |
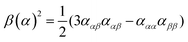 | (9) |
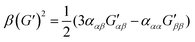 | (10) |
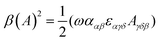 | (11) |
A quantitative experimental ROA observable that can be useful for biomolecular analysis is the dimensionless circular intensity difference (CID), introduced by Barron and Buckingham, as given by eqn (12);1
| Δ = (IR − IL)/(IR + IL) | (12) |
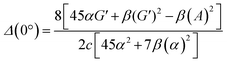 | (13) |
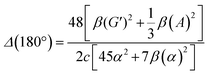 | (14) |
eqn (13) shows the CID expression for a forward scattering geometry and eqn (14) shows the expression for a backscattering geometry. Where a molecule is composed of idealised axial symmetric achiral bonds, a situation where β(G′)2 = β(A)2 and αG′ = 0, ROA is generated entirely by anisotropic scattering and the forward scattering and backscattering CID expressions are reduced to eqn (15) and (16), respectively.18,19
| Δ(0°) = 0 | (15) |
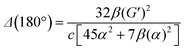 | (16) |
This shows that the ROA intensity is maximised in the back scattering geometry. As Raman scattering intensities are equal for the forward and backwards geometries, this increase in the ROA signal relative to the Raman shows that this is generally the best experimental strategy. A more extensive analysis of the theory of ROA can be found in one of several reviews on this subject.20–24
Instrumentation and experiment
ROA can be measured as a small circularly polarized component in either the incident or scattered beams.8,25,26 Other ROA measurement strategies are possible and are described elsewhere.27–30 A simple bond polarisability model has shown that a backscattering geometry is essential for the routine measurement of ROA spectra of biomolecules.31,32 Backscattering ROA spectra may be acquired using a number of different measurement strategies, with the ICP and SCP approaches being by far the most commonly used. A backscattering ICP measurement strategy was utilized in Glasgow from the 1970s and these instruments were responsible for most reported ROA spectra until the first few years of the 21st century. A detailed description of the optical layout of the main version of the Glasgow backscattering ICP ROA instrument operating at 532 nm can be found elsewhere.33 Since 2003, a new design of ROA instrument based on the SCP strategy34 has been commercially available and is now the most widely used type of ROA spectrometer worldwide.As stated above, in the absence of electronic resonance effects the ROA spectra obtained from these different instruments are directly comparable. In each case, laser powers used for biological molecules are typically from 1–1.4 W (measured at the laser source), concentrations usually are in the range of ∼30–100 mg ml−1 for proteins and nucleic acids while those of intact viruses and complex polysaccharides are ∼5–30 mg ml−1. For smaller molecules concentrations are usually in the range of 50–200 mg ml−1. While measurements can be conducted on concentrations lower than those mentioned here, the higher the concentration the faster the measurement will be. Under these conditions ROA spectra over the spectral range of ∼300–2000 cm−1 are typically obtained in minutes to a few hours for small molecules, ∼5–24 hours for proteins and nucleic acids, and ∼1–4 days for intact viruses and complex carbohydrates.
History of computational ROA
Whilst the definitive theory of ROA was developed in 1971,1 and the first experimental spectrum was recorded in 1972,2 it took until 1989 for the first calculated results to be published.35 This was reported by Polavarapu and co-workers, studying the molecule (+)-R-methylthiirane with Hartree Fock (HF) and the 6-31G* basis set, resulting in reasonable agreement with experimental results, with the exception of generally overestimated intensities. Many of the publications in the early years of computational ROA spectroscopy came from the groups of Barron and Polavarapu, who produced experimental spectra and ab initio calculations on a wide range of small organic molecules, including three-membered rings,36–38 five-membered rings,39 six-membered rings,40 alanine,41 and tartaric acid.42 The computational limitations at the time meant that it was difficult to advance beyond systems of this size and they were studied using HF approaches with relatively small basis sets. One of the earliest calculations that advanced beyond the level of HF was also reported by Polavarapu et al.,43 using MP2 for the force field calculation in the study of substituted oxiranes. However, issues arose where different oxiranes produced results of varying quality for the same level of theory. The authors brought up the question of basis set dependence on the sensitivity of the normal mode composition and Cartesian polarisability.With the increase in computing power the capability of calculating ROA spectra also increased, with access to larger basis sets and more advanced methods than those used in the early studies. As well as these improvements, deficiencies in the calculations were also able to be addressed. Helgaker et al.44 examined issues in the calculation of magnetic properties with finite basis sets, causing errors in the calculation of the electric dipole – magnetic dipole tensor. Magnetic properties are dependent on the gauge origin of the magnetic vector potential. Hence, as a solution, gauge-invariant atomic orbitals (GIAOs) were used, as they yield intensities independent of the gauge origin.
Density functional theory (DFT) methods are widely used in computational chemistry and have a wide range of applications. As such, they have become the standard approach in the calculation of ROA intensities. The first reported studies using DFT were from Ruud et al.,45 using the hybrid functional B3LYP with a combination of Pople and Dunning basis sets. Results for methyloxirane, α-pinene, and trans-pinene were compared to those using HF, as well as experiment. Spectra calculated using DFT were found to be superior to the earlier methods, and a significant improvement in the calculation of harmonic vibrational frequencies was also noted.
In one of the early computational ROA studies by Polavarapu in 1990,46 the author noted that ROA calculations were hindered by the need to obtain the derivatives of the electric dipole – magnetic dipole polarizability tensor. As no analytical differentiation approaches were available, numerical differentiation was used, complicating the computations and causing much greater computational expense. It was also noted that the development of an analytical method to evaluate the derivatives would greatly facilitate the ROA prediction of larger molecular systems. Early analytic protocols originated in 2007 from Liegeois et al.47 with an analytical time-dependent HF algorithm for calculation of the derivatives of the electric dipole – magnetic dipole polarisability tensor. This work allowed for the first time fully analytical evaluation of the three frequency-dependent invariants needed for ROA calculation. Although this method utilised non-London orbitals, resulting in erroneous gauge origin dependence, further advancements have since been made allowing for the use of GIAOs and DFT.48–51
Method and basis set dependence
The advancements in theory as well as the general advancements in computing mean it is now routinely possible to calculate the ROA spectra of small to medium sized systems. However, an important facet still to consider is the choice of method and basis set, together referred to as the level of theory. As mentioned earlier, the question of basis set dependence was posed in some of the early publications and as such several benchmark studies have been undertaken to determine the most suitable basis sets for performing calculations.Early studies by Pecul and Rizzo52 examined the basis set dependence of ROA using a selection of Dunning's correlation consistent basis sets, in augmented and non-augmented forms. Using MCSCF methods they found aug-cc-pVDZ to be suitable for qualitative analysis but more importantly they noted that basis sets with diffuse functions were able to reproduce experimental spectra more accurately than those without. This was also noted by Hug,53 and that description of the diffuse part of the electron distribution on hydrogen nuclei was essential for basis sets used for ROA calculations. This led to a more extensive benchmark study by Zuber and Hug,54 which also led to the development of a new basis set, rDPS. This basis set is in the form 3–21++G, with semidiffuse p functions on hydrogens, with an exponent of 0.2. In their tests, rDPS performed very well, giving better results than a selection of Pople and Dunning basis sets, with only aug-cc-pVDZ outperforming it against the benchmark Sadlej basis set.
The most recent benchmark study was carried out by Cheeseman and Frisch,55 where they examined the basis set dependence of the ROA tensor invariants and force field calculations separately. This study took advantage of the fully analytical derivative methods as well as examining the onestep and twostep procedures (2n + 1 and n + 1 algorithms, respectively) as described by Ruud and Thorvaldsen.20 The twostep approach allows for the calculation ROA tensor invariants at a different level of theory than the optimisation and force field calculation, whereas the onestep approach calculates everything at the same level of theory. Cheeseman and Frisch noted that the influence of the basis set is different in the calculation of the Raman/ROA tensor invariants compared to the force field calculation and concluded from this that the twostep procedure is the more efficient, particularly for large molecules. A selection of basis set combinations for twostep calculations, based on system size, was also reported. For intermediate-sized system aug(sp)-cc-pVDZ//cc-pVTZ was suggested, while for large systems rDPS//6-31G* for the ROA tensor invariant and force field calculations, respectively.
There are comparatively fewer benchmark studies that explore the dependence on the method rather than on the basis set. Reiher et al.56 presented one of the first studies with a combined basis set and DFT functional. Local density approximation, generalised gradient approximation, and hybrid DFT methods were explored using SVWN, BLYP, and B3LYP, respectively. Results showed that BLYP and B3LYP outperformed SVWN.
A more extensive study was carried out by Danecek et al.57 using a mix of 23 pure and hybrid DFT functionals, as well as HF and MP2. Comparison between experimental spectra and those calculated with the DFT methods, for alanine and proline zwitterions, found that the hybrid functionals generally performed best, noting that B3LYP and B3PW91 performed particularly well. Sebek et al.58 also noted that, overall, the B3LYP functional provides a well-balanced model between accuracy and cost, as such this functional has been widely used in recent computational ROA studies.
The calculation of ROA spectra is now possible through several commercially available programs, including Gaussian03,59 Gaussian09,60 and the Amsterdam Density Functional code (ADF).61 Gaussian09 also includes the necessary subroutines for analytical derivatives of all the required ROA tensors. As well as these packages, there are several other programs for ROA calculation including Dalton,62 CADPAC,63 and SNF.64
Solvent models
An important aspect to consider when carrying out ab initio simulations is the inclusion of solvent. The lack of a solvent model, particularly when carrying out calculations on biologically relevant molecules, can lead to large errors in the simulated spectra.65,66 As such, solvent inclusion has become routine in many ab initio calculations, leading to better descriptions of the dynamics and energetics of experimentally studied systems. It is of particular importance in the simulation of ROA, because direct interactions with solvent molecules can have a drastic effect on the spectra, particularly for vibrational modes in the low wavenumber region.67The inclusion of solvent in the ab initio calculation of ROA spectra can be carried out in two ways, broadly defined as implicit and explicit solvation. Implicit solvent models place the solute within a cavity in a uniform polarisable medium with a dielectric constant. There are two widely used implicit solvent models called PCM68 and COSMO,69 which treat the solvent as a dielectric and a conductor, respectively.
The explicit solvation approach includes explicit solvent molecules in the ab initio calculation, which can be modelled at several different levels of theory. A small number of solvent molecules can be added and treated at the quantum mechanics level along with the solute, if the solvent molecule is relatively small, such as water. It is also possible to include large numbers of solvent molecules and model them using hybrid quantum mechanics/molecular mechanics (QM/MM) methods. This approach treats the solute at the QM level and the solvent with a computationally much cheaper molecular mechanics approach. Electrostatic embedding can also be included for more accurate calculation by incorporating the MM charges in the QM Hamiltonian. Such an approach is able to model systems with large solvation shells, with solvent molecules numbering in the hundreds.
It is also possible to combine implicit and explicit solvation approaches. When carrying out calculations on systems with small numbers of explicit molecules it is trivial to include a continuum method. Recent work by Biczysko et al.70 has also explored the possibility of incorporating implicit solvent models within QM/MM frameworks.
The suitability of the solvation approach used depends greatly on the molecular property of interest. Implicit models offer reasonable accuracy for energy and structure calculations, with a minimal increase in computational expense compared to gas phase calculations.71,72 However, the accuracy of vibrational frequencies increases less from the gas phase to an implicit solvent model and a small number of explicit water molecules has been shown to have a dramatic effect on calculated spectra, resulting in much better agreement with experiment.65,73
The addition of explicit solvent molecules to a system can present issues, however. The simplest approach to add solvent molecules is ad hoc solvation, where the solvent is added manually to regions of each of the molecular conformers, such as water molecules being added to the polar groups of a biomolecule. Studies have shown that this approach can offer significant improvement in the reproduction of several features within ROA spectra.74,75 However, this approach does have a shortcoming in that systems may converge very slowly to an optimised geometry, as a result of the shallow nature of the potential energy surface.57,75
Given the importance of including the major conformers of a molecule for the simulation of ROA spectra, a more practical approach for the addition of solvent molecules is a dynamic method. The use of molecular dynamics (MD) simulations offers the benefits of being able to obtain accurate solvated structures, closer to optimised geometries, as well as giving valuable conformational information.
Several recently published studies explore the area of implicit and explicit modelling of solvent. Hopmann et al.75 studied the effect solvation had on the Raman and ROA spectra of lactamide and 2-aminopropanal, using PCM, ad hoc hydration, classical MD, and Car-Parrinello MD. Results showed that although the PCM gave basic conformational information, energies and ROA intensity patterns, the inclusion of explicit solvent provided better agreement with experiment. Inclusion of at least ad hoc hydration was recommended and it was noted that Car-Parrinello MD gave better agreement than classical MD. However, the additional computational cost of ab initio Car-Parrinello MD might mean it is not possible to fully sample the conformational space of systems in question.
Cheeseman et al.7 utilised a full MD simulation to model the hydration effects of methyl-β-D-glucose for ROA calculation. Carbohydrates are a class of biomolecules that benefit greatly from ROA studies as the larger, more complex polysaccharides are inherently difficult to study with traditional structural biology techniques. Calculation of ROA spectra is often difficult for these molecules due to their high conformational flexibility and the need for accurate solvent modelling. This study incorporated solvated structures from the MD trajectories as starting points for the QM/MM calculations. The explicitly solvated structures resulted in spectra with excellent agreement with experiment, particularly when compared to the PCM models, which offered comparatively poor agreement, as shown in Fig. 1. The authors concluded that the implicitly solvated models fail to accurately model the sensitivity of ROA features to hydration effects and that adopting a full MD approach to handle the aqueous environment is essential for carbohydrates.
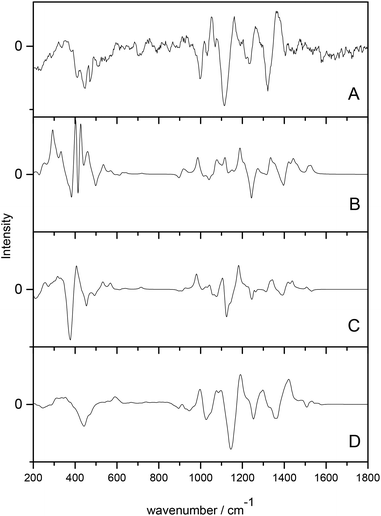 | ||
| Fig. 1 ROA spectra of methyl-β-D-glucose. (A) experimental spectrum, (B) gas phase calculated spectrum, (C) PCM calculated spectrum, (D) QM/MM explicitly solvated calculated spectrum. Modified with permission from ref. 7. | ||
Urago et al.76 carried out a similar study to that undertaken above, on a cyclic dipeptide. They found good agreement with experiment but found that a large number of MD snapshots were required to achieve this, particularly in the 1580–1800 cm−1 region, which required 120 snapshots. In comparison, Cheeseman et al. required only 16 snapshots for each of the two conformers for excellent agreement across the entire frequency range examined. However, it should be noted that different snapshot optimisation approaches were used in these two publications, where Urago et al. used a technique analogous to OPTSOLUTE and Cheeseman et al. used OPTALL, as described below. This difference in optimisation approach likely results in the difference of number of snapshots required for accurate spectral reproduction.
Simulation of ROA spectra
As a result of the success of the work on carbohydrates carried out by Cheeseman et al.7 we have further developed the approach they presented. The protocols have been utilised for successfully studying carbohydrates, which as test cases are particularly difficult to study, but could equally be applied to any other system of interest with strong solvent interaction. Fig. 2 shows the approach that we have designed for accurate computation of ROA spectra.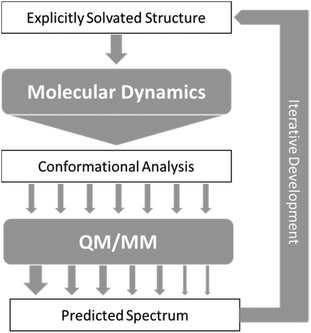 | ||
| Fig. 2 Schematic of the approach to calculation of ROA spectra, with arrows representing flow of data between steps. | ||
In general terms, this approach consists of exploring the configurations accessible to the explicitly solvated system, for temperature and pressure conditions similar to experiment. When no reference data are available, it becomes crucial to extensively sample the conformational space to obtain reliable quantitative information. For flexible molecules such as carbohydrates, the required simulation time can then dramatically rise as the space to explore gets more complex and features more dimensions. Dynamic sampling was used in our work, but Monte–Carlo methods would be appropriate as well. Obviously, for such time-scales, it is an understatement to say that ab Initio MD is impractical. Currently, the only alternative is the use of atomistic molecular models based on classical mechanics (force-fields). So far, most of these rely on fitting methods, parametrisation, and a number of approximations (such as the point-charge description of atomic charge densities, neglecting all polarisation effects) that may severely limit accuracy and transferability.77,78 A number of initiatives and developments are progressing toward maturity and will become available in the near future, among them the new generation force-field presented below. In the meantime, special care needs to be dedicated to the choice and testing of the optimal molecular model among the readily available alternatives.
From the sheer mass of data generated during sampling, it is possible to extract qualitative and quantitative information about the energetically favoured configurations. If done carefully, even a superficial conformational analysis can yield very helpful data that can be used to lighten the computational cost of the subsequent QM/MM computation steps. Indeed, by focusing the selection of MD snapshots toward the most probable conformers, in their most average form, one can then lighten the subsequent steps by a reduction in the number of snapshots, and optimisation starting structures being closer to their energetic minima. Eventually, any quantitative insight on the relative occurrence probability of these conformers can be used as weights (represented by arrows of different size in Fig. 2) for the averaging of each snapshot's spectrum into the final prediction.
The term explicit solvation refers to the inclusion of solvent molecules in the simulation. Although implicit solvation models are far less computationally demanding, they rely on a number of approximations that have been shown several times to impede the proper description of solvent effects the spectroscopic responses of carbohydrates.7,79,80 As a result, we strongly recommend sticking to explicit solvation when considering carbohydrates.
A possible starting point can be the gas-phase optimised structure of the considered carbohydrate. If not readily available from the literature or the Glycam project,81 one can quickly obtain a sufficient estimate through optimisation thanks to a force field, or a quantum chemical computation at a low level of theory. Afterwards, this isolated molecule has to be immersed in a solvent bath: cubic cells of side 30 Å (approximately 900 water molecules) have been a safe choice so far for monosaccharides, while remaining relatively cost effective regards computing time. As interest tends to larger systems, this size is expected to evolve accordingly, so that the overall solvent bath increases in size with the increasing size of the solutes, as to ensure molecules stay surrounded from every side by at least 10 Å of explicit solvent molecules (within a single periodic cell).
Any molecular dynamics or Monte–Carlo computer program with basic features would be suited to the task at hand, provided it can handle a carbohydrate-specific force field (such as Glycam82). Periodic boundary conditions have to be applied to the cubic cell previously described, thus we recommend handling electrostatic interactions with a method adapted to such a system (e.g. Ewald Sums or one of its derivatives).77
Special care must be dedicated to bringing the system to proper equilibrium at experimental conditions (298 K, 1 atm). An explicitly solvated system is likely to be, at first, lying far from its minimal energy configuration, depending on the way the system has been prepared and the software tool used. In our experience, preliminary optimisation, progressive heating, and force-capping can sometimes be necessary. Similarly, we recommend letting the cell volume adjust until reaching a safe convergence threshold within the NPT ensemble, prior to moving toward production simulation (NVT).
In principle, a random sampling of a molecule's dynamic trajectory would provide the time-averaged conformational diversity necessary to predict the spectroscopic response.75,76 However, accuracy cannot be guaranteed until the sampling coverage reaches statistical significance. Instead, we advocate an alternative that aims at reducing the number of MD snapshots to process by QM/MM. Indeed, it is possible to maximise the statistical significance of the extracted snapshots by targeting the most probable structures, as identified by conformational analysis of the MD trajectory. Since it is already necessary to run long simulations (at least 50 ns for a monosaccharide83) to ensure exhaustive sampling, the conformer populations can be expected to be reliable enough. As a result, it is possible to use ratios between these populations in order to weight the snapshots’ spectra into an average spectrum representative of the molecule's dynamic and complex conformational space.
To conduct a conformational analysis appropriate for our purposes, it is preferable to focus on general structural features since slight structural changes are to be expected through the QM/MM optimisation. Bond lengths and 3-atom angles are indeed more prone to readjustment and change during optimisation, whereas dihedral angles can be expected to be more constrained. The latter type of geometrical feature typically describes the orientation of chemical groups and ring puckering, which can be expected to be held into place by the environment's general influence. It is unlikely to see dramatic changes during optimisation.
In order to scan a geometrical feature's evolution and detect the occurrence of multiple conformers, it can be sufficient to plot its value against simulation time, as in Fig. 3. As we need a clear picture of the favoured structures and to define their corresponding domain of values, we recommend to push further the analysis and plot histograms, as in Fig. 4, i.e. the occurrence of the considered feature values within regular intervals (bins). Such a graph enables the ability to easily notice any overlap between conformers, shoulders or minor structures. Once each conformer's domain is determined, their populations and average values can be accurately calculated.
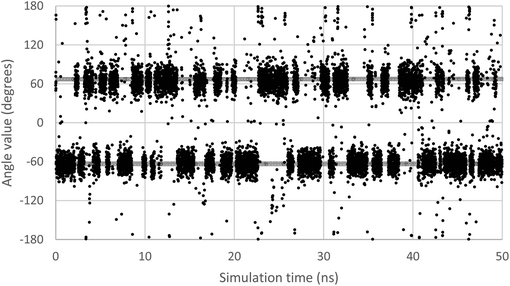 | ||
| Fig. 3 Evolution of the ω dihedral angle (O5–C5–C6–O6) in GlcNAc, a relevant monosaccharide, along simulation time. Two grey lines mark the average value for each of the two observable conformers. | ||
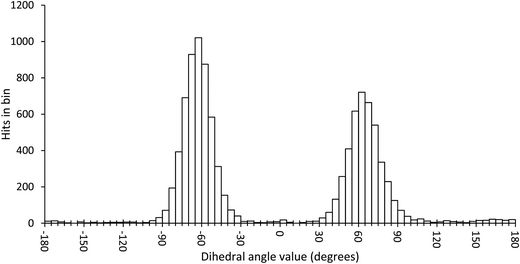 | ||
| Fig. 4 Histogram plot of the occurrence of the ω dihedral angle values in GlcNAc, with bins of 5 degrees. | ||
Once these last data are calculated, they can be used as combinations of target values to filter the MD frames and obtain representative snapshots of each conformer. The closer a snapshot assumes dihedral values from the conformer's average, the quicker it can be expected to optimise. Furthermore, selecting frames as far from each other in the trajectory ensures that the diversity of solvent layer configurations is properly sampled. In cases where it is necessary to include a counter ion in the simulation, it is advised to select only frames where the ion is lying as far as possible from the molecule of interest. It is still unclear what the ideal number of snapshots is in order to obtain an average spectrum in agreement with experiment. Even though good results have been obtained with as few as 6 snapshots, the number is likely to scale up with the conformational variety. Further investigations are currently in progress to address this concern.
The selection of MD frames, taken from the conformational analysis, is then used as a starting point for the QM/MM calculations. The initial step is optimisation of the system. Whilst this may seem contradictory, as it results in loss of dynamic information from the MD simulations, it is necessary, because the vibrational normal modes and frequencies are only valid for minima on the potential energy surface. There are two main approaches used for QM/MM optimisation, carried out using ONIOM84 as implemented in Gaussian 09. The first is to optimise the solute and freeze the solvent molecules in the MD geometry, which is dubbed OPTSOLUTE. The second approach is allowing the entire system to optimise, with full geometrical freedom for all molecules, named OPTALL. The second approach, OPTALL, is arguably more accurate as the optimisation of the solvent close to the solute creates a better model of solvent–solute interactions when calculating ROA. However, OPTALL does have a practical disadvantage as convergence to optimisation is difficult and, on occasion, these systems will never reach full optimisation. In these situations the electronic energies of each optimisation step oscillate but do not decrease in value overall. However, they can be considered to be optimised if the maximum and root-mean-square values of the forces meet the convergence criteria of 0.00045 and 0.00030 a.u., respectively, in Gaussian 09. The level of theory recommended for optimisation is B3LYP/6-31G* for the solute and AMBER/TIP3P for the aqueous solvent.
After optimisation of the solvent–solute clusters, harmonic frequency calculations are carried out at the same level of theory as the optimisation. Using the two step approach the ROA tensor invariants for the optimised clusters can be calculated at a different level of theory to that of the optimisation. Based on the benchmark studies of Cheeseman and Frisch55 B3LYP/rDPS is recommended, because for large system sizes a combination of 6-31G* and rDPS for force field and ROA calculation, respectively, has proven to be successful.
Raman and ROA intensities are obtained from the appropriate combinations of tensor invariants, and we have included the ν4 and Boltzmann factors, which are essential for experimental comparison.7 The most common experimental ROA set up utilises SCP in the backscattering geometry, at a laser excitation of 532 nm, such that spectra can be calculated for these experimental parameters.
A simulated spectrum for a single snapshot only takes into account the single conformer present in that cluster, as such conformational averaging over multiple snapshots needs to be carried out. Averaging can be done with equal weighting for all snapshots if a large number have been taken at regular intervals along the trajectory. When conformational analysis has been carried out to find the major conformers the more appropriate approach is to weight the snapshots based on the conformer populations of the MD simulations. Averaging of the spectra should be carried out with the lineshape form (average of the curves) and not the ROA intensities at individual frequencies.
With the steps outlined above it is possible to accurately simulate Raman and ROA spectra for many different chiral systems. These calculations account for not only conformational dynamics but also include explicit modelling of solvent interactions and offer great improvements over implicit solvent models.
Analysis of vibrational modes
ROA spectra calculated using the approaches above can be used to reveal important information about molecular systems. The simplest approach to analysing spectra is a visual comparison between experimental and calculated data. This can confirm that the structural and conformational data obtained from calculation are correct and can be used as a description of molecules in experimental conditions. On top of visual analysis, there are several coefficients that aim to quantify the similarity between experimental and simulated spectra.85–87 However, these coefficients have a much greater focus on vibrational circular dichroism (VCD), a related chiroptical technique, and while applicable to ROA, they have not been extensively tested and as such are not, so far, readily used.One of the most important aspects of ROA analysis is the ability to assign the absolute configuration of chiral molecules. While other techniques are more commonly applied to this problem, such as X-ray diffraction and VCD, ROA possesses considerable advantages for such studies. A study by Haesler et al.6 proved this by means of the assignment of absolute configuration of chirally deuterated neopentane. This molecule is chemically inert and its chirality results from dissymmetric mass distribution, with configuration studies unable to be carried out successfully by any other method but ROA.
As ROA exhibits such a high sensitivity to stereochemistry, a large amount of structural and vibrational data can be elucidated from the spectral bands. Therefore, it is important to understand the origins of the aforementioned bands so that they can be used as identifiers of structural motifs. Some spectral regions already have well defined peak assignments, such as in peptides and proteins for which there are a number of bands known to be markers of secondary structure. For other molecules, such as carbohydrates and chiral transition metal complexes, relatively little insight into the details of higher order conformation have been obtained so far. New tools and approaches are still needed to explore the vibrational nature of such complex molecules.
Using software such as Gaussview88 or pyvib2,89 calculation output from ROA simulations can be visualised in terms of vibrational modes, from which the bands originate. Visualisation of these modes can then lead to the assignment of peaks, as exhibited by Cheeseman et al.7 for methyl-β-D-glucose and Humbert-Droz et al.90 for rhodium trisethylenediamine. This approach can be successful but has the disadvantage that assignments are limited to a spectrum simulated from one conformer in the gas phase or with implicit solvent models. Individual conformer assignments do offer interesting structural information but it is also important to consider origins of bands for spectra simulated with the more accurate combined approach, outlined above. In order to do so, it is important to consider all the snapshots used to generate the final spectrum. The calculation outputs for each individual snapshot's spectrum can be examined visually, using the software mentioned above. Initially, this can be problematic due to the difficulty of visual analysis when explicit solvent molecules are present, but options can enable them to be presented in different ways, such as wireform, to increase clarity. A preliminary examination of the final spectrum generated from all the snapshots should be carried out to determine the features of greatest interest on which to focus assignments for. Comparison between the assignments of individual snapshots at the frequency of the peaks of interest in the final spectrum can then lead to a final assignment, thus offering analysis of systems modelled in environments closer to that observed experimentally.
In cases where molecules have very diffuse vibrational modes it can be difficult to assign the most important vibrations. Small carbohydrates exemplify this, as nuclear motions arising from most, if not all, of the molecule often contribute to many of the observed vibrations. In these situations, for each individual mode, the analysis of the molecular displacement data (obtained from calculation outputs) can offer deeper insight. Corroboration of the molecular displacements and visual analysis can confirm which atoms make either larger or smaller/negligible contributions to the modelled vibrations.
Combined, visual analysis and molecular displacement data can enable deeper understanding of simulated spectra, and can be used to great effect when assigning peaks in a spectrum generated from several solvated snapshots. Better insight can be obtained regarding the origin of these bands than is possible from examining individual conformers in the gas phase or with PCM. However, this approach is much more laborious and can become much more time-consuming as more snapshots are used. Consequently, such an analysis is much more practical when ROA simulations are based on an optimally limited number of snapshots, as in the presented MD and quantum approaches that incorporates conformational analysis to identify the preferred conformers.
Development of simulation approaches
Over the last few decades ROA spectroscopy has matured from being a relatively unknown analytical technique to its realisation as a powerful tool for the study of chiral molecules. Fig. 2 shows that it is possible to carry out accurate simulations of ROA spectra, even for molecules exhibiting high conformational flexibility, such as carbohydrates. It also shows that by using combined experimental and theoretical methods it is possible to exploit the complementarity of the two approaches. The iterative development strategy outlined in Fig. 2 aims to improve the accuracy of computation and this can be achieved through further research in several key areas. One important facet of this analytical process that is currently being explored by the authors is the development of more accurate force fields.Biomolecular modelling urgently needs more realistic force field potentials. In order to enhance its utility for experimentalists, force field design needs an urgent overhaul because current force-field architecture has remained largely stagnant since the 1980s. This overhaul must be guided by both rigour and imagination, while respecting the quantum physics ultimately underpinning biomolecular structure and behaviour. A long-term concerted research effort91–93 in this direction is currently ongoing. At the core of a future-proof force-field is a maximally energy-transferable atom. In this respect, the best atom,94 according to literature evidence, is that defined by Quantum Chemical Topology (QCT).
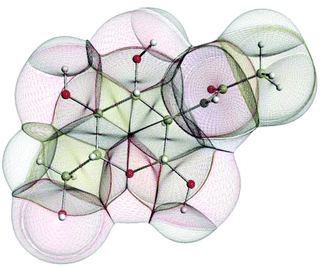
In the condensed matter phase QCT atoms are parameter-free three-dimensional fragments of finite volume, appearing in the electron density. Fig. 5 shows an example in the gas phase, where an outer boundary is fixed for visual purposes. This figure shows how QCT naturally partitions a carbohydrate derivative into its constituent (topological) atoms. These atoms have sharp boundaries, they do not overlap, and they leave no gaps. A change in any nucleus's position will change the electron density and hence the shape of the atoms. Each atomic property (i.e. kinetic energy, charge, dipole moment, volume, etc.) is obtained from the same universal formula, which embodies a 3D integral of the atom's volume.
Combining this QCT partitioning with the universal quantum expression of energy, leads to four types of fundamental energy contributions from which all chemical features and phenomena can be derived. These fundamental energy contributions are (i) intra-atomic energy, (ii) inter-atomic exchange energy, (iii) inter-atomic Coulomb energy and (iv) inter-atomic correlation energy. The first energy covers stereo-electronic effects (e.g. rotation barriers, steric hindrance), the second governs chemical bonding (including weakly covalent interactions) and (hyper)conjugation effects, the third accounts for the ubiquitous electrostatics, while the fourth covers dynamic correlation, which gives rise to dispersion. These contributions are all physically well-defined. They are all derived under the same Ansatz, both conceptually and computationally. This means that they are properly balanced and give the best guarantee to describe energetics of large systems at atomistic level. This approach resolves typical debates in force–field design such as the one on the nature of torsion potentials and that on the need for dedicated hydrogen bonding terms. The QCT force field does not directly mimic energy terms but faithfully expresses what is behind them. It should also be emphasised that the Coulomb interaction will be categorically represented by atomic multipole moments.95 This accurate representation of the anisotropy, i.e. the deformation of atomic electron densities eliminates the inaccuracy of point charges.78
Finally, machine learning captures the response of these four fundamental energy contributions upon any change in geometry of the system including its environment. We pioneered the use of kriging in the context of potential design.96 The machine learning method of kriging97 best handles the complexity98 of distant geometrical changes, and models pivotal polarisation effects. Kriging learns the mapping between an atomic quantity (as output, e.g. an atomic multipole moment or self-energy) and the coordinates of the neighbouring atoms (as input, called features).
There are a number of attractive features to Kriging, the main one being that this machine learning method is excellent in handling the high-dimensional complexity of configurational change in condensed matter. The four advantages of kriging are: (i) ranking of feature values according to importance: chemical insight, (ii) performance scales linearly with the dimension of feature space, (iii) trained model is analytical and differentiable, so forces can be computed quickly and accurately and, finally (iv) the knowledge of how an environment influences an atom is stored in Kriging parameters. The latter act as the trained memory of the atoms. Hence, there is no need to perform iterative calculations to self-consistent energies during a MD simulation.
Work is under way at Manchester that aims at demonstrating proof-of-concept that the QCT force field (which is still being developed) can be used in a molecular dynamics simulation. The analytically obtained forces, acting on the nuclei, and due to the interatomic multipolar electrostatic potential99 are currently being implemented in the molecular simulation program DL_POLY_4.100 The forces caused by the other fundamental forces are also added and the first ever simulation is expected in 2015.
Conclusions
Raman optical activity is an analytical technique offering many advantages in terms of structural sensitivity that was discovered and extensively developed in the UK. More specifically, recent instrumental and computational advancements have opened up an avenue toward the structural elucidation of families of molecules that are difficult to study with mainstream analytical techniques. However, it is only by working hand-in-hand that experiment and theory will be able to provide the methodological overhaul necessary to cope with complex challenges such as carbohydrate solvation, or new molecular model development. An approach successfully developed in the UK to address the former is presented and discussed, whereas perspectives on the latter open up new opportunities for more accurate analysis in chemistry and biology. Our presented approach has recently been successfully utilised for two monosaccharides and the use of vibrational analysis has led to new insights into the origin of carbohydrate ROA bands.102Acknowledgements
We are grateful to Tim Hughes for producing Fig. 5 using the in-house package IRIS, which incorporates special versions101 of the program MORPHY. We would like to thank the EPSRC for funding this research (EP/J019623/1).References
- L. D. Barron and A. D. Buckingham, Mol. Phys., 1971, 20, 1111 CrossRef CAS.
- L. D. Barron, M. P. Bogaard and A. D. Buckingham, J. Am. Chem. Soc., 1973, 95, 603 CrossRef CAS.
- J. Haesler, I. Schindelholz, E. Riguet, C. G. Bochet and W. Hug, Nature, 2007, 446, 526 CrossRef CAS PubMed.
- Y. He, B. Wang, R. K. Dukor and L. A. Nafie, Appl. Spectrosc., 2011, 65, 699 CrossRef CAS PubMed.
- F. J. Zhu, G. E. Tranter, N. W. Isaacs, L. Hecht and L. D. Barron, J. Mol. Biol., 2006, 363, 19 CrossRef CAS PubMed.
- J. Haesler, I. Schindelholz, E. Riguet, C. G. Bochet and W. Hug, Nature, 2007, 446, 526 CrossRef CAS PubMed.
- J. R. Cheeseman, M. S. Shaik, P. L. A. Popelier and E. W. Blanch, J. Am. Chem. Soc., 2011, 133, 4991 CrossRef CAS PubMed.
- P. W. Atkins and L. D. Barron, Mol. Phys., 1969, 16, 453 CrossRef CAS.
- S. T. Mutter, S. Ostavarpour and E. W. Blanch, Raman Optical Activity, in Encyclopedia of Analytical Chemistry, ed. R. A. Meyers, John Wiley, Chichester, 2014 Search PubMed.
- Y. A. He, B. Wang, R. K. Dukor and L. A. Nafie, Appl. Spectrosc., 2011, 65, 699 CrossRef CAS PubMed.
- E. W. Blanch and L. D. Barron, Raman Optical Activity of Biological Molecules, in Emerging Raman Applications and Techniques in Biomedical and Pharmaceutical Fields, ed. P. Matousek and M. D. Morris, Springer, New York, 2010, p. 153 Search PubMed.
- (a) N. R. Yaffe, A. Almond and E. W. Blanch, J. Am. Chem. Soc., 2010, 132, 10654 CrossRef CAS PubMed; (b) T. R. Rudd, R. Hussain, G. Siligardi and E. A. Yates, Chem. Commun., 2010, 46, 4124 RSC.
- L. Ashton, P. D. A. Pudney, E. W. Blanch and G. E. Yakubov, Adv. Colloid Interface Sci., 2013, 199, 66 CrossRef PubMed.
- (a) A. N. L. Batista, J. M. Batista Jr., V. S. Bolzani, M. Furlan and E. W. Blanch, Phys. Chem. Chem. Phys., 2013, 15, 20147 RSC; (b) A. N. L. Batista, J. M. Batista Jr., L. Ashton, V. S. Bolzani, M. Furlan and E. W. Blanch, Chirality, 2014, 26, 497 CrossRef CAS PubMed.
- C. M. Templeton, S. Ostavarpour, J. R. Hobbs, E. W. Blanch, S. D. Munger and G. L. Conn, Chem. Senses, 2011, 36, 425 CrossRef CAS PubMed.
- L. D. Barron, L. Hecht, I. H. McColl and E. W. Blanch, Mol. Phys., 2004, 102, 731 CrossRef CAS.
- L. D. Barron and A. D. Buckingham, Chem. Phys. Lett., 2010, 492, 199 CrossRef CAS.
- L. D. Barron, E. W. Blanch and L. Hecht, Adv. Protein Chem., 2002, 62, 51 CrossRef CAS PubMed.
- E. W. Blanch, L. Hecht and L. D. Barron, Methods, 2003, 29, 196 CrossRef CAS PubMed.
- K. Ruud and A. J. Thorvaldsen, Chirality, 2009, 21, E54–E67 CrossRef CAS PubMed.
- M. Pecul, Chirality, 2009, 21, E98–E104 CrossRef CAS PubMed.
- L. A. Nafie, Annu. Rev. Phys. Chem., 1997, 48, 357 CrossRef CAS PubMed.
- M. Pecul and K. Ruud, Int. J. Quantum Chem., 2005, 104, 816 CrossRef CAS.
- P. L. Polavarapu, Chem. Rec., 2007, 7, 125 CrossRef CAS PubMed.
- L. D. Barron and A. D. Buckingham, Annu. Rev. Phys. Chem., 1975, 26, 381 CrossRef CAS.
- L. D. Barron, Molecular Light Scattering and Optical Activity, Cambridge University Press, Cambridge, 2nd edn, 2009 Search PubMed.
- P. L. Polavarapu, Vibrational Spectra: Principles and Applications with Emphasis on Optical Activity, Elsevier, Amsterdam, 1998 Search PubMed.
- L. A. Nafie, Vibrational Optical Activity: Principles and Applications, Wiley, Chichester, 2011 Search PubMed.
- L. A. Nafie, Theor. Chem. Acc., 2008, 119, 39 CrossRef CAS.
- H. G. Li and L. A. Nafie, J. Raman Spectrosc., 2012, 43, 89 CrossRef CAS.
- L. Hecht, L. D. Barron and W. Hug, Chem. Phys. Lett., 1989, 158, 341 CrossRef CAS.
- L. Hecht and L. D. Barron, Appl. Spectrosc., 1990, 44, 483 CrossRef CAS.
- L. Hecht, L. D. Barron, E. W. Blanch, A. F. Bell and L. A. Day, J. Raman Spectrosc., 1999, 30, 815 CrossRef CAS.
- W. Hug and G. Hangartner, J. Raman Spectrosc., 1999, 30, 841 CrossRef CAS.
- P. K. Bose, L. D. Barron and P. L. Polavarapu, Chem. Phys. Lett., 1989, 155, 423 CrossRef CAS.
- P. L. Polavarapu, S. T. Pickard, H. E. Smith, T. M. Black, L. D. Barron and L. Hecht, Talanta, 1993, 40, 545 CrossRef CAS PubMed.
- P. L. Polavarapu, L. Hecht and L. D. Barron, J. Phys. Chem., 1993, 97, 1793 CrossRef CAS.
- T. M. Black, P. K. Bose, P. L. Polavarapu, L. D. Barron and L. Hecht, J. Am. Chem. Soc., 1990, 112, 1479 CrossRef CAS.
- P. L. Polavarapu, P. K. Bose, L. Hecht and L. D. Barron, J. Phys. Chem., 1993, 97, 11211 CrossRef CAS.
- P. L. Polavarapu, T. M. Black, L. D. Barron and L. Hecht, J. Am. Chem. Soc., 1993, 115, 7736 CrossRef CAS.
- L. D. Barron, A. R. Gargaro, L. Hecht and P. L. Polavarapu, Spectrochim. Acta, Part A, 1991, 47, 1001 CrossRef.
- L. D. Barron, A. R. Gargaro, L. Hecht, P. L. Polavarapu and H. Sugeta, Spectrochim. Acta, Part A, 1992, 48, 1051 CrossRef.
- P. L. Polavarapu, L. Hecht and L. D. Barron, J. Phys. Chem., 1993, 97, 1793 CrossRef CAS.
- T. Helgaker, K. Ruud, K. L. Bak, P. Jorgensen and J. Olsen, Faraday Discuss., 1994, 99, 165 RSC.
- K. Ruud, T. Helgaker and P. Bour, J. Phys. Chem. A, 2002, 106, 7448 CrossRef CAS.
- P. L. Polavarapu, J. Phys. Chem., 1990, 94, 8106 CrossRef CAS.
- V. Liegeois, K. Ruud and B. Champagne, J. Chem. Phys., 2007, 127, 204105 CrossRef PubMed.
- A. J. Thorvaldsen, B. Gao, K. Ruud, M. Fedorovsky, G. Zuber and W. Hug, Chirality, 2012, 24, 1018 CrossRef CAS PubMed.
- R. Bast, U. Ekstrom, B. Gao, T. Helgaker, K. Ruud and A. J. Thorvaldsen, Phys. Chem. Chem. Phys., 2011, 13, 2627 RSC.
- A. J. Thorvaldsen, K. Ruud and M. Jaszunski, J. Phys. Chem. A, 2008, 112, 11942 CrossRef CAS PubMed.
- A. J. Thorvaldsen, K. Ruud, K. Kristensen, P. Jorgensen and S. Coriani, J. Chem. Phys., 2008, 129, 164110 CrossRef PubMed.
- M. Pecul and A. Rizzo, Mol. Phys., 2003, 101, 2073 CrossRef CAS.
- W. Hug, Chem. Phys., 2001, 264, 53 CrossRef CAS.
- G. Zuber and W. Hug, J. Phys. Chem. A, 2004, 108, 2108 CrossRef CAS.
- J. R. Cheeseman and M. J. Frisch, J. Chem. Theor. Comput., 2011, 7, 3323 CrossRef CAS.
- M. Reiher, V. Liegeois and K. Ruud, J. Phys. Chem. A, 2005, 109, 7567 CrossRef CAS PubMed.
- P. Danecek, J. Kapitan, V. Baumruk, L. Bednarova, V. Kopecky and P. Bour, J. Chem. Phys., 2007, 126, 224513 CrossRef PubMed.
- J. Sebek, J. Kapitan, J. Sebestik, V. Baumruk and P. Bour, J. Phys. Chem. A, 2009, 113, 7760 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford CT, 2004 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- ADF2013, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands; http://www.scm.com/.
- Dalton, a molecular electronic structure program, Release DALTON2013 (2013), see http://daltonprogram.org/.
- I. L. Alberts, J. S. Andrews, S. M. Colwell, N. C. Handy, D. Jayatilaka, P. J. Knowles, R. Kobayashi, K. E. Laidig, G. Laming, A. M. Lee, P. E. Maslen, C. W. Murray, J. E. Rice, E. D. Simandiras, A. J. Stone, M.-D. Su and D. J. Tozer, Cambridge Analytical Derivatives Package (CADPAC), Cambridge University, Cambridge, 6.5 edn, 2001 Search PubMed.
- J. Neugebauer, M. Reiher, C. Kind and B. A. Hess, J. Comput. Chem., 2002, 23, 895 CrossRef CAS PubMed.
- K. J. Jalkanen, R. M. Nieminen, M. Knapp-Mohammady and S. Suhai, Int. J. Quantum Chem., 2003, 92, 239 CrossRef CAS.
- E. Tajkhorshid, K. J. Jalkanen and S. Suhai, J. Phys. Chem. B, 1998, 102, 5899 CrossRef CAS.
- J. Kapitan, V. Baumruk, V. Kopecky Jr., R. Pohl and P. Bour, J. Am. Chem. Soc., 2006, 128, 13451 CrossRef CAS PubMed.
- S. Miertus, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117 CrossRef CAS.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799 RSC.
- M. Biczysko, J. Bloino, G. Brancato, I. Cacelli, C. Cappelli, A. Ferretti, A. Lami, S. Monti, A. Pedone, G. Prampolini, C. Puzzarini, F. Santoro, F. Trani and G. Villani, Theor. Chem. Acc., 2012, 131, 1201 CrossRef.
- V. Barone and M. J. Cossi, Phys. Chem. A, 1998, 102, 1995 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. J. Barone, Comput. Chem., 2002, 24, 669 CrossRef PubMed.
- K. J. Jalkanen, I. M. Degtyarenko, R. M. Nieminen, X. Cao, L. A. Nafie, F. Zhu and L. D. Barron, Theor. Chem. Acc., 2008, 119, 191 CrossRef CAS.
- S. Luber and M. Reiher, J. Phys. Chem. A, 2009, 113, 12044 CrossRef CAS.
- K. H. Hopmann, K. Ruud, M. Pecul, A. Kudelski, M. Dracinsky and P. Bour, J. Phys. Chem. B, 2011, 115, 4128 CrossRef CAS PubMed.
- H. Urago, T. Suga, T. Hirata, H. Kodama and M. Unno, J. Phys. Chem. B, 2014, 118, 6767 CrossRef CAS PubMed.
- V. Babin and C. Sagui, J. Chem. Phys., 2010, 132, 104108 CrossRef PubMed.
- S. Cardamone, T. J. Hughes and P. L. A. Popelier, Phys. Chem. Chem. Phys., 2014, 16, 10367 RSC.
- S. Luber and M. Reiher, J. Phys. Chem. A, 2009, 113, 8268 CrossRef CAS PubMed.
- J. Kaminsky, J. Kapitan, V. Baumruk, L. Bednarova and P. Bour, J. Phys. Chem. A, 2009, 113, 3594 CrossRef CAS PubMed.
- Woods Group. (2005–2014) GLYCAM Web. Complex Carbohydrate Research Center, University of Georgia, Athens, GA ( http://www.glycam.com).
- B. L. Foley, M. B. Tessier and R. J. Woods, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2, 652 CrossRef CAS PubMed.
- K. N. Kirschner and R. J. Woods, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10541 CrossRef CAS PubMed.
- S. Dapprich, I. Komaromi, K. S. Byun, K. Morokuma and M. J. Frisch, J. Mol. Struct. (THEOCHEM), 1999, 462, 1 CrossRef.
- J. Vandenbussche, P. Bultinck, A. K. Przybyl and W. A. Herrebout, J. Chem. Theory Comput., 2013, 9, 5504 CrossRef CAS.
- B. Simmen, T. Weymuth and M. Reiher, J. Phys. Chem. A, 2012, 116, 5410 CrossRef CAS PubMed.
- P. L. Polavarapu and C. L. Covington, Chirality, 2014, 26, 539 CrossRef CAS PubMed.
- R. Dennington, T. Keith and J. Millam, GaussView, Version 5, Semichem Inc., Shawnee Mission, KS, 2009 Search PubMed.
- M. Fedorovsky, PyVib2, a program for analysing vibrational motion and vibrational spectra, http://pyvib2.sourceforge.net, 2007 Search PubMed.
- M. Humbert-Droz, P. Oulevey, L. M. L. Daku, S. Luber, H. Hagemann and T. Burgi, Phys. Chem. Chem. Phys., 2014, 16, 23260 RSC.
- P. L. A. Popelier, AIP Conf. Proc., 2012, 1456, 261 CrossRef CAS.
- P. L. A. Popelier, Curr. Top. Med. Chem., 2012, 12, 1924 CrossRef CAS PubMed.
- P. L. A. Popelier, in Drug Design Strategies: Computational Techniques and Applications, ed. L. Banting and T. Clark, Roy. Soc. Chem., 2012, vol. 20, ch. 6, p. 120 Search PubMed.
- P. L. A. Popelier, in The Nature of the Chemical Bond Revisited, ed. G. Frenking and S. Shaik, Wiley-VCH, 2014, ch. 8, p. 271 Search PubMed.
- S. Y. Liem and P. L. A. Popelier, Phys. Chem. Chem. Phys., 2014, 16, 4122 RSC.
- C. M. Handley, G. I. Hawe, D. B. Kell and P. L. A. Popelier, Phys. Chem. Chem. Phys., 2009, 11, 6365 RSC.
- N. Cressie, Statistics for Spatial Data, Wiley, New York, USA, 1993 Search PubMed.
- T. Fletcher, S. J. Davie and P. L. A. Popelier, J. Chem. Theor. Comput., 2014, 10, 3708 CrossRef CAS.
- M. J. L. Mills and P. L. A. Popelier, J. Chem. Theor. Comput., 2014, 10, 3840 CrossRef CAS.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1911 RSC.
- M. Rafat, M. Devereux and P. L. A. Popelier, J. Mol. Graphics Modell., 2005, 24, 111 CrossRef CAS PubMed.
- S. T. Mutter, F. Zielinski, J. R. Cheeseman, C. Johannessen, P. L. A. Popelier and E. W. Blanch, Phys. Chem. Chem. Phys., 2015 10.1039/C4CP05517A , in press.
Footnote |
| † Current address: School of Applied Sciences, RMIT University, GPO Box 2476, Melbourne VIC 3001, Australia. |
| This journal is © The Royal Society of Chemistry 2015 |