Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Soft-patchy nanoparticles: modeling and self-organization
Emanuela
Bianchi
*a,
Barbara
Capone
b,
Gerhard
Kahl
c and
Christos N.
Likos
b
aInstitut für Theoretische Physik, Technische Universität Wien, Wiedner Hauptstraße 8-10, A-1040 Vienna, Austria. E-mail: emanuela.bianchi@tuwien.ac.at
bFaculty of Physics, University of Vienna, Boltzmanngasse 5, A-1090, Vienna, Austria
cInstitut für Theoretische Physik and Center for Computational Materials Science (CMS), Technische Universität Wien, Wiedner Hauptstraße 8-10, A-1040 Vienna, Austria
First published on 16th January 2015
Abstract
We consider a novel class of patchy particles inspired by polymer-based complex units where the limited valence in bonding is accompanied by soft interactions and incessant fluctuations of the patch positions, possibly leading to reversible modifications of the patch number and size. We introduce a simple model that takes into account the aforementioned features and we focus on the role played by the patch flexibility on the self-organization of our patchy units in the bulk, with particular attention to the connectivity properties and the morphology of the aggregated networks.
1 Introduction
Self-organization at the atomic or molecular level is a fundamental mechanism of paramount relevance in nature. During the past years this mechanism has been exploited increasingly more frequently in materials science to fabricate target mesoscopic structures for technological applications.1 A successful way to produce materials with well-defined architectures and properties often relies on anisotropy-driven self-organization.2 At the nano- or micro-scale level, inter-particle interactions can indeed be designed to be anisotropic, for instance by creating patterns on the surface of the self-organizing entities: surface regions with chemical or physical properties different from those of the bare colloid are usually referred to as patches. By virtue of their directional and selective bonding capacities, patchy3,4 and inverse patchy5 particles, i.e., patchy particles with charged patches, can assemble in a large variety of mesoscopic structures.3,4,6–13In most of the patchy and inverse patchy systems investigated so far, the accurate design of the particle surface pattern (in terms of position, shape and extent of the patches) has been a key ingredient for the assembly of the desired mesoscopic architectures. When some patch rearrangement was allowed, units with reduced bonding valence were shown to favor disordered phases and stabilize the liquid with respect to the crystal in the zero-temperature limit.14 Additionally, as soon as patchy particles with a low number of mobile, directional bonds were designed to interact in a soft fashion, the solid–liquid phase separation was suppressed in favor of a coexistence between two disordered phases: a single and a double network, the latter consisting of two inter-penetrating, non-interacting single networks.15 Patchy systems combining low valence, bond flexibility and soft interactions were designed to neglect double bonding between patches as well as possible energy penalties associated with the distortion of the equilibrium patch arrangement. These features can, for instance, be realized in associating fluids or DNA-coated colloid systems. On the other side of the spectrum, tetravalent DNA nanostars, i.e., extremely flexible patchy units with four bonding patches, have been shown to never crystallize and form instead a thermodynamically stable, fully bonded equilibrium gel.16,17
In the present contribution we introduce a class of patchy particles where directional bonding, soft interactions, and incessant patch rearrangements are complemented with energy penalties associated with the mobility of the patches, reversible modifications of the patch number/size and the possible formation of more than two bonds per patch. Our model is inspired by deformable patchy units that self-assemble in a bulk system of star polymers with functionalized arms. Such functionalized star polymers, also known as telechelic star polymers (TSPs), are macromolecules made of diblock polymeric chains grafted on a common center in a selective solvent: each arm has a solvophilic part, which is located in the interior of the star, and an attractive, solvophobic end. The propensity of the solvophobic ends of different arms to associate gives rise to a number of particular intra-star and inter-star association phenomena.18–20 In particular, it was recently shown that the functionalized ends of the arms self-organize into soft, attractive patches, while the non-functionalized parts of the arms act as ultra-soft, repulsive cores:21,22 in the zero density limit, the number of patches per star and the equilibrium patch positions can be controlled by changing the percentage of attractive monomers per arm and the number of arms per star; at finite density, the intra-star association, which is faster than the inter-star association, leads to systems composed of equilibrium patchy aggregates, which maintain the same number of patches as their zero-density counterparts. These self-assembled, polymer-based patchy units are thus equilibrium structures that can interact with each other while keeping, on average, a well-defined internal structure. The possibility of tuning the number and the equilibrium arrangement of the patches, in combination with the capability of these patchy assemblies to maintain their internal structure at finite density, strongly motivates the investigation of these systems in the bulk. In this contribution we consider a simple patchy model that keeps a close connection to the described polymer-based complex units, while dealing with interaction potentials that are computationally easier to handle. Our aim is to explore the role of the softness and of the patch rearrangement on the formation of particle networks at a coarse-grained level where both physical features can be controlled by suitably chosen parameters.
Our soft and flexible patchy colloid (SFPC) model features a soft, repulsive core on which a fixed number of soft, attractive patches is attached. Both the patch–core distance and the patch–patch angle within the same particle are allowed to fluctuate around their respective equilibrium values. The movements of the patches are controlled by two flexibility parameters: one describes the patch elongation along the radial direction, while the other is associated with the angular patch freedom. The internal energy of each patchy unit is the result of pair interactions occurring between the single entities – either cores or patches – belonging either to the same particle or to two different particles. The functional form and the specific values of the parameters of the pair interaction are chosen in such a way that, in the limit of non-flexible patches, our model can be related to a rigid counterpart whose phase diagram is reported in the literature.23
In the present contribution we explore by means of Monte Carlo (MC) simulations the bulk behavior of the fluid phase at a fixed density; this value corresponds to the density at which the rigid reference model forms a fully bonded, homogeneous phase with an open architecture; different temperatures (or interaction strengths) are considered. We put particular focus on the impact of the patch flexibility on the features of the percolating structures formed in our SFPC systems.
The manuscript is organized as follows: in Section 2 we describe our SFPC model, in Section 3 we provide details of the MC simulations, in Section 4 we report our results, and in Section 5 we present our conclusions.
2 The model
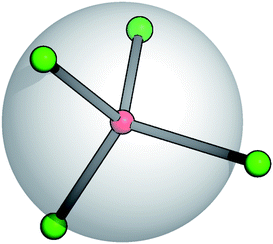
Recent studies on TSPs showed that systems with an average spherical repulsive core and functionalized sites, flexibly distributed around the core, allow the mechanical stabilization of crystals over a portion of the phase diagram that is one order of magnitude wider than in systems with the same particle valence where the patches are fixed in rigid geometries on the particle surface.21 At the same time, the occurrence of gel states in TSP systems has also been observed.22 It is thus important to analyze the effect of the patch flexibility on the self-organization of patchy units into extended structures. Starting from the fully rigid reference system,23 we hereby introduce suitable potentials characterized by two specific flexibility parameters that allow for angular and radial displacements of the patches with respect to the core of the units they belong to.A soft and flexible patchy colloid (SFPC) consists of a fixed number of mutually attractive spheres, referred to as patches (index “p”), connected to the center of a soft repulsive sphere, referred to as the core (index “c”). A schematic representation of such a patchy unit is reported in Fig. 1 for the four patch case. The internal energy of a collection of SFPCs can be split into two distinct contributions: the inter-particle (or mutual) interaction and the intra-particle (or self) energy.
2.1 Inter-particle interactions
The inter-particle or mutual interaction is the sum of three contributions: the attraction between the patches (index “pp”), the repulsion between the cores (index “cc”), and the patch–core repulsion (index “pc”); the entities (either patches or cores) involved in these pair interactions belong to different SFPCs.We consider a 2n–n potential for the attractive pp interaction:
| Vmpp(rpp) = 4εpp[(σpp/rpp)2n − (σpp/rpp)n], | (1) |
 | (2) |
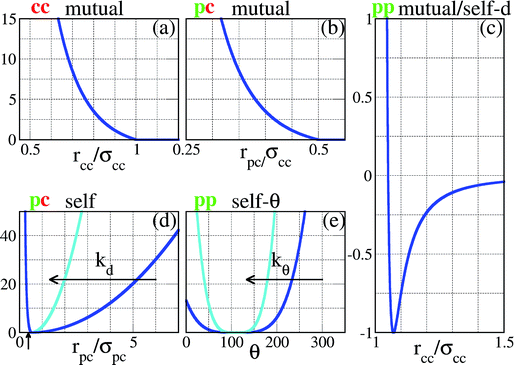 | ||
| Fig. 2 Representation of the interaction potentials between the different components of our SFPCs (the vertical axes correspond to energies, measured in units of εpp). In panels (a)–(c), the core–core, the patch–core and the patch–patch potentials between entities belonging to two distinct SFPCs are reported (labeled as cc mutual, pc mutual and pp mutual, respectively). In panels (c)–(e), the radius-dependent patch–patch, the patch–core and the angle-dependent patch–patch potentials between entities belonging to the same SFPC are reported (labeled as pp self-d, pc self, and pp self-θ, respectively). To facilitate the comparison with the pair potential of the rigid system reported in ref. 23, the pp mutual potential is reported versus the distance between the SFPC cores, assuming that the patch–core distance is exactly σpc; the pp self-d potential must thus be shifted by a distance σpc in order to visualize it as a function of the distance between two patches on the same patchy units. The pc self and the pp self-θ potentials represent the constraints on the patch mobility; the flexibility of the patchy unit is described via two parameters, namely kd, responsible for the patch elongation along radial directions, and kθ, related to the angular patch freedom; in the figure the cases kd = kθ = 1 (blue) and 10 (turquoise) are depicted. | ||
2.2 Intra-particle interactions
The intra-particle or self energy is the sum of the interactions within a single SFPC. The patch–patch interaction consists of a distance-dependent, attractive part, expressed by the same patch–patch potential described above, i.e. Vspp(rpp) = Vmpp(rpp), and an angular constraint Sspp(θ) which prevents the patches on the same particle from collapsing on top of each other. This constraint is an efficient way for capturing the self-avoiding behavior of the branches of the functionalized star polymers that represent the basis of our SFPC model. The functional form of such a constraint is a generalized spring potential with an average value equal to the equilibrium angle of a regular patch decoration, i.e. θ0pp = 109.5° in the case of four patches, arranged on a regular tetrahedron; the functional form is given by| Sspp(θ) = kθ(θ − θ0pp)4, | (3) |
The patch–core interaction consists of a repulsive part, expressed by the same patch–core potential described above, i.e. Vspc(rpp) = Vmpc(rpp), plus an attractive constraint Sspc(rpc) which keeps the patches attached to their respective particle core. The equilibrium patch–core position is σpc: when a patch is closer than σpc to its core then it feels the repulsion, while when the patch is farther than σpc from its core it feels the attraction. The fluctuations around the equilibrium position are again described by a spring potential, namely
| Sspc(rpc) = kd(rpc − σpc)2, | (4) |
3 Monte Carlo simulations
We perform Monte Carlo (MC) simulations in the NVT ensemble, where N = 512 is the number of patchy units, V = 970.299 is the volume of the simulations box in units of σcc3, and T is the temperature in units of εpp (with kB = 1). It is worth noting that in our simulations, while T is varied, the number density of the systems is fixed to ρ ≈ 0.5277 in units of σcc−3; this choice corresponds to the density at which the rigid reference system23 is able to form a fully bonded, homogeneous and open structure—namely the diamond cubic lattice—which spans the whole simulation box.23Each MC move consists, on average, of N trial displacements; in order to take into account the internal degrees of freedom of our SFPCs, ∼50% of the trial displacements are particle moves, while ∼50% are patch displacements. An intra-particle move is defined as a rigid displacement of the whole SFPC by a random quantity distributed uniformly between ±δrm; an inter-particle move is defined as a displacement of a single patch by a random quantity distributed uniformly between ±δrs. The choice of the maximum amount of these displacements keeps an acceptance ratio of the corresponding move between 30% and 40%.
In the present contribution, we focus on the role played by the patch flexibility on the self-organization of SFPCs in the bulk; we thus consider a selection of systems characterized by different sets of (kd, kθ)-values at three different temperatures, namely T = 0.10, 0.30 and 0.70. We select a grid of flexibility parameters on a logarithmic scale: both kd and kθ range from 1 to 1000 in units of εpp/σcc2 and εpp rad−4, respectively. We initialize all the simulations in the fluid phase and analyze the morphology of the system using the respective final configuration of the MC simulation. The shortest MC simulations (corresponding to systems in the fluid phase) extend over at least 106 MC steps, while the longest simulations (corresponding to systems in the gel states) cover 107 MC steps. Gels observed in the selected SFPC systems are out of equilibrium structures that show a small annealing even after long equilibration times.
We characterize the morphology of the systems via different quantities, namely the intra-particle and the inter-particle energies, the number of bonds formed between patches either on different particles (mutual bonds) or on the same particle (self bonds), the average angle between patches linked to the same core, and the average distance between a patch and its core. Finally, we also evaluate if the system is percolating or not; our percolation analysis is based on a minimum energy criterion: we consider two patches to be bonded when their interaction energy amounts to less than 10% εpp.
4 Results
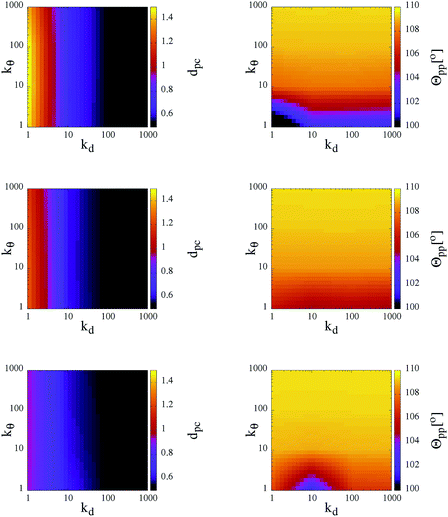
As observed in the previous studies on TSPs,21,22 soft and flexible patchy units tend to form percolating gel networks; we thus expect to observe similar behavior in our SFPC systems. For TSPs the radial and angular flexibilities, as well as the attraction strength between the patches, depend on the microscopic details of the underlying systems and are consequently coupled to each other. In contrast, with our SFPC model we are able to investigate separately the role of the radial and angular flexibilities, on one side, and the effect of a change in the attraction strength (or equivalently, a change in temperature), on the other side. In particular, we aim to describe how the morphology of the self-organized structures depends on the flexibility parameters kd and kθ at three selected T-values (namely, T = 0.10, 0.30 and 0.70) and at a fixed density (namely, ρ ≈ 0.5277).In order to classify the self-organized structures, we first characterize the single particle architecture by considering two distinct features: the average distance between the patches and their corresponding core, dpc, and the average angle between two patches belonging to the same unit, Θpp. In Fig. 3, both quantities are represented at fixed temperature in contour plots in the kdvs. kθ plane; data for all selected systems are reported for the three investigated temperatures. As expected, while the average patch–core distance depends mainly on kd, fluctuations of the average patch–patch angle are predominantly influenced by kθ. On lowering the temperature, both sets of data show rapidly diminishing deviations from their respective equilibrium values, i.e., both (dpc − σpc) and (Θpp − θ0pc) grow with T. In particular, while at the highest temperature investigated, dpc attains values of almost 3σpc for kd < 10; it is on average less than 2σpc for the corresponding cases at the lowest temperature considered. In a similar way, in systems with kθ < 10, Θpp is smaller than θ0pp by about 2° at T = 0.10, while it is about 10° smaller than θ0pp at T = 0.70.
The trends of the single particle structural features with temperature have two consequences. First of all, the increase of the patch–core distance enhances the effective packing fraction of the system: as dpc varies from 0.5σcc (in the most rigid systems at the lowest temperature) to almost 1.5σcc (in the most flexible cases at the highest temperature), the packing fraction becomes seven times bigger. Moreover, the increase of both the radial and the angular patch fluctuations leads to effectively larger bonding volumes, thus favoring the formation of more than one bond per patch. The changes of the effective packing fraction of the system and of the bonding volume per particle have an impact on the inter-particle bonding, as demonstrated in the following.
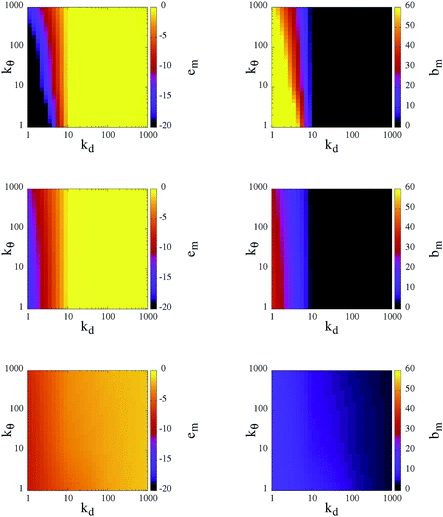
To classify the different self-organized morphologies emerging in SFPC systems, we consider the average inter-particle (or mutual) energy, em, the corresponding average number of bonds between patches belonging to different particles (or mutual bonds), bm, and the percolation threshold, signaled by the presence of at least one cluster that extends over the entire simulation box.
At T = 0.10, the rigid reference system is able to form a fully bonded diamond crystal, where the average energy per particle, due to inter-particle bonding, is ≈−1.65.23 In contrast, at T = 0.30 and 0.70, the system is in the fluid state, characterized by an almost vanishing inter-particle energy. It must be noted that, even though the diamond crystal is the thermodynamically stable phase, when the system is initialized in the fluid phase and instantaneously quenched at T = 0.10 (the same procedure that we use for our SFPCs), particles self-organize into a disordered percolating structure, where the average inter-particle energy is ≈−0.96. In other words, while the number of bonds of a rigid patchy particle in the lattice is four, in the disordered network not all patches are bonded and thus a rigid patchy particle in the gel state at T = 0.10 forms less than four bonds.
In Fig. 4, the corresponding data for em and bm for our SFPCs are reported as contour plots in the kdvs. kθ plane for all selected systems; again, each panel in the figure corresponds to one temperature. Similar to the rigid case, em and bm provide a consistent picture of the system: when the system is in the fluid phase em ≈ 0, then also bm ≈ 0; in contrast, extended bonded structures are characterized by em ≪ 0, or equivalently, by bm ≫ 0. While at T = 0.10 particles self-organize into extended gel networks over the entire (kd, kθ)-range, for T > 0.10 two different scenarios can be identified according to the radial flexibility: for kd ≥ 10 the systems are in the fluid phase irrespective of the value of kθ, while for kd < 10 the systems form deeply inter-connected networks over the entire kθ range. The data provide evidence that the transition between the two scenarios at kd ≃ 10 is rather well-defined. Such a sharp distinction suggests that kd is the key parameter that governs the self-organization of our SFPCs; thus it can be used to distinguish between percolating and fluid states at intermediate and high temperatures. By softening the radial localization, i.e., by decreasing kd, the particle interaction range is indeed effectively increased (or, as mentioned before, the effective packing fraction is augmented), and thus even particles that are farther away from each other are able to form bonds. The angular flexibility starts only to play a role at the highest temperature investigated: the softer the angular localization is, the more interconnected the system is. All branched networks are found to be percolating.
Different characteristic features in the gel structure can be observed at different state points. In contrast to rigid patchy colloids, the number of bonds that a patch forms can be greater than one in SFPC systems: as mentioned before, the bonding volume increases together with either the temperature or the (radial and angular) flexibility. At the lowest temperature investigated, the differences in em and bm are small for the chosen (kd, kθ)-value; nonetheless, the emerging percolating structures have different morphologies, discussed more thoroughly in the following. It is worth noting that at T = 0.10 and for large kd, em assumes slightly smaller values (and bm assumes slightly bigger values) with respect to the rigid case for large kd. In contrast, at the highest temperature considered, em can decrease (and bm can increase) by up to a factor of ten when the angular and radial flexibilities are large. Thus, even in the stiff limit at low temperatures, the percolating structures formed by SFPCs are more inter-connected than their rigid counterpart; this fact is due to the release of the single bond per patch constraint in the present model.
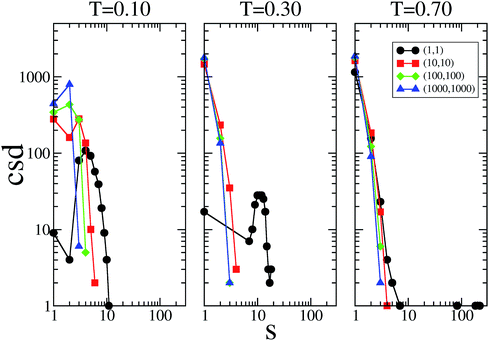
The cluster size distribution of the patches, i.e., the number of patch clusters with size s, are reported in Fig. 5 for selected systems at the three temperatures investigated; data are only shown along the main diagonal in the plane of the flexibility parameters. These data provide additional information on how the patch flexibility affects the connectivity of the system; they also shed some light on the extremely large values for em and bm observed in some of the most flexible cases. In the rigid reference system, clusters of patches can be composed of only two patches; however, as soon as the single bonding constraint is released, the size of the clusters can grow, since patches can rearrange around their core, paying an increasingly small energetic penalty on decreasing the flexibility parameters.
At T = 0.10, a peak in the cluster size distribution of the patches is observed at s = 2 for (kd, kθ) = (1000, 1000) and (100, 100); the rest of the patches are mainly in the monomeric state, while a small percentage of them are in clusters of size three. The presence of clusters bigger than size two explains why, even in the stiff limit, bm is bigger in SFPCs than in the rigid reference system where the constraint of the single bond per patch is implemented. On increasing the patch flexibility (i.e., when decreasing kd and kθ), the s corresponding to the peak increases monotonically: to be more specific, when (kd, kθ) = (10, 10), s = 3, while for (kd, kθ) = (1, 1), s = 4. At T = 0.30 the cluster size distribution peaks at s = 1 for all systems in the fluid phase; in contrast it has a peak at s ≈ 12 in the percolating gel network which emerges when (kd, kθ) = (1, 1). At T = 0.70, the cluster size distribution in the fluid systems does not change significantly, while the cluster size of the gel system changes distinctively: while most of the patches are in the monomeric state, big clusters of more than 200 bonds can be found. In the final part of this section, where we select typical configurations of SFPC systems, we further analyze how strongly the morphology of the system is affected by the clustering of the patches.
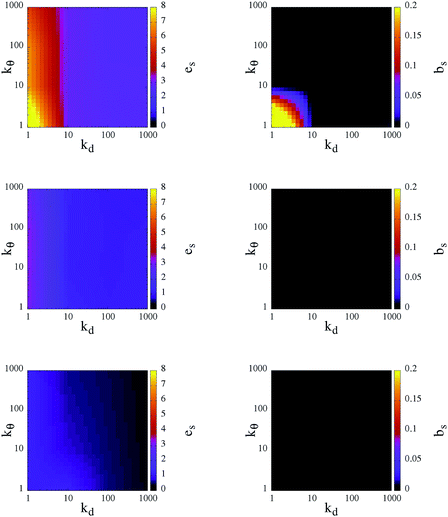
As already discussed above, the bonding volume of a patch is increased on softening the patch constraints. This increase has an impact not only on the inter-particle properties but possibly also on the intra-particle properties. Indeed, the morphology of the percolating network can be affected by the formation of bonds between patches on the same unit. Fig. 6 reports in a contour plot the average intra-particle (or self) energy, es, and the average number of intra-particle (or self) bonds, bs, at the chosen three temperatures and for all selected systems. Again, both quantities have a stronger dependence on kd rather than on kθ: at a given temperature, es and bs are completely determined by the radial flexibility (quantified by kd), which governs whether the system is in the fluid or gel state. In fluid systems no internal bonds are formed and the energy price of the continuously rearranging patches is very close to zero. In contrast, in percolating gels a small percentage of self bonds can occur, according to the angular flexibility of the patches: when kθ is large, particles do not form internal bonds and hence on an inter-particle level the particles assemble as four coordinated patchy particles; when kθ < 10 a small percentage of internal bonds are formed only at the highest temperature analyzed. The energy cost associated with the movements of the patches increases with increasing T and attains a maximum at T = 0.70 when both kd and kθ assume values that are less than 10. This fact is due to the formation of both inter- and intra-particle bonds: as mentioned before, as a consequence of a deformation of the patch unit, which increases es, the patches prefer to assemble into big clusters to maximize the number of bonds, thus lowering their em.
We conclude this section by showing a selection of simulation snapshots of our system in Fig. 7. We report system configurations with kd = kθ at T = 0.10 and 0.70. As discussed above, at T = 0.10 all systems form a percolating gel structure, while among the systems at T = 0.70 only the one with (kd, kθ) = (1, 1) is percolating. The fluid systems are in a homogeneous phase characterized by a spatially random distribution of the entities – either patches or cores – in the simulation box; a visual inspection of the panels provides evidence that the respective configurations bear strong similarities with each other (as suggested by the previous quantitative analysis on the single particle structural features). In contrast, the gel structures have different morphologies, as anticipated before. At T = 0.10 the network in the very stiff limit, i.e., when kd, kθ = (1000, 1000), is quite homogeneous, resembling the configurations found for the rigid reference case. On increasing the patch flexibility, voids emerge in the gel structure that are related to the formation of clusters with more than two patches. Interestingly, on further increasing the patch flexibility, the percolating network again becomes homogeneous: in striking contrast to the stiff case, the homogeneous gel at (kd, kθ) = (1, 1) is characterized by a deeply inter-connected structure. On increasing the temperature, extremely big clusters form in the system. It is worth noting that at T = 0.70 patches are either unbonded or belong to big clusters; in contrast, at T = 0.30 most of the patches are bonded and belong to relatively smaller clusters.
5 Conclusions
Motivated by recent investigations on the self-assembly scenarios of telechelic star polymers (TSPs),21,22 we have introduced a simple, soft and flexible patchy colloid (SFPC) model that captures the main features of TSPs in the regime where they behave as complex patchy particles. Introducing a soft core linked to four mobile patches as the building unit of our model, we parameterize the effective interactions between the different entities (either patches or cores) via simple potentials, that are able to capture on a qualitative level the main features of the underlying TSP systems. In addition to conventional Lennard-Jones-type interactions between the different entities, we allow patch displacements in both radial and tangential directions. The Lennard-Jones-type interactions are parameterized to closely reproduce, when the patches are fixed in their equilibrium positions, a model with immobile patches which is used as a reference.23 The radial and tangential constraints acting on patches belonging to the same particle are parameterized via generalized spring-potentials, whose stiffness is quantified by two respective flexibility parameters. In contrast to the original TSP model, we are able to obtain a deeper insight into the self-organization strategies of SFPCs via systematic variation of the two flexibility parameters. While the density was kept fixed to the value at which the reference system can stabilize a diamond cubic lattice, the temperature (or equivalently the energy interaction strength) was varied over a relatively broad range. All investigations are based on extensive Monte Carlo simulations.Investigating first the single particle features, i.e., the average distance of the patches from their respective core and the average relative angle between two patches on the same particle, provides clear evidence of the strong impact of the radial flexibility on the former property and of the temperature on the latter property. These features lead to a substantial increase of the effective packing fraction of the system and to an enlarged bonding volume. By analyzing the average inter-particle energy and the average number of bonds between patches belonging to different particles, unambiguous fingerprints can be identified whether a system forms a liquid or a gel phase. Among the latter ones, significantly different morphologies can be identified. Additional insight on the impact of patch flexibility on the connectivity is obtained via a detailed analysis of the cluster size distribution of the patches.
Previous progress in synthesis techniques allowed for the precise and reliable fabrication of star-shaped macromolecules with functionalized end groups.24–26 Block copolymer stars have been experimentally analyzed by the group of Fetters27,28 in the concentrated density regime; such macromolecules were shown to assemble in structures that depend both on the number of arms and on the percentage of attractive monomers per arm. At the time of the experimental study, no explanation was given about how the functionality of the polymers influences the self-assembly scenario, as the ordered phase was not related directly to the number of arms of each polymer. The theoretical study of ref. 21 and 22 provided an explanation to the experimentally observed phenomena by demonstrating that each single star polymer can undergo a two-stage hierarchical self-assembly: first the polymer stars assemble at the local scale into soft and flexible patchy particles and then they assemble at the global scale into a crystalline structure compatible with the patchiness of the self-aggregated patchy units.
Given the experimental results and the interesting theoretical predictions, the present work aimed at analyzing how the introduction of flexibility into a patchy particle model could affect the behavior of functionalized particle systems. We have presented a very versatile model of a soft and flexible patchy model, that allows to analyze the different types of flexibility independently of each other. The self-assembly scenarios of our model are dictated by the competition between the energy penalties associated with the patch fluctuations and the energy gains due to the patch bonding, giving rise to different self-organization scenarios. Our preliminary results indicate that disordered networks with connectivity properties that can be controlled by tuning the flexibility of the patchy units have come within reach. The design of such disordered architectures will be of high relevance for the development of self-repairing and biomimetic systems.
It should be noted that systems with related features were recently studied either experimentally or via simulations: (i) in systems where DNA strands were grafted to the liquid interface of emulsions, tuning the valence (via the flexibility of the DNA strands) led to different emulsion architectures,29 (ii) in systems of single-stranded DNA-coated colloids tuning the valence (via nonspecific repulsions between the particles) led to different aggregation scenarios.30
Acknowledgements
EB, GK and CNL acknowledge support from the Austrian Science Fund (FWF) under Proj. no. V249-N27 (EB's Elise Richter Grant), P23910-N16, and F41 (SFB ViCoM). BC acknowledges support from the ÖAW, through her APART Fellowship 11723. Computer time at the Vienna Scientific Cluster (VSC) is gratefully acknowledged.References
- G. M. Whitesides and M. Boncheva, Science, 2002, 295, 2418 CrossRef CAS PubMed.
- S. C. Glotzer, Science, 2004, 306, 419–420 CrossRef CAS PubMed.
- A. B. Pawar and I. Kretzschmar, Macromol. Rapid Commun., 2010, 31, 150 CrossRef CAS PubMed.
- E. Bianchi, R. Blaak and C. N. Likos, Phys. Chem. Chem. Phys., 2011, 13, 6397 RSC.
- E. Bianchi, G. Kahl and C. N. Likos, Soft Matter, 2011, 7, 8313 RSC.
- C. E. Snyder, M. Ong and D. Velegol, Soft Matter, 2009, 5, 1263 RSC.
- S. Gangwal, A. Pawar, I. Kretzschmar and O. D. Velev, Soft Matter, 2010, 6, 1413 RSC.
- Q. Chen, S. C. Bae and S. Granick, Nature, 2011, 469, 381 CrossRef CAS PubMed.
- B. Ruzicka, E. Zaccarelli, L. Zulian, R. Angelini, M. Sztucki, A. Moussaïd, T. Narayanan and F. Sciortino, Nat. Mater., 2011, 10, 56 CrossRef CAS PubMed.
- F. Romano and F. Sciortino, Nat. Mater., 2011, 10, 171 CrossRef CAS PubMed.
- E. Bianchi, C. N. Likos and G. Kahl, ACS Nano, 2013, 7, 4657 CrossRef CAS PubMed.
- E. Bianchi, C. N. Likos and G. Kahl, Nano Lett., 2014, 14, 3412 CrossRef CAS PubMed.
- E. Noya, I. Kolovos, G. Doppelbauer, G. Kahl and E. Bianchi, Soft Matter, 2014, 10, 8464 RSC.
- F. Smallenburg and F. Sciortino, Nat. Phys., 2013, 9, 554 CrossRef CAS.
- F. Smallenburg, L. Filion and F. Sciortino, Nat. Phys., 2014, 10, 653 CrossRef CAS PubMed.
- L. Rovigatti, F. Bomboi and F. Sciortino, J. Chem. Phys., 2014, 140, 154903 CrossRef PubMed.
- L. Rovigatti, F. Smallenburg, F. Romano and F. Sciortino, ACS Nano, 2014, 8, 3567 CrossRef CAS PubMed.
- F. Lo Verso, C. N. Likos, C. Mayer and H. Löwen, Phys. Rev. Lett., 2006, 96, 187802 CrossRef.
- F. Lo Verso, C. N. Likos and H. Löwen, J. Phys. Chem. C, 2007, 111, 15803 CAS.
- F. Lo Verso, A. Z. Panagiotopoulos and C. N. Likos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 010401(R) CrossRef.
- B. Capone, I. Coluzza, F. Lo Verso, C. N. Likos and R. Blaak, Phys. Rev. Lett., 2012, 109, 238301 CrossRef.
- B. Capone, I. Coluzza, R. Blaak, F. Lo Verso and C. N. Likos, New J. Phys., 2013, 15, 095002 CrossRef.
- E. Noya, C. Vega, J. P. K. Doye and A. A. Louis, J. Chem. Phys., 2010, 132, 234511 CrossRef PubMed.
- D. Vlassopoulos, T. Pakula, G. Fytas, M. Pitsikalis and N. Hadjichristidis, J. Chem. Phys., 1999, 111, 1760 CrossRef CAS PubMed.
- M. Pitsikalis, E. Siakali-Kioulafa and N. Hadjichristidis, Macromolecules, 2000, 33, 5460 CrossRef CAS.
- S. Strandman and H. Tenhu, Polymer, 2007, 48, 7008 CrossRef CAS PubMed.
- D. B. Alward, D. J. Kinning, E. L. Thomas and L. J. Fetters, Macromolecules, 1986, 19, 215 CrossRef CAS.
- E. L. Thomas, D. B. Alward, D. J. Kinning, D. C. Martin, D. L. Handlin Jr and L. J. Fetters, Macromolecules, 1986, 19, 2197 CrossRef CAS.
- L. Feng, L.-L. Pontani, R. Dreyfus, P. Chaikin and J. Brujic, Soft Matter, 2013, 9, 9816 RSC.
- S. Angioletti-Uberti, P. Varilly, B. M. Mognetti and D. Frenkel, Phys. Rev. Lett., 2014, 113, 128303 CrossRef.
| This journal is © The Royal Society of Chemistry 2015 |