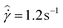Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A comprehensive constitutive law for waxy crude oil: a thixotropic yield stress fluid†
Christopher J.
Dimitriou‡
and
Gareth H.
McKinley
*
Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: gareth@mit.edu
First published on 16th June 2014
Abstract
Guided by a series of discriminating rheometric tests, we develop a new constitutive model that can quantitatively predict the key rheological features of waxy crude oils. We first develop a series of model crude oils, which are characterized by a complex thixotropic and yielding behavior that strongly depends on the shear history of the sample. We then outline the development of an appropriate preparation protocol for carrying out rheological measurements, to ensure consistent and reproducible initial conditions. We use RheoPIV measurements of the local kinematics within the fluid under imposed deformations in order to validate the selection of a particular protocol. Velocimetric measurements are also used to document the presence of material instabilities within the model crude oil under conditions of imposed steady shearing. These instabilities are a result of the underlying non-monotonic steady flow curve of the material. Three distinct deformation histories are then used to probe the material's constitutive response. These deformations are steady shear, transient response to startup of steady shear with different aging times, and large amplitude oscillatory shear (LAOS). The material response to these three different flows is used to motivate the development of an appropriate constitutive model. This model (termed the IKH model) is based on a framework adopted from plasticity theory and implements an additive strain decomposition into characteristic reversible (elastic) and irreversible (plastic) contributions, coupled with the physical processes of isotropic and kinematic hardening. Comparisons of experimental to simulated response for all three flows show good quantitative agreement, validating the chosen approach for developing constitutive models for this class of materials.
1 Introduction
The term “yield stress fluid” is used to describe soft rheologically-complex materials that behave like a solid at low levels of imposed stress, yet flow when subjected to stresses that exceed a critical value.1,2 These types of materials are ubiquitous in nature and in industrial applications, so predicting their rheology with a constitutive model is an important challenge. The term yield stress fluid is a rather broad classification for materials which exhibit this general behavior of transitioning from solid to liquid, and these materials can exhibit additional complexities in their rheological behavior. Møller et al.3 proposed using thixotropy as a distinguishing behavior that separates “ideal” yield stress fluids from “non-ideal” yield stress fluids. Thixotropy describes the ability of a material to exhibit a continuous and reversible time-dependent change (usually a decrease) in viscosity at a particular constant imposed shear rate.4–6 These time-dependent changes in viscosity are due to a gradual change in the microstructure of the material resulting from the application of shear; this mechanism is commonly referred to as shear rejuvenation. Thixotropic materials also exhibit aging, which describes the ability of the material to reacquire its initial structure under the absence of shear (hence the reversibility of the initial time-dependent change). The aging phenomenon is commonly the result of thermally activated Brownian motion causing a sufficient rearrangement of the material's microconstituents. When this rearrangement occurs, the attractive forces between these microconstituents can cause a reformation of the sample spanning network in the material structure.5,6The classification used by Møller et al. is a simplified view of yield stress fluids. For example, Divoux et al.7,8 showed that even Carbopol, widely considered to be an “ideal” yield stress fluid,3 can exhibit some non-idealities (e.g. shear banding) that are associated with thixotropic yield stress fluids. Given the ubiquity of thixotropic behavior in yield stress fluids, it is important to have an appropriate constitutive framework for modeling the rheology of these fluids. The development of such a framework is a critical issue which remains to be addressed.6 There is a significant body of literature which has strived towards this goal.9–19 Many of the models in the literature adopt a scalar structure parameter (frequently, but not always, denoted as λ) to describe some appropriate measure of the internal material structure. This material structure can build up or break down over time due to the application of shear, and the evolution equation for the structure parameter therefore typically contains an aging term, and a shear rejuvenation term. The structure parameter is then related to macroscopic rheological parameters in the fluid, such as the yield stress, shear viscosity, or elastic modulus.
Other models in the literature take a different approach by modeling the underlying microstructural physics in these materials. Rather than prescribing a constitutive behavior based on bulk rheological measurements of the material, the constitutive relations are formally derived by considering interactions between the material's microstructural elements. Some of the more prominent examples of such models include the Soft Glassy Rheology (SGR) model,13,20 the Shear Transformation Zone (STZ) model14,21 and the Kinetic Elastoplastic (KEP) model.18,22 As a testament to the capability of these models, several important experimental observations are predicted including shear banding/nonlocal effects,23,24 power law dependency of linear viscoelastic moduli on frequency, and stress overshoots.13 Together with their generality and the added intuition developed from the microstructural approach, these models are quite appealing. However considerable mathematical manipulation is often required in order to express them in terms of macroscopic variables such as stress or strain, and they have not often been used to quantitatively describe experimental data sets for real elastoplastic materials. On the other hand, models such as those of Quemada,15 Mujumdar et al.17 as well as many others, are explicitly written in terms of stress and strain. This form facilitates the fitting and use of such models in engineering applications.
The particular subclass of thixotropic yield stress fluids studied here are model waxy crude oils. Wax is a commonly encountered component of crude oils that can be present as a solid precipitate at low temperatures. These solid precipitates have adverse effects on the rheology of the crude oil during production scenarios,25,26 so engineers and scientists must be aware of the thixotropic nature of waxy crude oils.4,27 Detailed studies of the rheology of these fluids emphasized the importance of sample preparation protocol (or beneficiation28) in order to ensure repeatable rheological data.29–31 However, one of the issues presented when measuring the rheology on these fluids is the variability in sample composition across different crudes (asphaltene content, wax content32). For these reasons, we utilize a model waxy crude oil in the present study, the composition of which can be tightly controlled by formulating the fluid in the laboratory.
The thixotropic behavior of these fluids also makes reproducible rheological data difficult to obtain. Comprehensive, quantitative comparisons with model predictions are therefore scarce. Many of the models employed in the literature are simplified inelastic models, e.g. the frequently used Houska model9,33 does not account for material elasticity, and the Pedersen model28,34 assumes a generalized Newtonian fluid with temperature dependency. A more complete and experimentally-substantiated constitutive law would be useful for developing flow assurance strategies.35 The goal of flow assurance is to ensure continuous flow of production fluids (crude oils) under adverse scenarios, such as the presence of precipitates or non-Newtonian behavior.26 As an illustration, we note that the pressure drop ΔP required to restart a gelled pipeline typically scales with the material yield stress σy. In the simplest case, a force balance on a gelled plug of wax gives ΔPπR2 ∼ σyπDL, where D is the diameter of the pipe and L is the length. Designing a pipeline network with a fixed pumping capacity ΔP therefore requires a priori knowledge of how the yield stress σy varies in the gelled crude oil (especially when aging processes and shear history cause large variations of σy with time). This necessitates a constitutive law that can be both fit to rheological data, and has predictive capabilities.
A more comprehensive approach to the rheology of elastoviscoplastic materials, both in terms of experiments and modeling, is therefore required. Coussot et al.10 and Mujumdar et al.17 propose several different rheological experiments, among them startup of steady shear and large amplitude oscillatory shear (LAOS) as methods to validate and discriminate between constitutive models. There have also been many recent experimental studies which have combined bulk rheological measurements with velocimetry. These are important experimental efforts, because thixotropic yield stress fluids often exhibit shear banding and other types of heterogeneities in simple viscometric flows. This behavior is commonplace and is observed in a number of specific materials, including suspensions of star polymers,36 Laponite gels,37,38 emulsions,24 Carbopol micro gels7 and other colloidal gels.39 Shear banding or inhomogenous flow can significantly affect interpretation of experimental data, so the use of velocimetric techniques has become an important part of the experimentalist's toolbox.
Hence, combined with a detailed preparation protocol for our model fluid (which is validated using direct measurements of flow kinematics), we will use a suite of well-defined viscometric flows to evaluate a constitutive model. The model we develop will be verified across a wide range of data. Once the model parameters are fixed, the constitutive equations are solved for an additional independent test protocol in order to explore the predictive capabilities of the model. This gives further experimental validation to future numerical studies which would utilize the model to predict pipeline restart.40,41
We endeavor to expand the approaches for describing thixotropic materials by introducing ideas from plasticity that have not been widely used in prior studies of such phenomena. The term “yield stress fluid” generally describes a yielding material with rate-dependent plastic flow above a critical stress. This behavior is generic, and is even exhibited by metals at elevated temperatures.42,43 The strengthening/softening processes that characterize thixotropy are similar to hardening mechanisms that are used in plasticity, which also utilize an internal microstructural variable of the form of the scalar parameter λ.42 These similarities suggest that there are underlying links between the models employed to describe thixotropic yield stress fluids, and the models used in plasticity.44 Early work hinted at the utility of employing concepts from plasticity to model yield stress fluids,45 but only recently have these mechanisms been used to successfully predict the behavior of a (non-thixotropic) yield stress fluid.46 In the present contribution, we show for the first time how a constitutive model can quantitatively predict the rheology of waxy crude oil (a specific thixotropic yield stress fluid) across a comprehensive set of experimental data. The data includes steady and transient tests, as well as linear and nonlinear rheological measurements.
This is accomplished by utilizing detailed experiments on a model crude oil to motivate the development of the constitutive equations. We take a modeling approach that allows us to rapidly express our elastoviscoplastic equations of state in terms of macroscopic variables (stress and strain), which are the variables that are of interest to the practicing engineer or scientist who deals with flow of a real crude oil. While this approach may not give as detailed an account of the microstructural yielding and thixotropic mechanisms as other approaches,13,14,18 we will still take care to provide a general discussion of the microstructural interpretation of these plasticity mechanisms. We will also illustrate the links between this model, and other models that have been employed to predict thixotropic behavior. The constitutive framework can describe the material response to a number of different rheometric test protocols, and also has a general 3D continuum mechanics formulation. It will therefore ultimately be useful for numerical simulations of complex flows of waxy crude oils that can then be used to guide flow assurance strategies.
2 Experimental
2.1 Model fluids & rheometry
The class of thixotropic yield stress fluids used here has been characterized in detail in a previous study.47 They are created by combining a heavy mineral oil (Sigma Aldrich 330760) with a paraffin wax (Sigma Aldrich 327212). The components are combined together at a high temperature (≥60 °C) and stirred continuously to fully dissolve the wax in the oil. The model fluid behaves as a Newtonian liquid in this state, and can be loaded into the rheometer and cooled in situ.Two different rheometers are used to probe the response of this fluid to imposed deformations. A controlled strain rheometer (ARES LS, TA Inst.) is used for large amplitude oscillatory shear (LAOStrain) measurements. The ARES rheometer is equipped with a lower Peltier plate for temperature control of the sample. The upper fixture is a cone with a diameter of 50 mm and an angle of 2°. The upper and lower surfaces are also roughened (root mean squared roughness Rq ≃ 30 μm) in order to suppress wall slip.
A stress controlled rheometer (AR-G2, TA Inst.) is also used. This rheometer is utilized in two different configurations. The first of these is the standard configuration, which incorporates a lower Peltier plate for temperature control, and an upper cone (diameter 60 mm and angle of 2°). This configuration also utilizes roughened upper and lower surfaces, with Rq ≃ 30 μm. The second configuration is a custom-designed Rheo-PIV configuration, which allows in situ measurements of the flow field within the fluid to be extracted. This apparatus is described in detail in Section 2.2.
In Fig. 1, we illustrate one of the characteristic thermorheological features of these model waxy crude oils – the wax appearance temperature, Twa. Fig. 1 presents measurements of the viscosity of the heavy oil, and a 5% and 10% wax in oil mixture over a range of temperatures (obtained using the standard AR-G2 configuration). In Fig. 1, a shear rate of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 50 s−1 is imposed on the fluid, while lowering the temperature at a rate of 1 °C min−1 from 55 °C to 25 °C. As seen in Fig. 1, the mineral oil exhibits an Arrhenius-like exponential dependence of viscosity on temperature. Both the 10% and 5% wax in oil systems exhibit a similar Arrhenius-like variation of viscosity on temperature for large values of T. However, they rapidly diverge from this dependency at a temperature known as the wax appearance temperature, Twa. This temperature corresponds to the point at which wax crystals first begin to precipitate in a sufficient amount to affect the viscosity of the fluid. The morphology of these crystals is typically sheet-like or needle like,30,48 and the high aspect ratio of the crystallites results in mechanical percolation and formation of a gel at low concentrations of precipitated wax.49
= 50 s−1 is imposed on the fluid, while lowering the temperature at a rate of 1 °C min−1 from 55 °C to 25 °C. As seen in Fig. 1, the mineral oil exhibits an Arrhenius-like exponential dependence of viscosity on temperature. Both the 10% and 5% wax in oil systems exhibit a similar Arrhenius-like variation of viscosity on temperature for large values of T. However, they rapidly diverge from this dependency at a temperature known as the wax appearance temperature, Twa. This temperature corresponds to the point at which wax crystals first begin to precipitate in a sufficient amount to affect the viscosity of the fluid. The morphology of these crystals is typically sheet-like or needle like,30,48 and the high aspect ratio of the crystallites results in mechanical percolation and formation of a gel at low concentrations of precipitated wax.49
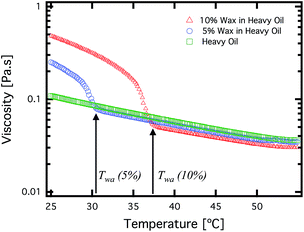 | ||
Fig. 1 Temperature sweep of viscosity for 3 different model fluids, at an imposed shear rate of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 50 s−1. Temperature is ramped at a rate of 1 °C min−1. = 50 s−1. Temperature is ramped at a rate of 1 °C min−1. | ||
2.2 Rheo-PIV configuration
A Rheo-PIV apparatus was used to obtain in situ measurements of the velocity/displacement field within the model fluids as they are sheared in the rheometer. This Rheo-PIV apparatus is based on a previous design,47,50 and a schematic diagram is shown in Fig. 2(a). A laser light sheet (10 mW, 635 nm wavelength), created by a plano-concave lens, is directed vertically downward into the sample at a location rl. Displacements of illuminated tracer particles are then tracked to extract the deformation field of suspended particles across the gap between the upper plate and lower cone (with angle ϕ). The fluid is seeded with reflective TiO2 particles of average size 3 μm, at a volume fraction of 2 × 10−5 (this volume fraction is low enough not to affect the rheology of the fluid being studied). Cross correlation PIV software (Digiflow, Dalziel Research Partners, Cambridge UK) was used to process sequences of images and obtain the 2-dimensional velocity field within the fluid from a sequence of particle displacements. The 2-dimensional field is averaged along the direction of flow, providing a velocity profile of the form v(y). In this case, y is the position between the lower cone and upper plate, with y = 0 at the lower cone, and y = H ≡ rl tan ϕ at the upper plate. This configuration differs from the standard configuration of the AR-G2 by using a lower cone and an upper plate. A stepped lower Peltier plate (TA Instruments part #531052.901) is utilized that allows for interchangeable lower geometries to be used. All measurements made using the Rheo-PIV configuration use either a 4° or 2° lower machined aluminum cone. The cone is black anodized in order to suppress reflection of the laser sheet from this surface. The upper and lower geometries are smoother than the geometries used in the standard configuration (Rq ∼ 0.1 μm) – a polished upper geometry is necessary to provide a clear optical path for the reflected light from the tracer particles.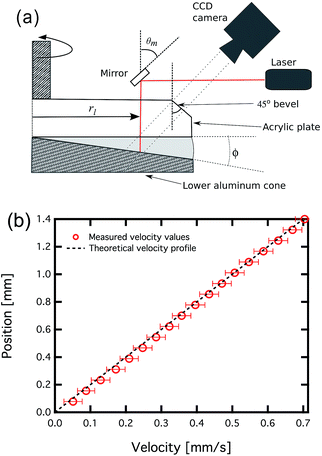 | ||
Fig. 2 (a) Schematic diagram of the RheoPIV configuration mounted on the AR-G2. (b) Calibration velocity profile for a Newtonian mineral oil under an applied shear rate of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.5 s−1. = 0.5 s−1. | ||
The RheoPIV fixture shown in Fig. 2 has one important alteration from previous versions – the upper rotating plate, which is made from a transparent acrylic disc of diameter 50 mm, has a polished 45° bevel machined into the upper corner. This allows the laser-illuminated plane in the sample to be imaged through the flat beveled surface, rather than through the curved fluid meniscus at the edge of the geometry. The fluid meniscus may change in shape over the course of an experiment due to sample shrinkage (which waxy crude oils are known to exhibit51), or edge instabilities.52 The flat beveled edge avoids local image distortion which arises from refraction of light across the irregularly shaped air–fluid meniscus. The index of refraction of the acrylic and model oils (n = 1.49 and n = 1.47 respectively) is very close. This refractive index matching, combined with the bevel, avoids optical aberrations and systematic errors that could arise from the lens/camera axis not being positioned orthogonally to an interface between two media with different values of refractive index n1 ≠ n2.
The apparatus shown in Fig. 2(a) allows for the location of the laser light sheet rl and the angle of the reflective mirror θm to be adjusted and optimized. For the experiments presented in this work, the value of rl was kept constant at 20 mm, while θm was held constant at 45° (creating a vertical laser light sheet). It is possible to decrease θm so that the plane of illuminated particles is orthogonal to the camera's imaging axis. However, this was not necessary because the camera/lens assembly had a high enough focal depth (>2 mm), and all of the illuminated particles across the gap were sufficiently in focus. The laser light sheet is also very thin (approximately 50 μm), resulting in radial variations in particle location having a negligible effect on the velocity profile. A velocity calibration profile of a heavy mineral oil undergoing steady shear of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.5 s−1 in a 50 mm diameter, ϕ = 4° cone-plate geometry is shown in Fig. 2(b). The profile is averaged from 100 frames of video taken over a course of 3 seconds. It shows excellent agreement with the linear, theoretical profile predicted for a Newtonian fluid with no wall slip at either fixture surface.
= 0.5 s−1 in a 50 mm diameter, ϕ = 4° cone-plate geometry is shown in Fig. 2(b). The profile is averaged from 100 frames of video taken over a course of 3 seconds. It shows excellent agreement with the linear, theoretical profile predicted for a Newtonian fluid with no wall slip at either fixture surface.
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) and shear rate
and shear rate 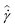 as follows:
as follows: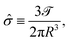 | (1) |
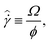 | (2) |
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) is the torque that the rheometer imposes on the sample, Ω is the angular rotation rate of the geometry, R is the radial size of the geometry, and ϕ is the cone angle. We also define an average strain accumulated as
is the torque that the rheometer imposes on the sample, Ω is the angular rotation rate of the geometry, R is the radial size of the geometry, and ϕ is the cone angle. We also define an average strain accumulated as 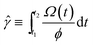 . Under homogenous shearing with no wall slip, these average quantities reduce to the local true stress σ, the local true shear rate
. Under homogenous shearing with no wall slip, these average quantities reduce to the local true stress σ, the local true shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and the local true strain γ. Due to the presence of wall slip and other shear localization events in the fluids, we will reserve the symbols σ and
and the local true strain γ. Due to the presence of wall slip and other shear localization events in the fluids, we will reserve the symbols σ and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) to refer to the stress and shear rate under homogenous deformations only.
to refer to the stress and shear rate under homogenous deformations only.
2.3 Preparation methods of the model fluid – slurry vs. strong gel
In order to carry out reproducible bulk rheological measurements on waxy crude oil, an appropriate sample preparation protocol must be selected. Waxy crude oils are extremely sensitive to variations in their thermal and shear history as they are cooled to below their wax appearance temperature.55 Here we justify the selection of one particular preparation protocol which minimizes the impacts of wall slip and material instabilities. This provides reproducible rheometric data, which can subsequently be used for the development of a constitutive model.We envision two distinct flow assurance scenarios under which waxy crude oils are transported through pipelines. For the first scenario, consider a length of pipeline containing waxy crude at a temperature T > Twa, under quiescent (zero flow-rate) conditions. If the temperature of this fluid slowly and uniformly drops to below Twa, then a gel network forms in the material due to the presence of solid wax precipitates. The cooling of this fluid occurs under no flow conditions with zero shear rate. The crystallite aggregates therefore grow to large sizes and the percolated gel structure formed in the crude oil will be stiff (high viscosity and modulus). Restarting the flow in the pipeline after cooling will therefore require large applied pressure drops, with the possibility that the fluid undergoes an adhesive failure (or wall slip) at the pipe wall.51
The second scenario involves cooling the waxy crude oil under non-quiescent (flowing) conditions. For these conditions, the gel structure formed in the oil will be softer (lower modulus and viscosity), due to the disruptive effect of shearing the aggregates of wax crystals as they form. Smaller pressure drops will be required in order to maintain the flow of the fluid through the pipeline, and wall slip will be less likely.
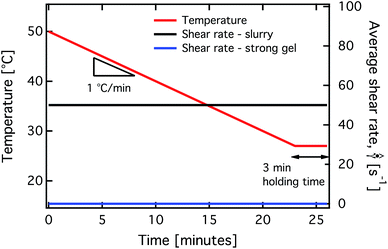
We refer to the state of the crude oil in the first scenario as a “strong gel” and the state of the material in the second scenario as a “slurry”. The strong gel and slurry states of the oil are reproduced in a laboratory scale setup by cooling the model wax–oil mixture from a single phase mixture at T > Twa in the rheometer either quiescently (under zero imposed shear rate) or under a high shear rate 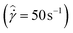 . These two sample preparation protocols are illustrated in Fig. 3. In previous work47 we focused on the behavior of the wax–oil system in its strong gel state, which is dominated by wall slip and other interfacial failure processes. Here, we restrict our focus to the rheology of the material in its slurry state. In the slurry state, bulk rheological behavior is easier to interpret, due to the absence of these failure processes.
. These two sample preparation protocols are illustrated in Fig. 3. In previous work47 we focused on the behavior of the wax–oil system in its strong gel state, which is dominated by wall slip and other interfacial failure processes. Here, we restrict our focus to the rheology of the material in its slurry state. In the slurry state, bulk rheological behavior is easier to interpret, due to the absence of these failure processes.
Fig. 4 illustrates the critical differences between the response of a 5% wax–oil mixture in the two different states to a step in the shear rate to 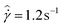 . The response of the model fluid in the slurry state is shown in Fig. 4(a). The model fluid is brought to this state by cooling the sample from 55 °C to 27 °C at a cooling rate of 1 °C min−1, under an applied shear rate of
. The response of the model fluid in the slurry state is shown in Fig. 4(a). The model fluid is brought to this state by cooling the sample from 55 °C to 27 °C at a cooling rate of 1 °C min−1, under an applied shear rate of 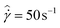 . Once the fluid reaches the final temperature of 27 °C, the shear rate of
. Once the fluid reaches the final temperature of 27 °C, the shear rate of 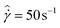 is held for an additional 3 minutes, so that any thermal transients in the system die out. After these 3 minutes, the shear rate is immediately reduced to
is held for an additional 3 minutes, so that any thermal transients in the system die out. After these 3 minutes, the shear rate is immediately reduced to 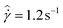 . This sequence of steps is administered using the AR-G2 in its RheoPIV configuration with a 2° lower cone (discussed in Section 2.2). Both the spatially averaged values of
. This sequence of steps is administered using the AR-G2 in its RheoPIV configuration with a 2° lower cone (discussed in Section 2.2). Both the spatially averaged values of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) and
and 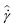 , and the local flow field within the sample are measured.
, and the local flow field within the sample are measured.
The response of the model fluid in its strong gel state is shown in part (b) of Fig. 4. The fluid reaches this state by undergoing the same protocol for the slurry state, however for the cooling step and the subsequent 3 minute holding time, the shear rate is held at 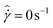 . This results in an essentially unperturbed gel network before the startup of steady shear of
. This results in an essentially unperturbed gel network before the startup of steady shear of 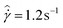 is imposed.
is imposed.
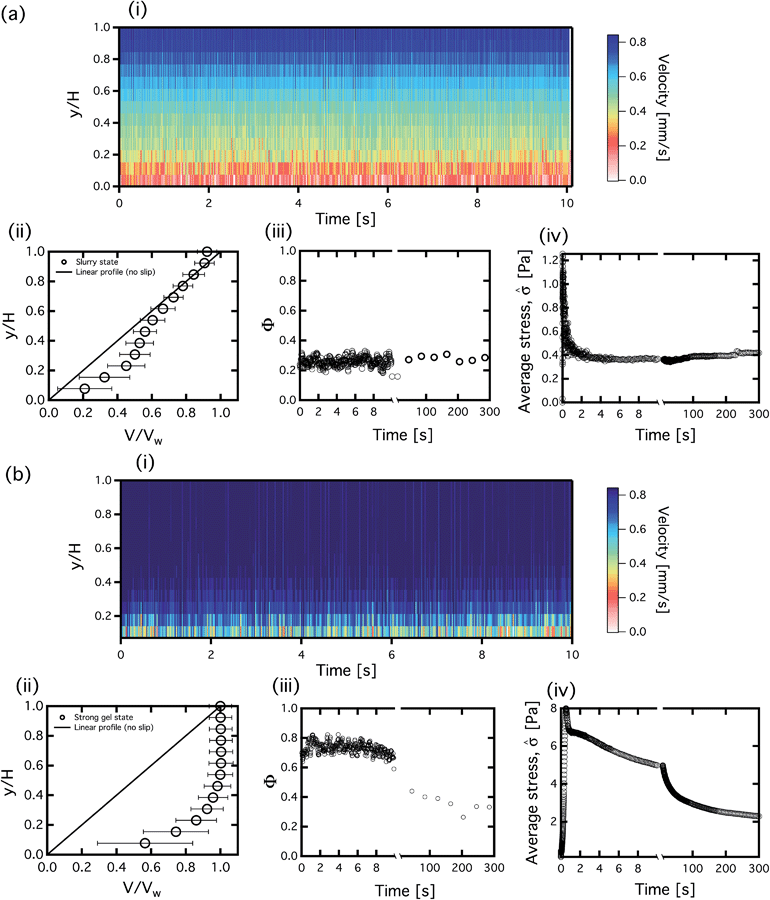
The RheoPIV configuration enables measurements of the average stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) in the fluid, as well as measurements of the local velocity field during the 300 second application of the shear rate
in the fluid, as well as measurements of the local velocity field during the 300 second application of the shear rate 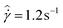 . In the slurry state, the spatially average stress
. In the slurry state, the spatially average stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) shows a constant measured value of 0.4 Pa. The strong gel state shows an initial peak in the stress, followed by a slow decay in the measured value of
shows a constant measured value of 0.4 Pa. The strong gel state shows an initial peak in the stress, followed by a slow decay in the measured value of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) , occurring over the course of several minutes. The velocity field within the fluid in the two states (illustrated through the use of spatiotemporal diagrams for the first 10 seconds, as well as the average velocity profiles shown in (ii)) is markedly different for the two cases. For the strong gel state, larger stresses are needed to break the gel structure in the bulk of the fluid. The stiff material therefore flows through the mechanism of wall slip at the lower surface, and remains adhered to the upper surface. The velocity profile in this state is plug-like, in contrast to what is seen for the material in the slurry state. In the slurry state, a velocity profile closer to linear is observed, with a non-zero shear rate in the bulk.
, occurring over the course of several minutes. The velocity field within the fluid in the two states (illustrated through the use of spatiotemporal diagrams for the first 10 seconds, as well as the average velocity profiles shown in (ii)) is markedly different for the two cases. For the strong gel state, larger stresses are needed to break the gel structure in the bulk of the fluid. The stiff material therefore flows through the mechanism of wall slip at the lower surface, and remains adhered to the upper surface. The velocity profile in this state is plug-like, in contrast to what is seen for the material in the slurry state. In the slurry state, a velocity profile closer to linear is observed, with a non-zero shear rate in the bulk.
We quantify the long term evolution of the velocity profiles in these two states by utilizing a non-dimensional metric Φ, defined in a previous study.47 This dimensionless scalar measures deviations from homogenous linear shear and varies from 0, for a perfectly linear velocity profile with 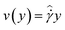 , to 1, for a plug-like profile with velocity v(y) = Vp. Φ is evaluated using the following equation:
, to 1, for a plug-like profile with velocity v(y) = Vp. Φ is evaluated using the following equation:
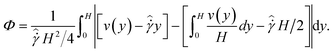 | (3) |
A single value of Φ can be determined for each frame of video, so measured values of Φ corresponding to each frame of video are plotted for the first 10 seconds of the experiment. Subsequently, values of Φ which have been averaged over 10 seconds of video are plotted at 30 second intervals (and the time axis on the figure is expanded in this region). The material in the slurry state shows constant values of Φ ≤ 0.25 over the entire 300 second duration of the test. Measurements of Φ = 0 are difficult to obtain for wax–oil fluids below Twa, due to some residual wall slip, and due to the turbidity of the fluid. This turbidity introduces errors in the velocity measurements that always positively contribute towards Φ. However this behavior can still be compared to the behavior of the material in the strong gel state. In the strong gel state, Φ ≃ 0.7 initially, then subsequently decreases. This process has been observed and documented previously in these fluids47 and is the result of erosion37 whereby the wax crystal structure breaks down into smaller aggregates and the gel weakens.
The measurements of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) and Φ in Fig. 4 show that the strong gel response to an imposed shear rate is dominated by localized failure events at the wall. This is followed by long transients in the evolution of the heterogenous microstructure. These circumstances are different from the uniform distribution of stress and shear rate typically assumed for a fluid being deformed in a cone and plate rheometer. In order to avoid the impact that these complicated yielding scenarios have on interpreting bulk rheological data, we choose to utilize the slurry preparation protocol for all experiments that follow. As is seen in Fig. 4(a), the 5% wax–oil system in its slurry state exhibits significantly less wall slip. It also does not exhibit a prolonged decay in the stress signal due to fluctuating stick-slip events and erosion of the microstructure. Some deviations of the velocity profile from the linear form for values of y/H < 0.4 are observed – these are due to the turbidity of the material decreasing the precision of the velocity measurements deeper into the fluid (and consequently the error bars are much larger for these values of y/H < 0.4). Bulk rheological data for material prepared in this slurry state is more congruent with a continuum mechanics constitutive modeling framework (especially when roughened surfaces are used to eliminate residual wall slip).
and Φ in Fig. 4 show that the strong gel response to an imposed shear rate is dominated by localized failure events at the wall. This is followed by long transients in the evolution of the heterogenous microstructure. These circumstances are different from the uniform distribution of stress and shear rate typically assumed for a fluid being deformed in a cone and plate rheometer. In order to avoid the impact that these complicated yielding scenarios have on interpreting bulk rheological data, we choose to utilize the slurry preparation protocol for all experiments that follow. As is seen in Fig. 4(a), the 5% wax–oil system in its slurry state exhibits significantly less wall slip. It also does not exhibit a prolonged decay in the stress signal due to fluctuating stick-slip events and erosion of the microstructure. Some deviations of the velocity profile from the linear form for values of y/H < 0.4 are observed – these are due to the turbidity of the material decreasing the precision of the velocity measurements deeper into the fluid (and consequently the error bars are much larger for these values of y/H < 0.4). Bulk rheological data for material prepared in this slurry state is more congruent with a continuum mechanics constitutive modeling framework (especially when roughened surfaces are used to eliminate residual wall slip).
Fig. 5 graphically illustrates the difference between the “strong gel” and “slurry” states. The figure contains two bright-field microscopy images of the wax crystal microstructure for a 5% wax–oil mixture at 25 °C in its slurry state (a), and in the strong gel state (b). The wax crystals appear as dark particles in a light background. These crystals are discotic, but appear needle-like when viewed edge-on in the two-dimensional plane. The wax network formed in the slurry state is looser with more vacant (light gray) regions where no precipitates are present. The strong gel state consists of fewer vacant regions with a more closely packed network of wax precipitates. The wax crystals in the strong gel are non-Brownian in character, and form a sample-spanning jammed structure. However in the slurry the discrete crystals (with typical sizes 10–50 μm) can be aligned by the shearing flow. This results in strong shear thinning in the apparent viscosity observed in the steady-state flow curve (see Fig. 6).
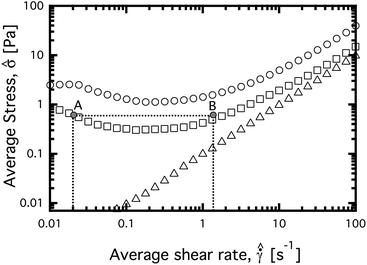 | ||
| Fig. 6 Measured flow-curves of the various systems used in this study using the standard configuration of the AR-G2 rheometer. (Δ) Heavy mineral oil, (○) 10% wax in oil, and (□) 5% wax in oil. Points A and B correspond to the shear rates imposed in Fig. 7. | ||
3 Experimental results and discussion
3.1 Rheology of wax–oil system in slurry state
We propose three different rheometric tests as canonical flows to probe the material response of the wax–oil mixture, and provide a set of data for fitting to a constitutive model. In what follows, we describe these three different test protocols, and discuss implications of the experimental results for constitutive modeling.3.2 Steady state flow curve
For thixotropic systems, steady state flow curves (that is, plots of viscosity vs. shear rate, or shear stress vs. shear rate) are difficult to obtain.5 The measured viscosity will depend on the duration of the experiment, due to the thixotropic transients exhibited by the material. However, flow curves are commonly used in fitting of constitutive models to thixotropic yielding materials.31,56 de Souza Mendes and Thompson57 argue that the steady state flow curve describes the equilibrium locus of the dynamic thixotropic system. For constitutive models which incorporate an evolving internal structural parameter (commonly denoted generically as λ(t)5), this implies that the steady state flow curve can be fit to the constitutive model predictions for the special case when![[small lambda, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e152.gif) = 0. This significantly simplifies the fitting procedure.
= 0. This significantly simplifies the fitting procedure.
In Fig. 6 we plot the measured flow curves for the heavy mineral oil, and the 5% and 10% wax–oil systems in their slurry state (T = 27 °C). These measured flow curves are obtained by using the AR-G2 in its standard configuration. The measurements are carried out by shearing at a given globally averaged rate 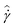 , and are determined to have reached a steady state by using a “steady state sensing” option on the rheometer. Using this option we measure the temporally averaged torque
, and are determined to have reached a steady state by using a “steady state sensing” option on the rheometer. Using this option we measure the temporally averaged torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) over successive 30 second periods, and determine that the measurement has reached a steady state when three successive sampling periods are within 5% of the same value. Each measurement point usually requires 5 minutes to reach a steady state, and the measurement of the entire flow curve requires 2–3 hours.
over successive 30 second periods, and determine that the measurement has reached a steady state when three successive sampling periods are within 5% of the same value. Each measurement point usually requires 5 minutes to reach a steady state, and the measurement of the entire flow curve requires 2–3 hours.
Several key features can be identified from the flow curves shown in Fig. 6. First, both the 5% and 10% model fluids exhibit Newtonian-like behavior at high shear rates, with the average stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) being linearly proportional to average shear rate
being linearly proportional to average shear rate 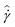 . Second, the 10% system has a larger steady state viscosity than the 5% system, due to the higher volume fraction of solid precipitates. Third, the flow curves of the model crude oils exhibit a non-monotonicity, i.e. there is a region at lower applied shear rates
. Second, the 10% system has a larger steady state viscosity than the 5% system, due to the higher volume fraction of solid precipitates. Third, the flow curves of the model crude oils exhibit a non-monotonicity, i.e. there is a region at lower applied shear rates 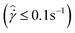 where the average stress decreases as the shear rate is increased.
where the average stress decreases as the shear rate is increased.
Non-monotonic flow curves (NMFC's) point towards the presence of a material instability.58–61 Some shear banding fluids, for example wormlike micellar solutions, exhibit an underlying non-monotonic flow curve.62 This non-monotonic flow curve cannot be measured, because at imposed shear rates in the decreasing region of the flow curve, the material bifurcates into two63 or more64 coexisting regions with different local shear rates. We refer to this as a “standard shear banding scenario”.61
There are several examples in the literature of measured NMFC's. Dijksman et al.65 measured NMFC's in granular media in a number of different geometries, while Michel et al.66 measured non-monotonic flow curves in microemulsions of oil in water which form transient networks. In the latter, the authors observe “wavy deformations of the sample surface” and “progressive cavitation-like proliferation of bubbles in the bulk”. These manifestations are indicative of an unstable flow within the material, even though the imposed deformation is steady. This differs from the standard shear banding scenario envisioned for wormlike micellar solutions, in which a steady (banded) velocity field is established in the material. The underlying non-monotonic constitutive curve is then manifested as a stress plateau with an approximately constant value of the average stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) .61
.61
For our model crude oil, the data shown in Fig. 6 indicates that a NMFC of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) vs.
vs.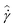 is measurable. We therefore emphasize that the results shown in Fig. 6 correspond to temporally converged values of average stress
is measurable. We therefore emphasize that the results shown in Fig. 6 correspond to temporally converged values of average stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) in the material at an imposed global shear rate
in the material at an imposed global shear rate 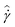 . However, as pointed out by Michel et al.,66 substantial temporal and spatial fluctuations in microstructure and local stress must persist.
. However, as pointed out by Michel et al.,66 substantial temporal and spatial fluctuations in microstructure and local stress must persist.
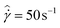 for 5 minutes. Then, a sequence of three steps in shear rate is imposed. The first step is to
for 5 minutes. Then, a sequence of three steps in shear rate is imposed. The first step is to 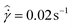 (at a time denoted as t = 0 s), followed by a step to
(at a time denoted as t = 0 s), followed by a step to 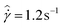 at t = 1432 s, and finally a step back to
at t = 1432 s, and finally a step back to  at t = 3232 s. The measured stress and velocity profiles for this test are shown in Fig. 7.
at t = 3232 s. The measured stress and velocity profiles for this test are shown in Fig. 7.
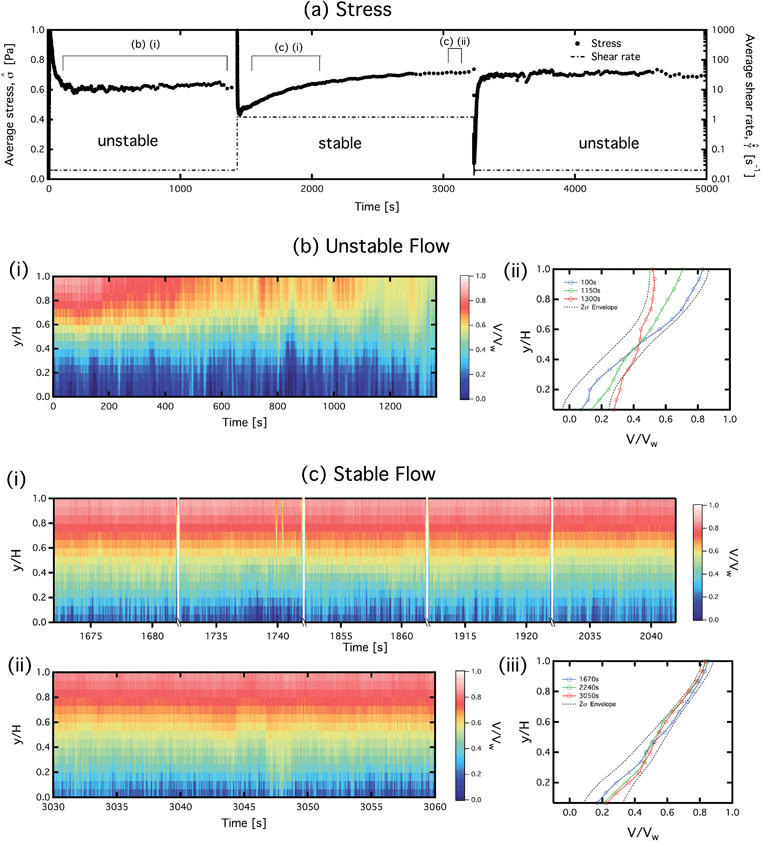 | ||
Fig. 7 Switching between the stable  and unstable and unstable  regions of the flow curve in Fig. 6 (5% wax–oil mixture). The steady (averaged) measured stress values are the same for the two different shear rates, however in the unstable region (b), substantially enhanced fluctuations are observed in the velocity profile, as indicated by the 2Σv (standard deviation) envelope of the profiles. Within the stable region, velocity profiles are sampled at several 10 second intervals (c) (i), and then for a longer 30 second interval (c) (ii) beginning at t = 3030 s. Fluctuations in the instantaneous shear rate across the gap are more than a factor of two lower in this stable region. Measurements are carried out using the RheoPIV configuration of the AR-G2 (smooth cone-plate geometry). regions of the flow curve in Fig. 6 (5% wax–oil mixture). The steady (averaged) measured stress values are the same for the two different shear rates, however in the unstable region (b), substantially enhanced fluctuations are observed in the velocity profile, as indicated by the 2Σv (standard deviation) envelope of the profiles. Within the stable region, velocity profiles are sampled at several 10 second intervals (c) (i), and then for a longer 30 second interval (c) (ii) beginning at t = 3030 s. Fluctuations in the instantaneous shear rate across the gap are more than a factor of two lower in this stable region. Measurements are carried out using the RheoPIV configuration of the AR-G2 (smooth cone-plate geometry). | ||
From Fig. 7(a) it is apparent that the rheometer imposes an apparent shear rate in the two cases which differs by a factor of 60, however the steady state value of the average stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) is roughly equal (within ±12%) for both values of
is roughly equal (within ±12%) for both values of 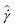 . This is indicative of the extreme shear thinning exhibited by the model waxy crude oil, and is consistent with the non-monotonicity in the measured flow curve of Fig. 6. Transient responses are also exhibited in the response of the material to the steps in shear rate. At t = 1432 s, when the shear rate is stepped to
. This is indicative of the extreme shear thinning exhibited by the model waxy crude oil, and is consistent with the non-monotonicity in the measured flow curve of Fig. 6. Transient responses are also exhibited in the response of the material to the steps in shear rate. At t = 1432 s, when the shear rate is stepped to 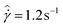 , an instantaneous increase in the stress occurs, followed by a subsequent decrease with the stress reaching a minimum at approximately t = 1452 s. Then, there is a gradual increase (from t = 1452–2800 s) in the stress towards a steady value of
, an instantaneous increase in the stress occurs, followed by a subsequent decrease with the stress reaching a minimum at approximately t = 1452 s. Then, there is a gradual increase (from t = 1452–2800 s) in the stress towards a steady value of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) = 0.71 ± 0.01 Pa. At t = 3232 s, when the shear rate is suddenly dropped back to
= 0.71 ± 0.01 Pa. At t = 3232 s, when the shear rate is suddenly dropped back to 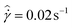 , the stress instantaneously decreases, followed by a subsequent increase in the stress reaching a maximum (and steady value) at t = 3280 s.
, the stress instantaneously decreases, followed by a subsequent increase in the stress reaching a maximum (and steady value) at t = 3280 s.
These long transient responses are consistent with a thixotropic material undergoing cycles of structuring and destructuring.67 In particular, from t = 1432 s to t = 1452 s, the material evolves from a structured state (due to the low value of the shear rate imposed for t ≤ 1432 s) to a destructured state. The high shear rate after the jump results in a sudden increase in the stress, which subsequently breaks the wax structure. The structure breaks down completely and the stress reaches a minimum at t = 1452 s. From t = 3232 s to t = 3280 s when the shear rate is decreased, the material starts from a destructured state due to the high value of the shear rate imposed previously. A smaller stress is required to drive the flow, but this stress progressively increases due to a build up in the structure at the lower imposed shear rates. From t = 1452 s to t = 2800 s we also observe the additional effect of a long-time structuring which results in an increase in the measured or apparent viscosity within the fluid 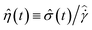 . This presence of multiple timescales for restructuring of the fluid is to be expected. Fig. 5(a) indicates that for the material in the slurry state, there is a distribution of characteristic sizes of the wax precipitates and aggregates. The characteristic rotary diffusion time for rearrangement of the discotic microstructure is a strong function of the size of these crystals and aggregates.5 The evolution of the bulk fluid rheology should therefore reflect this distribution of timescales.
. This presence of multiple timescales for restructuring of the fluid is to be expected. Fig. 5(a) indicates that for the material in the slurry state, there is a distribution of characteristic sizes of the wax precipitates and aggregates. The characteristic rotary diffusion time for rearrangement of the discotic microstructure is a strong function of the size of these crystals and aggregates.5 The evolution of the bulk fluid rheology should therefore reflect this distribution of timescales.
The measurements of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) in Fig. 7(a) provide clear evidence that the model waxy crude oil is highly thixotropic. The larger temporal fluctuations in the average stress
in Fig. 7(a) provide clear evidence that the model waxy crude oil is highly thixotropic. The larger temporal fluctuations in the average stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t) at lower shear rates is also notable. However, Fig. 7(a) provides no indication whether the flow field within the material is heterogenous or shear-banded. Rheo-PIV evidence supporting a material instability is given in Fig. 7(b) and (c). In these two sub-figures we contrast the measured velocity field within the fluid as two different values of
(t) at lower shear rates is also notable. However, Fig. 7(a) provides no indication whether the flow field within the material is heterogenous or shear-banded. Rheo-PIV evidence supporting a material instability is given in Fig. 7(b) and (c). In these two sub-figures we contrast the measured velocity field within the fluid as two different values of 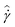 are imposed. At the lower imposed shear rate of
are imposed. At the lower imposed shear rate of 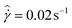 , we observe stochastic fluctuations in the average shear rate across the gap, in the slip velocity at the upper plate, and in the general form of the velocity profile. From t = 0–100 s, the velocity profile indicates a region of higher shear rate near the center of the gap. This is reminiscent of the 3-banded velocity profiles which have been observed in wormlike micellar solutions under imposed steady shear in cone-plate geometries.50,64,68 However, this structure in the velocity profile is ephemeral. The velocity profiles at later times (e.g. t = 1150 s and t = 1300 s plotted in Fig. 7(b)(ii)) show a more uniform shear rate across the gap with larger slip velocities at the upper and lower plates. The velocity profile plotted for t = 1300 s is nearly plug-like (Φ = 0.73) with scaled slip velocities of (1 − v(y)/Vw) = 0.48 at the upper surface and (v(y)/Vw) = 0.28 at the lower surface.
, we observe stochastic fluctuations in the average shear rate across the gap, in the slip velocity at the upper plate, and in the general form of the velocity profile. From t = 0–100 s, the velocity profile indicates a region of higher shear rate near the center of the gap. This is reminiscent of the 3-banded velocity profiles which have been observed in wormlike micellar solutions under imposed steady shear in cone-plate geometries.50,64,68 However, this structure in the velocity profile is ephemeral. The velocity profiles at later times (e.g. t = 1150 s and t = 1300 s plotted in Fig. 7(b)(ii)) show a more uniform shear rate across the gap with larger slip velocities at the upper and lower plates. The velocity profile plotted for t = 1300 s is nearly plug-like (Φ = 0.73) with scaled slip velocities of (1 − v(y)/Vw) = 0.48 at the upper surface and (v(y)/Vw) = 0.28 at the lower surface.
We quantify these fluctuations by considering a Reynolds decomposition of the velocity field v(y, t) such that:
v(y, t) = ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) (y) + v′(y, t), (y) + v′(y, t), | (4) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) (y) is the average part of the velocity defined as follows:
(y) is the average part of the velocity defined as follows: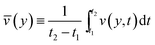 | (5) |
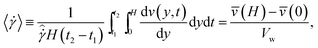 | (6) |
![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) (H) and
(H) and ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) (0) are the temporally-averaged velocities of the upper and lower walls. To quantify the effect that the fluctuating part of the velocity v′(y) has on the shear rate, we define a standard deviation of the shear rate as follows:
(0) are the temporally-averaged velocities of the upper and lower walls. To quantify the effect that the fluctuating part of the velocity v′(y) has on the shear rate, we define a standard deviation of the shear rate as follows: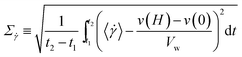 | (7) |
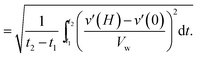 | (8) |
For the velocity data in Fig. 7(b), the average shear rate measured across the gap is 〈![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 〉 ± 2Σ
〉 ± 2Σ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , where the ± represents the 95% confidence bound in this average over time, and is indicative of the extent of the fluctuations in the local shear rate
, where the ± represents the 95% confidence bound in this average over time, and is indicative of the extent of the fluctuations in the local shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) over time. For Fig. 7(b), we compute 〈
over time. For Fig. 7(b), we compute 〈![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 〉 = 0.59 and Σ
〉 = 0.59 and Σ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.13.
= 0.13.
In Fig. 7(c), we show measured profiles for the case when 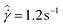 . At this higher shear rate, images are acquired at a higher frame rate due to the increased velocity of the tracer particles. Due to limited digital storage space, sampling of the velocity field is limited to several smaller intervals in time. The velocity field is therefore sampled for 5 different 10 second intervals from t = 1670 s to t = 2040 s, which coincides with the region of increasing measured stress. The velocity is also sampled for 30 seconds at t = 3030 s, where the spatially averaged stress
. At this higher shear rate, images are acquired at a higher frame rate due to the increased velocity of the tracer particles. Due to limited digital storage space, sampling of the velocity field is limited to several smaller intervals in time. The velocity field is therefore sampled for 5 different 10 second intervals from t = 1670 s to t = 2040 s, which coincides with the region of increasing measured stress. The velocity is also sampled for 30 seconds at t = 3030 s, where the spatially averaged stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) has approached and remains at a constant value. In these regions, the average shear rate across the gap fluctuates considerably less, with 〈
has approached and remains at a constant value. In these regions, the average shear rate across the gap fluctuates considerably less, with 〈![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 〉 = 0.66 and Σ
〉 = 0.66 and Σ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.068. The 95% confidence bounds for the velocity profiles have been reduced by a factor of 2 compared to the lower shear rate. The velocity field also appears linear for all times, with some wall slip still occurring at both the upper ((1 −
= 0.068. The 95% confidence bounds for the velocity profiles have been reduced by a factor of 2 compared to the lower shear rate. The velocity field also appears linear for all times, with some wall slip still occurring at both the upper ((1 − ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) (H)/Vw) = 0.14) and lower ((
(H)/Vw) = 0.14) and lower ((![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) (0)/Vw) = 0.21) surfaces. The fluctuations in shear rate and slip velocity that are observed in Fig. 7(b) are therefore markedly reduced when compared to Fig. 7(b).
(0)/Vw) = 0.21) surfaces. The fluctuations in shear rate and slip velocity that are observed in Fig. 7(b) are therefore markedly reduced when compared to Fig. 7(b).
Fig. 7(b) (ii) and (c)(ii) also include envelopes which represent the magnitude of the fluctuations in the velocity v′(y). These envelopes are defined as ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) (y) ± 2Σv(y), where Σv(y) is the standard deviation of the velocity as a function of position across the gap, and is defined as follows:
(y) ± 2Σv(y), where Σv(y) is the standard deviation of the velocity as a function of position across the gap, and is defined as follows:
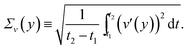 | (9) |
We find that 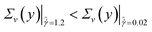 for all values of y, indicating that there are more fluctuations in the velocity when the applied shear rate is
for all values of y, indicating that there are more fluctuations in the velocity when the applied shear rate is 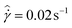 . The difference in the magnitude of these fluctuations is highest near the upper surface (y = H), where fluctuations are 4.8 times larger for the case when
. The difference in the magnitude of these fluctuations is highest near the upper surface (y = H), where fluctuations are 4.8 times larger for the case when 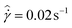 . Incidentally, at y = H the velocity measurements are most accurate due to diminished effects of sample turbidity. The RheoPIV data and associated statistical analysis presented in Fig. 7 provides strong evidence of spatiotemporal fluctuations in the velocity field associated with a material instability in the wax–oil mixture. This unstable flow is most pronounced at low shear rates (which lie in the decreasing region of the NMFC).
. Incidentally, at y = H the velocity measurements are most accurate due to diminished effects of sample turbidity. The RheoPIV data and associated statistical analysis presented in Fig. 7 provides strong evidence of spatiotemporal fluctuations in the velocity field associated with a material instability in the wax–oil mixture. This unstable flow is most pronounced at low shear rates (which lie in the decreasing region of the NMFC).
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) under startup of steady shear. These tests probe the effect of the “aging time” that elapses between sample preparation, and imposing the step in shear rate. The initial sample preparation is typically carried out by shearing (or rejuvenating) the material at a high and constant deformation rate (well within the stable region of the flow curves shown in Fig. 6) for an extended period of time. Then, during the period of aging, the sample is left unperturbed in the rheometer so that the material microstructure starts to build up. When the step in shear rate is subsequently imposed, the gelled and structured material will go through a yielding transition which depends on the initial structure, which in turn depends on the aging time. These tests have been used previously to quantify the effect that internal microstructure has on the rheology of a thixotropic system, and to quantify the characteristic time scales which may be associated with the formation of this structure.69
under startup of steady shear. These tests probe the effect of the “aging time” that elapses between sample preparation, and imposing the step in shear rate. The initial sample preparation is typically carried out by shearing (or rejuvenating) the material at a high and constant deformation rate (well within the stable region of the flow curves shown in Fig. 6) for an extended period of time. Then, during the period of aging, the sample is left unperturbed in the rheometer so that the material microstructure starts to build up. When the step in shear rate is subsequently imposed, the gelled and structured material will go through a yielding transition which depends on the initial structure, which in turn depends on the aging time. These tests have been used previously to quantify the effect that internal microstructure has on the rheology of a thixotropic system, and to quantify the characteristic time scales which may be associated with the formation of this structure.69
The tests presented here are carried out on the 10% model waxy crude oil prepared to its slurry state at a temperature of 27 °C. The AR-G2 in its standard configuration is used, which utilizes roughened cone-plate surfaces to eliminate wall slip. We adopt the nomenclature of Fielding et al.70 and denote the aging/waiting time as tw. After the sample is prepared, an initial waiting time of tw = 2 s is applied, and then a step in shear rate to 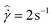 is imposed for 10 minutes. Following this step, the material is left unperturbed for a waiting time tw = 5 s, and an applied steady shear rate of
is imposed for 10 minutes. Following this step, the material is left unperturbed for a waiting time tw = 5 s, and an applied steady shear rate of 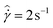 is imposed for 10 minutes. In total, seven startup tests of steady shear are imposed successively, with the waiting time between these steps being incremented in a logarithmic fashion up to a maximum value of tw = 200 s. For each value of tw, measurements of the stress
is imposed for 10 minutes. In total, seven startup tests of steady shear are imposed successively, with the waiting time between these steps being incremented in a logarithmic fashion up to a maximum value of tw = 200 s. For each value of tw, measurements of the stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) are obtained for the 10 minute step in shear rate. For consistency, the measurements of stress and strain rate in this section will be indicated as averages (
are obtained for the 10 minute step in shear rate. For consistency, the measurements of stress and strain rate in this section will be indicated as averages (![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) and
and 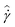 ). However, the average strain rate
). However, the average strain rate 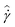 here is high enough, and wall slip is suppressed by the roughened geometry, so deviations of the average values from the local shear rate
here is high enough, and wall slip is suppressed by the roughened geometry, so deviations of the average values from the local shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and local stress σ will be small.
and local stress σ will be small.
In Fig. 8 we plot the measured response of the average stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) as a function of the imposed strain
as a function of the imposed strain ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) , for seven different values of tw. An overshoot is seen at applied deformations of approximately
, for seven different values of tw. An overshoot is seen at applied deformations of approximately 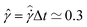 dimensionless strain units. The magnitude of this overshoot increases with tw, however it appears to saturate for tw ≥ 20 s. The overshoot is clearly the result of structuring within the fluid that occurs over the course of the aging time tw. There is also a gradual monotonic increase in the long time steady state value of
dimensionless strain units. The magnitude of this overshoot increases with tw, however it appears to saturate for tw ≥ 20 s. The overshoot is clearly the result of structuring within the fluid that occurs over the course of the aging time tw. There is also a gradual monotonic increase in the long time steady state value of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) which occurs over much longer time scales, and over multiple steps in the shear rate. This slower increase in
which occurs over much longer time scales, and over multiple steps in the shear rate. This slower increase in ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) is a manifestation of the same slow aging process that is observed in Fig. 7(a) – even at a (stable) applied shear rate of 1.2 s−1 it takes a long time (on the order of tens of minutes) for the value of
is a manifestation of the same slow aging process that is observed in Fig. 7(a) – even at a (stable) applied shear rate of 1.2 s−1 it takes a long time (on the order of tens of minutes) for the value of ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t) (and hence
(t) (and hence ![[small eta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e108.gif) (t)) to stabilize. This slow structuring occurs on time constants that are much larger than the waiting time of tw = 20 s which is approximately required for the peak stress to saturate. This is additional experimental evidence of a distribution of processes and time scales associated with the internal material structuring.
(t)) to stabilize. This slow structuring occurs on time constants that are much larger than the waiting time of tw = 20 s which is approximately required for the peak stress to saturate. This is additional experimental evidence of a distribution of processes and time scales associated with the internal material structuring.
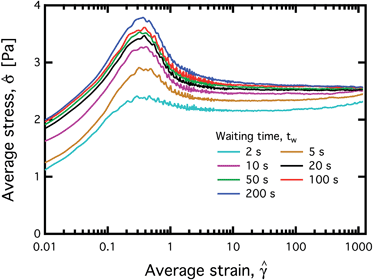 | ||
Fig. 8 Stress overshoots for different waiting times tw in the 10% model waxy crude oil system. Fluid is prepared to its slurry state at 27 °C. The applied shear rate is 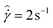 . . | ||
Our constitutive model will primarily focus on predicting the transient yield peak in the stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t) at intermediate strains
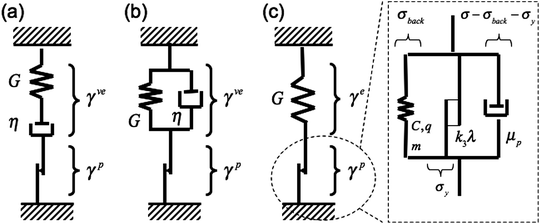
(t) at intermediate strains ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) ≃ 0.3. This is frequently of greater relevance to flow assurance than the very long time response of the material stress. These initial yield peaks observed in Fig. 8 would be responsible for relatively large additional pressure drops being required to restart a pipeline where flow has ceased for a short period of time. Several other constitutive models have had success in predicting these types of overshoots (e.g. see the SGR model,13 or the thixo-elastic Maxwell model,15 among any others). In the present work, we develop a model capable of predicting these overshoots by incorporating mechanisms from plasticity theory. The model will quantitatively predict these stress overshoots, as well as several other key experimental observations. Although lacking the more detailed microstructural physics interpretation of some other models,13,14,18 the model introduced here will be written in terms of a set of evolution equations in macroscopic variables, rather than in integral form. This differential form is more suitable for implementation in common Eulerian flow solvers. Furthermore, the mechanisms utilized in this model are grounded in a robust continuum mechanics framework, so the model can also be generalized to tensorial form in a straightforward manner (see the table in the ESI†).
≃ 0.3. This is frequently of greater relevance to flow assurance than the very long time response of the material stress. These initial yield peaks observed in Fig. 8 would be responsible for relatively large additional pressure drops being required to restart a pipeline where flow has ceased for a short period of time. Several other constitutive models have had success in predicting these types of overshoots (e.g. see the SGR model,13 or the thixo-elastic Maxwell model,15 among any others). In the present work, we develop a model capable of predicting these overshoots by incorporating mechanisms from plasticity theory. The model will quantitatively predict these stress overshoots, as well as several other key experimental observations. Although lacking the more detailed microstructural physics interpretation of some other models,13,14,18 the model introduced here will be written in terms of a set of evolution equations in macroscopic variables, rather than in integral form. This differential form is more suitable for implementation in common Eulerian flow solvers. Furthermore, the mechanisms utilized in this model are grounded in a robust continuum mechanics framework, so the model can also be generalized to tensorial form in a straightforward manner (see the table in the ESI†).
To quantify the magnitude of the yield peak, which will in turn assist in the fitting of the constitutive model, we define our stress overshoot Δσ0 as the difference between the peak stress during each test and the measured stress 10 seconds (i.e. 20 strain units) after the step in shear rate is imposed. At this level of imposed strain it is clear that the initial transients associated with the thixotropic yield peak have died out. The measured value of Δσ0 is plotted as a function of tw in Fig. 9. In this figure, the magnitude of the yield peak saturates with Δσ0 approaching a value close to 1 Pa, or approximately 40% of the final flow stress. Some further increases at longer times (between 100–200 s) are also evident, and these smaller increases are evidence of the same long time restructuring behavior that was discussed in Section 3.2.1.
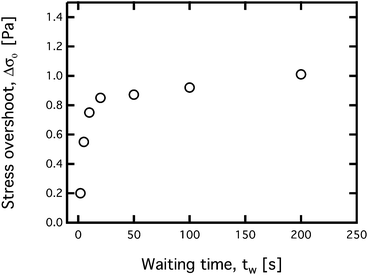 | ||
| Fig. 9 Thixotropic evolution in the stress overshoot Δσ0 as a function of waiting time tw extracted from the startup experiments presented in Fig. 8. | ||
γ(t) = γ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt. ωt. | (10) |
For the measurements presented here an oscillatory average strain will be imposed on the material, ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) = γ0
= γ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt. Even though we suppress wall slip, we will utilize the averaged quantities
ωt. Even though we suppress wall slip, we will utilize the averaged quantities ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) ,
, ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) and
and 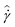 to represent the measured rheological data. This is to account for the possibility of small fluctuations in the local variables σ, γ and
to represent the measured rheological data. This is to account for the possibility of small fluctuations in the local variables σ, γ and 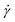 .
.
Two independent test parameters can be modified in LAOS; the oscillation frequency ω and the strain amplitude γ0. When the strain amplitude is small enough, the stress in the material σ(t) is linear in strain and can be decomposed into in phase and out of phase components as follows:
σ(t) = γ0{G′(ω)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt + G′′(ω)cos ωt + G′′(ω)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt}, ωt}, | (11) |
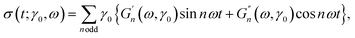 | (12) |
The LAOStrain measurements presented here will be used primarily as a fitting tool in order to guide the development of a suitable elasto-viscoplastic model, and then to compare the model response to the response of the real fluid. One benefit of using LAOS tests to fit constitutive models is that several key aspects of the rheological behavior of the fluid are revealed under LAOS forcing. At low values of γ0, the linear viscoelastic behavior of the fluid is probed. Larger values of γ0 can then probe the plastic yielding transition of the test material. It is also possible to observe transients in the LAOS response which result from the thixotropic behavior of these fluids. These transients are represented clearly in the Lissajous curves as decays towards a periodic attractor. Hence, if a constitutive model can predict the response of a material to LAOS, then it is likely to predict other time- and strain-varying responses that occur over a wide range of deformations.
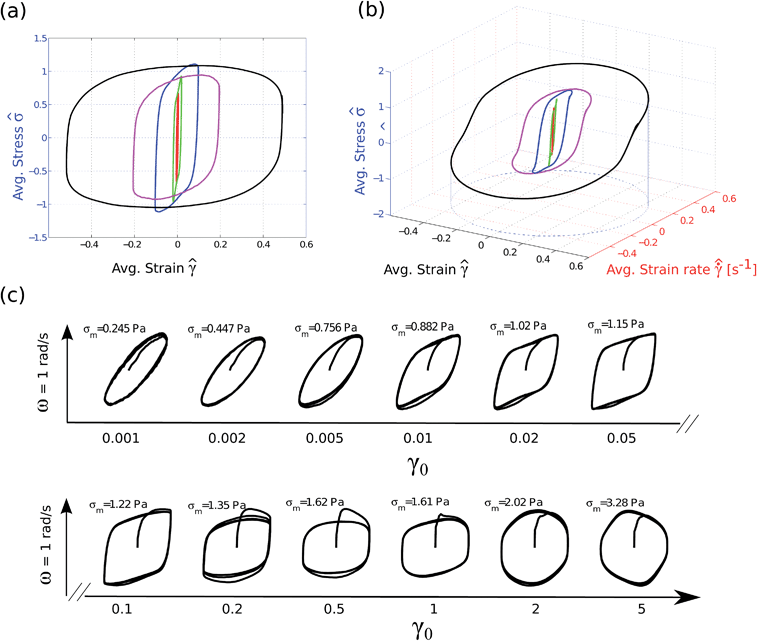
Several researchers have used cyclic stress–strain loading curves, or Lissajous–Bowditch curves, as signatures that are used to fit material responses to a constitutive model.17,46,74 We represent the response of our model crude oil to LAOS through the use of these Lissajous–Bowditch curves (with strain as the abscissa and stress as the ordinate). A series of these curves can be plotted for a number of different strain amplitudes γ0 and frequencies ω. We carry out a series of LAOS tests on the 10% model crude oil fluid in its slurry state at a temperature of 27 °C. These measurements are done on the ARES rheometer, with a roughened cone-plate geometry configuration. A series of measurements at progressively larger strain amplitudes γ0 and at a single fixed frequency of ω = 1 rad s−1 is shown in Fig. 10. Between each measurement, a waiting time of tw = 100 s is applied so that the structure associated with the transient yield peaks shown in Fig. 8 has enough time to build up. For each measurement at a given strain amplitude, four complete oscillation periods are applied.
In Fig. 10(b) we represent the Lissajous curves as 3D trajectories with the measured stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) plotted against the sinusoidally varying strain
plotted against the sinusoidally varying strain ![[small gamma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b2.gif) , and the strain rate
, and the strain rate 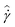 which varies in quadrature. We are primarily interested in the stress–strain projection of these 3D curves, as shown in Fig. 10(a), because this reveals the elastoviscoplastic character of the material response. The curves in Fig. 10(a) and (b) are only shown for their stable limit cycle or “alternance state”.75 This alternance state is reached after multiple cycles of oscillation. In Fig. 10(c), we illustrate the transients which occur before reaching the alternance state by plotting these Lissajous curves on independent (rescaled) axes for each strain amplitude γ0. The magnitude of the maximum stress σm and strain at each strain amplitude is shown by each figure. In Fig. 10(c), overshoots and prolonged transients are clearly evident in the response of the material.
which varies in quadrature. We are primarily interested in the stress–strain projection of these 3D curves, as shown in Fig. 10(a), because this reveals the elastoviscoplastic character of the material response. The curves in Fig. 10(a) and (b) are only shown for their stable limit cycle or “alternance state”.75 This alternance state is reached after multiple cycles of oscillation. In Fig. 10(c), we illustrate the transients which occur before reaching the alternance state by plotting these Lissajous curves on independent (rescaled) axes for each strain amplitude γ0. The magnitude of the maximum stress σm and strain at each strain amplitude is shown by each figure. In Fig. 10(c), overshoots and prolonged transients are clearly evident in the response of the material.
From Fig. 10(c) we can see that at low values of γ0 the material response is that of a linear viscoelastic solid, with G′ > G′′. This can be distinguished from the elliptical shape of the loading curve, which implies a linear response. As γ0 is progressively increased, the maximum stress σm also increases. However σm then saturates at moderate strain amplitudes, a behavior typically associated with a yield-like response. For moderate strain amplitudes between 5% and 50% the characteristic shape of the cyclic loading curves changes and indicates yielding. At these values of γ0 the material undergoes a sequence of processes which involve elastic loading, followed by saturation of the stress and subsequent viscoplastic flow, before elastically unloading when the direction of straining is reversed. This sequence of events occurs within each cycle (i.e. it occurs on an intra-cycle basis), and is responsible for the transition from elliptical to rhomboidal shaped loading curves.76,77
There is additional valuable information contained in the material's inter-cycle response, i.e. in the prolonged transients exhibited, especially for intermediate strain amplitudes of 20% ≤ γ0 ≤ 100%. These transients are manifested in the form of an initial stress overshoot which occurs as the material is first strained. This stress overshoot is evidence of the same transient yield peak that was documented in Section 3.2.2 for the startup of steady experiments. Several cycles are required (spanning a time period on the order of 10 seconds) for the stress to settle into its steady alternance state.
Several key features of Fig. 10 can be used to guide the development of our constitutive model (the detailed formulation of which will be given in Section 4). First, there is no observable inter-cycle change in the linear viscoelastic behavior between each cycle of loading. This implies that G′ and G′′ remain constant with time for the material. If both G′ and G′′ are to be non-constant functions of some microstructure parameter λ, which in turn depends on tw, then deformations in the linear regime cannot cause a change in the microstructural parameter λ. This will be accounted for by specifying a plastic strain as being responsible for changing the structure parameter λ, and this plastic strain is only allowed to accumulate when the material yields at larger stresses and strains. Thus, a central component of our modeling approach will be to additively decompose the total strain into plastic and viscoelastic contributions, with plastic strain only accumulating when the shear stress in the sample exceeds some critical value. As a mechanical analog representation, this model can be visualized as a viscoelastic element in series with a nonlinear plastic yielding element. The yielding element will then utilize two important concepts from plasticity theory – isotropic hardening and kinematic hardening – in order to capture both the nonlinear intra-cycle behavior of the material, as well as the transient inter-cycle behavior (i.e. stress overshoots) which is exhibited under LAOS.
4 Constitutive model
4.1 Formulation of the isotropic-kinematic hardening model (IKH model)
In this section we outline the development of a constitutive model that quantitatively predicts the salient features of the model crude oil's rheological response. As noted above, a central component of our approach is to additively decompose the total shear strain in our material into linear viscoelastic (γve) and plastic (γp) components, such that| γ = γve + γp. | (13) |
Irreversible plastic strain accumulates in the material when the applied stress is above a certain critical value, so for low stresses γ = γve and the response of the material is linear and viscoelastic. This decomposition differs slightly from classical descriptions of viscoplasticity, where strain is additively decomposed into plastic and purely elastic components. Here we rename our elastic strain a viscoelastic strain in order to account for some linear viscoelastic effects that are present in our material below the yielding point. This linear viscoelastic response can specified further by decomposing the viscoelastic strain γve into elastic and viscous components, such that γve = γv + γe. This would correspond to specifying a Maxwell-like linear viscoelastic behavior below the yield stress, with γe = σ/G and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) v = σ/η. Alternatively, a Kelvin–Voigt viscoelastic behavior can be specified. In fact any LVE-type behavior can be specified within this general constitutive framework, depending on the characteristics of the soft gel and the desired fidelity of the model prediction. We show three canonical forms in Fig. 11 in the form of corresponding mechanical analog elements. Because the flows of interest are nonlinear, we will predominantly focus on prescribing the correct behavior of the nonlinear yielding element that is characterized by the plastic strain γp. As a result, we will not discuss fitting of linear viscoelastic behavior in detail. Interested readers can consult any of the classical textbooks on linear viscoelasticity78–80 and replace the simple linear viscoelastic elements shown in Fig. 11 with the elements of their choice (and this will not significantly affect the large strain nonlinear behavior).
v = σ/η. Alternatively, a Kelvin–Voigt viscoelastic behavior can be specified. In fact any LVE-type behavior can be specified within this general constitutive framework, depending on the characteristics of the soft gel and the desired fidelity of the model prediction. We show three canonical forms in Fig. 11 in the form of corresponding mechanical analog elements. Because the flows of interest are nonlinear, we will predominantly focus on prescribing the correct behavior of the nonlinear yielding element that is characterized by the plastic strain γp. As a result, we will not discuss fitting of linear viscoelastic behavior in detail. Interested readers can consult any of the classical textbooks on linear viscoelasticity78–80 and replace the simple linear viscoelastic elements shown in Fig. 11 with the elements of their choice (and this will not significantly affect the large strain nonlinear behavior).
For most of the calculations below, the simplest canonical form of LVE behavior is considered, i.e. a linear Maxwell-like behavior as shown in Fig. 11(a) with elastic modulus G and damping η. Incidentally, this MIKH form of the model is compatible with the classical description of yielding materials with γ = γe + γp, since the plastic strain can be redefined to include the linear dampling element with viscosity η. In addition to this, two assumptions are made about the nature of the linear viscoelastic behavior. First, we observed in Section 3.2.3 that under small amplitude oscillatory shear, G′ and G′′ remain constant in time – i.e. imposed deformations in the linear regime do not affect material structure. Therefore, only the plastic accumulated strain γp can drive a thixotropic restructuring of the fluid. The second, stronger assumption is based on measurements of G′ and G′′ as a function of tw. These measurements show that both G′ and G′′ are in fact at most weak functions of waiting time tw, with G′ only varying by 20% and G′′ varying by even less as tw is changed (see ESI†). For this data, the LVE parameters G and η are therefore assumed to be constant, and do not vary significantly with changes in material structure. This assumption has been discussed by Quemada,15 and is utilized here to reduce the number of constitutive parameters associated with this model. However, the IKH model will still quantitatively capture the three nonlinear flows discussed in Section 3.
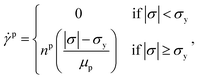 | (14) |
The simple Bingham equation given in eqn (14) captures some of the basic features of the flow curve in Fig. 6, however it lacks the ability to predict the transient behavior and nonlinear stress overshoots that were documented in Section 3. To predict these transients, the flow rule in eqn (14) must be modified to account for the constitutive processes of kinematic hardening and isotropic hardening/softening.42 We have used the concept of kinematic hardening in previous work to model the response of simple (non-thixotropic) yield stress fluids,46 Kinematic hardening accounts for a movement of the center of the yield surface in stress space. Isotropic hardening, on the other hand, accounts for an expansion or contraction of the yield surface, and is frequently used to model the strengthening of polycrystalline metals under imposed deformations.43
These hardening mechanisms are abundantly used in the plasticity literature, and full three-dimensional versions of models with combined isotropic and kinematic hardening have been developed82,83 that are both frame invariant and thermodynamically consistent. For simplicity, we only describe here a one-dimensional version of the model. To capture these two additional microstructural mechanisms, the Bingham equation given in eqn (14) is modified as follows:
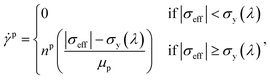 | (15) |
| σeff = σ − σback. | (16) |
In addition to the presence of the back stress in eqn (15), the yield stress σy is now a function of a single internal structure parameter λ. Furthermore, the direction of plastic strain np is now codirectional with the effective stress, so that:
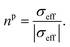 | (17) |
With the formulation in eqn (15)–(17), the center of the yield surface can change through the variation of the back stress σback with the imposed plastic strain (kinematic hardening) and the yield surface itself can contract/expand through the variation of σy with microstructure (isotropic hardening). The incorporation of two yield parameters (center of yield surface σback and size of yield surface σy) bears some similarity to the Houska model used by Sestak et al.84 and Cawkwell and Charles,9 in which the yield stress is decomposed into two components (a constant term and a varying component). This model is commonly used to predict the rheology of crude oils, however as an inelastic model, it cannot capture the full behavior of waxy crude oils, especially in large amplitude oscillatory flows.
The variation of the back stress σback and the yield stress σy for a given deformation must be specified. The back stress is related to an internal structural variable A which was utilized in previous work to model ideal (non-thixotropic) yield stress fluids:46
| σback = CA. | (18) |
The linear relationship between σback and A results from taking the derivative with respect to A of a quadratic form of a defect energy in the material that accumulates with the plastic strain γp.46,83,85 This is analogous to an additional elastic free energy for the defects, so C can be thought of as the back stress modulus, and has units of stress.85 The internal variable A can be physically interpreted as a dimensionless strain-like variable, or a back strain. The defect energy accumulates because of a rearrangement of the material microstructure, which in our case consists of the interlocking wax crystal network. For three-dimensional versions of constitutive models that include kinematic hardening, the variable A necessarily takes on a tensorial form.83
The back strain A follows an evolution equation that is a more general form of the Armstrong–Frederick equation86 discussed by Jiang and Kurath87 that can be used to capture the Bauschinger effect,88
Ȧ = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p − f(A)| p − f(A)|![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p|. p|. | (19) |
The Bauschinger effect refers to a decrease in the yield strength of a material upon reversal of the direction of stress.42 In the above equation, when f(A) = qA (with q a dimensionless material constant) the classical Armstrong–Frederick equation is recovered, which is typically used to describe cyclic loading in metals, but was more recently used to describe the LAOS behavior of soft Carbopol microgels.46 To more accurately capture the intra-cycle behavior under LAOS model waxy crude oil over a wide range of imposed strain amplitudes γ0, a power law function of f(A) is specified:
f(A) = (q|A|)m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sign(A), sign(A), | (20) |
When the plastic strain rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p is nonzero, the back strain A will initially increase in the direction of the plastic strain γp. This results in an increase in the back stress, or a “hardening” of the material in the direction of flow. However, the back strain A eventually saturates due to the second term in eqn (19). The saturation value of A is ±1/q, with the back stress therefore saturating at ±C/q (with the sign depending on the direction of the plastic straining
p is nonzero, the back strain A will initially increase in the direction of the plastic strain γp. This results in an increase in the back stress, or a “hardening” of the material in the direction of flow. However, the back strain A eventually saturates due to the second term in eqn (19). The saturation value of A is ±1/q, with the back stress therefore saturating at ±C/q (with the sign depending on the direction of the plastic straining ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p). The value C/q therefore corresponds to the center of the yield surface under steady flowing conditions (
p). The value C/q therefore corresponds to the center of the yield surface under steady flowing conditions (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p ≠ 0) and for the case of a material with σy = 0, and purely elastic behaviour below yielding, then C/q would also correspond to the steady state yield stress of the material as the flow curve is ramped to zero.
p ≠ 0) and for the case of a material with σy = 0, and purely elastic behaviour below yielding, then C/q would also correspond to the steady state yield stress of the material as the flow curve is ramped to zero.
Finally, the variation of the additional contribution to the yield stress σy(λ) is specified. Here we select the simplest linear relationship between the yield stress σy and the dimensionless microstructural variable λ
| σy = k3λ, | (21) |
A differential equation which determines how λ evolves over time is then specified. The following canonical form, which is frequently encountered in thixotropic material models, will be used here5,17,89
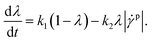 | (22) |
The change in λ is therefore determined by the competition between a microstructural build up term (first term in eqn (22)) and a breakdown term (second term of eqn (22)). The buildup term is assumed to be the result of Brownian motion or other internal aging processes causing a rearrangement in the local wax microstructure which increases the stiffness of the gel. The breakdown term results from the irreversible plastic shearing of this microstructure. The two new material constants in eqn (22) are the rate constant k1 (with units s−1) and the coefficient k2 which is dimensionless. The constant k1 sets the scale for the waiting time tw ∼ 1/k1 required for a build up of the wax microstructure, while the constant k2 determines the rate at which the wax microstructure breaks down for a given shear rate. An important distinction of the evolution equation proposed in eqn (22) compared to other proposed models is that only the plastic strain rate, and not the total strain rate, is responsible for destroying the material structure. This reflects the fact that only large and irreversible strains should cause a significant change in the material microstructure. Furthermore, small strains which result in primarily elastic behavior should not perturb the material microstructure, and should not have an effect on the microstructural parameter λ or on the back strain A. This distinction is frequently made in the plasticity literature,42 but is less common in thixotropic rheological models.
The evolution equation for λ, also requires specifying an initial condition. The initial value of λ will depend on how long the material has been aging (λ can build up under the absence of any type of deformation). Typically an initial condition of λ = 0 is used when a deformation begins immediately after a long history of preshearing at a high shear rate. If a deformation begins immediately after a long aging time, then an initial condition of λ = 1 is used.
Eqn (22) allows for both isotropic hardening and softening. The isotropic hardening only results from a build up in structure in the material which occurs even when the shear rate is zero. This contrasts to some of the hardening equations that are used in the plasticity literature, where shear can cause an increase in the yield stress of the material.82,85 For our model crude oil, shear only results in a nonzero softening term (i.e. the second term in eqn (22)) which causes the yield stress σy(λ) to decrease.
4.1.1.1 Physical interpretation of the internal parameters. In most thixotropic models, a single variable λ is frequently used to characterize the material structure.5 The model introduced here bears more similarities to the approach taken in plasticity,82 due to the introduction of two variables, λ and A. Here we discuss the significance of these two variables with respect to the material microstructure.
Mujumdar et al.17 argued that the scalar parameter λ quantifies the ratio of the number of links in a transient network at a particular level of structure, to the number of links in the network when it is fully structured. For the wax microstructure, we envision λ as being representative of the total number of links per unit volume between the wax particles that form aggregates. Assuming that the force required to break such links is always the same, then the yield stress σy can be approximated as a linear function of λ. Because the variable λ quantifies the number of links, it will necessarily be a positive scalar parameter, even in a 3-dimensional version of the model. Furthermore, this scalar parameter can only be used to quantify an isotropic resistance to deformations (i.e. a resistance which is the same in all directions of loading).
However, an additional parameter is necessarily required to characterize anisotropy in the local material microstructure and the resulting non-isotropic resistance, i.e. a stiffening of the material along the direction of imposed deformation. Non-isotropic resistance to deformation is most important when considering oscillatory loading, where the direction of deformation changes (e.g. LAOS), or more complex 3-dimensional deformations. Capturing this non-isotropic resistance is the purpose of the back strain A and the resulting back stress σback, which are allowed to take on both negative and positive values for the one-dimensional case of this model (unlike λ and σy which are always positive scalar quantities). Furthermore, a fully three-dimensional version of this model would generalize A to a tensor valued quantity (A), and the back stress σback to a tensor valued quantity (Tback).46 Thus, in contrast to the scalar variable λ which only measures the total number of links between wax particles, this tensor valued internal variable A additionally characterizes the orientation of the wax microstructure. This aspect of the microstructure will be affected by the orientation of the wax sheets observed in Fig. 5 (a property which cannot be described by a simple scalar), which will in turn play a role in determining how these particles resist deformation along a certain direction. The inclusion of both of these internal variables therefore provides a more complete picture of the material microstructure.
| γ = γve + γp. | (23) |
The linear viscoelastic strain is specified through the introduction of an appropriate LVE constitutive element (Maxwell, Kelvin–Voigt, or simple elastic solid as shown in Fig. 11), while the rate of change of the plastic strain is given by the following:
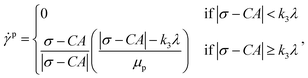 | (24) |
Ȧ = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p − (q|A|)m p − (q|A|)m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sign(A)| sign(A)|![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p| p| | (25) |
![[small lambda, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e152.gif) = k1(1 − λ) − k2λ| = k1(1 − λ) − k2λ|![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p|. p|. | (26) |
With the Maxwell model specified as the LVE behavior shown in Fig. 11(a), this model has 9 fitting parameters, which are: G, η, μp, k1, k2, k3, C, q, m. This is one additional parameter compared to the Houska model, which is commonly used to describe the rheology of crude oils.27
For the reader interested in more general tensorial forms of this model, the additive strain decomposition for the case of the EIKH model shown in Fig. 11(c) can be generalized to a multiplicative Kroner Decomposition90 of the deformation gradient F such that
| F = FeFp, | (27) |
4.2 Quantitative predictions
The IKH model can be used to predict the model crude oil rheological response in the three canonical flows given in Section 3. We use data sets for the 10% model waxy crude system in its slurry state at a temperature of 27 °C. First the steady state flow curve given in Fig. 6 is considered. Under steady flowing conditions, the IKH model reduces to the limiting case where![[small lambda, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e152.gif) = 0 and Ȧ = 0. The relationship between the magnitude of the plastic flow rate |
= 0 and Ȧ = 0. The relationship between the magnitude of the plastic flow rate |![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p| and the magnitude of the stress |σ| in eqn (15) simplifies to the following:
p| and the magnitude of the stress |σ| in eqn (15) simplifies to the following: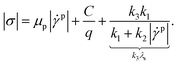 | (28) |
In the case where the KIKH or EIKH variants of the model are used, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p is the only contribution towards the strain rate. Eqn (28) therefore gives a functional form of the IKH model which can be fitted to steady state flow curves such as that in Fig. 6. In Fig. 12 we show such a fit, and it correctly predicts the important features of the flow curve. It predicts a Newtonian limit at high shear rates, as well as locally nonmonotonic decreasing region of the flow curve at the intermediate shear rates. As the shear rate approaches zero, the EIKH and KIKH variants predict a constant stress |σ| = C/q + k3. The MIKH variant however will predict a high viscosity Newtonian region at lower shear rates with σ ≃ η
p is the only contribution towards the strain rate. Eqn (28) therefore gives a functional form of the IKH model which can be fitted to steady state flow curves such as that in Fig. 6. In Fig. 12 we show such a fit, and it correctly predicts the important features of the flow curve. It predicts a Newtonian limit at high shear rates, as well as locally nonmonotonic decreasing region of the flow curve at the intermediate shear rates. As the shear rate approaches zero, the EIKH and KIKH variants predict a constant stress |σ| = C/q + k3. The MIKH variant however will predict a high viscosity Newtonian region at lower shear rates with σ ≃ η![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (which our model crude oil does not appear to exhibit). These types of high viscosity, Newtonian regions at very low imposed shear rates often appear for thixotropic yield stress fluids,1 but are difficult to measure precisely. Tuning the LVE element in the IKH model allows for flexibility in the model in capturing this type of behavior.
(which our model crude oil does not appear to exhibit). These types of high viscosity, Newtonian regions at very low imposed shear rates often appear for thixotropic yield stress fluids,1 but are difficult to measure precisely. Tuning the LVE element in the IKH model allows for flexibility in the model in capturing this type of behavior.
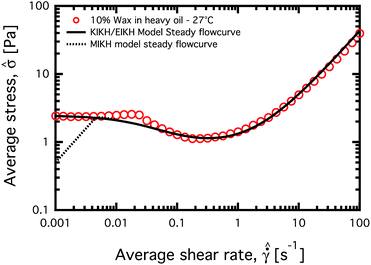 | ||
| Fig. 12 Fitting of the IKH model to the flow curve of Fig. 6. Values of model constants are C/q = 0.85 Pa, μp = 0.42 Pa s, k3 = 1.5 Pa, k1/k2 = 0.033 s−1 and η = 500 Pa s. | ||
The values of the model parameters used in Fig. 12 are C/q = 0.85 Pa, μp = 0.42 Pa s, k3 = 1.5 Pa, k1/k2 = 0.033 s−1 and η = 500 Pa s. The fitting to the steady state flow curve only depends on the ratios k1/k2 and C/q, and not the specific values of the individual constants. The fitting also does not depend on the modulus G or the softening exponent m (or the viscosity η in the case of the MIKH and KIKH variants). It is therefore necessary to fit the model to additional deformation histories in order to determine the values of these parameters.
Although the simple equation given in eqn (28) predicts a non-monotonic dependency of stress σ on shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , it does so assuming the case of homogenous shear, i.e. a spatially and temporally uniform shear rate within the material. Such a nonmonotonic response can also lead to shear banding.91 In Section 3.2.1 we indicated experimentally that for shear rates where we observe a decrease in the average stress
, it does so assuming the case of homogenous shear, i.e. a spatially and temporally uniform shear rate within the material. Such a nonmonotonic response can also lead to shear banding.91 In Section 3.2.1 we indicated experimentally that for shear rates where we observe a decrease in the average stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) as the average shear rate
as the average shear rate  is increased, unstable flow occurs within the material and the local shear rate is not homogenous across the gap. Therefore, eqn (28) should only be viewed as a first order approximation of what the local stress is within the material as a function of the globally applied shear rate. A more complete prediction for the stress in Fig. 12 would account for these heterogeneities and material instabilities in the flow. In Section 4.3 we briefly discuss possible avenues for predicting this complex flow behavior using the IKH model.
is increased, unstable flow occurs within the material and the local shear rate is not homogenous across the gap. Therefore, eqn (28) should only be viewed as a first order approximation of what the local stress is within the material as a function of the globally applied shear rate. A more complete prediction for the stress in Fig. 12 would account for these heterogeneities and material instabilities in the flow. In Section 4.3 we briefly discuss possible avenues for predicting this complex flow behavior using the IKH model.
The stress overshoots that were measured in Section 3.2.2 can also be quantitatively predicted by the IKH model using the same values of the model parameters used in Fig. 12. Values of G = 250 Pa, k1 = 0.1 s−1, C = 70 Pa and m = 0.25 are specified (and the Maxwell variant of the model illustrated in Fig. 11 is used). Initial conditions for the internal variables are A(t = 0) = 0 and λ(t = 0) = λ(tw). Fig. 13(a) shows that the IKH model does indeed capture the key features of the response of the 10% wax oil system to startup of steady shear. Stress overshoots are predicted, and these increase as a function of waiting time tw due to the magnitude of the microstructure parameter λ increasing during the waiting time as a result of rheological aging. The value of the stress overshoot also saturates beyond waiting times of tw ∼ 1/k1 = 10 s, in accordance with our experimental observations.
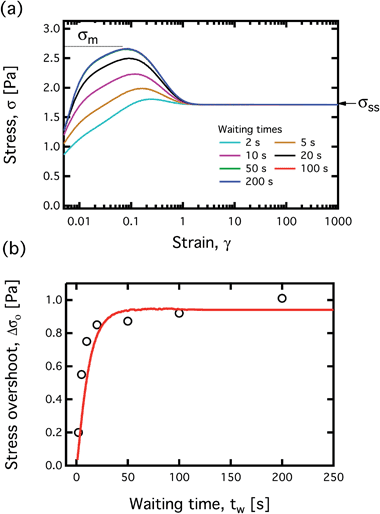 | ||
Fig. 13 Prediction of stress overshoots under startup of steady shear for the IKH model. In (a), the imposed shear rate is 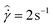 . In (b), we plot the predicted stress overshoot (red line) from the IKH model simulated in (a) vs. the experimental data from Fig. 9 (circles). The model parameters are the same for (a) and (b), and are as follows: C/q = 0.85 Pa, μp = 0.42 Pa s, k3 = 1.5 Pa, k1/k2 = 0.033 s−1, G = 250 Pa, η = 500 Pa s, k1 = 0.1 s−1, C = 70 Pa, m = 0.25. . In (b), we plot the predicted stress overshoot (red line) from the IKH model simulated in (a) vs. the experimental data from Fig. 9 (circles). The model parameters are the same for (a) and (b), and are as follows: C/q = 0.85 Pa, μp = 0.42 Pa s, k3 = 1.5 Pa, k1/k2 = 0.033 s−1, G = 250 Pa, η = 500 Pa s, k1 = 0.1 s−1, C = 70 Pa, m = 0.25. | ||
Fig. 13(b) gives a quantitative comparison between the predicted value of the stress overshoot Δσ0 ≡ σm − σss with its measured value. At a shear rate of 2 s−1, which is far from the unyielded state, the steady state stress is approximately σss ≃ C/q + μp![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . The maximum in the stress scales as σm ∼ (C/q + k3 + μp
. The maximum in the stress scales as σm ∼ (C/q + k3 + μp![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ), so the stress overshoot will scale as Δσ0 ∼ k3. The IKH model correctly predicts the overshoot saturating at approximately 1 Pa, and it predicts the critical waiting time tw ∼ 1/k1 required for this overshoot to saturate.
), so the stress overshoot will scale as Δσ0 ∼ k3. The IKH model correctly predicts the overshoot saturating at approximately 1 Pa, and it predicts the critical waiting time tw ∼ 1/k1 required for this overshoot to saturate.
One aspect of the material response that the IKH model does not predict is the long term increase in the steady measured stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t) which is observed in Fig. 8. This slow transient aging in
(t) which is observed in Fig. 8. This slow transient aging in ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (t) can be attributed to the presence of additional longer time scales for restructuring in the wax. The IKH model can be readily modified to account for this behavior by introducing a third internal variable, and making the high shear rate plastic viscosity μp a function of this variable (similar dependencies are also adopted for some isotropic hardening models83). An evolution equation for this third variable that is similar to eqn (22) could be specified. However the associated parameters determining time scales (e.g. the aging rate k1) would have to be modified in order to reflect this slow restructuring. This would result in the introduction of several new material parameters, making the model significantly more complex. For the sake of simplicity and compactness, we choose to focus on predicting the relative stress overshoot Δσ0 (which is more important for flow assurance restart procedures), and therefore avoid introducing a third internal variable. The introduction of a third internal variable also requires a subtle distinction in the microstructural interpretation for the λ variable used here. This can be justified by considering rearrangement of the individual wax crystals vs. rearrangement of flocs of crystals. Due to the difference in size, the flocs rearrange much slower than the individual crystals, and have different impacts on the fluid rheology (e.g. the slow floc rearrangement will impact long term changes in steady state viscosity whereas the local rapid rotary diffusion of the wax crystals will affect initial yielding transients).
(t) can be attributed to the presence of additional longer time scales for restructuring in the wax. The IKH model can be readily modified to account for this behavior by introducing a third internal variable, and making the high shear rate plastic viscosity μp a function of this variable (similar dependencies are also adopted for some isotropic hardening models83). An evolution equation for this third variable that is similar to eqn (22) could be specified. However the associated parameters determining time scales (e.g. the aging rate k1) would have to be modified in order to reflect this slow restructuring. This would result in the introduction of several new material parameters, making the model significantly more complex. For the sake of simplicity and compactness, we choose to focus on predicting the relative stress overshoot Δσ0 (which is more important for flow assurance restart procedures), and therefore avoid introducing a third internal variable. The introduction of a third internal variable also requires a subtle distinction in the microstructural interpretation for the λ variable used here. This can be justified by considering rearrangement of the individual wax crystals vs. rearrangement of flocs of crystals. Due to the difference in size, the flocs rearrange much slower than the individual crystals, and have different impacts on the fluid rheology (e.g. the slow floc rearrangement will impact long term changes in steady state viscosity whereas the local rapid rotary diffusion of the wax crystals will affect initial yielding transients).
We also assess the predictive capabilities of the IKH model with respect to the measured LAOS response of the waxy crude oil presented in Fig. 10. For the LAOS response, the values of the model parameters used for the fits in Fig. 12 and 13 are kept constant, other than k3 and C/q which are both set to 0.7 Pa (while keeping C constant at 70 Pa). With a value of k3 = 1.5 Pa, the general features under LAOS are still captured (see supplemental information), however a lower value of k3 more accurately predicts the absolute value of σm under LAOS. In Fig. 14(a), the fit of the MIKH variant to the LAOS response is shown for the 10% wax oil system in its slurry state at 27 °C. The simulated LAOS response of the IKH model always uses the initial conditions of A = 0 and λ = 1. For visual clarity Fig. 14 only illustrates the limit cycle, or alternance state of these LAOS tests.
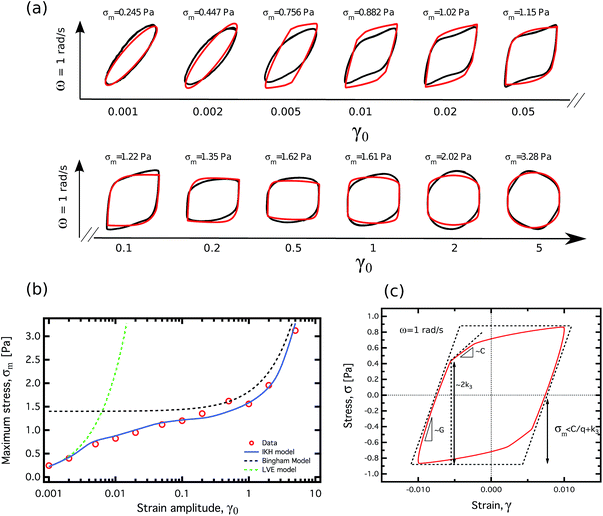 | ||
| Fig. 14 Modeling of the alternance state in (a) of LAOS tests shown in Fig. 10 (ω = 1 rad s−1). Model parameters are C/q = 0.7 Pa, μp = 0.42 Pa s, k3 = 0.7 Pa, k1/k2 = 0.033 s−1, G = 250 Pa, η = 500 Pa s, k1 = 0.1 s−1, C = 70 Pa, m = 0.25. The red line is the IKH model, the black line shows data for a 10% model crude oil. In (b) the prediction of the maximum stress σm from the IKH model is compared to the experimentally measured values of σm. The predictions of a Maxwell LVE model (green dashed line) and a Bingham model (black dotted line) are also shown. (c) Illustrates the key features of the rhomboidal Lissajous curve for the IKH model, when γ0 = 1%. | ||
There is good agreement between the experimental data and the IKH model for the limit cycles observed under LAOS. Both material and model exhibit a transition from linear viscoelastic behavior (corresponding to elliptical Lissajous curves) to nonlinear behavior at strain amplitudes of approximately γ0 = 0.2%. This very small linear range of strains implies that at moderate strain amplitudes (1–10%), the IKH response is dominated by the behavior of the nonlinear yielding element with strain γp.
In Fig. 14(b) we compare the values of the maximum stress σm determined from the experimental data and from the IKH model. The maximum stress σm is defined as the maximum stress over all cycles of oscillation, so it includes the initial transients (overshoots) that are not included in the alternance plots of Fig. 14(a) (but are shown below in Fig. 15). Fig. 14(b) includes the predicted values of σm for a Maxwell LVE element (with η = 500 Pa s and G = 250 Pa), and a Bingham model (with μp = 0.42 Pa s and σy = 1.4 Pa). The MIKH model reduces to the LVE model for small strains, and to the Bingham model for large strains, while also maintaining the ability to predict the behavior at intermediate strains.
 | ||
| Fig. 15 Transient LAOS data for the IKH model (red line) and the 10% model crude oil (points) at two strain amplitudes; (a) γ0 = 0.1% and (b) γ0 = 20%. Frequency is ω = 1 rad s−1 in both cases the same model coefficients as in Fig. 14 are used. | ||
Fig. 14(c) decomposes the “sequence of physical processes”77 that the IKH model undergoes as the stress and strain vary under LAOS at moderate strain amplitudes. Starting from the lower left point of the curve, the material undergoes an initial (primarily) elastic loading, characterized by a slope/modulus of G = 250 Pa. When the stress has increased by a value of 2k3, the material yields in the forward direction. As soon as yielding starts, there is an onset of kinematic hardening (relative to a perfect yield plateau), leading to an increase in the stress with 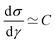 initially. The recovery term in the evolution equation for A (eqn (19)) causes this initial slope to decrease as the imposed deformation continues to increase. A rhomboidal shape in the curve arises, and this is indicative of the presence of the Bauschinger effect.42 For low shear rates (i.e. μpωγ0 ≪ (k3 + C/q)), the maximum stress σm never exceeds the value of k3 + C/q, corresponding to the limiting value of static yield stress in Fig. 12 at low shear rates. For larger strain amplitudes (and hence larger shear rates), the plastic viscosity contribution to the stress μp
initially. The recovery term in the evolution equation for A (eqn (19)) causes this initial slope to decrease as the imposed deformation continues to increase. A rhomboidal shape in the curve arises, and this is indicative of the presence of the Bauschinger effect.42 For low shear rates (i.e. μpωγ0 ≪ (k3 + C/q)), the maximum stress σm never exceeds the value of k3 + C/q, corresponding to the limiting value of static yield stress in Fig. 12 at low shear rates. For larger strain amplitudes (and hence larger shear rates), the plastic viscosity contribution to the stress μp![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) becomes more prominent, resulting in Lissajous curves with a diminished rhomboidal shape and increasing convexity.
becomes more prominent, resulting in Lissajous curves with a diminished rhomboidal shape and increasing convexity.
The IKH model is also capable of predicting the initial transient response of the material as it undergoes large amplitude deformations. Before each test is carried out at a given amplitude γ0, a waiting time tw = 100 s is applied, resulting in the material being fully structured before the oscillatory deformation is imposed. For this reason, the IKH simulation begins with the initial condition λ = 1, and over the course of several oscillations λ will decrease as a result of a nonzero plastic strain rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p, resulting in a decrease in the size of the Lissajous orbits.
p, resulting in a decrease in the size of the Lissajous orbits.
Fig. 15 shows two representative transient Lissajous curves of the material undergoing an initial three cycles of deformation at two different amplitudes, γ0 = 0.1% and γ0 = 20%. For the small amplitude case in Fig. 15(a), the material requires one half of a cycle of oscillation before the behavior settles into a steady state. Furthermore, no overshoots are observed in the stress when the oscillatory deformation is initialized. This behavior is consistent with a standard linear viscoelastic response, where no thixotropy is present. The IKH model predicts this behavior, validating our argument that only the plastic contribution to the strain γp should appear in the evolution equation of λ in eqn (22). Thixotropic effects only become apparent at larger strain amplitudes when γp is no longer zero. These thixotropic effects are apparent in the LAOS measurements at a higher strain amplitude in Fig. 15(b). An initial stress overshoot is observed, and multiple cycles of oscillation are required for the material to settle into an alternance state. The IKH model quantitatively predicts the magnitude of this overshoot, and also predicts the slow contraction of the Lissajous orbits towards the ultimate limit cycle. At a given frequency, the ratio of parameters k2/k1 = 30 s controls the rate of the contraction; as k2/k1 increases the orbits will contract more rapidly.
The LAOS tests in Fig. 14 only show the dependency of the material response on the imposed strain amplitude γ0. The oscillation frequency ω was also varied at a moderate strain amplitude (γ0 = 2%) to further illustrate the nature of the material's response in the nonlinear regime of deformations. The specific strain amplitude of 2% was chosen because it lies in the intermediate regime of Fig. 14(b) between linear viscoelastic (LVE) behavior and Bingham-plastic behavior. In each of these limiting regimes, the effect of varying ω is well understood. In the LVE regime, varying ω enables the appropriate viscoelastic mechanical model for the material properties below yield to be probed. In the Bingham-plastic regime, the dependency on ω is dominated by the plastic viscosity μp, since the instantaneous shear rates are high leading to increasing circular trajectories (as shown in Fig. 14(a)).
However, in the intermediate regime where strains are between 1 and 20%, the material exhibits a rate-independent behavior. Fig. 16(a) illustrates this by showing the cyclic Lissajous curves of the first 3 cycles of oscillation for the material undergoing LAOS at 4 frequencies spanning an order of magnitude (ω = 0.5 rad s−1 to ω = 5 rad s−1). At this moderate strain amplitude, the material response is clearly nonlinear, with a small amount of thixotropic contraction occurring in the orbits over multiple cycles. However, there is little dependency of the material response on the frequency ω. This is indicative of a deformation rate-independent response at moderate strain amplitudes. The predicted model response shown in Fig. 16(b) captures this type of behavior. This is because of the rate-independent nature of the kinematic hardening behavior prescribed in eqn (19). This equation can be rewritten in terms of increments in A and γp as follows:
| dA = dγp − f(A)|dγp|. | (29) |
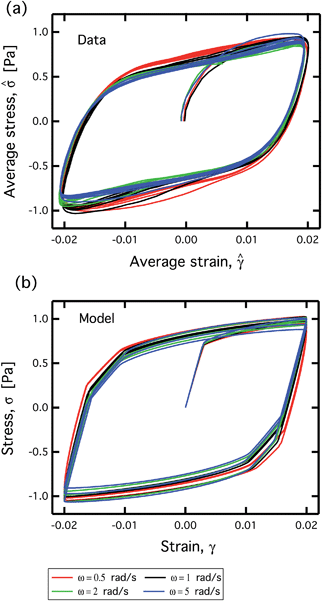 | ||
| Fig. 16 Frequency dependent behavior under LAOS at moderate strain amplitudes (γ0 = 2%) for both the 10% model crude oil (a) and the IKH model (b). The IKH model model coefficients are the same as in Fig. 14 and 15. | ||
The back strain A therefore evolves independently of the rate of plastic strain ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p. For the strain amplitude shown in Fig. 16, σm ≃ 1 Pa, so γve ∼ (σm/G + σm/(ηω)) ≃ 0.006 when ω = 1 rad s−1. A large proportion of the total imposed strain, γ0 = 0.02, is therefore taken up by the plastic strain γp = γ − γve. As a result, the behavior at this strain amplitude is primarily rate independent. The other internal variable, λ, evolves in a rate-dependent fashion set by the ration k2/k1, but on a time scale longer than the period of a single orbit 2π/ω. Hence, the overall response of the material at this range of frequencies is characterized by rate-independent kinematic hardening – a behavior which is most appropriately described by equations of the Armstrong–Frederick type86 used in eqn (29).
p. For the strain amplitude shown in Fig. 16, σm ≃ 1 Pa, so γve ∼ (σm/G + σm/(ηω)) ≃ 0.006 when ω = 1 rad s−1. A large proportion of the total imposed strain, γ0 = 0.02, is therefore taken up by the plastic strain γp = γ − γve. As a result, the behavior at this strain amplitude is primarily rate independent. The other internal variable, λ, evolves in a rate-dependent fashion set by the ration k2/k1, but on a time scale longer than the period of a single orbit 2π/ω. Hence, the overall response of the material at this range of frequencies is characterized by rate-independent kinematic hardening – a behavior which is most appropriately described by equations of the Armstrong–Frederick type86 used in eqn (29).
The IKH model predicts all of the important features of the material response to the three canonical rheological flows outlined in Section 3. To end this subsection, we will discuss one additional flow, and compare it to the predicted response of the IKH model.
In Fig. 6, the particular experimental protocol that was used to measure the flow curve of the material controlled the applied global (or spatially averaged) deformation rate  on the material. An alternative way to control the flow in the material would be to ramp the applied average stress
on the material. An alternative way to control the flow in the material would be to ramp the applied average stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) on the material at a very slow rate, and measure the corresponding average shear rate at subsequent points in time. This “stress ramp” test was conducted with the 10% wax–oil system in its slurry state at 27 °C using the AR-G2 in its standard configuration. The material is initially brought to its fully structured state by applying a wait time of tw = 300s, and then a stress ramp from 0.1 Pa to 5 Pa is imposed over the course of 2 hours (this results in a constant value of d
on the material at a very slow rate, and measure the corresponding average shear rate at subsequent points in time. This “stress ramp” test was conducted with the 10% wax–oil system in its slurry state at 27 °C using the AR-G2 in its standard configuration. The material is initially brought to its fully structured state by applying a wait time of tw = 300s, and then a stress ramp from 0.1 Pa to 5 Pa is imposed over the course of 2 hours (this results in a constant value of d![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) /dt = 0.00136 Pa s−1). Once the stress reaches the maximum value of 5 Pa, the ramp is immediately reversed and brought down to 0.1 Pa at a rate of d
/dt = 0.00136 Pa s−1). Once the stress reaches the maximum value of 5 Pa, the ramp is immediately reversed and brought down to 0.1 Pa at a rate of d![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) /dt = −0.00136 Pa. The average shear rate within the fluid (as measured by the rate of rotation of the conical fixture) is sampled at regular intervals over the course of the increasing and decreasing ramps in stress.
/dt = −0.00136 Pa. The average shear rate within the fluid (as measured by the rate of rotation of the conical fixture) is sampled at regular intervals over the course of the increasing and decreasing ramps in stress.
In Fig. 17, we show the experimental results of this stress test, as well as the predicted response of the IKH model to such a stress ramp using the same model parameters that were determined from Fig. 12 and 13. For comparison with the average shear rate measurements, the flow curve obtained in Fig. 6 is also included on this figure. The non-monotonicity in the IKH model results in hysteresis being captured in the stress ramp experiments. Specifically, a larger imposed stress (asymptotic value of σs ≃ 2 Pa) is required to start the flow from the structured state, and as the stress is decreased, the same shear rates can be sustained at lower values of the applied stress (asymptotic value of σd ≃ 1.1 Pa). This essentially corresponds to different measurements for the static and dynamic yield stress within the material,92 and the nonzero value of the microstructural parameter λ is responsible for this difference. While σ approaches the limit of C/q + k3 = 2.35 Pa in the limit ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0 for the rate-controlled experiment, the asymptotic values of σ determined from the stress ramp experiments are both different from this value. The difference between the static and dynamic yield stress is responsible for the “avalanche effect” that is frequently observed in thixotropic yield stress fluids93 – the supplementary information shows how the IKH model can predict this avalanche effect.
→ 0 for the rate-controlled experiment, the asymptotic values of σ determined from the stress ramp experiments are both different from this value. The difference between the static and dynamic yield stress is responsible for the “avalanche effect” that is frequently observed in thixotropic yield stress fluids93 – the supplementary information shows how the IKH model can predict this avalanche effect.
 | ||
| Fig. 17 Rheological measurements for an imposed stress ramp shown in (a), and measured (points) and simulated (lines) shear rates in (b). The different static and dynamic yield stresses are also annotated. The resulting flow curves of the model crude oil (red data points) and the IKH model (solid and dashed lines) are given in (c). The data is for the same model system at the same temperature shown in Fig. 12–16, with the same model parameters as in Fig. 12 and 13. | ||
The microstructural physics captured by the IKH model is thus extremely versatile and is able to capture the complex rheology of a structured and aging material such as an elastoviscoplastic crude oil. It can capture the salient features of the response exhibited by the fluid to a number of different steady and time-varying rheological flows. The numerical values of the model parameters were consistent among these different flows, so the measurements in Fig. 17 constitute a true test of the predictive nature of the model.
4.3 Further discussion
To conclude our discussion of the IKH model, we expand on a few important points related to the current form of the model. We will also comment on how this model is related to other constitutive models that are commonly encountered in the literature.Shear banding is also predicted by the IKH model under deformations in geometries with sufficiently large stress gradients. We illustrate this in Fig. 18 by simulating startup of shearing flow for the IKH model in a Taylor–Couette cell under a steady applied torque ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) . For the simulations in Fig. 18, the inner radius of the cell is set to Rin = 23.7 mm and the outer radius is Rout = 25 mm, corresponding to a typical experimental cup and bob. The dimensionless radial position is defined as ρ ≡ (r − Rin)/(Rout − Rin), and thus varies from 0 to 1. The torque is set so as to impose a stress which varies (in a 1/r2 fashion) from σ = 2.05 Pa at ρ = 0 to σ = 1.85 Pa at ρ = 1. The IKH simulation presented in Fig. 18 assumes that the fluid is initially in a fully structured state with spatially uniform values of λ = 1 and back strain A = 0. The model parameters used were G = 250 Pa, η = 500 Pa s, μp = 0.42 Pa s, k1 = 0.1 s−1, k2 = 3, k3 = 1.5 Pa, C = 70 Pa, q = 82 and m = 0.25 (these are consistent with the parameter values for the real model waxy crude oil). The data in Fig. 18 is plotted against dimensionless time t/tc, where tc = k2/(k1q). The timescale tc arises from equating the natural timescales for the kinematic hardening and isotropic softening/hardening processes.
. For the simulations in Fig. 18, the inner radius of the cell is set to Rin = 23.7 mm and the outer radius is Rout = 25 mm, corresponding to a typical experimental cup and bob. The dimensionless radial position is defined as ρ ≡ (r − Rin)/(Rout − Rin), and thus varies from 0 to 1. The torque is set so as to impose a stress which varies (in a 1/r2 fashion) from σ = 2.05 Pa at ρ = 0 to σ = 1.85 Pa at ρ = 1. The IKH simulation presented in Fig. 18 assumes that the fluid is initially in a fully structured state with spatially uniform values of λ = 1 and back strain A = 0. The model parameters used were G = 250 Pa, η = 500 Pa s, μp = 0.42 Pa s, k1 = 0.1 s−1, k2 = 3, k3 = 1.5 Pa, C = 70 Pa, q = 82 and m = 0.25 (these are consistent with the parameter values for the real model waxy crude oil). The data in Fig. 18 is plotted against dimensionless time t/tc, where tc = k2/(k1q). The timescale tc arises from equating the natural timescales for the kinematic hardening and isotropic softening/hardening processes.
At time t/tc = 0, the step increase in the torque is imposed and the material starts to deform away from its fully structured state (corresponding to λ = 1). There is initially a nonzero shear rate across the gap, which decreases up until t/tc = 1. During this initial deformation stage, the material deforms elastically, begins to yield, and then kinematically hardens, resulting in an increase in A and a strengthening of the material in the flow direction. Consequently, the shear rate across the gap decreases during this time period.
For t/tc > 1, the fluid begins to shear band. For the region of the fluid located closest to the inner wall, i.e. for values of ρ < 0.4, the isotropic softening process (accounted for by the term −k2|![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p|λ in the evolution equation for λ) begins to dominate over the kinematic hardening process. The value of λ decreases in this region, and a high shear rate band forms in the material closest to the inner wall. For times t/tc ≫ 1 the material near the inner wall has fully yielded, and at ρ = 0 the velocity reaches its maximum value, v = vm = 1.52 mm s−1. The material closer to the outer wall experiences lower shear rates and continues to harden and age, until it exhibits a negligibly small shear rate at long times. These steady shear banded profiles (with one strongly sheared band and one stationary, unsheared band) have been observed in numerous thixotropic yield stress fluids; for example they are carefully documented in the work by Martin and Hu.94
p|λ in the evolution equation for λ) begins to dominate over the kinematic hardening process. The value of λ decreases in this region, and a high shear rate band forms in the material closest to the inner wall. For times t/tc ≫ 1 the material near the inner wall has fully yielded, and at ρ = 0 the velocity reaches its maximum value, v = vm = 1.52 mm s−1. The material closer to the outer wall experiences lower shear rates and continues to harden and age, until it exhibits a negligibly small shear rate at long times. These steady shear banded profiles (with one strongly sheared band and one stationary, unsheared band) have been observed in numerous thixotropic yield stress fluids; for example they are carefully documented in the work by Martin and Hu.94
The IKH model can also be readily simplified to the kinematic hardening model used by Dimitriou et al.46 to describe non-thixotropic yield stress fluids. This is accomplished by setting k3 = 0. While the KH model was shown in that work to predict the correct LAOS behavior for a “simple yield stress fluid”,91 it is not able to predict stress overshoots or prolonged transients under multiple cycles of large amplitude deformation.
The limit of the inelastic Houska model studied by Cawkwell and Charles9 and others33,41 can be realized by taking the limit of C → ∞ while keeping the ratio C/q constant and equal to their “fixed” component of the yield stress. The dependence of σy on λ however remains with an evolution equation for λ resulting in the second component of the yield stress not varying. The Houska model also does not account for any elastic behavior below yield, corresponding to the limit G → ∞.
Finally, the IKH model can be reduced to the “toy” λ-model employed by Coussot et al.95 This limit can be achieved by setting both yield parameters σy and σback equal to zero, taking the limit of G → ∞, and making the viscosity μp a function of λ. Coussot employs a different evolution equation for λ, which results in λ growing unbounded in time when the shear rate is zero.
The IKH model is more broadly related to the Mujumdar17 and de Souza Mendes19 models. These models exhibit key differences from the IKH model. The Mujumdar model does not explicitly decompose strain into elastic and plastic components – as a result the authors necessarily introduce a critical strain γc into the model which is used to determine whether or not the structure of the material is breaking. The Mujumdar model does utilize the same form of the evolution equation for λ that is employed here.
The de Souza Mendes family of models19,57,96 use a different form for the evolution equation of λ, specifically the stress σ enters this equation and is assumed to be the driving force for disrupting the material microstructure. de Souza Mendes and Thompson take this approach in order to avoid disruption of the material microstructure in any elastic, reversible regime of deformation.57 The use of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) p in our evolution equation in λ achieves this same goal. de Souza Mendes also writes the linear viscoelastic moduli G and η as functions of λ, resulting in additional material parameters that must be determined by regression to data.19 This may be required for a more complete form of the IKH model, however for simplicity and compactness these dependencies are neglected in the IKH model.
p in our evolution equation in λ achieves this same goal. de Souza Mendes also writes the linear viscoelastic moduli G and η as functions of λ, resulting in additional material parameters that must be determined by regression to data.19 This may be required for a more complete form of the IKH model, however for simplicity and compactness these dependencies are neglected in the IKH model.
5 Conclusions
The primary goal of this work has been to develop a suitable elasto-viscoplastic constitutive model that can predict the rheology of a thixotropic yield stress fluid. The fluid studied here is a waxy crude oil that is relatively easy to formulate and prepare in a repeatable manner, but still captures the rheological complexity of a real crude oil.To develop this model, Rheo-PIV measurements were first used to distinguish between the material behavior under different sample preparation protocols. We distinguished between the material in a “slurry” state vs. a “strong gel” state. In the former, the material exhibits a weaker gel network and is less likely to flow through the mechanism of interfacial wall slip. In the latter, the material can undergo irreversible breakdown of an initially strong gel network. Furthermore, the material in its “strong gel” state is more likely to exhibit localized fracture and failure at the fluid/solid interface.
Second, we outlined three canonical flow scenarios to probe the rheology of the model fluid in its slurry state. These are measurements of the steady (spatially averaged) flow curve of the material (![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) vs.
vs. ), startup of steady shear flow following different waiting times tw, and large amplitude oscillatory shear strain (LAOStrain). Furthermore, we used Rheo-PIV measurements to elucidate the nature of flow instabilities that occur in the material at low shear rates. These coincide with a non-monotonic region in the material's flow curve. The material instabilities consist of spatially and temporally fluctuating values of local shear rate and shear stress within the material, with a constant globally applied shear rate
), startup of steady shear flow following different waiting times tw, and large amplitude oscillatory shear strain (LAOStrain). Furthermore, we used Rheo-PIV measurements to elucidate the nature of flow instabilities that occur in the material at low shear rates. These coincide with a non-monotonic region in the material's flow curve. The material instabilities consist of spatially and temporally fluctuating values of local shear rate and shear stress within the material, with a constant globally applied shear rate 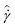 and average shear stress
and average shear stress ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) .
.
Third, we developed an elastoviscoplastic constitutive model (referred to for simplicity as the IKH model) which quantitatively captures the material response to these three flow scenarios. The key features of this model are the additive decomposition of strain into two components (γve and γp) and the use of the isotropic and kinematic hardening mechanisms adapted from plasticity theory. An added benefit of this approach is that the model is extendable to a frame invariant, 3-dimensional tensorial form that can be utilized in simulations of more complex flow scenarios. The IKH model was fitted to the 10% wax in oil model system in its “slurry state” at 27 °C. Under these isothermal conditions it was capable of capturing the rheological aging behavior exhibited by the fluid, and the subsequent effects of this aging process on the material response to deformations. Values of the model parameters were generally consistent across the three different rheological flows. The IKH model was also shown to be capable of predicting transient shear banding behavior under deformations in geometries with sufficiently large gradients in the stress.
There are several avenues for a continuation of this work on the IKH model – some of which we have already highlighted. These include accounting for additional slower restructuring timescales which affect the high shear rate plastic viscosity. In the present study we have taken this viscosity to be a constant, μp. The IKH model could also be improved by introducing nonlocal terms into the constitutive model, to better describe the nature of the flow instabilities that are observed at low globally-applied shear rates.18,97 Other than the results presented in Section 4.3, all of the predictions of the IKH model were obtained by assuming homogenous flow. The work by Moorcroft et al.98,99 suggested that instances of inhomogenous flow may be more ubiquitous than previously thought (in particular where stress overshoots are present). Thus, understanding how the IKH framework might be able to predict these instabilities in more detail would be a worthwhile endeavor. Finally, the model could be modified to capture the continuous, temperature-dependent transition that the material exhibits as it is cooled from above Twa (where it behaves as a Newtonian liquid) to below Twa where it begins to exhibit thixotropic, elastoviscoplastic behavior. The ultimate goal of such work would be to develop a temperature-dependent IKH model, which can then be implemented into simulations of non-isothermal flow in pipelines for flow assurance applications. This would substantially build on the temperature-dependent models that are available today, which typically assume a generalized Newtonian fluid and do not account for elastic or yielding behavior.28,34 Practical applications for such a model would be widespread, and would greatly assist in optimizing operating conditions for pipelines that transport waxy crude oil.
Acknowledgements
The authors would like to thank L. Anand and K. Kamrin for fruitful discussions on developing the constitutive model framework employed in this paper. They would also like to acknowledge the help of R. Venkatesan, as well as Chevron Energy Technology Company for funding this research.References
- H. A. Barnes, J. Non-Newtonian Fluid Mech., 1999, 81, 133–178 CrossRef CAS.
- D. Bonn and M. M. Denn, Science, 2009, 324, 1401–1402 CrossRef CAS PubMed.
- P. Møller, A. Fall, V. Chikkadi, D. Derks and D. Bonn, Philos. Trans. R. Soc., A, 2009, 367, 5139–5155 CrossRef PubMed.
- J. Mewis, J. Non-Newtonian Fluid Mech., 1979, 6, 1–20 CrossRef CAS.
- H. A. Barnes, J. Non-Newtonian Fluid Mech., 1997, 70, 1–33 CrossRef CAS.
- J. Mewis and N. J. Wagner, Adv. Colloid Interface Sci., 2009, 147–148, 214–227 CrossRef CAS PubMed.
- T. Divoux, D. Tamarii, C. Barentin and S. Manneville, Phys. Rev. Lett., 2010, 104, 208301 CrossRef.
- T. Divoux, C. Barentin and S. Manneville, Soft Matter, 2011, 7, 9335–9349 RSC.
- M. G. Cawkwell and M. E. Charles, J. Pipelines, 1987, 7, 41–52 Search PubMed.
- P. Coussot, A. I. Leonov and J. M. Piau, J. Non-Newtonian Fluid Mech., 1993, 46, 179–217 CrossRef CAS.
- D. De Kee and C. F. Chan Man Fong, Polym. Eng. Sci., 1994, 34, 438–445 CAS.
- E. Toorman, Rheol. Acta, 1997, 36, 56–65 CrossRef CAS.
- P. Sollich, F. Lequeux, P. Hébraud and M. E. Cates, Phys. Rev. Lett., 1997, 78, 2020–2023 CrossRef CAS.
- M. L. Falk and J. S. Langer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 7192–7205 CrossRef CAS.
- D. Quemada, Eur. Phys. J. Appl. Phys., 1999, 5, 191–207 CrossRef CAS.
- F. Yziquel, P. Carreau, M. Moan and P. Tanguy, J. Non-Newtonian Fluid Mech., 1999, 86, 133–155 CrossRef CAS.
- A. Mujumdar, A. N. Beris and A. B. Metzner, J. Non-Newtonian Fluid Mech., 2002, 102, 157–178 CrossRef CAS.
- L. Bocquet, A. Colin and A. Ajdari, Phys. Rev. Lett., 2009, 103, 036001 CrossRef.
- P. R. de Souza Mendes, Soft Matter, 2011, 7, 2471–2483 RSC.
- P. Sollich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 738–759 CrossRef CAS.
- J. S. Langer and L. Pechenik, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 061507 CrossRef CAS.
- V. Mansard, A. Colin, P. Chauduri and L. Bocquet, Soft Matter, 2011, 7, 5524–5527 RSC.
- J. Goyon, A. Colin, G. Ovarlez, A. Ajdari and L. Bocquet, Nature, 2008, 454, 84–87 CrossRef CAS PubMed.
- J. Goyon, A. Colin and L. Bocquet, Soft Matter, 2010, 6, 2668–2678 RSC.
- H. Petter Rønningsen, J. Pet. Sci. Eng., 1992, 7, 177–213 CrossRef.
- A. Hammami and J. Ratulowski, Asphaltenes, Heavy Oils, and Petroleomics, 2007, pp. 617–660 Search PubMed.
- M. Cawkwell and M. Charles, J. Pipelines, 1989, 7, 251–256 Search PubMed.
- K. S. Pedersen and H. P. Rønningsen, Energy Fuels, 2000, 14, 43–51 CrossRef CAS.
- L. T. Wardhaugh and D. V. Boger, J. Rheol., 1991, 35, 301–308 CrossRef.
- R. Venkatesan, N. Nagarajan, K. Paso, Y. Yi, A. Sastry and H. Fogler, Chem. Eng. Sci., 2005, 60, 3587–3598 CrossRef CAS PubMed.
- R. F. G. Visintin, R. Lapasin, E. Vignati, P. D'Antona and T. P. Lockhart, Langmuir, 2005, 21, 6240–6249 CrossRef CAS PubMed.
- J. G. Speight, The Chemistry and Technology of Petroleum, CRC Press, 4th edn, 2007 Search PubMed.
- K. Paso, T. Kompalla, H. J. Oschmann and J. Sjöblom, J. Dispersion Sci. Technol., 2009, 30, 472–480 CrossRef CAS.
- E. Ghanaei and D. Mowla, Energy Fuels, 2010, 24, 1762–1770 CrossRef CAS.
- W. C. Chin, Offshore, 2000, 60, 92 Search PubMed.
- S. A. Rogers, D. Vlassopoulos and P. T. Callaghan, Phys. Rev. Lett., 2008, 100, 128304 CrossRef CAS.
- T. Gibaud, C. Barentin and S. Manneville, Phys. Rev. Lett., 2008, 101, 258302 CrossRef.
- T. Gibaud, C. Barentin, N. Taberlet and S. Manneville, Soft Matter, 2009, 5, 3026–3037 RSC.
- P. C. F. Møller, S. Rodts, M. A. J. Michels and D. Bonn, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 041507 CrossRef.
- A. Wachs, G. Vinay and I. Frigaard, J. Non-Newtonian Fluid Mech., 2009, 159, 81–94 CrossRef CAS PubMed.
- C. Chang, O. Nguyen and H. Rønningsen, J. Non-Newtonian Fluid Mech., 1999, 87, 127–154 CrossRef CAS.
- M. Gurtin, E. Fried and L. Anand, The Mechanics and Thermodynamics of Continua, Cambridge, 2010 Search PubMed.
- J. Lemaitre and J.-L. Chaboche, Mechanics of Solid Materials, Cambridge, 1990 Search PubMed.
- M. Rubin and A. Yarin, J. Non-Newtonian Fluid Mech., 1993, 50, 79–88 CrossRef CAS.
- D. Doraiswamy, A. N. Mujumdar, I. Tsao, A. N. Beris, S. C. Danforth and A. B. Metzner, J. Rheol., 1991, 35, 647–685 CrossRef CAS.
- C. J. Dimitriou, R. H. Ewoldt and G. H. McKinley, J. Rheol., 2013, 57, 1–44 CrossRef.
- C. J. Dimitriou, G. H. McKinley and R. Venkatesan, Energy Fuels, 2011, 25, 3040–3052 CrossRef CAS.
- M. Kanè, M. Djabourov, J.-L. Volle, J.-P. Lechaire and G. Frebourg, Fuel, 2002, 82, 127–135 CrossRef.
- A. Aiyejina, D. P. Chakrabarti, A. Pilgrim and M. Sastry, Int. J. Multiphase Flow, 2011, 37, 671–694 CrossRef CAS PubMed.
- C. J. Dimitriou, L. Casanellas, T. Ober and G. McKinley, Rheol. Acta, 2012, 51, 395–411 CrossRef CAS.
- H. S. Lee, P. Singh, W. H. Thomason and H. S. Fogler, Energy Fuels, 2008, 22, 480–487 CrossRef CAS.
- M. Keentok and S. Xue, Rheol. Acta, 1999, 38, 321–348 CrossRef CAS.
- J. M. Piau, J. Non-Newtonian Fluid Mech., 2007, 144, 1–29 CrossRef CAS PubMed.
- W. B. Russel and M. C. Grant, Colloids Surf., A, 2000, 161, 271–282 CrossRef CAS.
- L. T. Wardhaugh and D. V. Boger, AIChE J., 1991, 37, 871–885 CrossRef CAS.
- P. Coussot, L. Tocquer, C. Lanos and G. Ovarlez, J. Non-Newtonian Fluid Mech., 2009, 158, 85–90 CrossRef CAS PubMed.
- P. R. de Souza Mendes and R. L. Thompson, J. Non-Newtonian Fluid Mech., 2012, 187–188, 8–15 CrossRef CAS PubMed.
- R. G. Larson, Rheol. Acta, 1992, 31, 213–263 CrossRef CAS.
- F. Pignon, A. Magnin and J.-M. Piau, J. Rheol., 1996, 40, 573–587 CrossRef CAS.
- J. D. Goddard, Annu. Rev. Fluid Mech., 2003, 35, 113–133 CrossRef.
- P. Olmsted, Rheol. Acta, 2008, 47, 283–300 CrossRef CAS PubMed.
- J.-F. Berret, Langmuir, 1997, 13, 2227–2234 CrossRef CAS.
- J.-B. Salmon, A. Colin, S. Manneville and F. Molino, Phys. Rev. Lett., 2003, 90, 228303 CrossRef.
- M. M. Britton and P. T. Callaghan, Phys. Rev. Lett., 1997, 78, 4930–4933 CrossRef CAS.
- J. A. Dijksman, G. H. Wortel, L. T. H. van Dellen, O. Dauchot and M. van Hecke, Phys. Rev. Lett., 2011, 107, 108303 CrossRef.
- E. Michel, J. Appell, F. Molino, J. Kieffer and G. Porte, J. Rheol., 2001, 45, 1465–1477 CrossRef CAS.
- K. Dullaert and J. Mewis, J. Rheol., 2005, 49, 1–18 CrossRef.
- P. Callaghan, Rheol. Acta, 2008, 47, 243–255 CrossRef CAS.
- S. A. Rogers, P. T. Callaghan, G. Petekidis and D. Vlassopoulos, J. Rheol., 2010, 54, 133–158 CrossRef CAS.
- S. M. Fielding, P. Sollich and M. E. Cates, J. Rheol., 2000, 44, 323–369 CrossRef CAS.
- J. S. Dodge and I. M. Krieger, Trans. Soc. Rheol., 1971, 15, 589–601 CrossRef.
- K. Hyun, M. Wilhelm, C. O. Klein, K. S. Cho, J. G. Nam, K. H. Ahn, S. J. Lee, R. H. Ewoldt and G. H. McKinley, Prog. Polym. Sci., 2011, 36, 1697–1753 CrossRef CAS PubMed.
- S. A. Rogers, J. Rheol., 2012, 56, 1129–1151 CrossRef CAS.
- T. S.-K. Ng, G. H. McKinley and R. H. Ewoldt, J. Rheol., 2011, 55, 627–654 CrossRef CAS.
- A. J. Giacomin, R. B. Bird, L. M. Johnson and A. W. Mix, J. Non-Newtonian Fluid Mech., 2011, 166, 1081–1099 CrossRef CAS PubMed.
- R. H. Ewoldt, P. Winter, J. Maxey and G. H. McKinley, Rheol. Acta, 2010, 49, 191–212 CrossRef CAS PubMed.
- S. A. Rogers, B. M. Erwin, D. Vlassopoulos and M. Cloitre, J. Rheol., 2011, 55, 435–458 CrossRef CAS.
- M. Reiner, Advanced Rheology, H. K. Lewis, 1971 Search PubMed.
- J. D. Ferry, Viscoelastic Properties of Polymers, John Wiley and Sons, 3rd edn, 1980 Search PubMed.
- R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of Polymeric Liquids, John Wiley and Sons, 2nd edn, 1987, vol. 1 Search PubMed.
- A. Slibar and P. R. Paslay, in Intern Symp on Second Order Effects in Elasticity, Plasticity and Fluid Dynamics, ed. M. Reiner and D. Abir, Pergamon Press, 1964, pp. 1–314 Search PubMed.
- L. Anand, N. M. Ames, V. Srivastava and S. A. Chester, Int. J. Plast., 2008, 25, 1474–1494 CrossRef PubMed.
- D. L. Henann and L. Anand, Int. J. Plast., 2009, 25, 1833–1878 CrossRef PubMed.
- J. Sestak, M. E. Charles, M. G. Cawkwell and M. Houska, J. Pipelines, 1987, 6, 15–24 Search PubMed.
- N. M. Ames, V. Srivastava, S. A. Chester and L. Anand, Int. J. Plast., 2009, 25, 1495–1539 CrossRef CAS PubMed.
- P. J. Armstrong and C. O. Frederick, Mater. High Temp., 1966, 24, 1–26 Search PubMed.
- Y. Jiang and P. Kurath, Int. J. Plast., 1996, 12, 387–415 CrossRef CAS.
- J. Bauschinger, Mitteilung aus dem Mechanisch-technischen Laboratorium der Königlichen polytechnischen Hoschschule in München, 1886, vol. 13, pp. 1–115 Search PubMed.
- F. Moore, Trans. Br. Ceram. Soc., 1959, 58, 470–494 CAS.
- E. Kroner, Arch. Ration. Mech. Anal., 1960, 4, 273–334 CrossRef.
- G. Ovarlez, S. Cohen-Addad, K. Krishan, J. Goyon and P. Coussot, J. Non-Newtonian Fluid Mech., 2013, 193, 68–79 CrossRef CAS PubMed.
- D. C.-H. Cheng, Rheol. Acta, 1986, 25, 542–554 CrossRef CAS.
- P. Coussot, Q. D. Nguyen, H. T. Huynh and D. Bonn, Phys. Rev. Lett., 2002, 88, 128302 Search PubMed.
- J. D. Martin and Y. Thomas Hu, Soft Matter, 2012, 8, 6940–6949 RSC.
- P. Coussot, Q. D. Nguyen, H. T. Huynh and D. Bonn, J. Rheol., 2002, 46, 573–589 CrossRef CAS.
- P. R. de Souza Mendes and R. L. Thompson, Rheol. Acta, 2013, 52, 673–694 CrossRef CAS.
- D. L. Henann and K. Kamrin, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6730–6735 CrossRef CAS PubMed.
- R. L. Moorcroft and S. M. Fielding, Phys. Rev. Lett., 2013, 110, 086001 CrossRef.
- R. L. Moorcroft and S. M. Fielding, J. Rheol., 2014, 58, 103–147 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sm00578c |
| ‡ Current address: Nike Inc. Polymers R&D, 13630 SW Terman Rd., Beaverton, OR 97005. |
| This journal is © The Royal Society of Chemistry 2014 |