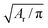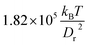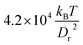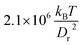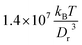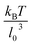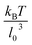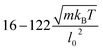Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Deformation and dynamics of red blood cells in flow through cylindrical microchannels†
Dmitry A.
Fedosov
*,
Matti
Peltomäki
and
Gerhard
Gompper
Theoretical Soft Matter and Biophysics, Institute of Complex Systems and Institute for Advanced Simulation, Forschungszentrum Jülich, 52425 Jülich, Germany. E-mail: d.fedosov@fz-juelich.de
First published on 14th March 2014
Abstract
The motion of red blood cells (RBCs) in microcirculation plays an important role in blood flow resistance and in the cell partitioning within a microvascular network. Different shapes and dynamics of RBCs in microvessels have been previously observed experimentally including the parachute and slipper shapes. We employ mesoscale hydrodynamic simulations to predict the phase diagram of shapes and dynamics of RBCs in cylindrical microchannels, which serve as idealized microvessels, for a wide range of channel confinements and flow rates. A rich dynamical behavior is found, with snaking and tumbling discocytes, slippers performing a swinging motion, and stationary parachutes. We discuss the effects of different RBC states on the flow resistance, and the influence of RBC properties, characterized by the Föppl–von Kármán number, on the shape diagram. The simulations are performed using the same viscosity for both external and internal fluids surrounding a RBC; however, we discuss how the viscosity contrast would affect the shape diagram.
1 Introduction
The behavior of soft mesoscopic particles (e.g., polymers, vesicles, capsules, and cells) in flow has recently received enormous attention due to the wide range of applications of such suspensions and their rich physical properties.1 To better control and/or manipulate the suspension's properties, for example in lab-on-chip applications,2,3 a deeper understanding of the interplay among flow forces, elastic response and dynamics of soft objects is required. An important example is the motion of red blood cells (RBCs) in microcirculation, which influences many vital processes in microvasculature;4 however, similar mechanisms and phenomena encompass a much wider class of capsule suspensions.5,6 RBCs are extremely flexible and experience strong deformation in microcirculation due to the flow and/or geometrical constraints. RBC deformation is important for the reduction of blood flow resistance7–11 and for ATP release and oxygen delivery.12,13RBCs in microcirculation may attain various shapes including parachutes and slippers.7,14–21 Parachutes are characterized by a rather symmetric shape resembling a semi-spherical cap and are located at a position near the tube center. Slippers correspond to asymmetric RBC shapes, and therefore their membranes are typically in motion (e.g., tank-treading). Both non-centered slipper20 and centered slipper shapes17 have been observed experimentally, where the latter may only differ slightly from parachute shapes. The stable slipper shapes are well established at higher hematocrits due to hydrodynamic cell–cell interactions.14,15,19 However, it is still not fully clear whether slippers are stable or transient states for single cells in flow.7,9,17,20,21 The most convincing evidence so far comes from simulations in two dimensions (2D).9,10,21
Simulations of 2D vesicles in slit channels have shown the existence of stable parachutes, slippers, and a snaking dynamics of discocytes9,10—where snaking refers to an oscillating RBC dynamics near the tube center. A phase diagram of various shapes was predicted, depending on relative confinement and flow rate. Simulations of single RBCs in three dimensions (3D)7,8,11,18 have been restricted so far to a limited number of studies, which only reveal (except for fluctuations and transient states) stationary parachutes and discocytes. It is important to note that these shapes (averaged over thermal fluctuations) are characterized by different symmetry classes, ranging from cylindrical symmetry (parachutes) to a single mirror plane containing the capillary axis and the RBC center (slippers). This raises several important questions: are slipper shapes also stable in 3D capillary flow? Is snaking dynamics around the center line possible in cylindrical microchannels in 3D? Do thermal fluctuations destroy the regular snaking oscillations? What is the role of the membrane shear modulus (absent in 2D) in the phase diagram?
In this paper, we present a systematic study of single RBCs flowing in microchannels. We construct diagrams of RBC shapes for different flow conditions and analyze RBC deformation. Changes in RBC properties (e.g., shear elastic modulus, bending rigidity) are also considered, since they are of importance in various blood diseases and disorders.22 The presented 3D shape diagrams describe RBC deformation in microchannels, which mimic small vessels in microcirculation, and show that the parachute shape occurs mainly in small channels, while in large channels the slipper shape may occur. All simulations assume the same viscosity for both cytosol and suspending fluid; however, we discuss how the viscosity contrast would affect the shape diagram. We also compare the 3D results with the 2D shape diagrams in ref. 9 and 10 and emphasize essential differences. For instance, due to membrane shear elasticity, there exists a region of RBC tumbling in 3D, which is absent in 2D. Finally, the simulation results are compared to available experimental data.17,20,23
The article is organized as follows. In Section 2 we briefly describe the mesoscopic method employed for fluid flow, a RBC model, and simulation setup and parameters. In Section 3 we first present the shape diagram for cell parameters typical of a healthy RBC. Then, RBC membrane properties are varied in order to elucidate their effects on the RBC shape and dynamics in microchannel flow. We also discuss the effect of viscosity contrast between external and internal fluids on the shape diagram and the effects of different shapes on the flow resistance. We conclude briefly in Section 4.
2 Models & methods
To model tube flow, we employ the smoothed dissipative particle dynamics (SDPD) method24 for the suspending fluid. SDPD is a particle-based mesoscopic simulation technique, where each SDPD particle represents a small volume of fluid rather than individual atoms or molecules. The RBC membrane is represented by a triangulated network model7,8,25,26 and coupled to a fluid through friction forces.2.1 Red blood cell model
The RBC membrane is modeled by a triangulated network of springs,7,8,25,26 which includes elastic, bending, and viscous properties. A RBC is represented by a collection of Nv particles connected by Ns = 3(Nv − 2) springs with the potential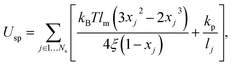 | (1) |
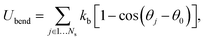 | (2) |
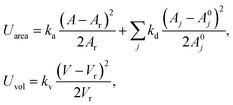 | (3) |
To relate the model parameters in the spring potential (1) (e.g., ξ, kp) and the bending potential (2) to the macroscopic membrane properties (e.g., Young's modulus Yr, bending rigidity κr), we use analytic relationships derived for a regular hexagonal network.8,27 The ratio lm/l0 is set to 2.2 for all springs.26 To relate simulation parameters to the physical properties of RBCs, we need a basic length and energy scale. Therefore, we define an effective RBC diameter 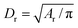 with Ar being the RBC membrane area. From Ar we can also calculate the average bond length l0 for a given number of membrane vertices
with Ar being the RBC membrane area. From Ar we can also calculate the average bond length l0 for a given number of membrane vertices 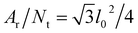 where Nt = 2Nv − 4 is the total number of triangular elements on a membrane. Experimental results28 for the RBC area imply that Dr = 6.5 μm. Table 1 summarizes the parameters for the RBC model in units of Dr and the thermal energy kBT, and the corresponding average values for a healthy RBC in physical units. The global area (ka) and volume (kv) constraint coefficients are chosen large enough to approximate closely the area-incompressibility of the lipid bilayer and incompressibility of the inner cytosol. Finally, a relationship for time scale is based on the characteristic RBC relaxation time, which is defined further below in the text.
where Nt = 2Nv − 4 is the total number of triangular elements on a membrane. Experimental results28 for the RBC area imply that Dr = 6.5 μm. Table 1 summarizes the parameters for the RBC model in units of Dr and the thermal energy kBT, and the corresponding average values for a healthy RBC in physical units. The global area (ka) and volume (kv) constraint coefficients are chosen large enough to approximate closely the area-incompressibility of the lipid bilayer and incompressibility of the inner cytosol. Finally, a relationship for time scale is based on the characteristic RBC relaxation time, which is defined further below in the text.
2.2 Smoothed dissipative particle dynamics
SDPD24 is a mesoscopic particle method, which combines two frequently used fluid-dynamics approaches: the smoothed particle hydrodynamics29,30 and dissipative particle dynamics31,32 methods. The SDPD system consists of N point particles of mass mi, position ri and velocity vi. SDPD particles interact through three pairwise forces: conservative (C), dissipative (D), and random (R), so that the force on particle i is given by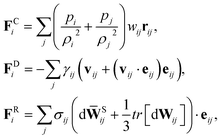 | (4) |
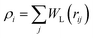 with weight function
with weight function 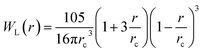 being the Lucy function, where rc is the cutoff radius. Note that ∇WL(r) = −rw(r) so that
being the Lucy function, where rc is the cutoff radius. Note that ∇WL(r) = −rw(r) so that 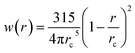 and wij = w(rij). The (distance-dependent) coefficients γij and σij define the strength of dissipative and random forces and are equal to
and wij = w(rij). The (distance-dependent) coefficients γij and σij define the strength of dissipative and random forces and are equal to 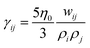 and
and 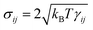 , where η0 is the desired fluid's dynamic viscosity and kBT is the thermal energy unit. The notation tr[dWij] corresponds to the trace of a random matrix of independent Wiener increments dWij, and d
, where η0 is the desired fluid's dynamic viscosity and kBT is the thermal energy unit. The notation tr[dWij] corresponds to the trace of a random matrix of independent Wiener increments dWij, and d![[W with combining macron]](https://www.rsc.org/images/entities/b_char_0057_0304.gif) Sij is the traceless symmetric part.
Sij is the traceless symmetric part.
The time evolution of velocities and positions of particles is determined by Newton's second law of motion
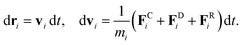 | (5) |
The SDPD fluid parameters are given in Table 2. A natural length scale in the fluid is the cut-off radius rc; however, since we investigate the dependence of fluid properties on rc, we use the membrane bond length l0 instead, which is very similar in magnitude to rc. In addition, the exponent α in the equation of state is chosen to be α = 7, and ρ0 = n, where n is the fluid's number density (in particles per l03). A relatively large value of α provides a good approximation of fluid incompressibility, since even small changes in local density may lead to strong local pressure changes. Furthermore, the speed of sound, c, for the selected equation of state can be given as c2 = p0α/ρ0. The corresponding Mach numbers have been kept below 0.1 in all simulations providing a good approximation for an incompressible fluid flow.
To span a wide range of flow rates, we employed different values of fluid viscosities η in simulations with an input parameter η0 ∈ [15; 120] 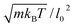 (m is the fluid's particle mass), since the fluid viscosity modifies linearly the RBC relaxation time scale defined further below. Large values of viscosity were used to model high flow rates of the physical system in order to keep the Reynolds number in simulations, based on characteristic RBC size, sufficiently low (see also an argument at the end of Section 2.3). Even though we can directly input the desired fluid viscosity η0 in SDPD, the assumption that η0 equals the actual fluid viscosity η is reliable only when each SDPD particle has large enough number of neighboring particles, which may require a large enough cutoff radius and/or a density of fluid particles. Therefore, it is always advisable to calculate the fluid viscosity directly (e.g., in shear-flow setup) to check validity of the approximation of the simulated fluid viscosity by η0. Note that for the fluid viscosity we have always used the precalculated values of η rather than input values of η0.
(m is the fluid's particle mass), since the fluid viscosity modifies linearly the RBC relaxation time scale defined further below. Large values of viscosity were used to model high flow rates of the physical system in order to keep the Reynolds number in simulations, based on characteristic RBC size, sufficiently low (see also an argument at the end of Section 2.3). Even though we can directly input the desired fluid viscosity η0 in SDPD, the assumption that η0 equals the actual fluid viscosity η is reliable only when each SDPD particle has large enough number of neighboring particles, which may require a large enough cutoff radius and/or a density of fluid particles. Therefore, it is always advisable to calculate the fluid viscosity directly (e.g., in shear-flow setup) to check validity of the approximation of the simulated fluid viscosity by η0. Note that for the fluid viscosity we have always used the precalculated values of η rather than input values of η0.
The tube wall has been modeled by frozen particles which assume the same structure as the fluid, while the wall thickness is equal to rc. Thus, the interactions of fluid particles with wall particles are the same as the interactions between fluid particles, and the interactions of a RBC with the wall are identical to those with a suspending fluid. The wall particles also provide a contribution to locally calculated density of fluid particles near a wall, while the local density of wall particles is set to n. To prevent wall penetration, fluid particles as well as vertices of a RBC are subject to reflection at the fluid–solid interface. We employed bounce-back reflections, because they provide a better approximation for the no-slip boundary conditions in comparison to specular reflection of particles. To ensure that no-slip boundary conditions are strictly satisfied, we also add a tangential adaptive shear force33 which acts on the fluid particles in a near-wall layer of a thickness rc.
Coupling between the fluid flow and RBC deformation is achieved through viscous friction between RBC nodes and surrounding fluid particles, which is implemented via dissipative particle dynamics interactions.8 Each membrane vertex interacts with fluid particles within a spherical volume with a radius r′c using dissipative and random forces similar to those in SDPD. The strength of dissipative (friction) coupling depends on the fluid viscosity and particle density as well as on the choice of r′c. The RBC membrane also separates inner and outer fluids, which is implemented through bounce-back reflections of fluid particles on a membrane surface.8 Finally, the local density of fluid particles near the membrane includes contributions of both inner and outer fluid particles.
2.3 Simulation setup
The simulation setup consists of a single periodic tube-like channel characterized by a diameter D and the length L = 10Dr, filled with a fluid and a single suspended RBC. For simplicity, the fluid viscosity inside a RBC is set to be the same as that of blood plasma. The flow is driven by a constant force f applied to each fluid particle, which is equivalent to a constant pressure gradient ΔP/L = fn, where ΔP is the pressure drop. To characterize the flow we define a non-dimensional shear rate given by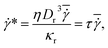 | (6) |
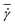 =
= ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) /D = Dfn/(32η) is the average shear rate (or pseudo-shear rate),
/D = Dfn/(32η) is the average shear rate (or pseudo-shear rate), ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) = Q/A is the average flow velocity with cross-sectional area A = πD2/4 and volumetric flow rate Q = πD4fn/(128η), and τ = ηDr3/κr is a characteristic relaxation time of a RBC. Note that we define
= Q/A is the average flow velocity with cross-sectional area A = πD2/4 and volumetric flow rate Q = πD4fn/(128η), and τ = ηDr3/κr is a characteristic relaxation time of a RBC. Note that we define 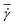 based on the Poiseuille flow solution for a Newtonian fluid without a RBC, since a single RBC does not significantly affect the total flow rate. This assumption for Q also results in
based on the Poiseuille flow solution for a Newtonian fluid without a RBC, since a single RBC does not significantly affect the total flow rate. This assumption for Q also results in ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * to be proportional to the pressure drop, which would be a convenient parameter to control in experiments. Furthermore, the flow behavior is determined by the cell confinement χ = Dr/D and the Föppl–von Kármán number Γ = YrDr2/κr = 2662 (average value for a healthy RBC), which characterizes relative importance of cell elasticity to bending rigidity.
* to be proportional to the pressure drop, which would be a convenient parameter to control in experiments. Furthermore, the flow behavior is determined by the cell confinement χ = Dr/D and the Föppl–von Kármán number Γ = YrDr2/κr = 2662 (average value for a healthy RBC), which characterizes relative importance of cell elasticity to bending rigidity.
To interpret the non-dimensional shear rate with respect to experimental measurements, we can compute the characteristic RBC relaxation time from eqn (6) to be τ = 1.1 s. Thus, the pseudo-shear rate 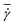 used in experiments is roughly equivalent in magnitude to
used in experiments is roughly equivalent in magnitude to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * in inverse seconds. It is important to note that since we employ distinct viscosity values in different simulations, the RBC relaxation time in simulation units also changes. Therefore, the same shear rate in simulations with different viscosities corresponds to different shear rates in physical units. This approach allows us to keep the Reynolds number low in the simulations, while a large range of shear rates in physical units can be spanned.
* in inverse seconds. It is important to note that since we employ distinct viscosity values in different simulations, the RBC relaxation time in simulation units also changes. Therefore, the same shear rate in simulations with different viscosities corresponds to different shear rates in physical units. This approach allows us to keep the Reynolds number low in the simulations, while a large range of shear rates in physical units can be spanned.
2.4 Sensitivity of simulation results to the discretization of fluid and RBC membrane
A too coarse discretization of fluid and RBC membrane may affect simulation results. To check whether our RBC discretization is fine enough, a number of simulations have been performed using significantly different numbers of membrane vertices, Nv = 1000 and Nv = 3000. The comparison reveals that Nv = 1000 is sufficient to obtain accurate results for the investigated range of flow rates. Much larger flow rates may require finer RBC discretization due to strong membrane deformation.Another potential source of error arises from the discretization of fluid flow. There are two main parameters here, which are related to each other: the particle density n and the cutoff radius rc within the SDPD fluid. The value of rc cannot be arbitrarily small, since the SDPD method properly functions only if each particle has a large enough number of neighboring particles. Thus, the choice of rc is directly associated with the particle density and can be selected smaller in magnitude for higher number densities. To study the sensitivity of the results to fluid discretization, the fluid density has been varied between n = 0.2l0−3 and n = 0.8l0−3, while the corresponding rc values were between 3.8l0 and 2.3l0. Simulation results show that values of rc ≲ 3l0 and n ≳ 0.4l0−3 are small and large enough, respectively, to properly reproduce the flow around a RBC for the studied flow rates. Note that the cutoff radius does not directly reflect strong local correlations, since local interactions are scaled by the weights wij, which decay to zero at distance rc.
Finally, coupling between the RBC and fluid flow is also performed over a smoothing length r′c. Even though generally there are no restrictions on the choice of r′c, it has to be small enough to impose properly the coupling between RBC vertices and local fluid flow. To test the sensitivity of our simulation results to the choice of this parameter, we varied the coupling radius between 1.2l0 and 2.4l0. A comparison of simulation results indicated that r′c ≲ 1.9l0 appears to be sufficient to obtain results independent of r′c for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≲ 100. All results in the paper are obtained using the discretization parameters which comply with the estimations made above.
* ≲ 100. All results in the paper are obtained using the discretization parameters which comply with the estimations made above.
3 Results and discussion
3.1 Shapes and dynamics of a healthy RBC
Fig. 1 shows several RBC shapes for χ = 0.58 (corresponding to a channel diameter D = 1.72Dr), which are typically encountered in microcirculatory blood flow; see also Movies S1–S4.† For slow flows, see Fig. 1(a), the RBC shape is similar to the biconcave discocyte shape in equilibrium. For higher flow rates, see Fig. 1(b), a slipper shape may be observed, which is characterized here by an off-center position within the tube so that the membrane displays a tank-treading motion due to local shear gradients resembling the tank-treading in shear flow.34,35 At the highest flow rate, see Fig. 1(c), a parachute shape is obtained, where the cell flows at the channel center and the membrane is practically not moving in the lab frame.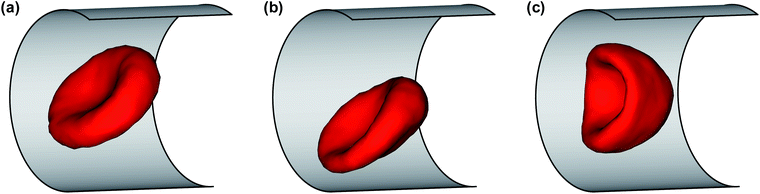 | ||
Fig. 1 Simulation snapshots of a RBC in flow (from left to right) for χ = 0.58. (a) A biconcave RBC shape at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = 5; (b) an off-center slipper cell shape at * = 5; (b) an off-center slipper cell shape at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = 24.8; and (c) a parachute shape at * = 24.8; and (c) a parachute shape at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = 59.6. See also Movies S1–S4.† * = 59.6. See also Movies S1–S4.† | ||
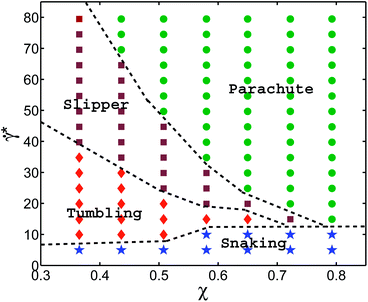
Fig. 2 presents our main result, the shape diagram for different flow rates and confinements, where the cell parameters are similar to those of a healthy RBC. The parachute RBC shape is predominantly observed in the region of strong confinements and high enough flow rates, where large flow forces are able to strongly deform a RBC. Here, it should be noticed that parachutes are also stable for weak or no confinement when the curvature of the parabolic flow in the center exceeds a critical value.9,36 At weak confinements, we find off-center slippers with tank-treading motion for higher flow rates, and discocytes with tumbling motion for lower flow rates. Both regions arise from the transition from strongly deformed parachute to more relaxed (discocyte and slipper) shapes, similar to the transition seen in the diagram for 2D vesicles.9,10 However, the boundary between slippers and discocytes is governed by the critical shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *ttt of the tumbling-to-tank-treading transition of a RBC;37,38 tumbling occurs off the tube center, when the local shear rate drops below
*ttt of the tumbling-to-tank-treading transition of a RBC;37,38 tumbling occurs off the tube center, when the local shear rate drops below ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *ttt. In the case of small viscosity contrast between inner and outer fluids (equal to unity here), the origin of the tumbling-to-tank-treading transition is the anisotropic shape of the spectrin network, which requires stretching deformation in the tank-treading state,37,38 and therefore cannot be captured by simulations of 2D vesicles. In addition, near the tumbling-slipper boundary, tumbling motion of a RBC exhibits a noticeable orbital drift so that the tumbling axis is not fixed and oscillates in the vorticity direction (see Movie S2†). This effect is qualitatively similar to a rolling motion (also called kayaking) found in experiments39 and in simulations40 of a RBC in shear flow. Orbital oscillations of a tumbling RBC are attributed to local membrane stretching deformation due to small membrane displacements whose effect becomes reduced if a RBC transits to a rolling motion.39
*ttt. In the case of small viscosity contrast between inner and outer fluids (equal to unity here), the origin of the tumbling-to-tank-treading transition is the anisotropic shape of the spectrin network, which requires stretching deformation in the tank-treading state,37,38 and therefore cannot be captured by simulations of 2D vesicles. In addition, near the tumbling-slipper boundary, tumbling motion of a RBC exhibits a noticeable orbital drift so that the tumbling axis is not fixed and oscillates in the vorticity direction (see Movie S2†). This effect is qualitatively similar to a rolling motion (also called kayaking) found in experiments39 and in simulations40 of a RBC in shear flow. Orbital oscillations of a tumbling RBC are attributed to local membrane stretching deformation due to small membrane displacements whose effect becomes reduced if a RBC transits to a rolling motion.39
At small shear rates ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *, there also exists a so-called snaking region, first observed for 2D vesicles in ref. 9 and 10, where a RBC performs a periodic oscillatory motion near the center line. In contrast to snaking in 2D, the snaking motion in 3D is fully three dimensional and exhibits an orbital drift (see Movie S1†), which is similar to that for a RBC rolling motion in shear flow occurring in a range of shear rates between RBC tumbling and tank-treading.39,40 The origin of orbital oscillations in the snaking regime might be similar to that for a rolling RBC; however, this issue requires a more detailed investigation. Note that at very low
*, there also exists a so-called snaking region, first observed for 2D vesicles in ref. 9 and 10, where a RBC performs a periodic oscillatory motion near the center line. In contrast to snaking in 2D, the snaking motion in 3D is fully three dimensional and exhibits an orbital drift (see Movie S1†), which is similar to that for a RBC rolling motion in shear flow occurring in a range of shear rates between RBC tumbling and tank-treading.39,40 The origin of orbital oscillations in the snaking regime might be similar to that for a rolling RBC; however, this issue requires a more detailed investigation. Note that at very low ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * ≲ kBT/κr, the rotational diffusion of RBCs becomes important, and RBC dynamics is characterized by random cell orientation. Another striking difference between the phase diagrams in Fig. 2 and in ref. 9 and 10 is that at high confinements the “confined slipper” found in the 2D vesicle simulations is suppressed in 3D. The confined slipper in 2D found for χ ≳ 0.6 is qualitatively similar to a slipper at low confinements, which is also called “unconfined slipper” in ref. 9 and 10, since this vesicle state exists in unbound parabolic flow. Note that the regions of confined and unconfined slippers in 2D have no common boundary. The absence of slippers at high confinements in 3D is due to the cylindrical shape of a channel, which would cause the confined slipper to conform to the wall curvature, which is energetically unfavorable.
* ≲ kBT/κr, the rotational diffusion of RBCs becomes important, and RBC dynamics is characterized by random cell orientation. Another striking difference between the phase diagrams in Fig. 2 and in ref. 9 and 10 is that at high confinements the “confined slipper” found in the 2D vesicle simulations is suppressed in 3D. The confined slipper in 2D found for χ ≳ 0.6 is qualitatively similar to a slipper at low confinements, which is also called “unconfined slipper” in ref. 9 and 10, since this vesicle state exists in unbound parabolic flow. Note that the regions of confined and unconfined slippers in 2D have no common boundary. The absence of slippers at high confinements in 3D is due to the cylindrical shape of a channel, which would cause the confined slipper to conform to the wall curvature, which is energetically unfavorable.
To better understand the differences between various RBC states, we now analyze the cell orientational angle, displacement from the channel center, and asphericity. The RBC orientational angle is defined as an angle between the eigenvector of the gyration tensor corresponding to the smallest eigenvalue (RBC thickness) and the tube axis. The RBC displacement r is computed as a distance between the RBC center of mass and the tube center. The RBC asphericity characterizes the deviation of a cell from a spherical shape and is defined as [(λ1 − λ2)2 + (λ2 − λ3)2 + (λ3 − λ1)2]/(2Rg4), where λ1 ≤ λ2 ≤ λ3 are the eigenvalues of the gyration tensor and Rg2 = λ1 + λ2 + λ3. The asphericity for a single RBC in equilibrium is equal to 0.15. Fig. 3 presents the temporal dependence of these properties for different RBC states, including snaking and tumbling discocyte, slipper, and parachute. For the snaking dynamics, the orientational angle oscillates between 40 and 90 degrees (Fig. 3(a)), the cell remains close to the channel center (Fig. 3(b)), and it shows only slight deformation compared to the equilibrium shape (Fig. 3(c)). The parachute shape is characterized by a small orientational angle (aligned with the tube axis), a cell position right in the tube center, and a small asphericity which indicates that the RBC shape attains a more spherical shape. Both tumbling discocytes and tank-treading slippers are displaced further from the channel center (Fig. 3(b)) than snaking discocytes and parachutes, and show an oscillating orientational angle. However, tumbling discocytes clearly show cell rotations, while slippers display a swinging motion characterized by small orientational oscillations around the tank-treading axis.37 Moreover, a tumbling RBC does not experience strong deformation (Fig. 3(c)), while a slipper shows large oscillations in cell asphericity. Note that to determine the RBC shape under given conditions, we used both visual assessment of the corresponding RBC shapes in flow and the analysis of the characteristics discussed above.
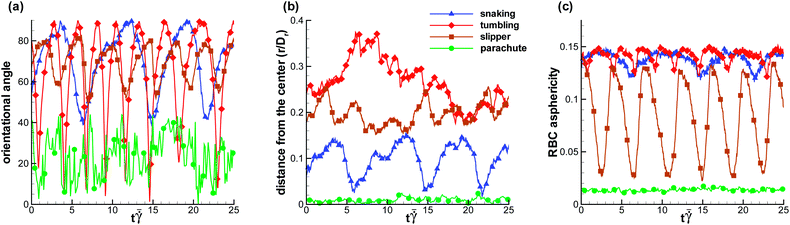 | ||
Fig. 3 Characteristics of different RBC states: blue triangle – snaking discocyte (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = 9.9, χ = 0.72), red diamond – tumbling discocyte ( * = 9.9, χ = 0.72), red diamond – tumbling discocyte (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = 14.9, χ = 0.44), brown square – slipper ( * = 14.9, χ = 0.44), brown square – slipper (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = 49.7, χ = 0.44), and green circle – parachute ( * = 49.7, χ = 0.44), and green circle – parachute (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = 64.6, χ = 0.65). (a) Cell orientational angle between the eigenvector of the gyration tensor corresponding to the smallest eigenvalue (RBC thickness) and the tube axis. (b) Distance between the RBC center of mass and the tube center normalized by Dr. (c) RBC asphericity, which characterizes the deviation from a spherical shape. The asphericity is defined as [(λ1 − λ2)2 + (λ2 − λ3)2 + (λ3 − λ1)2]/(2Rg4), where λ1 ≤ λ2 ≤ λ3 are the eigenvalues of the gyration tensor and Rg2 = λ1 + λ2 + λ3. The asphericity for a single RBC in equilibrium is equal to 0.15. See also Movies S1–S4.† * = 64.6, χ = 0.65). (a) Cell orientational angle between the eigenvector of the gyration tensor corresponding to the smallest eigenvalue (RBC thickness) and the tube axis. (b) Distance between the RBC center of mass and the tube center normalized by Dr. (c) RBC asphericity, which characterizes the deviation from a spherical shape. The asphericity is defined as [(λ1 − λ2)2 + (λ2 − λ3)2 + (λ3 − λ1)2]/(2Rg4), where λ1 ≤ λ2 ≤ λ3 are the eigenvalues of the gyration tensor and Rg2 = λ1 + λ2 + λ3. The asphericity for a single RBC in equilibrium is equal to 0.15. See also Movies S1–S4.† | ||
3.2 Comparison with experiments
There exist several experimental studies of a RBC in microchannel flow.17,20,23,41 In the experiments of ref. 23, the rotation of single RBCs and of their rouleaux structures in tube flow with radii ranging from 30 μm to 100 μm has been investigated. Even though the tube diameters in the experiments were larger than those used in our simulations, these experiments provide direct evidence of the existence of RBC off-center tumbling dynamics for low confinements and low flow rates with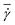 ≲ 50 s−1, in agreement with the simulation results in Fig. 2.
≲ 50 s−1, in agreement with the simulation results in Fig. 2.
In the experiments of ref. 17, the imposed flow velocities were very large, ranging from 1 cm s−1 to 30 cm s−1 in a capillary with the diameter of 9 μm. This is much faster than the typical flow velocities in microcirculation, where for venules and arterioles with a similar diameter flow velocities are in the range of 0.2–7 mm s−1.4,42 The range of flow velocities we span in our simulations is about 0.2–1.0 mm s−1, and is therefore comparable with that in microcirculation. The results in ref. 17 show the existence of parachute and slipper shapes, where a weak confinement favors non-centered slipper shapes, which is in qualitative agreement with the simulations in Fig. 2. Furthermore, a good agreement between experiments and simulations is found for low confinements, where parachute shapes are observed for flow rates with the velocities lower than 4–7 cm s−1.17 At flow velocities larger than approximately 7 cm s−1 and at low confinements, centered slippers are observed which resemble parachutes, but become slightly asymmetric.17 Recent 2D simulations10 have also found that at high enough flow rates centered slippers and parachutes may coexist. Currently, we are not able to reach such high flow rates in 3D simulations due to numerical limitations. In addition, this region might be of limited interest, since the corresponding flow rates are far beyond the physiologically relevant values.
Experimental data in ref. 20 were obtained for narrow capillaries with diameters ranging from 4.7 μm to 10 μm; however, the flow velocities are considerably smaller than those in ref. 17, in the range of 1–40 mm s−1. For strong confinements χ ≳ 1, centered bullet-like shapes are observed which resemble an elongated cylindrical shape with a semi-spherical cap at the front end and a semi-spherical dip at the rear end. A comparison with our simulation results for the weaker confinement of χ = 0.65 shows a good agreement since centered parachute shapes are found in both experiments and simulations. The transition to the parachute shape for χ = 0.65 occurred at the RBC velocity of about 0.5 mm s−1 in the experiments,20 while our simulations predict the transition velocity of about 0.45 mm s−1.
3.3 The effects of membrane properties on the shape diagram
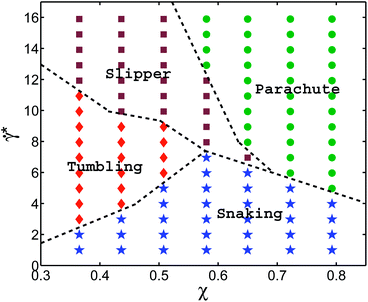
In order to investigate the effects of membrane elastic parameters on the RBC phase diagram in capillary flow, we calculated phase diagrams for both reduced Young's modulus and increased bending rigidity. The state diagram for membrane bending rigidity increased by a factor of five, which leads to κr = 1.5 × 10−18 J and Γ = 532, is shown in Fig. 4. We expect a dependence of the transition lines on the membrane parameters and geometry of the channel to be of the form![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *c =
*c = ![[capital Omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e133.gif) (Γ, χ, κr/kBT), where
(Γ, χ, κr/kBT), where ![[capital Omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e133.gif) is a universal function for each transition. In addition, a more general form of
is a universal function for each transition. In addition, a more general form of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *c should also include the strength of thermal fluctuations characterized by ambient temperature as an independent variable. As an example, different temperatures would affect the rotational diffusion of RBCs, which may become important at very low
*c should also include the strength of thermal fluctuations characterized by ambient temperature as an independent variable. As an example, different temperatures would affect the rotational diffusion of RBCs, which may become important at very low ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * and lead to random cell orientation modifying potentially a snaking region. Also, recent experiments on vesicles43 and a corresponding theory44 suggest that the transition lines might be affected by thermal noise due to the sensitivity of a nonlinear dynamics to small perturbations near transition lines. A comparison of the results of Fig. 4 with those of Fig. 2 shows that for stiffer cells, the parachute and slipper/tumbling regions shift to lower values of
* and lead to random cell orientation modifying potentially a snaking region. Also, recent experiments on vesicles43 and a corresponding theory44 suggest that the transition lines might be affected by thermal noise due to the sensitivity of a nonlinear dynamics to small perturbations near transition lines. A comparison of the results of Fig. 4 with those of Fig. 2 shows that for stiffer cells, the parachute and slipper/tumbling regions shift to lower values of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *. This behavior is consistent with the roughly linear dependence of the shear rate
*. This behavior is consistent with the roughly linear dependence of the shear rate 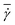 at the parachute-to-discocyte transition on RBC bending rigidity and shear modulus reported in ref. 7, which is equivalent to
at the parachute-to-discocyte transition on RBC bending rigidity and shear modulus reported in ref. 7, which is equivalent to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * = c1(χ) + c2(χ)Γ. Similarly, the snaking region shrinks towards lower
* = c1(χ) + c2(χ)Γ. Similarly, the snaking region shrinks towards lower ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * values.
* values.
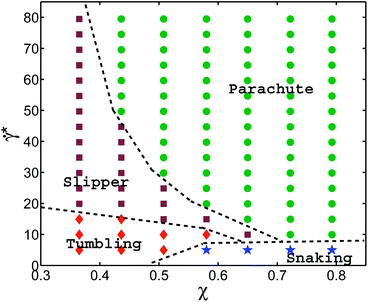
Fig. 5 shows the state diagram for a RBC in tube flow with the membrane Young's modulus reduced by the factor of three (Yr = 6.3 μN m−1) in comparison to that of a healthy RBC. This diagram should be compared with Fig. 2 and 4, which are for healthy RBCs and cells with an increased bending rigidity, respectively. In Fig. 5, the transition from snaking discocytes and swinging slippers to the parachute shape, as well as the transition from tumbling discocytes to swinging slippers occur at lower flow rates than those for a healthy RBC (Fig. 2). As a consequence, the snaking region shrinks substantially and is observed primarily at very low ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *. Another feature is that the tumbling region is significantly reduced in comparison to that in the diagram for healthy cells (Fig. 2). These results are consistent with the fact that the transition from discocyte to parachute shapes in Poiseuille flow depends roughly linearly on the RBC elastic properties and bending rigidity,7 as well as that the tumbling-to-tank-treading transition of a RBC in shear flow depends nearly linearly on the RBC elastic properties such as Young's modulus.37,38 This implies that the transition lines for a fixed ambient temperature are linear functions of the Föppl–von Kármán number Γ, as discussed above. A comparison with the results of ref. 7 for RBCs with considerably smaller bending and shear rigidities indicates that strong thermal fluctuations destroy the regular snaking oscillations.
*. Another feature is that the tumbling region is significantly reduced in comparison to that in the diagram for healthy cells (Fig. 2). These results are consistent with the fact that the transition from discocyte to parachute shapes in Poiseuille flow depends roughly linearly on the RBC elastic properties and bending rigidity,7 as well as that the tumbling-to-tank-treading transition of a RBC in shear flow depends nearly linearly on the RBC elastic properties such as Young's modulus.37,38 This implies that the transition lines for a fixed ambient temperature are linear functions of the Föppl–von Kármán number Γ, as discussed above. A comparison with the results of ref. 7 for RBCs with considerably smaller bending and shear rigidities indicates that strong thermal fluctuations destroy the regular snaking oscillations.
Correspondence of different systems with a fixed Föppl–von Kármán number Γ is also supported by the argument that the RBC relaxation time τ is a linear function of RBC membrane elastic parameters (κr or equivalently Yr for a fixed Γ). Thus, a simulation with the parameters {Dr, Yr, sκr, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *} should lead to identical results as those obtained from a simulation with {Dr, Yr/s, κr,
*} should lead to identical results as those obtained from a simulation with {Dr, Yr/s, κr, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) */s}, where s is a scaling constant. Even though this argument is quite general, other characteristics of a system also need to be properly considered including thermal fluctuations and Reynolds number of the flow. Finally, the assumption of linear dependence of τ on the membrane properties may become invalid for strong enough flow rates, which may lead to non-linear membrane deformation. A semi-quantitative comparison of cell shape regions can be done by looking at the state diagram of Fig. 5 for the reduced membrane Young's modulus and the state diagram of Fig. 4 for an increased membrane bending rigidity. The corresponding Föppl–von Kármán numbers are not the same, but similar in magnitude and both are considerably smaller than those for healthy RBCs. Thus, we expect that the two state diagrams for Γ = 532 (Fig. 4) and Γ = 887 (Fig. 5) should be similar, and show the same trends in comparison with the diagram for healthy cells (Fig. 2). This comparison further supports our argument about the existence of universal functions
*/s}, where s is a scaling constant. Even though this argument is quite general, other characteristics of a system also need to be properly considered including thermal fluctuations and Reynolds number of the flow. Finally, the assumption of linear dependence of τ on the membrane properties may become invalid for strong enough flow rates, which may lead to non-linear membrane deformation. A semi-quantitative comparison of cell shape regions can be done by looking at the state diagram of Fig. 5 for the reduced membrane Young's modulus and the state diagram of Fig. 4 for an increased membrane bending rigidity. The corresponding Föppl–von Kármán numbers are not the same, but similar in magnitude and both are considerably smaller than those for healthy RBCs. Thus, we expect that the two state diagrams for Γ = 532 (Fig. 4) and Γ = 887 (Fig. 5) should be similar, and show the same trends in comparison with the diagram for healthy cells (Fig. 2). This comparison further supports our argument about the existence of universal functions ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *c to describe the transition lines.
*c to describe the transition lines.
3.4 The effect of cytosol viscosity on the shape diagram
We have focused in our simulations on the investigation of the effect of membrane elasticity on RBC dynamics in microcapillary flow, and have therefore employed same viscosity for the suspending fluid and RBC cytosol. For a healthy RBC, the viscosity contrast λ, defined as the ratio of cytosol over blood plasma viscosity, is approximately λ = 5. Therefore, we want to discuss briefly the possible effect of the viscosity contrast on the dynamical states. Clearly, cytosol viscosity only plays a role when the internal fluid (or equivalently membrane) is in motion, i.e., only when the cell tank-treads in the slipper state. Thus, we mainly need to discuss how the slipper region will be modified. Recent experiments45 and simulations46 indicate that the viscosity contrast indeed strongly affects the tumbling-to-tank-treading transition characterized by![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *ttt.
*ttt.
An increase in λ is known to shift ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *ttt of the tumbling-to-tank-treading transition to higher shear rates.46 Therefore, we expect that the boundary between the tumbling and slipper regions in Fig. 2 would shift to higher values of
*ttt of the tumbling-to-tank-treading transition to higher shear rates.46 Therefore, we expect that the boundary between the tumbling and slipper regions in Fig. 2 would shift to higher values of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * for a real RBC leading to the expansion of the tumbling region. A very large viscosity of either RBC membrane or cytosol, which may occur in some blood-related diseases or disorders,22 may also lead to a complete disappearance of the slipper region, which would be replaced by the RBC tumbling state. Recent simulations of 2D vesicles with λ = 1 in ref. 9 and λ = 5 in ref. 10 have shown an expansion of the snaking region toward the slipper region, since the RBC tank-treading becomes less favorable. Note that since RBC tumbling due to membrane elastic anisotropy is not possible in 2D, the snaking region in ref. 9 and 10 has a large common boundary with the slipper region, while in 3D the snaking region has practically no boundary with the dynamical slipper region and is mainly connected to the tumbling region (Fig. 2). Thus, no significant changes in the snaking region due to the viscosity contrast is expected in 3D. In analogy with the expansion of the snaking region in 2D, an expansion of the tumbling region in 3D can be expected.
* for a real RBC leading to the expansion of the tumbling region. A very large viscosity of either RBC membrane or cytosol, which may occur in some blood-related diseases or disorders,22 may also lead to a complete disappearance of the slipper region, which would be replaced by the RBC tumbling state. Recent simulations of 2D vesicles with λ = 1 in ref. 9 and λ = 5 in ref. 10 have shown an expansion of the snaking region toward the slipper region, since the RBC tank-treading becomes less favorable. Note that since RBC tumbling due to membrane elastic anisotropy is not possible in 2D, the snaking region in ref. 9 and 10 has a large common boundary with the slipper region, while in 3D the snaking region has practically no boundary with the dynamical slipper region and is mainly connected to the tumbling region (Fig. 2). Thus, no significant changes in the snaking region due to the viscosity contrast is expected in 3D. In analogy with the expansion of the snaking region in 2D, an expansion of the tumbling region in 3D can be expected.
An effect of the viscosity contrast on the boundary between the slipper and parachute regions is not obvious. 2D simulations for different viscosity contrasts9,10 indicate that the boundary is slightly altered that makes the slipper region get mildly expanded. Thus, it is plausible to expect a similarly weak effect in 3D; however, a definite statement on this issue is only possible after a systematic numerical investigation of the effect of viscosity contrast has been performed in 3D.
3.5 Snaking, tumbling, and swinging frequencies
The simulations also provide interesting information about the dependence of the snaking, tumbling (both in the discocyte state) and swinging (in the slipper state) frequencies ω on shear rate, as shown in Fig. 6 for three different confinements extracted from the state diagram of Fig. 4. In all regimes, the frequencies increase linearly with shear rate. However, the prefactors of this linear dependence are very different. The strongest dependence is found in the swinging regime, somewhat larger than that in the snaking regime, while the frequency is almost independent of![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * in the tumbling regime. Increasing confinement significantly reduces the snaking, tumbling and swinging frequencies. Note that the swinging frequencies are likely to be overpredicted in Fig. 6 in comparison with those of real RBCs due to the assumption of having the same viscosity of the suspending medium and RBC cytosol.
* in the tumbling regime. Increasing confinement significantly reduces the snaking, tumbling and swinging frequencies. Note that the swinging frequencies are likely to be overpredicted in Fig. 6 in comparison with those of real RBCs due to the assumption of having the same viscosity of the suspending medium and RBC cytosol.
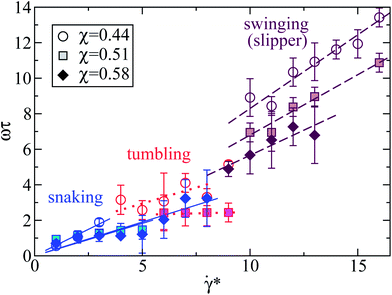 | ||
Fig. 6 Normalized snaking, tumbling, and swinging (slipper state) frequencies ω of RBCs as a function of the dimensionless shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) *. The elastic membrane parameters are the same as in Fig. 4 (Yr = 18.9 × 10−6 N m−1, κr = 1.5 × 10−18 J), i.e. the bending rigidity is five times larger than that used for a healthy RBC, and Γ = 532. Three confinements are shown, as indicated. The symbols depict simulation results for various confinements. The regions of *. The elastic membrane parameters are the same as in Fig. 4 (Yr = 18.9 × 10−6 N m−1, κr = 1.5 × 10−18 J), i.e. the bending rigidity is five times larger than that used for a healthy RBC, and Γ = 532. Three confinements are shown, as indicated. The symbols depict simulation results for various confinements. The regions of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * corresponding to different RBC states can be distinguished in the plot by colors and line types – swinging (brown, dashed line), tumbling (red, dotted line), and snaking (blue, solid line). * corresponding to different RBC states can be distinguished in the plot by colors and line types – swinging (brown, dashed line), tumbling (red, dotted line), and snaking (blue, solid line). | ||
3.6 Flow resistance
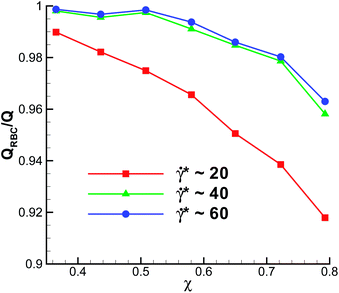
Fig. 7 presents the volumetric flow rate QRBC with a RBC measured in simulations and normalized by the flow rate Q without a RBC. Data are shown for different![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * for the case of Γ = 2662, corresponding to the shape diagram in Fig. 2. The volumetric flow rate at low confinements remains essentially unaffected by the presence of a RBC. As the confinement is increased, the flow rate decreases and the effect of a RBC on the flow rate appears to be stronger at low
* for the case of Γ = 2662, corresponding to the shape diagram in Fig. 2. The volumetric flow rate at low confinements remains essentially unaffected by the presence of a RBC. As the confinement is increased, the flow rate decreases and the effect of a RBC on the flow rate appears to be stronger at low ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * values. Note that Fig. 7 also presents the change in flow resistance, since the apparent viscosity is inversely proportional to the volumetric flow rate. Thus, the apparent viscosity increases with increasing confinement. A reduction in the flow resistance with the increase of
* values. Note that Fig. 7 also presents the change in flow resistance, since the apparent viscosity is inversely proportional to the volumetric flow rate. Thus, the apparent viscosity increases with increasing confinement. A reduction in the flow resistance with the increase of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * (represented by different curves in Fig. 7) is due to the transition from discocyte to parachute and slipper shapes, since for large enough
* (represented by different curves in Fig. 7) is due to the transition from discocyte to parachute and slipper shapes, since for large enough ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) * no significant further changes in flow resistance occur.
* no significant further changes in flow resistance occur.
Even though Fig. 7 shows the effect of confinement on QRBC, the flow resistance for different χ may be also affected by the change in hematocrit. In all simulations, the length of the channel was kept the same, while the tube diameter was varied, which means that the tube hematocrit (Ht), calculated as the ratio of the RBC volume to total tube volume, is inversely proportional to D2. For the strongest confinement χ = 0.79 (D = 8.2 μm) Ht is equal to 0.027, while for the lowest confinement χ = 0.37 (D = 17.8 μm) Ht = 0.0057.
4 Conclusions
Even though the phase diagrams of RBC shapes show some qualitative similarities with the corresponding diagram of 2D vesicles,9,10 there are several qualitative and quantitative differences. In 3D, slippers are essentially absent at high confinements (χ ≳ 0.7) and low flow rates due to the cylindrical channel geometry, which requires the RBC slipper to comply with the channel wall curvature and cannot be captured by a 2D model. Therefore, parachute shapes are preferred at high χ – in agreement with the 3D results of ref. 7. At even higher confinements than those in this study, RBCs are expected to attain bullet shapes.20 Another evident difference between RBCs in 3D and vesicles in 2D9,10 is the existence of a RBC tumbling region, which appears in 3D due to anisotropic elastic properties of RBCs.37,38 For vesicles in 2D, the only possibility to include tumbling is to introduce a high enough viscosity contrast between the fluids inside and outside a RBC.The calculated state diagrams in 3D provide a better description of RBC shapes and dynamics in microvascular flow than the previous 2D results. The flow resistance is affected only weakly by the transition from discocyte to parachute and slipper shapes, most significantly at high confinements (χ ≳ 0.6). The geometrical complexity of microvasculature induces non-trivial partitioning of RBCs, which often leads to very low cell volume fractions within various vessel structures, so that our simulation results provide an important step towards an understanding of blood flow and RBC behavior in microcirculation. Finally, similar physical mechanisms are expected for capsule suspensions.
Acknowledgements
A CPU time grant by the Jülich Supercomputing center is gratefully acknowledged. Dmitry A. Fedosov acknowledges funding by the Alexander von Humboldt Foundation. We also thank the DFG Research Unit FOR 1543 “SHENC – Shear Flow Regulation in Hemostasis” for support.References
- R. G. Larson, The structure and rheology of complex fluids, Oxford University Press, Oxford, NY, 1999 Search PubMed.
- J. A. Davis, D. W. Inglis, K. M. Morton, D. A. Lawrence, L. R. Huang, S. Y. Chou, J. C. Sturm and R. H. Austin, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 14779–14784 CrossRef CAS PubMed.
- H. Craighead, Nature, 2006, 442, 387–393 CrossRef CAS PubMed.
- A. S. Popel and P. C. Johnson, Annu. Rev. Fluid Mech., 2005, 37, 43–69 CrossRef PubMed.
- T. Omori, Y. Imai, T. Yamaguchi and T. Ishikawa, Phys. Rev. Lett., 2012, 108, 138102 CrossRef.
- A. Kumar and M. D. Graham, Phys. Rev. Lett., 2012, 109, 108102 CrossRef.
- H. Noguchi and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 14159–14164 CrossRef CAS PubMed.
- D. A. Fedosov, B. Caswell and G. E. Karniadakis, Biophys. J., 2010, 98, 2215–2225 CrossRef CAS PubMed.
- B. Kaoui, N. Tahiri, T. Biben, H. Ez-Zahraouy, A. Benyoussef, G. Biros and C. Misbah, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041906 CrossRef CAS.
- N. Tahiri, T. Biben, H. Ez-Zahraouy, A. Benyoussef and C. Misbah, Microvasc. Res., 2013, 85, 40–45 CrossRef CAS PubMed.
- D. A. Fedosov, H. Noguchi and G. Gompper, Biomech. Model. Mechanobiol., 2014, 13, 239–258 CrossRef PubMed.
- R. S. Sprague, M. L. Ellsworth, A. H. Stephenson, M. E. Kleinhenz and A. J. Lonigro, Am. J. Physiol., 1998, 275, H1726–H1732 CAS.
- A. M. Forsyth, J. Wan, P. D. Owrutsky, M. Abkarian and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10986–10991 CrossRef CAS PubMed.
- R. Skalak, Science, 1969, 164, 717–719 CAS.
- P. Gaehtgens, C. Dührssen and K. H. Albrecht, Blood Cells, 1980, 6, 799–812 CAS.
- U. Bagge, P.-I. Branemark, R. Karlsson and R. Skalak, Blood Cells, 1980, 6, 231–237 CAS.
- M. Abkarian, M. Faivre, R. Horton, K. Smistrup, C. A. Best-Popescu and H. A. Stone, Biomed. Mater., 2008, 3, 034011 CrossRef PubMed.
- I. V. Pivkin and G. E. Karniadakis, Phys. Rev. Lett., 2008, 101, 118105 CrossRef.
- J. L. McWhirter, H. Noguchi and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 6039–6043 CrossRef CAS PubMed.
- G. Tomaiuolo, M. Simeone, V. Martinelli, B. Rotoli and S. Guido, Soft Matter, 2009, 5, 3736–3740 RSC.
- B. Kaoui, G. Biros and C. Misbah, Phys. Rev. Lett., 2009, 103, 188101 CrossRef.
- M. Diez-Silva, M. Dao, J. Han, C.-T. Lim and S. Suresh, MRS Bull., 2010, 35, 382–388 CrossRef CAS.
- H. L. Goldsmith and J. Marlow, Proc. R. Soc. London, Ser. B, 1972, 182, 351–384 CrossRef.
- P. Espanol and M. Revenga, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 026705 CrossRef.
- D. E. Discher, D. H. Boal and S. K. Boey, Biophys. J., 1998, 75, 1584–1597 CrossRef CAS.
- D. A. Fedosov, B. Caswell and G. E. Karniadakis, Comput. Methods Appl. Mech. Eng., 2010, 199, 1937–1948 CrossRef PubMed.
- H. S. Seung and D. R. Nelson, Phys. Rev. A, 1988, 38, 1005–1018 CrossRef.
- E. A. Evans and R. Skalak, Mechanics and thermodynamics of biomembranes, CRC Press, Inc., Boca Raton, Florida, 1980 Search PubMed.
- L. B. Lucy, Astron. J., 1977, 82, 1013–1024 CrossRef.
- J. J. Monaghan, Annu. Rev. Astron. Astrophys., 1992, 30, 543–574 CrossRef.
- P. J. Hoogerbrugge and J. M. V. A. Koelman, Europhys. Lett., 1992, 19, 155–160 CrossRef.
- P. Espanol and P. Warren, Europhys. Lett., 1995, 30, 191–196 CrossRef CAS.
- D. A. Fedosov and G. E. Karniadakis, J. Comput. Phys., 2009, 228, 1157–1171 CrossRef PubMed.
- R. Tran-Son-Tay, S. P. Sutera and P. R. Rao, Biophys. J., 1984, 46, 65–72 CrossRef CAS.
- T. M. Fischer, Biophys. J., 2007, 93, 2553–2561 CrossRef CAS PubMed.
- J. L. McWhirter, H. Noguchi and G. Gompper, Soft Matter, 2011, 7, 10967–10977 RSC.
- M. Abkarian, M. Faivre and A. Viallat, Phys. Rev. Lett., 2007, 98, 188302 CrossRef.
- J. M. Skotheim and T. W. Secomb, Phys. Rev. Lett., 2007, 98, 078301 CrossRef CAS.
- J. Dupire, M. Socol and A. Viallat, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 20808–20813 CrossRef CAS PubMed.
- D. Cordasco and P. Bagchi, Phys. Fluids, 2013, 25, 091902 Search PubMed.
- G. Tomaiuolo, V. Preziosi, M. Simeone, S. Guido, R. Ciancia, V. Martinelli, C. Rinaldi and B. Rotoli, Ann. Ist. Super. Sanita, 2007, 43, 186–192 Search PubMed.
- A. R. Pries, T. W. Secomb and P. Gaehtgens, Am. J. Physiol., 1995, 269, H1713–H1722 CAS.
- M. Levant and V. Steinberg, Phys. Rev. Lett., 2012, 109, 268103 CrossRef.
- D. Abreu and U. Seifert, Phys. Rev. Lett., 2013, 110, 238103 CrossRef.
- V. Vitkova, M.-A. Mader, B. Polack, C. Misbah and T. Podgorski, Biophys. J., 2008, 95, L33–L35 CrossRef CAS PubMed.
- A. Z. K. Yazdani and P. Bagchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 026314 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Four movies of different RBC shapes in capillary flow: snaking discocytes, tumbling discocytes, swinging slippers, and parachutes. Blue particles on the RBC are firmly attached to the membrane and serve as tracers in order to visualize the membrane dynamics; these particles have no physical meaning. See DOI: 10.1039/c4sm00248b |
| This journal is © The Royal Society of Chemistry 2014 |