Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Influence of interfacial rheology on drainage from curved surfaces†
M. Saad
Bhamla
a,
Caroline E.
Giacomin
b,
Caroline
Balemans
c and
Gerald G.
Fuller
*a
aDepartment of Chemical Engineering, Stanford University, Stanford, California 94305, USA. E-mail: ggf@stanford.edu
bDepartment of Chemical Engineering, McGill University, Montreal, Quebec, Canada
cDepartment of Mechanical Engineering, Eindhoven University of Technology, Eindhoven, The Netherlands
First published on 11th February 2014
Abstract
Thin lubrication flows accompanying drainage from curved surfaces surround us (e.g., the drainage of the tear film on our eyes). These draining aqueous layers are normally covered with surface-active molecules that render the free surface viscoelastic. The non-Newtonian character of these surfaces fundamentally alters the dynamics of drainage. We show that increased film stability during drainage can occur as a consequence of enhanced surface rheology. Increasing the surfactant layer viscosity decreases the rate of drainage; however, this retarding influence is most pronounced when the insoluble surfactant layer has significant elasticity. We also present a simple theoretical model that offers qualitative support to our experimental findings.
1 Introduction
In this work, we examine the drainage of liquids from curved surfaces and focus on an important aspect of this problem that has not received previous attention: the interaction of rheologically complex, insoluble lipid layers at the surface of the draining liquid. One application of our work is drainage and thinning of the tear film atop silicone hydrogel contact lenses.Osbourne Reynolds originally formulated the problem of drainage between two approaching rigid parallel surfaces in 1886.1 In his seminal paper, Reynolds proposed the lubrication theory equations that govern thin film flow and showed that the draining film thickness decayed as a square-root in time (h ∼ t−1/2), also known as Reynolds thinning law. Today, drainage of thin films finds diverse applications from drop–drop coalescence,2–5 to drainage of foams,6–8 and biologically relevant applications, such as the stability of the tear film.9–11
Important developments on the problem of drainage from curved surfaces came about a century later, when Hartland12 reported on experiments measuring the transient thickness of a thin liquid film squeezed beneath an approaching solid sphere. In his experiment, the thin film is of a lighter liquid and is sandwiched between the sphere at the top and a denser, immiscible liquid at the bottom. Hartland offered a simple theory assuming a uniform thickness of the draining film, and his prediction for the diminishing film thickness was identical to Reynolds thinning law. Interestingly though, Hartland observed that as the thin, lighter liquid was squeezed out beneath the sphere, changes in the dynamic pressure led to the formation of a dimple, which he revealed by impressive photographic evidence. These dimples in the free surface were a result of the pressure field arising from the interplay of gravity, viscous stresses, and interfacial tension. Not surprisingly these dimples were unexplained by his simple theoretical model. However, in a later paper,13 he offered a numerical analysis that predicted the observed dimple formation by assuming a non-uniform film thickness.
Over the years, various other researchers have contributed to the understanding of drainage from a curved surface: Jones and Wilson14 employed matched asymptotic expansions to predict the shape of the free interface of the thin liquid film sandwiched underneath a translating solid sphere; Smith and Van De Ven15 considered the long time stages of film drainage; Leal and coworkers16 considered the possibility that a solid sphere might “break through” the fluid interface and drag a long tail of liquid behind its wake; and more recently, Dietrich et al.17 offered recent experimental results for conditions where impacting solid spheres drag long tails, adding further physical insight into the complex interfacial phenomenon involved in drainage from curved surfaces.
In addition to the drainage of liquid films sandwiched between solid spheres and free interfaces, researchers have investigated the case of advancing drops and bubbles as these problems are linked to important questions concerning emulsion and foam stability. In the literature, there are numerous studies on film drainage associated with advancing droplets,4,18–21 as well as advancing bubbles.6,22,23 Chan et al.24 have compiled a critical review covering literature up to 2010, on film drainage associated with advancing drops and bubbles.
However, the problem of drainage in the presence of rheologically complex fluid–fluid interfaces has received scant attention. Park25 considered the problem of dip coating in the presence of insoluble surfactants. In his analysis, Park models the process of Langmuir–Blodgett deposition, where a planar substrate is withdrawn through a layer of insoluble surfactant that is initially deposited on a liquid interface (normally water). The associated coating flow is the classic Landau–Levich–Derjaguin (LLD) dip-coating process,26,27 which was originally developed for a Newtonian liquid in the absence of surfactants. Park does not explicitly incorporate interfacial shear rheology into his model but rather employs a convection–diffusion equation for surfactant concentration at the interface, which leads to a prediction of Marangoni interfacial flows. An important outcome of Park's analysis is that the layer of the coating liquid is thickened in the presence of insoluble surfactants. More recently, Scheid et al.28 improved on this analysis, but in the limit where Marangoni stresses are absent and where the surfactant layer is characterized by a surface viscosity. Those authors also demonstrated that the coating layer thickness increases with the interfacial viscosity of the surfactant layer. A complete review of the literature on drainage in the presence of rheologically active species at the interface has been recently compiled by Langevin.29
This work is aimed at understanding drainage from a curved surface that approaches the air–liquid interface in the presence of viscoelastic, insoluble monolayers and multilayers. Unlike the Landau–Levich–Derjaguin coating problem, where steady state profiles can be assumed, drainage from a spherical cap is inherently transient, which poses an additional layer of complexity. With this background, we first discuss the theoretical description using a model that describes the thinning of a film coated with an insoluble but Newtonian lipid layer. We compare the results of our model with drainage experiments on films coated with dipalmitoylphosphatidylcholine (DPPC) and meibomian lipids, which are known to be viscoelastic.30–32 Finally, a discussion on the consequences of surface rheology on film drainage is presented with some ideas for future work.
2 Theoretical description
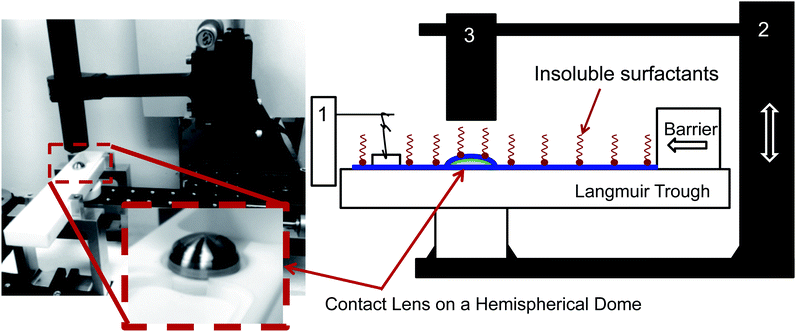
Consider a hemispherical dome that is raised through a bath of liquid resulting in the entrainment of a liquid film of thickness h(θ, t), which is shrouded by an insoluble monolayer (see Fig. 1). The surface of the hemispherical dome is covered with a hydrogel (soft contact lens). By design, our experimental platform enables the analysis of osmotic pressure flow through the hydrogel, which is worth considering and will be addressed in a future publication. However, our focus in this current work is on the possible influence of the viscoelastic monolayer on drainage atop this hydrogel. Consequently, we assume that the lower boundary of the porous layer (lens) is impermeable and stationary.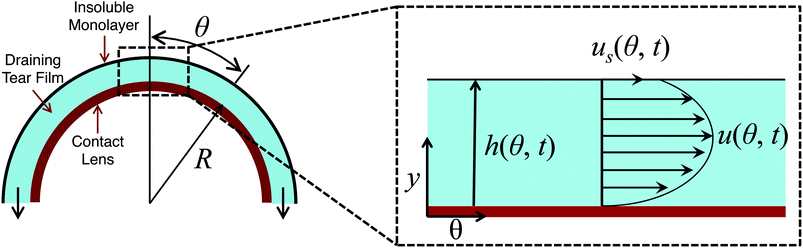 | ||
| Fig. 1 Schematic showing the problem modeled using eqn (8) where a film of thickness h(θ, t) is drained off a hemispherical dome of radius R. The inset shows the details of the flow at the apex of the dome. | ||
Our theory is based on the following five conditions.
(1) The draining flow at the surface of the lens (r = R), is axisymmetric (i.e., all the quantities are independent of the azimuthal coordinate).
(2) The draining liquid layer is thin compared with the dome radius, i.e., the aspect ratio is small, h0/R ∼ 10−3, which enables the application of lubrication theory (h0 is the initial film thickness at θ = 0).
(3) The Bond number, Bo = ρgR3/(γh0) ∼ 104, is large, so that the effects of surface tension can be neglected during drainage flow. The surface tension of the layer is γ, and ρ is the liquid's density.
(4) Marangoni stresses are neglected in our simple model. Justification for this assumption, based on the relative Gibbs elasticities of the insoluble surfactants reported in this work, is presented in the Discussion section.
(5) The insoluble surfactant layer is characterized by a constant surface shear viscosity (μs).
In the lubrication limit, the equation of motion in the aqueous layer is
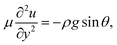 | (1) |
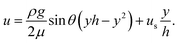 | (2) |
This result is then combined with the following equation of mass conservation:
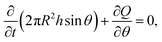 | (3) |
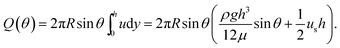 | (4) |
Introducing the dimensionless variables, H = h/h0, τ = tρgh02/(μR), and Us = usμ/(ρgh02), eqn (3) results in the following dimensionless evolution equation,
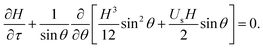 | (5) |
It is left to specify the interfacial stress balance from which the surface velocity field, us, can be evaluated. In general, this requires a balance of interfacial stresses with tractions exerted on the interface by the bulk fluid. Assuming the interface is Newtonian and only characterized by a surface shear viscosity, us, this is given by the tangential stress balance,
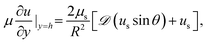 | (6) |
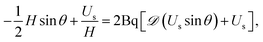 | (7) |
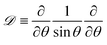 and Bq = μsh0/(μR2) is a modified Boussinesq number. This dimensionless group gauges the relative strength of interfacial stress to bulk stresses. In the asymptotic limit that Bq = 0, we have the simple case of an air–liquid interface that amounts to forcing gradients in the subphase velocity to be zero at the interface and is equivalent to the no-stress condition on the surface. On the other hand, as Bq → ∞, the interface resists lateral deformation (tangentially immobile), and this leads to a no-slip boundary condition at the interface. Intermediate values of the Boussinesq number (0 < Bq < ∞) produce drainage dynamics between the limiting cases of a zero stress and no-slip condition at the free surface.
and Bq = μsh0/(μR2) is a modified Boussinesq number. This dimensionless group gauges the relative strength of interfacial stress to bulk stresses. In the asymptotic limit that Bq = 0, we have the simple case of an air–liquid interface that amounts to forcing gradients in the subphase velocity to be zero at the interface and is equivalent to the no-stress condition on the surface. On the other hand, as Bq → ∞, the interface resists lateral deformation (tangentially immobile), and this leads to a no-slip boundary condition at the interface. Intermediate values of the Boussinesq number (0 < Bq < ∞) produce drainage dynamics between the limiting cases of a zero stress and no-slip condition at the free surface.
The solutions of the film drainage problem for the limiting cases of either a zero stress condition or the no-slip condition at the free surface are easily obtained and that analysis is not elaborated here. The final solutions for the film thickness at the apex of a hemispherical dome H(θ = 0, τ) in these two limits are of the form
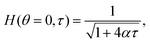 | (8) |
Predictions of the dimensionless film thickness as a function of dimensionless time are shown in Fig. 2 for several values of the Boussinesq number. Shown in this figure are numerical solutions to eqn (5) and (7) along with fits of those numerical predictions to eqn (8) with α used as a fitting parameter. As expected, when Bq = 0, the zero stress condition yielding α = 1/3 is reproduced. Likewise, as Bq → ∞ (the values Bq = 100, 1000 in the figure), the expected response for a tangentially immobile surface (α = 1/12) is reproduced. Interestingly, when intermediate values of Bq are chosen, the simple square-root dependence of eqn (8) can be used successfully to fit the numerical results.
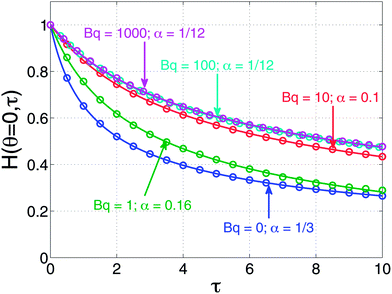 | ||
| Fig. 2 Predictions of dimensionless apex film thickness as a function of dimensionless time by simultaneously solving eqn (5) and (7). The numerical solutions are shown as open symbols. Also plotted are solid curves that are the fits to the numerical solutions using eqn (8) with α as a fitting parameter. | ||
It must be emphasized that the initial film thickness captured at the apex, h0, is simply specified and is not a prediction of this simple model. As the experimental results will reveal, this captured thickness is a strong function of interfacial rheology and its prediction remains an important, unsolved problem.
3 Experimental section
3.1 Materials
Bovine meibum is a complex mixture of waxy esters, cholesterol esters, polar lipids and fatty acids. Unlike DPPC, the viscoelastic properties of meibum will vary slightly from source to source. We have therefore carefully measured the viscoelastic properties of the meibum samples used in this study. Furthermore, an appreciation of how this viscoelastic material influences drainage was essential for one of the central applications of these studies, which concerns the stability of the tear film.
3.2 Interfacial rheology
An interfacial shear rheometer (KSV NIMA Ltd., Helsinki, Finland) was used to measure the interfacial shear rheology of the insoluble materials.34 A detailed analysis of the device is available elsewhere.35,36 The protocol that was followed to make these measurements is described in detail in Leiske et al.30 Briefly, insoluble materials dissolved in chloroform were spread droplet wise on a clean water subphase (Milli-Q) using a clean Hamilton syringe. Chloroform was allowed to evaporate for 15 minutes, and the interface was compressed using symmetric teflon barriers at 1.5 cm2 min−1. Dynamic interfacial moduli of the insoluble surfactants were measured by imposing interfacial, oscillating strains. Strain amplitudes of 0.029 and 0.0174 were used for DPPC and meibum, respectively, which fall within the linear viscoelastic regimes of the respective materials. The data was measured at a frequency of 1 Hz.3.3 Film thickness measurements
The aqueous film thickness measurements were made using a Filmetrics F70 thin-film measurement system (Filmetrics, Inc.) with a High-Brightness White LED light source over a wavelength of 400–720 nm. The incident light was reflected normally at the apex of the hemispherical interface. The working distance was 3 mm and the spot size was 10 μm. Due to the similar refractive indices of the contact lens (1.42) and the aqueous layer (1.33), the interference data was fit to a single-layer model to obtain the combined thickness of the contact lens and the aqueous film, with a combined refractive index (1.42) chosen to accurately reproduce the known thickness of the contact lens. The possible error on the thickness measurements of the aqueous film is less than 10%. As the aqueous film drained, the thickness measurements as a function of time would monotonically decay to a constant value, which represents the thickness of the contact lens. This thickness was then subtracted from the measurements to obtain the actual thickness of the draining aqueous film. The average thickness at the center of the lens using our measurement technique is 100 ± 10 μm, which is in good agreement with the values reported by the manufacturer.373.4 Drainage apparatus
The instrument consists of several main elements (Fig. 3). A Teflon mini-Langmuir trough is fixed onto a stationary support structure. This trough allows one to spread an insoluble layer of material (DPPC, meibum) on top of an aqueous subphase at a controlled surface pressure. This control is important since it is well established that the interfacial rheology is a strong function of surface pressure. For most insoluble amphiphiles, increasing the surface pressure will increase the surface viscosity and surface moduli.30,31 The surface pressure is monitored using a paper Wilhelmy balance connected to a surface pressure sensor (KSV NIMA Ltd., Helsinki, Finland). Surrounding the trough is a moving platform that can elevate a hemispherical surface (supporting a contact lens) from an initial position slightly beneath the interface and lift it at computer-controlled speeds (10 mm s−1). The curvature of the hemispherical surface can potentially diminish the surface pressure due to dilatational effects – the consequences of which will be discussed in the Results section. However, the change in surface area as a result of elevation of the dome is small (15%) and this minimizes the possible influence of Marangoni flows and dilatational stresses. Additionally, the surface pressure is continuously monitored during the experiment and only a small deviation of ±0.5 mN m−1 is observed during the duration of the experiment. So, the surface pressure remains practically constant during the experiment. The inset photograph on the left side of Fig. 3 shows the lens placed onto a small titanium dome, which has the same base curvature as a commercial silicone hydrogel contact lens. Attached to the moving platform is a high speed interferometer that is focussed on the apex of the lens. The schematic in Fig. 1 shows a contact lens having captured a thin layer of draining fluid. On top of the draining layer, an insoluble lipid layer may have been deposited. Once the elevation motion is commenced, the interferometer begins measuring the thickness of the aqueous layer on top of the lens as a function of time. The top of the lens is located at θ = 0 (Fig. 1).4 Results and discussion
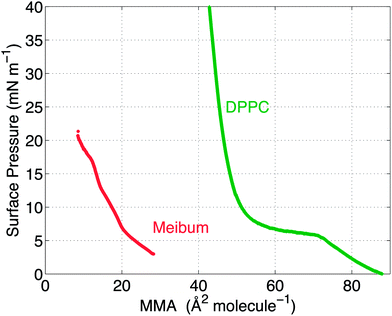
The surface pressure versus mean molecular area (MMA) isotherms for the two insoluble materials are shown in Fig. 4. The isotherm measures the surface pressure of the insoluble layer as a function of decreasing area (proceeding right to left on the horizontal axis). As the layer is compressed, DPPC shows a characteristic transition from a liquid-expanded state to a liquid-condensed state at 6 mN m−1, evidenced by the presence of a plateau in the curve. Upon further compression, DPPC molecules are packed closely together, resulting in a steep rise in the surface pressure. Meibum, on the other hand, does not exhibit any distinctive plateaus or the corresponding phase transitions.Furthermore, from the slopes of the isotherms in Fig. 4, the Gibbs modulus (EGibbs = −∂Π/∂ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A) can be estimated, where A is the mean molecular area and Π is the surface pressure. As shown in Fig. 5, both the insoluble materials exhibit relatively constant Gibbs moduli at surface pressures greater than 10 mN m−1. At 15 mN m−1, EGibbs,DPPC ∼ 100 mN m−1 and is an order higher than EGibbs,meibum ∼ 10 mN m−1.
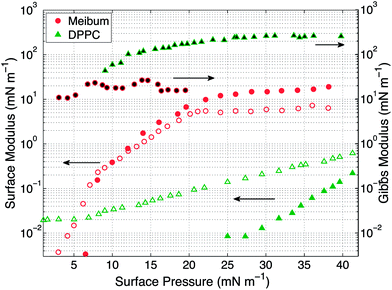
A) can be estimated, where A is the mean molecular area and Π is the surface pressure. As shown in Fig. 5, both the insoluble materials exhibit relatively constant Gibbs moduli at surface pressures greater than 10 mN m−1. At 15 mN m−1, EGibbs,DPPC ∼ 100 mN m−1 and is an order higher than EGibbs,meibum ∼ 10 mN m−1.
The interfacial rheology for the insoluble materials at room temperature is presented in Fig. 5. Over the range of surface pressures accessible to our instrument, the viscous interfacial modulus of DPPC remains greater than its elastic modulus. Additionally, the elastic modulus for DPPC becomes measurable only above 25 mN m−1. Compared with DPPC, meibum exhibits high surface elasticity, with the surface elastic modulus larger than the surface viscous modulus. The surface moduli for meibum increase over four orders of magnitude, from 0.008 mN m−1 to 20 mN m−1. Both the elastic and viscous moduli of meibum are one and two orders higher than DPPC, respectively. It is important to note that even though both the materials demonstrate viscoelastic behavior, DPPC is viscous-dominated, whereas meibum is highly elastic. From these measurements, the surface shear viscosity for DPPC at 15 mN m−1 is 0.005 mN s m−1 and is in good agreement with values published in the literature.32 Also, at surface pressures below 20 mN m−1, the surface rheology of DPPC is independent of frequency.38 It is important to note that over the range of surface pressures from 15 to 20 mN m−1 (the range explored in the drainage experiments), the interfacial moduli of the two insoluble surfactants increase more dramatically than do the Gibbs moduli.
The results of several drainage experiments are shown in Fig. 6 as a function of dimensionless time, as defined previously. Four curves are shown: the blue (diamond) symbols are for a layer of water in the absence of an insoluble layer, the green (squares) and teal (triangle) symbols are the result of depositing DPPC on top of the water at surface pressures of 15 mN m−1 and 20 mN m−1, respectively, and lastly, the red (circles) for meibum on top of water at a surface pressure of 15 mN m−1.
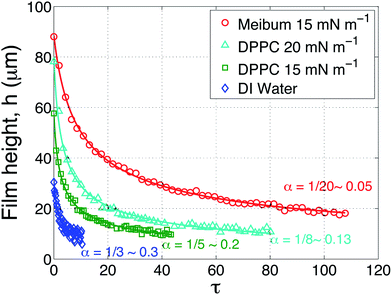 | ||
| Fig. 6 Aqueous layer thickness as a function of dimensionless time above a AirOptix Aqua (Lotrafilcon B) lens. Curves are shown for an uncoated layer of deionized water (diamonds), a layer of deionized water coated with DPPC at 15 mN m−1 (squares) and 20 mN m−1 (triangles), and bovine meibum at 15 mN m−1 (circles). The solid lines are fits to eqn (8) using α as a fitting parameter. | ||
As shown in Fig. 5, the interfacial viscoelasticity of DPPC monotonically increases with surface pressure. Increasing the surface pressure of DPPC produces two noticeable effects, both of which are beneficial to the retention of aqueous films above the lens: (1) the presence of viscoelastic layers allows the capture of much thicker aqueous films; (2) the time scale for thinning of the layers is increased substantially with the presence of the insoluble layers. In the same figure, the drainage dynamics of bovine meibum are compared to those of DPPC at the surface pressure of 15 mN m−1. The meibum layer is observed to capture a substantially thicker film of water and the time taken for drainage is also much longer.
The solid curves that accompany the data in Fig. 6 are fits to eqn (8) using α as a fitting parameter. This simple square root law fits the data remarkably well. The data for an uncoated film of water (blue) is well-fit using α = 1/3, which is the value expected for a stress-free air surface. The surface pressure values for water were 0 ± 0.5 mN m−1. The possibility that there is some minor contamination in the water cannot be ruled out, although this effect is minor.
The values of α required to fit the DPPC drainage data depend on the surface pressure of the surfactant. At a surface pressure of 15 mN m−1 (the green symbols), α = 0.2 fits the data quite well. As the surface pressure is increased to 20 mN m−1 (the teal colored symbols) and the surface viscous modulus increases by approximately 50%, the data is best fit using a value of α = 0.13. Thus, increasing the viscoelasticity of DPPC requires a progressively smaller value of α. The data in Fig. 6 also reveal that the captured, initial film thickness increases substantially when the surface pressure of DPPC is increased.
The value used to fit the bovine meibum coated surface (red), however, is α = 0.05, which is substantially less that the value of α = 1/12 ∼ 0.083 that is appropriate for an infinite Boussinesq number and a no-slip air surface. This suggests that the highly viscoelastic response of bovine meibum presents qualitatively different dynamical responses and these are explored below.
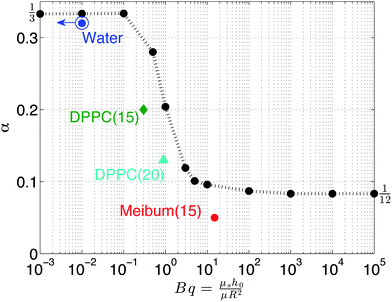
The parameter α provides a convenient means of comparing experiment and theory and Fig. 7 provides such a comparison. From the numerical results (black), it is observed that, as the Boussinesq number increases, α decreases from 1/3 to 1/12 with a strong transition when α = 1 These results indicate the dampening of drainage dynamics due to pure surface shear viscosity effects. The best empirical fit in the transition region is α ∼ Bq−2/5. On the same plot, experimental values are shown as well. The drainage of water is fit using a value of α = 1/3 and Bq → 0. The experimental Boussinesq values for DPPC are 0.1 and 0.9 at surface pressures of 15 mN m−1 and 20 mN m−1, respectively. These experimental values are on the same order of magnitude as the corresponding numerical predictions, however, the actual values are slightly smaller, which may be due to the assumption of a simple Newtonian interface to model these viscoelastic materials. For meibum, a high Boussinesq value (15) is observed but the α value is smaller than 1/12. Thus, the experimental values are in good, qualitative agreement with the model and match the transition in the drainage dynamics at a critical Boussinesq number on the order of unity. A quantitative comparison, however, would require the use of more sophisticated interfacial rheological constitutive models, which is not within the scope of the present paper.
Two possible sources for the slower-than-expected drainage are both linked to the deformation of the interface as the hemispherical domed substrate is elevated. As the hemisphere is pushed upward, it will stretch the interface, leading to two possible outcomes: (1) elongational stretching of the viscoelastic meibum interface may result in a recoil of this interface and a subsequent back flow at the surface, which will slow down drainage; (2) stretching of the interface could result in a polar gradient in the surfactant from the apex of the dome that can induce an upward Marangoni flow that will also slow down drainage.
To quantify the existence of back flow kinematics retarding drainage, surface flow in meibum coated films was monitored using a CCD camera, looking normally down on to the curved draining surface. At a moderately high surface pressure of 15 mN m−1, meibum forms a waxy viscoelastic skin at the air–water interface which is translucent and is highly textured. These textures have been imaged in past studies using Brewster Angle Microscopy (BAM),39 and provide a means of tracking the time dependent position of identifiable features in the insoluble meibum layer. Using this imaging system, the displacement vectors joining the initial locations of microstructures at 4 s and their locations after 44 s of drainage are shown in Fig. 8. The result is a family of displacement vectors that clearly indicate a non-zero, upward flow towards the apex is, which is against the direction of gravity-driven flow.
The presence of a non-zero upward surface flow qualitatively explains the slower dynamical response for meibum. We suspect that this upward flow is a consequence of the surface shear elasticity of meibum and not due to Marangoni flows or dilatational rheological effects. In fact, if the upward flow was a manifestation of surface tension gradients, then this flow would be greater in DPPC, since it has a larger Gibbs modulus than meibum. However, this is clearly not the case as meibum retards drainage more substantially than DPPC. Furthermore, the Gibbs modulus for DPPC is largely independent of surface pressure whereas the drainage dynamics are a strong function of this variable.
Our experimental results indicate that the presence of an insoluble surfactant layer has a two-fold effect on film drainage: (1) the initial capture thickness is higher with increases in surface viscosity and even more pronounced in the presence of surface elasticity, and (2) the film drainage rates are retarded as the surface viscoelasticity is increased.
Interfacial viscoelasticity plays a major role in foam stability and many authors have investigated the effect of both the surface shear and dilatational viscosity, on drainage of thin films.2,5,40–43 These studies have shown that increasing the interfacial shear viscosity has a retarding effect on the film thinning rate. However, most of these investigations treat the interface as either rigid plane or a Newtonian interface. Tambe and Sharma,5 were the first to offer a numerical analysis that attributed viscoelastic properties to the interface bounding plane-parallel films. Using a simple Maxwell constitutive model for their interface, they revealed that the rate of drainage was strongly influenced by the surface rheology of the bounding layer. Moreover, they found that the retarding influence of surface viscosity was more pronounced if the interface possessed finite elasticity. The predictions of these authors are in good qualitative agreement with our experimental findings.
It is important to underscore that these enhancements in film stability are a consequence of enhanced interfacial rheology as surface pressure is increased and not a lowering of surface tension. This was established with experiments using simple, soluble surfactants (SDS) at a concentration of 0.003 mol L−1, where it was found that drainage was not retarded (data not shown). Thus, this work eliminates the complication of bulk-to-interface diffusion since we employ insoluble surfactants. An important implication of our findings is to suggest that the interfacial rheology of meibomian lipids on our eyes may play an extremely important role in enhancing tear film stability and reduced drainage on our eyes.
5 Conclusions
We have shown that increased film stability during drainage on a curved surface can occur as a consequence of enhanced surface rheology. Specifically, we find that insoluble surfactants such as DPPC with finite interfacial viscosity stabilize drainage. Moreover, the rate of drainage decreases as the surface pressure of the surfactant layer is increased. Importantly, the retarding influence is most pronounced when the insoluble surfactant has significant elasticity, as in the case of meibum. We present a simple theoretical model which enables qualitative comparison of the influence of surface viscoelasticity on drainage from curved surfaces.Acknowledgements
The authors would like to thank Danielle L. Leiske and Liat Rosenfeld for their help in the interfacial rheology experiments, Colin F. Cerretani for assistance in acquiring the meibomian lipids and Joseph M. Barakat for a critical reading of the manuscript. William Sin (Filmetrics, Inc.) is acknowledged for his support and guidance in setting up the interferometer. Finally, we are indebted to Karlheinz Merkle and John Kirk at the Varian Physics Machine Shop (Stanford University) for their help in building our experimental setup.References
- O. Reynolds, Proc. R. Soc. London, 1886, 40, 191–203 CrossRef.
- J. C. Lee and T. D. Hodgson, Chem. Eng. Sci., 1968, 23, 1375–1397 CrossRef CAS.
- Y. T. Hu, D. J. Pine and L. G. Leal, Phys. Fluids, 2000, 12, 484–489 CrossRef CAS PubMed.
- D. G. A. L. Aarts and H. N. W. Lekkerkerker, J. Fluid Mech., 2008, 606, 275–294 CAS.
- D. E. Tambe and M. M. Sharma, J. Colloid Interface Sci., 1991, 147, 137–151 CrossRef CAS.
- G. Debrégeas, P. De Gennes and F. Brochard-Wyart, Science, 1998, 279, 1704–1707 CrossRef.
- A. Sonin, A. Bonfillon and D. Langevin, Phys. Rev. Lett., 1993, 71, 2342–2345 CrossRef CAS.
- M. Durand and D. Langevin, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 7, 35–44 CrossRef CAS PubMed.
- H. Wong, I. Fatt and C. Radke, J. Colloid Interface Sci., 1996, 184, 44–51 CrossRef CAS.
- K. Nong and D. M. Anderson, SIAM J. Appl. Math., 2010, 70, 2771–2795 CrossRef.
- R. J. Braun and A. D. Fitt, Math. Med. Biol., 2003, 20, 1–28 CrossRef CAS PubMed.
- S. Hartland, J. Colloid Interface Sci., 1968, 26, 383–394 CrossRef CAS.
- S. Hartland, Chem. Eng. J., 1970, 1, 67–75 CrossRef CAS.
- A. F. Jones and S. Wilson, J. Fluid Mech., 1978, 87(2), 263–288 CrossRef CAS.
- P. G. Smith and T. Van De Ven, J. Colloid Interface Sci., 1984, 100, 456–464 CrossRef CAS.
- A. S. Geller, S. H. Lee and L. G. Leal, J. Fluid Mech., 1986, 169, 27–69 CrossRef CAS.
- N. Dietrich, S. Poncin and H. Z. Li, Exp. Fluids, 2011, 50, 1293–1303 CrossRef.
- J. M. Frostad, J. Walter and L. G. Leal, Phys. Fluids, 2013, 25, 052108 CrossRef PubMed.
- K. D. Danov, S. D. Stoyanov, N. K. Vitanov and I. B. Ivanov, J. Colloid Interface Sci., 2012, 368, 342–355 CrossRef CAS PubMed.
- D. G. A. L. Aarts, H. N. W. Lekkerkerker, H. Guo, G. H. Wegdam and D. Bonn, Phys. Rev. Lett., 2005, 95, 164503 CrossRef.
- Z. Zapryanov, A. K. Malhotra, N. Aderangi and D. T. Wasan, Int. J. Multiphase Flow, 1983, 9, 105–129 CrossRef CAS.
- H. Kočárková, F. Rouyer and F. Pigeonneau, Phys. Fluids, 2013, 25, 022105 CrossRef PubMed.
- F. Pigeonneau and A. Sellier, Phys. Fluids, 2011, 23, 092102 CrossRef PubMed.
- D. Y. Chan, E. Klaseboer and R. Manica, Soft Matter, 2011, 7, 2235–2264 RSC.
- C.-W. Park, J. Colloid Interface Sci., 1991, 146, 382–394 CrossRef CAS.
- V. G. Levich, Physicochemical Hydrodynamics, Prentice-Hall, 1962 Search PubMed.
- L. Landau and B. Levich, Acta Physicochim. URSS, 1942, 17, 42 Search PubMed.
- B. Scheid, J. Delacotte, B. Dollet, E. Rio, F. Restagno, E. A. van Nierop, I. Cantat, D. Langevin and H. A. Stone, Europhys. Lett., 2010, 90, 24002 CrossRef.
- D. Langevin, Annu. Rev. Fluid Mech., 2014, 46, 47–65 CrossRef.
- D. Leiske, C. Monteux, M. Senchyna, H. Ketelson and G. Fuller, Soft Matter, 2011, 7, 7747–7753 RSC.
- L. Rosenfeld and G. G. Fuller, Langmuir, 2012, 28, 14238–14244 CrossRef CAS PubMed.
- E. Hermans and J. Vermant, Soft Matter, 2014, 10, 175–186 RSC.
- N. Nicolaides, J. K. Kaitaranta, T. N. Rawdah, J. I. Macy, F. M. Boswell and R. E. Smith, Invest. Ophthalmol. Visual Sci., 1981, 20, 522–536 CAS.
- C. Brooks, G. Fuller, C. Frank and C. Robertson, Langmuir, 1999, 15, 2450–2459 CrossRef CAS.
- T. Verwijlen, P. Moldenaers, H. A. Stone and J. Vermant, Langmuir, 2011, 27, 9345–9358 CrossRef CAS PubMed.
- S. Reynaert, C. Brooks, P. Moldenaers, J. Vermant and G. Fuller, J. Rheol., 2008, 52, 261–285 CrossRef CAS.
- D. Luensmann, F. Zhang, L. Subbaraman, H. Sheardown and L. Jones, Curr. Eye Res., 2009, 34, 683–697 CrossRef CAS PubMed.
- K. Kim, S. Q. Choi, J. A. Zasadzinski and T. M. Squires, Soft Matter, 2011, 7, 7782–7789 RSC.
- D. Leiske, S. Raju, H. Ketelson, T. Millar and G. Fuller, Exp. Eye Res., 2010, 90, 598–604 CrossRef CAS PubMed.
- W. Johannes and S. Whitaker, J. Phys. Chem., 1965, 69, 1471–1477 CrossRef CAS.
- A. D. Barber and S. Hartland, Can. J. Chem. Eng., 1976, 54, 279–284 CrossRef CAS.
- I. B. Ivanov and D. S. Dimitrov, Colloid Polym. Sci., 1976, 254, 450 Search PubMed.
- D. Langevin, Adv. Colloid Interface Sci., 2000, 88, 209–222 CrossRef CAS.
Footnote |
| † The authors dedicate this paper to Professor Dominique Langevin, whose illustrious career has been an important influence in our work. |
| This journal is © The Royal Society of Chemistry 2014 |