 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mathematically modelling competitive ion absorption in a polymer matrix
Stanley J.
Miklavcic
*ab,
Magnus
Nydén
c,
Johan B.
Lindén
c and
Jordan
Schulz
a
aPhenomics and Bioinformatics Research Centre, University of South Australia, Mawson Lakes, SA 5095, Australia. E-mail: stan.miklavcic@unisa.edu.au; Fax: +61 8 830 25785; Tel: +61 8 830 23788
bAustralian Centre for Plant Functional Genomics, Hartley Grove, Urrbrae, SA 5064, Australia
cIan Wark Research Institute, University of South Australia, Mawson Lakes, SA 5095, Australia
First published on 3rd November 2014
Abstract
A recent publication [Lindén et al., RSC Adv., 2014, 4, 25063–25066] describing a material with extreme efficiency and selectivity for adsorbing copper opens up the possibility of large scale purification technologies and new materials for prevention of biological growth, both in bulk and on surfaces. On the molecular scale, the material’s efficiency and selectivity depends on competitive metal ion diffusion into a nanometer thin polymer film and on competitive binding of metal ions to specific ligand sites. We present and explore two reaction-diffusion models describing the detailed transport and competitive absorption of metal ions in the polymer matrix studied in [Lindén et al., RSC Adv., 2014, 4, 25063–25066]. The diffusive transport of the ions into an interactive, porous polymer layer of finite thickness, supported by an impermeable substrate and in contact with an infinite electrolyte reservoir, is governed by forced diffusion equations, while metal ion binding is modelled by a set of coupled reaction equations. The qualitative behavior observed in experiments can be reproduced and explained in terms of a combination of (a) differing ion diffusive rates and, effectively, (b) an ion exchange process that is superimposed on independent binding processes. The latter’s origin is due to conformational changes taking place in the polymer structure in response to the binding of one of the species. The results of simulations under a diverse set of parameter conditions are discussed in relation to experimental observations.
1 Introduction
Water contaminated with toxic metal ions is often a result of industrial processes2 but also occurs through antifouling paints leaching metal-based biocides.3,4 Increased awareness of the toxic effects and economic aspects of reuse of water, sludge and sediment and recovery of metal waste are driving forces for research in new and improved metal-removal technologies2,5. A wide range of techniques has been studied over past decades, including chemical precipitation, ion-exchange, adsorption, membrane filtration, coagulation–flocculation, flotation and electrochemical methods.6Adsorption and ion-exchange technologies have proven to be effective methods for the removal of various metals from aqueous solutions.6,7 In both methods a selectivity for specific metal ions is attributed to functional groups on either the natural or chemically modified surface of the material.6–8
The separation process of the metal ions from the aqueous phase is typically described as adsorption onto the surface of the solid phase of either the adsorbent9 or the ion-exchange resin.2 Wan Ngah et al.9 evaluated the adsorption capacities and rates of Cu(II) ions onto chitosan and chitosan blended with poly(vinyl alcohol) (PVA). They found that the Langmuir model correlated well with the adsorption isothermal data and that the kinetic experimental data correlated well with the second-order kinetic model which would indicate the rate-limiting step as chemical sorption. Beatty et al.2 also analysed the performance of their ion-exchange resin using a Langmuir isotherm and second-order kinetic model. They described their slower rate of adsorption in comparison to a commercially available resin as being dependant on a longer ion diffusion path into the polymer layer on the silica support material.
Although adsorption isotherms such as the Langmuir isotherm play an important role in the search for an ideal metal ion adsorbent, they might face limitations when the metal ion uptake is not solely adsorption.10 In one study of chitosan and its glutaraldehyde cross-linked derivative it was concluded that the metal ion uptake mechanism was absorption within the polymers rather than adsorption on the polymer surface.11 This indicates the importance of investigating the possibility of considering the metal ion uptake of a pure polymer sorbent or polymer modified sorbent as an absorption process. Furthermore, the effect of conformational changes within polymers could also play an important role in the metal uptake mechanism.12,13
We address the following problem: to model the temporal and spatial development of competitive absorption of metal ions within a polymer matrix. The example system we have in mind to model is a polyethyleneimine (PEI) layer adsorbed onto an impermeable planar surface and exposed to a bulk electrolyte mixture. Recently, Lindén and coworkers1 experimented with a surface-bound, cross-linked PEI layer exposed to either an artificial sea water solution or actual sea water. They found that the PEI layer exhibited preferential absorption for certain metal cations, namely copper (Cu2+), zinc (Zn2+) and cadmium (Cd2+), in that order of preference. The competitive absorption of metal ions into the PEI layer was performed at an equimolar concentration of about 3 μM,1 which is roughly 200 times higher than the levels at which the ions are present in sea water.14,15 However, this concentration is considerably lower than that employed in other metal ion uptake studies involving PEI.2,5,16–18
Linden1 has recently shown that polyethyleneimine (PEI) is extremely effective and selective to copper in salt and fresh water and that it self-adsorbs into a thin film on porous silica particles. The latter allows for very large surface area exposure. Furthermore, the cross-linked polymer is mechanically and chemically stable in a wide pH range. Taken together, the material properties of PEI and porous silica particles allow for large scale technologies for purifying water from copper as well as preventing biological growth at surfaces and in bulk. Given the need for copper purification and the large scale potential of the PEI/silica particle system we aim to increase our understanding of the molecular-scale processes by addressing the following problem in more detail: to model the temporal and spatial development of competitive absorption and chemical binding of metal ions within a polymer matrix.
That PEI can take up metal ions through chemical binding is known.19–21 Rivas et al.,20 working with PEI tetramers (TETA) in solution, showed that the TETA molecules could take up copper, and Kobayashi with coworkers in ref. 19, who also worked in solution, found that the branched structure of PEI gave a more favourable complexation than the linear structure. Metal ion uptake studies have also been reported for cases where PEI was attached to the surface of a support material.2,5,16–18 However, what was not explored prior to the work of Lindén et al.1 was the competitive absorption behavior of PEI in the presence of a solution mixture, the predominant results of which are shown in Fig. 1. In particular, Lindén et al.1 found that the cross-linked PEI matrix displayed an anomalous preference for copper in the following sense. At a very early stage post exposure, zinc ions, and to a lesser extent cadmium ions, were rapidly absorbed forming complexes with specific sites in the matrix. Later, increasing amounts of copper complexes were detected. However, rather than each metal ion complex increasing in number monotonically with prolonged exposure to a bulk electrolyte reservoir, it was found that the copper ion complexes increased significantly, reaching a steady state plateau value, while the zinc and cadmium complexes reached a maximum amount and then decreased to levels below instrument sensitivity. Effectively, the quantities of bound zinc and cadmium approached zero at steady state. It is this entire time series of phenomena that we seek to address in this paper. Reasons for the findings were postulated, as were the possible applications of the phenomena, such as the extraction of minerals from seawater (specifically, the extraction of copper from the oceans), the refinement and purification of industry waste water, as well as the more community-based treatment of recycled water.1
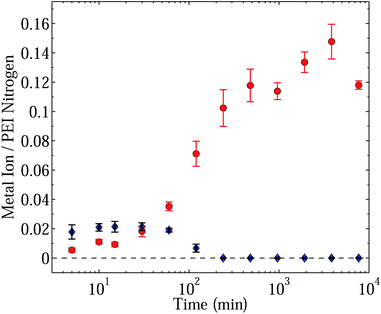 | ||
| Fig. 1 Graph showing metal ion uptake over time in terms of a metal ion to (PEI) nitrogen ratio as a function of time after immersion in artificial seawater (pH 8). Blue diamonds denote Zn/N ratios, while red circles denote Cu/N ratios. In this experiment 12 different metal ions were present at the same time: Al3+, Cd2+, Co2+, Cr3+, Cu2+, Fe2+, Mn2+, Mo6+, Ni2+, Pb2+, V3+, Zn2+: [Men+] = 3 μM ([Cu2+] = 200 ppb). Data shown in this figure was adapted from ref. 1. | ||
In explanation for the two phases of uptake, Lindén et al.1 stated that “the binding kinetics were faster for zinc but with copper binding being thermodynamically favored”. On the face of it, this would seem a natural conclusion to draw. However, the physical system proves to be more complex. In this paper we present and investigate quantitatively two alternate scenarios which explain the competitive behavior, at least qualitatively. In the first scenario we postulate that the differential binding phenomenon is simply not due to faster binding kinetics on the part of Zn2+ and a steady state or thermodynamic preference toward Cu2+ binding, but rather to a difference in the diffusive properties of the two ions in conjunction with an ion exchange reaction. In the second scenario, in recognition of the findings of Nurchi et al.,13 who argued that the binding of Cu2+ induces a conformational change in the matrix structure, we postulate that the competitive binding phenomenon is due to a conjunction of differential diffusion and a conformational change upon Cu2+ binding that both precludes the binding of Zn2+ ions as well as ejecting already bound Zn2+ in the neighborhood of the copper binding site.
Although the (two) models we introduce and explore below target the aforementioned experimental system directly, it is not unreasonable to anticipate that the models and the simulation results derived from them have applicability in other contexts, notably in biology, dealing, for instance, in ion specific membrane transport.22
The remainder of this paper is organized as follows. In Section 2 we describe the two scenarios hypothesized to explain the findings, as well as introducing other essential particulars of the models. In Section 3, the mathematical descriptions of the physical models are outlined. Here, the key model parameters are introduced. In that section we also outline the numerical solution method followed. Section 4 presents some illustrative example simulations, which explore the important regions of parameter space. We summarize our findings and provide concluding remarks in Section 5.
2 Polymer matrix geometry & kinetic transport mechanisms
In line with the experimental system, we adopt the model of a thin, charged polymer matrix of thickness D that has been adsorbed to an uncharged, solid and impermeable substrate. We assume in the following that D remains a constant and is not responsive to ion uptake (an alternate model approach showing this effect can be found in ref. 23 and 24). We further assume the polymer matrix to be homogeneous and uniformly porous. Moreover, it is homogeneously permeable to mobile ions. We assume the matrix to possess a constant (total) density of binding sites, nPEItot, which are either equally accessible to both binding cations (Scenario I) or are equally divided into a number that are accessible to only Cu2+ (nPEI1,tot) or only Zn2+ (nPEI2,tot) (Scenario II). In either case, the binding sites are assumed to be negatively charged with unit valence (zPEI = zPEI1 = zPEI2 = −1). The adsorbed layer is in contact with a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixed bulk electrolyte comprising Cu2+, Zn2+ and Cl− ions.
1 mixed bulk electrolyte comprising Cu2+, Zn2+ and Cl− ions.
The important processes taking place in this problem include mobile ion diffusion into or out from the polymer matrix, with ions sourced from the electrical double layer adjacent to the polymer matrix. In addition, there are two fundamental chemical binding reactions, one for each of the cations Cu2+ and Zn2+ and their respective binding sites within the matrix. The details of these intrinsic reactions are given in the next section. In Section 4 we show that these effects alone are insufficient to explain the experimental observations. Therefore, in addition to the core binding reactions we invoke a secondary reaction mechanism, which will be explained in Section 3 via two model formulations, that completes the picture and quite convincingly accounts for observed phenomenon. Finally, the outcome of all the binding events (as well as the underlying charged state of the matrix) results in an inhomogeneous distribution of charge that establishes an inhomogeneous electric potential field. The field gradient in turn influences the rate of influx of ions (indeed it influences which ions enter the matrix as well as their diffusion rates).
With respect to the electric field, we envisage that the mobile ions external to the matrix diffuse sufficiently fast that the ionic double layer outside the matrix is always in a state of quasi equilibrium. That is, the ions are sufficiently responsive on the time scale of the processes taking place within the layer that the double layer adjusts immediately in response to changes in the state of polymer charge. At the low values of accumulated charge and low bulk electrolyte concentrations considered, we assume that the electrical double layer outside the matrix is adequately described by the Poisson–Boltzmann model.25,26 We remark that although we will associate differences in ion diffusivities with differences in effective ionic radii (see Section 4), our models do not include any explicit ion size effects, which could not only influence the double layer structure adjacent to the polymer layer at high concentrations,27 but would likely play an influential role in shifting the balance in the competition for absorption sites even at low electrolyte concentrations. We envisage the latter effect to be akin to the site exclusion phenomenon simulated in the hydrated ion model of competitive ion adsorption.28 We reserve for the future the task of considering this effect, whose significance is comparable to and indeed warrants a more accurate description of the polymer structure itself, which is presently unavailable.
3 Governing equations
The charge distribution within the polymer matrix comprises free ions, here denoted by the index i = 1,…,n and bound charges, here denoted by the index j = 1,…,m. As our focus is on the competitive binding of Cu2+ and Zn2+ in a polymer matrix, we restrict attention to determining the distribution of these two ions plus that of a common counterion, Cl−. Thus, n = 3. In this same context, the bound species are PEI−, CuPEI+ and ZnPEI+, as explained below. Thus, m = 3 or 4, as explained below. The charge density is given as,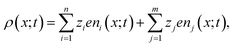 | (1) |
3.1 Competitive binding scenario I: Ion exchange model
To describe the competitive absorption of Cu and Zn ions, we model the ion binding event here assuming a single type of binding site, denoted PEI−. In this case we first identify two binding reactions, one for each of the ions. These reactions involve a mix of free ions and bound charge sites: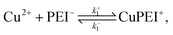 | (2) |
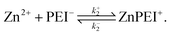 | (3) |
Thus far, these reactions take place explicitly independent of each other and occur at different rates given by
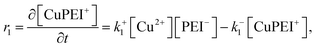 | (4) |
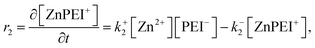 | (5) |
In addition to these binding reactions we include in this scenario the following exchange reaction,
 | (6) |
| r3 = k+3[Cu2+][ZnPEI+] − k−3[Zn2+][CuPEI+]. | (7) |
The rates, r1 and r2, describe the rates of production of CuPEI+ and ZnPEI+, respectively, as well as the consumption of Cu2+ and Zn2+, the latter being the free mobile ions. Given the additional exchange reaction, the rate equations (4) and (5) must be supplemented by the effect of the exchange rate r3:
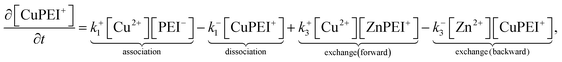 | (8) |
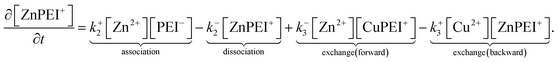 | (9) |
These equations are explicit, ordinary differential equations in time, but are also implicitly functions of position x through the dependencies of the respective concentrations on position. That is, these equations must be solved locally (at x) throughout the polymer matrix.
This binding model must satisfy the conservation condition that the total number of sites remains fixed irrespective of whether there is binding or not. The relevant equation is
| nPEItot = NA10−3[[PEI−] + [CuPEI+] + [ZnPEI+]] = constant. | (10) |
3.2 Competitive binding scenario II: Polymer relaxation model
We formulate this model situation by assuming, at least initially, that there are two types of binding sites (labelled with subscripts 1 and 2), one for each of the divalent metal ions, Cu2+ and Zn2+. In addition to the standard binding reaction equations, we presume here that site type 2 can exist in one of two binding states, an active binding state, labelled {2, a}, and an inactive binding state, labelled {2, ia}. The fundamental reaction equations are then slightly modified versions of eqn (2) and (3),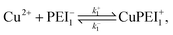 | (11) |
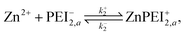 | (12) |
A point of major differentiation between this scenario and that of Scenario I is the assumption that the binding of Cu2+ to its specific binding site induces a local conformational change in the polymer matrix which converts an active type-2 binding site to its inactive binding state. This conversion, which may be structural or chemical, either prevents the binding of Zn2+ to its specific binding site or induces an unbinding of an existing bound Zn2+. For the latter possibility, we imagine the two-step reaction process
 | (13) |
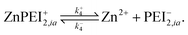 | (14) |
Once in the inactive state, the forward reaction in eqn (14) is considered to be sufficiently rapid as to be a spontaneous event. Hence, one would expect k+4 ≫ k−4. Indeed, assuming the limiting case of complete forward reaction, we can summarize eqn (13) and (14) in one reaction equation,
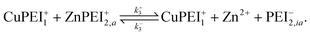 | (15) |
The rate of production of free Zn2+ (assuming complete dissociation) is then governed by the rate at which reaction (15) proceeds, which is given by
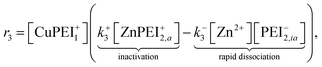 | (16) |
As for the case of converting the state of a vacant type-2 binding site, we invoke the model reaction
 | (17) |
 | (18) |
In all probability, the latter rate constants should satisfy the inequality k+5 ≫ k−5, implying that the reverse reaction all but never takes place. Note also that based on our intuitive understanding of the conformational change process, we expect the k+5 value to be different, but perhaps not significantly different, from the k+3 value.
As in the case of the single site binding model, this two-site binding model must satisfy conservation conditions: the total number of sites remains fixed irrespective of whether there is binding or not. The relevant equations are
| nPEI1,tot = NA10−3[[PEI−1] + [CuPEI+1]] = constant, | (19) |
| nPEI2,tot = NA10−3[[PEI−2,ia] + [PEI−2,a] + [ZnPEI+2,a] + [ZnPEI+2,ia] = constant. | (20) |
It is important to point out that Scenario I and II are different in two major respects. Firstly, Scenario I describes a process of physical exchange of Cu2+ for Zn2+, with no alteration of the polymer matrix, while Scenario II describes a conformational reaction within the polymer resulting from the binding of Cu2+. These are quite distinct phenomena. The second point of differentiation is that Scenario I assumes a common type of binding site, equally accessible to both Zn2+ and Cu2+, while Scenario II assumes specific sites for the respective ions. It is not difficult to imaging other scenarios that are intermediate or hybrids of the two cases. However, it is not the purpose of this paper to establish which of these is most applicable to the given experimental system. Our purpose is only to demonstrate that an additional interaction involving the ions (such as described by Scenarios I and II) is necessary to produce behavior reminiscent of the experiments.
3.3 Ion diffusion
The intrusion of ions into the polymer matrix is assumed to take place by means of (forced) diffusion. Exposure of the matrix to an electrolyte solution with ions at a finite bulk concentration and thus a larger chemical potential induces the transport of ions into the polymer layer. The process is largely driven by concentration gradients but also by an electric field gradient arising from the inhomogeneous charge distribution. Three ions are assumed sufficiently mobile to diffuse into the matrix: Cu2+, Zn2+ and Cl−. The rates at which ions diffuse into the matrix are here governed by their intrinsic diffusion constants and their respective ionic conductivities. However, it is well known that diffusion of dissolved molecules is reduced, relative to bulk diffusion, by polymer chains through several mechanisms.29 While it is necessary for a quantitative evaluation with experiments to consider these effects, for the present task of illustrating qualitative behavior, and in the absence of detailed quantitative experimental information about the present system, we shall assume, unless otherwise stated, that the values of the ion diffusion parameters are equal to their bulk values.30 The equations governing forced ion diffusion are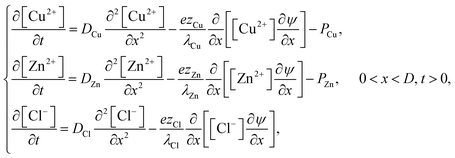 | (21) |
Eqn (21) are complemented by boundary and initial conditions. Initially, we suppose there are no mobile ions present. Thus,
| [X](x;0) = 0, X = {Cu2+,Zn2+,Cl−}, 0 ≤ x ≤ D, t = 0. | (22) |
At x = 0 we suppose there is no flux of ions through the substrate
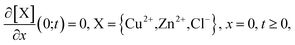 | (23) |
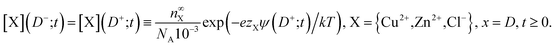 | (24) |
3.4 Electric potential
Given that the bound ions are also charged contributions, the concentrations will also need to be incorporated into the expression for the charge density. The explicit expression for the charge density is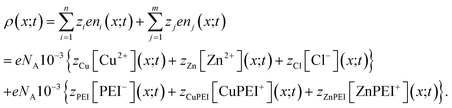 | (25) |
The non-uniform charge content of the polymer layer generates an electric field which influences both the rate and extent of ion intrusion into the polymer layer. The electric potential associated with that field satisfies Poisson’s equation,
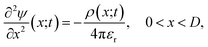 | (26) |
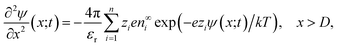 | (27) |
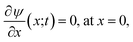 | (28) |
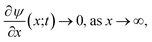 | (29) |
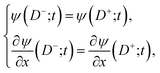 | (30) |
Although the equations for the electric potential depend explicitly only on the spatial variable, x, the potential itself is also implicitly dependent on time, t, through its dependence on the charge density which depends explicitly and implicitly on time. Consequently, Poisson’s equation and the Poisson–Boltzmann equation need to be solved self-consistently throughout the time period of interest. Incidentally, the application of the Poisson–Boltzmann equation in the bulk solution implies the assumption of rapid equilibrium in the bulk. That is, irrespective of the time development within the polymer matrix, the electrolyte in the adjacent electrical double layer is taken to relax sufficiently fast to always be in a state of (quasi-)equilibrium given the prevailing conditions within the matrix.
3.5 Numerical solution approach
To solve the coupled systems of equations we first nondimensionalise all variables and equations using the time and spatial scales of Dmκ2 and κ−1, respectively, where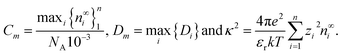 | (31) |
We then introduce dimensionless dependent and independent variables and related parameters: y = κx, s = tDmκ2, K = κD
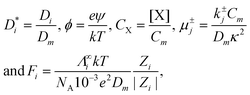 | (32) |
The equations to be solved are then written in dimensionless form. For example, non-dimensional versions of the diffusion equations take the form
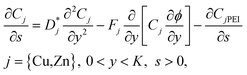 | (33) |
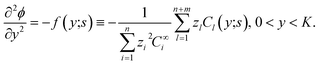 | (34) |
Finally, the reaction equations (e.g., eqn (2) and (3)) typically appear in the form
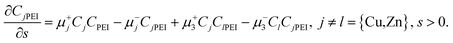 | (35) |
Note that some dimensionless reaction rate constants are not defined as per eqn (32), depending on their original dimensions. Nevertheless, dimensionless reaction rates are implicit in all of our working. We point out that for convenience we subsequently refrain from quoting the units of the different reaction rate constants. Instead, we document here that the units of k+1, k+2, k+3, k−3 (Scenario I and II), k−4 and k±5 are cm3 mole−1 s−1, while the units of k−1, k−2 and k+4 are s−1. The units of k−3 (rapid dissociation version of Scenario II) are cm6 molec−2 s−1.
It is possible in principle to consider all three sets of equations (dimensional or nondimensional versions) as subsystems of a larger system of partial differential equations (pdes) involving both time (t or s) and space (x or y) derivatives. Those equations not possessing explicit time (space) derivatives can be considered as pdes with zero time (space) derivative coefficients. The complete system could theoretically be solved as one self-consistent system. Unfortunately, this turns out to be problematic in practice. In this work, we have adopted an iterative approach whereby we cycle through the solution of each subsystem in turn, assuming that the dependent variables not being solved for explicitly are inhomogeneous inputs in that calculation. The outputs of each subsystem calculation are then used as inputs for the solution of the other subsystems. The entire cycle of calculation is iterated until we achieve self-consistent results for a given set of initial parameter conditions. The code developed was written in the Matlab® environment utilizing some of the inbuilt subroutines. The subsystem of reaction equations of the form in eqn (35) was solved using the function routine ode45, while the set of diffusion equations, eqn (33), was solved using the solver pdepe. With regard to eqn (34), this equation was integrated explicitly to give the result
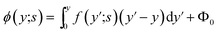 | (36) |
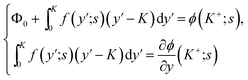 | (37) |
In eqn (37), the right hand side of the second of the continuity equations is the derivative of the Poisson–Boltzmann solution:
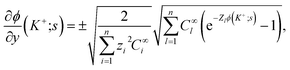 | (38) |
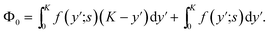 | (39) |
4 Results and discussion
4.1 Scenario I
In this section we shall focus on Scenario I as an example of a system exhibiting the type of qualitative behavior found in the experiments of ref. 1. The working hypothesis of this scenario is that although both ions have a similar binding affinity for the PEI binding sites (or possibly that Cu2+ has a greater affinity for binding than Zn2+), the Zn2+ metal ion has a more rapid diffusive entry into the polymer matrix and therefore has an earlier binding association with the polymer than does Cu2+. However, the hypothesis then proposed is that once in, the Cu2+ ions preferentially replace already bound Zn2+ ions to either a significant fractional extent or completely, depending on the respective binding constants. Clearly, the important parameters to focus on in order to explore and test the hypothesis are the diffusion constants of the respective ions and the binding reaction rate constants introduced in the previous section. To this end (and so as to limit the very large parameter space inherent in the model) we focus attention on the principal parameters: k±1,2, k±3 and D1,2, keeping other quantities constant. Quantities such as the thickness of the polymer matrix, w, the bulk concentrations of free electrolyte ions, C∞Cu, C∞Zn, C∞Cl and the density of binding sites serve only to adjust the total number of bound Cu2+ and Zn2+ ions (i.e., the steady state) for a given set of our designated principal parameters. It is possible that under extreme parameter conditions, these secondary parameters may influence even the qualitative behavior. However, it will become clear that under quite reasonable parameter conditions, the model described in Section 3 does support the hypothesis. Table 1 summarizes the fixed parameters used in these calculations.| Parameter | Value | Comment |
|---|---|---|
| n, m | 3, 3/4 | Scenario I/Scenario II |
| [Cu2+]∞, [Zn2+]∞, [Cl−]∞ | 1.0 mM, 1.0 mM, 4.0 mM | |
| n PEItot | 6.022 × 1017 cm−3 ≡ 1.0 mM | |
| n PEI1,tot | 3.011 × 1017 cm−3 ≡ 0.5 mM | |
| n PEI2,tot | 3.011 × 1017 cm−3 ≡ 0.5 mM | |
| z PEI = zPEI1 = zPEI2 | −1 | |
| R Cu | 1.074 Å | Unless otherwise stated |
| R Zn | 1.069 Å | |
| R Cl | 1.181 Å | |
| Polymer thickness, D | 10−6 cm | |
| Λ ∞Cu | 73.5 cm2 Ohm−1 | |
| Λ ∞Zn | 75 cm2 Ohm−1 | |
| Λ ∞Cl | 76.35 cm2 Ohm−1 | |
| Temperature, T | 298 K | |
| ε r | 78 | For the bulk solution |
| ε r | 78 | Assumed for the polymer region |
It has been shown30 that the diffusion constants of the mobile electrolyte ions vary, depending on solution conditions. The ranges of diffusion constants, 0.5–1.0 × 10−5 cm2 s−1 and 2–5 × 10−6 cm2 s−1, determined experimentally for Cu2+ and Zn2+ under concentrated electrolyte conditions, are not too dissimilar to what can be deduced from the ideal Stokes–Einstein relation
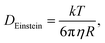 | (40) |
We first establish the reference case of ion binding, assuming all but equal diffusion constants and equal binding affinities. Under such conditions there is identical time and space development of the density of CuPEI+ and ZnPEI+ complexes within the polymer layer. One should note that steady state densities are obtained for all mobile ions well within the non-dimensional time frame adopted. The steady state concentrations of CuPEI+ and ZnPEI+ are dictated solely by the respective bulk ion concentrations and the underlying density of binding sites. The equivalence of the two ions results in negligible difference in either diffusive or absorptive behavior. This is summarized by the coincident curves in the centre of Fig. 2. The figure shows the time evolution of the integral amounts of CuPEI+ and ZnPEI+ in the matrix. Mobile metal ions occupying space in the matrix are not included in these integral quantities. The curves have converged to the theoretical limit depicted by the dashed line, which represents the case of equal share of binding sites to Cu and Zn. The separated curves (blue solid curves for CuPEI+ and red broken curves for ZnPEI+) on either side of the coincident pair depict the result of delaying the influx of Cu2+ by reducing this ion’s diffusion constant. The two values of RCu = 3.5 Å and 4.5 Å show progressively reduced Cu2+ uptake with corresponding increased Zn2+ uptake. The accumulating ZnPEI+, however, reaches a maximum and then decreases as CuPEI+ continues to increase. However, the behavior is not due to any extraneous exchange process as negligible exchange has been assumed here (k±3 = 1.0). Instead, what we observe is a natural approach of the two corresponding curves to their equal steady state values shown by the black dashed line in the figure centre. All things being equal, the differences in diffusive rates only affect the approach to equilibrium, not the equilibrium state itself. Thus, although we have not been able to track numerically the time development further, we surmise that the two sets of curves will each ultimately asymptote to the theoretical non-dimensional limit of 0.3153. (Numerical difficulties were experienced in solving the coupled system of diffusion equations, presumably because the faster species achieves steady state values in significant regions of the matrix before the overall system reached steady state. We aim to address this problem mathematically in future work.)
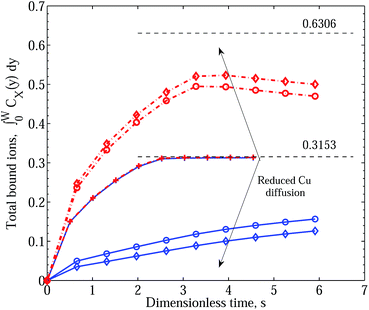 | ||
| Fig. 2 Integral graphs showing the rates of accumulation of CuPEI+ and ZnPEI+ assuming independent binding reactions. Blue solid lines denote CuPEI+ accumulation, while red broken lines depict ZnPEI+ accumulation. Values shown are nondimensional. The thin black dashed lines indicate the level of saturated binding; the upper line denotes the level of saturated binding by one species, while the lower line indicates the level of equally shared saturated binding. The results were generated assuming direct binding rate constants of k+1 = k+2 = 5 × 1011 and k−1 = k−2 = 4 × 106 and negligible exchange reaction, k±3 = 1.0. In the order depicted by the arrows, we assume increasing effective Cu2+ ion radius: RCu = 1.074 (pluses), 3.5 (circles) and 4.5 (diamonds) Å, respectively, or equivalently decreasing Cu diffusion constant: DCu = 2.26 × 10−6, 6.94 × 10−7 and 5.40 × 10−7 cm2 s−1, respectively, compared with DZn = 2.27 × 10−6 cm2 s−1. Other parameters are as given in Table 1. | ||
As our interest is with competitive absorption of metal ions over and above the intrinsic process depicted by the curves in Fig. 2 and governed by eqn (2) and (3), we show in Fig. 3 the time development of total metal ions bound in the matrix under equivalent diffusive and equal binding conditions, but with increasing influence of the forward exchange reaction. Three cases are demonstrated: k+3 = 1.0, 1.0 × 109 and 1.0 × 1012. The blue solid curves again follow the accumulation of bound Cu2+ throughout the polymer, while the red broken lines follow the accumulation of Zn2+. A nine order of magnitude increase in forward exchange reaction is required to see a separation of the integral responses. Initially, however, the two curves closely follow one another with the marginal diffusive advantage of Zn2+ over Cu2+ being insufficient to curtail the Cu2+ binding dominance. At roughly twice the characteristic diffusion time, the two curves deviate markedly, with the CuPEI+ integral curve increasing somewhat faster than linearly, while the ZnPEI+ integral curve decreases linearly. The transition point is quite abrupt and common for the two curves. However, increasing k+3 another three orders of magnitude results in complete separation of the two integral quantities, with the CuPEI+ curve increasing monotonically with no apparent inflection point and plateauing to a steady state value (of 0.622), well above the maxima reached by the other two cases (k+3 values) during the simulation period. In contrast, the ZnPEI+ curve reaches a maximum at approximately twice the characteristic time before decreasing linearly for another two characteristic time units to then asymptote to zero. The latter trend reflects the plateauing of CuPEI+ at the high positive value. We point out that the plateau reached by the CuPEI+ complex content asymptotes to the theoretical limit (0.6306) of all binding sites being occupied by the one species; this is indicated by the upper black dashed line. The implication here is that the added effect of an additional exchange process drives the system to consider Cu2+ being the preferred binding species. Unfortunately again, we are unable to track the time course of metal ion accumulation in the case of the smaller value of k+3 = 109 beyond the values shown. However, we anticipate that the two profiles for this case will ultimately asymptote to the same steady state limits as for the k+3 = 1012 profiles, namely zero for ZnPEI+ and 0.6306 for CuPEI+.
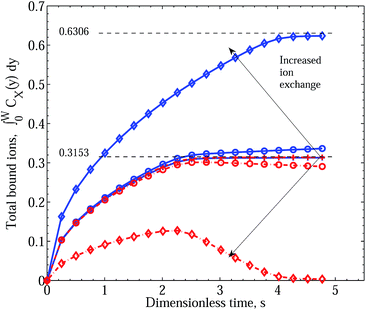 | ||
| Fig. 3 Integral graphs showing CuPEI+ and ZnPEI+ accumulation rates according to Scenario I. Line references as in Fig. 2. This data was generated assuming equivalent direct binding rate constants: k+1 = k+2 = 5 × 1011 and k−1 = k−2 = 4 × 106 and (practically) equivalent diffusion rates, while the different curves, in the order depicted by the arrows, result from increasing exchange reaction rate constants k+3 = 1.0 (pluses), 109 (circles) and 1012 (diamonds), respectively. Other parameters are as given in Table 1. | ||
The detailed time and space development of the concentrations of the metal ion–ligand complexes, CuPEI+ and ZnPEI+, for the case of k+3 = 1.0 × 1012, clearly exhibits the more rapid increase in ZnPEI+ concentration initially. However, as Cu2+ spreads into the matrix and the concentration of CuPEI+ increases, the depletion of ZnPEI+ in favorable exchange with CuPEI+ is apparent (data not shown). The exchange effect is complete in the long term (i.e., asymptotically) throughout the polymer matrix, but occurs sooner near to the edge of the polymer layer as this region is first to become saturated with Cu2+ ions.
While we see a trend reflecting the differing degree of binding, and specifically the replacement of bound Zn2+ for bound Cu2+, we have yet to encounter the observed event of initial dominant accumulation of Zn2+ that is then overshadowed by the binding of Cu2+. If we now modify the diffusive process to disadvantage the diffusion of Cu by increasing the effective Cu2+ radius to 4.5 Å, we find, other things being equal, the qualitative behavior observed in the experiments of ref. 1. In Fig. 4, we compare the different cases of increased Cu2+ radius RCu = 1.074, 4.5 and 6.5 Å, corresponding to a steady decrease in Cu2+ diffusion constant. As in the case of Fig. 2, the rate of intrusion of Cu2+ is slower as RCu increases, allowing Zn to diffuse uninhibited into the matrix and bind with free PEI− sites. Only when a sufficient number of Cu2+ ions have entered is there any decline in the rate of increase of bound Zn2+. However, in contrast to the results of Fig. 2, the rate at which the metal ions bind is dominated by Zn2+ only initially, when diffusion of Cu2+ is much slower (RCu = 4.5 Å compared with RZn = 1.069 Å). A cross-over point is reached beyond which the rate of uptake of Cu2+ dominates over Zn2+ binding through the action of the exchange mechanism (eqn (6)). Increasing RCu to 6.5 Å reinforces the effect, although the peak value of ZnPEI+ is only slightly higher and is reached at only a slightly later time (s = 3.32 for RCu = 6.5 Å compared with s = 3.19 for RCu = 4.5 Å). The cross-over point, however, is significantly delayed in the slower diffusive case (s = 5.26 for RCu = 6.5 Å compared with s = 3.22 for RCu = 4.5 Å). Although we are not able to access later simulation times in the cases of RCu = 4.5 Å and RCu = 6.5 Å due to numerical difficulties, we again anticipate that the subsequent behavior of the profiles will mimic the asymptotic behavior exhibited by the faster Cu2+ diffusion case (RCu = 1.074 Å), since once again the only difference between the cases (difference in the diffusion constant of Cu2+) only affects the rate of approach to steady state and not the steady state condition itself.
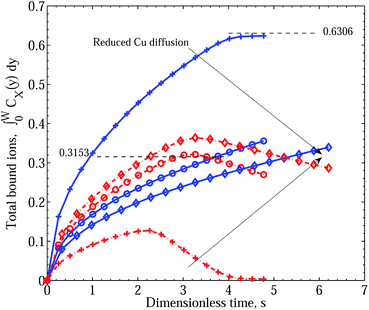 | ||
| Fig. 4 Integral graphs showing CuPEI+ and ZnPEI+ accumulation rates according to Scenario I. Line references as in Fig. 2. The results were generated assuming: binding rate constants of k+1 = k+2 = 5 × 1011 and k−1 = k−2 = 4 × 106; significant exchange reaction rate constants of k+3 = 1012k−3 = 1.0. The different cases, in the order indicated by the arrows, refer to increasing effective Cu2+ ion radius: RCu = 1.074 (pluses), 4.5 (circles) and 6.5 (diamonds) Å, respectively, or equivalently decreasing Cu diffusion constant: DCu = 2.26 × 10−6, 5.40 × 10−7 and 3.74 × 10−7 cm2 s−1, respectively. All other parameters are as given in Table 1. | ||
The combination of the observed short term behavior, depicted by the RCu = 4.5 Å and RCu = 6.5 Å results, with the expected asymptotic limit, demonstrated by the RCu = 1.074 Å result, correlates well with the behavior observed in the Lindén et al. experiments.
4.2 Scenario II
In the following calculations we shall assume the same total number density of absorption sites as assumed for Scenario I. This is to allow for some commonality between the two models. In the majority of cases, however, half of these are assumed selective binding sites for Cu2+ and half are selective binding sites for Zn2+. Again, in the majority of cases, the binding of metal ions will be limited only to their respective sites. As a point of model differentiation, this scenario models, more explicitly than in Scenario I, the situation of Cu2+ binding having a direct impact on the binding of Zn2+ through two mechanisms.The first mechanism is akin to the mechanism underpinning Scenario I, but rather than being considered an exchange process, the mechanism implies an induced conformational change to the polymer structure that destabilizes existing ZnPEI+ complexes. A destabilized complex then undergoes a dissociation reaction to produce a free Zn2+ ion and an inactive PEI−2,ia binding site. The second mechanism is not considered at all in Scenario I. Here, the binding of Cu2+ impacts directly on a bare PEI−2,a binding site, converting it to its inactive state thus precluding any subsequent Zn2+ binding. With regard to the former mechanism, we treat it here in two ways. First, by modelling explicitly the dissociation process as a separate, but coupled, reaction step, with its own dissociation rate constants (k±4 in eqn (14)); as already mentioned a nonzero k−4 constant allows for the finite probability of a reverse reaction, however slight. Nevertheless, we choose k−4 values that have negligible effect on the simulation outcome. In the second approach, we assume that the forward dissociation reaction proceeds spontaneously and completely without the possibility of reversal. The two cases are clearly distinguished in the figures. In this case, there is no reference to k±4 constants and we invoke eqn (15) (again with negligible k−3 values). For the right choice of reaction rate constants, the second approach is largely equivalent to the first, although it circumvents the need to identify possible k±4 values.
In Fig. 5 we demonstrate the effect of increasing the effect of polymer reconfiguration triggered by the binding of Cu2+ ions, manifested in the destabilisation of existing ZnPEI+2,a complexes and the inactivation of bare PEI−2,a sites. In this figure both treatments of the two-site model, with and without an intermediate dissociation step, are included to indicate their essential equivalence. Two points should be noted. First, with the separation into two site types, the theoretical limit of site saturation is equal for each binding species. This is indicated by the black dashed line and value of 0.3153. However, in contrast to Scenario I, as the binding of Zn2+ decreases through the destabilisation mechanisms there is no corresponding increase in the level of Cu2+ binding. Hence, in all the cases shown in this figure, the CuPEI+1 integral curve is largely unaffected by the changes experienced by the ZnPEI+2,a content in the matrix. The second point of note is that the curves were generated assuming equivalent ion diffusive rates (equal diffusion constants). Note also the absence of the experimentally observed behavior of initial dominance of bound Zn2+ over bound Cu2+ and subsequent reversal of binding trends. This sought-after behavior, quite convincingly demonstrated in Fig. 6, is found when differences in diffusivities are introduced. Specifically, as the rate of Cu2+ intrusion into the matrix is successively reduced (by reducing the ion’s diffusion constant relative to that of Zn2+), there is a progressively stronger take up of Zn2+, at least in relative terms. However, the uptake of Zn2+ never exceeds the theoretical limit (of 0.3153), and indeed it is always lower and slower than the amount taken up in the case of completely independent binding, which thus represents an upper limiting envelope in time for Zn2+ uptake. This observation is to be contrasted with the results of Scenario I in which the ZnPEI+ amounts can surpass the equal binding curve. Naturally, as the Cu2+ diffusion constant is reduced, the ZnPEI+2,a accumulation is larger, lying closer to the independent binding envelope. In all cases of Cu2+ diffusion, however, the ZnPEI+2,a curve attains a maximum after which the level of bound Zn2+ decreases linearly (at first) before approaching the zero asymptote in the steady state limit, as more Cu2+ binds to its specific binding site. The results in this figure were generated assuming an intermediate dissociation step.
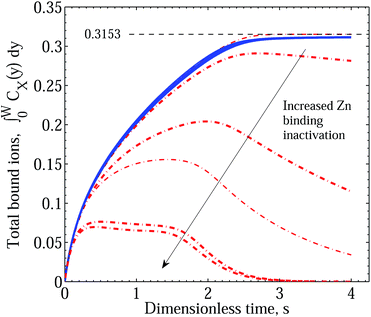 | ||
| Fig. 5 Integral graphs showing CuPEI+ and ZnPEI+ accumulation rates according to Scenario II with and without an intermediate dissociation step. Values shown are nondimensional. Blue solid lines denote CuPEI+ accumulation, while red broken lines depict total ZnPEI+ accumulation (in some cases being the sum of both ZnPEI+2,a and ZnPEI+2,ia). Values shown are nondimensional. The results were generated assuming equivalent binding rate constants k+1 = k+2 = 5 × 1011 and k−1 = k−2 = 4 × 106 and equivalent ion diffusion rates. Thin lines correspond to the case of an intermediate dissociation reaction, while thick lines assume no intermediate reaction step. The thin black dashed line indicates the level of saturated binding for both site types. In the order depicted by the arrow, the ZnPEI+ curves result from increased site inactivation reaction (eqn (13) and eqn (17)): k±3 = k±4 = k±5 = 1.0; k+3 = 109, k−3 = 1.0, k±5 = 1.0; k+3 = 1011, k−3 = 1.0, k±5 = 1.0; k+3 = 1012, k−3 = 1.0, k+4 = 107, k−4 = k±5 = 1.0; k+3 = 1011, k−3 = 1.0, k+5 = 109, k−5 = 1.0; k+3 = 1011, k−3 = 1.0, k+5 = 1011, k−5 = 1.0. All other parameters are as given in Table 1. | ||
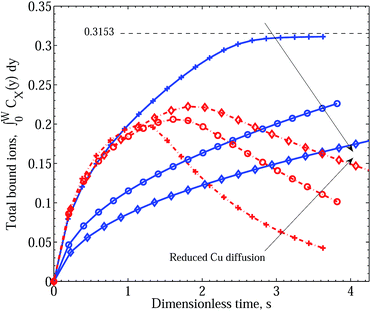 | ||
| Fig. 6 Integral graphs showing CuPEI+ and ZnPEI+ accumulation rates according to Scenario II with an intermediate dissociation step. Line references as in Fig. 5. In the order depicted by the arrows, we assume increasing effective Cu radius: RCu = 1.074 (pluses), 3.5 (circles) and 6.5 (diamonds) Å, respectively, or equivalently decreasing Cu diffusion constant: DCu = 2.26 × 10−6, 6.94 × 10−7 and 3.74 × 10−7 cm2 s−1. Reaction rate constants assumed are: equivalent binding rate constants k+1 = k+2 = 5 × 1011 and k−1 = k−2 = 4 × 106; binding site inactivation k+3 = 1012, k+5 = 109 and k−3 = k−5 = 1.0; and intermediate step dissociation rate k+4 = 107 and k−4 = 1.0. All other parameters are as given in Table 1. | ||
It should be noted that as we have assumed an equal number of binding sites for Cu2+ as for Zn2+, the steady state limit for the amount of ZnPEI+2,a complexes will be zero. This limit would apply for any choice of underlying site densities satisfying the inequality nPEI1,tot ≥ nPEI2,tot. However, a nonzero steady state ZnPEI+2,a limit exists under the current binding scenario should the underlying Cu2+ binding site density nPEI1,tot be less than nPEI2,tot. Since experimental findings indicate complete depletion of bound Zn2+, this would suggest the number of Cu2+ binding sites to be greater than or equal to the number of Zn2+ binding sites.
Fig. 7A shows the time and space development of the ZnPEI+2,a complex under the condition of reduced Cu2+ diffusion and significant rates of inactivation and destabilisation. In Fig. 7B we show the corresponding increase in the density of inactive Zn2+ binding sites, PEI−2,ia. The latter quantity appears in response to the level of influx of Cu2+ and thus the time and space dependent CuPEI+1 density.
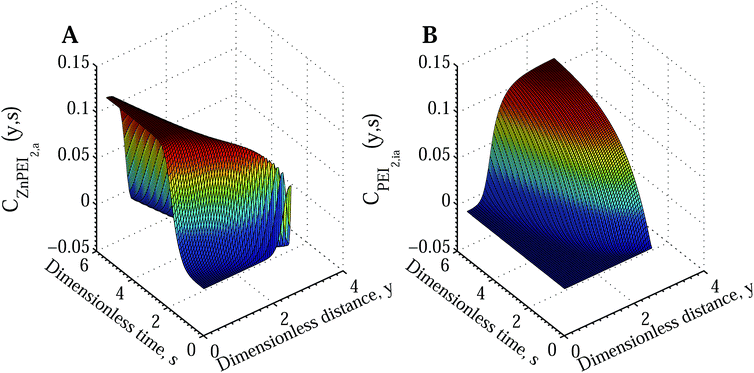 | ||
| Fig. 7 Surface plots showing the temporal and spatial increase of bound species and inactivated Zn binding sites according to Scenario II with an intermediate dissociation step. The results assume the conditions of Fig. 6 for the extreme case of reduced Cu2+ diffusion rate (DCu = 3.74 × 10−7 cm2 s−1 compared with DZn = 2.27 × 10−6 cm2 s−1). The subplots show (A) ZnPEI+2,a density and (B) PEI−2,ia density. All variables are nondimensional. | ||
For completeness, we show in Fig. 8 results of the model assuming no intermediate dissociation step in Scenario II, again for significant inactivation and destabilisation reactions and for progressively reduced Cu2+ diffusion. No major qualitative differences appear in comparison with the results shown in Fig. 6.
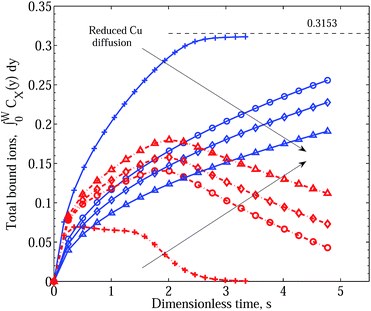 | ||
| Fig. 8 Integral graphs showing CuPEI+ and ZnPEI+ accumulation rates according to Scenario II with no intermediate dissociation step. Line references as in Fig. 5. In the order depicted by the arrows, we assume increasing effective Cu radius: RCu = 1.074 (pluses), 3.5 (circles), 4.5 (diamonds) and 6.5 (triangles) Å, respectively, or equivalently decreasing Cu diffusion constant: DCu = 2.26 × 10−6, 6.94 × 10−7, 5.40 × 10−7 and 3.74 × 10−7 cm2 s−1. We assume the following rate constants: equivalent binding rate constants k+1 = k+2 = 5 × 1011 and k−1 = k−2 = 4 × 106; inactivation rates of k+3 = 1011, k+5 = 1011 and k−3 = k−5 = 1.0. All other parameters are as given in Table 1. | ||
5 Summary remarks
With regard to Scenario I, we have shown that with the right combination of two influential factors,• a low relative Cu2+ diffusion constant,
• a high Cu2+ for Zn2+ exchange rate,
we can reproduce qualitatively, if not quantitatively, the experimental findings of ref. 1. Naturally, it is necessary for the Cu2+ binding rate/strength to be sufficiently high for the Cu2+ binding to be at all competitive with Zn2+. However, the results indicate that it is not necessary for Cu2+ binding to be significantly stronger than the binding strength of Zn2+. The combination of the above two factors is sufficient to substantiate the hypothesis of a simple competitive mechanism (or mechanisms) for the reported experimental results. We remark that this scenario is the simpler of the two presented here. Advocates of Occam’s razor would argue that this may be the most reasonable explanation. We remark also that nothing has actually been said of, nor does the model itself suggest, any specific physical or chemical processes that are being represented by the rate constants themselves.
With regard to Scenario II, analogous summary comments can be made. A diffusion differential alone is not sufficient to explain the experimental findings. Nor is a polymer matrix rearrangement triggered by Cu2+ binding sufficient to account for the observed competitive binding behavior. The qualitative effect can be achieved through a suitable blend of these two mechanisms:
• significant differential diffusion, and
• significant destabilization of Zn2+–PEI− complexes and/or inactivation of Zn2+ binding sites.
Incidentally, this is true whether Cu2+ and Zn2+ have different selective binding sites or they are attracted to and compete for the same binding sites (data not shown).
The features that distinguish the single site model from the two site model are points of differentiation that are potentially useful in aiding the interpretation of experiments on the real systems as well as for the design of new experiments for hypothesis testing.
In this work we have not made any attempt to accurately model the experimental system. Instead, we have taken the opportunity to explore the temporal and spatial details that physically underlie the competitive binding process. We have achieved the goal of identifying the essential processes that lead to preferential competitive binding. In our ongoing efforts, which will be the subject of future communications, we are undertaking the necessary rigorous quantitative comparison between theory and a more extensively characterized experimental system. In so doing, the model will be refined to improve its representation of the experimental system. This will include a more appropriate spatial account of ion diffusion through the porous matrix29 and allowance for the possibility of matrix swelling during the absorption process. More accurate modelling, however, requires in turn a more accurate characterisation of the experimental situation as well as a more extensive survey of experimental conditions. Not only will this establish a solid benchmark of experimental data for a comparison, it will help to identify trademark behavior that could be used to distinguish between the different possible mechanisms responsible for the observed competitive ion absorption.
Acknowledgements
The authors thank Dr Mikael Larsson for useful discussions. We also thank Drs Hamid Laga and Pankaj Kumar and Ms Julie Sleep for technical assistance with Matlab programming and Latex formatting, respectively.References
- J. B. Lindén, M. Larsson, B. R. Coad, W. M. Skinner and M. Nydén, Polyethyleneimine for Copper Absorption: Kinetics, Selectivity and Efficiency in Artificial Seawater, RSC Adv., 2014, 4, 25063–25066 RSC.
- S. T. Beatty, R. J. Fischer, D. L. Hagers and E. Rosenberg, A Comparative Study of the Removal of Heavy Metal Ions from Water Using a Silica–Polyamine Composite and a Polystyrene Chelator Resin, Ind. Eng. Chem. Res., 1999, 38, 4402–4408 CrossRef CAS.
- L. Kiaune and N. Singhasemanon, Pesticidal Copper(I) Oxide: Environmental Fate and Aquatic Toxicity, Rev. Environ. Contam. Toxicol., 2011, 213, 1–26 CAS.
- K. Schiff, D. Diehl and A. Valkirs, Copper Emissions from Antifouling Paint on Recreational Vessels, Mar. Pollut. Bull., 2004, 48, 371–377 CrossRef CAS PubMed.
- P. E. Duru, S. Bektas, Ö. Genc, S. Patir and A. Denizli, Adsorption of Heavy-Metal Ions on Poly(Ethyleneimine)-Immobilized Poly(Methyl Methacrylate) Microspheres, J. Appl. Polym. Sci., 2001, 81, 197–205 CrossRef CAS.
- F. Fu and Q. Wang, Removal of Heavy Metal Ions from Wastewaters: A Review, J. Environ. Manage., 2011, 92, 407–418 CrossRef CAS PubMed.
- S. D. Alexandratos, Ion-Exchange Resins: A Retrospective from Industrial and Engineering Chemistry Research, Ind. Eng. Chem. Res., 1999, 48, 388–398 CrossRef.
- W. Chouyyok, Y. Shin, J. Davidson, W. D. Samuels, N. H. LaFemina, R. D. Rutledge, G. E. Fryxell, T. Sangvanich and W. Yantasee, Selective Removal of Copper(II) from Natural Waters by Nanoporous Sorbents Functionalized with Chelating Diamines, Environ. Sci. Technol., 2010, 44, 6390–6395 CrossRef CAS PubMed.
- W. S. Wan Ngah, A. Kamari and Y. J. Koay, Equilibrium and Kinetics Studies of Adsorption of Copper(II) on Chitosan and Chitosan/PVA Beads, Int. J. Biol. Macromol., 2004, 34, 155–161 CrossRef CAS PubMed.
- K. Y. Foo and B. H. Hameed, Insights into the Modeling of Adsorption Isotherm Systems, Chem. Eng. J., 2010, 156, 2–10 CrossRef CAS PubMed.
- A. Webster, M. D. Halling and D. M. Grant, Metal Complexation of Chitosan and its Glutaraldehyde Cross-Linked Derivatives, Carbohydr. Res., 2007, 342, 1189–1201 CrossRef CAS PubMed.
- A. Debbaudt, M. Zalba, M. L. Ferreira and M. E. Gschaider, Theoretical and Experimental Study of Pb2+ and Hg2+ Adsorption on Biopolymers. 2. Experimental Part, Macromol. Biosci., 2001, 1, 6249–6257 CrossRef.
- V. M. Nurchi, G. Crisponi, M. Crespo-Alonso, J. I. Lachowicz, Z. Szewczuk and G. J. S. Cooper, Complex Formation Equilibria of CuII and ZnII with Triethylenetetramine and its Mono-and Di-acetyl Metabolites, Dalton Trans., 2013, 42, 6161–6170 RSC.
- S. Hirata, Y. Ishida, M. Aihara, K. Honda and O. Shikino, Determination of Trace Metals in Seawater by On-line Column Preconcentration Inductively Coupled Plasma Mass Spectrometry, Anal. Chim. Acta, 2001, 438, 205–214 CrossRef CAS.
- M. E. Lagerström, M. P. Field, M. Séguret, L. Fischer, S. Hann and R. M. Sherrell, Automated On-line Flow-Injection ICP-MS Determination of Trace Metals (Mn, Fe, Co, Ni, Cu and Zn) in Open Ocean Seawater: Application to the GEOTRACES Program, Mar. Chem., 2013, 155, 71–80 CrossRef PubMed.
- Y. Chen, B. Pan, H. Li, W. Zhang, L. Lv and J. Wu, Selective Removal of Cu(II) Ions by Using Cation-exchange Resin-Supported Polyethyleneimine (PEI) Nanoclusters, Environ. Sci. Technol., 2010, 44, 3508–3513 CrossRef CAS PubMed.
- M. Ghoul, M. Bacquet and M. Morcellet, Uptake of Heavy Metals from Synthetic Aqueous Solutions using Modified PEI-Silica Gels, Water Res., 2003, 37, 729–734 CrossRef CAS.
- B. Gao, F. An and K. Liu, Studies on Chelating Adsorption Properties of Novel Composite Material Polyethyleneimine/Silica Gel for Heavy-Metal Ions, Appl. Surf. Sci., 2003, 256, 1946–1952 Search PubMed.
- S. Kobayashi, K. Hiroishi, M. Tokunoh and T. Saegusa, Chelating Properties of Linear and Branched Polyethylenimines, Macromolecules, 1987, 20, 1496–1500 CrossRef CAS.
- B. L. Rivas and K. E. Geckeler, Polymer Synthesis Oxidation Processes, Springer, 1992 Search PubMed.
- V. N. Kislenko and L. P. Oliynyk, Complex Formation of Polyethyleneimine with Copper(II), Nickel(II), and Cobalt(II) Ions, J. Polym. Sci., Part A: Polym. Chem., 2002, 40, 914–922 CrossRef CAS.
- P. L. Yeagle, The Structure of Biological Membranes, CRC Press, 2nd edn, 2004 Search PubMed.
- S. J. Miklavic and B. W. Ninham, Conformation of Surface Bound Polyelectrolytes: I Implications for Cell Electrophoresis, J. Theor. Biol., 1989, 137, 71–89 CrossRef CAS.
- M. K. Granfeldt, S. J. Miklavic, S. Marcelja and C. E. Woodward, Conformation of Surface Bound Polyelectrolytes: II A Monte Carlo study of Medium Length Lattice Chains, Macromolecules, 1990, 23, 4760–4768 CrossRef CAS.
- E. J. W. Verwey and J. Th. G. Overbeek, Theory of the Stability of Lyophobic Colloids, Elsevier Publishing Company, 1948 Search PubMed.
- D. F. Evans and H. Wennerström, The Colloidal Domain, VCH, New York, 1994 Search PubMed.
- P. A. Attard and S. J. Miklavic, The Electrical Double Layer in the Wall-Wall Hypernetted Chain Approximation with Bridge Functions, J. Chem. Phys., 1993, 99, 6078–6086 CrossRef CAS PubMed.
- S. J. Miklavic and B. W. Ninham, Competition for Adsorption Sites by Hydrated Ions, J. Colloid Interface Sci., 1990, 134, 305–311 CrossRef CAS.
- J. T. Kim and J. L. Anderson, Diffusion and Flow Through Polymer-Lined Micropores, Ind. Eng. Chem. Res., 1991, 29, 1008–1016 CrossRef.
- S. Kariuki and H. D. Dewald, Evaluation of Diffusion Coefficients of Metallic Ions in Aqueous Solutions, Electroanalysis, 1996, 8, 307–313 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2014 |
