Metallophilicity-assisted assembly of phosphine-based cage molecules

Abstract

A family of supramolecular cage molecules has been obtained via self-assembly of the phosphine–gold coordination complexes following an aurophilicity-driven aggregation approach. Use of the di- (PP) or tridentate (PPP) phosphine ligands P_n (n = 2, 3) with rigid polyaromatic backbones leads to clean formation of the coordination P_n(Au(tht))_nⁿ⁺ species, sequential treatment of which with H₂O/NEt₃ and excess of H₂NBu^t gives the finite 3D structures of two major types. The cylindrical-like hexametallic cages [(PPAu₂)₃(μ₃-NBu^t)₂]²⁺ are based on the diphosphines PP = 1,4-bis(diphenylphosphino)benzene (1), 4,4′-bis(diphenylphosphino)biphenyl (2), 4,4′′-bis(diphenylphosphino)terphenyl (3), while the triphosphine PPP (1,3,5-tris(diphenylphosphinophenyl)benzene) produces a tetrahedral dodecagold complex [(PPPAu₃)₄(μ₃-NBu^t)₄]⁴⁺ (4). The cages 1–4 have been studied using the ESI-MS and ¹H, ³¹P NMR spectroscopy, and the crystal structures of 1 and 4 were determined by an X-ray diffraction study. The NMR spectroscopic investigations showed that cylindrical complexes 1–3 undergo twisting-like interconversion of the helical P↔M isomers in solution, while 4 is a stereochemically rigid compound retaining its axially chiral architecture. The difference in dynamic behavior was rationalized using computational studies with density functional methods.

---

Introduction

Remarkable progress in supramolecular coordination chemistry has been observed during the past two decades. Using a combination of discrete metal coordination geometry and rationally designed organic ligands, an impressively large number of finite supramolecular assemblies and extended inorganic polymers showing unique physical and chemical properties were successfully prepared via a self-assembly approach.^1,2 By varying the nature of metal ion and tuning the stereochemistry of the organic linker, one can control the formation of fascinating polygonal 2D and polyhedral 3D aggregates of regular architectures. The latter type of compounds is particularly attractive as they possess well-defined nanosized hollows and can efficiently serve as molecular containers demonstrating rich host–guest chemistry, e.g. selective molecular recognition,³ stabilization of the reactive or unstable species,^4,5 unconventional catalysis,^2,6 photochemistry⁴ and molecular transportation including drug delivery.⁷

Most of the work dedicated to the metal–organic cage complexes is based on the mononuclear coordinating centers (i.e. metal ions) and polydentate hard N and/or O donor ligands of suitable geometry.^1,2 The general synthetic methodology is based on so-called coordination-driven self-assembly that involves spontaneous formation of the metal–ligand bonds upon reacting the ligands with coordinatively unsaturated metal precursors or those having easy to substitute groups (e.g. weakly bound solvent molecules, counterions, labile ligands like alkenes, nitriles, etc.).

The soft P donor ligands have been extensively used in coordination chemistry of late transition metals, but their utilization for the construction of supramolecular 2D/3D molecules is quite uncommon in comparison to the N, O building blocks. Some homo- and heteroleptic diphosphine-based coinage metal rings, which mainly contain the bridging ligands with flexible backbones, were reported in the literature.⁸ The use of rigid multidentate phosphine ligands allowed for the preparation of certain interesting hollow aggregates of copper subgroup metals,⁹ such as adamantanoid,¹⁰ bowl-shaped,¹¹ nanotubular¹² and tetrahedral¹³ coordination clusters. Despite the well-reported ability of d¹⁰ metal ions and of Au(I) in particular to form extensive metal–metal bonding,¹⁴ this phenomenon is scarcely considered as a potential directing force in constructing three-dimensional cage ensembles.

We described earlier the assembly of gold(I)–diphosphine cages built of the planar tetragold Au₄ coordinating centers¹⁵ that was one of the first examples where polynuclear metal clusters were used in the construction of 3D hollow complexes.¹⁶ Herein we report on the further development of metallophilicity-assisted cage compound synthesis using the combination of Au₃ cluster units together with di- and tridentate stereochemically rigid phosphine ligands.

Experimental

General comments

The ligands 1,4-bis(diphenylphosphino)benzene,¹⁷ 4,4′-bis(diphenylphosphino)biphenyl,¹⁷ 4,4′′-bis(diphenylphosphino)terphenyl,¹⁸ 1,3,5-tris(4-diphenylphosphinophenyl)benzene¹⁹ and the complex Au(tht)Cl (tht = tetrahydrothiophene)²⁰ were synthesized according to published procedures. Other reagents and solvents were used as received. Solution ¹H and ³¹P NMR spectra were recorded using a Bruker Avance 400 spectrometer. Mass spectra were measured using a Bruker APEX-Qe ESI FT-ICR instrument in the ESI⁺ mode. Microanalyses were carried out in the analytical laboratory of St.-Petersburg State University.

Synthesis of the complexes [(Bu^tNAu₃)₂(PP)₃]²⁺ (1–3) and [(Bu^tNAu₃)₄(PP)₄]⁴⁺ (4) exemplified by PP = 1,4-PPh₂C₆H₄PPh₂ (PP = diphosphine, PPP = triphosphine)

Step A. Au(tht)Cl (100 mg, 0.31 mmol) and 1,4-PPh₂C₆H₄PPh₂ (70 mg, 0.16 mmol) were mixed in dichloromethane (15 cm³) and a solution of AgPF₆ (79 mg, 0.31 mmol) in acetone (5 cm³) was added. The reaction mixture was stirred for 30 min in the absence of light. A precipitate of AgCl was filtered off and the solvents were removed under vacuum to give a glassy pale yellow residue of the [{Au(tht)}₂PP](PF₆)₂ compound.

Step B. The solid obtained was dissolved in acetone (10 cm³) and treated with H₂O (4 drops) and NEt₃ (2 drops) to give a flaky white solid formulated as [(OAu₃)₂PP₃](PF₆)₂. The suspension was stirred for 20 min in the absence of light, and then it was evaporated; the solid product was washed with methanol (2 × 3 cm³) and diethyl ether (2 × 3 cm³) and dried to give [(OAu₃)₂PP₃](PF₆)₂ as a light beige solid, which was used in the next stage without purification.

Step C. [(OAu₃)₂PP₃](PF₆)₂ (140 mg, 0.049 mmol) was suspended in acetone (10 cm³), and NH₂Bu^t (0.1 cm³) was added. The reaction mixture was stirred for 20 minutes in the absence of light to give a nearly transparent colorless solution. The reaction mixture was evaporated, and the resulting amorphous solid was washed with methanol (2 × 3 cm³) and diethyl ether (2 × 3 cm³) and dried to give [(Bu^tNAu₃)₂(PP)₃](PF₆)₂ as a colorless solid.

[(μ₃-Bu^tNAu₃)₂(PPh₂C₆H₄PPh₂)₃](PF₆)₂ (1). Recrystallization of the crude material by gas-phase diffusion of diethyl ether into concentrated acetone solution at room temperature gave a colorless crystalline material (97 mg, 63%). Single crystals were obtained by slow evaporation of dichloromethane–ethanol solution of 1 at room temperature. ESI MS (m/z): [(Bu^tNAu₃)₂(PPh₂C₆H₄PPh₂)₃]²⁺ 1331.69 (calcd 1331.68). ³¹P{¹H} NMR (acetone-d₆; δ): 28.7 (s, 6P), −144.8 (sept, 2PF₆). ¹H NMR (acetone-d₆; δ): diphosphine 7.67 (t, para-H, 12H, J(H–H) 7.3 Hz), 7.57 (dm(AXX′), ortho-H, 24H, J(H–H) 7.6, J(P–H) 12.7 Hz), 7.49 (t, meta-H, 24H, J(H–H), 7.3 Hz), 7.23 (m(A₂X₂), {P–C₆H₄–P}, 12H); Bu^tN 1.59 (s, 18H). Anal. Calc. for C₉₈H₉₀Au₆F₁₂N₂P₈: C, 39.86; H, 3.07; N, 0.95. Found: C, 40.04; H, 3.09; N, 0.94.

[(μ₃-Bu^tNAu₃)₂(PPh₂(C₆H₄)₂PPh₂)₃](PF₆)₂ (2). Recrystallization of the crude material by gas-phase diffusion of diethyl ether into a concentrated dichloromethane solution at +5 °C gave a colorless crystalline material (125 mg, 76%). ES MS (m/z): [(Bu^tNAu₃)₂(PPh₂(C₆H₄)₂PPh₂)₃]²⁺ 1445.73 (calcd 1445.73). ³¹P{¹H} NMR (acetone-d₆; δ): 28.4 (s, 6H), −144.8 (sept, 2PF₆). ¹H NMR (acetone-d₆; δ): diphosphine 7.51–7.70 (m, ortho, meta, para-H (Ph–P), 60H), 7.39 (dd, meta-H, (–C₆H₄–P), 12H, J(H–H) 8.3, J(P–H) 1.9 Hz), 7.02 (dd, ortho-H, (–C₆H₄–P), 12H, J(H–H) 8.3, J(P–H) 12.1 Hz); Bu^tN 1.64 (s, 18H). Anal. Calc. for C₁₁₆H₁₀₂Au₆F₁₂N₂P₈: C, 43.79; H, 3.23; N, 0.88. Found: C, 43.84; H, 3.25; N, 0.86.

[(μ₃-Bu^tNAu₃)₂(PPh₂(C₆H₄)₃PPh₂)₃](PF₆)₂ (3). Recrystallization of the crude material by gas-phase diffusion of diethyl ether into an acetone solution at room temperature gave a colorless crystalline material (126 mg, 71%). ES MS (m/z): [(Bu^tNAu₃)₂(PPh₂(C₆H₄)₃PPh₂)₃]²⁺ 1559.77 (calcd 1559.77). ³¹P{¹H} NMR (acetone-d₆; δ): 27.9 (s, 6P), −144.8 (sept, 2PF₆). ¹H NMR (acetone-d₆; δ): diphosphine 7.51–7.74 (m, ortho, meta, para-H (Ph–P), ortho-H, (–C₆H₄–P), 72H), 7.34 (d, meta-H, (–C₆H₄–P), 12H, J(H–H) 8.0), 7.22 (s, –C₆H₄–, 12H); Bu^tN 1.67 (s, 18H). Anal. Calc. for C₁₃₄H₁₁₄Au₆F₁₂N₂P₈: C, 47.20; H, 3.37; N, 0.82. Found: C, 47.04; H, 3.09; N, 0.94.

[(μ₃-Bu^tNAu₃)₄{(PPh₂C₆H₄)₃C₆H₃}₃](PF₆)₄ (4). Recrystallization of the crude material by gas-phase diffusion of diethyl ether into a dichloromethane solution at room temperature gave a colorless crystalline material (128 mg, 74%). ES MS (m/z): [(Bu^tNAu₃)₄{(PPh₂C₆H₄)₃C₆H₃)₃]⁴⁺ 1520.76 (calcd 1520.75). ³¹P{¹H} NMR (acetone-d₆; δ): 28.7 (s, 12P), −144.8 (sept, 4PF₆). ¹H NMR (acetone-d₆; δ): triphosphine 7.77 (m, ortho-H, (Ph¹–P), 24 H, J(H–H) 7.6, J(P–H) 13.3 Hz), 7.57–7.8 (m, ortho, meta, para-H (Ph²–P), 60H), 7.66–7.74 (m, ortho-H, (–C₆H₄–P), 24 H, J(H–H) 8.0, J(P–H) 12.7 Hz), 7.42 (t, para-H, (Ph¹–P), 12 H, J(H–H) 7.6 Hz), 7.24 (m, meta-H, (Ph¹–P), 24 H, J(H–H) 7.6, J(P–H) 1.9 Hz), 6.60 (dd, meta-H, (–C₆H₄–P), 24 H, J(H–H) 8.0, J(P–H) 1.9 Hz), 6.31 (s, –C₆H₃–, 12 H); Bu^tN 1.59 (s, tBu, 36H). Anal. Calc. for C₂₅₆H₂₁₆Au₁₂F₂₄N₄P₁₆: C, 46.14; H, 3.27; N, 0.84. Found: C, 45.92; H, 3.10; N, 0.81.

X-ray structural determination

Single crystals of 1 and 4 were immersed in cryo-oil, mounted on a Nylon loop, and measured at the temperatures of 120 K and 210 K, respectively. The X-ray diffraction data were collected on Bruker Smart Apex II and Bruker Kappa Apex II Duo diffractometers using Mo Kα radiation. The APEX2²¹ program package was used for cell refinements and data reductions. The structures were solved by direct methods using the SHELXS-2013²² programs with the WinGX²³ graphical user interface and the SHELXS-97 program²² incorporated into the OLEX2 program package.²⁴ A semi-empirical absorption correction (SADABS)²⁵ was applied to all data. Structural refinements were carried out using SHELXS-97 and SHELXL-2013.²² One of the phenyl rings in 1 was disordered over two positions (C38–C43, C138–C143) and was refined with occupancies 0.66/0.34. The displacement parameters of the carbon atoms of both components were constrained to be equal. The aromatic ring C138–C143 was geometrically idealized. Some of the solvent molecules in the unit cells of 1 and 4 were omitted as they were disordered and could not be resolved unambiguously. The missing solvent was taken into account using a SQUEEZE routine of PLATON²⁶ and was not included in the cell content. The H₂O hydrogens in 1 were positioned manually and were constrained to ride on their parent atoms O1 and O2, with U_iso = 1.5U_eq (parent atom). All other hydrogen atoms were positioned geometrically and constrained to ride on their parent atoms, with C–H = 0.95–0.99 Å, U_iso = 1.2–1.5U_eq (parent atom). The crystallographic details are summarized in Table 1.

Table 1 Crystal data for 1 and 4

	1	4
a R 1 = ∑||Fo| − |Fc||/∑|Fo|. b wR2 = [∑[w(Fo^2 − Fc^2)^2]/∑[w(Fo^2)^2]]^1/2.
Empirical formula	C98H98Au6F12N2O4P8	C260.47H224.70Au12Cl8.95F24N4P16
Fw	3025.34	7043.03
T (K)	120(2)	210(2)
λ (Å)	0.71073	0.71073
Cryst syst	Monoclinic	Monoclinic
Space group	P2/n	C2/c
a (Å)	16.2957(9)	30.2941(17)
b (Å)	18.2873(10)	34.3378(19)
c (Å)	18.9512(10)	26.6065(15)
α (°)	90	90
β (°)	91.857(2)	99.7320(10)
γ (°)	90	90
V (Å^3)	5644.6(5)	27 279(3)
Z	2	4
ρ calc (Mg m^−3)	1.780	1.715
μ(Mo Kα) (mm^−1)	7.946	6.673
No. reflns	41 225	108 842
Unique reflns	9723	24 020
GOOF (F^2)	1.078	0.988
R int	0.0482	0.0860
R 1 ^a (I ≥ 2σ)	0.0789	0.0677
wR2 ^b (I ≥ 2σ)	0.1808	0.1997

---

Computational details

The gold–phosphine cage compounds 1–4 were studied using the hybrid PBE0 density functional method combined with Grimme's D3 dispersion correction (DFT-PBE0-D).²⁷ The gold atoms were described by a triple-zeta-valence quality basis set with polarization functions (def2-TZVP).²⁸ Scalar relativistic effects were taken into account by applying a 60-electron relativistic effective core potential for Au.²⁹ A split-valence basis set with polarization functions on non-hydrogen atoms was used for all the other atoms.³⁰ All electronic structure calculations were carried out with the TURBOMOLE program package (version 6.4).³¹

Results and discussion

Synthesis

The metallophilicity-assisted approach to the synthesis of gold–phosphine cages involves the formation of the metal–ligand stereochemically rigid building units P_n(AuS*)_nⁿ⁺ (P_n = di- or triphosphine, i.e. n = 2, 3; S* = labile ligand, e.g. tetrahydrothiophene C₄H₈S), which can subsequently undergo a self-assembly process directed by a suitable single atom μ₃- or μ₄-bridging group X (e.g. μ₄-CR³⁻, μ₃-NR²⁻, Scheme 1).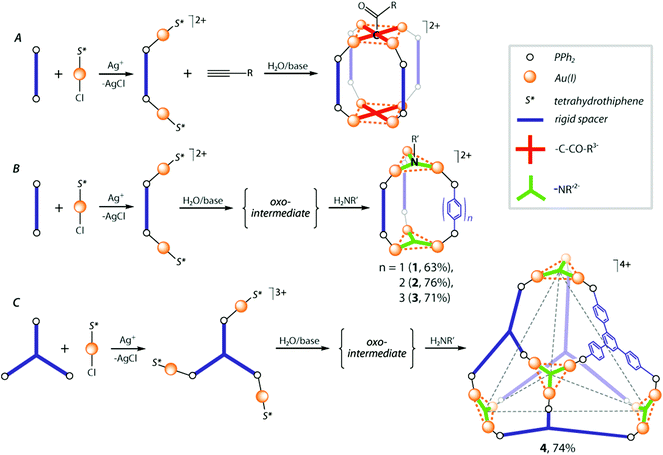

Scheme 1 Metallophilicity-assisted assembly of the gold–phosphine cages (A – ref. 15, B and C – the current work).

A key point in the preparation of 3D finite structures is an appropriate choice of a ligand X which can stabilize a gold(I) cluster coordinating center. Among these X moieties, reported in the literature for a number of clusters [P_nAu_n(μ_n-X)]^m+ (n = 3, 4; P = phosphine; X = O, S, Se, As, CR, NR, PR, R₃P:B),^32–34 the fragments R₃P:B³⁻, PR²⁻, NR²⁻, CR³⁻ seem to be the most promising templates as they can be introduced into the cage structures under mild conditions using the main group element nucleophiles (NH₂R, PH₂R, HC≡CR) and simultaneously prevent the formation of intermolecular {Au_n}⋯{Au_n} bonding in the solid state, often found for chalcogenido complexes.³³

As we reported earlier, terminal alkynes can be easily converted into the μ₄-methylydine group under basic conditions in the presence of diphosphine–gold cationic species, to give the stable cage complexes (Scheme 1A), which exist not only in the solid state, but retain their structures in solution.¹⁵ However, application of this protocol to the star-shaped triphosphines, e.g. 1,3,5,-tris(4-diphenylphosphinophenyl)benzene, did not bring positive results leading to insoluble material that was difficult to characterize. In order to expand this concept we investigated a possibility to use the imido μ₃-NR²⁻ bridging groups for the cage assembly (exemplified by R = Bu^t, Scheme 1B and C).

The auration of the primary amines with the gold–phosphine species requires initial preparation of the intermediate trinuclear oxo-complexes [(PR₃Au)₃(μ₃-O)]⁺,³⁵ which then readily react with NH₂R compounds.^34,36 Following this method, treatment of Au(tht)Cl (tht = tetrahydrothiophene) with stoichiometric amounts of a diphosphine ligand PP (PP = PPh₂-(C₆H₄)_n-PPh₂, n = 1–3) and AgPF₆ led to clean formation of the cationic PP{Au(tht)}₂²⁺ species. A reaction of the latter with H₂O/NEt₃ caused nearly quantitative precipitation of pale solids, virtually insoluble in common organic solvents that unfortunately prevented their characterization. Assuming that the obtained materials were the oxo-intermediates, they were tentatively formulated as [(PPAu₂)₃(μ₃-O)₂]_n(PF₆)_2n complexes. Indeed, according to the expectations, their interactions with an excess of NH₂Bu^t gave clear solutions from which tubular-like cage clusters [(PPAu₂)₃(μ₃-NBu^t)₂](PF₆)₂ (1–3) were isolated as colorless crystalline solids in moderate-to-good overall yields (see the Experimental section and Scheme 1B). Using the rigid triphosphine ligand PPP (PPP = 1,3,5,-tris(4-diphenylphosphinophenyl)benzene) in this reaction sequence, an unprecedented tetrahedral cage complex based on the cluster coordinating units, [(PPPAu₃)₄(μ₃-NBu^t)₄](PF₆)₄ (4), was successfully obtained (Scheme 1C).

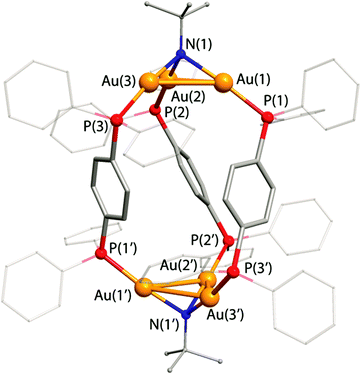
Structural analysis

The structures of the cages 1 and 4 in the solid state were determined by an X-ray diffraction analysis (Fig. 1 and 2, ORTEP views are shown in Fig. S1 and S2, ESI†). The molecule of 1 contains two Au₃(μ₃-NBu^t) units, which are linked by three diphosphine ligands thus forming a trigonal antiprism-like arrangement. Similarly to the congener compounds with planar Au₄ coordinating sites, [(PPAu₂)₄(μ₄-CCOPh)₂]²⁺,¹⁵ the trigold cluster cores in 1 are twisted with respect to each other to give the P and M helical geometries both found in the crystal cell.

Fig. 1 Molecular view of the complex 1²⁺. Hydrogen atoms and counterions are omitted for clarity. Selected interatomic distances (Å) are: N(1)–Au(1) 2.060(14), N(1)–Au(2) 2.055(14), N(1)–Au(3) 2.057(13), P(1)–Au(1) 2.242(4), P(2)–Au(2) 2.229(5), P(3)–Au(3) 2.238(5), Au(1)–Au(2) 2.9830(10), Au(1)–Au(3) 3.0698(10), Au(2)–Au(3) 2.9631(12). Symmetry transformations used to generate equivalent atoms: (′) 1.5 − x, y, −0.5 − z.

Fig. 2 Molecular view of the complex 4⁴⁺. Hydrogen atoms and counterions are omitted for clarity. The interstitial CH₂Cl₂ solvent molecule is shown in a spacefill mode. Selected interatomic distances (Å) are: N(1)–Au(1) 2.075(14), N(1)–Au(2) 2.044(13), N(1)–Au(3) 2.050(13), N(2)–Au(4) 2.068(13), N(2)–Au(5) 2.056(14), N(2)–Au(6) 2.070(14), P(1)–Au(1) 2.263(5), P(2)–Au(2) 2.236(5), P(3)–Au(3) 2.234(4), P(4)–Au(4) 2.235(5), P(5)–Au(5) 2.236(5), P(6)–Au(6) 2.229(5), Au(1)–Au(2) 2.9426(10), Au(1)–Au(3) 3.1480(10), Au(2)–Au(3) 3.0538(10), Au(4)–Au(5) 3.0244(10), Au(4)–Au(6) 3.0272(10), Au(5)–Au(6) 3.1446(11). Symmetry transformations used to generate equivalent atoms: (′) 1 − x, y, 0.5 − z.

Complex 4 adopts a tetrahedral geometry with the Au₃(μ₃-NBu^t) cluster fragments occupying the vertices, while the triphenylbenzene backbones of the phosphines form the faces of the cage. The non-linear environment of P atoms together with the coordination geometry of the Au₃ framework results in the appearance of axial chirality in the molecule of 4, which was also observed in the tetrahedral triphosphine compounds of coinage metal iodides M₄(PPP)I₄.³⁷ The trinuclear Au₃ cluster units in 1 and 4 are stabilized by the μ₃-bridging imido ligands NBu^t and effective aurophilic bonding. The metal–metal distances in these complexes lie in the range 2.9426(10)–3.1480(10) Å and are in good agreement with those found in the other trigold-imido clusters of the [(PR₃Au)₃(μ₃-NR)]⁺ type (2.926–3.333 Å).^34,36

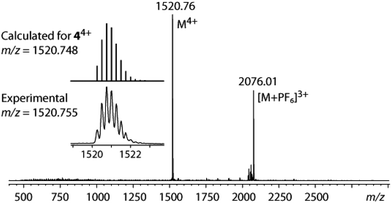
In the solid state the cage 4 was found to host a disordered dichloromethane crystallization molecule. According to the elemental analysis data, the CH₂Cl₂ guest can be easily removed under vacuum from the crystalline sample. The ESI-MS (see below) did not show any appreciable signs of solvent inclusion under the conditions of mass-spectroscopic experiment.

Spectroscopic characterization

In solution the complexes 1–4 were studied by ¹H and ³¹P NMR spectroscopy. The positive ion mode ESI-MS data confirm that the clusters retain their composition in solution showing the signals of the dications 1–3 with characteristic isotopic distributions at m/z 1331, 1445 and 1559, respectively (Fig. S3†). The mass-spectrum of 4 as well displays a dominant peak of the quadruply charged ion at m/z 1520.76 that exactly matches the stoichiometry of the intact [(PPPAu₃)₄(μ₃-NBu^t)₄]⁴⁺ cation (Fig. 3).

Fig. 3 ESI-MS of the complex 4.

The ³¹P NMR spectra of 1–4 show singlet resonances in a narrow range of δ (27.9–28.7) that is indicative of all equivalent phosphorus atoms coordinated to Au ions and is in agreement with the solid state structures. The ¹H NMR of 1–3 displays the spectroscopic patterns, which correspond to the idealized D_3h point symmetry group that is, however, higher than that found in the crystal of 1 (D₃). All the signals of the ortho–meta–para protons of the –PPh₂ groups represent a single set of resonances that points to the equivalence of the phenyl rings. The protons of the PP spacers –(C₆H₄)_n–, n = 1 (1), 2 (2), 3 (3), also give rise to the groups of signals which fit well the D_3h symmetry of the molecules. These spectroscopic patterns can be explained in terms of the fast (on the NMR timescale) right–left twisting of the “Au₆PP₃” framework that results in a flip motion of the helical isomers P↔M, which eventually leads to equivalence of the phenyl rings and increases the molecular symmetry in comparison with the crystalline state (Scheme 2).¹⁵

Scheme 2 A simplified top view of the complexes 1–3 showing possible interconversion of two helical isomers.

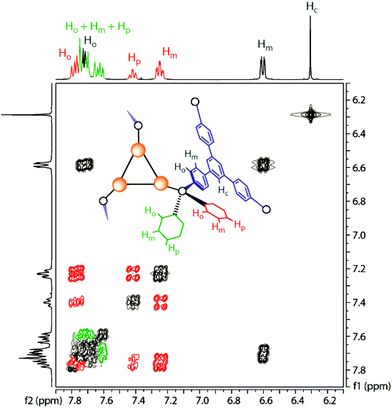
The solution behavior of the tetrahedral cage 4 is somewhat different from that of 1–3. The idealized symmetry of the molecule in the solid state corresponds to T point group. The architecture of the complex that exhibits axial chirality makes the triphosphine phenyl rings non-equivalent in every –PPh₂ fragment. In contrast to 1–3, which display a fast P↔M equilibrium, cluster 4 retains its configuration in solution according to the ¹H NMR data, as indicated by two clearly distinguishable sets of resonances corresponding to non-equivalent Ph protons in the phosphorus atoms environment (Fig. 4). One unresolved group of signals is found in a narrow region from 7.57 to 7.80 ppm and contains all the resonances of ortho, meta, and para-H atoms. In another group of Ph ring signals there are well resolved resonances at 7.77, 7.42 and 7.24 ppm corresponding to ortho, para and meta-H, respectively. This observation clearly points to high robustness of the tetrahedral cage and the absence of intramolecular dynamics found in the other tetrahedral complexes built of the mononuclear metal centers.³⁷

Fig. 4 ¹H–¹H COSY NMR (aromatic region) spectrum of 4, acetone-d₆, 298 K; the inset shows schematic representation of the non-equivalent phenyl rings in the molecule; the assignment of the signals to the –PPh₂ phenyl rings is arbitrary.

Computational results

We elucidated the structural characteristics of the gold–phosphine cages 1–4 by means of quantum chemical calculations at the DFT-PBE0-D level of theory (see the Experimental section for the details). First, the geometries of the cages were fully optimized using the ideal point group symmetries derived from the solid state structures of 1 and 4 (1–3: D₃; 4: T). We also carried out harmonic frequency calculations to confirm that the optimized structures are true local minima. The optimized geometries are illustrated in Fig. 5.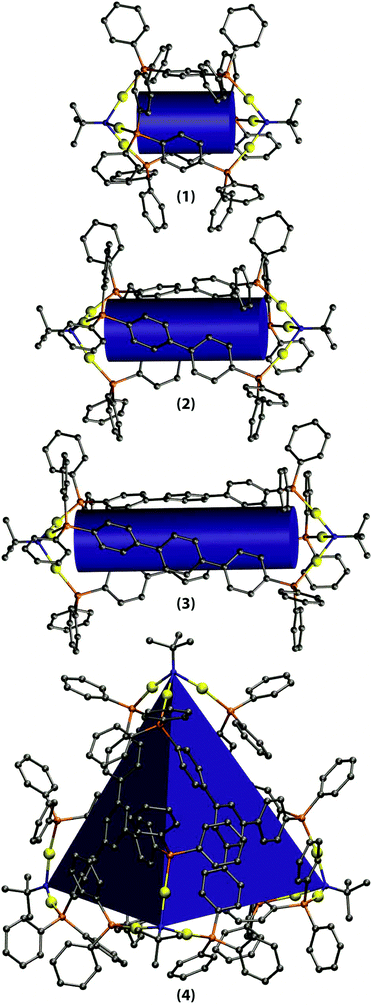

Fig. 5 Optimized structures of the gold–phosphine cages 1–4. The cylinders and the tetrahedron demonstrate the hollow cavities within the cages. Hydrogen atoms have been left out for clarity.

Even though the DFT calculations were carried out in the gas phase, the resulting geometries for 1 and 4 are in very good agreement with the respective solid state structures. For 1, the Au–Au distances in the X-ray structure are 2.96–3.07 Å, while the DFT-optimized distance is 3.09 Å. The N–N distance describing the overall dimensions of the cage is 10.7 Å in the X-ray structure and 10.4 Å in the optimized structure. Various bond distances such as Au–P and Au–N are reproduced with good accuracy (differences <0.05 Å). For 4, the Au–Au distances in the X-ray structure are 2.94–3.15 Å and the DFT-optimized distance of 3.06 Å is very close to the average Au–Au contact in the solid state structure. The N–N distances in the X-ray structure are 15.5–17.3 Å and also here the respective value for the DFT-optimized structure (16.7 Å) is practically similar to the average N–N separation in the X-ray structure. In the case of the cages 2 and 3, where no X-ray structure is available, the Au–Au distances are very similar to 1 (3.06 Å). The N–N distances of 2 and 3 are 14.8 and 19.3 Å, respectively. Including the D3 dispersion corrections in the structural optimizations clearly improved the agreement between the X-ray and DFT-optimized structures with respect to non-dispersion corrected results.

Since the applied computational method describes the structural characteristics of the gold–phosphine cages very well, we also investigated the difference in solution behavior of the cylindrical cages 1–3 and the tetrahedral cage 4. As discussed above, in solution the cages 1–3 display NMR patterns that correspond to the ideal D_3h point group symmetry, while the cage 4 retains the T-symmetric structure, instead of showing an NMR pattern corresponding to the ideal T_d point group. This difference between the two types of cages arises from the twisting-type interconversion of the gold–phosphine framework, which occurs in the case of 1–3, but not in the case of 4. We investigated the energetic barriers for the twisting-type interconversion for all four clusters. During the twisting, the cages 1–3 pass through a D_3h-symmetric transition state, where the capping gold triangles are in an eclipsed conformation instead of the staggered one in the D₃-symmetry (see Scheme 2). Similarly, the cage 4 should pass through a T_d-symmetric transition state when twisting from one T-symmetric minimum to another. We optimized the D_3h- and T_d-symmetric transition states by means of a constrained optimization where the positions of the P atoms were fixed (if no atoms are fixed, the cages will revert back to D₃ or T symmetry during the optimization). The energy barriers for the D₃ → D_3h → D₃ conversion in the cages 1–3 turned out to be significantly smaller than for the T → T_d → T conversion in the cage 4. The twisting barrier is the lowest for the cage 1, where it is 82 kJ mol⁻¹. The true twisting barriers in solution are expected to be lower than this since the transition states here are obtained from constrained optimization, but the relative twisting barriers of the cages show a very clear trend. The twisting barriers of the cages 2 and 3 relative to the cage 1 are only 24 and 3 kJ mol⁻¹ higher (cage 3 is slightly more flexible than cage 2 due to the longer phenyl spacer). For comparison, the twisting barrier in cage 4 relative to the cage 1 is an order of magnitude higher, 230 kJ mol⁻¹. Hence, the difference in solution behavior of 1–3 and 4 can be attributed to the significantly higher energy barrier for the twisting-type interconversion in the cage 4.

Conclusions

In summary, we have demonstrated a so far rare possibility of using the phosphine ligands and polynuclear coordination centers for the effective construction of supramolecular cage molecules. The synthetic approach is based on aurophilicity-driven aggregation of the Au(I) ions into the small Au₃ clusters stabilized by the μ₃-NR²⁻ bridging imido groups. Conducting this process in the presence of the di- or triphosphine ligands P_n (n = 2, 3) of suitable stereochemistry results in self-assembly of the coordination precursors P_n(AuS*)_nⁿ⁺ (S* = labile ligand) into the finite 3D structures. Depending on the denticity of the phosphines used the tubular-like cage clusters [(P₂Au₂)₃(μ₃-NBu^t)₂]²⁺ (1–3) and the tetrahedral complex [(P₃Au₃)₄(μ₃-NBu^t)₄]⁴⁺ (4) were isolated. All the compounds under study retain their composition in solution according to the NMR and ESI-MS data. The cylindrical cages 1–3 were shown to undergo fast interconversion of the helical P↔M isomers, while the architecture of the tetrahedron 4 having axial chirality found in the crystalline state remains intact in the fluid medium. The computational studies of the geometries of the complexes and of the twisting-type dynamic behavior are in good agreement with experimental observations suggesting a significantly higher energy barrier for the P↔M isomerization in the cage 4.

Acknowledgements

This research has been supported by the strategic funding of the University of Eastern Finland (Russian-Finnish collaborative project and Spearhead project), Saint-Petersburg State University research grant 12.37.132.2011, the Academy of Finland (grant 268993, I.O.K.; grant 138560/2010, A.J.K.) and the Russian Foundation for Basic Research (grants 11-03-00541 and 13-03-12411). NMR and XRD studies were performed at the Centers for Magnetic Resonance and X-ray Diffraction of St. Petersburg State University. A.J.K. gratefully acknowledges computing time from the CSC – the Finnish IT Center for Science.

Notes and references

1. M. Fujita and M. Yoshizawa, in Modern Supramolecular Chemistry: Strategies for Macrocycle Synthesis, ed. F. Diederich, P. J. Stang and R. R. Tykwinski, Wiley-VCH, Weinheim, 2008, pp. 277–314; R. W. Saalfrank, H. Maid and A. Scheurer, Angew. Chem., Int. Ed., 2008, 47, 8794–8824; S. J. Dalgarno, N. P. Power and J. L. Atwood, Coord. Chem. Rev., 2008, 252, 825–841; M. D. Ward, Chem. Commun., 2009, 4487–4499; M. D. Pluth, R. G. Bergman and K. N. Raymond, Acc. Chem. Res., 2009, 42, 1650–1659; R. Chakrabarty, P. S. Mukherjee and P. J. Stang, Chem. Rev., 2011, 111, 6810–6918; Y. Inokuma, M. Kawano and M. Fujita, Nat. Chem., 2011, 3, 349–358; H. Amouri, C. Desmarets and J. Moussa, Chem. Rev., 2012, 112, 2015–2041; K. N. Raymond and C. J. Brown, Top. Curr. Chem., 2012, 323, 1–18; T. K. Ronson, S. Zarra, S. P. Black and J. R. Nitschke, Chem. Commun., 2013, 49, 2476–2490; T. R. Cook, Y.-R. Zheng and P. J. Stang, Chem. Rev., 2013, 113, 734–777.
2. M. Yoshizawa, J. K. Klosterman and M. Fujita, Angew. Chem., Int. Ed., 2009, 48, 3418–3438.
3. M. Yoshizawa, M. Tamura and M. Fujita, J. Am. Chem. Soc., 2004, 126, 6846–6847; D. H. Leung, R. G. Bergman and K. N. Raymond, J. Am. Chem. Soc., 2008, 130, 2798–2805.
4. M. Yoshizawa, S. Miyagi, M. Kawano, K. Ishiguro and M. Fujita, J. Am. Chem. Soc., 2004, 126, 9172–9173.
5. P. Mal, B. Breiner, K. Rissanen and J. R. Nitschke, Science, 2009, 324, 1697–1699; S. Horiuchi, T. Murase and M. Fujita, J. Am. Chem. Soc., 2011, 133, 12445–12447; H. Takezawa, T. Murase and M. Fujita, J. Am. Chem. Soc., 2012, 134, 17420–17423.
6. Z. J. Wang, C. J. Brown, R. G. Bergman, K. N. Raymond and F. D. Toste, J. Am. Chem. Soc., 2011, 133, 7358–7360.
7. M. A. Furrer, F. Schmitt, M. Wiederkehr, L. Juillerat-Jeanneret and B. Therrien, Dalton Trans., 2012, 41, 7201–7211; B. Therrien, Top. Curr. Chem., 2012, 319, 35–56; F. Schmitt, J. Freudenreich, N. P. E. Barry, L. Juillerat-Jeanneret, G. Suss-Fink and B. Therrien, J. Am. Chem. Soc., 2012, 134, 754–757; B. Therrien, Chem.–Eur. J., 2013, 19, 8378–8838.
8. J. H. K. Yip and J. Prabhavathy, Angew. Chem., Int. Ed., 2001, 40, 2159–2162; R. Lin, J. H. K. Yip, K. Zhang, L. L. Koh, K.-Y. Wong and H. K. Piu, J. Am. Chem. Soc., 2004, 126, 15852–15869; R. Lin and J. H. K. Yip, Inorg. Chem., 2006, 45, 4423–4430; R. J. Puddephatt, Chem. Soc. Rev., 2008, 37, 2012–2027; S. Bhargava, K. Kitadai, T. Masashi, D. W. Drumm, S. P. Russo, V. W.-W. Yam, T. Kwok-Ming Lee, J. Waglere and N. Mirzadeh, Dalton Trans., 2012, 41, 4789–4798.
9. S. L. James, Chem. Soc. Rev., 2009, 38, 1744–1758.
10. S. L. James, D. M. P. Mingos, A. J. P. White and D. J. Williams, Chem. Commun., 1998, 2323–2324.
11. J. Zhang, M. Nieuwenhuyzen, J. P. H. Charmant and S. L. James, Chem. Commun., 2004, 2808–2809.
12. X. Wang, J. Huang, S. Xiang, Y. Liu, J. Zhang, A. Eichhöfer, D. Fenske, S. Baic and C.-Y. Su, Chem. Commun., 2011, 47, 3849–3851.
13. S. H. Lim, Y. Su and S. M. Cohen, Angew. Chem., Int. Ed., 2012, 51, 5106–5109.
14. C. Silvestru, in Modern Supramolecular Gold Chemistry, ed. A. Laguna, Wiley-VCH, Weinheim, 2008, pp. 181–295; H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2012, 41, 370–412.
15. I. O. Koshevoy, M. Haukka, S. I. Selivanov, S. P. Tunik and T. A. Pakkanen, Chem. Commun., 2010, 46, 8926–8928.
16. P. Sevillano, T. Langetepe and D. Fenske, Z. Anorg. Allg. Chem., 2003, 629, 207–214.
17. R. A. Baldwin and M. T. Cheng, J. Org. Chem., 1967, 32, 1572–1577.
18. I. O. Koshevoy, A. J. Karttunen, S. P. Tunik, M. Haukka, S. I. Selivanov, A. S. Melnikov, P. Y. Serdobintsev, M. A. Khodorkovskiy and T. A. Pakkanen, Inorg. Chem., 2008, 47, 9478–9488.
19. I. O. Koshevoy, L. Koskinen, E. S. Smirnova, M. Haukka, T. A. Pakkanen, A. S. Melnikov and S. P. Tunik, Z. Anorg. Allg. Chem., 2010, 636, 795–802.
20. R. Uson, A. Laguna and M. Laguna, Inorg. Synth., 1989, 26, 85–91.
21. APEX2 – Software Suite for Crystallographic Programs, Bruker AXS, Inc., Madison, WI, USA, 2009.
22. G. M. Sheldrick, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2008, 64, 112–122.
23. L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849–854.
24. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
25. G. M. Sheldrick, SADABS-2008/1 – Bruker AXS area detector scaling and absorption correction, Bruker AXS, Madison, Wisconsin, USA, 2008.
26. A. L. Spek, PLATON, A Multipurpose Crystallographic Tool, Utrecht University, Utrecht, The Netherlands, 2005.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868; S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
28. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
29. D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chem. Acc., 1990, 77, 123–141.
30. A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
31. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
32. H. Schmidbaur, E. Zeller, G. Weidenhiller, O. Steigelmann and H. Beruda, Inorg. Chem., 1992, 2370–2376; A. Blumenthal, H. Beruda and H. Schmidbaur, J. Chem. Soc., Chem. Commun., 1993, 1005–1006; J. Vicente, M. T. Chicote, R. Guerrero and P. G. Jones, J. Am. Chem. Soc., 1996, 118, 699–700; E. Zeller, H. Beruda, A. Kolb, P. Bissinger, J. Riede and H. Schmidbaur, Nature, 1991, 352, 141–143.
33. O. Crespo, M. C. Gimeno, A. Laguna, C. Larraz and M. D. Villacampa, Chem.–Eur. J., 2007, 13, 235–246; S. Canales, O. Crespo, C. Gimeno, P. G. Jones and A. Laguna, Chem. Commun., 1999, 679–680.
34. V. Ramamoorthy and P. R. Sharp, Inorg. Chem., 1990, 29, 3336–3339.
35. Y. Yang, V. Ramamoorthy and P. R. Sharp, Inorg. Chem., 1993, 32, 1946–1950.
36. H. Schmidbaur, A. Kolb and P. Bissinger, Inorg. Chem., 1992, 31, 4370–4375.
37. S. H. Lim and S. M. Cohen, Inorg. Chem., 2013, 52, 7862–7872.

---

Footnote

† Electronic supplementary information (ESI) available: X-ray crystallographic data in CIF for 1 and 4, additional spectroscopic data, optimized Cartesian coordinates of the studied systems in atomic units. CCDC 977750 and 952114. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c3dt53645a

---