A partial differential equation for pseudocontact shift
Received
15th July 2014
, Accepted 31st July 2014
First published on 4th August 2014
Abstract
It is demonstrated that pseudocontact shift (PCS), viewed as a scalar or a tensor field in three dimensions, obeys an elliptic partial differential equation with a source term that depends on the Hessian of the unpaired electron probability density. The equation enables straightforward PCS prediction and analysis in systems with delocalized unpaired electrons, particularly for the nuclei located in their immediate vicinity. It is also shown that the probability density of the unpaired electron may be extracted, using a regularization procedure, from PCS data.
Introduction
Pseudocontact shift (PCS) is an effective additional contribution to the nuclear chemical shift that arises in open-shell chemical systems due to partial polarization of the electron spin by the applied magnetic field.1 The primary application of PCS is in structural biology, where it provides additional distance restraints for molecular geometry determination.2,3Pseudocontact shift is different from the contact shift in that it does not require electron-nuclear overlap and propagates instead through the dipolar coupling.1
It can be verified by direct inspection that the commonly used point electron dipole expression for the PCS4 has a zero Laplacian everywhere except the origin:
| | 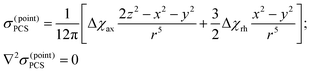 | (1) |
where Δ
χax and Δ
χrh are axiality and rhombicity of the electron magnetic susceptibility tensor
χ and the nucleus is located at [
x,
y,
z] relative to the electron. This is to be expected – all classical electromagnetic phenomena must obey Maxwell's equations – but the singularity at the origin also suggests the possibility of an elliptic partial differential equation existing for the harder case of the PCS generated by a
non-point electron probability density
ρ(
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
):
| | σ(non-point)PCS = ∫σ(point)PCS(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) − − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′)ρ( ′)ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′)d3 ′)d3![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′; ∇2σ(non-point)PCS = κ(χ, ′; ∇2σ(non-point)PCS = κ(χ, ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) ) | (2) |
in which the source term
κ(
χ,
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
) is unknown and has so far resisted all derivation attempts: a direct calculation of the Laplacian of the convolution of
eqn (1) with a finite unpaired electron density comes across singular integrals that cannot be regularized.
5 Yet the prize is tempting – elliptic PDEs are a classical topic in mathematics: a simple enough equation would generalize all PCS prediction and analysis problems, improve data interpretation close to the unpaired electron and enable direct measurement of spin label probability distributions in double electron-electron resonance (DEER) experiments.
6 It would also be convenient – numerical PDE solvers are standard functionality in modern technical computing software. In this communication we derive the equation and comment on some of its properties.
Hyperfine shift as a total energy derivative
To facilitate subsequent mathematics, and also for the sake of completeness, we provide in this section succinct derivations, using the relatively modern total energy derivative formalism,7 of the classical expressions for the various components of the hyperfine shift tensor.1,4 For historical reasons we shall separate the hyperfine shift tensorσHF into the contact shift tensorσCS and the dipolar shift tensorσDS. Their isotropic parts shall be called contact shift and pseudocontact shift, and denoted σCS and σPCS respectively.
Placed in a magnetic field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) 0, a point electron at the origin with a magnetic susceptibility tensor χ ≪ 1 would acquire an average magnetic moment:
0, a point electron at the origin with a magnetic susceptibility tensor χ ≪ 1 would acquire an average magnetic moment:
| | ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) e = χ· e = χ·![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) 0/μ0 0/μ0 | (3) |
The additional magnetic field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) 1 generated by this dipole at the point
1 generated by this dipole at the point ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) is:
is:
| | 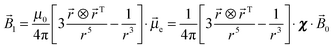 | (4) |
The change in energy E for a nuclear magnetic dipole ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) N located at that point would be:
N located at that point would be:
| | 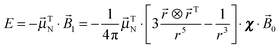 | (5) |
and therefore, the additional chemical shift tensor experienced by the nucleus, measured relative to the unperturbed conditions, would be:
| | 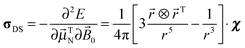 | (6) |
where the minus appears because of the relationship between chemical shielding and chemical shift.
8,9 The isotropic part of this tensor is:
| | 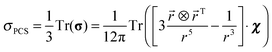 | (7) |
For a point electron located at ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) e and a point nucleus located at
e and a point nucleus located at ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) N the final expression is:
N the final expression is:
| | 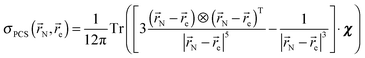 | (8) |
A neat derivation for the hyperfine shift can also be given in terms of the hyperfine coupling tensor A. The spin Hamiltonian for the hyperfine interaction is 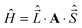 and therefore the corresponding energy change for the k-th nucleus in the system is:
and therefore the corresponding energy change for the k-th nucleus in the system is:
| | 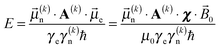 | (9) |
After using the same derivative expression for the chemical shielding,7 we obtain:
| | 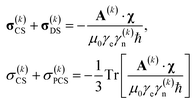 | (10) |
A significant advantage of these equations over other physically equivalent formulations is that the excitation structure of the quantum chemistry part of the problem is hidden from the user – both the hyperfine tensor and the susceptibility tensor are effective quantities that already incorporate all of the formidable complexities of the electronic structure theory.7 The derivations given above are classical, but the only assumption in eqn (10) is that χ ≪ 1 (meaning also that magnetic hyperpolarizability terms in the electronic structure theory are negligible) and that the electron relaxes sufficiently rapidly for eqn (3) to always remain valid.
Eqn (8), in its various forms, has done considerable service to the NMR community over the last forty years – naturally occurring calcium, magnesium and other metals in biological systems can often be substituted with lanthanides and pseudocontact shift then used to obtain distance restraints for structure determination purposes.2,3 The point electron dipole assumption does, however, have its validity range – eqn (8) is not applicable in close proximity of the metal centre, most notably in lanthanide spin labels, and also in the cases where the electron probability density is broadly distributed within the molecular structure.
Derivation of the elliptic PDE
The source term κ(χ, ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) in eqn (2) for pseudocontact shift induced by a distributed electron is not currently known. The most straightforward derivation is to notice that:
) in eqn (2) for pseudocontact shift induced by a distributed electron is not currently known. The most straightforward derivation is to notice that:| | 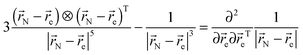 | (11) |
and to note that the Laplacian of the reciprocal distance is:| | 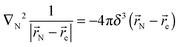 | (12) |
With these observations in place, we can conclude that:
| | 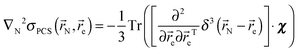 | (13) |
The convolution of this expression with a finite electron probability density distribution ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) e) then yields (after dropping the N subscript on the nuclear coordinate vector
e) then yields (after dropping the N subscript on the nuclear coordinate vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) N):
N):
| | 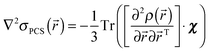 | (14) |
After abbreviating the Hessian of ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) in square brackets
) in square brackets
| | 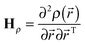 | (15) |
we arrive at a neat final result:
| | | ∇2σPCS = −(1/3)Tr[Hρ·χ] | (16) |
A similar derivation for the full 3 × 3 dipolar shift tensor in eqn (6) yields:
If chemical shielding is considered instead of the chemical shift, the minus sign on the right hand side disappears. Simplicity of eqn (16) and (17) stands in sharp contrast with the unfathomable spherical harmonic expansions10 generated by ab initio treatments using the ligand field theory. It should be noted that eqn (16) and (17) only apply to pseudocontact and dipolar shift respectively. For contact shifts a convenient description is provided by eqn (10), where the isotropic part of the hyperfine tensor is proportional to the local spin density.
Analytical and numerical solutions
General solution strategies for eqn (16) and (17) are identical to those of Poisson's equation.11 The special case of the point electron in eqn (7) is recovered by observing that the Green's function of the Laplacian is:| | 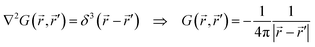 | (18) |
and taking its convolution with the right hand side of eqn (16) for the point electron:| | 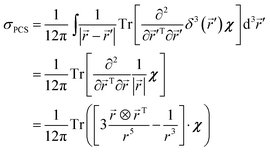 | (19) |
Analytical treatments of more general unpaired electron probability density distributions may be simplified significantly by noting that the Laplacian in eqn (16) and (17) leaves spherical harmonics intact. General solutions of those equations therefore simply inherit the multipolar expansion from the source term in the same way as Poisson's equation solutions do:12
| | 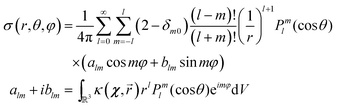 | (20) |
where
κ(
χ,
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
) is either the right hand side of
eqn (16), or each of the nine matrix elements on the right hand side of
eqn (17).
This is the general analytical solution for eqn (16) and for each matrix element of eqn (17), but in practice the interpretation of multipole moments with l > 2 is difficult. We would argue here that numerical treatment is easier computationally and also more interpretable from the physical point of view because the fundamental quantity there is the unpaired electron probability density ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ). Sparse matrix representations of 3D Laplacians with Dirichlet, Neumann or periodic boundary conditions are readily available,13 and the numerical solution of eqn (16) and (17) requires a single sparse matrix-inverse-times-vector operation:
). Sparse matrix representations of 3D Laplacians with Dirichlet, Neumann or periodic boundary conditions are readily available,13 and the numerical solution of eqn (16) and (17) requires a single sparse matrix-inverse-times-vector operation:
| | | σPCS = −(1/3)L−1 vec[Tr(Hρ·χ)] | (21) |
where
L is a matrix representation of the 3D Laplacian with appropriate boundary conditions
13 and vec[Tr(
Hρ·
χ)] denotes the index transformation that stretches [Tr(
Hρ·
χ)], which is a three-dimensional array, into a column vector.
Eqn (21) has been implemented into versions 1.5 and later of our
Spinach library.
14
A practical example of pseudocontact shift field being computed for a lanthanide complex using eqn (16) is shown in Fig. 1. Nuclear coordinates, electron probability density and the susceptibility tensor have all been estimated using DFT methods in Gaussian09 (see figure caption for the details of the methods used). The conclusion from Fig. 1 is, at least for this complex, that the accuracy of the point PCS model is very high, presumably due to the localized nature of the f orbitals under the relatively low ligand field of the C4-symmetric N8 cyclen ligand, and it is mostly the contact shift that is making PCS interpretation difficult.
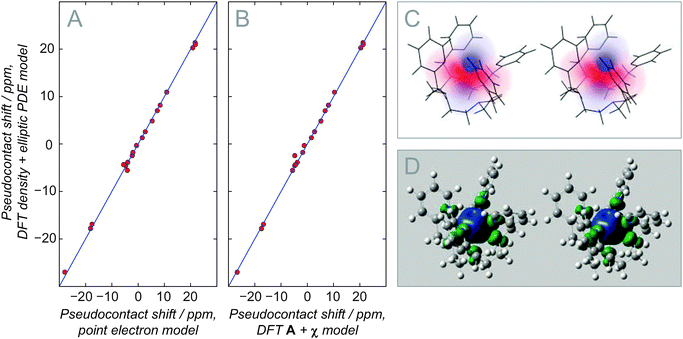 |
| | Fig. 1 An example of the forward problem solution and a demonstration of the mutual consistency of eqn (8), (10) and (17). The red points refer to the symmetry-unique atoms in the ligand, including carbons and protons, but excluding nitrogens that have significant contact shifts. (A) Point model versus the elliptic PDE in eqn (16) for the PCS in the complex of europium(III) with 1,4,7,10-tetrakis(2-pyridylmethyl)-1,4,7,10-tetraazacyclododecane24 using the magnetic susceptibility tensor obtained from a DFT calculation. (B) Point model versus the PCS part of eqn (10) using hyperfine tensors and the magnetic susceptibility tensor from a DFT calculation. (C) Volumetric stereo plot of the PCS field computed using eqn (16) with the electron probability density and the susceptibility tensor obtained from a DFT calculation. (D) Stereo plot of electron spin density isosurface (at the isovalues of ±0.0004) in the complex. In all cases, the molecular geometry was optimized and the electron spin density estimated using DFT UB3LYP method25,26 in vacuum with cc-pVTZ basis set27 on light atoms and Stuttgart ECP basis set on europium.28 CSGT DFT UB3LYP29 method with the same combination of basis sets was used to estimate the magnetic susceptibility tensor. Simulation source code is available within the example set of Spinach library version 1.5 and later.14 | |
Inverse problems
The most interesting possibility offered by eqn (16) and (17) is model-free recovery of the electron probability density distribution ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) and the susceptibility tensor χ from nuclear coordinates and pseudocontact shifts, in particular, for spin label conformation analysis in DEER experiments. The problem may be formulated as a minimization condition, with respect to
) and the susceptibility tensor χ from nuclear coordinates and pseudocontact shifts, in particular, for spin label conformation analysis in DEER experiments. The problem may be formulated as a minimization condition, with respect to ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) = vec[ρ(
= vec[ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )] and χ, for the following regularized least squares error functional:
)] and χ, for the following regularized least squares error functional:
Ω(![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) ) = ‖PL−1K ) = ‖PL−1K![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) − − ![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) expt‖2 + λ1〈 expt‖2 + λ1〈![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) |ln( |ln(![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) )〉 + λ2‖L )〉 + λ2‖L![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) ‖2 ‖2 |
| | K![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) = −(1/3)vec[Tr(Hρ·χ)] = −(1/3)vec[Tr(Hρ·χ)] | (22) |
where P is the matrix that projects out pseudocontact shifts at nuclear locations, ![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) expt is a vector of experimental PCS data and λ1,2 are Tikhonov regularization parameters.15 The uncommon choice of regularization operators (maximum entropy and minimum Laplacian norm) is dictated by two practical considerations:
expt is a vector of experimental PCS data and λ1,2 are Tikhonov regularization parameters.15 The uncommon choice of regularization operators (maximum entropy and minimum Laplacian norm) is dictated by two practical considerations:
1. Electron probability distribution is expected to be localized in at least one dimension – even extended conjugated systems, such as porphyrin and carotene radicals, have electron spin densities that closely follow the bonding network. Maximum entropy regularization is known to favour local solutions unencumbered by baseline noise,16 hence the presence of λ1〈![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) |ln(
|ln(![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) )〉 term in eqn (22).
)〉 term in eqn (22).
2. Electron probability distribution is not infinitely sharp – some penalty should be placed that enforces a measure of broadening. Because electron spin densities often have symmetric distributions in PCS systems, high multipoles should also be discouraged in the solution. Both objectives are accomplished by λ2‖L![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) ‖2 term in eqn (22).
‖2 term in eqn (22).
Ω(![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) ) is non-linear with respect to
) is non-linear with respect to ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) , necessitating the use of numerical minimization methods (the memory-conserving version of the quasi-Newton method proposed by Broyden, Fletcher, Goldfarb and Shanno17 is used here), but good initial guesses may be obtained by noting that, for λ1 = 0, the global minimum of Ω(
, necessitating the use of numerical minimization methods (the memory-conserving version of the quasi-Newton method proposed by Broyden, Fletcher, Goldfarb and Shanno17 is used here), but good initial guesses may be obtained by noting that, for λ1 = 0, the global minimum of Ω(![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) ) with respect to
) with respect to ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) is analytical:
is analytical:
| | ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) min = (ATA + λ2LTL)−1AT min = (ATA + λ2LTL)−1AT![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) expt, A = PL−1K expt, A = PL−1K | (23) |
A synthetic example of computing the PCS field generated by multiple paramagnetic centres and then recovering their distribution from PCS data is given in Fig. 2. Additional constraints on the probability density are non-negativity, fixed integral and zero boundary conditions:
| | ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) ≥ 0; ∫ρ( ) ≥ 0; ∫ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )d3 )d3![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) = N; ρ(∞) = ρ′(∞) = 0 = N; ρ(∞) = ρ′(∞) = 0 | (24) |
where
N is the number of unpaired electrons in the system. Because the error functional in
eqn (22) has two regularization parameters, a generalization of the
L-curve method
18 to surfaces
19 is used here. Better regularization methods for
eqn (16) that could improve the fidelity of the reconstruction in
Fig. 2C are undoubtedly possible, but are beyond the scope of the present work.
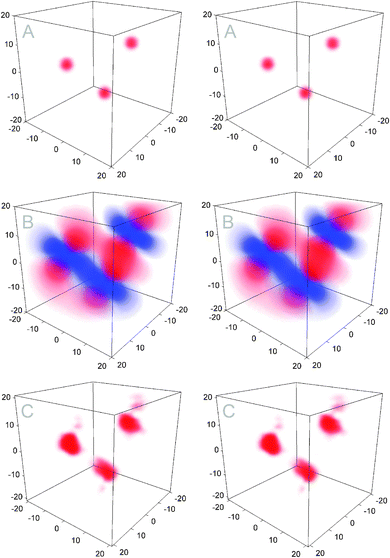 |
| | Fig. 2 An example of the inverse problem solution where the electron probability distribution is recovered from PCS data. (A) Volumetric stereo plot of a model system with three electrons with a randomly assigned susceptibility tensor and Gaussian probability distributions randomly positioned within a 20 × 20 × 20 Angstrom cube. (B) Volumetric stereo plot of the PCS field obtained from the probability density cube shown in (A) using eqn (21). (C) Volumetric stereo plot of the electron probability distribution obtained by solving the inverse problem as described in the main text. Pseudocontact shift was sampled at 500 random points emulating nuclear locations within the volume and fed into eqn (22), which was then minimized from a random initial guess. Simulation source code is available within the example set of Spinach library version 1.5 and later.14 | |
Conclusions
Eqn (16) and (17) provide a simple and numerically friendly alternative to voluminous and abstruse multipolar expansions in situations where electron probability distributions deviate significantly from the point electron case. Both forward (PCS from ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) and χ) and backward (χ and ρ(
) and χ) and backward (χ and ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) from PCS) calculations are straightforward – the former is accomplished in a single sparse matrix-inverse-times-vector operation prescribed by eqn (21) and the latter is an instance of Tikhonov regularization of the well-researched source recovery problem for an elliptic PDE20 with the error functional specified in eqn (22).
) from PCS) calculations are straightforward – the former is accomplished in a single sparse matrix-inverse-times-vector operation prescribed by eqn (21) and the latter is an instance of Tikhonov regularization of the well-researched source recovery problem for an elliptic PDE20 with the error functional specified in eqn (22).
Attention should also be drawn again to the simple general connection between hyperfine shift and hyperfine coupling provided by eqn (10) – modern electronic structure theory packages are able to compute both hyperfine tensors and magnetic susceptibility tensors, meaning that hyperfine shift may be obtained essentially for free after standard magnetic property runs in ADF,21 ORCA22 or Gaussian,23 subject only to the electron spin relaxation time being sufficiently short for the approximation made in eqn (3) to be valid.
The source code for all examples provided above, as well as numerical infrastructure functions (3D finite difference operators, 3D interpolation operators, Tikhonov solvers, volumetric scalar field visualizer, etc.), are available in versions 1.5 and later of Spinach library.14
Acknowledgements
The authors are grateful to Alan Kenwright, Claudio Luchinat, Gottfried Otting, Giacomo Parigi, David Parker and Guido Pintacuda for stimulating discussions. This work is supported by EPSRC (EP/H003789/1).
References
- I. Bertini, C. Luchinat and G. Parigi, Magnetic susceptibility in paramagnetic NMR, Prog. Nucl. Magn. Reson. Spectrosc., 2002, 40, 249–273 CrossRef CAS.
- I. Bertini, C. Luchinat and G. Parigi, Paramagnetic constraints: an aid for quick solution structure determination of paramagnetic metalloproteins, Concepts Magn. Reson., 2002, 14, 259–286 CrossRef CAS PubMed.
- G. Otting, Protein NMR Using Paramagnetic Ions, Annu. Rev. Biophys., 2010, 39, 387–405 CrossRef CAS PubMed.
-
I. Bertini, C. Luchinat and G. Parigi, Solution NMR of paramagnetic molecules: applications to metallobiomolecules and models, Elsevier, 2001 Search PubMed.
-
G. T. P. Charnock, Computational Spin Dynamics and Visualisation of Large Spin Systems, DPhil thesis, Department of Computer Science, University of Oxford, 2012 Search PubMed.
- G. Jeschke, V. Chechik, P. Ionita, A. Godt, H. Zimmermann, J. Banham, C. R. Timmel, D. Hilger and H. Jung, DeerAnalysis2006 – a comprehensive software package for analyzing pulsed ELDOR data, Appl. Magn. Reson., 2006, 30, 473–498 CrossRef CAS.
-
M. Kaupp, M. Bühl and V. G. Malkin, Calculation of NMR and EPR parameters: theory and applications, Wiley, 2004 Search PubMed.
- R. K. Harris, Conventions for tensor quantities used in NMR, NQR and ESR, Solid State Nucl. Magn. Reson., 1998, 10, 177–178 CrossRef CAS.
- C. J. Jameson, Reply to “Conventions for tensor quantities used in nuclear magnetic resonance, nuclear quadrupole resonance and electron spin resonance spectroscopy”, Solid State Nucl. Magn. Reson., 1998, 11, 265–268 CrossRef CAS.
- R. M. Golding and L. C. Stubbs, The theory of the pseudocontact dontribution to NMR shifts of d1-transition and d2-transition metal-ion systems in sites of octahedral symmetry, J. Magn. Reson., 1980, 40, 115–133 CAS.
- S. D. Poisson, Remarques sur l'équation qui se présente dans la théorie des attractions des sphéroïdes, Nouveau Bulletin des Sciences par la Société Philomatique de Paris, 1812–1813, 3, 388–392 Search PubMed.
- N. Takaaki and A. Shigeru, A projective method for an inverse source problem of the Poisson equation, Inverse Probl., 2003, 19, 355 CrossRef.
- A. Knyazev, M. Argentati, I. Lashuk and E. Ovtchinnikov, Block Locally Optimal Preconditioned Eigenvalue Xolvers (BLOPEX) in Hypre and PETSc, SIAM J. Sci. Comput., 2007, 29, 2224–2239 CrossRef.
- H. J. Hogben, M. Krzystyniak, G. T. P. Charnock, P. J. Hore and I. Kuprov, Spinach - a software library for simulation of spin dynamics in large spin systems, J. Magn. Reson., 2011, 208, 179–194 CrossRef CAS PubMed.
-
A. N. Tikhonov, Numerical methods for the solution of ill-posed problems, Kluwer, 1995 Search PubMed.
- P. Hodgkinson, H. R. Mott, P. C. Driscoll, J. A. Jones and P. J. Hore, Application of maximum entropy methods to 3-dimensional NMR spectroscopy, J. Magn. Reson., 1993, 101, 218–222 CrossRef CAS.
- D. C. Liu and J. Nocedal, On the Limited Memory BFGS Method for Large-Scale Optimization, Math. Program., 1989, 45, 503–528 CrossRef.
- P. Hansen and D. O'Leary, The Use of the L-Curve in the Regularization of Discrete Ill-Posed Problems, SIAM J. Sci. Comput., 1993, 14, 1487–1503 CrossRef.
- B. Murat, E. K. Misha and L. M. Eric, Efficient determination of multiple regularization parameters in a generalized L-curve framework, Inverse Probl., 2002, 18, 1161 CrossRef.
- I. Kazufumi and L. Ji-Chuan, Recovery of inclusions in 2D and 3D domains for Poisson's equation, Inverse Probl., 2013, 29, 075005 CrossRef.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS PubMed.
- F. Neese, The ORCA program system, Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS PubMed.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009 Search PubMed.
- L. S. Natrajan, N. M. Khoabane, B. L. Dadds, C. A. Muryn, R. G. Pritchard, S. L. Heath, A. M. Kenwright, I. Kuprov and S. Faulkner, Probing the Structure, Conformation, and Stereochemical Exchange in a Family of Lanthanide Complexes Derived from Tetrapyridyl-Appended Cyclen, Inorg. Chem., 2010, 49, 7700–7709 CrossRef CAS PubMed.
- A. D. Becke, A New Mixing of Hartree–Fock and Local Density-Functional Theories, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS PubMed.
- C. T. Lee, W. T. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron-Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS PubMed.
- M. Kaupp, P. V. Schleyer, H. Stoll and H. Preuss, Pseudopotential Approaches to Ca, Sr, and Ba Hydrides - Why Are Some Alkaline-Earth MX2 Compounds Bent, J. Chem. Phys., 1991, 94, 1360–1366 CrossRef CAS PubMed.
- T. A. Keith and R. F. W. Bader, Calculation of magnetic response properties using a continuous set of gauge transformations, Chem. Phys. Lett., 1993, 210, 223–231 CrossRef CAS.
|
| This journal is © the Owner Societies 2014 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ):
):![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) −
− ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′)ρ(
′)ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′)d3
′)d3![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′; ∇2σ(non-point)PCS = κ(χ,
′; ∇2σ(non-point)PCS = κ(χ, ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )
)![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is unknown and has so far resisted all derivation attempts: a direct calculation of the Laplacian of the convolution of eqn (1) with a finite unpaired electron density comes across singular integrals that cannot be regularized.5 Yet the prize is tempting – elliptic PDEs are a classical topic in mathematics: a simple enough equation would generalize all PCS prediction and analysis problems, improve data interpretation close to the unpaired electron and enable direct measurement of spin label probability distributions in double electron-electron resonance (DEER) experiments.6 It would also be convenient – numerical PDE solvers are standard functionality in modern technical computing software. In this communication we derive the equation and comment on some of its properties.
) is unknown and has so far resisted all derivation attempts: a direct calculation of the Laplacian of the convolution of eqn (1) with a finite unpaired electron density comes across singular integrals that cannot be regularized.5 Yet the prize is tempting – elliptic PDEs are a classical topic in mathematics: a simple enough equation would generalize all PCS prediction and analysis problems, improve data interpretation close to the unpaired electron and enable direct measurement of spin label probability distributions in double electron-electron resonance (DEER) experiments.6 It would also be convenient – numerical PDE solvers are standard functionality in modern technical computing software. In this communication we derive the equation and comment on some of its properties.
![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) 0, a point electron at the origin with a magnetic susceptibility tensor χ ≪ 1 would acquire an average magnetic moment:
0, a point electron at the origin with a magnetic susceptibility tensor χ ≪ 1 would acquire an average magnetic moment:![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) e = χ·
e = χ·![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) 0/μ0
0/μ0![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) 1 generated by this dipole at the point
1 generated by this dipole at the point ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) is:
is: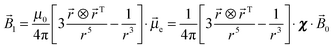
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) N located at that point would be:
N located at that point would be: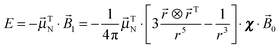
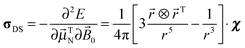
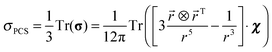
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) e and a point nucleus located at
e and a point nucleus located at ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) N the final expression is:
N the final expression is: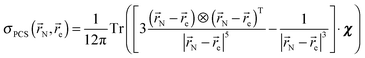
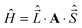 and therefore the corresponding energy change for the k-th nucleus in the system is:
and therefore the corresponding energy change for the k-th nucleus in the system is: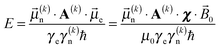
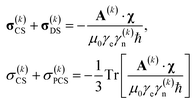
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) in eqn (2) for pseudocontact shift induced by a distributed electron is not currently known. The most straightforward derivation is to notice that:
) in eqn (2) for pseudocontact shift induced by a distributed electron is not currently known. The most straightforward derivation is to notice that: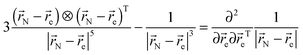
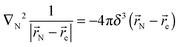
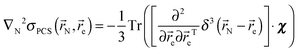
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) e) then yields (after dropping the N subscript on the nuclear coordinate vector
e) then yields (after dropping the N subscript on the nuclear coordinate vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) N):
N):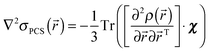
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) in square brackets
) in square brackets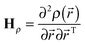
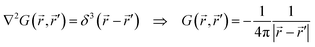
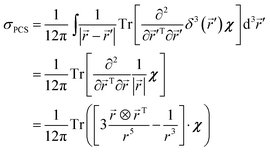
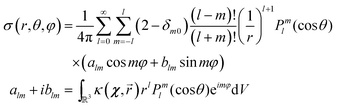
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is either the right hand side of eqn (16), or each of the nine matrix elements on the right hand side of eqn (17).
) is either the right hand side of eqn (16), or each of the nine matrix elements on the right hand side of eqn (17).
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ). Sparse matrix representations of 3D Laplacians with Dirichlet, Neumann or periodic boundary conditions are readily available,13 and the numerical solution of eqn (16) and (17) requires a single sparse matrix-inverse-times-vector operation:
). Sparse matrix representations of 3D Laplacians with Dirichlet, Neumann or periodic boundary conditions are readily available,13 and the numerical solution of eqn (16) and (17) requires a single sparse matrix-inverse-times-vector operation:
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) and the susceptibility tensor χ from nuclear coordinates and pseudocontact shifts, in particular, for spin label conformation analysis in DEER experiments. The problem may be formulated as a minimization condition, with respect to
) and the susceptibility tensor χ from nuclear coordinates and pseudocontact shifts, in particular, for spin label conformation analysis in DEER experiments. The problem may be formulated as a minimization condition, with respect to ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) = vec[ρ(
= vec[ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )] and χ, for the following regularized least squares error functional:
)] and χ, for the following regularized least squares error functional:![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) ) = ‖PL−1K
) = ‖PL−1K![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) −
− ![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) expt‖2 + λ1〈
expt‖2 + λ1〈![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) |ln(
|ln(![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) )〉 + λ2‖L
)〉 + λ2‖L![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) ‖2
‖2![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) = −(1/3)vec[Tr(Hρ·χ)]
= −(1/3)vec[Tr(Hρ·χ)]![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) expt is a vector of experimental PCS data and λ1,2 are Tikhonov regularization parameters.15 The uncommon choice of regularization operators (maximum entropy and minimum Laplacian norm) is dictated by two practical considerations:
expt is a vector of experimental PCS data and λ1,2 are Tikhonov regularization parameters.15 The uncommon choice of regularization operators (maximum entropy and minimum Laplacian norm) is dictated by two practical considerations:
![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) |ln(
|ln(![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) )〉 term in eqn (22).
)〉 term in eqn (22).![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) ‖2 term in eqn (22).
‖2 term in eqn (22).![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) ) is non-linear with respect to
) is non-linear with respect to ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) , necessitating the use of numerical minimization methods (the memory-conserving version of the quasi-Newton method proposed by Broyden, Fletcher, Goldfarb and Shanno17 is used here), but good initial guesses may be obtained by noting that, for λ1 = 0, the global minimum of Ω(
, necessitating the use of numerical minimization methods (the memory-conserving version of the quasi-Newton method proposed by Broyden, Fletcher, Goldfarb and Shanno17 is used here), but good initial guesses may be obtained by noting that, for λ1 = 0, the global minimum of Ω(![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) ) with respect to
) with respect to ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) is analytical:
is analytical:![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) min = (ATA + λ2LTL)−1AT
min = (ATA + λ2LTL)−1AT![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) expt, A = PL−1K
expt, A = PL−1K![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) ≥ 0; ∫ρ(
) ≥ 0; ∫ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )d3
)d3![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) = N; ρ(∞) = ρ′(∞) = 0
= N; ρ(∞) = ρ′(∞) = 0
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) and χ) and backward (χ and ρ(
) and χ) and backward (χ and ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) from PCS) calculations are straightforward – the former is accomplished in a single sparse matrix-inverse-times-vector operation prescribed by eqn (21) and the latter is an instance of Tikhonov regularization of the well-researched source recovery problem for an elliptic PDE20 with the error functional specified in eqn (22).
) from PCS) calculations are straightforward – the former is accomplished in a single sparse matrix-inverse-times-vector operation prescribed by eqn (21) and the latter is an instance of Tikhonov regularization of the well-researched source recovery problem for an elliptic PDE20 with the error functional specified in eqn (22).
