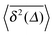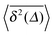Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Scaled Brownian motion: a paradoxical process with a time dependent diffusivity for the description of anomalous diffusion
Jae-Hyung
Jeon
a,
Aleksei V.
Chechkin
bcd and
Ralf
Metzler
*ad
aDepartment of Physics, Tampere University of Technology, FI-33101 Tampere, Finland
bInstitute for Theoretical Physics, Kharkov Institute of Physics and Technology, Kharkov 61108, Ukraine
cMax-Planck Institute for the Physics of Complex Systems, Nöthnitzer Straße 38, 01187 Dresden, Germany
dInstitute of Physics & Astronomy, University of Potsdam, 14776 Potsdam-Golm, Germany. E-mail: rmetzler@uni-potsdam.de
First published on 18th June 2014
Abstract
Anomalous diffusion is frequently described by scaled Brownian motion (SBM), a Gaussian process with a power-law time dependent diffusion coefficient. Its mean squared displacement is 〈x2(t)〉 ≃ 2![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) (t)t with
(t)t with ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) (t) ≃ tα−1 for 0 < α < 2. SBM may provide a seemingly adequate description in the case of unbounded diffusion, for which its probability density function coincides with that of fractional Brownian motion. Here we show that free SBM is weakly non-ergodic but does not exhibit a significant amplitude scatter of the time averaged mean squared displacement. More severely, we demonstrate that under confinement, the dynamics encoded by SBM is fundamentally different from both fractional Brownian motion and continuous time random walks. SBM is highly non-stationary and cannot provide a physical description for particles in a thermalised stationary system. Our findings have direct impact on the modelling of single particle tracking experiments, in particular, under confinement inside cellular compartments or when optical tweezers tracking methods are used.
(t) ≃ tα−1 for 0 < α < 2. SBM may provide a seemingly adequate description in the case of unbounded diffusion, for which its probability density function coincides with that of fractional Brownian motion. Here we show that free SBM is weakly non-ergodic but does not exhibit a significant amplitude scatter of the time averaged mean squared displacement. More severely, we demonstrate that under confinement, the dynamics encoded by SBM is fundamentally different from both fractional Brownian motion and continuous time random walks. SBM is highly non-stationary and cannot provide a physical description for particles in a thermalised stationary system. Our findings have direct impact on the modelling of single particle tracking experiments, in particular, under confinement inside cellular compartments or when optical tweezers tracking methods are used.
The passive, thermally driven diffusion of fluorescently labelled molecules or optically visible submicron particles is routinely measured inside living cells and complex liquids by methods such as single particle tracking1 and fluorescence correlation spectroscopy.2 Often the observed diffusion patterns deviate from the laws of Brownian motion and display anomalous diffusion characterised by the mean squared displacement (MSD)
| 〈x2(t)〉 ≃ 2Kαtα | (1) |
In biological contexts one often invokes the concept of apparent subdiffusion, which is in fact a transient crossover between free normal diffusion with α = 1 and the thermal plateau of the MSD in confinement.6 However, there is clear experimental evidence of long-ranged subdiffusion (1) in living biological cells4,7–12 and in artificially crowded or structured liquids.13–17 The physical mechanisms for such anomalous diffusion are very varied, even considering the most common approaches: we mention the continuous time random walk approach,3,5,18 in which subdiffusion is effected by multiple trapping or sticking events with an emerging power-law distribution of waiting times, as seen in the data of ref. 9, 10 and 12. Alternatively, subdiffusion arises in fractal geometries with their dead ends and bottlenecks across spatial scales,19 an additional mechanism pinpointed in ref. 12. We also mention diffusion processes in which the anomaly arises from the spatial dependence of the diffusion coefficients,20–22 or from interaction of the tracer particle with a structured environment.23–26
A special role play the Gaussian models for anomalous diffusion which belong to two families, that can best be distinguished on the Langevin equation level. The Mandelbrot–van Ness fractional Brownian motion (FBM) follows the stochastic equation ẋ(t) = ζfGn(t), where ζfGn(t) represents fractional Gaussian noise characterised by the covariance 〈ζfGn(t1)ζfGn(t2)〉 ≃ α(α − 1)|t1 − t2|α−2 which has long-ranged negative or positive correlations, respectively, for subdiffusion (0 < α < 1) or superdiffusion (1 < α < 2).27,28 FBM and the closely related fractional Langevin equation motion are physically related to the motion in a viscoelastic environment.29 In various experiments this type of motion was identified as single or partial component.9–11,15,30
Here we focus on the second family of Gaussian anomalous diffusion models, namely, scaled Brownian motion (SBM).31 SBM is governed by the Langevin equation
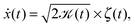 | (2) |
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) (t) = αKαtα−1, (t) = αKαtα−1, | (3) |
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) (t) × t. Originally, the diffusion process with a time dependent diffusivity was introduced by Batchelor in the description of relative diffusion in turbulence.39
(t) × t. Originally, the diffusion process with a time dependent diffusivity was introduced by Batchelor in the description of relative diffusion in turbulence.39
For unconfined SBM the probability density function is the Gaussian31
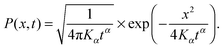 | (4) |
Time averaged mean squared displacement for unconfined SBM
While we are used to think of a diffusion process in terms of the MSD (1) calculated as the spatial average of x2 over the probability density function P(x,t), single particle tracking experiments typically provide few but long individual time series x(t). These are evaluated in terms of the time averaged MSD5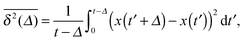 | (5) |
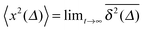 for different trajectories are identical. For anomalous diffusion the behaviour of the MSD (1) and the time averaged MSD (5) may be fundamentally different. Simultaneously
for different trajectories are identical. For anomalous diffusion the behaviour of the MSD (1) and the time averaged MSD (5) may be fundamentally different. Simultaneously 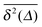 for different trajectories may become intrinsically irreproducible. This phenomenon of irreproducibility and disparity
for different trajectories may become intrinsically irreproducible. This phenomenon of irreproducibility and disparity 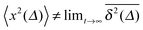 is usually called weak ergodicity breaking5 and was discussed in detail for the subdiffusive CTRW.5,41–45
is usually called weak ergodicity breaking5 and was discussed in detail for the subdiffusive CTRW.5,41–45
For SBM the mean of the time averaged MSD over multiple trajectories i, 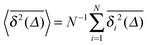 can be derived from the Langevin eqn (2), yielding48
can be derived from the Langevin eqn (2), yielding48
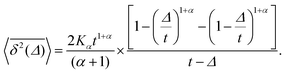 | (6) |
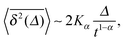 | (7) |
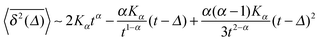 | (8) |
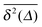 when Δ approaches t, as shown in Fig. 5 in the Appendix.
when Δ approaches t, as shown in Fig. 5 in the Appendix.
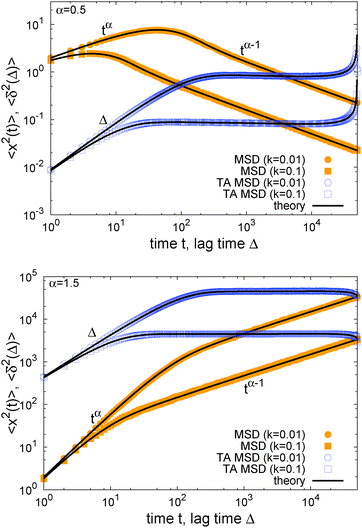
In Fig. 1 we show results from simulations of the SBM process for both sub- and superdiffusion, observing excellent agreement with the analytical findings. We also see that the scatter between individual trajectories is very small. Such scatter is a characteristic for anomalous diffusion models and can be used, e.g., to reliably distinguish FBM from subdiffusive CTRW processes.40,46 For CTRW subdiffusion we find pronounced scatter between 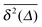 from individual trajectories even in the limit of extremely long trajectories t → ∞,5,40,41 while for FBM the scatter vanishes for longer t, a signature of the ergodic nature of FBM.29,40,46,50 The amplitude scatter of individual
from individual trajectories even in the limit of extremely long trajectories t → ∞,5,40,41 while for FBM the scatter vanishes for longer t, a signature of the ergodic nature of FBM.29,40,46,50 The amplitude scatter of individual 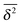 can be characterised in terms of the dimensionless variable
can be characterised in terms of the dimensionless variable 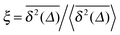 . If ξ has a narrow distribution around ξ = 1 and the width decreases with increasing t, the process is usually considered ergodic. This width is characterised in terms of the ergodicity breaking parameter EB = 〈ξ2〉 − 〈ξ〉2. For SBM it was found49
. If ξ has a narrow distribution around ξ = 1 and the width decreases with increasing t, the process is usually considered ergodic. This width is characterised in terms of the ergodicity breaking parameter EB = 〈ξ2〉 − 〈ξ〉2. For SBM it was found49
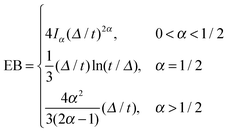 | (9) |
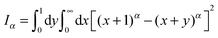 .49 The EB parameter for SBM thus clearly decays to zero for increasing t. For α = 1 we obtain the known form EB =
.49 The EB parameter for SBM thus clearly decays to zero for increasing t. For α = 1 we obtain the known form EB = ![[/]](https://www.rsc.org/images/entities/char_e12a.gif) Δ/t for Brownian motion. The Δ/t scaling also characterises FBM for α < 3/2.50 Our analysis for SBM shows that the scatter distribution ϕ(ξ) is indeed narrow and bell shaped, albeit it is broader than the Gaussian form predicted for FBM in ref. 46 (see Fig. 6). It decreases with the ratio Δ/t and thus indicates a reproducible behaviour between individual trajectories. The coexistence of the disparity
Δ/t for Brownian motion. The Δ/t scaling also characterises FBM for α < 3/2.50 Our analysis for SBM shows that the scatter distribution ϕ(ξ) is indeed narrow and bell shaped, albeit it is broader than the Gaussian form predicted for FBM in ref. 46 (see Fig. 6). It decreases with the ratio Δ/t and thus indicates a reproducible behaviour between individual trajectories. The coexistence of the disparity 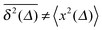 and asymptotically vanishing ergodicity breaking parameter, limt→∞EB = 0 is a new class of non-ergodic processes the more detailed mathematical nature of which remains to be examined.
and asymptotically vanishing ergodicity breaking parameter, limt→∞EB = 0 is a new class of non-ergodic processes the more detailed mathematical nature of which remains to be examined.
 | ||
Fig. 1 MSD and time averaged MSD for SBM with α = 1/2 (top) and α = 3/2 (bottom). The simulations of the SBM-Langevin eqn (2) show excellent agreement with the analytical results, eqn (1) and (6). We also show results for the time averaged MSD for 20 individual trajectories. Apart from the region where the lag time Δ approaches the length t of the time series and statistics worsen, there is hardly any amplitude scatter between individual 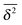 . . | ||
From the analysis so far for free motion we can see that the SBM process has a truly split personality. Thus, on the one hand SBM's PDF is identical to that for free FBM. On the other hand, however, in contrast to the ergodic behaviour 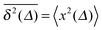 of FBM for sufficiently long t,40,50 SBM exhibits weak ergodicity breaking
of FBM for sufficiently long t,40,50 SBM exhibits weak ergodicity breaking 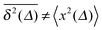 , as demonstrated by comparison of eqn (7) with eqn (1). This scaling form
, as demonstrated by comparison of eqn (7) with eqn (1). This scaling form 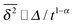 exactly matches the result for CTRW subdiffusion5,40,41 or diffusion processes with space-dependent diffusivity.20,21 Unlike the weakly non-ergodic dynamics of the latter two, for SBM the fluctuations around the mean
exactly matches the result for CTRW subdiffusion5,40,41 or diffusion processes with space-dependent diffusivity.20,21 Unlike the weakly non-ergodic dynamics of the latter two, for SBM the fluctuations around the mean 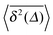 measured by the distribution ϕ(ξ) are narrow and decrease with longer t. We now show that the behaviour of confined SBM is also unconventional.
measured by the distribution ϕ(ξ) are narrow and decrease with longer t. We now show that the behaviour of confined SBM is also unconventional.
Confined SBM
An important physical property of a stochastic process is its response to external forces or spatial confinement. From an experimental point of view, this is of relevance to tracer particles moving in the confines of cellular compartments or when the particle is traced by the help of optical tweezers, which exert an Hookean restoring force on the particle.9 We study the paradigmatic case of an harmonic potential V(x) ∝ ½kx2, for which the motion is governed by the Fokker–Planck equation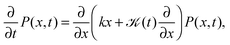 | (10) |
| 〈x2(t)〉 = 2Kαtαe−2ktM(α,1 + α,2kt), | (11) |
| 〈x2(t)〉 ∼ αKαk−1tα−1 | (12) |
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) (t) corresponds to a time dependent temperature52 or a time dependent viscosity. Thus SBM is a most non-stationary process that never reaches stationarity. Fig. 2 corroborates this analytical result with simulations based directly on the Langevin eqn (2): after the free anomalous diffusion behaviour of the MSD for a particle starting at the vertex of the potential, we observe a turnover to a power-law behaviour with negative or positive scaling exponent.
(t) corresponds to a time dependent temperature52 or a time dependent viscosity. Thus SBM is a most non-stationary process that never reaches stationarity. Fig. 2 corroborates this analytical result with simulations based directly on the Langevin eqn (2): after the free anomalous diffusion behaviour of the MSD for a particle starting at the vertex of the potential, we observe a turnover to a power-law behaviour with negative or positive scaling exponent.
The result for the time averaged MSD is similarly remarkable. As shown in Fig. 2 for SBM simulations based on the Langevin eqn (2) with the Hookean forcing, it exhibits a pronounced apparent plateau for lag times Δ ≫ 1/k for both sub- and superdiffusive SBM. This behaviour is in excellent agreement with the full analytical solution (16) provided in the Appendix in terms of Kummer functions. Taking the limit Δ ≪ t we obtain
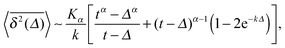 | (13) |
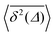 converges to the value of the MSD 〈x2(t)〉 due to the pole in expression (5). This behaviour is analysed in more detail in Fig. 5 in the Appendix.
converges to the value of the MSD 〈x2(t)〉 due to the pole in expression (5). This behaviour is analysed in more detail in Fig. 5 in the Appendix.
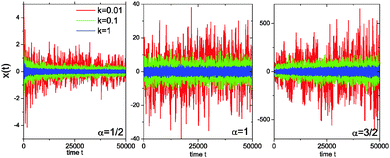
Fig. 3 analyses this behaviour in the harmonic potential further by showing the time series x(t) for subdiffusive SBM, Brownian motion, and superdiffusive SBM. Indeed we see that for subdiffusive and superdiffusive confined SBM the fluctuations continue to decrease and increase with time, while those in the Brownian limit become stationary. This is the direct effect of the time dependent temperature or viscosity encoded in the SBM diffusivity ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) (t). If the system is stationary or thermalised this behaviour clearly underlines the unsuitability of SBM for the description of anomalous diffusion.
(t). If the system is stationary or thermalised this behaviour clearly underlines the unsuitability of SBM for the description of anomalous diffusion.
The behaviour of SBM dynamics under confinement is the central result of our study. The continued temporal decay or increase of the MSD that we obtained for SBM is in stark contrast to the behaviour of confined CTRW subdiffusion, for which the MSD 〈x2〉 saturates to the thermal plateau, while the time averaged MSD continues to grow in the power-law form 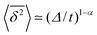 up until the lag time Δ approaches t.40,43 It strongly differs from FBM, which relaxes to a plateau for both the MSD and the time averaged MSD, and for which only a transient disparity between 〈x2〉 and
up until the lag time Δ approaches t.40,43 It strongly differs from FBM, which relaxes to a plateau for both the MSD and the time averaged MSD, and for which only a transient disparity between 〈x2〉 and 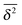 exists.15 Finally, SBM is also at variance with heterogeneous diffusion processes with a space dependent diffusion coefficient that relax to a plateau for both 〈x2〉 and
exists.15 Finally, SBM is also at variance with heterogeneous diffusion processes with a space dependent diffusion coefficient that relax to a plateau for both 〈x2〉 and 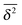 .53
.53
Discussion
As we showed SBM is a truly paradoxical stochastic process. Somewhat similar to a chameleon, each time we compare SBM with other established anomalous diffusion processes we find certain similarities. Looking at the sum of its features, however, SBM is an independent process with a range of remarkable properties.For free SBM the probability density function P(x,t) equals that of FBM, despite the fact that both processes are governed by different stochastic (Langevin) equations. SBM's time averaged MSD scales equally to those of the weakly non-ergodic CTRW subdiffusion and diffusion processes with space-dependent diffusivity. Despite this weakly non-ergodic character of the mean time averaged MSD 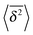 , the amplitude scatter between the time averaged MSD
, the amplitude scatter between the time averaged MSD 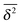 of individual realisations is small and the distribution is bell shaped, as otherwise observed for the ergodic FBM or for Brownian motion of finite time t. In that sense SBM represents a new class of non-ergodic processes. The most striking behaviour of SBM is, however, its strongly non-stationary behaviour under confinement. Instead of relaxing to a plateau the MSD acquires a power-law decay or growth mirroring a continuously decreasing or increasing temperature encoded in SBM's time dependent diffusion coefficient
of individual realisations is small and the distribution is bell shaped, as otherwise observed for the ergodic FBM or for Brownian motion of finite time t. In that sense SBM represents a new class of non-ergodic processes. The most striking behaviour of SBM is, however, its strongly non-stationary behaviour under confinement. Instead of relaxing to a plateau the MSD acquires a power-law decay or growth mirroring a continuously decreasing or increasing temperature encoded in SBM's time dependent diffusion coefficient ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) (t).
(t).
SBM is thus at variance with the currently available experimental observations in complex liquids using single particle tracking by video microscopy or by optical tweezers tracking of single submicron particles. Thus the free anomalous diffusion data garnered so far was classified into FBM-like and CTRW-like behaviour, or combinations thereof.8,10,12 Note that also for fluorescence correlation spectroscopy experiments recent analysis tools corroborated an FBM nature of the data.13 For optical tweezers tracking of lipid granules in different complex liquids the subdiffusive time averaged MSD either continues to grow under confinement, reflecting the non-ergodic features of CTRWs,5,9 or it relaxes to a plateau value mirroring an ergodic dynamics.15,54
How can FBM and SBM have the same distribution (4) in free space? Simply put for FBM, the viscoelastic properties of the environment effecting the long-range correlations of FBM lead to a frequency dependent response of the environment to a disturbance, while the materials properties remain unchanged in time. For free FBM this gives rise to the subdiffusive MSD (1), in which the time dependent diffusivity effectively encodes the frequency dependent response of the viscoelastic environment. The distribution (4) for FBM and its description in terms of a Fokker–Planck equation of the form (10) is treacherous, however. This can already be seen when we use the PDF (4) or the dynamics eqn (10) to calculate the first passage behaviour. This procedure leads to the wrong result,55 and the full analytical description of FBM in the presence of boundaries remains elusive, a difficulty imposed by the highly correlated fractional Gaussian noise driving its Langevin equation. In contrast, SBM, according to its Langevin description (2), is driven by uncorrelated noise but the environment itself is changing as function of time, effecting an extremely non-stationary process. The equivalence of the PDF (4) of both processes is thus simply due to the fact that a Gaussian PDF is completely defined by its second moment, the MSD (1).
With its interesting behaviour that is so different from the other conventional anomalous diffusion models, SBM may indeed have relevant applications to weakly coupled or fully adiabatic systems, as well as for active systems, in which the existence of a temperature is not meaningful. In particular, in the superdiffusive case SBM or analogous dynamics with other increasing effective diffusivities may represent an alternative approach to active Brownian motion.56
The difference of SBM to other processes can also be seen in Fig. 4. For the subdiffusive case a sample trajectory of SBM is compared to that of FBM and the noisy CTRW,47 in which the pure subdiffusive CTRW is superimposed with Ornstein–Uhlenbeck noise to accommodate the thermal noise of the environment observed in experiments.25 We see that SBM with its Gaussian probability density function and uncorrelated driving noise appears more similar to the noisy CTRW motion, albeit it has a more pronounced tendency to reach larger amplitudes than the CTRW with its waiting time periods. The fluctuations of SBM are dramatically less than those of the anticorrelated FBM, which also shows the largest amplitudes in x(t). For superdiffusion, we compare SBM with a noisy version of the Lévy walk process57 and again with FBM. Note the vastly different size of the window shown on the ordinate. This time, the persistent FBM shows pronouncedly larger excursions and a distinct reduction of the noise compared to SBM. The shape of x(t) of the latter does not appear to be qualitatively different from the subdiffusive case. The noisy CTRW is fundamentally different from both SBM and FBM. Despite their disparate physical nature and their dissimilarity when setting one against the other in a direct comparison, we note that generally it is difficult to identify a stochastic process solely from the appearance of the recorded trajectory.
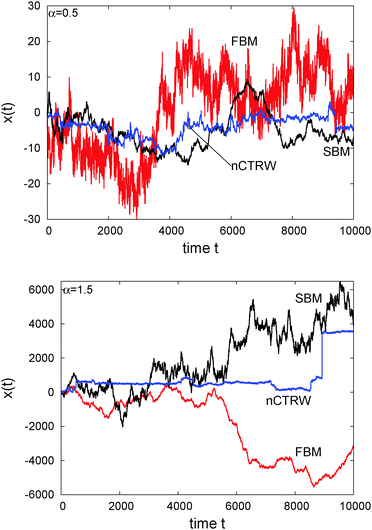 | ||
| Fig. 4 Individual trajectories of anomalous stochastic processes: FBM, SBM, and noisy CTRW (nCTRW), for subdiffusion with α = 1/2 (top) and superdiffusion with α = 3/2 (right). | ||
From this discussion it is obvious that one thing is to have at our disposal a handy and easy-to-use description for anomalous diffusion processes: SBM with its Gaussian and uncorrelated nature appears deceivingly simple and is therefore easy to implement in numerical analyses and descriptions such as diffusion limited reactions. However, it is yet another thing to consider the physical relevance of a model process. Using SBM with its time-dependent diffusion coefficient violates the physical setting in typical experiments, in which the system is held at approximately constant temperature and its predictions are at odds with actual observations. The unphysical nature for the kind of processes we have in mind is most obvious for confined motion. In contrast, FBM and fractional Langevin equation motion are ergodic processes with the physical background of an effective particle motion in a viscoelastic multi-body environment. FBM and fractional Langevin equation motion exhibit a transient disparity between the MSD and the time averaged MSD under confinement.15 Weakly non-ergodic CTRW processes emerge due to immobilisation periods that are imprinted on the dynamics by the structure of the environment or binding events to the environment. Finally, diffusion processes with space dependent diffusivities arise naturally in non-homogeneous systems such as biological cells or subsurface aquifers. To extract physically meaningful information from anomalous diffusion data one needs to have some physical insight into the observed process and properly analyse the data using complementary tools5,10–12,15,47,58–60 before settling for the appropriate physical model.
We finally note that it will be interesting to compare the predictions of the SBM model in the superdiffusive range 1 < α < 2 with that of active processes in viscoelastic environments, which in the relevant overdamped limit are of FBM type.61,62
Appendix
The covariance of the position for SBM in an harmonic potential follows from the Langevin eqn (2). Our result is| 〈x(t1)x(t2)〉 = 2Kαtα1e−k(t1+t2)M(α,1 + α,2kt1) | (14) |
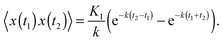 | (15) |
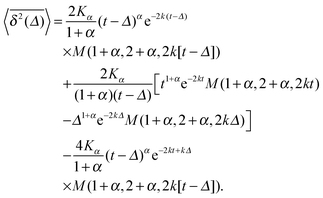 | (16) |
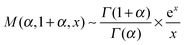 | (17) |
In Fig. 5 we illustrate the convergence of the time averaged MSD 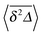 to the value of the MSD 〈x2(t)〉 in the limit Δ → t.
to the value of the MSD 〈x2(t)〉 in the limit Δ → t.
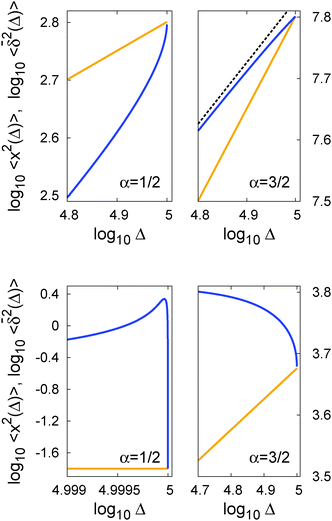 | ||
Fig. 5 Convergence of the time averaged MSD  to the MSD 〈x2(Δ)〉 when the lag time Δ approaches the measurement time t. The remarkable behaviour is due to the pole in the defining expression (5). We show the result for α = 1/2 and α = 3/2. The measurement time t = 105. Top: free SBM. For the superdiffusive case the dashed black line of unity slope aids in demonstrating the non-linear behaviour of to the MSD 〈x2(Δ)〉 when the lag time Δ approaches the measurement time t. The remarkable behaviour is due to the pole in the defining expression (5). We show the result for α = 1/2 and α = 3/2. The measurement time t = 105. Top: free SBM. For the superdiffusive case the dashed black line of unity slope aids in demonstrating the non-linear behaviour of  . Bottom: SBM in an harmonic potential with k = 0.1. Note the different ranges of the abscissa in the two cases. For the extremely small window for the subdiffusive case needed to illustrate the cusp at Δ → t and the relatively large variation of . Bottom: SBM in an harmonic potential with k = 0.1. Note the different ranges of the abscissa in the two cases. For the extremely small window for the subdiffusive case needed to illustrate the cusp at Δ → t and the relatively large variation of  the MSD 〈x2(Δ)〉 appears almost constant. the MSD 〈x2(Δ)〉 appears almost constant. | ||
In Fig. 6 we demonstrate the bell shaped scatter around the ergodic value ξ = 1 of the relative amplitude 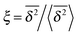 . For smaller values of Δ/t, the scatter clearly decreases and is almost Gaussian. At the larger Δ value the distribution is somewhat more asymmetric. The dashed lines in both panels of Fig. 6 indicate the Gaussian shape calculated for the ergodic FBM process in ref. 46. Clearly, the distribution ϕ(ξ) for SBM is broader.
. For smaller values of Δ/t, the scatter clearly decreases and is almost Gaussian. At the larger Δ value the distribution is somewhat more asymmetric. The dashed lines in both panels of Fig. 6 indicate the Gaussian shape calculated for the ergodic FBM process in ref. 46. Clearly, the distribution ϕ(ξ) for SBM is broader.
 | ||
Fig. 6 Scatter PDF ϕ(ξ) of the relative amplitude  around the ergodic value ξ = 1, for Δ = 1 (top) and Δ = 10 (bottom), as well as α = 1/2. around the ergodic value ξ = 1, for Δ = 1 (top) and Δ = 10 (bottom), as well as α = 1/2. | ||
We acknowledge funding from the Academy of Finland within the FiDiPro scheme.
References
- Single Particle Tracking an Single Molecule Energy Transfer, ed. C. Bräuchle, D. C. Lamb and J. Michaelis, Wiley-VCH, Weinheim, 2009 Search PubMed.
- Fluorescence Correlation Spectroscopy: Theory and Applications, ed. R. Rigler and E. S. Elson, Springer, Berlin, 2001 Search PubMed.
- R. Metzler and J. Klafter, Phys. Rep., 2000, 339, 1 CrossRef CAS.
- F. Höfling and T. Franosch, Rep. Prog. Phys., 2013, 76, 046602 CrossRef PubMed.
- E. Barkai, Y. Garini and R. Metzler, Phys. Today, 2012, 65(8), 29 CrossRef CAS PubMed.
- M. J. Saxton and K. Jacobson, Annu. Rev. Biophys. Biomol. Struct., 1997, 26, 373 CrossRef CAS PubMed.
- I. Golding and E. C. Cox, Phys. Rev. Lett., 2006, 96, 098102 CrossRef PubMed.
- S. C. Weber, A. J. Spakowitz and J. A. Theriot, Phys. Rev. Lett., 2010, 104, 238102 CrossRef.
- J.-H. Jeon, V. Tejedor, S. Burov, E. Barkai, C. Selhuber-Unkel, K. Berg-Sørensen, L. Oddershede and R. Metzler, Phys. Rev. Lett., 2011, 106, 048103 CrossRef.
- S. M. A. Tabei, S. Burov, H. Y. Kim, A. Kuznetsov, T. Huynh, J. Jureller, L. H. Philipson, A. R. Dinner and N. F. Scherer, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4911 CrossRef PubMed.
- K. Burnecki, E. Kepten, J. Janczura, I. Bronshtein, Y. Garini and A. Weron, Biophys. J., 2012, 103, 1839 CrossRef CAS PubMed.
- A. V. Weigel, B. Simon, M. M. Tamkun and D. Krapf, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6438 CrossRef CAS PubMed.
- J. Szymanski and M. Weiss, Phys. Rev. Lett., 2009, 103, 038102 CrossRef.
- W. Pan, L. Filobelo, N. D. Q. Pham, O. Galkin, V. V. Uzunova and P. G. Vekilov, Phys. Rev. Lett., 2009, 102, 058101 CrossRef.
- J.-H. Jeon, N. Leijnse, L. Oddershede and R. Metzler, New J. Phys., 2013, 15, 045011 CrossRef.
- M. J. Skaug, A. M. Lacasta, L. Ramirez-Piscina, J. M. Sancho, K. Lindenberg and D. K. Schwartz, Soft Matter, 2014, 10, 753 RSC.
- D. Ernst, J. Köhler and M. Weiss, Phys. Chem. Chem. Phys., 2014, 16, 7686 RSC.
- H. Scher and E. W. Montroll, Phys. Rev. B: Solid State, 1975, 12, 2455 CrossRef CAS.
- S. Havlin and D. Ben-Avraham, Adv. Phys., 1987, 36, 695 CrossRef CAS.
- A. G. Cherstvy, A. V. Chechkin and R. Metzler, New J. Phys., 2013, 15, 083039 CrossRef.
- A. G. Cherstvy and R. Metzler, Phys. Chem. Chem. Phys., 2013, 15, 20220 RSC.
- P. Massignan, C. Manzo, J. A. Torreno-Pina, M. F. Garca-Parajo, M. Lewenstein and G. J. Lapeyre, Jr., Phys. Rev. Lett., 2014, 112, 150603 CrossRef CAS.
- A. Godec, M. Bauer and R. Metzler, e-print arXiv:1403.3910.
- M. Bauer, A. Godec and R. Metzler, Phys. Chem. Chem. Phys., 2014, 16, 6118 RSC.
- I. Y. Wong, M. L. Gardel, D. R. Reichman, E. R. Weeks, M. T. Valentine, A. R. Bausch and D. A. Weitz, Phys. Rev. Lett., 2004, 92, 178101 CrossRef CAS.
- Q. Xu, L. Feng, R. Sha, N. C. Seeman and P. M. Chaikin, Phys. Rev. Lett., 2011, 106, 228102 CrossRef CAS.
- B. B. Mandelbrot and J. W. van Ness, SIAM Rev., 1968, 10, 422 CrossRef.
- FBM was originally addressed in A. N. Kolmogorov, C. R. (Dokl.) Acad. Sci. URSS, 1940, 26, 115 Search PubMed.
- I. Goychuk, Adv. Chem. Phys., 2012, 150, 187 CrossRef CAS.
- G. Guigas, C. Kalla and M. Weiss, Biophys. J., 2007, 93, 316 CrossRef CAS PubMed.
- S. C. Lim and S. V. Muniandy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 021114 CrossRef CAS.
- G. Guigas, C. Kalla and M. Weiss, FEBS Lett., 2007, 581, 5094 CrossRef CAS PubMed.
- N. Periasmy and A. S. Verkman, Biophys. J., 1998, 75, 557 CrossRef.
- J. Wu and M. Berland, Biophys. J., 2008, 95, 2049 CrossRef CAS PubMed.
- J. Szymaski, A. Patkowski, J. Gapiski, A. Wilk and R. Hoyst, J. Phys. Chem. B, 2006, 110, 7367 CrossRef PubMed.
- P. P. Mitra, P. N. Sen, L. M. Schwartz and P. Le Doussal, Phys. Rev. Lett., 1992, 68, 3555 CrossRef CAS.
- J. F. Lutsko and J. P. Boon, Phys. Rev. Lett., 2013, 88, 022108 Search PubMed.
- M. J. Saxton, Biophys. J., 2001, 81, 2226–2240 CrossRef CAS.
- G. K. Batchelor, Math. Proc. Cambridge Philos. Soc., 1952, 48, 345 CrossRef.
- S. Burov, J.-H. Jeon, R. Metzler and E. Barkai, Phys. Chem. Chem. Phys., 2011, 13, 1800 RSC.
- Y. He, S. Burov, R. Metzler and E. Barkai, Phys. Rev. Lett., 2008, 101, 058101 CrossRef CAS.
- A. Lubelski, I. M. Sokolov and J. Klafter, Phys. Rev. Lett., 2008, 100, 250602 CrossRef.
- S. Burov, R. Metzler and E. Barkai, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13228 CrossRef CAS PubMed.
- I. M. Sokolov, E. Heinsalu, P. Hänggi and I. Goychuk, Europhys. Lett., 2009, 86, 30009 CrossRef.
- M. Khoury, A. M. Lacasta, J. M. Sanchom and K. Lindenberg, Phys. Rev. Lett., 2011, 106, 090602 CrossRef CAS.
- J.-H. Jeon and R. Metzler, J. Phys. A: Math. Theor., 2010, 43, 252001 CrossRef.
- J.-H. Jeon, E. Barkai and R. Metzler, J. Chem. Phys., 2013, 139, 121916 CrossRef PubMed.
- A. Fuliński, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 061140 CrossRef.
- F. Thiel and I. M. Sokolov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 012115 CrossRef.
- W. Deng and E. Barkai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 011112 CrossRef.
- M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions, Dover, Publications, New York, NY, 1965 Search PubMed.
- A. Fuliński, J. Chem. Phys., 2013, 138, 021101 CrossRef PubMed.
- A. G. Cherstvy and R. Metzler, unpublished.
- M. A. Taylor, J. Janousek, V. Daria, J. Knittel, B. Hage, H.-A. Bachor and W. P. Bowen, Nat. Photonics, 2013, 7, 229 CrossRef CAS.
- J.-H. Jeon, A. V. Chechkin and R. Metzler, EPL, 2011, 94, 20008 CrossRef , and references therein.
- F. Schweitzer, W. Ebeling and B. Tilch, Phys. Rev. Lett., 1998, 80, 5044 CrossRef CAS.
- J.-H. Jeon, A. V. Chechkin and R. Metzler, unpublished.
- V. Tejedor, O. Bénichou, R. Voituriez, R. Jungmann, F. Simmel, C. Selhuber-Unkel, L. Oddershede and R. Metzler, Biophys. J., 2010, 98, 1364 CrossRef CAS PubMed.
- T. Albers and G. Radons, Europhys. Lett., 2013, 102, 40006 CrossRef.
- A. M. Berezhkovsky, L. Dagdug and S. M. Bezrukov, Biophys. J., 2014, 106, L09 CrossRef PubMed.
- D. Robert, T. H. Nguyen, F. Gallet and C. Wilhelm, PLoS One, 2010, 4, e10046 Search PubMed.
- I. Goychuk, V. O. Kharchenko and R. Metzler, PLoS One, 2014, 9, e91700 Search PubMed.
- N. G. van Kampen, Stochastic processes in physics and chemistry, North-Holland, Amsterdam, 1981 Search PubMed.
| This journal is © the Owner Societies 2014 |