Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Lithium-ion diffusion mechanisms in the battery anode material Li1+xV1−xO2†
Pooja M.
Panchmatia
ab,
A. Robert
Armstrong
c,
Peter G.
Bruce
c and
M. Saiful
Islam
*a
aDepartment of Chemistry, University of Bath, Bath BA2 7AY, UK. E-mail: m.s.islam@bath.ac.uk
bDepartment of Chemical Sciences, University of Huddersfield, Huddersfield, UK
cSchool of Chemistry, University of St. Andrews, St. Andrews, Fife, UK
First published on 3rd July 2014
Abstract
Layered Li1+xV1−xO2 has attracted recent interest as a potential low voltage and high energy density anode material for lithium-ion batteries. A greater understanding of the lithium-ion transport mechanisms is important in optimising such oxide anodes. Here, stoichiometric LiVO2 and Li-rich Li1.07V0.93O2 are investigated using atomistic modelling techniques. Lithium-ion migration is not found in LiVO2, which has also previously shown to be resistant to lithium intercalation. Molecular dynamics simulations of lithiated non-stoichiometric Li1.07+yV0.93O2 suggest cooperative interstitial Li+ diffusion with favourable migration barriers and diffusion coefficients (DLi), which are facilitated by the presence of lithium in the transition metal layers; such transport behaviour is important for high rate performance as a battery anode.
1. Introduction
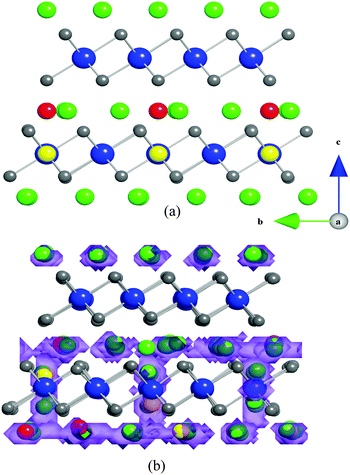
The revolution in portable electronic devices has been powered by rechargeable lithium-ion batteries. Alternative electrode materials for new generations of lithium batteries are generating considerable research activity, particularly for large-scale applications (such as electric vehicles and grid storage).1–9 Graphite is currently the dominant anode material in Li-ion batteries. Metal oxide anodes such as TiO2(B) are attracting interest since they can offer twice the volumetric energy density of graphite.10–12 However, the anode voltage for titanium oxides of ∼1.6 V vs. Li+/Li compared to ∼0.1 V for graphite compromises the cell voltage and hence energy storage.Recent studies have shown that Li can be intercalated into the layered oxide Li1+xV1−xO2, at an unusually low voltage of ∼0.1 V vs. Li+/Li,13–20 with a theoretical volumetric capacity of 1360 mA h cm−3 compared to graphite at 790 mA h cm−3. Previously we investigated the intercalation process for Li1+xV1−xO2 and in particular the key role that non-stoichiometry or excess lithium (x > 0) plays in switching on intercalation.16 Lithium does not intercalate into stoichiometric layered LiVO2 (Fig. 1). However, substituting a small amount of the V on the transition metal sites by Li (typically Li1.07V0.93O2) is sufficient to promote a two-phase intercalation process at a potential of ∼0.1 V.
 | ||
| Fig. 1 Schematic representation of the layered structures of (a) LiVO2, and (b) Li1.07V0.93O2. Key: LiO6 octahedra (green); VO6 octahedra (blue); Li on V site (yellow). | ||
Other recent studies on this system17 include an investigation of doping on the V site with Cr or Fe leading to improved rate capabilities and cyclability. A combination of solid state NMR, pair distribution function analysis and density functional theory calculations has provided further insights into the crystal and electronic structures of Li1+xV1−xO2, indicating magnetically-induced distortions of the V sublattice to form trimers.18
To fully understand the factors influencing the electrochemical behaviour of the Li1+xV1−xO2 anode material it is clear that greater insight into the underlying lithium transport properties is needed at the atomic scale. Indeed, a major puzzle is what is the atomistic mechanism controlling lithium-ion diffusion in this new oxide anode? Such transport features are important factors for charge/discharge rates and high power, but are often difficult to determine from experimental methods. Here, we extend our previous electrode work with a combination of energy minimization and molecular dynamics (MD) simulation techniques to probe, for the first time, the lithium-ion diffusion mechanisms in the vanadate material. In particular, the results comparing stoichiometric LiVO2 and Li-rich Li1.07V0.93O2 from long time-scale MD provide new insights into the mechanistic features of interstitial lithium-ion transport.
2. Methods
Atomistic modelling techniques are well suited to the investigation of defect and transport properties and have been applied successfully to a variety of studies on lithium battery materials.21–26 In the present study, potentials-based energy minimization and molecular dynamics (MD) were employed.25–27 The GULP code28 was used for the interatomic potential refinement, and the Mott–Littleton29 method was used to investigate the isolated point defects. The interactions between ions were represented in terms of a long-range Coulombic term plus an analytical function representing short-range repulsive and van der Waals forces. The empirically-derived potential parameters for Li–O, V–O and O–O were transferred from our previous successful study of the LiVO2 system.16 The Buckingham shell-model potentials used in this study are presented in ESI,† Table S1.The MD technique consists of an explicit dynamical simulation of the ensemble of ions for which Newton's equations of motion are solved (and were carried out using the DLPOLY 2.20 code).27 For this work two key structural compositions were compared: stoichiometric LiVO2 and the lithiated non-stoichiometric Li1.07+yV0.93O2 (where y = 0.09). The LiVO2 simulation box was constructed using a 10 × 10 × 2 P1 supercell consisting of 2400 atoms. Our previous work showed that Li intercalation into the Li-rich Li1.07V0.93O2 phase was energetically more favourable and that the Li interstitials preferred to go on a tetrahedral site adjacent to a Li on a vanadium site.16 The initial Li1.07+yV0.93O2 configuration contained 10% Li interstitial ions placed on these tetrahedral sites leading to a total of 2454 atoms in the supercell. The charge-compensation for Li on the V sites and Li interstitials was delocalised across all the V ions to make the supercell charge neutral. More than three initial configurations of the lithiated lithium vanadium oxide were explored via full bulk optimisations; their energetic stabilities were compared and the lowest energy configuration was used for the subsequent MD simulations.
After initial equilibration (100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps), MD simulations were performed with a 0.5 fs time step for long runs of 1.1 ns at temperatures in the range 200–600 K (Nóse–Hoover thermostat27) at intervals of 100 K. The NPT ensemble was used to allow for any thermal expansion after which the NVT ensemble was employed for the full production runs of 1.1 ns, which are important for good statistics. Such potentials-based MD techniques have been applied to other lithium battery materials23,24 and to oxide-ion conductors for solid oxide fuel cells.30 It is worth remarking that we are employing much larger supercells and an order of magnitude longer timescales than the majority of ab initio MD simulations.
000 steps), MD simulations were performed with a 0.5 fs time step for long runs of 1.1 ns at temperatures in the range 200–600 K (Nóse–Hoover thermostat27) at intervals of 100 K. The NPT ensemble was used to allow for any thermal expansion after which the NVT ensemble was employed for the full production runs of 1.1 ns, which are important for good statistics. Such potentials-based MD techniques have been applied to other lithium battery materials23,24 and to oxide-ion conductors for solid oxide fuel cells.30 It is worth remarking that we are employing much larger supercells and an order of magnitude longer timescales than the majority of ab initio MD simulations.
3. Results and discussion
3.1 Structures and defect chemistry
LiVO2 and Li1.07V0.93O2 are both ccp structures (space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) with alternating LiO6 and VO6 layers shown schematically in Fig. 1; the lithium present in the transition metal layers in Li1.07V0.93O2 is highlighted. The modelling study first attempted to reproduce the observed crystal structures. A comparison between the calculated unit cell parameters based on effective potentials and those of the experimental structure is given in Table 1. The calculated unit cell parameters deviate from experiment by at most 1.9%, and in most cases much less; the same is found for the Li–O and V–O bond lengths. This reproduction of the structures of both LiVO2 and Li1.07V0.93O2 compositions gives us confidence that the interatomic potential model can be used reliably in the defect and migration calculations. In ESI,† we have listed the calculated elastic and dielectric constants for LiVO2 and Li1.07V0.93O2. Although there are no experimental data for the LiVO2 system for direct comparison, our calculated values are consistent with observed and DFT values for similar layered oxides31 including static dielectric constants for LiCoO2.
m) with alternating LiO6 and VO6 layers shown schematically in Fig. 1; the lithium present in the transition metal layers in Li1.07V0.93O2 is highlighted. The modelling study first attempted to reproduce the observed crystal structures. A comparison between the calculated unit cell parameters based on effective potentials and those of the experimental structure is given in Table 1. The calculated unit cell parameters deviate from experiment by at most 1.9%, and in most cases much less; the same is found for the Li–O and V–O bond lengths. This reproduction of the structures of both LiVO2 and Li1.07V0.93O2 compositions gives us confidence that the interatomic potential model can be used reliably in the defect and migration calculations. In ESI,† we have listed the calculated elastic and dielectric constants for LiVO2 and Li1.07V0.93O2. Although there are no experimental data for the LiVO2 system for direct comparison, our calculated values are consistent with observed and DFT values for similar layered oxides31 including static dielectric constants for LiCoO2.
| Expt. | Calc. | Δ | |
|---|---|---|---|
(a) LiVO2 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
|||
| a/Å | 2.8377 | 2.8608 | 0.023 |
| b/Å | 2.8377 | 2.8608 | 0.023 |
| c/Å | 14.8230 | 14.5516 | −0.271 |
| α/β deg | 90.0 | 90.0 | 0.0 |
| γ/deg | 120.0 | 120.0 | 0.0 |
| Li–O/Å | 2.102 | 2.103 | 0.001 |
| V–O/Å | 2.004 | 2.058 | 0.054 |
| O–O/Å | 2.830 | 2.905 | 0.075 |
(b) Li1.07V0.93O2 (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) m) |
|||
| a/Å | 2.8430 | 2.9370 | 0.094 |
| b/Å | 2.8430 | 2.8920 | 0.049 |
| c/Å | 14.7675 | 14.6355 | −0.132 |
| α/β deg | 90.0 | 90.0 | 0.0 |
| γ/deg | 120.0 | 120.0 | 0.0 |
| Li–O/Å | 2.020 | 2.064 | 0.044 |
| Li+V–O/Å | 2.046 | 2.030 | −0.016 |
| V–O/Å | 2.037 | 2.030 | −0.007 |
| O−O/Å | 2.834 | 2.832 | 0.002 |
A series of isolated point defect (vacancy and interstitial) energies were then calculated, and combined to give the relative energies of formation of the Li Frenkel defect. We also examined the Li/M “anti-site” pair defect, which involves the exchange of a V ion (radius 0.64 Å) with a Li ion (radius 0.76 Å); this type of defect is worth investigating since cation exchange effects have been observed in other layered oxide electrodes.1,2
Table 2 lists the formation energies of Li Frenkel and anti-site defects in the two compositions. The high unfavourable energies suggest that the inability to intercalate into stoichiometric LiVO2 is not due to the presence of site-exchange disorder involving V ions in the alkali metal layers pinning them together; this result is in agreement with previous structural studies indicating that there is no V in the Li layers of LiVO2. The site exchange energy in Li1.07V0.93O2 is the most favourable, although the magnitude still suggests that intrinsic concentrations will not be significant. The calculated defect energies also suggest that intrinsic lithium vacancies and interstitials are unlikely to be found in stoichiometric LiVO2.
| Compound | Frenkel defect energy (eV) | Antisite defect energy (eV) |
|---|---|---|
| LiVO2 | 3.58 | 3.44 |
| Li1.07V0.93O2 | 1.67 | 1.36 |
3.2 Li ion diffusion
Examination of the Li-ion transport properties of Li1+xV0.93O2 is of vital importance when considering electrode kinetics. Of primary interest here is information on the atomistic mechanism of lithium-ion diffusion, which is difficult to probe purely by experimental methods. Molecular dynamics (MD) techniques are well suited to probing transport mechanisms, especially cooperative or correlated ion motion. Here, MD calculations over long simulation time scales were carried out at temperatures more than covering typical battery operating temperatures for the two compositions for direct comparison: stoichiometric LiVO2 and the lithiated non-stoichiometric Li1.07+yV0.93O2 (y = 0.09).First, the mean squared displacements (MSDs), 〈[r(t)]2〉, of lithium ions have been resolved and shown in Fig. 2; the results clearly show that there is significant lithium-ion diffusion only in the Li-rich composition. For LiVO2 the MSD of the Li-ions tends rapidly to a constant value and confirms that there is no ion diffusion in this stoichiometric composition.
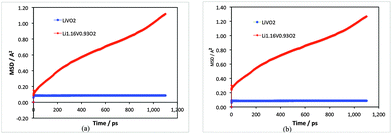 | ||
| Fig. 2 Mean squared displacement (MSD) plots for LiVO2 (blue) and Li1.07+yV0.93O2 (red) for 1.1 ns at (a) 400 K and (b) 500 K. | ||
The Li-ion diffusion coefficient (DLi) can be derived from the MSD data given by D = (1/6t) 〈[r(t)]2〉. We calculate a DLi value of about 10−9 cm2 s−1 for Li1.07+yV0.93O2 (y = 0.09) at 300 K. Although there are currently no measured diffusion data for direct comparison, the magnitude is comparable to other electrode materials; for example, graphite has lithium diffusivity of about 10−8 to 10−9 cm2 s−1,32 and experimental diffusion coefficients of 10−8 to 10−11 cm2 s−1 have been reported33 for Li+ diffusion in layered oxide cathodes such as LiCoO2 and Li(Ni,Mn,Co)O2.
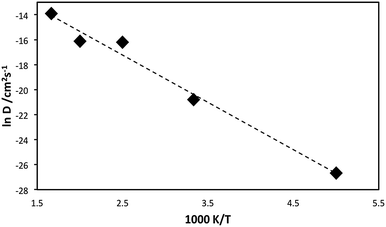
An Arrhenius plot (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D versus 1/T) for lithiated Li1.16V0.93O2 is presented in Fig. 3. Analysis of such data provides an estimate of the migration activation energy (Eact) using the standard Arrhenius relation:
D versus 1/T) for lithiated Li1.16V0.93O2 is presented in Fig. 3. Analysis of such data provides an estimate of the migration activation energy (Eact) using the standard Arrhenius relation:
D = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Eact/kT) exp(−Eact/kT) | (1) |
A migration activation energy of 0.32 eV is derived, indicating high Li ion mobility in this Li-rich oxide anode, which is important for good rate capability. Despite the lack of Li ion conductivity data for direct comparison, our calculated migration energy is compatible with low activation energies for other layered oxides such as LixCo0.95Mg0.05O2,34 LixCoO226 and LixNiO2,35 albeit for Li vacancy migration.
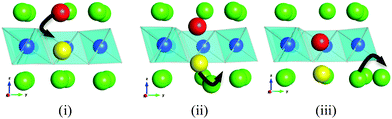
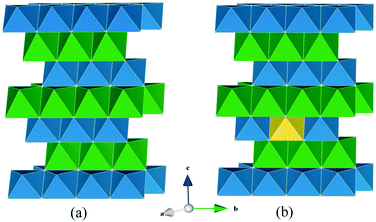
Scatter or density plots of the accumulated density of lithium ion trajectories over the simulated time scale enables useful visualization of the migration pathways and the lattice regions most frequently traversed by the mobile Li-ions. Fig. 4a shows the starting configuration of the Li1.07+yV0.93O2 (y = 0.09) structure where the Li+V atoms are in the vanadium layers and the interstitial lithiums are on tetrahedral sites. As shown previously,16 substitution of Li for V on the octahedral transition metal sites renders tetrahedral sites in the alkali metal layers energetically accessible by Li.
The lithium diffusion density plots and final configuration of ions in Li1.07+yV0.93O2 (y = 0.09) at the end of the MD simulation are shown in Fig. 4b. The diffuse distribution and overlapping of different lithium positions indicate that numerous different lithium ions are moving between octahedral lattice and tetrahedral interstitial sites. These results show that long-range lithium-ion migration is highly anisotropic, restricted to within the lithium layers adjacent to vanadium layers that contain a small amount of lithium ions. Interestingly, there is also evidence of ion migration between adjacent layers via the lithium ions on the V sites. In contrast, the lithium layers that are not adjacent to Li on V sites, do not exhibit diffusion within or across the layers. A key feature is that the Li-rich composition with Li on V sites plays a vital role in not only switching on the lithium intercalation process,16 but also in aiding facile lithium-ion diffusion.
A major thrust of fundamental transport studies has been the examination of the atomistic mechanisms controlling bulk transport phenomena. Indeed, the unravelling of mechanistic detail at the microscopic level is a powerful feature of the MD technique. Fig. 5 shows a series of snapshots of the lithium ions as they migrate within the alkali-ion layer and via the Li ions in the vanadium layers. This illustration suggests that lithium-ion diffusion takes place by a cooperative interstitialcy or knock-on type mechanism in which the migrating interstitial Li-ion displaces the Li in the V layer into a neighbouring interstitial position in the alkali-metal layer. Such a cooperative type mechanism facilitates lithium-ion diffusion despite the lack of open conduction pathways. Similar cooperative mechanisms have been discussed in connection with lithium migration in LiMgSO4F24 and with interstitial oxide-ion conduction in electrolytes for solid oxide fuel cells,30 but have not been widely elucidated in Li-rich layered oxides.
4. Conclusions
Atomic-scale mechanistic features of Li-ion transport in vanadium oxide anode materials have been investigated, revealing three main results.First, the defect formation energies indicate that the inability to intercalate into stoichiometric LiVO2 is not due to the presence of cation exchange disorder involving V ions in the lithium ion layers pinning them together, which is in agreement with structural studies. It is known that the Li-rich composition Li1.07V0.93O2 with lithium on the vanadium layers switches on lithium intercalation.
Second, the MD simulations indicate facile Li+ diffusion in the lithiated composition, Li1.07+yV0.93O2, with a low activation barrier (0.32 eV) for interstitial Li+ transport, and diffusion coefficients (DLi) of ca. 10−9 cm2 s−1; these values are consistent with other layered oxide electrodes and suggest favourable rate performance. Finally, long-range Li+ diffusion is found to be highly anisotropic, largely restricted to within the lithium layers adjacent to vanadium layers that contain lithium ions. Interestingly, there is also evidence of interlayer diffusion via the lithium ions on the vanadium sites, and involving a cooperative interstitial mechanism.
These insights into transport mechanisms and electrode kinetics are valuable in developing strategies for optimizing this low voltage oxide anode.
Acknowledgements
We acknowledge EPSRC for funding (EP/H019596/1) and the Materials Chemistry consortium (EP/L000202/1) for access to high-end supercomputer resources. PMP would like to thank D. J. Cooke for useful discussions.Notes and references
- J. B. Goodenough, Chem. Mater., 2010, 22, 587 CrossRef CAS.
- B. L. Ellis, K. T. Lee and L. F. Nazar, Chem. Mater., 2010, 22, 691 CrossRef CAS.
- M. S. Whittingham, MRS Bull., 2008, 33, 411 CrossRef CAS.
- M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652 CrossRef CAS PubMed.
- P. G. Bruce, B. Scrosati and J. M. Tarascon, Angew. Chem., Int. Ed., 2008, 47, 2930 CrossRef CAS PubMed; B. Scrosati, J. Hassoun and Y.-K. Sun, Energy Environ. Sci., 2011, 4, 3287 Search PubMed.
- M. R. Palacín, Chem. Soc. Rev., 2009, 38, 2565 RSC.
- M. M. Thackeray, C. Wolverton and E. D. Isaacs, Energy Environ. Sci., 2012, 4, 7854 Search PubMed.
- J. Liu, J.-G. Zhang, Z. Yang, J. P. Lemmon, C. Imhoff, G. L. Graff, L. Li, J. Hu, C. Wang, J. Xiao, G. Xia, V. V. Viswanathan, S. Baskaran, V. Sprenkle, X. Li, Y. Shao and B. Schwenzer, Adv. Funct. Mater., 2013, 23, 929 CrossRef CAS.
- N. S. Choi, J. S. Kim, R. Z. Yin and S. S. Kim, Mater. Chem. Phys., 2009, 116, 603 CrossRef CAS PubMed.
- G. Zhu, Y.-G. Wang and Y.-Y. Xia, Energy Environ. Sci., 2012, 5, 6652 CAS.
- M. V. Reddy, G. V. Subba Rao and B. V. R. Chowdari, Chem. Rev., 2013, 113, 5364 CrossRef CAS PubMed.
- L. Ji, Z. Lin, M. Alcoutlabi and X. Zhang, Energy Environ. Sci., 2011, 4, 2682 CAS.
- J. H. Song, H. J. Park, K. J. Kim, Y. N. Jo, J.-S. Kim, Y. U. Jeong and Y. J. Kim, J. Power Sources, 2010, 195, 6157 CrossRef CAS PubMed.
- S.-S. Kim, J. Kim, M. Koike and N. Kobayashi, 14th International Meeting on Lithium Batteries, Tianjin, Abstract #20, 2008.
- S.-S. Kim, Y. Nitta, T. I. Nedoseykina and J.-C. Lee, US Pat., 2006/0088766, 2006 Search PubMed.
- A. R. Armstrong, C. Lyness, P. M. Panchmatia, M. S. Islam and P. G. Bruce, Nat. Mater., 2011, 10, 223 CrossRef CAS PubMed.
- W.-T. Kim, Y. U. Jeong, H. C. Choi, Y. J. Lee, Y. J. Kim and J. H. Song, J. Power Sources, 2013, 221, 366 CrossRef CAS PubMed.
- F. Pourpoint, X. Hua, D. S. Middlemiss, P. Adamson, D. Wang, P. G. Bruce and C. P. Grey, Chem. Mater., 2012, 24, 2880 CrossRef CAS.
- J. Yi, J. Key, F. Wang, Y.-G. Wang, C. Wang and Y.-Y. Xia, Electrochim. Acta, 2013, 106, 534 CrossRef CAS PubMed; J. M. Gaudet and J. R. Dahn, Can. J. Phys., 2013, 91, 444 CrossRef.
- Y. C. K. Chen-Wiegart, P. Shearing, Q. Yuan, A. Tkachuk and J. Wang, Electrochem. Commun., 2012, 21, 58 CrossRef CAS PubMed.
- C. A. J. Fisher and M. S. Islam, J. Mater. Chem., 2008, 18, 1208 RSC; M. Schroeder, C. Eames, D. A. Tompsett, G. Lieser and M. S. Islam, Phys. Chem. Chem. Phys., 2013, 15, 20473 RSC.
- M. S. Islam, D. J. Driscoll, C. A. J. Fisher and P. R. Slater, Chem. Mater., 2005, 17, 5085 CrossRef CAS; G. R. Gardiner and M. S. Islam, Chem. Mater., 2010, 22, 1242 CrossRef; N. Kuganathan and M. S. Islam, Chem. Mater., 2009, 21, 5196 CrossRef.
- S. Lee and S. S. Park, J. Phys. Chem. C, 2012, 116, 6484 Search PubMed; C. Tealdi, C. Spreafico and P. Mustarelli, J. Mater. Chem., 2012, 22, 24870 RSC; S. Adams and R. P. Rao, Solid State Ionics, 2011, 184, 57 CrossRef CAS PubMed; M. Vijayakumar, S. Kerisit, K. M. Rosso, S. D. Burton, J. A. Sears, Z. Yang, G. L. Graff, J. Liu and J. Hu, J. Power Sources, 2011, 196, 2211 CrossRef PubMed; S. E. Boulfelfel, G. Seifert and S. Leoni, J. Mater. Chem., 2011, 21, 16365 RSC.
- M. Salanne, M. Marrocchelli and G. W. Watson, J. Phys. Chem. C, 2012, 116, 18618 CAS.
- Computer Modelling in Inorganic Crytallography, ed. C. R. A. Catlow, Academic Press, San Diego, 1997 Search PubMed.
- M. S. Islam and C. A. J. Fisher, Chem. Soc. Rev., 2014, 43, 185 RSC.
- W. Smith, C. W. Yong and P. M. Rodger, Mol. Simul., 2002, 28, 385 CrossRef CAS; S. Nóse, J. Chem. Phys., 1984, 81, 511 CrossRef PubMed; W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629 RSC.
- N. F. Mott and M. J. Littleton, Trans. Faraday Soc., 1938, 34, 485 RSC.
- C. Tealdi, P. Mustarelli and M. S. Islam, Adv. Funct. Mater., 2010, 20, 3874 CrossRef CAS; E. Kendrick, J. Kendrick, K. S. Knight, M. S. Islam and P. R. Slater, Nat. Mater., 2007, 6, 871 CrossRef PubMed; P. M. Panchmatia, A. Orera, G. J. Rees, M. E. Smith, J. V. Hanna, P. R. Slater and M. S. Islam, Angew. Chem., Int. Ed., 2011, 50, 9328 CrossRef PubMed; A. Chroneos, D. Parfitt, J. A. Kilner and R. W. Grimes, J. Mater. Chem., 2010, 20, 266 RSC.
- K. Hoang and M. D. Johannes, J. Mater. Chem. A, 2014, 2, 5224 Search PubMed; F. X. Hart and J. B. Bates, J. Appl. Phys., 1998, 83, 7560 CrossRef CAS PubMed.
- K. Persson, V. A. Sethuraman, L. J. Hardwick, Y. Hinuma, Y.-S. Meng, A. van der Ven, V. Srinivasan, R. Kostecki and G. Ceder, J. Phys. Chem. Lett., 2010, 1, 1176 CrossRef CAS; S. Bhattacharya, A. R. Riahi and A. T. Alpas, Carbon, 2014, 67, 597 CrossRef PubMed; D. R. Baker and M. W. Verbugge, J. Electrochem. Soc., 2012, 159, A1341 CrossRef PubMed; P. Maire, H. Kaiser, W. Scheifele and P. Novak, J. Electroanal. Chem., 2010, 644, 127 CrossRef PubMed.
- Q. S. Wang, J. H. Sun, C. H. Chen and X. M. Zhou, J. Therm. Anal. Calorim., 2008, 92, 563 CrossRef CAS; M. Park, X. Zhang, M. Chung, G. B. Less and A. M. Sastry, J. Power Sources, 2010, 195, 7904 CrossRef PubMed; P. Jeevan-Kumar, K. Jayanth-Babu, O. M. Hussain and C. M. Julien, Solid State Ionics, 2013, 19, 421 Search PubMed; M. Shui, S. Gao, J. Shu, W. D. Zheng, D. Xu, L. L. Chen, L. Feng and Y. L. Ren, Solid State Ionics, 2013, 19, 47 Search PubMed; W. C. West, J. Soler, M. C. Smart, B. V. Ratnakumar, S. Firdosy, V. Ravi, M. S. Anderson, J. Hrbacek, E. S. Lee and A. Manthiram, J. Electrochem. Soc., 2011, 158, A883–A889 CrossRef PubMed; M. Gozu, K. Swierczek and J. Molenda, J. Power Sources, 2009, 194, 38 CrossRef PubMed; K. M. Shaju, G. V. S. Rao and B. V. R. Chowdari, J. Electrochem. Soc., 2004, 151, A1324 CrossRef PubMed.
- F. Nobili, S. Dsoke, F. Croce and R. Marassi, Electrochim. Acta, 2005, 50, 2307 CrossRef CAS PubMed.
- K. Nakamura, H. Ohno K. Okamura, Y. Michihiro, I. Nakabayashi and T. Kanashiro, Solid State Ionics, 2000, 135, 143 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp01640h |
| This journal is © the Owner Societies 2014 |