 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Negative area compressibility in silver(I) tricyanomethanide†
Sarah A.
Hodgson
a,
Jasper
Adamson
a,
Sarah J.
Hunt
a,
Matthew J.
Cliffe
a,
Andrew B.
Cairns
a,
Amber L.
Thompson
a,
Matthew G.
Tucker
bc,
Nicholas P.
Funnell
a and
Andrew L.
Goodwin
*a
aDepartment of Chemistry, University of Oxford, Inorganic Chemistry Laboratory, South Parks Road, Oxford OX1 3QR, UK. E-mail: andrew.goodwin@chem.ox.ac.uk; Fax: +44 (0)1865 274690; Tel: +44 (0)1865 272137
bISIS Facility, Rutherford Appleton Laboratory, Chilton, Didcot, OX11 0QX, UK
cDiamond Light Source, Harwell Campus, Didcot, OX11 0DE, UK
First published on 9th December 2013
Abstract
The molecular framework Ag(tcm) (tcm− = tricyanomethanide) expands continuously in two orthogonal directions under hydrostatic compression. The first of its kind, this negative area compressibility behaviour arises from the flattening of honeycomb-like layers during rapid pressure-driven collapse of the interlayer separation.
In the absence of a structural phase transition, it is a thermodynamic requirement that a system reduce its volume under hydrostatic pressure.1 The phenomenon of negative compressibility is the counterintuitive effect whereby this volume reduction couples to an expansion of the material in at least one linear dimension.2 Examples of such behaviour are rare even amongst anisotropic materials because buckling and bond compression mechanisms are almost always more effective at reducing crystal volume than is uniaxial or biaxial lattice expansion. Not only does the existence of negative compressibility challenge our understanding of the ways in which materials can respond to external stimuli, but the phenomenon is also of practical importance. It promises a means of developing artificial muscles, nanoscale actuators and high-performance pressure sensors for sonar and altitude measurements.2,3 In principle, the most extreme such response allowed thermodynamically is that of negative area compressibility (NAC), whereby a material expands along two orthogonal directions on increasing hydrostatic pressure. The possibility that tetragonal PbTiO3 might show an extremely weak NAC effect has been raised4 and disputed;5 similarly weak effects are thought to occur at high pressure in NaV2O5 (ref. 6) and are predicted for TlGaSe2.7 Instead the remarkably few negative compressibility materials that have been characterised unambiguously expand only along one principal axis when compressed hydrostatically (i.e., negative linear compressibility, NLC).8–12 The distinction between NLC and NAC is more fundamental than magnitude alone: NAC materials increase their surface area under hydrostatic pressure, and so they can be used as substrates to provide order-of-magnitude amplification of piezoelectric response in e.g. ferroelectric sensors.2
One strategy for identifying negative compressibility candidates is to target framework materials that exhibit anisotropic negative thermal expansion (NTE): a material that shrinks in one direction on heating is likely to expand in that same direction on compression.13 While there is no requirement that deformation mechanisms under temperature and pressure be identical,14 there is empirical evidence of such a correspondence amongst molecular framework materials.8,9,12,15 The natural strategy then for identifying NAC candidates is to investigate framework materials that exhibit area-NTE. It is for this reason that we chose to investigate silver(I) tricyanomethanide, Ag(tcm): its layer-like network topology [Fig. 1(a)] is of a form often associated with area-NTE.16,17 In this compound, each Ag+ cation is coordinated by three tcm− anions in an approximately trigonal arrangement; likewise each tcm− anion is coordinated by three Ag+ centres.18,19 The resulting hexagonal (6,3) topology is sufficiently open that two honeycomb networks interpenetrate within each layer of the crystal structure [Fig. 1(b)]. Adjacent layers interact via long Ag⋯N contacts [d(Ag⋯N) > 3 Å] that are sufficiently weak that the material behaves essentially as a two-dimensional framework, capable even of intercalation chemistry.19
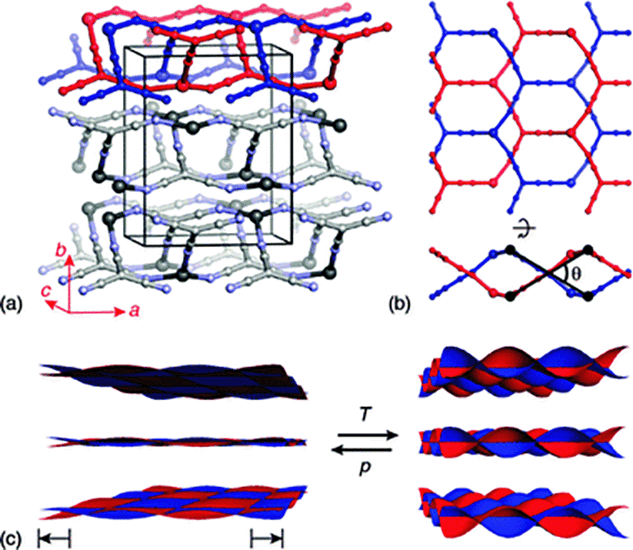 | ||
| Fig. 1 (a) The crystal structure of Ag(tcm) is composed of stacked, doubly-interpenetrating (6,3)-nets in which both Ag+ (large spheres) and tcm− ions (smaller spheres) function as trigonal nodes. (b) The extent of rippling of layers (viewed along b and a in the top and bottom parts of this panel, respectively) can be quantified by the inter-network angle θ (see ESI†). (c) The generic mechanical response of a layered material links volume expansion to increasing interlayer separation and increasing layer rippling. The cross-sectional area of each layer is maximised by reducing θ, and hence increases during volume reduction under hydrostatic compression. | ||
Using single-crystal X-ray diffraction, we first established the thermal expansion behaviour of Ag(tcm) to verify whether or not the material exhibits area-NTE. Because the material crystallises in the orthorhombic (polar) space group Ima2,18 its thermal expansivity is uniquely determined by the relative rate of change of the unit cell lengths with temperature.17 We observe essentially linear thermal variation in these parameters over the temperature range 100–250 K [Fig. 2(a)], yielding coefficients of thermal expansion of −48(3), +200(2) and −54.0(4) MK−1 along the a, b, and c axes, respectively.17 As is increasingly found to be the case for molecular frameworks,13,20 the magnitudes of these values are large compared to those obtained for traditional engineering materials, for which one expects linear coefficients of thermal expansion in the vicinity of +20 MK−1 (i.e., a 0.2% increase in linear dimension for each 100 K temperature rise).21 What is clear is that Ag(tcm) does exhibit area-NTE, with an area coefficient of thermal expansion for the (a,c)-plane, α(010) = −102(3) MK−1, that is the most extreme negative value reported for a layered material. The material undergoes a 1% reduction in area for each 100 K rise in temperature—more than an order of magnitude larger than the corresponding values for area-NTE systems such as graphite and Ni(CN)2 (αA = −2.4 and −13 MK−1, respectively).17,22,23
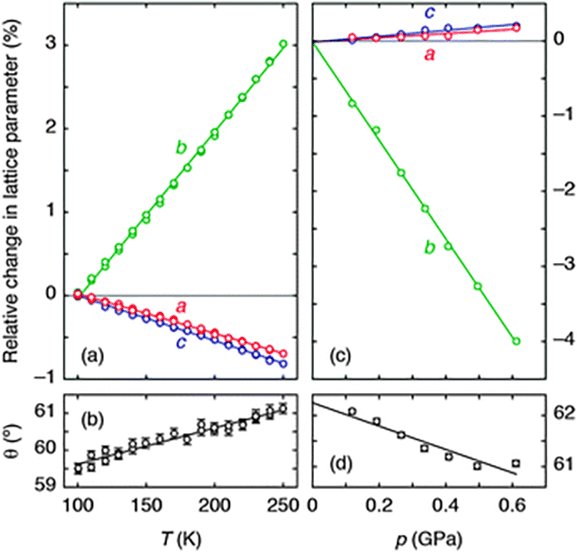 | ||
| Fig. 2 (a) The thermal variation of lattice parameters, determined using single-crystal X-ray diffraction measurements, is illustrated here for ease of comparison as a % change relative to the extrapolated value at 100 K. Solid lines are weighted linear fits to the data obtained using the program PASCal.17 (b) The corresponding variation in inter-network angle θ indicates an increase in layer rippling on heating. (c) The pressure dependence of lattice parameters, measured using variable-pressure neutron diffraction, is represented as a % change relative to the extrapolated value at 0 GPa. (d) The corresponding variation in θ now indicates a decrease in layer rippling under compression. | ||
The microscopic mechanism responsible for this behaviour can be deduced from the variation in framework geometry during heating. The established model of area-NTE in layered materials predicts coupling between NTE and the extent of layer ‘rippling’, as quantified by the inter-network torsion angle θ [Fig. 1(b and c)].16 Our measurements indeed indicate an increase in θ with temperature [Fig. 2(b)].24 Using simple geometric arguments, the temperature dependence of θ can be used to estimate the value of αA attributable to layer rippling:
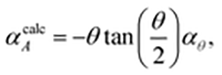 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/dT (see ESI† for derivation). Our data give αcalcA = −101 MK−1, which is within experimental error of the observed value of −102(3) MK−1. Consequently, we can be confident that the mechanism illustrated in Fig. 1(c) is responsible for area-NTE in Ag(tcm).
θ)/dT (see ESI† for derivation). Our data give αcalcA = −101 MK−1, which is within experimental error of the observed value of −102(3) MK−1. Consequently, we can be confident that the mechanism illustrated in Fig. 1(c) is responsible for area-NTE in Ag(tcm).
In order to determine whether or not Ag(tcm) exhibits the target property of NAC, we performed a series of neutron diffraction measurements across the pressure range 0 < p < 2 GPa using the PEARL instrument at ISIS. The use of neutron radiation maximises the scattering sensitivity to C/N atoms in the presence of Ag atoms, which is all the more important for measurements performed in the high-background sample environments required for variable-pressure experiments. We found that, for powdered samples, the ambient phase is stable up to 0.615(6) GPa, but by 0.672(7) GPa it has transformed reversibly to a related phase with symmetry not higher than monoclinic. The same transformation occurs at higher pressures (0.83 < pc < 1.47 GPa) in single-crystal experiments (see ESI† for further discussion); our focus here is on the pressure-dependent behaviour of the ambient phase rather than the nature of the phase transition or the high-pressure phase. Rietveld refinement against the corresponding neutron diffraction patterns revealed the anticipated increase in a and c parameters [Fig. 2(c)], with the anomalous expansion of the material in these directions being allowed by a much more rapid decrease in the interlayer spacing (given by the lattice parameter b). Our variable-pressure lattice parameter data can be converted into compressibilities using the relationship K![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) = −[∂(ln
= −[∂(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) )/∂p]T, from which we obtain Ka = −3.5(6) TPa−1, Kb = +66(20) TPa−1, and Kc = −4.0(6) TPa−1. Consequently, the compressibility is negative everywhere within the (a,c)-plane, with the magnitude of NAC quantified by the corresponding area compressibility K(010) = Ka + Kc = −7.5(8) TPa−1.
)/∂p]T, from which we obtain Ka = −3.5(6) TPa−1, Kb = +66(20) TPa−1, and Kc = −4.0(6) TPa−1. Consequently, the compressibility is negative everywhere within the (a,c)-plane, with the magnitude of NAC quantified by the corresponding area compressibility K(010) = Ka + Kc = −7.5(8) TPa−1.
Conventional engineering materials (e.g. iron) have linear compressibilities K ∼ 5 TPa−1 that correspond to a decrease of ca. 0.5% in length for each 1 GPa pressure increase;25 consequently, the NAC behaviour of Ag(tcm) is essentially as strong as the positive area compressibility of these ‘normal’ phases. Moreover, despite the fact that the orthorhombic symmetry of Ag(tcm) allows for different behaviour in the a and c directions, we find that both its compressibility and its thermal expansivity are essentially isotropic within the entire (a,c) plane. Isotropy is important for NAC applications because it avoids composite warping and performance breakdown.2
That NAC is driven by the same layer-rippling mechanism as area-NTE is evident in the variation of the parameter θ with increasing pressure [Fig. 2(d)]. The volume reduction accommodated by rapid collapse of the interlayer spacing (note Kb ≫ 5 TPa−1) evidently couples with a reduction in the degree of layer rippling: dθ/dp < 0. To substantiate further our interpretation of the NAC mechanism, we recast eqn (1) in terms of compressibilities; our refined values of θ give KcalcA = −θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan(θ/2)Kθ = −26 TPa−1. That the measured area compressibility K(010) = −7.5(8) TPa−1 is somewhat smaller in magnitude reflects the expected ∼10 TPa−1 contribution from (positive) bond compressibilities omitted from the geometric formalism of eqn (1), as discussed elsewhere for NLC materials.13 Indeed, that the p/T correspondence inferred in Fig. 1(c) holds qualitatively for Ag(tcm) is immediately evident in the close relationship between the temperature- and pressure-induced lattice parameter and layer rippling parameter variations documented in Fig. 2.
tan(θ/2)Kθ = −26 TPa−1. That the measured area compressibility K(010) = −7.5(8) TPa−1 is somewhat smaller in magnitude reflects the expected ∼10 TPa−1 contribution from (positive) bond compressibilities omitted from the geometric formalism of eqn (1), as discussed elsewhere for NLC materials.13 Indeed, that the p/T correspondence inferred in Fig. 1(c) holds qualitatively for Ag(tcm) is immediately evident in the close relationship between the temperature- and pressure-induced lattice parameter and layer rippling parameter variations documented in Fig. 2.
In conclusion, we find that silver(I) tricyanomethanide exhibits NAC over the pressure range 0 < p < 0.615 GPa with an essentially isotropic area compressibility of similar magnitude (but opposite sign) to that of established engineering materials. From a structural viewpoint, the phenomenon can be understood in terms of pressure-driven damping of layer ‘rippling’, acting to increase the layer cross-sectional area at larger hydrostatic pressures. Variable-pressure spectroscopic measurements may provide valuable additional insight into the subtle variations in bonding interactions that occur throughout this process.26 In favour of immediate application of Ag(tcm) in ultra-high-precision sensing devices are (i) the ease with which large single-crystal samples can be prepared under ambient conditions and using readily-available solvents, and (ii) its optical transparency. Moreover, the polarity of its crystal structure offers the possibility of designing multifunctional devices based on Ag(tcm) in which the interplay between responses to electric field, temperature, and pressure are exploited to produce piezoelectric and thermoelectric devices.
The authors gratefully acknowledge financial support from the E.P.S.R.C. (EP/G004528/2) and the E.R.C. (Grant Ref.: 279705), the provision of neutron beamtime on the PEARL instrument at ISIS, and the assistance of Dr Marek Jura (ISIS).
References
- Z. G. Nicolaou and A. E. Motter, Nat. Mater., 2012, 11, 608–613 CrossRef CAS PubMed.
- R. H. Baughman, S. Stafström, C. Cui and S. O. Dantas, Science, 1998, 279, 1522–1524 CrossRef CAS.
- A. E. Aliev, J. Oh, M. E. Kozlov, A. A. Kuznetsov, S. Fang, A. F. Fonseca, R. Ovalle, M. D. Lima, M. H. Haque, Y. N. Gartstein, M. Zhang, A. A. Zakhidov and R. H. Baughman, Science, 2009, 323, 1575–1578 CrossRef CAS PubMed.
- R. J. Nelmes and A. Katrusiak, J. Phys. C: Solid State Phys., 1986, 19, L725–L730 CrossRef CAS.
- A. Sani, M. Hanfland and D. Levy, J. Phys.: Condens. Matter, 2002, 14, 10601–10604 CrossRef CAS.
- I. Loa, K. Syassen, R. K. Kremer, U. Schwarz and M. Hanfland, Phys. Rev. B, 1999, 60, R6945–R6948 CrossRef CAS.
- M. Y. Seyidov and R. A. Suleymanov, J. Appl. Phys., 2010, 108, 063540 CrossRef PubMed.
- A. L. Goodwin, D. A. Keen and M. G. Tucker, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18708–18713 CrossRef CAS PubMed.
- W. Li, M. R. Probert, M. Kosa, T. D. Bennett, A. Thirumurugan, R. P. Burwood, M. Parinello, J. A. K. Howard and A. K. Cheetham, J. Am. Chem. Soc., 2012, 134, 11940–11943 CrossRef CAS PubMed.
- H. J. Shepherd, T. Palamarciuc, P. Rosa, P. Guionneau, G. Molnár, J.-F. Létard and A. Bousseksou, Angew. Chem., Int. Ed., 2012, 51, 3910–3914 CrossRef CAS PubMed.
- A. B. Cairns, J. Catafesta, C. Levelut, J. Rouquette, A. van der Lee, L. Peters, A. L. Thompson, V. Dmitriev, J. Haines and A. L. Goodwin, Nat. Mater., 2013, 12, 212–216 CrossRef CAS PubMed.
- A. D. Fortes, E. Suard and K. S. Knight, Science, 2011, 331, 742–745 CrossRef CAS PubMed.
- J. M. Ogborn, I. E. Collings, S. A. Moggach, A. L. Thompson and A. L. Goodwin, Chem. Sci., 2012, 3, 3011–3017 RSC.
- R. W. Munn, J. Phys. C: Solid State Phys., 1972, 5, 535–542 CrossRef CAS.
- A. B. Cairns, A. L. Thompson, M. G. Tucker, J. Haines and A. L. Goodwin, J. Am. Chem. Soc., 2012, 134, 4454–4456 CrossRef CAS PubMed.
- I. M. Lifshits, Zh. Eksp. Teor. Fiz., 1952, 22, 475–486 CAS.
- M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329 CrossRef CAS.
- J. Konnert and D. Britton, Inorg. Chem., 1966, 5, 1193–1196 CrossRef CAS.
- S. R. Batten, B. F. Hoskins and R. Robson, New J. Chem., 1998, 22, 173–175 RSC.
- A. L. Goodwin, M. Calleja, M. J. Conterio, M. T. Dove, J. S. O. Evans, D. A. Keen, L. Peters and M. G. Tucker, Science, 2008, 319, 794–797 CrossRef CAS PubMed.
- R. E. Newnham, Properties of Materials, Oxford University Press, Oxford, 2005 Search PubMed.
- A. C. Bailey and B. Yates, J. Appl. Phys., 1970, 41, 5088–5091 CrossRef CAS PubMed.
- S. J. Hibble, A. M. Chippindale, A. H. Pohl and A. C. Hannon, Angew. Chem., Int. Ed., 2007, 46, 7116–7118 CrossRef CAS PubMed.
- P. Betteridge, J. Carruthers, R. Cooper, K. Prout and D. Watkin, J. Appl. Crystallogr., 2003, 36, 1487 CrossRef CAS.
- H. L. Zhang, S. Lu, M. P. J. Punkkinen, Q.-M. Hu, B. Johannson and L. Vitos, Phys. Rev. B, 2010, 82, 132409 CrossRef.
- K. Kamali, C. Ravi, T. R. Ravindran, R. M. Sarguna, T. N. Sairam and G. Kaur, J. Phys. Chem. C, 2013, 117, 25704–25713 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis; experimental methods; X-ray single-crystal diffraction refinement details (variable-temperature and variable-pressure); neutron powder diffraction refinement details; calculations. CCDC 961474–961482. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c3cc47032f |
| This journal is © The Royal Society of Chemistry 2014 |
