 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Counterion release in membrane–biopolymer interactions
Daniel Harries
a,
Sylvio May
*b and
Avinoam Ben-Shaul
a
aInstitute of Chemistry and the Fritz Haber Research Center, The Hebrew University of Jerusalem, Jerusalem 91904, Israel
bDepartment of Physics, North Dakota State University, Fargo, North Dakota 58108, USA. E-mail: sylvio.may@ndsu.edu
First published on 7th August 2013
Abstract
When two oppositely charged macroions are brought into contact, a large fraction of the mobile counterions that previously surrounded each isolated macromolecule is released into the bulk solution, thereby increasing the counterions' translational entropy. The entropy gain associated with this counterion release mechanism is the driving force for various macroion binding processes, such as protein–membrane, protein–DNA, and DNA–membrane complexation. In this review we focus on the role of counterion release in the interaction between charged macromolecules and oppositely charged lipid membranes. The electrostatic interaction is generally coupled to other degrees of freedom of the membrane, or of the adsorbed macroion. Thus, for example, when a basic protein adsorbs onto a binary fluid membrane comprising anionic and neutral lipids then, in addition to the release of the mobile counterions to the bulk solution, the protein polarizes the membrane composition by attracting the charged lipids to its immediate vicinity. This process, which enhances the electrostatic attraction, is partly hampered by the concomitant loss of two-dimensional (2D) lipid mixing entropy, so that the resulting lipid distribution reflects the balance between these opposing tendencies. In membranes containing both monovalent and multivalent lipids, as is often the case with biological membranes, the peripheral protein preferentially interacts with (and thus immobilizes) the multivalent lipids, because a smaller number of these lipids are needed to neutralize its charge. The monovalent “counterlipids” are thus free to translate in the remaining area of the membrane. This entropy-driven counterlipid release mechanism in 2D is analogous to the extensively studied phenomenon of DNA condensation by polyvalent cations in 3D. Being self-assembled fluid aggregates, lipid bilayers can respond to interactions with peripheral or integral (whether charged or neutral) macromolecules in various ways. Of particular interest in this review is the interplay between electrostatic interactions, the lipid composition degrees of freedom mentioned above, and the membrane curvature elasticity, as will be discussed in some detail in the context of the thermodynamic stability and phase behavior of lipid–DNA complexes (also known as “lipoplexes”). This article is primarily theoretical, but the systems and phenomena considered are directly related to and motivated by specific experiments. The theoretical modeling is generally based on mean-field level approaches, specifically the Poisson–Boltzmann theory for electrostatic interactions, sometimes in conjunction with coarse grained computer simulations.
 Daniel Harries | Daniel Harries is an Associate Professor in the Institute of Chemistry at the Hebrew University of Jerusalem. He received his PhD in 2002 from the same University, and was a postdoctoral fellow at the National Institutes of Health in Bethesda, MD. His main research interests involve interactions between macromolecules and how these are modified in biologically realistic solutions that are stressed, confined, or crowded by numerous additional cosolutes. |
 Sylvio May | Sylvio May is an Associate Professor in the Department of Physics at North Dakota State University. He received his PhD degree in 1996 from Friedrich-Schiller University Jena and then worked as a postdoctoral associate at the Hebrew University of Jerusalem. His research focuses on modeling physical properties of lipid membranes and their interactions with biopolymers. |
 Avinoam Ben-Shaul | Avinoam Ben-Shaul received his PhD from the Hebrew University of Jerusalem in 1972, to which he returned in 1975 and has been a professor of theoretical chemistry since 1984. His research in soft matter has been concerned with the statistical thermodynamics of self-assembly, elasticity and phase behavior of micelles and membranes, and membrane interactions with proteins and DNA. In the last decade his research has focused on the physical mechanisms of cell adhesion and the structure and thermodynamics of DNA and RNA in and out of viral capsids. |
1 Introduction
Most of the counterions neutralizing the surface charge of a bilayer that contains ionic lipids reside within a thin layer parallel to the membrane plane. The shape and thickness of this counterion layer depend on the surface charge density, the valence and structure of the counterions, and the concentration of electrolytes in the ambient solution.1,2 For instance, divalent counterions such as Ca2+ are more strongly attracted to the surface of an anionic lipid membrane than monovalent counterions, such as Na+. Hence, Ca2+ ions added to solution will efficiently replace “membrane-bound” Na+ ions, sending them to the bulk solution, as illustrated in Fig. 1 and detailed in the next section. This “ion exchange” process is a simple demonstration of the entropy-driven counterion release mechanism, whereby many weakly charged counterions are replaced by fewer, strongly charged ones. Our interest in this review focuses on processes involving the release of small counterions by polyvalent ions or multivalent “macroions”, in which case the entropic component constitutes a major, often the dominant, contribution to the ensuing change in free energy.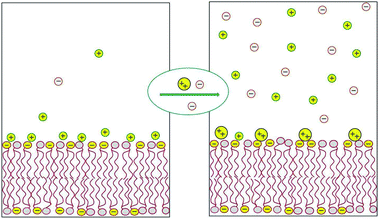 | ||
| Fig. 1 Schematic illustration of the release of monovalent counterions induced by the binding of divalent cations to an acidic lipid membrane. | ||
The electric field around linear, quasi one-dimensional (1D) macroions, e.g., DNA, is qualitatively different from the one generated by 2D macroions such as ionic lipid membranes. Specifically, in the low salt regime, the field is inversely proportional to the distance from an infinitely long 1D charged wire, while remaining independent of the distance from an extended 2D charged plate. Yet, similar to charged membranes, DNA in solution is surrounded by a thin cylindrical mantle of counterions, the shape and thickness of which depend on whether, how much, and which kind of salt is present in solution. But in practically all cases of interest, most of the DNA charge is balanced by a cloud of low-entropy counterions that are either “condensed” on the DNA surface or only confined to its immediate vicinity.3–5 Here again, monovalent counterions, such as Na+, can be efficiently replaced by polyvalent ions such as cobalt hexamine [Co(NH3)63+], or the biologically abundant polyamines spermidine and spermine, both serving to condense double stranded DNA (dsDNA) in bacterial viruses. Upon adding these polyvalent ions to an aqueous solution of dsDNA/Na+, they replace and release to solution DNA-bound Na+ ions carrying the equivalent amount of charge.6 When the polyvalent ion concentration in solution increases to a point that they neutralize all the dsDNA phosphate charges, they also mediate attractive interactions between neighboring dsDNAs, inducing a process known as DNA condensation, whereby the dsDNA molecules condense into hexagonally packed double helices.7 Different mechanisms have been suggested to explain this DNA condensation process, such as the formation of a Wigner lattice comprising phosphate and counterion charges,8,9 or the bridging of neighboring DNA strands by polyamines.10
Of special interest are the condensates of isolated, long dsDNA molecules, such as the ∼50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 base-pair (∼16
000 base-pair (∼16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 nm) long genome of the λ-phage. In the presence of polyvalent cations in a dilute solution of these dsDNAs, each molecule winds on itself to form an hexagonally packed toroidal aggregate,11–13 as illustrated in Fig. 2. Note that in this case, the attraction mediated by the counterions is strong enough to overcome the elastic curvature energy associated with bending the rather stiff dsDNA.14,15 At very high polyvalent concentrations DNA condensates re-dissolve into isolated double helices, each decorated with more polyvalent counterions than needed to neutralize its charge, resulting in “charge reversal” (or “charge inversion”) of the DNA surface, from negative to positive.16
500 nm) long genome of the λ-phage. In the presence of polyvalent cations in a dilute solution of these dsDNAs, each molecule winds on itself to form an hexagonally packed toroidal aggregate,11–13 as illustrated in Fig. 2. Note that in this case, the attraction mediated by the counterions is strong enough to overcome the elastic curvature energy associated with bending the rather stiff dsDNA.14,15 At very high polyvalent concentrations DNA condensates re-dissolve into isolated double helices, each decorated with more polyvalent counterions than needed to neutralize its charge, resulting in “charge reversal” (or “charge inversion”) of the DNA surface, from negative to positive.16
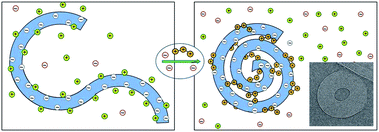 | ||
| Fig. 2 Schematic illustration of dsDNA condensation mediated by the release of monovalent counterions and their replacement by polyvalent ones, resulting in the formation of a toroidal condensate. The inset (adapted from Hud and Vilfan12) shows a cryo-electron microscopy image of the hexagonally packed, dsDNA torus of λ-phage condensed by trivalent cobalt hexamine ions. | ||
Lipid assemblies display a rich repertoire of aggregation morphologies, with a correspondingly complex interplay between elastic and electrostatic degrees of freedom. Upon changes in lipid composition, or upon their interactions with other molecules in solution, notably proteins and DNA, lipid bilayers often undergo curvature or stretching deformations. Furthermore, since lipid bilayers constitute self-assembled aggregates, upon changing solution conditions or due to interaction with other macromolecules, they may rearrange into topologically different structures, e.g., inverse hexagonal or cubic phases. A striking example of this behavior, as well as a dramatic demonstration of counterion release, is the formation of cationic lipid–DNA complexes. These complexes, also known as lipoplexes,17–20 were originally designed and are currently used as gene delivery vectors.21–23 Lipoplexes are spontaneously formed in aqueous solution upon bringing together dsDNA and cationic lipid bilayers into the same volume.20,24,25 As a concrete example, consider the mixing of two similar salt (e.g., 0.1 M NaCl) solutions: one containing dsDNA molecules, totaling N−D phosphate charges (balanced by the same number of sodium ions), and the other containing binary lipid vesicles composed of N+l monovalent cationic lipids (balanced by as many chloride ions) and, say, N0l ≈ N+l electrically neutral lipids. The latter is often referred to as a “helper lipid”,26 because it helps to determine the structure of the desired lipoplex, and hence its transfection efficiency. Within the complexes, the cationic lipids replace the mobile counterions that had originally balanced the DNA charge, and are therefore sometimes referred to as “counterlipids”, a term that we shall occasionally use in the forthcoming discussion. In fluid lipid membranes the lipids, charged and neutral, are free to diffuse in the membrane plane, enabling their redistribution in this plane upon interacting with peripheral macroions in order to enhance the electrostatic attraction. This, in turn, results in localization of the charged lipids within the interaction region, and hence in a loss of translational entropy. Nonetheless, this loss of 2D lipid entropy is considerably smaller than the gain of 3D translational entropy resulting from the release of the mobile counterions to the bulk solution.27
Experiments reveal that in the special case of “iso-electricity”, when N−D = N+l, all the dsDNA and the cationic lipids (accompanied by N0l neutral lipids) co-assemble into lamellar or hexagonal, electrically neutral lipoplexes, as illustrated in Fig. 3.25,28,29 The experiment also reveals that at the isoelectric point practically all the N−D + N+l mobile counterions, both positive and negative, are released into the solution.30 The complete release of the counterions is a direct consequence of the fact that in these complexes two macroions mutually neutralize each other, rendering the mobile counterions “unnecessary”. In thermodynamic terms, the free energy for lipoplex formation is minimized by maximizing the gain in entropy due to the release of the mobile counterions to the solution.
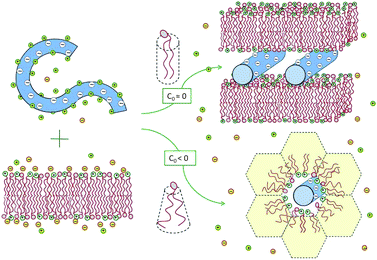 | ||
| Fig. 3 Spontaneous lipoplex formation by mixing dsDNA and cationic lipid membranes. Hexagonal complexes are formed when one of the lipid components (in this illustration the helper lipid) is characterized by a negative spontaneous curvature, c0 < 0, or when the lipid membrane is soft enough to allow for the change in its curvature. | ||
Two related factors determine which lipoplex morphology is more favorable: the bending rigidity, κ, of the lipid layers and the spontaneous curvature, c0, of their constituent lipids. When both the cationic and helper lipids favor the planar bilayer geometry, the lipoplexes formed are generally lamellar. Hexagonal complexes are formed when either the helper or the cationic lipid is characterized by a negative spontaneous curvature, and hence a propensity for the inverse-hexagonal phase. It should be noted, however, that in the absence of DNA, these honeycomb-like structures are rather unstable, owing to strong electrostatic repulsion between the charged lipid headgroups. This is why, in most experiments, the lipids are initially assembled into bilayers, while the hexagonal complexes are spontaneously formed only upon mixing with dsDNA, as shown in Fig. 3, and further discussed in Section 3.
Lipoplex formation emphasizes the role of the counterion release mechanism in mediating a real thermodynamic phase transition. In a way, this is analogous to other entropy-driven transitions, such as those attributed to the attractive depletion forces associated with the release of small particles from the space between macroscopic surfaces.31 But the analogy is limited, because in the systems of interest here the surfaces are charged and the interactions are electrostatic rather than steric.
The concept of “counterion release” has been coined long ago,32 and the underlying mechanism has been extensively appreciated, analyzed and verified, primarily in the context of chemical reactions between charged molecules, specifically, in bimolecular ligand–protein or DNA–protein binding,33 and in the unimolecular helix–coil transition of nucleic acid chains.34 These topics have been reviewed previously35,36 and need not be repeated here. Counterion release also plays an important role in the adsorption of flexible polyelectrolytes on flat surfaces37 or the formation of complexes of such polyelectrolytes with other rigid macroions;38,39 these scenarios have been reviewed comprehensively, too.40 Therefore, here we shall mainly focus on membrane–macroion interactions, with which we are also more familiar from our own work. We find these interactions particularly interesting and challenging because the membranes, and often the macroion too (e.g., a flexible protein), can respond to such interactions in various ways, including elastic deformations, morphological phase transformations, as well as local or global variations in lipid composition.
The discussion in this review is primarily theoretical, yet with close reference to relevant experiments. The electrostatic interactions are generally treated within the framework of Poisson–Boltzmann theory, which in several cases is integrated into computer simulation approaches. We begin the discussion in Section 2 with a brief outline of some of the relevant expressions and notions of Poisson–Boltzmann theory. Section 3 is devoted to the energetics, structure, and thermodynamics of the complexes formed between DNA and either mixed cationic–zwitterionic or only zwitterionic lipid membranes. Section 4 begins with a description of the local changes in lipid composition dependent upon the adsorption of model macroions, mimicking globular proteins. The discussion is then extended to the 2D phase transitions mediated by the adsorption of charged macroions on membranes composed of non-ideal lipid mixtures. Section 5 is concerned with the interaction of flexible (natively unfolded) proteins with mixed lipid membranes comprising neutral, monovalent, and polyvalent lipids, demonstrating the ability of the adsorbed proteins to preferentially attract and become neutralized by the multivalent counter-lipids; revealing a new type of 2D, or “in-plane counterlipid” release mechanism. We end this section by discussing the coupled diffusion dynamics of lipids and proteins and its biological relevance. We conclude with summarizing remarks in Section 6.
2 Excerpts from Poisson–Boltzmann theory
A transparent theoretical account of the principles underlying the counterion release mechanism is provided by mean-field electrostatics. This approach, often referred to as the Poisson–Boltzmann (PB) theory,41 and sometimes as the Gouy–Chapman theory,42 ignores correlations between the mobile salt ions and is therefore mainly applicable to monovalent electrolyte solutions. We thus consider an aqueous electrolyte solution containing a symmetric, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, (i.e., monovalent) salt of bulk concentration n0, and one or few macroions of low dielectric constant εL (much smaller than the dielectric constant of water, εW ≈ 80) and surface charge density σ. These conditions are relevant to most biological macroions, including membranes, proteins, and DNA. The present discussion will focus on systems where the number of macroion charges is negligible compared to that of the mobile ions, so that the overall counterion and coion concentrations are practically equal.
1, (i.e., monovalent) salt of bulk concentration n0, and one or few macroions of low dielectric constant εL (much smaller than the dielectric constant of water, εW ≈ 80) and surface charge density σ. These conditions are relevant to most biological macroions, including membranes, proteins, and DNA. The present discussion will focus on systems where the number of macroion charges is negligible compared to that of the mobile ions, so that the overall counterion and coion concentrations are practically equal.
Coulomb forces attract the counterions to (and repel the coions from) the macroion surfaces, thus screening part of the fixed surface charges. This, in turn, reduces the electric fields around the macroions, resulting in lower electrostatic energy of the system. In principle, the Coulomb energy would become minimal if all surface charges were exactly neutralized by an equivalent amount of adsorbed counterions. Clearly, however, localizing the counterions to the macroion surfaces entails an unfavorable demixing penalty associated with their loss of translational entropy. The balance between these two opposing tendencies – electrostatic attraction energy on the one hand and ion “demixing” entropy on the other hand – is dictated, as usual, by the requirement for thermodynamic equilibrium, which means minimal free energy. The structural consequence of this energy-entropy compromise is that each macroion surface is surrounded by a diffuse layer of mobile ions that is enriched with counterions and depleted of coions.
The structure of the diffuse layer is quantitatively characterized by the local volume densities of mobile cations and anions, n+(r) and n−(r), at every point of the aqueous solution, r. These, in turn, determine the local charge density, ρ(r) = e[n+(r) − n−(r)], and the local electrostatic potential distribution, Φ = Φ(r), which are related via the Poisson equation: εWε0∇2Φ = −ρ. Here, e denotes the elementary charge, ∇2 is the Laplacian, and ε0 is the permittivity of vacuum. At a given temperature T, the equilibrium ion densities n+(r) and n−(r) are those that minimize the electrostatic free energy of the system, Fel = Uel − TS. For arbitrary n+(r), n−(r), (or n+, n− for brevity) the mean-field expression for Fel is
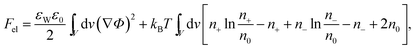 | (1) |
At equilibrium δFel(n+, n−) = 0 for any arbitrary variation of the mobile ion distributions in the system. By using Poisson's equation, εWε0∇2Φ = −e(n+ − n−), the identity ∇Φ∇(δΦ) = ∇(Φ∇(δΦ)) − Φ∇2(δΦ), and the boundary condition on the normal component of the electric field on the macroion surface, −(∇Φ·n)A = σ/(εWε0) (the unit vector n points toward the electrolyte), one finds43 that the first variation of Fel is given by
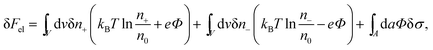 | (2) |
n± = n0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(∓eΦ/kBT). exp(∓eΦ/kBT).
| (3) |
It should be emphasized, however, that there are many important cases where the macroion surface charges are mobile rather than fixed, in which case σ can adjust in order to further reduce the electrostatic free energy. This is the case for example with a binary lipid membrane composed of electrically charged and neutral species, the local composition of which can adjust in response to interactions with charged macroions such as DNA or proteins, as will be discussed in Sections 3–5.
Substituting the Boltzmann distributions, eqn (3), into Poisson's equation leads to the Poisson–Boltzmann equation,
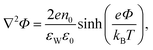 | (4) |
According to PB theory, for any given σ the mobile ion distributions are given by eqn (3) and the electrostatic potential must satisfy eqn (4). Thus, based on eqn (2) the electrostatic free energy can alternatively be calculated through the hypothetical charging process
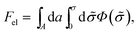 | (5) |
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) is increased from zero to its final value σ everywhere on the macroion surface A. The electrostatic potential Φ(
is increased from zero to its final value σ everywhere on the macroion surface A. The electrostatic potential Φ(![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ) on the surface A must be determined as a function of
) on the surface A must be determined as a function of ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) , such that n± = n0
, such that n± = n0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(∓eΦ/kBT) throughout the charging process.44 Eqn (5) implies that to evaluate Fel all we need is the electrostatic potential on the macroion surface, which must be known for all surface charge densities σ. This is often the most efficient way to calculate Fel, as demonstrated below for the case of a uniformly charged planar surface.
exp(∓eΦ/kBT) throughout the charging process.44 Eqn (5) implies that to evaluate Fel all we need is the electrostatic potential on the macroion surface, which must be known for all surface charge densities σ. This is often the most efficient way to calculate Fel, as demonstrated below for the case of a uniformly charged planar surface.
First, let us re-express the PB equation and its boundary conditions in terms of the dimensionless electrostatic potential Ψ = eΦ/(kBT), and introduce two important length scales: the Bjerrum length, lB = e2/(4πεWε0kBT), expressing the distance at which two elementary charges experience an interaction energy of kBT (in water lB = 0.7 nm), and the Debye length, 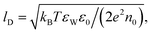 which provides a convenient measure for the range of electrostatic interactions in electrolyte solutions. (In physiological solutions, where salt concentrations are on the order of 0.1 M, lD ≈ 1 nm.) The PB equation now reads,
which provides a convenient measure for the range of electrostatic interactions in electrolyte solutions. (In physiological solutions, where salt concentrations are on the order of 0.1 M, lD ≈ 1 nm.) The PB equation now reads,
lD2∇2Ψ = sinh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ψ, Ψ,
| (6) |
| −(∇Ψ·n)A = 4πlBσ/e. | (7) |
For small values of the electrical potential, |Ψ| ≪ 1, the PB equation can be linearized, yielding lD2∇2Ψ = Ψ, which is known as the Debye–Hückel limit of PB theory. At room temperature this approximation is appropriate for |Φ| ≪ 25 mV. In this limit the electrolyte mediates a screened Coulomb (Yukawa-like) interaction ∼exp(−r/lD)/r between any two charges that are separated by a distance r. The Debye length lD is the screening length associated with this interaction.
We conclude this section with one specific example, demonstrating the relative importance of the energetic and entropic contributions to the electrostatic free energy as a function of the surface charge density and the bulk ion concentration. Consider a planar surface carrying a uniform and fixed charge density σ, which extends along the x = 0 plane of a Cartesian coordinate system. The surface is in contact with a symmetric 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte solution, present in the region 0 < x < ∞. The area of the surface A is large enough so that edge effects can be ignored. The PB equation, lD2Ψ′′(x) = sinh
1 electrolyte solution, present in the region 0 < x < ∞. The area of the surface A is large enough so that edge effects can be ignored. The PB equation, lD2Ψ′′(x) = sinh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ψ(x), must then be solved subject to the boundary conditions Ψ′(0) = −4πlBσ/e and Ψ(x → ∞) = 0. A first integration yields lDΨ′(x) = ±2
Ψ(x), must then be solved subject to the boundary conditions Ψ′(0) = −4πlBσ/e and Ψ(x → ∞) = 0. A first integration yields lDΨ′(x) = ±2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh(Ψ(x)/2) and thus Ψ0(σ) = 2
sinh(Ψ(x)/2) and thus Ψ0(σ) = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) arsinh(2πlBlDσ/e) for the σ-dependence of the surface potential Ψ0(σ) = Ψ(x = 0; σ). By using eqn (5) we obtain the electrostatic free energy per unit area
arsinh(2πlBlDσ/e) for the σ-dependence of the surface potential Ψ0(σ) = Ψ(x = 0; σ). By using eqn (5) we obtain the electrostatic free energy per unit area
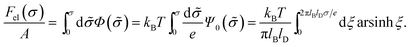 | (8) |
This is one of the few analytical results of the nonlinear PB model. By using the thermodynamic relationship S = −∂Fel/∂T and noting that lBlD ∼ T−1/2, eqn (8) leads to the following expressions for the energetic (Uel) and entropic (−TS) contributions to the free energy of the system, Fel:
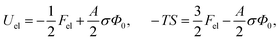 | (9) |
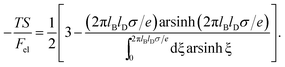 | (10) |
Fig. 4 shows −TS/Fel as a function of 2πlBlDσ/e, calculated according to eqn (10). In the linear (Debye–Hückel) limit of small surface charge density, 2πlBlDσ/e ≪ 1, we obtain −TS/Fel = 0.5; i.e., the electrostatic energy and demixing entropy contribute equally to the free energy. Typical charge densities of biologically relevant macroions are on the order of ∼1 e nm−2. With lB = 0.7 nm for water and lD = 1 nm under physiological conditions we obtain 2πlBlDσ/e = 4.4, so that −TS/Fel = 0.7. That is, in the nonlinear PB regime the diffuse ion cloud is more condensed and thinner than the prediction of the linear Debye–Hückel model. In other words, the entropic penalty for the salt ions is more pronounced than the energy stored in the remaining electric field.45–47
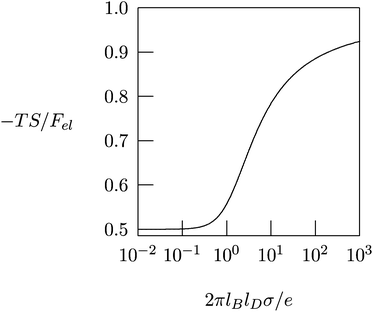 | ||
| Fig. 4 The fraction, −TS/Fel, of the entropic contribution to the total electrostatic free energy of a single charged planar surface with surface charge density σ, in contact with a salt solution of Debye length lD, according to eqn (10). | ||
The results in Fig. 4 provide important insights regarding the role of counterion release when two oppositely charged macroions interact with each other, at least for the special case that their surfaces are uniformly and oppositely charged, σ1 = σ and σ2 = −σ. At large separation, each macroion is surrounded by its own diffuse counterion layer with free energies as in eqn (8). At contact, the two macroions neutralize each other electrostatically, and all the mobile counterions are set free to the solution. Now there are no charged surfaces in the system and its free energy, by definition, is zero. Hence, the gain in free energy is −2Fel with Fel given in eqn (8). As discussed above, in the nonlinear PB regime the free energy gain is predominantly entropic, reflecting the increased translational freedom of the mobile ions. Similar, entropy-driven, counterion release mechanisms are the basis of various macroion–macroion interaction processes.36,48
A particularly subtle case of macroion attraction driven by counterion release concerns heterogeneously charged surfaces that are overall neutral. Surfaces with charged domains of finite size in thermodynamic equilibrium can form due to the competition of long-range electrostatic interactions and line tension.49 Even if random charge distributions on both surfaces are quenched and uncorrelated, experiments demonstrate a long-range attractive interaction of electrostatic origin.50–52 This attraction, which is driven by the release of counterions, can be caused by ion–ion correlations.53 However, it can also be reproduced by the non-linear Poisson–Boltzmann model47,54 but not if modeled using the linearized Debye–Hückel limit.54
Extension of the PB formalism to di- (or higher) valent mobile ions is, in principle, straightforward. It should be pointed out, however, that ion–ion correlations become increasingly important for higher valence species and/or close to highly charged surfaces.55–57 Ignoring these correlations can render the PB approach unreliable, even on a qualitative level. This is particularly evident for like-charged macroions (such as two parallel surfaces or stiff rods) where in contrast to computer simulations5,58 mean-field electrostatics strictly fails59 to predict attractive interactions that arise from ion–ion correlations. The influence of correlations is further amplified by image charges at dielectric boundaries.60–62
Still, qualitatively, we can use the mean-field approach to illustrate the concept of counterion release from an anionic membrane. For example, as discussed in Section 1, Ca2+ is able to replace monovalent “membrane bound” Na+. The prediction based on the Poisson–Boltzmann formalism is that the addition of 1 mM divalent salt to a solution of 100 mM monovalent salt releases 26% of the initially bound monovalent cations. The addition of 10 mM divalent salt instead increases the fraction of released cations to 60%, and for 100 mM as much as 80% will be exchanged. These numbers refer to a membrane charge density of −1 e nm−2. The maximal release, 100%, would correspond to the complete replacement of two Na+ by one Ca2+.
3 Membrane–DNA interactions
With dramatic precipitation, mixing of solutions of cationic lipids (CL) with DNA results in spontaneous formation of CL–DNA aggregates with submicron size.19,25,28,29,63–65 Driven to form by counterion release, these CL–DNA aggregates are routinely used for cell transfection in vitro, and afford potential gene delivery vehicles for in vivo gene therapy (for reviews see, e.g., ref. 28 and 66–68). In recent years this strategy has been extended to complex DNA with anionic or zwitterionic lipids into aggregates that should have lower cytotoxicity than the alternative CL.69–71 To form these complexes, polyvalent ions are used to mediate DNA and lipid complex formation, even for lipids that are net neutral or anionic, as is DNA. Lipoplexes have also attracted interest from a basic physical point of view as convenient tools for studying the link between intermolecular lipid–DNA interactions and the macroscopic ordered phases that they form. Specifically, these complexes have allowed some of the most compelling and direct demonstrations of counterion release.3.1 Structure of CL–DNA complexes
By forming composite phases, the CL–DNA structures combine the pure-lipid and pure-DNA phases. While double-stranded DNAs are rather stiff, and tend to align in parallel within domains, with a typical persistence length of 50 nm, lipid membranes can adopt different topologies. Crucial to the thermodynamic stability of all structural phases are the identity and ratio of CL and the so-called “helper lipids”72 (HL) that are added to form the lipoplexes. This in turn determines fundamental material properties, such as the lipid bilayer's curvature elasticity, which can be described in terms of the familiar Helfrich free energy.73 For the bending deformation of a membrane along one single spatial direction this free energy reads
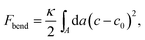 | (11) |
Lamellar complexes, illustrated in Fig. 3, typically form out of rigid membranes that prefer uncurved phases (low spontaneous curvature, c0), such as a mixture of CL (e.g., dioleoyltrimethylammonium propane, DOTAP76) and neutral HL (such as dioleoylphosphatidylcholine, DOPC). Intercalated between stacks of these lipids lie monolayers of DNA strands within the intervening water gaps. This complex has been termed Lcα because it is somewhat similar to a lipid bilayer stack in the Lα phase.
In Lcα lipoplexes, the DNA strands within each “gallery” tend to lie parallel to each other with a well-defined average repeat distance d that typically exhibits considerable fluctuations around its mean. The average spacing between two apposed lipid monolayers is nearly constant at ∼2.6 nm, corresponding to the diameter of double-stranded B-DNA, ca. 2.0 nm, surrounded by a thin hydration shell. In contrast, d can vary significantly and sensitively depends on the ratio between the total number of positive lipid charges to negative DNA charges, ρ = N+l/N−D, and on the fraction of charged lipids out of the total number of lipids, ϕ0 = N+l/(N+l + N0l).
As described in Section 1, the main driving force for lipoplex formation is the entropic gain in counterion release. Therefore, at the so-called “isoelectric point”, ρ = 1, the number of released counterions can be maximized, because fixed DNA and lipid charges match exactly, and the free energy of the complex is thus minimized.30,77
Additional equilibrium ordered-phases form when other HLs are used. For example, dioleoylphosphatidylethanolamine (DOPE) is known to promote the formation of inverted hexagonal (“honeycomb”78 or HcII79) organization of the lipid. This difference in preferred structure is due to the curvature-loving character of DOPE (c0 < 0). The HcII structure is analogous to the inverted hexagonal (HII) lipid phase, with DNA strands replacing most of its water tubes; see the illustration in Fig. 3. Here too, the diameter of the water tubes is only slightly larger than the diameter of the DNA “rods”. Other CL–DNA phases have also been observed. These include a hexagonal arrangement of rod-like micelles intercalated between hexagonally packed DNA,20,80 cubic phases,81 and the “spaghetti” structure,79 which is probably a metastable intermediate.78,82 Even more structures have been observed in computer simulations,83 yet without experimental verification so far.
3.2 Lamellar lipid–DNA complexes
The consequences of counterion release are well exemplified by the phase evolution of Lcα complexes. As revealed by a series of exacting X-ray measurements,25,29 the DNA–DNA distance, d, depends on the thermodynamic variables ρ, ϕ0, and n0, and reflects the DNA packing density within the complex. Both theory and experiment indicate that a lipid mixture with a given composition ϕ0 results in spacings d that are small and constant throughout the low ρ range, where the complex coexists with excess DNA; see Fig. 5. In the high ρ range, where the complex coexists with excess lipid, the spacings are larger and also nearly constant. In between these limits, which includes the isoelectric point ρ = 1, there exists a single-phase region, where all the DNA and lipids are complexed, and therefore d varies linearly with ρ.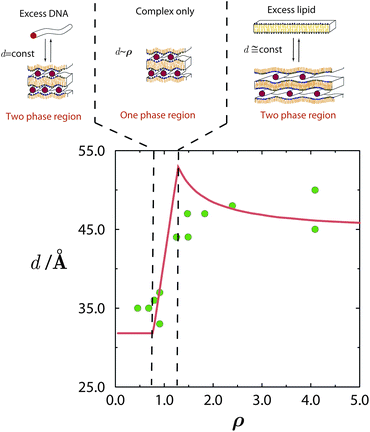 | ||
| Fig. 5 Phase evolution of lamellar CL–DNA complexes. The DNA–DNA distances within the multilamellar structure, d, change with ρ, increasing from their low value in the excess DNA region to a higher value in the excess lipid region. Around the isoelectric point, ρ = 1, the gain in entropy from counterion release is maximal, and all DNA and lipid are associated in complexes. Adapted from Harries et al.84 Copyright (1998), with permission from Biophysical Society. | ||
Most of the experimental findings can be explained within the scope of an extended PB theory.84,85 The model is based on the free energy in eqn (1) for a unit cell of the Lcα lipoplex, as illustrated in Fig. 6 (with additional curvature corrugations as discussed below in Section 3.3). Let us first assume that lipid bilayers are very rigid. That is, κ in eqn (11) is large and c0 ≈ 0 so that the free energy for bending is prohibitively large and, consequently, membranes are perfectly planar. The lateral mobility of the lipid molecules within the membrane plane is explicitly taken into account by adding to eqn (1) the “demixing entropy” term
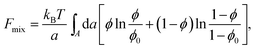 | (12) |
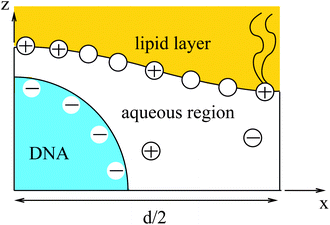 | ||
| Fig. 6 Unit cell of the lamellar Lcα–lipoplex. Curvature modulation of the surface of the lipid region (yellow) allows for a more favorable electrostatic interaction with the DNA (blue). | ||
Functional minimization of the total free energy, Fel + Fmix, leads to the familiar PB equation for the bulk solution, as detailed in Section 2, as well as to an additional equation that defines the charge regulation boundary condition for the membrane,
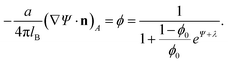 | (13) |
The equality on the left hand side of eqn (13) corresponds to the boundary condition in eqn (7), relating the charge density on the interface, σ = ϕe/a, to the derivative of the potential along the membrane normal n. However, unlike in eqn (7), here the local membrane composition ϕ is not fixed, but is rather regulated according to the local potential, Ψ, and subject to another Lagrange multiplier, λ, conjugated to the conservation of the total lipid charge in the membrane. For the DNA, a constant charge density boundary condition is assumed (corresponding to one negative elementary charge per 1.1 nm2), and the remaining boundary conditions result from the structure's periodicity. The resulting equations are solved self-consistently to determine the total free energy of the lipoplexes for specific values of d and ϕ0.
Inclusion of the lipid mobility degree of freedom turns out to be important for the mixed fluid bilayers considered here, because it enables lipids to greatly enhance the free energy gain upon complexation, and to increase the stability of the Lcα complex.27 Generally, it was found that the lipid mobility favors optimal (local) charge matching of the apposed DNA and lipid membrane. This is the state in which a maximal number of mobile counterions are expelled from the volume limited by the “interaction zone” of the membrane and DNA macroions, which results in a maximal free energy gain upon complex formation. Nevertheless, the tendency for charge matching (hence migration of lipids to and from the region of proximity) is opposed by an unfavorable lipid demixing entropy loss; see eqn (12). This entropic penalty somewhat suppresses the membrane's tendency to polarize in the vicinity of the DNA molecule. The extent to which the membrane will polarize is determined by an intricate balance between the electrostatic and lipid mixing entropy contributions to the free energy of the complex. The contribution of lipid demixing to the stabilization of the complex is most pronounced when the membrane's average composition is far from matching the charge density of the DNA, namely for low ϕ0. Here, the largest gain in counterion release can be made by ensuring local charge matching.
The total free energy associated with complexes, Fel + Fmix (see eqn (1) and (12)), can be used to determine the equilibrium proportions of three phases: free lipid, free DNA and lamellar lipoplexes. By equating the chemical potentials of each component in a mixture, it is possible to determine the compositions for which coexistence of two or more phases is expected, as well as regions with single phases at equilibrium. The different phase regions in Fig. 5 can therefore directly be derived from the model. The lipid composition in the complex and the free membrane need not be the same, because the average lipid composition in the system is generally different from the one that minimizes the complex's free energy, corresponding to exact charge matching and maximal counterion release. Nevertheless, since the equilibrium state of the system is dictated by the minimum of the total free energy of the system (not only of the complexes), it is often the case that the complexes are not “isoelectric” (i.e., ρ ≠ 1). Instead, they may become either negatively or positively “overcharged” away from the isoelectric point, thus accommodating an excess amount of either CL or DNA. This additional accommodation lowers the free energy of otherwise bare CL or DNA.
Further and direct support to the counterion release mechanism was given by counting released ions upon complex formation.30 By using conductivity measurements of the lipoplex supernatant, it was possible to determine that, as expected, a maximal number of counterions were released at the isoelectric point; see Fig. 7. This outcome is also accurately predicted using PB theory. Away from the isoelectric point (excess lipid or DNA) some counterions must remain to ensure charge neutralization, and the gain in free energy drops. Calorimetric measurements also confirm this finding, and show furthermore that complexation could in fact be endothermic, so that CL–DNA association is only favorable entropically.86 Theoretical predictions and estimates from calorimetry show that for a salt solution of concentration n0 = 4 mM, and a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 CL/HL mole ratio, the gain in free energy upon adsorption at the isoelectric point is large: 7.5 kBT per fixed charge pair (DNA and CL).30 This value translates to over 2000 kBT when considering the energy per persistence length of DNA (about 50 nm), carrying approximately 300 charges.
1 CL/HL mole ratio, the gain in free energy upon adsorption at the isoelectric point is large: 7.5 kBT per fixed charge pair (DNA and CL).30 This value translates to over 2000 kBT when considering the energy per persistence length of DNA (about 50 nm), carrying approximately 300 charges.
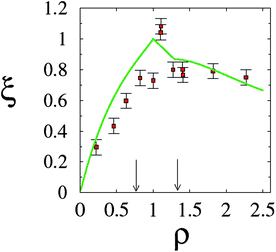 | ||
| Fig. 7 Fractional degree of counterion release, ξ, as a function of the lipid-to-DNA charge ratio, ρ. Experimental results (red solid squares) refer to an equimolar DOPC–DOTAP mixture in a 4 mM NaCl solution. The corresponding prediction according to the Poisson–Boltzmann model is also shown (green solid line). Recall the isoelectric point, ρ = 1. The two vertical arrows mark the phase boundaries (see Fig. 5). Adapted from Wagner et al.30 Copyright (2000), with permission from the American Chemical Society. | ||
Salt has a significant effect on the phase behavior, mainly because higher salt concentration lowers the entropic gain associated with the release of a counterion into the (denser) solution. Moreover, added salt causes a significant decrease in d, probably due to the screening of the repulsive DNA–DNA interaction. This response is more pronounced when divalent salts are added in increasing amounts, causing a 2D analogue of DNA condensation.87 A sharp decrease in d is observed above a certain salt concentration, resulting in very highly condensed DNA in each gallery.88 Another interesting observation is that the identity of the CL's counterion considerably changes the (endothermic) association enthalpy, particularly in the excess DNA region. This probably reflects the non-electrostatic interaction energies of different ions with membranes and other macromolecules, sometimes referred to as the “Hofmeister effect”.89–91
3.3 Curvature effects and structural transitions
So far the theoretical model has assumed that membranes remain flat. However, if κ is low or c0 is nonzero, additional counterion release may be achieved if membranes wrap more tightly around DNA in the lipoplex, Fig. 3. Indeed, when lipid membranes are soft or have a sufficiently negative spontaneous curvature, the hexagonal HcII phase becomes stable.74 This is because the free energy of bending will be lower when either the lipid monolayer's spontaneous curvature matches closely the complementary curvature of the DNA or when the lipid layer has low bending rigidity. Usually, a neutral HL is used for adjusting the spontaneous curvature to the required negative curvature, since pure CL tends to form planar or positively curved aggregates. However, while more HL in the mixed membranes may lower the elastic penalty, it also lowers the monolayer's charge density, compromising the electrostatic energy gain upon association.29 Theoretically, we have been able to account for these considerations by deriving detailed phase diagrams for lipid–DNA complexes with various electrostatic and bending properties.Fig. 8 shows an example of the complex phase behavior of lipoplexes, taking into account the bare lipid phases Lα and HII, naked DNA, and the complex phases Lcα and HcII. The phase diagram is computed for lipids forming soft membranes85 by numerically minimizing the total free energy, which included electrostatic, elastic, and lipid demixing contributions. This diagram (and similar phase diagrams for other material properties85) reflects the subtle interplay between the different contributions, including the release of counterions.
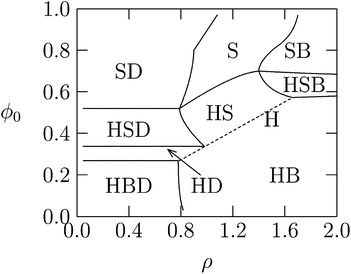 | ||
| Fig. 8 Calculated phase diagram of a lipid–DNA mixture, for lipids forming very soft planar membranes with κ = 0.2 kBT and vanishing spontaneous curvature. The symbols S, B, H, and D denote, respectively, the Lcα, Lα, HcII, and uncomplexed DNA phases. The straight dashed line marks the single HcII phase region. Adapted from May et al.85 Copyright (2000), with permission from the Biophysical Society. | ||
It is also possible to directly probe the competition of elastic and electrostatic energies in osmotic stress experiments.92 Interestingly, by measuring the associated Π V work, it has been possible to determine, both experimentally and theoretically, that the energy required to transit from the lamellar to hexagonal geometry is almost identical to the predicted membrane bending energy involved in the transition.92
More subtle effects may be observed if the bending energy cost of forming the HcII complexes is too high. To the extent allowed by elastic energy penalties, calculations show that the membranes in the Lcα complexes may corrugate and partially bend around DNA, thus further maximizing their contact with DNA and the degree of counterion release.93 A possible consequence of membrane corrugation, as well as a weak electrostatic interaction between galleries in the Lcα phase is an induced inter-locking between neighboring galleries (see Fig. 5), following the formation of “troughs”.94–97 An interplay between direct electrostatic repulsion and membrane-mediated elastic attraction between DNA strands in a lamellar lipoplex has also been suggested and analyzed by Dan.98,99
3.4 Zwitterionic lipoplexes
The two major drawbacks of using cationic lipids as non-viral gene delivery vectors are the low transfection efficiency of the lipoplexes100 and their cytotoxicity.101 The latter drawback may, in principle, be overcome by using only naturally occurring, biodegradable lipids. Yet, replacing cationic lipids by zwitterionic lipids apparently also eliminates the electrostatic attraction between the condensing agent (i.e., the lipid) and the DNA – the very reason to form lipoplexes in the first place. A method to regain this electrostatic attraction is to add divalent metal cations (such as Ca2+, Mg2+, Mn2+, and Zn2+) to an uncharged lipid membrane. Binding then effectively leaves the lipids with a cationic charge.102 Initial experimental indications that divalent cations facilitate the interaction of DNA with zwitterionic lipids103–105 have been confirmed for planar membranes,71,106,107 inverse hexagonal aggregates,108–110 and lipid monolayers.111–113 Indeed, zwitterionic lipoplexes are able to transfect DNA114 and are believed to be promising vectors for human gene delivery.115DNA adsorption onto a zwitterionic membrane is not driven by the release of counterions because the entropy gained by releasing to solution one “DNA-bound” divalent cation is, to a good approximation, similar to the entropy lost by one divalent cation upon becoming membrane bound. Instead, an extended PB model116,117 suggests that the adsorption is mediated by an ion exchange mechanism that is schematically illustrated in Fig. 9. Upon adsorption, divalent cations bound to the phosphate groups of the DNA migrate toward the membrane surface and bind to the phosphate groups of the lipids. Concomitantly, the headgroups of the zwitterionic lipids stretch out toward the DNA so as to interact with the DNA's phosphate groups. The migration of the divalent cations to the lipid region is favorable because their lateral area density (≈1.5 nm−2) is larger than that of the phosphate groups in the DNA (≈0.9 nm−2). In addition, lipids exhibit in-plane mobility, which allows them to further optimize the interaction with the divalent cations.
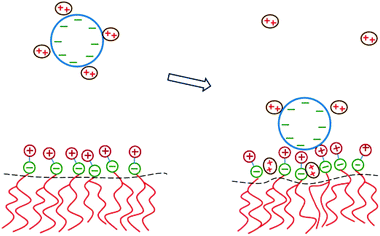 | ||
| Fig. 9 Schematic illustration of the physical mechanism that underlies the adsorption of DNA onto a zwitterionic lipid layer according to PB theory. Left: prior to adsorption, the DNA is screened by divalent cations. Right: upon the adsorption of DNA, some divalent cations redistribute in between the phosphate groups of the lipid heads. This enables the headgroups to extend toward the DNA where the positive headgroup charges contribute to screening the DNA charge. This ion exchange mechanism dominates the adsorption energetics. | ||
4 Role of lipid mobility
In this section we consider the adsorption of “midsized” macroions – finite, but larger than a lipid headgroup, e.g., peptides or globular proteins – on charged lipid membranes, highlighting two additional aspects of this lipid degree of freedom and their thermodynamic consequences. First, in Section 4.1, we consider the adsorption equilibrium between macroions in solution and those adsorbed on a binary lipid membrane, taking into account the electrostatic repulsion between the adsorbed proteins and assuming the 2D lipid mixture to be ideal. Then, in Section 4.2 the treatment is extended to nonideal lipid mixtures, revealing that macroion adsorption enhances the propensity of the lipid mixture to phase separate. These two scenarios are illustrated pictorially in Fig. 10. To feature the qualitative aspects of the two types of systems, the macroions are modeled as simple symmetric objects with uniform surface charge distributions.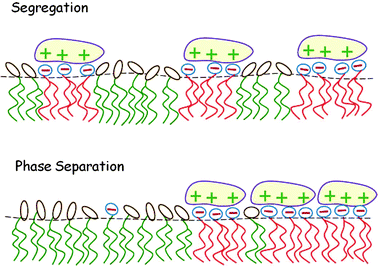 | ||
| Fig. 10 Local segregation of charged lipids by adsorbed macroions (top). When the lipid mixture is non-ideal, the adsorption of oppositely charged macroions may induce macroscopic 2D phase separation (bottom). | ||
4.1 Macroion-induced lipid segregation
As a simple model system consider the adsorption of a positively charged, spherical macroion of radius Rp = 1 nm with uniform surface charge density σp onto a binary lipid mixture composed of neutral and monovalent acidic lipids, all having equal cross-sectional headgroup area a. The average 2D membrane charge density is σm = −ϕ0e/a where ϕ0 is the mole fraction of anionic lipids in the membrane. Treating e as the unit of charge and a as the unit of area, −ϕ0 provides a dimensionless measure of the membrane surface charge density. In these units the dimensionless charge density on the macroion surface is given by ϕp = σpa/e. Consider now the special case of a strongly charged macroion with ϕp = 0.7, interacting with a fluid phospholipid membrane where the mole fraction of acidic lipids is ϕ0 = 0.2. This case, which is most representative for biological membranes, and various other scenarios were studied by May et al.118 The area per molecule in a fluid lipid membrane is typically, a ≈ 0.65 nm2, implying σm = −0.31 e nm−2 and σp = 1.07 e nm−2. The membrane–macroion system is assumed to bathe in monovalent ∼0.1 M salt solution, corresponding to a Debye screening length of lD = Rp = 1 nm. The minimal distance between the macroion and the membrane is fixed at 0.3 nm; all these are typical values for membrane-associated peripheral proteins.The model accounts for the electrostatic repulsion between the adsorbed macroions using a mean-field approximation, whereby the total membrane area is divided into hexagonal 2D (Wigner–Seitz) cells, such that the distance between the projections of neighboring macroion centers is 2R, as depicted in the inset of Fig. 11. Allowing for lipid mobility as in Section 3, the electrostatic free energy of the membrane–macroion system can be calculated based on PB theory for different cell sizes, reflecting different values of θ = (Rp/R)2, the surface coverage by macroions, which ranges between θ = 0 and θ ≈ 1 (maximal coverage). In addition to the boundary conditions on the dimensionless electrostatic potential Ψ on the macroion and membrane surfaces (allowing for lipid mobility; see eqn (13)), it is also required that (∂Ψ/∂r)r=R = 0 at the cell boundary. Fig. 11 shows the radial distribution of charged lipids around the projected center of the macroion, revealing the extensive enrichment of charged lipids “in the shadow of the macroion's southern hemisphere”, especially at low surface coverage.
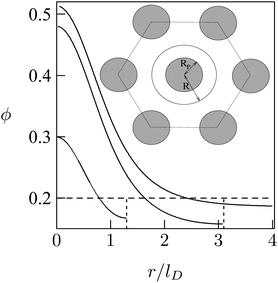 | ||
| Fig. 11 Radial distribution of charged lipid, ϕ(r), around the center (of the projection) of the adsorbed macroion, for lD = 1 nm, Rp = 1 nm, ϕP = 0.7, ϕ0 = 0.2. The three different curves correspond to R/lD = 6, R/lD = 3.1, and R/lD = 1.3. The inset shows the Wigner–Seitz cell with the macroion. Adapted from May et al.118 Copyright (2000), with permission from the Biophysical Society. | ||
As expected, the electrostatic adsorption free energy of the system, ΔF(θ), increases steeply as the average distance between macroions decreases (R → Rp); see Fig. 12. Adsorption isotherms can be derived by adding to ΔF(θ) the 2D (ideal mixing) entropy of the adsorbed macroions −TS = kBT[θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + (1 − θ)
θ + (1 − θ)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 − θ)] and, on a similar level of approximation, assuming ideal mixing behavior of the macroions in solution. This leads to Langmuir adsorption isotherms θ = αc/(1 + αc) where c is the volume fraction of macroions in solution, with α = α(θ) = exp{−[ΔF(θ) + θ(∂ΔF/∂θ)]/kBT}. The adsorption isotherm corresponding to the case considered here is shown in the inset of Fig. 12, indicating that the lipid mobility (solid curve) enhances the adsorption as compared to the case of a fixed and uniform lipid distribution (dashed curve); this follows from the fact that adsorption sets in at significantly lower bulk concentrations. Note, however, that as the macroion concentration in solution (and hence on the membrane) increases, the difference between the two curves diminishes. This is due to the steeply increasing electrostatic repulsion between the adsorbed macroions once their counterion clouds begin to overlap, i.e., when R ≈ Rp + lD, marking the onset of the saturation limit, which for the special case considered in Fig. 12 corresponds to θ ≈ 0.16 (slightly lower than [Rp/(Rp + lD)]2 = 0.25). At such high macroion surface densities the modulation of the lipid composition weakens (see Fig. 11) and hence the lipid mobility plays a lesser role. Finally, we note that the net charge on the macroion-decorated membrane in this limit is given by σnet = σm + 4θσp ≈ [−0.2 + 4 × 0.16 × 0.7] e nm−2 = +0.25 e nm−2, which is roughly equal in magnitude but opposite in sign to the charge on the bare membrane. This can be rationalized by noting that the upper hemisphere of the macroion does not contribute to membrane neutralization. The net charge on the surface is thus reversed.
ln(1 − θ)] and, on a similar level of approximation, assuming ideal mixing behavior of the macroions in solution. This leads to Langmuir adsorption isotherms θ = αc/(1 + αc) where c is the volume fraction of macroions in solution, with α = α(θ) = exp{−[ΔF(θ) + θ(∂ΔF/∂θ)]/kBT}. The adsorption isotherm corresponding to the case considered here is shown in the inset of Fig. 12, indicating that the lipid mobility (solid curve) enhances the adsorption as compared to the case of a fixed and uniform lipid distribution (dashed curve); this follows from the fact that adsorption sets in at significantly lower bulk concentrations. Note, however, that as the macroion concentration in solution (and hence on the membrane) increases, the difference between the two curves diminishes. This is due to the steeply increasing electrostatic repulsion between the adsorbed macroions once their counterion clouds begin to overlap, i.e., when R ≈ Rp + lD, marking the onset of the saturation limit, which for the special case considered in Fig. 12 corresponds to θ ≈ 0.16 (slightly lower than [Rp/(Rp + lD)]2 = 0.25). At such high macroion surface densities the modulation of the lipid composition weakens (see Fig. 11) and hence the lipid mobility plays a lesser role. Finally, we note that the net charge on the macroion-decorated membrane in this limit is given by σnet = σm + 4θσp ≈ [−0.2 + 4 × 0.16 × 0.7] e nm−2 = +0.25 e nm−2, which is roughly equal in magnitude but opposite in sign to the charge on the bare membrane. This can be rationalized by noting that the upper hemisphere of the macroion does not contribute to membrane neutralization. The net charge on the surface is thus reversed.
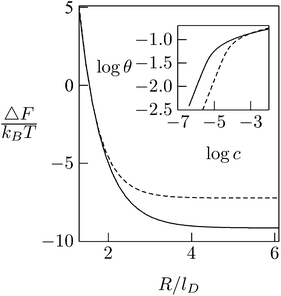 | ||
| Fig. 12 Adsorption free energies ΔF(R), as a function of the average distance between adsorbed macroion centers, 2R, for ϕP = 0.7 and ϕ0 = 0.2. The inset shows the corresponding adsorption isotherms. Solid curves correspond to the case of a fluid membrane composed of mobile lipids. For comparison we show the corresponding results (dashed curve) for a membrane composed of immobile lipids where ϕ(r) = ϕ0 = 0.2. In both cases Rp = lD = 1 nm. Adapted from May et al.118 Copyright (2000), with permission from the Biophysical Society. | ||
4.2 Macroion-induced phase separation
In addition to the local segregation of lipids into protein size domains, the binding of proteins onto mixed lipid membranes can sometimes result in macroscopic phase separation, whereby the two phases differ in both the lipid composition and the protein 2D concentration. Such phase transitions were observed, for example, in the adsorption of α-synuclein119 and annexin A2 (ref. 120) on supported binary (charged/uncharged) membranes. Particularly dramatic is the case of the cholera toxin subunit B that induces phase separation by cross-linking the lipid GM1 in both model121 and biological122 membranes. The extent to which proteins are involved in the regulation of membrane domains remains poorly understood but is likely of relevance in connection with the formation and stability of rafts in biomembranes.123,124Membrane phase separation is a consequence of non-ideal lipid mixing, which is known to prevail in (and has been quantified for) many model membranes.125,126 Even small differences in the acyl chain lengths of otherwise identical lipids can give rise to non-ideal mixing behavior of a binary membrane.127 Ternary mixtures of cholesterol with two lipids that differ in the degree of chain saturation can also lead to lipid phase separation. Suggested as models for rafts in biomembranes,128 these lipid mixtures exhibit non-ideality because of the more favorable interaction of cholesterol with saturated than with unsaturated acyl chains.
In the mean-field approximation of a 2D lattice model for a bare (“protein-free”) binary mixture of two electrically neutral lipid species, “1” and “2”, the free energy of the non-ideal mixture is given by
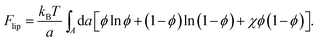 | (14) |
Here, ϕ is the mole fraction of lipid “1”, with χ = z[(ω11 + ω22)/2 − ω12] measuring the extent of non-ideality, defined as the difference between the average of the interaction energies of lipids of the same type, (ω11 + ω22)/2, and the interaction energy between unlike lipids, ω12. The two lipid species are assumed to occupy the same cross-sectional (i.e., the lattice site) area, a, and z is the lattice coordination number. For uncharged lipids, where the non-ideality originates mainly from interactions between the lipid acyl chains, macroscopic phase separation occurs when χ > χc = 2. If one lipid component, say “1”, is charged, the ensuing electrostatic headgroup repulsion renders the net interaction ω11 less negative, thus demanding an even larger non-ideality parameter χ for phase separation. Adding the electrostatic mean-field free energy, eqn (8), to the non-electrostatic contribution, eqn (14), yields χ > χc = 3.7 for the charged membrane,129 as expected, since like-charged lipids tend to avoid each other.
If, however, proteins of opposite charge are adsorbed onto the charged–neutral lipid mixture, macroscopic phase separation may take place even if the non-ideality parameter of the lipid chains is far lower than the critical value for phase separation in the bare membrane. As noted in the previous section, the adsorbed proteins not only neutralize the charge of the counter-lipids but also sequester these lipids to their vicinity, forming lipid–protein micro-domains, as illustrated in the upper diagram of Fig. 10. These protein-decorated micro-domains are enriched with acidic lipids and diffuse collectively as “rafts” or “barges” in the membrane plane; they may, or may not, condense into a separate phase, depending on their lateral interactions. If the interactions are attractive and strong enough, the lipid–protein barges will form a separate phase, as schematically depicted in the lower diagram of Fig. 10.
The phase behavior of the protein-decorated membrane can again be described in terms of a 2D lattice gas model, where the lipid–protein barges play the role of individual units, the size aP of which dictates the area per lattice site. In analogy to eqn (14), the mean-field free energy of this system is given by
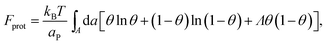 | (15) |
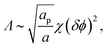 | (16) |
Similarly to χ, Λ can be expressed in the form Λ = z[(WPP + WLL)/2 − WPL], where WPP = (n/2)[ϕP2ω11 + (1 − ϕP)2ω22 + 2ϕP(1 − ϕP)ω12] is the interaction energy between two neighboring lipid–protein barges, with n denoting the number of lipid molecules along their mutual boundary; WLL and WPL are defined analogously. After some algebra, and noting that the number of lipids along the circumference of one barge, and hence n, is proportional to 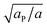 , we arrive at eqn (16). If the effective attraction between the barges is strong enough (Λ > 2 in the mean-field approximation), the protein-decorated binary membrane will split into a condensed phase enriched in acidic lipids and proteins that coexists with an essentially bare membrane of mostly uncharged lipids; see the lower diagram of Fig. 10. Notably, this phase separation can take place even if the lipid non-ideality is weak, namely χ < 2, provided of course that the surface area of the adsorbed protein aP (and hence its perimeter length) is large enough to ensure that Λ is larger than its critical value. This behavior is qualitatively similar to the phase behavior of polymer solutions, where a rather small non-ideality parameter χ between monomers and solvent molecules suffices to render the polymer insoluble, owing to the fact that the effective polymer–solvent non-ideality parameter is on the order of Mχ, where M is the degree of polymerization.131 All these qualitative notions are supported by detailed Poisson–Boltzmann based calculations132 and other modeling methods.133–135
, we arrive at eqn (16). If the effective attraction between the barges is strong enough (Λ > 2 in the mean-field approximation), the protein-decorated binary membrane will split into a condensed phase enriched in acidic lipids and proteins that coexists with an essentially bare membrane of mostly uncharged lipids; see the lower diagram of Fig. 10. Notably, this phase separation can take place even if the lipid non-ideality is weak, namely χ < 2, provided of course that the surface area of the adsorbed protein aP (and hence its perimeter length) is large enough to ensure that Λ is larger than its critical value. This behavior is qualitatively similar to the phase behavior of polymer solutions, where a rather small non-ideality parameter χ between monomers and solvent molecules suffices to render the polymer insoluble, owing to the fact that the effective polymer–solvent non-ideality parameter is on the order of Mχ, where M is the degree of polymerization.131 All these qualitative notions are supported by detailed Poisson–Boltzmann based calculations132 and other modeling methods.133–135
5 Counterlipid exchange and enrichment
5.1 Thermodynamics
Biological membranes are multicomponent mixtures of various lipid species and proteins. In many cases, anionic phospholipids comprise a substantial fraction of the lipid population. Some 10–30% of the lipids in the inner leaflet of many cell membranes are anionic, the majority of which are singly charged phosphatidylserine (PS), and 1% are multivalent lipids, of which phosphatidylinositol 4,5-bisphosphate (PIP2) is the most abundant one, serving as the source of two second messengers in a variety of biological chain events.136 The net charge of PIP2 ranges between −3 and −5, depending on pH and other factors.Substantial experimental evidence reveals that PIP2, despite its rarity, is strongly attracted to the adsorption zone of basic peripheral proteins.137–141 An extensively studied case is that of the natively unfolded protein MARCKS (myristoylated alanine-rich C kinase substrate), whose central (“effector”) domain (ED) comprises 25 amino acid residues, 13 of which are positively charged. This domain is flanked by two flexible chains, each 150 residues long, with a hydrophobic myristate membrane anchor at the N terminus, as illustrated in Fig. 13. Phosphorylation of three serine residues by protein kinase C reduces the charge of ED to +7, triggering the detachment of the protein from the membrane, thus exposing the 3 PIP2 molecules formerly shielded by the basic domain to enzymatic reactions. This chain of events is sometimes termed the “electrostatic switch mechanism”.142–146
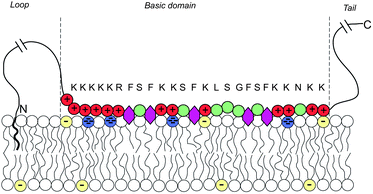 | ||
| Fig. 13 Schematic representation of a membrane-adsorbed MARCKS protein. Red and green circles represent charged and neutral amino acids, respectively. Purple hexagons stand for the phenyl groups which tend to insert into the membrane's hydrophobic core. The blue and yellow lipid headgroups represent the tetravalent PIP2 and monovalent PS lipids, respectively. The amino acid sequence of the basic domain is shown explicitly. The effector domain of MARCKS sequesters and binds to 3 (tetravalent) anionic PIP2 lipids. Adapted from Tzlil et al.142 Copyright (2008), with permission from the Biophysical Society. | ||
The system described above has also been studied using Monte Carlo (MC) simulations.142 The membrane was modeled as a ternary mixture of neutral zwitterionic lipids (mimicking phosphatidylcholine, PC), and two acidic lipids: monovalent (PS) and tetravalent (PIP2). MARCKS was modeled as a freely jointed heteropolymer chain of charged, neutral, and hydrophobic residues, with electrostatic interactions treated using screened Coulomb potentials. An extended version147 of the Rosenbluth MC algorithm of polymer statistics was employed in order to account for the simultaneous 2D diffusion of the mobile lipids, and the conformational changes of the flexible protein arms. A snapshot from one of the simulation runs is shown in Fig. 14. In addition, in Fig. 15 we display the radial distribution of the charged lipids around the (projected) center of the protein for a PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PS
PS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PIP2 = 89
PIP2 = 89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 lipid mixture. By now it should not be surprising that although PIP2 constitutes just 1% of the lipids, its local concentration in the adsorption zone is enormously enriched, whereas practically all of the (10-fold more abundant) PS lipids have been released to the bulk of the membrane where they experience unrestricted translational entropy. This behavior is yet another (2D in this case) manifestation of the counterion release mechanism.147,148
1 lipid mixture. By now it should not be surprising that although PIP2 constitutes just 1% of the lipids, its local concentration in the adsorption zone is enormously enriched, whereas practically all of the (10-fold more abundant) PS lipids have been released to the bulk of the membrane where they experience unrestricted translational entropy. This behavior is yet another (2D in this case) manifestation of the counterion release mechanism.147,148
 | ||
Fig. 14 A snapshot from the MC simulation of an entire MARCKS protein model, for a system where PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PS PS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PIP2 = 89 PIP2 = 89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; the red and green spheres represent the anionic and neutral residues. Blue, purple and white spheres represent PIP2, PS and PC, respectively. The yellow sphere is the myristoyl anchor. Adapted from Tzlil et al.142 Copyright (2008), with permission from the Biophysical Society. 1; the red and green spheres represent the anionic and neutral residues. Blue, purple and white spheres represent PIP2, PS and PC, respectively. The yellow sphere is the myristoyl anchor. Adapted from Tzlil et al.142 Copyright (2008), with permission from the Biophysical Society. | ||
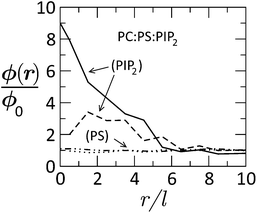 | ||
Fig. 15 Radial distribution of tetravalent (PIP2) and monovalent (PS) lipids in a membrane of lipid composition PC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PS PS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PIP2 = 89 PIP2 = 89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, as a function of the distance from the (membrane-projected) center of the basic effector domain (ED). ϕ(r)/ϕo is the ratio between the local and bulk populations of the corresponding lipid. The dashed curve describes the distribution of PIP2 after phosphorylation of ED, whereby its charge is reduced from +13 to +7. The dashed-dotted and dotted curves describe the distribution of PS before and after phosphorylation, respectively. While PIP2 is highly enriched in the adsorption zone, PS is hardly affected. Adapted from Tzlil et al.142 Copyright (2008), with permission from the Biophysical Society. 1, as a function of the distance from the (membrane-projected) center of the basic effector domain (ED). ϕ(r)/ϕo is the ratio between the local and bulk populations of the corresponding lipid. The dashed curve describes the distribution of PIP2 after phosphorylation of ED, whereby its charge is reduced from +13 to +7. The dashed-dotted and dotted curves describe the distribution of PS before and after phosphorylation, respectively. While PIP2 is highly enriched in the adsorption zone, PS is hardly affected. Adapted from Tzlil et al.142 Copyright (2008), with permission from the Biophysical Society. | ||
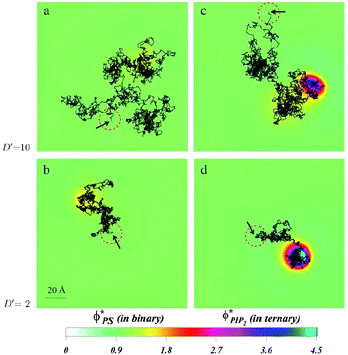 | ||
| Fig. 16 Diffusion of a charged spherical macroion on mixed membranes. Protein diffusion is most strongly impacted when fast diffusing proteins are adsorbed on membranes containing even small amounts of PIP2. The high valency lipids migrate quickly to the interaction zone and retard the protein motion, by making the entire “complex” diffuse together. The panels show the local surface charge densities after 0.6 ms of simulations (color scale) and the entire macroion trajectories in that time (connected black lines) for a protein with high diffusion rate on a binary (PC–PS) mixture, (a), and on a ternary (PC–PS–PIP2) mixture (c), and for a slowly diffusing protein on a binary (PC–PS) mixture (b), and on a ternary (PC–PS–PIP2) mixture (d). The red-dashed circles on each panel represent the projected size of the macroion with black arrows indicating the starting position of the macroion center of mass. For clarity, the figures are zoomed in on the relevant membrane surface region explored by the macroion. Adapted from Khelashvili et al.149 Copyright (2008), with permission from the Biophysical Society. | ||
5.2 Kinetics
Together with the stronger sequestration of high valency lipids to the interaction zone of oppositely charge macroions, the dynamics of lipid segregation is also significantly impacted. The same expressions for the free energy, eqn (1), can be used to derive the local, nonequilibrium, chemical potentials of lipids in the membrane. These expressions can be used in dynamic Cahn–Hilliard equations that describe the continuum kinetics of lipid diffusion in the membrane upon oppositely charged macroion absorption.149,150 These dynamics can be followed from the time of absorption to the steady state. By using this formalism, it has been possible to determine that PIP2 lipids not only sequester more strongly to the interaction zone of the oppositely charged polylysine peptides, but that they also diffuse more quickly into the interaction zone. This should not be surprising, because more highly charged lipids not only enjoy a larger chemical potential difference when they enter the interaction zone relative to the bulk free membrane, but they are also subjected to larger gradients of the chemical potential, and therefore migrate faster than monovalent lipids. This is true even if the diffusion constants of all lipids in the membrane are assumed equal. In a way, this can be viewed as lipids “sensing” the favorable prospects of lowering the free energy due to counterion release, and their subsequent preferential drive in that direction.It is interesting to also determine how the diffusion of an adsorbed peptide changes due to the chemical potential difference in the presence of PIP2 versus monovalent lipids. Experiments show that peptide diffusion is retarded significantly in the presence of PIP2 lipids compared with when a monovalent lipid such as PS is used.143,144 By allowing a model protein to diffuse into a membrane in a dynamic Monte Carlo scheme, it was possible to determine the differences in protein diffusion in the presence and absence of PIP2 and monovalent lipids, Fig. 16. We have found that lipid segregation slows protein diffusion, as PIP2 lipids introduce an effective drag on the motion of the adsorbate. In contrast, in the presence of monovalent lipids such as PS that only weakly segregate, the diffusion of proteins and lipids remains largely uncorrelated.
6 Concluding remarks
Originally described as a driving force for initial DNA–protein association,35 counterion release is now recognized to pervade interactions between many types of oppositely charged macromolecules.29,67,150,151 We described here several biophysical and biomedical implications of this phenomenon, yet the same general and robust principles play a major role in many systems that we have not even mentioned. One example of practical importance is the powerful directed self-assembly technique, termed layer-by-layer deposition,152 that enables easy fabrication of multilayers on surfaces by successive adsorption of polyanions and polycations. The adsorption and subsequent charge reversal at each stage are driven primarily by the release of the polyelectrolyte counterions.In our analysis we have mainly relied on Poisson–Boltzmann theory. However, since the systems considered involve complex geometries and additional, “non-electrostatic”, degrees of freedom (e.g., protein flexibility, lipid mobility, or membrane curvature), the solution of the corresponding PB equations has unavoidably been numerical. Only in Section 2 did we briefly discuss the case of a single planar membrane, for which an analytical solution is well known. It should nevertheless be mentioned that there are several other cases, where the mechanism of counterion release has been analyzed rigorously. This includes in particular the interaction between two planar membranes in the linearized Debye–Hückel limit,153 as well as in the non-linear regime.46,47,154,155
Other theoretical tools have also been used to describe counterion release or the related process of lipoplex formation, including analytical treatment,156 methodologies that go beyond the mean-field description,157 and coarse-grained83 or all-atom molecular dynamics simulations.158 It is appropriate to reiterate that counterion release also plays an important role in the process of DNA condensation, which has received enormous analytical and numerical attention.4,159
From the three decades since it was first described, the principle of counterion release has been found to be one of the most important mechanisms for macromolecular associations in solution. It will be interesting to see the inevitable emergence of additional examples for its importance in biologically relevant interactions as well as for future technological fabrication applications.
Acknowledgements
This work was supported by the Israel Science Foundation (ISF grant 1448/10 to ABS). The Fritz Haber research center is supported by the Minerva foundation, Munich, Germany.References
- D. F. Evans and H. Wennerström, The Colloidal Domain: Where Physics, Chemistry, Biology, and Technology Meet, VCH publishers, 2nd edn, 1994 Search PubMed.
- D. Andelman, Structure and Dynamics of Membranes, Elsevier, Amsterdam, 2nd edn, 1995, vol. 1, ch. 12, pp. 603–642 Search PubMed.
- F. Oosawa, Polyelectrolyes, Marcel-Dekker, New York, 1971 Search PubMed.
- G. S. Manning, Q. Rev. Biophys., 1978, 11, 179–246 CrossRef CAS.
- N. Gronbech-Jensen, R. J. Mashl, R. F. Bruinsma and W. M. Gelbart, Phys. Rev. Lett., 1999, 78, 2477–2480 CrossRef PubMed.
- V. A. Bloomfield, Biopolymers, 1996, 44, 269–282 CrossRef.
- S. Leikin, V. A. Parsegian, D. C. Rau and R. P. Rand, Annu. Rev. Phys. Chem., 1993, 44, 369–395 CrossRef CAS PubMed.
- B. I. Shklovskii, Phys. Rev. Lett., 1999, 82, 3268–3271 CrossRef CAS.
- I. Rouzina and V. A. Bloomfield, J. Phys. Chem., 1996, 100, 9977–9989 CrossRef CAS.
- E. Raspaud, M. Olvera de la Cruz, J. L. Sikorav and F. Livolant, Biophys. J., 1998, 74, 381–393 CrossRef CAS.
- V. A. Bloomfield, Curr. Opin. Struct. Biol., 1996, 6, 334–341 CrossRef CAS.
- N. V. Hud and I. D. Vilfan, Annu. Rev. Biophys. Biomol. Struct., 2005, 34, 295–318 CrossRef CAS PubMed.
- O. Lambert, L. Letellier, W. M. Gelbart and J. L. Rigaud, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 7248–7253 CrossRef CAS PubMed.
- J. Ubbink and T. Odijk, Europhys. Lett., 1996, 33, 353–358 CrossRef CAS PubMed.
- S. Tzlil, J. T. Kindt, W. M. Gelbart and A. Ben-Shaul, Biophys. J., 2003, 84, 1616–1627 CrossRef CAS.
- K. Besteman, K. V. Eijk and S. G. Lemay, Nat. Phys., 2007, 3, 641–644 CrossRef CAS.
- R. Fraley, S. Subramani, P. Berg and D. Papahadjopoulos, J. Biol. Chem., 1980, 255, 10431–10435 CAS.
- P. Felgner, T. Gadek, M. Holm, R. Roman, H. Chan, M. Wenz, J. Northrop, G. Ringold and M. Danielsen, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 7413–7417 CrossRef CAS.
- P. L. Felgner and G. M. Ringold, Nature, 1989, 331, 461–462 Search PubMed.
- R. Ghirlando, E. J. Wachtel, T. Arad and A. Minsky, Biochemistry, 1992, 32, 7143–7151 Search PubMed.
- A. Elouahabi and J. M. Ruysschaert, Mol. Ther., 2005, 11, 336–347 CrossRef CAS PubMed.
- M. S. Al-Dosari and X. Gao, AAPS J., 2009, 11, 671–681 CrossRef CAS PubMed.
- E. N. Smyth Templeton, Gene and Cell Therapy: Therapeutic Mechanisms and Strategies, CRC press, Boca Raton, 3rd edn, 2008 Search PubMed.
- D. D. Lasic, H. Strey, M. C. A. Stuart, R. Podgornik and P. M. Frederik, J. Am. Chem. Soc., 1997, 119, 832–833 CrossRef CAS.
- J. O. Rädler, I. Koltover, T. Salditt and C. R. Safinya, Science, 1997, 275, 810–814 CrossRef.
- S. W. Hui, M. Langner, Y.-L. Zhao, R. Patrick, E. Hurley and K. Chan, Biophys. J., 1996, 71, 590–599 CrossRef CAS.
- P. M. M. P. Mitrakos, Biochemistry, 1996, 35, 16714–16722 CrossRef CAS PubMed.
- C. R. Safinya, Curr. Opin. Struct. Biol., 2001, 11, 440–448 CrossRef CAS.
- I. Koltover, T. Salditt, J. O. Rädler and C. R. Safinya, Science, 1998, 281, 78–81 CrossRef CAS.
- K. Wagner, D. Harries, S. May, V. Kahl, J. O. Rädler and A. Ben-Shaul, Langmuir, 2000, 16, 303–306 CrossRef CAS.
- S. Asakura and F. Oosawa, J. Polym. Sci., 1958, 33, 183–192 CrossRef CAS.
- P. L. Dehaseth, T. M. Lohman and M. T. Record, Biochemistry, 1977, 16, 4783–4790 CrossRef CAS.
- S. Tomac, M. Sarkar, T. Ratilainen, P. Wittung, P. E. Nielsen, B. Norden and A. Graslund, J. Am. Chem. Soc., 1996, 118, 5544–5552 CrossRef CAS.
- J. Q. Wu and R. B. Macgregor, Biopolymers, 1995, 35, 369–376 CrossRef CAS PubMed.
- M. T. Record, C. F. Anderson and T. M. Lohman, Q. Rev. Biophys., 1978, 11, 103–178 CrossRef CAS.
- C. F. Anderson and M. T. Record, Annu. Rev. Phys. Chem., 1995, 46, 657–700 CrossRef CAS PubMed.
- P. Sens and J. F. Joanny, Phys. Rev. Lett., 2000, 84, 4862–4865 CrossRef CAS.
- R. R. Netz and J. F. Joanny, Macromolecules, 1999, 32, 9026–9040 CrossRef CAS.
- K. K. Kunze and R. R. Netz, Europhys. Lett., 2002, 58, 299–305 CrossRef CAS.
- R. R. Netz and D. Andelman, Phys. Rep., 2003, 380, 1–95 CrossRef CAS.
- M. R. Wright, An Introduction to Aqueous Electrolyte Solutions, John Wiley & Sons, New York, 2007 Search PubMed.
- E. J. W. Verwey and J. T. G. Overbeek, Theory of the Stability of Lyophobic Colloids, Elsevier, New York, 1948 Search PubMed.
- R. E. Goldstein, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 5504–5515 CrossRef CAS.
- R. J. Hunter, Foundations of Colloid Science, Oxford University Press, 1987 Search PubMed.
- J. T. G. Overbeek, Colloids Surf., 1990, 51, 61–75 CrossRef CAS.
- A. A. Meier-Koll, C. C. Fleck and H. H. von Grunberg, J. Phys.: Condens. Matter, 2004, 16, 6041–6052 CrossRef CAS.
- S. A. Safran, Europhys. Lett., 2005, 69, 826–831 CrossRef CAS.
- A. L. Becker, K. Henzler, N. Welsch, M. Ballauff and O. Borisov, Curr. Opin. Colloid Interface Sci., 2012, 17, 90–96 CrossRef CAS PubMed.
- A. Naydenov, P. A. Pincus and S. A. Safran, Langmuir, 2007, 23, 12016–12023 CrossRef CAS PubMed.
- S. Perkin, N. Kampf and J. Klein, Phys. Rev. Lett., 2006, 96, 038301 CrossRef.
- Y. S. Jho, R. Brewster, S. A. Safran and P. A. Pincus, Langmuir, 2011, 27, 4439–4446 CrossRef CAS PubMed.
- G. Silbert, D. Ben-Yaakov, Y. Dror, S. Perkin, N. Kampf and J. Klein, Phys. Rev. Lett., 2012, 109, 168305 CrossRef.
- A. Naji and R. Podgornik, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 041402 CrossRef.
- D. Ben-Yaakov, D. Andelman and H. Diamant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 022402 CrossRef.
- V. Vlachy, Annu. Rev. Phys. Chem., 1999, 50, 145–165 CrossRef CAS PubMed.
- Y. Levin, Rep. Prog. Phys., 2002, 65, 1577–1632 CrossRef CAS.
- H. Boroudjerdi, Y. W. Kim, A. Naji, R. R. Netz, X. Schlagberger and A. Serr, Phys. Rep., 2005, 416, 129–199 CrossRef CAS PubMed.
- M. Kanduc, M. Trulsson, A. Naji, Y. Burak, J. Forsman and R. Podgornik, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 061105 CrossRef CAS.
- J. C. Neu, Phys. Rev. Lett., 1999, 82, 1072–1074 CrossRef CAS.
- M. M. Hatlo and L. Lue, EPL, 2010, 89, 25002 CrossRef.
- S. Buyukdagli, M. Manghi and J. Palmeri, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 041601 CrossRef.
- M. Kanduc, A. Naji, J. Forsman and R. Podgornik, J. Chem. Phys., 2012, 137, 174704 CrossRef PubMed.
- P. L. Felgner, Y. Barenholz, J. P. Behr, S. H. Cheng, P. Cullis, L. Huang, J. A. Jessee, L. Seymour, F. Szoka, A. R. Thierry, E. Wagner and G. Wu, Hum. Gene Ther., 1997, 8, 511–512 CrossRef CAS PubMed.
- Y. Barenholz, Curr. Opin. Colloid Interface Sci., 2001, 6, 66–77 CrossRef CAS.
- J. O. Rädler, Electrostatic effects in soft matter and biophysics, Kluwer, Dordrecht, 2001, pp. 441–458 Search PubMed.
- S. May and A. Ben-Shaul, Curr. Med. Chem., 2004, 11, 151–167 CrossRef CAS.
- R. Podgornik, D. Harries, J. DeRouchey, H. H. Strey and V. A. Parsegian, Gene and Cell Therapy: Therapeutic Mechanisms and Strategies, CRC press, Boca Raton, 3rd edn, 2008, pp. 443–485 Search PubMed.
- C. R. Safinya, K. K. Ewert and C. Leal, Liq. Cryst., 2011, 38, 1715–1723 CrossRef CAS PubMed.
- H. Liang, D. Harries and G. C. L. Wong, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 11173–11178 CrossRef CAS PubMed.
- A. Lakkaraju, J. Dubinsky, W. Low and Y. Rahman, J. Biol. Chem., 2001, 276, 32000–32007 CrossRef CAS PubMed.
- M. Pisani, P. Bruni, G. Caracciolo, R. Caminiti and O. Francescangeli, J. Phys. Chem. B, 2006, 110, 13203–13211 CrossRef CAS PubMed.
- S. W. Hui, M. Langner, Y. L. Zhao, P. Ross, E. Hurley and K. Chan, Biophys. J., 1996, 71, 590–599 CrossRef CAS.
- W. Helfrich, Z. Naturforsch., C: J. Biosci., 1973, 28, 693–703 CAS.
- C. R. Safinya, E. B. Sirota, D. Roux and G. S. Smith, Phys. Rev. Lett., 1989, 62, 1134–1137 CrossRef CAS.
- I. S. Zuhorn, V. Oberle, W. H. Visser, J. B. F. N. Engberts, U. Bakowsky, E. Polushkin and D. Hoekstra, Biophys. J., 2002, 83, 2096–2108 CrossRef CAS.
- D. Simberg, S. Weisman, Y. Talmon and Y. Barenholz, Crit. Rev. Ther. Drug Carrier Syst., 2004, 21, 257–317 CrossRef CAS.
- R. Bruinsma, Eur. Phys. J. B, 1998, 4, 75–88 CrossRef CAS.
- S. May and A. Ben-Shaul, Biophys. J., 1997, 73, 2427–2440 CrossRef CAS.
- B. Sternberg, F. L. Sorgi and L. Huang, FEBS Lett., 1994, 356, 361–366 CrossRef CAS.
- H. Gershon, R. Ghirlando, S. B. Guttman and A. Minsky, Biochemistry, 1993, 31, 7110–7119 Search PubMed.
- R. Koynova and R. C. MacDonald, Biophys. J., 2003, 85, 2449–2465 CrossRef CAS.
- N. Dan, Biochim. Biophys. Acta, 1998, 1369, 34–38 CrossRef CAS.
- O. Farago and N. Gronbech-Jensen, J. Am. Chem. Soc., 2009, 131, 2875–2881 CrossRef CAS PubMed.
- D. Harries, S. May, W. M. Gelbart and A. Ben-Shaul, Biophys. J., 1998, 75, 159–173 CrossRef CAS.
- S. May, D. Harries and A. Ben-Shaul, Biophys. J., 2000, 78, 1681–1697 CrossRef CAS.
- R. Zantl, L. Baicu, F. Artzner, I. Sprenger, G. Rapp and J. Rädler, J. Phys. Chem. B, 1999, 103, 10300–10310 CrossRef CAS.
- I. Koltover, K. Wagner and C. R. Safinya, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 14046–14051 CrossRef CAS PubMed.
- P. C. A. Barreleiro, G. Olofsson and P. Alexandridis, J. Phys. Chem. B, 2000, 104, 7795–7802 CrossRef CAS.
- W. Kunz and R. Neueder, Specific Ion effects, World Scientific, Dordrecht, 2010, ch. 1, pp. 3–54 Search PubMed.
- D. Ben-Yaakov, D. Andelman, R. Podgornik and D. Harries, Curr. Opin. Colloid Interface Sci., 2011, 16, 542–550 CrossRef CAS PubMed.
- S. Sukenik, L. Sapir, R. Gilman-Politi and D. Harries, J. Am. Chem. Soc., 2013, 160, 225–237 CAS.
- D. Danino, E. Kesselman, G. Saper, H. I. Petrache and D. Harries, Biophys. J., 2009, 96, L43–L45 CrossRef CAS PubMed.
- D. Harries, S. May and A. Ben-Shaul, J. Phys. Chem. B, 2003, 107, 3624–3630 CrossRef CAS.
- B. Battersby, R. Grimm, S. Huebner and G. Cevc, Biochim. Biophys. Acta, 1998, 379, 1372 Search PubMed.
- E. Henry, A. Dif, M. Schmutz, L. Legoff, F. Amblard, V. Marchi-Artzner and F. Artzner, Nano Lett., 2011, 11, 5443–5448 CrossRef CAS PubMed.
- H. Schiessel and H. Aranda-Espinoza, Eur. Phys. J. E, 2001, 5, 499–506 CrossRef CAS.
- A. J. Wagner and S. May, Eur. Biophys. J., 2007, 36, 293–303 CrossRef CAS PubMed.
- N. Dan, Biophys. J., 1996, 71, 1267–1272 CrossRef CAS.
- N. Dan, Biophys. J., 1997, 73, 1842–1846 CrossRef CAS.
- B. C. Ma, S. B. Zhang, H. M. Jiang, B. D. Zhao and H. T. Lv, J. Controlled Release, 2007, 123, 184–194 CrossRef CAS PubMed.
- C. R. Dass, J. Pharm. Pharmacol., 2002, 54, 593–601 CrossRef CAS.
- J. J. McManus, J. O. Rädler and K. A. Dawson, J. Phys. Chem. B, 2003, 107, 9869–9875 CrossRef CAS.
- V. G. Budker, Y. A. Kazatchkov and L. P. Naumova, FEBS Lett., 1978, 95, 143–146 CrossRef CAS.
- L. Vojcikova, E. Svajdlenka and P. Balgavy, Gen. Physiol. Biophys., 1989, 8, 399–406 CAS.
- Y. S. Tarahovsky, R. S. Khusainova, A. V. Gorelov, T. I. Nicolaeva, A. A. Deev, A. K. Dawson and G. R. Ivanitsky, FEBS Lett., 1996, 390, 133–136 CrossRef CAS.
- J. J. McManus, J. O. Rädler and K. A. Dawson, J. Am. Chem. Soc., 2004, 126, 15966–15967 CrossRef CAS PubMed.
- A. Lengyel, D. Uhrikova, M. Klacsova and P. Balgavy, Colloids Surf., B, 2011, 86, 212–217 CrossRef CAS PubMed.
- O. Francescangeli, V. Stanic, L. Gobbi, P. Bruni, M. Iacussi, G. Tosi and S. Bernstorff, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 011904 CrossRef CAS.
- O. Francescangeli, M. Pisani, V. Stanic, P. Bruni and T. M. Weiss, Europhys. Lett., 2004, 67, 669–675 CrossRef CAS.
- G. Tresset, W. C. D. Cheong and Y. M. Lam, J. Phys. Chem. B, 2007, 111, 14233–14238 CrossRef CAS PubMed.
- S. Gromelski and G. Brezesinski, Phys. Chem. Chem. Phys., 2004, 6, 5551–5556 RSC.
- D. McLoughlin, R. Dias, B. Lindman, M. Cardenas, T. Nylander, K. Dawson, M. Miguel and D. Langevin, Langmuir, 2005, 21, 1900–1907 CrossRef CAS PubMed.
- S. Gromelski and G. Brezesinski, Langmuir, 2006, 22, 6293–6301 CrossRef CAS PubMed.
- P. Bruni, M. Pisani, A. Amici, C. Marchini, M. Montani and O. Francescangeli, Appl. Phys. Lett., 2006, 88, 073901 CrossRef.
- P. Bruni, O. Francescangeli, M. Marini, G. Mobbili, M. Pisani and A. Smorlesi, Mini-Rev. Org. Chem., 2011, 8, 38–48 CrossRef CAS.
- D. H. Mengistu, K. Bohinc and S. May, J. Phys. Chem. B, 2009, 113, 12277–12282 CrossRef CAS PubMed.
- K. Bohinc, G. Brezesinski and S. May, Phys. Chem. Chem. Phys., 2012, 14, 10613–10621 RSC.
- S. May, D. Harries and A. Ben-Shaul, Biophys. J., 2000, 79, 1747–1760 CrossRef CAS.
- A. P. Pandey, F. Haque, J. C. Rochet and J. S. Hovis, Biophys. J., 2009, 96, 540–551 CrossRef CAS PubMed.
- M. Menke, V. Gerke and C. Steinem, Biochemistry, 2005, 44, 15296–15303 CrossRef CAS PubMed.
- A. T. Hammond, F. A. Heberle, T. Baumgart, D. Holowka, B. Baird and G. W. Feigenson, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6320–6325 CrossRef CAS PubMed.
- D. Lingwood, J. Ries, P. Schwille and K. Simons, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 10005–10010 CrossRef CAS PubMed.
- T. Harder, Philos. Trans. R. Soc. London, Ser. B, 2003, 358, 863–868 CrossRef CAS PubMed.
- R. M. Epand, Biochim. Biophys. Acta, Biomembr., 2008, 1778, 1576–1582 CrossRef CAS PubMed.
- P. Garidel, C. Johann and A. Blume, J. Liposome Res., 2000, 10, 131–158 CrossRef CAS.
- P. F. F. Almeida, A. Pokorny and A. Hinderliter, Biochim. Biophys. Acta, Biomembr., 2005, 1720, 1–13 CrossRef CAS PubMed.
- P. Garidel and A. Blume, Biochim. Biophys. Acta, Biomembr., 1998, 1371, 83–95 CrossRef CAS.
- K. Simons and W. L. C. Vaz, Annu. Rev. Biophys. Biomol. Struct., 2004, 33, 269–295 CrossRef CAS PubMed.
- W. M. Gelbart and R. Bruinsma, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 831–835 CrossRef CAS.
- S. May, D. Harries and A. Ben-Shaul, Phys. Rev. Lett., 2002, 89, 268102 CrossRef.
- T. L. Hill, An introduction to statistical thermodynamics, Reprint of 2nd edition (1962), Dover, New York, 1986 Search PubMed.
- E. C. Mbamala, A. Ben-Shaul and S. May, Biophys. J., 2005, 88, 1702–1714 CrossRef CAS PubMed.
- R. R. Netz, Phys. Rev. Lett., 1996, 76, 3646–3649 CrossRef CAS.
- B. J. Reynwar and M. Deserno, Biointerphases, 2008, 3, FA117–FA124 CrossRef PubMed.
- S. Loew, A. Hinderliter and S. May, J. Chem. Phys., 2009, 130, 045102 CrossRef PubMed.
- B. Vanhaesebroeck, S. J. Leevers, K. Ahmadi, J. Timms, R. Katso, P. C. Driscoll, R. Woscholski, P. J. Parker and M. D. Waterfield, Annu. Rev. Biochem., 2001, 70, 535–602 CrossRef CAS PubMed.
- J. Y. Wang, A. Gambhir, G. Hangyas-Mihalyne, D. Murray, U. Golebiewska and S. McLaughlin, J. Biol. Chem., 2002, 277, 34401–34412 CrossRef CAS PubMed.
- S. McLaughlin and D. Murray, Nature, 2005, 438, 605–611 CrossRef CAS PubMed.
- W. D. Heo, T. Inoue, W. S. Park, M. L. Kim, B. O. Park, T. J. Wandless and T. Meyer, Science, 2006, 314, 1458–1461 CrossRef CAS PubMed.
- T. Yeung, M. Terebiznik, L. M. Yu, J. Silvius, W. M. Abidi, M. Philips, T. Levine, A. Kapus and S. Grinstein, Science, 2006, 313, 347–351 CrossRef CAS PubMed.
- M. Nomikos, A. Mulgrew-Nesbitt, P. Pallavi, G. Mihalyne, I. Zaitseva, K. Swann, F. A. Lai, D. Murray and S. McLaughlin, J. Biol. Chem., 2007, 282, 16644–16653 CrossRef CAS PubMed.
- S. Tzlil, D. Murray and A. Ben-Shaul, Biophys. J., 2008, 95, 1745–1757 CrossRef CAS PubMed.
- U. Golebiewska, A. Gambhir, G. Hangyas-Mihalyne, I. Zaitseva, J. Rädler and S. McLaughlin, Biophys. J., 2006, 91, 588–599 CrossRef CAS PubMed.
- J. Y. Wang, A. Gambhir, S. McLaughlin and D. Murray, Biophys. J., 2004, 86, 1969–1986 CrossRef CAS.
- S. McLaughlin, J. Y. Wang, A. Gambhir and D. Murray, Annu. Rev. Biophys. Biomol. Struct., 2002, 31, 151–175 CrossRef CAS PubMed.
- V. B. Teif, D. Harries, D. Lando and A. Ben-Shaul, J. Pept. Sci., 2008, 14, 368–373 CrossRef CAS PubMed.
- S. Tzlil and A. Ben-Shaul, Biophys. J., 2005, 89, 2972–2987 CrossRef CAS PubMed.
- E. Haleva, N. Ben-Tal and H. Diamant, Biophys. J., 2004, 86, 2165–2178 CrossRef CAS.
- G. Khelashvili, H. Weinstein and D. Harries, Biophys. J., 2008, 94, 2580–2597 CrossRef CAS PubMed.
- G. Khelashvili, D. Harries and H. Weinstein, Biophys. J., 2009, 97, 1626–1635 CrossRef CAS PubMed.
- U. Raviv, D. J. Needleman, Y. Li, H. P. Miller, L. Wilson and C. Safinya, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 11167–11172 CrossRef CAS PubMed.
- G. Decher, Science, 1997, 277, 1232–1237 CrossRef CAS.
- V. A. Parsegian and D. Gingell, Biophys. J., 1972, 12, 1192–1204 CrossRef CAS.
- C. Russ, T. Heimburg and H. H. von Grunberg, Biophys. J., 2003, 84, 3730–3742 CrossRef CAS.
- D. Ben-Yaakov, Y. Burak, D. Andelman and S. A. Safran, EPL, 2007, 79, 48002 CrossRef.
- A. G. Cherstvy, Phys. Chem. Chem. Phys., 2011, 13, 9942–9968 RSC.
- A. Flores-Amado and M. Hernandez-Contreras, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 031404 CrossRef CAS.
- S. Bandyopadhya, M. Tarek and M. Klein, J. Phys. Chem. B, 1999, 51, 10075–10080 CrossRef.
- B. O'Shaughnessy and Q. Yang, Phys. Rev. Lett., 2005, 94, 048302 CrossRef.
| This journal is © The Royal Society of Chemistry 2013 |
