View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/C2SC21393A (Edge Article) Chem. Sci., 2013, 4, 503-508

Vibrationally mediated bond selective dissociative chemisorption of HOD on Cu(111)†

Bin Jiang ab, Daiqian Xie *a and Hua Guo *b
aInstitute of Theoretical and Computational Chemistry, Key Laboratory of Mesoscopic Chemistry, School of Chemistry and Chemical Engineering, Nanjing University, Nanjing 210093, China. E-mail: dqxie@nju.edu.cn
bDepartment of Chemistry and Chemical Biology, University of New Mexico, Albuquerque, New Mexico 87131, USA. E-mail: hguo@unm.edu

Received 30th August 2012 , Accepted 23rd October 2012

First published on 23rd October 2012

Abstract

The bond selectivity in dissociative chemisorption of HOD on Cu(111) is investigated using a six-dimensional quantum model. It includes all vibrational modes of the impinging molecule on a density functional theory based interaction potential between the molecule and metal surface. It is shown that excitations in the HOD local stretching modes selectively enhance cleavage of the excited bond. This pronounced bond selectivity is attributed to a “late” or “product-like” barrier on the potential energy surface for the dissociative chemisorption and the slow intramolecular vibrational energy redistribution in the water molecule. The existence of mode and bond selectivities also underscores the inadequacy of statistical based transition-state theory in describing this industrially important surface reaction.

The control of bond cleavage and formation represents a “holy grail” in chemistry, which has a potentially huge impact on various fields such as energy production, medicine, and environmental protection. The quantum mechanical nature of molecules naturally lends themselves to various control schemes. For example, it is possible to selectively excite a reactant to a particular internal state, which might lead to very different outcomes from those in the corresponding thermal reaction.1,2 Despite tremendous technological advances such as lasers, enhancement of reactivity and/or control of product branching remain a major challenge in modern chemistry. A key issue is the energy flow in the complex formed by colliding reaction partners, whether transient or long-lived. Efficient intramolecular vibrational energy redistribution, commonly known as IVR,3 can quickly randomize the energy in the complex, leading to equal partitioning in all degrees of freedom. Under such circumstances, the reaction rates and branching ratios are largely determined by statistical models such as the transition-state theory. However, it is known that in some systems, IVR is slower than the time required for the reaction, and as a result, control becomes possible.

One such example is methane (CH4) dissociative chemisorption on metal surfaces.4 This reaction, producing adsorbed CH3 and H species, is the rate-limiting step in the steam reforming of methane, which is a key heterogeneous catalytic process in the production of H2.5 It has recently been shown in several landmark experiments that vibrational excitation in methane is very efficient in promoting the reaction, sometimes more so than the same amount of translational energy.6–12 In addition, clear bond selectivity was found in dissociative chemisorption of partially deuterated methane, in which vibrational excitation controls the products by selectively cleaving a specific bond.13 Similar mode and bond selectivities have also been demonstrated in gas phase bimolecular reactions involving methane.14–17 The selectivities can be attributed to two major factors. First, these reactions have “late” or “product-like” transition states, for which the appropriate vibrational coordinate(s) are often more efficient in promoting barrier crossing, according to Polanyi's rules.18 Second, methane has relatively inefficient IVR due to its local mode nature of vibration,19 so that the energy deposited into a single vibrational mode does not easily leak out to other degrees of freedom. However, there have been several recent reports on departures from Polanyi's rules,20,21 underscoring the complexity of multidimensional dynamics.22–24

The mode and bond specificities found in these systems cannot be readily explained by the widely used transition-state theory,25 in which all types of energy contribute equally. Instead, a dynamical model is needed. However, a complete theoretical understanding of methane dissociative chemisorption dynamics has been hampered by the necessarily large number of degrees of freedom (fifteen if surface is assumed rigid) involved. The commonly used reduced-dimensional models are often difficult to correctly describe the vibrational modes in CH4, thus inadequate in addressing the mode and bond selectivity in this process.26–32 Recently, full-dimensional models for this system have been reported,33–35 some with approximate dynamical treatments.34,35 In addition, a quantum dynamic treatment, which is necessary because of the large zero-point energy and tunneling involved in the reaction, is still formidable if all dimensions are included,36 and the difficulties are compounded by the complexity in developing an accurate high-dimensional potential energy surface (PES).33–35,37

The mode and bond selectivities are not restricted to methane. With similar properties, H2O has, for example, been shown to exhibit similar behaviors in gas phase bimolecular reactions.38–42 Its dissociative chemisorption on most transition metal surfaces, which produces adsorbed H and OH species, should also behave in a similar fashion, because it has slow IVR due to its local mode nature,19 and the reaction also has a “late” barrier.43 This reaction is ubiquitous and often obligatory in many industrially important heterogeneous catalytic processes5 and represents the rate-limiting step in low-temperature water–gas shift (WGS) reaction on copper catalysts.44 Hence, the ability to control such a reaction may have important implications in many heterogeneous processes involving water. While there has not yet been any report of experimental exploration, we have recently demonstrated, using a reliable quantum mechanical model on a realistic PES based on ∼25[thin space (1/6-em)]000 density functional theory (DFT) points, that the dissociative chemisorption of H2O on Cu(111) exhibits strong mode selectivity.45 Specifically, vibrational energy in all three modes was found to be more effective in promoting the reaction than translational energy. In this publication, we address a different but related question: can vibrational excitation in the singly deuterated water (HOD) control the bond cleavage in its dissociative chemisorption on the same copper surface?

Since a detailed description of the DFT calculations of the PES and the six-dimensional (6D) dynamic model used for H2O dissociative chemisorption on the rigid Cu(111) surface has been presented in our recent publication,45 only a brief discussion concerning modifications for HOD will be given here. More details can be found in the ESI.† The Jacobi coordinates used in the 6D surface-triatom model is shown in Fig. 1 and the Hamiltonian can be expressed as follows (ℏ = 1 hereafter):

 
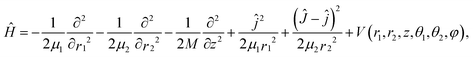ugraphic, filename = c2sc21393a-t1.gif(1)
where the r1 is the bond length of non-dissociative OH (or OD) bond, r2 the distance between the center of mass (COM) of OH (or OD) and D (or H), and z is the distance between the COM of HOD and the surface. μ1 = mH(D)mO/(mH(D) + mO), μ2 = mOH(OD)mD(H)/(mOH(OD) + mD(H)), M = mHOD. ĵ and Ĵ are the angular momenta for the OH (or OD) fragment and HOD triatom, respectively. While still reduced-dimensional in nature, this model includes the most important coordinates for the dissociative chemisorption of water, with a full description of its vibration. The degrees of freedom not treated include the translations of the molecule parallel to the surface and the rotational motion of the molecule along the surface normal, which are not considered essential for the reaction. This amounts to a flat surface approximation.46 In addition, the rigid surface approximation is partially justified because the surface reconstruction is small along the reaction coordinate.43 This rigid surface approximation, which does not allow exchange of energy with surface phonons, can be removed by introducing a moving surface atom, as shown by the recent work of Nave and Jackson.31,32


Coordinates used in the six-dimensional model for HOD dissociative chemisorption on Cu(111).
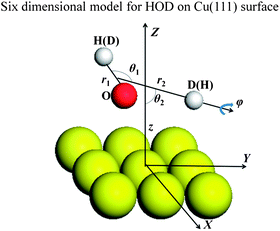Fig. 1 Coordinates used in the six-dimensional model for HOD dissociative chemisorption on Cu(111).

The Hamiltonian was represented with a mixed discrete variable representation (DVR) and finite basis representation (FBR).47 The z and r2 degrees of freedom were discretized with the sine DVR,48 while r1 was treated as non-reactive with a potential optimized DVR (PODVR).49,50 A non-direct product FBR basis ([P with combining macron]Kj(cos θ1)[P with combining macron]KJ(cos θ2)ΦK(ϕ)) was used to evaluate the rotational kinetic energy terms, where j, J, and K are the angular momentum quantum numbers associated with OH(OD), HOD, and the projection of Ĵ on the molecule-fixed z-axis which is along r2. 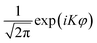[P with combining macron]Kj(cos θ1) and [P with combining macron]KJ(cos θ2) are normalized associated Legendre polynomials, and ΦK(ϕ) is the exponential Fourier function (ugraphic, filename = c2sc21393a-t2.gif). We further took advantage of the inversion symmetry of the potential with respect to φ in our model, so as to expand the wave function of even/odd parities in terms of cos(Kφ)/sin(Kφ) basis functions. In practice, three one-dimensional pseudo-spectral transformations were performed in sequence to transform the wavefunction from FBR to DVR, in order to evaluate the action of the potential energy operator on a grid.51

The dissociation probabilities were calculated with a modified version of the transition-state wave packet approach52 with the Chebyshev propagator,53 as discussed in detail in our recent work,45,54 and in ESI.† Briefly, two dividing surfaces are required. An initial wave packet is constructed on the first dividing surface placed in the asymptote as a direct product of the positive one-dimensional eigenstate of the flux operator and the specific rovibrational eigenstate for the reactant. This wavepacket is then propagated by the Chebyshev propagator toward the second dividing surface placed behind the transition state. The energy-dependent total reaction flux is calculated at the second dividing surface via a cosine Fourier transform of the Chebyshev propagation states, yielding the dissociation probability on a pre-specified energy grid.

While the O–H and O–D bond cleavages can in principle be treated within a single wave packet propagation, the grid needed to accommodate both processes is rather large. We chose to carry out two separate calculations for each initial state, one for the HOD → OH + D reaction and the other for the HOD → OD + H reaction. In both cases, the non-reactive bond can be described with a relatively small grid. This is possible because the two transition states for the dissociative chemisorption of HOD are well separated and have negligible interference, as in the gas phase HOD + H reaction.42

Numerous convergence tests have been performed and the final parameters used in the calculations are listed in Table 1. It is interesting to note that the number of grid points in θ1 for the OH bond cleavage is significantly larger than that for the OD bond cleavage, presumably due to the larger moment of inertia of the OD moiety. Similar observations have been made for the HOD + H reaction.42

Table 1 Numerical parameters used in calculations for two separate channels. (Atomic units are used unless stated otherwise)
Parameters HOD/Cu(111)
OD + H OH + D
Translational coordinate (z) 260 sine-DVR in [2.0,14.5] 280 sine-DVR in [2.0,14.5]
Internal coordinate (r2) 25 sine-DVR in [1.2,5.5] 25 sine-DVR in [1.2,5.5]
Nonreactive coordinate (r1) 5 PODVR 5 PODVR
Quadrature points in (θ1, θ2, φ) = (jmax + 1, Jmax + 1, Kmax + 1) (28, 30, 28) (18, 32, 18)
Dividing surface S1 z flux = 12.4 z flux = 12.4
Dividing surface S2 r 2flux = 3.2 r 2flux = 3.2
Absorbing potential in z
Absorbing potential in r2
Potential cut-off (eV) 5.0 5.0
Propagation step 4000 4000

Since the O–H and O–D stretches of HOD are well-defined local modes,19 the three vibrational modes of HOD are most conveniently labeled as the OD stretching, bending, and OH stretching modes, namely HOD(vOD, vb, vOH). Their calculated frequencies are 2561, 1353, and 3486 cm−1 on our PES, in reasonable agreement with the experimental values 2727, 1402, and 3707 cm−1.55 Experimentally, the excitation of individual quantum states in HOD can be readily achieved with IR lasers. The initial states in our wave packet calculations were chosen to be associated with the ground and first excited state of rotationless HOD in each of the three vibrational modes.

In Fig. 2, we first compare the dissociation probabilities for the ground (000) vibrational state of H2O and HOD as a function of the translational energy. The inset of the figure plots the dissociation probabilities in logarithmic scale, which shows an exponential increase of the reaction probabilities at low energies due apparently to tunneling. While the tunneling in the OD + H channel below the classical barrier of 0.96 eV is substantial, the OH + D channel shows much less reactivity due apparently to the heavier mass of the deuterium. It is interesting to note that the reaction threshold for the OD + H channel in the HOD(000) dissociation is somewhat lower than that for the other channel. This is in accord with the lower vibrational frequency of OD than that of OH. However, the dissociation probability in this channel becomes smaller than the OH + D channel at higher energies. Overall, the total dissociation probability for H2O(000) is much larger than the combined dissociation probabilities in both the OH and OD channels for HOD(000), which was also found in the gaseous H + HOD reaction.42 A clear explanation for this behavior is still lacking.


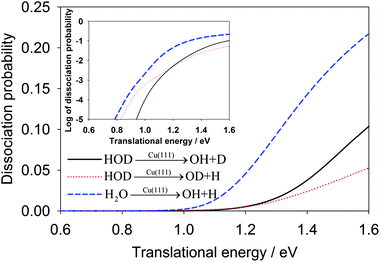Comparison of dissociative chemisorption probabilities for HOD and H2O on Cu(111) as a function of the translational energy. The probabilities are plotted in logarithmic scale in the inset.
Fig. 2 Comparison of dissociative chemisorption probabilities for HOD and H2O on Cu(111) as a function of the translational energy. The probabilities are plotted in logarithmic scale in the inset.

The influence of initial vibration excitations on the dissociation probabilities for the dissociative chemisorption of HOD is shown in Fig. 3 for the OH + D and OD + H channels. To facilitate a fair comparison, they are given as a function of the total energy relative to the reactant asymptote. As expected, vibrational excitation in the cleaving bond always enhances the reaction probability. For example, the first excited OD stretching state, HOD(100), has a much larger dissociation probability than HOD(000) for producing OH + D. On the other hand, the first OH stretching excited state, HOD(001), enhances the OD + H channel with a comparable magnitude. Interestingly, excitation of the vibration in the non-reactive bond typically inhibits the cleavage of the reactive bond. At 1.8 eV, for example, the dissociation probability for the OH bond cleavage into the OD + H channel in the dissociative chemisorption of HOD(100) (the OD stretching mode excited) is 0.00516, much lower than 0.0153 for HOD(000). In addition, the excitation of the bending mode also enhances moderately the reaction probabilities in both channels, relative to the vibrational ground state. This is presumably due to the geometry of the transition-state which has a different H–O–H angle than free H2O.45 The vibrational enhancement effects observed here bear many similarities with those found in the gas phase H + HOD reaction.42


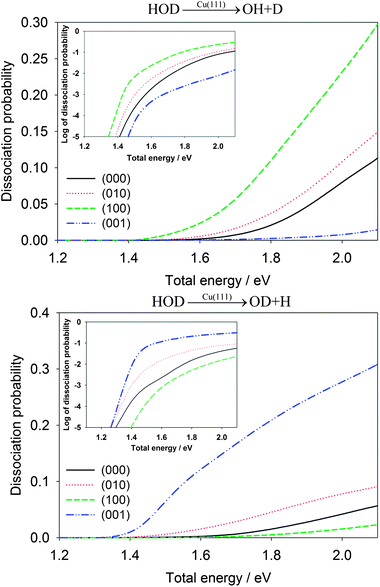Comparison of dissociative chemisorption probabilities for HOD into the OH + D channel (upper panel) and OD + H (lower panel) for several low-lying vibrational states of HOD as a function of the total energy (relative to the energy of H2O + Cu asymptote). The probabilities are plotted in logarithmic scale in the inset.
Fig. 3 Comparison of dissociative chemisorption probabilities for HOD into the OH + D channel (upper panel) and OD + H (lower panel) for several low-lying vibrational states of HOD as a function of the total energy (relative to the energy of H2O + Cu asymptote). The probabilities are plotted in logarithmic scale in the inset.

In Table 2, the OH/OD branching ratios are listed for the translational energies of 1.0 eV and 1.3 eV. At both energies, the HOD(100) state shows significant selectivity towards the OH product, while the HOD(001) state has a strong preference for the OD product. In Fig. 4, the dissociation probabilities are shown as a function of translational energy in the logarithmic scale. The enhancement effects of the vibrationally excited HOD are quite apparent. To make the comparison realistic, we plot in Fig. 5 the same reaction probabilities assumed Boltzmann weighting factors for these initial HOD states at 700 K, based on the nozzle temperature reported in the experiments on methane dissociative chemisorption.4 At this temperature, it is seen that the dissociative chemisorption is dominated at low translational energies by the vibrationally excited HOD in which the cleaving bond is excited.

Table 2 Dissociation probabilities for various vibrational states of HOD and the branching ratios for the OH/OD products at the translational energies of 1.0 eV and 1.3 eV
Vibrational state 1.0 eV 1.3 eV
OH + D OD + H OH/OD OH + D OD + H OH/OD
HOD(000) 1.03 × 10−4 5.98 × 10−4 1[thin space (1/6-em)]:[thin space (1/6-em)]5.8 1.62 × 10−2 1.21 × 10−2 1.3[thin space (1/6-em)]:[thin space (1/6-em)]1
HOD(010) 8.73 × 10−3 2.06 × 10−2 1[thin space (1/6-em)]:[thin space (1/6-em)]2.4 8.34 × 10−2 6.91 × 10−2 1.2[thin space (1/6-em)]:[thin space (1/6-em)]1
HOD(100) 1.04 × 10−1 4.84 × 10−3 21.5[thin space (1/6-em)]:[thin space (1/6-em)]1 2.91 × 10−1 2.22 × 10−2 13.1[thin space (1/6-em)]:[thin space (1/6-em)]1
HOD(001) 4.65 × 10−3 2.47 × 10−1 1[thin space (1/6-em)]:[thin space (1/6-em)]53.1 2.61 × 10−2 3.44 × 10−1 1[thin space (1/6-em)]:[thin space (1/6-em)]13.2


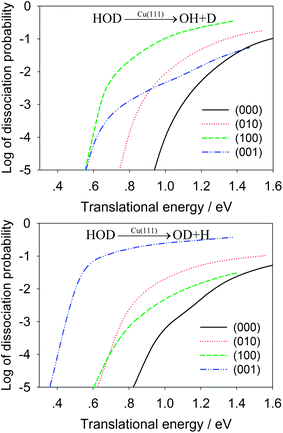Comparison of dissociative chemisorption probabilities for HOD into the OH + D (upper panel) and OD + H channels (lower panel) for several low-lying vibrational states of HOD as a function of the translational energy.
Fig. 4 Comparison of dissociative chemisorption probabilities for HOD into the OH + D (upper panel) and OD + H channels (lower panel) for several low-lying vibrational states of HOD as a function of the translational energy.

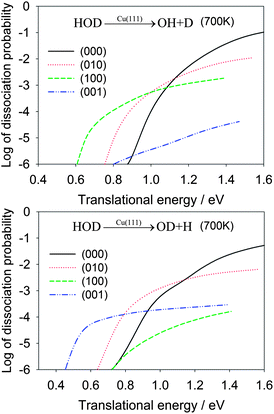Dissociative chemisorption probabilities for HOD into the OH + D (upper panel) and OD + H channels (lower panel) for several low-lying vibrational states of HOD weighted by Boltzmann factors for the initial vibrational states of HOD at 700 K, which was the nozzle temperature in a recent molecular beam experiment for methane dissociative chemisorption.4
Fig. 5 Dissociative chemisorption probabilities for HOD into the OH + D (upper panel) and OD + H channels (lower panel) for several low-lying vibrational states of HOD weighted by Boltzmann factors for the initial vibrational states of HOD at 700 K, which was the nozzle temperature in a recent molecular beam experiment for methane dissociative chemisorption.4

Most chemical reactions can be reasonably described by the transition-state theory, in which the probability to overcome a reaction barrier is solely determined by temperature or the total energy. In transition-state theory, the system is assumed to be ergodic and all modes have the same efficacy in promoting the reaction. Mode-selective reactions, in which the barrier crossing is preferentially promoted by energy in certain vibrational coordinate(s), suggest that all forms of energy are not equal. In other words, dynamics is essential in understanding the reactivity. In this work, we demonstrate, using a high-dimensional quantum dynamical model, the strong non-statistical nature of an industrially important heterogeneous catalytic process, namely the dissociative chemisorption of water.

Specifically, quantum dynamics studies on a DFT based PES have shown strong bond selectivity in the dissociative chemisorption of HOD on Cu(111), underscoring the central role of vibrational energy in the reaction. The mode and bond selectivities in this system can be attributed to the “late” transition state and the slow IVR rate in water. Despite the large body of work on the adsorption and dissociation of water on metal surfaces,56 there has not been any experimental report on water dissociative chemisorption dynamics. As our theoretical studies have demonstrated, significant control of the dissociative chemisorption of water can be achieved with vibrational excitation. Hence, it is hoped that our work will stimulate experimental explorations, particularly those with molecular beams and internal state resolution, of the mode and bond-selectivities in this important system in heterogeneous catalysis.

Acknowledgements

The NJU group was funded by the National Natural Science Foundation of China (Grant no. 21133006 and 91021010) and by the Ministry of Science and Technology (Grant no 2013CB834601), while the UNM team by the US National Science Foundation (CHE-0910828). The calculations were carried out on the IBM Blade cluster system in the High Performance Computing Center of Nanjing University and at NERSC.

References

  1. R. N. Zare, Science, 1998, 279, 1875 CrossRef CAS.
  2. F. F. Crim, Acc. Chem. Res., 1999, 32, 877 CrossRef CAS.
  3. D. J. Nesbitt and R. W. Field, J. Phys. Chem., 1996, 100, 12735 CrossRef CAS.
  4. L. B. F. Juurlink, D. R. Killelea and A. L. Utz, Prog. Surf. Sci., 2009, 84, 69 CrossRef CAS.
  5. I. Chorkendorff and H. Niemantsverdriet, Concepts of Modern Catalysis and Kinetics, Wiley-VCH, Weinheim, 2003 Search PubMed.
  6. L. B. F. Juurlink, P. R. MaCabe, R. R. Smith, C. L. DeCologero and A. L. Utz, Phys. Rev. Lett., 1999, 83, 868 CrossRef CAS.
  7. M. P. Schmid, P. Maroni, R. D. Beck and T. R. Rizzo, J. Chem. Phys., 2002, 117, 8603 CrossRef CAS.
  8. R. D. Beck, P. Maroni, D. C. Papageorgopoulos, T. T. Dang, M. P. Schmid and T. R. Rizzo, Science, 2003, 302, 98 CrossRef CAS.
  9. R. R. Smith, D. R. Killelea, D. F. DelSesto and A. L. Utz, Science, 2004, 304, 992 CrossRef CAS.
  10. P. Maroni, D. C. Papageorgopoulos, M. Sacchi, T. T. Dang, R. D. Beck and T. R. Rizzo, Phys. Rev. Lett., 2005, 94, 246104 CrossRef.
  11. L. B. F. Juurlink, R. R. Smith, D. R. Killelea and A. L. Utz, Phys. Rev. Lett., 2005, 94, 208303 CrossRef CAS.
  12. R. Bisson, M. Sacchi, T. T. Dang, B. Yoder, P. Maroni and R. D. Beck, J. Phys. Chem. A, 2007, 111, 12679 CrossRef CAS.
  13. D. R. Killelea, V. L. Campbell, N. S. Shuman and A. L. Utz, Science, 2008, 319, 790 CrossRef CAS.
  14. W. R. Simpson, T. P. Rakitzis, S. A. Kandel, A. J. Orr-Ewing and R. N. Zare, J. Chem. Phys., 1995, 103, 7313 CrossRef CAS.
  15. Z. H. Kim, H. A. Bechtel and R. N. Zare, J. Am. Chem. Soc., 2001, 123, 12714 CrossRef CAS.
  16. S. Yoon, R. J. Holiday, E. L. Sibert III and F. F. Crim, J. Chem. Phys., 2003, 119, 9568 CrossRef CAS.
  17. R. J. Holiday, C. H. Kwon, C. J. Annesley and F. F. Crim, J. Chem. Phys., 2006, 125, 133101 CrossRef.
  18. J. C. Polanyi, Acc. Chem. Res., 1972, 5, 161 CrossRef CAS.
  19. M. S. Child and L. Halonen, Adv. Chem. Phys., 1984, 57, 1 CrossRef CAS.
  20. S. Yan, Y. T. Wu, B. Zhang, X.-F. Yue and K. Liu, Science, 2007, 316, 1723 CrossRef CAS.
  21. W. Zhang, H. Kawamata and K. Liu, Science, 2009, 325, 303 CrossRef CAS.
  22. S. Yan, Y.-T. Wu and K. Liu, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12667 CrossRef CAS.
  23. G. Czakó and J. M. Bowman, Science, 2011, 334, 343 CrossRef.
  24. G. Czakó and J. M. Bowman, J. Am. Chem. Soc., 2009, 131, 17534 CrossRef.
  25. D. G. Truhlar, A. D. Isaacson and B. C. Garrett, in Theory of Chemical Reaction Dynamics, ed. M. Baer, CRC Press, Boca Raton, 1985, vol. 4 Search PubMed.
  26. A. C. Luntz and J. Harris, Surf. Sci., 1991, 258, 397 CrossRef CAS.
  27. A. P. J. Jansen and H. Burghgraef, Surf. Sci., 1995, 344, 149 CrossRef CAS.
  28. M.-N. Carre and B. Jackson, J. Chem. Phys., 1998, 108, 3722 CrossRef CAS.
  29. R. Milot and A. P. J. Jansen, Phys. Rev. B: Condens. Matter, 2000, 61, 15657 CrossRef CAS.
  30. Y. Xiang, J. Z. H. Zhang and D. Y. Wang, J. Chem. Phys., 2002, 117, 7698 CrossRef CAS.
  31. S. Nave and B. Jackson, Phys. Rev. Lett., 2007, 98, 173003 CrossRef.
  32. S. Nave and B. Jackson, J. Chem. Phys., 2007, 127, 224702 CrossRef.
  33. G. P. Krishnamohan, R. A. Olsen, A. Valdes and G.-J. Kroes, Phys. Chem. Chem. Phys., 2010, 12, 7654 RSC.
  34. S. Nave and B. Jackson, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 233408 CrossRef.
  35. B. Jackson and S. Nave, J. Chem. Phys., 2011, 135, 114701 CrossRef.
  36. G.-J. Kroes, A. Gross, E.-J. Baerends, M. Scheffler and D. A. McCormack, Acc. Chem. Res., 2002, 35, 193 CrossRef CAS.
  37. G. P. Krishnamohan, R. A. Olsen, G.-J. Kroes, F. Gatti and S. Woittequand, J. Chem. Phys., 2010, 133, 144308 CrossRef CAS.
  38. A. Sinha, M. C. Hsiao and F. F. Crim, J. Chem. Phys., 1991, 94, 4928 CrossRef CAS.
  39. M. J. Bronikowski, W. R. Simpson, B. Girard and R. N. Zare, J. Chem. Phys., 1991, 95, 8647 CrossRef CAS.
  40. J. M. Pfeifer, E. Woods, R. B. Metz and F. F. Crim, J. Chem. Phys., 2000, 113, 7982 CrossRef.
  41. D. H. Zhang and J. C. Light, J. Chem. Phys., 1996, 104, 4544 CrossRef CAS.
  42. D. H. Zhang and J. C. Light, J. Chem. Soc., Faraday Trans., 1997, 93, 691 RSC.
  43. A. A. Gokhale, J. A. Dumesic and M. Mavrikakis, J. Am. Chem. Soc., 2008, 130, 1402 CrossRef CAS.
  44. C. V. Ovesen, P. Stoltze, J. K. Norskov and C. T. Campbell, J. Catal., 1992, 134, 445 CrossRef CAS.
  45. B. Jiang, X. Ren, D. Xie and H. Guo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10224 CrossRef CAS.
  46. J. Sheng and J. Z. H. Zhang, J. Chem. Phys., 1992, 96, 3866 CrossRef CAS.
  47. J. C. Light and T. Carrington Jr, Adv. Chem. Phys., 2000, 114, 263 CrossRef.
  48. D. T. Colbert and W. H. Miller, J. Chem. Phys., 1992, 96, 1982 CrossRef CAS.
  49. J. Echave and D. C. Clary, Chem. Phys. Lett., 1992, 190, 225 CrossRef CAS.
  50. H. Wei and T. Carrington Jr, J. Chem. Phys., 1992, 97, 3029 CrossRef CAS.
  51. G. C. Corey, J. W. Tromp and D. Lemoine, in Numerical Grid Methods and Their Applications to Schroedinger's Equation, ed. C. Cerjan, Kluwer, Dordrecht, 1993, pp. 1–23 Search PubMed.
  52. D. H. Zhang and J. C. Light, J. Chem. Phys., 1996, 104, 6184 CrossRef CAS.
  53. D. Xie, S. Li and H. Guo, J. Chem. Phys., 2002, 116, 6391 CrossRef CAS.
  54. B. Jiang, D. Xie and H. Guo, J. Chem. Phys., 2011, 135, 084112 CrossRef.
  55. N. Gailar and E. K. Plyler, J. Chem. Phys., 1956, 24, 1139 CrossRef.
  56. M. A. Henderson, Surf. Sci. Rep., 2002, 46, 1 CrossRef CAS.

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c2sc21393a
This journal is © The Royal Society of Chemistry 2013