Revisiting the chemistry triplet: drawing upon the nature of chemical knowledge and the psychology of learning to inform chemistry education

Abstract

Much scholarship in chemical education draws upon the model of there being three ‘levels’ at which the teaching and learning of chemistry operates, a notion which is often represented graphically in terms of a triangle with the apices labelled as macroscopic, submicroscopic and symbolic. This model was proposed by Johnstone who argued that chemistry education needs to take into account ideas deriving from psychological research on cognition about how information is processed in learning. Johnstone's model, or the ‘chemistry triplet’, has been widely taken-up in chemistry education, but has also been developed and reconceptualised in diverse ways such that there is no canonical form generally adopted in the community. Three decades on from the introduction of Johnstone's model of the three levels, the present perspective article revisits both the analysis of chemical knowledge itself, and key ideas from the learning sciences that can offer insights into how to best teach the macroscopic, submicroscopic and symbolic aspects of chemical knowledge.

---

Introduction

It is now 30 years since Alex Johnstone (1982, p. 377) noted in a short paper about the nature of a chemistry curriculum suitable for all learners, that chemists “view our subject on at least three levels” and “jump freely from level to level in a series of mental gymnastics”. In later publications Johnstone (1989, 1991, 2000b), represented the levels as a triangle and related this description of chemistry to findings from the learning sciences – in particular the information processing perspective – to draw implications for teaching.

This notion that there are three ‘domains’ or ‘levels’ of chemical knowledge – often labelled as the macroscopic, the submicroscopic and the symbolic and sometimes referred to as the chemical knowledge ‘triplet’ (Talanquer, 2011) – has since become highly influential in the field of chemistry education. This idea has been found to be widely useful and has been adopted and adapted in a variety of ways that demonstrate its utility in the field. Indeed, Johnstone's triangle has in effect become a ‘taken-for-granted’ commitment (or assumption) for those working in the field of chemistry education.

The present perspective article in part celebrates the influence of Johnstone's insight. However given the passage of three decades since the original reference to the three levels, this article also looks to

(a) clarify the ontology of the ‘triplet’, and in particular questions how the ‘symbolic’ relates to the other ‘levels’ or ‘domains’; and

(b) revisit the implications of Johnstone's ideas in terms of widely accepted principles from the psychology of learning.

Johnstone's triangle, or the chemistry triplet

Johnstone's original presentation of his three levels is set out in Table 1. Johnstone's concern was that this offered too much complexity for the novice studying the subject at an introductory level, and, in particular, Johnstone argued for the potential for effectively teaching some aspects of chemistry without invoking the molecular explanatory level (cf. classical thermodynamics).

Table 1 The three levels at which chemists view the subject, after (and quoting) Johnstone (1982)

Level	Description	Notes
Descriptive and functional	We can see and handle materials, and describe their properties in terms of density, flammability, colour and so on.	We are also interested in the possibility of conversion of one material into another with consequent changes in properties.
Representational	We try to represent chemical substances by formulae and their changes by equations.	This is part of the sophisticated language of the subject.
Explanatory	We attempt to explain why chemical substances behave the way they do.	We invoke atoms, molecules, ions, structures, isomers, polymers etc. to give us a mental picture by which to direct our thinking and rationalize the descriptive level mentioned above.

---

Johnstone felt that ideas deriving from psychological research were potentially highly significant to chemistry educators (Johnstone, 1989, 1991). Indeed Johnstone also suggested that at the time such ideas were not getting the attention they deserved given the tendency of much research activity to be focused on work related to student ‘misconceptions’ and ‘alternative conceptions’ (Johnstone, 2000a).

An information processing perspective certainly need not be at odds with the constructivist perspective that informed the work on alternative conceptions, and indeed pioneering work to relate the two perspectives had been undertaken during the early 1980s (Osborne and Wittrock, 1983, 1985). (Arguably this work had not been as influential as it should have been due to the untimely early death in 1985 of Roger Osborne who had been developing the approach at the University of Waikato.) However, at the time that Johnstone was making his arguments, there was certainly a good deal of relatively under-theorised work focused on identifying student ideas, some of which at least offered limited guidance in relation to major issues of chemistry teaching (Taber, 2009b).

Johnstone (1991) suggested that one reason science was difficult for students, was that it involved what he termed ‘multilevel thought’. That is, in science subjects, students are commonly presented with explanations that involve being asked to think about very different types of things at once. Johnstone suggested that in physics this involved the levels of the ‘macro’, the invisible (such as forces), and the symbolic (such as the mathematical representations); and in biology this concerned the macro (animals and plants); the micro (cells) and the biochemical. In chemistry, Johnstone argued, learners were presented with and asked to make sense of teaching about the macro (tangible and visible ‘macrophenomena’), the submicro (molecules and ions) and the symbolic (for which Johnstone gave as an example a formula equation representing sodium chloride dissolving). It is interesting that Johnstone offered comparable arguments across the three main school science subjects, as his key point related to how learners are often asked to coordinate quite different kinds of ideas when learning science, which was not just a problem in chemistry classrooms.

Johnstone illustrated his point with a simple figure showing a triangle with the three apices labelled as ‘macro’, ‘sub-micro’ and ‘symbolics’ (see Fig. 1), and argued that rather than teaching being focused at one apex, or even along one side of the triangle, it often happened inside the triangle where students were expected to cope with all three ‘levels’ at once. The inspiration for using a triangle in this way was a standard diagram used in geology relating to mineral composition (Johnstone, 2009).

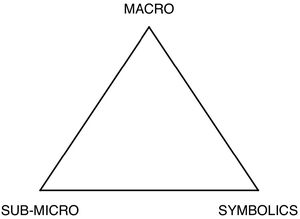Fig. 1 ‘Multilevel’ thought is required in learning chemistry if teaching relates different levels (after Johnstone, 1991, p. 78).

The triangle representation, in particular, was readily adopted by other chemical educators. Writing about Johnstone's ideas in the Journal of Chemical Education, Gabel (1993, p. 193) referred to Johnstone's triangle as representing “the three levels on which chemistry can be taught: atoms/molecules (microscopic level), sensory (macroscopic level), and the symbolic level” (present author's emphasis), and suggested it could be used as a device for monitoring teaching quantitatively as “using an equilateral triangle with a level at each vertex, any point within the triangle can represent the percentage of time allocated to using a given level in the teaching of chemistry”. She went on to claim that “at the present time most chemistry courses are taught at the symbolic level with little emphasis on the microscopic and the macroscopic levels” (p. 193). Johnstone later argued in this journal that the nature of chemistry is

“that it exists in three forms which can be thought of as corners of a triangle. No one form is superior to another, but each one complements the other. These forms of the subject are (a) the macro and tangible: what can be seen, touched and smelt; (b) the submicro: atoms, molecules, ions and structures; and (c) the representational: symbols, formulae, equations, molarity, mathematical manipulation and graphs.”

(Johnstone, 2000b, p. 11)

Johnstone also referred to these same descriptors in his original terms of there being ‘three levels of thought’,

“The psychology for the formation of most of chemical concepts is quite different from that of the ‘normal’ world. We have the added complication of operating on and interrelating three levels of thought: the macro and tangible, the sub micro atomic and molecular, and the representational use of symbols and mathematics. It is psychological folly to introduce learners to ideas at all three levels simultaneously. Herein lies the origins of many misconceptions. The trained chemist can keep these three in balance, but not the learner.”

(Johnstone, 2000b, p. 9)

So Johnstone brought attention to three aspects or domains of chemical knowledge, and the need to coordinate thinking within these three domains in chemistry – and the challenge this offered to the novice. Authors now commonly take these ideas for granted, as aspects of the shared intellectual commitments in the chemical education community. So among many recent references, Lorenzo write “nowadays, we can differentiate three levels of representation according to Johnstone's triangle” p. 14 (2010, p. 14). Jaber and BouJaoude (2011) refer to how the “multi-leveled way of thinking can be represented by the corners of a triangle” (2011, pp. 2–4).

Talanquer (2011, p. 179) has suggested that “the idea that chemical knowledge can be represented in three main ways: macro, submicro, and symbolic (chemistry triplet) has become paradigmatic in chemistry and science education. It has served both as the base of theoretical frameworks that guide research in chemical education and as a central idea in various curriculum projects”. Talanquer reasonably suggests that the triplet idea “has been one of the most powerful and productive ideas in chemical education for the past 25 years” (p. 179).

However, Talanquer has also noted that “this triplet relationship has been the subject of different adaptations and reinterpretations that sometimes lead to confusion and misunderstanding, which complicates the analysis of the triplet's nature and scope” (2011, p. 179). He observed that “this triplet view of our chemical knowledge has been adopted and adapted by many people who…have generated what can be identified as different faces, personalities or manifestations of the triplet” (p. 180). Talanquer suggested that while many of the modifications have been useful contributions, “they sometimes also generate confusion and misunderstanding as people tend to use different terms and concepts when describing the nature and scope of the major components of the triplet” (p. 180).

Indeed, when, in 2009, an edited volume was published exploring thinking about Johnstone's triangle and its implications in chemistry education (Gilbert and Treagust 2009b), the description of the triplet used to introduce this book by its editors was somewhat shifted from Johnstone's original model. Gilbert and Treagust (2009a, pp. 3–4) referred to the three types of representation in chemistry as phenomenological (which “seeks to represent phenomena as experienced with the senses”), model (“which seeks to support a qualitative explanation of these phenomena”) and symbolic (“which seeks to support a quantitative explanation of these phenomena”). So for some chemical educators, the triplet was conceptualised in terms of representational levels, whereas in Johnstone's initial presentation, the representational was one of his levels.

Talanquer (2011) has provided a very useful review of different adaptations and presentations of the triplet, and the present article does not look to repeat his work, to which interested readers are referred. Rather the present article has two aims:

(a) to revisit the triplet in the light of what I suggest are two common areas of confusion in the range of presentations of the triplet in common use; and then

(b) in the light of that analysis, to follow-through on the implications in relation to Johnstone's original intention of drawing upon a perspective based in cognitive science and the psychology of learning.

Revisiting the relationship between the macroscopic, the submicroscopic and the symbolic

Johnstone's triangle seemed to ‘capture the imagination’ of chemical educators, who commonly appreciated the strength of his argument. However, I will argue here that the adoption of the triangle symbol, and the common labels for its apices has led to two areas of confusion (which can be recognised in the diversity of terminology reported above):

(1) confusion between two possible foci for the macroscopic: the phenomena studied in chemistry, and the conceptual frameworks developed in chemistry to formalise knowledge about those phenomena;

(2) confusion over what is meant by a symbolic ‘level’ – how it fits in an ontology with ‘macroscopic’ and ‘submicroscopic’, and how it relates to notions of their being three different representational levels.

Two central problems in chemical education: theorising phenomena; and submicroscopic models

Modern chemistry has developed extensive theoretical models to explain chemical phenomena, based around the nature of conjectured entities at a scale far smaller than what can be observed with an optical microscope. The explanatory basis of a great deal of the chemistry we might teach in school, college and university concerns molecules, ions, and – in particular at higher levels – electrons and their associated orbitals and energy levels. The entities are often called ‘particles’, but, due to their scale, have properties unlike those of familiar particles such as grains of sand: for example, having no edges/perimeters and sometimes being able to overlap with each other. These ‘quanticles’ have wave-like as well as particle-like properties.

It is widely established that such abstract theoretical ideas are challenging for many learners (Brook et al., 1984; Harrison and Treagust, 1996, 2002; Johnson, 1998, 2005, 2012; Taber, 2005). In particular, the central assumption of this model – that the properties of the substances we study and can directly observe and handle, can be explained by the very different properties and interactions of the subatomic quanticles – is often not grasped (Taber, 2001). Instead, learners commonly ascribe to the subatomic entities the properties to be explained by the model: butter is soft as it is made of soft molecules; glass is transparent because its particles are transparent, etc. (Ben-Zvi et al., 1986).

So the submicroscopic explanations of chemistry are a major area of concern in teaching the subject, and make considerable demands on learners asked both to accept the existence (or at least, entertain the hypothesis) of these minute theoretical entities, and to learn about their nature (masses, charges, arrangements etc.), and then learn to use them as tools in building explanations – that is clearly quite advanced cognitive work (Shayer and Adey, 1981).

However, the macroscopic apex of Johnstone's triangle also brings challenges. In particular, although chemistry as a science is essential to understanding and developing materials, introductory chemistry often makes limited call upon most of the materials that learners are familiar with. Chemistry is primarily about substances, and substances are already a major abstraction from real-life experience (Taber, 2012). Pure samples of substances – elements and compounds – are commonly found in chemistry laboratories, and seldom anywhere else that most of our students venture.

Just as when studying introductory physics students are asked to deal with abstractions and simplifications – uniform gravitational fields, friction-less bearings, perfectly rigid-supports, negligible air resistance, etc. – so in chemistry lessons the real world of materials is replaced by the simplification of pure substances. For those of us who are chemists, it is quite easy to forget how significant a shift that is for young learners. So students must learn about the concepts of element, and compound, and of chemical reaction as a change into different substances that somehow retain an essence of the original elements whilst having quite different properties. These are themselves quite abstract notions, that students are asked to relate to the phenomena of the subject – their observations of different substances (many with unfamiliar names) and their reactions. So the conceptual demand is high even at the ‘macroscopic’ corner of the subject. This is without all the specific classifications of alkali metals, acids, reducing agents, transition metals, polymers etc.

Moreover, arguably, the key macroscopic concepts only begin to make sense for most learners in terms of the submicroscopic theoretical models (that can explain the basis of their being different elements and what is it of an element that is conserved when reactions occur to give new substances with different properties). So in learning chemistry, students are indeed usually asked to coordinate learning about the subject at two very different levels: in terms of the formal descriptions of the observed phenomena reconceptualised at the macroscopic level, and in terms of the theoretical models of the structure of matter at the submicroscopic scale. This is represented in Fig. 2 and is sufficient to make chemistry a challenging and demanding subject to learn and teach.

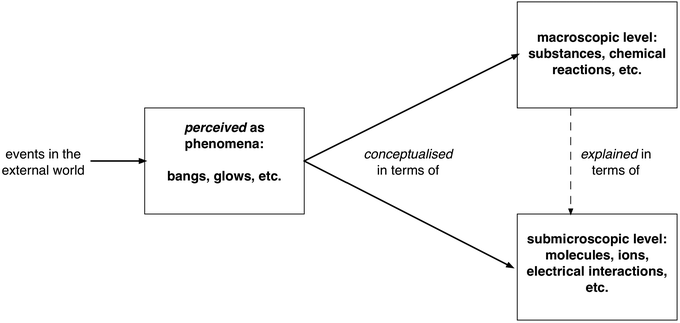Fig. 2 Two related levels of conceptualisation of chemical knowledge.

The importance of having a specialised language

Till this point I have had less to say about Johnstone's third domain or level – the symbolic. Talanquer (2011) notes that this ‘level’ has been conceptualised rather differently by various authors, and that there is no consensus on the extent of the symbolic level. The importance of the symbolic level relates to representation and communication (Taber, 2009a). Concepts of chemistry – whether from the macroscopic domain, such as ‘solution’, ‘element’, ‘reversible reaction’, or from the microscopic domain, such as ‘electron’, ‘orbital, ‘hydrated copper ion’ – need to be represented, both to facilitate the individual in thinking about and operating with them, and to communicate with others. In part this involves a technical vocabulary that can be used in conjunction with the ‘natural’ language (such as English) to stand for the concept of the subject.

However, there are other forms of representation that are just as useful in thinking about and communicating chemical concepts: such as graphs and diagrams of many forms (Taber, 2009a). There are also hybrid forms, which in part use written script, whilst adopting specialised formalisms (2NO₂ ⇄ N₂O₄; 1s² 2s² 2p⁶ 3s¹, etc.). Learning chemistry involves both forming concepts that are sufficiently aligned with those of other members of the chemical community, and adopting the systems of symbols commonly used within the chemical community so as to be able to communicate with others about these concepts.

The nature of the symbolic domain of chemical knowledge

The argument made here is that although the domain of symbolic knowledge, in effect the language for communicating and representing chemical concepts, is essential to effective chemistry learning, it is not helpful to think of this as a discrete ‘level’ of chemical knowledge that is one element of an ontological triad of macroscopic-submicroscopic-symbolic.

Johnstone's original point was that the symbolic domain provided an additional knowledge demand for students – just as it did in physics. Arguably, in physics, a key feature of the symbolic domain that learners have to master is mathematical representation – algebra, graphs, and later calculus – and that is part of the symbolic learning demand in chemistry as well. Learning chemistry, however, also involves mastering other symbolic systems (Taber, 2009a): for example, there are standard ways to represent bench apparatus set-ups. These symbols tend to relate largely to the macroscopic level.

In addition, there are various formalisms for representing atomic and molecular structures, and lattices, etc., relating to different aspects of our structural models (electron shells, orbitals, bonding, charge distributions, lone pairs, delocalisation, aromaticity, etc.). In effect there is a whole new graphical language, or iconic language (Grosholz and Hoffman, 2000), to be mastered here, largely related to the submicroscopic level. A particular challenge is that we often have a toolkit of alternative forms of representation that can be used to represent the same theoretical entity depending upon which models or features we wish to emphasise in a particular context or for a particular purpose (Taber, 2010). This clearly involves a considerable learning demand (Leach and Scott, 2002) for the student new to the subject.

However, of particular importance, it can be argued (Taber, 2009a), are the labels and symbols which are used to indicate particular substances (‘hydrogen’, ‘methane’, ‘H₂’, ‘CH₄’, etc.), because these may be ambiguous in terms of whether they refer to the substances themselves at the macroscopic level, or to the molecules and ions at the submicrosopic level. This is a potential source for confusion if a teacher or text book is not clear about how the symbol is being used in a particular context, again potentially adding to the demand on learners.

Combinations of these symbols may be used in the particular form of chemical equations, to represent chemical reactions and other processes of interest (e.g. phase changes). An equation such as

2H₂ + O₂→ 2H₂O

not only represents different entities, but their relationship in a chemical process. At the macroscopic level this set of symbols represents reactants and product, showing which substances react to form which new substance(s). At the submicroscopic level, this set of symbols shows which molecules are present before and after the change, and in what proportions, and is understood to be scaleable – referring to mole ratios as well as ratios of individual molecules. That the same representation can be used to stand for such different things offers potential for students to misinterpret what is signified: e.g., at a particular moment the teacher may be talking about molecules, but the student may be interpreting the signifiers as representing samples of substances.

Yet the affordance of this ambiguity is the potential for these symbols to allow us to shift between the macroscopic and submicroscopic levels. This is important because, as suggested above, much of modern chemistry involves explaining the phenomena we observe, and conceptualise at the macroscopic level – properties and reactions of substances – in terms of theoretical models of what is happening to molecules and ions and electrons. An equation for a chemical reaction, such as that presented above for example, can act as a bridge between the two levels by simultaneously representing both the macroscopic and submicrosopic, and aiding us in shifting between these levels in our explanations (see Fig. 3).

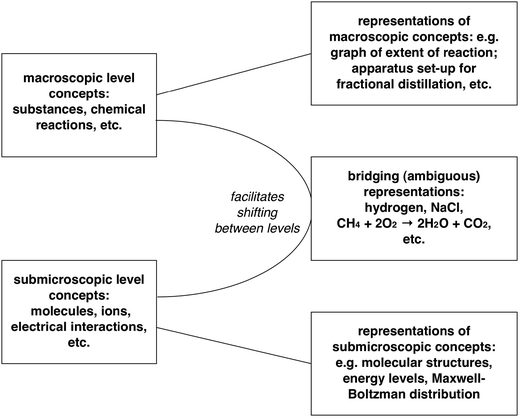Fig. 3 The symbolic domain as providing resources for representation and communication of chemical concepts, and in particular for supporting the development of explanations relating the two conceptual levels.

Grosholz and Hoffman (2000, p. 244) have argued that some iconic representations used in chemistry to represent, for example, aspects of molecular structure – despite illustrating features of submicroscopic models – come to be recognised as also referring to macroscopic samples of the corresponding substances as well. In this way, they suggest, such iconic representations can also come to be “productively ambiguous” in facilitating shifting between these levels. It is such shifts that are so important in building up the explanatory schemes that make chemistry a science (offering explanation and prediction) and not just a natural history that catalogues and characterises substances. Not all of the explanatory framework of chemistry relies on bridging these conceptual domains – but a good deal certainly does.

Relating the nature of chemistry to the science of learning

Johnstone not only sought to make chemistry educators aware of how complex our subject is from the perspective of the novice learner, but also sought to highlight implications in terms of what was understood about cognition as information processing. Johnstone's original concerns stand, although we are probably in a better position to explore the implications he highlighted in view of subsequent additions to the scholarship on the nature of learning. In particular, here I consider how the notion of teaching as scaffolding learning has in the past decades somewhat modified our ideas about the limitations on the types of conceptual learning possible by young learners (Mercer et al., 2004).

A learning science perspective 1: revisiting the information processing perspective

Johnstone's original argument reflected work in the psychology of learning (Johnstone, 2000b). Miller (1968) had reported on the limits to sensory channels in perception, and in particular the notion of the ‘magic number, 7 ± 2’ which seemed to describe limitations to information processing in various sensory modes. One of the features that Miller's work included was memory span. Commonly, if memory span is tested in adults (who are asked to repeat back arbitrary sequences of numbers, for example), then typically those tested tend to give an average correct response in the range 5–9 (i.e., 7 ± 2) items. Young children are often found to have even smaller memory spans (De Ribaupierre et al., 2011).

Nowadays this particular finding is linked to what is referred to as working memory, which is considered to be part a kind of ‘executive’ feature of human cognition that can access information from long-term memory, or from memory buffers holding material filtered through perception, and mentipulate (act upon) that information (Baddeley, 2003). So working memory is where we process information when doing a calculation, planning a piece of writing, developing a problem-solving strategy, and so forth. Research suggests this central feature of human cognition has very limited capacity – thus Miller's ‘magic’ number.

The limited information processing capacity of the typical human brain is a major restriction on cognition, and might often be considered the ‘bottleneck’ or ‘rate determining step’ that limits such activities as problem solving, and new learning. This is not the information processing capacity of the whole brain, but just of the part that deals with conscious thought: there may be a great deal of activity at preconscious levels, and what gets brought into consciousness at any one time represents a tiny fraction of the information represented in the brain (Kouider and Dehaene, 2007). Nonetheless, in terms of classroom learning, this feature is very significant. Consider, for example, the following string of symbols – a typical representation of a chemical reaction met in school chemistry:

H₂SO_4(aq) + 2NaOH_(aq)→ Na₂SO_4(aq) + 2H₂O_(l)

The amount of information represented here, if considered a string of characters, clearly well exceeds seven discrete units. Miller's principle would seem to suggest that few if any people should be able to hold this string of symbols in mind: i.e. be able to retrieve it intact from working memory when tested. Our experience as chemists might lead us to question this principle, as most readers of this journal could very easily hold this string in mind, and report it correctly on demand (a point returned to below). However, those of us who have taught introductory chemistry will also likely recognise that most novice learners would indeed struggle to hold such a string in mind, and would need to carry out a simple task like making a note of the equation by breaking it up into several smaller steps.

The severity of this restriction on working memory may seem something of an enigma as one might assume that evolving somewhat larger memory spans could radically improve cognitive ability. One theory is that the limitations on working memory may be adaptive in limiting the extent to which our knowledge shifts in response to environmental cues (Sweller, 2007): that is, if the physical world is generally fairly stable, then it may be an evolutionary advantage for the cognitive system not to be modifying our knowledge of that world too readily, perhaps based on atypical, transient or misperceived experiences. This certainly fits with the tenacious nature of some reported alternative conceptions in chemistry – which may survive secondary and even university level teaching in the subject (Taber and Tan, 2011).

Of course, if this is so, it reflects how during most of human evolution the amount of potentially useful new knowledge available from the environment was of a rather different order compared to the situation experienced by people in modern societies. We may have evolved cognition better adapted to a hunter-gatherer lifestyle than to learning in schools and university classes. However, it is also important to note that the highly limited memory span refers to the rather artificial task of remembering random and arbitrary information unaided. This explains why remembering the string of symbols in the chemical equation presented above is not a challenging task for chemistry ‘experts’. Human cognition can be applied quite differently.

A learning science perspective 2: meaningful learning and memory consolidation

For one thing, we find ways to use our environment to enhance our memory span. If a calculation is complex, we use pen and paper (or a computer, or stones, or lines in the sand) to help us plan a strategy and temporarily store intermediate results externally. This enables us to solve problems when we cannot ‘keep all the information in mind at once’. Successful students may have not greater memory spans than peers, but instead better metacognitive strategies (Shore and Dover, 2004).

Equally importantly, most information we deal with is not arbitrary at all, but is (potentially, at least) related to things we already know about. Although we have a limited capacity to deal with novel information, our brains are effective at ‘chunking’ together related information into quite complex structures (Baddeley, 2003). The ‘magic number’ supposedly refers to ‘chunks’ of information, so that the same data may overload one mind that sees it as arbitrary, but be readily addressed by another person with similar memory span, because they can relate it to existing mental schemes and accommodate it within working memory. As an example, the task of remembering the structural formula for a hormone molecule offers quite different demands for the typical secondary school student and a doctoral student specialising in natural products chemistry.

Capacity is not related to an inherent nature of the information, but to how it is perceived and related to existing knowledge. This allows some people to manage apparently incredible memory feats through various mnemonic tactics. One study reports the case of an undergraduate student (said to be of typical intelligence) who through practice managed to learn to demonstrate a highly superior memory span for numbers – eventually he could correctly recall lists of 79 digits. However, when the same student was tested with consonants, his memory span remained at 6 items (Ericsson et al., 1980), within the usual 7 ± 2 range.

Indeed, more recent research (Cowan et al., 2004; Mathy and Feldman, 2012), whilst supporting Miller's general principle, suggests that Miller's magic number may actually over-estimate the number of available ‘slots’ in working memory, because of our natural tendency to spot patterns that allow us to ‘chunk’ information. It seems that the real capacity of working memory may actually be more commonly around 4 rather than 7, because even when ‘arbitrary’ information is used to test memory span, people tend to be able to impose some order on the material to be remembered and so chunk it to some extent. It is suggested that the actual capacity may be better described as 4 ± 1 (more in keeping with what is often measured in young children), but appears to be 7 ± 2 when measured in most people due to automatic strategies used to chunk information.

This relates to Ausubel’s (1968, 2000) well-known distinction between rote and meaningful learning. From a constructivist perspective (Taber, 2009b) the learning process involves (a) a stage of interpretation where the learner has to make sense of what is being taught, drawing upon the interpretative resources available, and also (b) a process of modifying existing knowledge to incorporate new learning.

In some cases, internal cognitive resources (existing conceptual frameworks) may be supplemented by drawing upon external resources. One example might be a student referring to their previous notes or a textbook to help ‘make sense’ of teaching – although these additional resources still have to be interpreted in terms of existing cognitive resources ‘inside’ the mind. Perhaps more significantly, when the teacher uses a dialogic approach to teaching (Mortimer and Scott, 2003; Staarman and Mercer, 2010), and encourages students to share and discuss ideas, this allows students to express their own interpretations and compare them with those of others, so in effect allowing a moderation process to occur, and potentially the coming to a consensus (Bruner, 1987). However, ultimately, the learner is limited by what their existing conceptual frameworks allow them to understand.

The second stage of the learning process involves making changes to the internal conceptual structures (i.e. knowledge representations in the mind). There remains a significant gap between our models of learning processes and our understanding of what is occurring at the level of the material substrate (i.e. assumed to be the synaptic structure of the nervous system – circuits of neurons). So although it is widely assumed that learning involves changes in neural connections, we do not know enough about this to relate it directly to classroom learning in specific cases (Taber, forthcoming). Potentially, however, such changes can be considered to fall into qualitatively different types, with three main categories.

Ausubel (2000) refers to rote learning, where in effect the learner finds nowhere (sic, this is a spatial metaphor of course) in existing conceptual structure to ‘anchor’ new knowledge, and so it is learnt as an isolated ‘island’ that is not substantially connected to existing knowledge. There is no meaningful understanding in this case, and so anything learnt in this way is likely, if recalled at all, to only be available to be used in very limited situations where it is recognised that the task at hand is to recall that information. This is little more than a stimulus-response operation: we might imagine the hypothetical case of a student who can produce the utterance ‘delocalisation’ in response to hearing the cue ‘bonding in benzene’ without knowing what ‘benzene’ is, or what ‘bonding’ is; or what ‘delocalisation’ is, beyond being an appropriate response to that cue.

Such learning usually requires much reinforcement to become well established, and clearly is of limited value in terms of meaningful chemistry learning. That extreme case is considered here because it represents one pole of the useful construct ‘rote-meaningful’. Pure rote learning may be rare (if indeed possible in practice), but actual students’ learning is often only somewhat meaningful, being linked into conceptual structures in minimal and/or sub-optimal ways. Arguably, offering a student starting out on chemistry a formal definite of an element as a substance that cannot be broken down into any simpler substance(s) by chemical means is inviting rote learning, as the novice will lack sufficient prerequisite knowledge to understand what is meant by substance, simpler (in this context) or chemical means.

In relation to the opposite, meaningful, learning pole, one ideal is new learning that can be fitted into existing conceptual structures with minimal modification. A student who has learnt previously that hydrogen bonding occurs in HF, HCl and H₂O, may then learn that it also occurs in NH₃. Again, considering that such ‘addition’ leaves the rest of the structure unchanged is an in principle case (‘in principle’ as NH₃ will have other associations, and the nature of hydrogen bonding as a category may be considered to change in at least trivial ways as its group membership expands), and indeed in the Piagetian tradition which has informed this area of work (Piaget, 1970/1972) the ‘assimilation’ of new learning into existing structures is considered to be one component of a more extended process (assimilation → disequilibration → accommodation → equilibration) that always involves some level of restructuring to accommodate the new material.

However, it seems that much school learning is to a first approximation of this kind: just adding in examples or additional properties to categories represented in existing conceptual structures without bringing about substantive changes in those conceptual structures (Taber, forthcoming). It is common to distinguish this type of example from those cases where new learning disrupts existing understanding by creating internal contradictions within conceptual structures, and so leading to a sense of cognitive dissonance (Cooper, 2007) that motivates a restructuring of ideas to bring about greater ‘explanatory coherence’ (Thagard, 1992).

We should see these categories as ‘ideals’, whereas much real learning is intermediate between them – as suggested in Fig. 4. ‘Ideal’ does not here imply ‘perfect’ (or desirable), but just something that can be imagined in principle, regardless of whether such cases exist in reality or not (like purely ionic bonding) – something that is ideal in the Platonic sense of existing in what Popper (1979) referred to as the world of objective thought – that which can exist as ideas, even if not realisable in the material world.

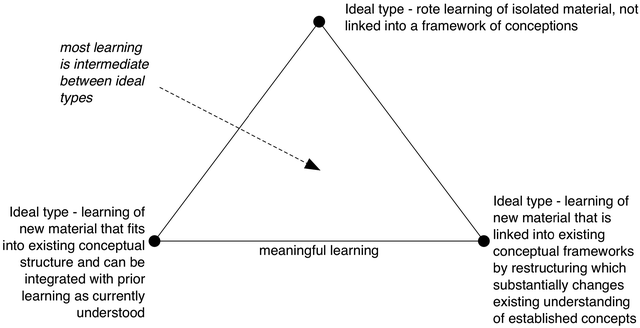Fig. 4 Ideal forms of learning.

The notion of meaningful learning, which allows existing conceptual structures that already integrate extensive aspects of prior learning to act as interpretive resources for new learning, to some extent nullifies the potentially problematic restrictions of working memory. The effective learner is often the one who has relevant prior learning, that is already structured in a highly organised way, and who is able to recognise how teaching can be related to what they already know. That learner can ‘chunk’ effectively to cope well with the stream of new information that may be presented in a classroom, as long as teaching is planned to make clear links with prior learning.

For example, we can consider again the string presented above:

H₂SO_4(aq) + 2NaOH_(aq) → Na₂SO_4(aq) + 2H₂O_(l)

Whilst for the novice to chemistry, this is a complex string of symbols – including letters (some parenthetical and as subscripts) and numbers (some but not all as subscripts) – the experienced chemist or science teacher can readily conceptualise this string in terms of a small number of items that could be held in working memory.

This is a neutralisation reaction, and so (for the chemistry expert) fits a familiar schema. That is, the chemist has represented in long-term memory the basic general structure of any reaction – reactant(s) → product(s) – and the specific form of this particular class of reaction – acid + alkali → salt + water – with its ‘slots’ for the specific acid, alkali and salt in any particular case (Taber, 2002). The ‘terms’ in the string (H₂SO_4(aq), etc.) are all familiar as representing particular reagents (sulphuric acid, etc.). So the chemist will most likely ‘re-cognise’ (sic) the string as the equation for neutralisation of sulphuric acid and sodium hydroxide; or, even more efficiently, as the equation for the formation of sodium sulphate by neutralisation.

In that form, very little information has to be held in working memory to allow the equation to be ‘recalled’ accurately by drawing upon existing knowledge in long-term memory. Memory commonly operates in a reconstructive way (Parkin, 1987; Taber, 2003), that is what we are conscious of ‘remembering’ is often a coherent scenario built from information that can be retrieved, with missing details ‘filled-in’ (in effect interpolation based on what preconscious cognitive processing suggests would be likely). Whilst this can lead to ‘false’ memories (so, for example, where learners have alternative conceptual frameworks, they will commonly ‘remember’ some things they are taught incorrectly, in ways consistent with those alternative frameworks), it allows us to effectively remember complex information as long as it fits well with our existing conceptual frameworks.

Many senior secondary level students will have conceptual structures which are somewhere between the complete novice and the expert in terms of both extent of knowledge and its organisation, and so will perceive the string as of intermediate complexity: perhaps not yet able to apply general reaction schemata, but able to recognise the reagents and draw upon other heuristics or common patterns (e.g. the number of atoms of each type are conserved in a balanced equation; sulphates often derive from sulphuric acid) that might have some utility in reconstructing the string (cf.Taber and Bricheno, 2009) from what can be held in working memory.

Whilst new learning may still prove labile even when initially made sense of in terms of existing conceptual structure, the human brain has (automatic) mechanisms to consolidate such learning so that over a period of time (which may be months) its integration into conceptual structures becomes more robust (Alvarez and Squire, 1994; Walker and Stickgold, 2004). Consolidation allows what was the subject of learning to become a potential resource to support future learning. In time, given suitable opportunities to learn, what is unfamiliar and strange, and part of the challenge of learning, becomes familiar and comfortable, and a mental tool to use in further learning. The crux is that learning must involve challenges, but carefully sequenced challenges that stimulate rather than overload the intellect.

A learning science perspective 3: teaching as scaffolding

An another important area of scholarship, and one which has been very actively developed since Johnstone first proposed his model, is that of sociocultural models of learning (Smardon, 2009), and in particular notions of scaffolding in learning (Wood, 1988), informed by the work of Vygotsky (1978). Vygosky offered a notion of the distinction between a learner's zone of actual development (ZAD, describing what they had already mastered) and their zone of next, or proximal, development (ZPD) where they were able to achieve with some support from a teacher or more advanced peer, but not yet unaided. The gist of Vygotsky's idea is that setting learning tasks beyond the ZPD does not support learning, and that tasks within the ZAD are only useful for drill, but usually do not lead to significant new learning. Rather, significant learning is most likely when tasks are initially beyond the competence of the student, who is supported to succeed by having the task ‘scaffolded’ (Taber, 2011).

Scaffolding involves structuring the task, offering cues and hints, and even modelling the activity for the learner, but gradually ‘fading’ the level of support as the learner begins to master the task – moving from a capacity to undertake single steps in a process when prompted, to developing an effective schema or mental framework that allows the organisation and completion of a complex task without support.

A task that is initially too unfamiliar and complex becomes manageable as it becomes better represented and integrated within the learner's conceptual frameworks (and so the representations can be more economically ‘chunked’ so that they can be mentipulated within working memory). Encouraging the use of dialogic teaching methods that allow students to take time to explore new ideas in terms of their own thinking – and which relates the formal material to be taught to learners’ ideas – has been found to be effective in supporting learning in this way (Mercer et al., 2004; Mortimer and Scott, 2003)

In terms of chemistry learning, the novice student will struggle to cope with teaching which flits back and forth between the observed phenomena and the formal conceptual categories at the macroscopic level (element, acid, oxidising agent, etc.), and the formal theoretical models at the submicroscopic level (electronic configurations, lattice arrangements etc.), especially when drawing upon technical vocabulary, various formulae, equations and other formalisms (e.g. dot and cross diagrams of molecules, etc.).

However, that does not mean that any of these key elements of chemistry as a subject need to be omitted from education at school level. As Johnstone recognised, it is important to limit what is presented at any one time. Students need time to make sense of the macroscopic concepts, and to become fluent in the technical terminology used to communicate them, before they should be asked to explain them using the highly abstract theoretical models of the molecular realm. When learning about molecules and ions and atoms and so forth, it is important that learners appreciate that our formal diagrams represent models, and that we need to have different types of models for the same entity (Taber, 2010): however, the student must be allowed sufficient time for each model that is introduced and represented to become familiar – with opportunities to consider its affordances, and to learn the formalisms of its canonical representation – before it can then be assumed to take its place as a useful tool to do the explanatory work of chemistry. So, certainly, some time does have to be given to learning the representations, and gaining confidence in working with them, before the teacher starts to model how they can be used to do the kind of intellectual work that we would like the student to eventually be able to undertake with them.

We know it is possible for students, some students at least, to master the complexity of our subject, and manage to coordinate the different domains of knowledge and formalisms used to represent chemical ideas – because as teachers we have made that journey, and often found it fascinating. The challenge is to allow all of our students to experience something of the wonder of chemical science, by carefully supporting their developing understanding of the subject, given (a) the limited amount of new information that can be held in mind at once, and (b) the need for considerable reinforcement before core ideas are consolidated enough to become resources for learning, rather than parts of the demand of learning the subject.

Revisiting the chemistry triplet: implications for developing pedagogy

Johnstone's triangle (1991) has arguably been one of the most adopted and applied ideas in the field of chemical education. This is undoubtedly because the core of Johnstone's argument was both accurate and important: (a) the nature of chemistry as a subject is complex because it involves two distinct levels of formal concepts that need to be related to each other and to observed phenomena, and it is communicated not only through specialised technical vocabulary but also in terms of a whole range of other symbolic forms of representation; (b) yet research on learning shows that the learner can only make sense of a restricted amount of new information at any one time, having a working memory of very limited capacity.

The analysis of the domains of chemical knowledge offered above suggests however that the symbolic knowledge domain cannot be readily separated from the macroscopic and submicroscopic domains as a discrete level of chemical knowledge, as this domain is concerned with representing and communicating the concepts and models developed at those two ‘levels’. The symbolic is inherent in how we think about chemistry; and the processes of learning, teaching and applying chemistry commonly involve re-descriptions into and between components of the specialised symbolic ‘language’ used to describe chemical ideas at the two levels. This is summarised in Fig. 5.

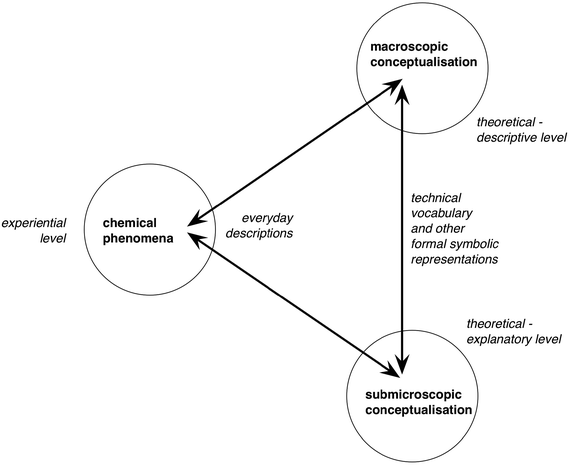Fig. 5 Learning chemistry involves re-descriptions (represented by the arrows) between the everyday language of direct experience and formal representations of the conceptualisation of the subject at two distinct levels.

Johnstone questioned the logic of introductory teaching that drew upon the different domains of knowledge all at once, and yet his analysis also suggested that the three domains of chemical knowledge were essential to expertise in the subject, and indeed a source of intellectual satisfaction once mastered. The advanced student certainly needs to be able to operate ‘in the triangle’ and so “jump freely…in a series of mental gymnastics” (Johnstone, 1982, p. 377).

Johnstone (1982) suggested that for at least some students chemistry should be largely restricted to the macroscopic level. It is certainly the case that different teaching approaches suit different students, and for some learners the extent of learning about the submicroscopic level may sensibly be more limited than for others. However, the nature of chemistry itself as a modern science relies on the molecular realm, and arguably an authentic chemistry education should introduce something of the explanatory power of the submicroscopic domain of chemical knowledge.

What is suggested here is that where students are not coping with the complexity of our subject, it may be better to slow the pace of introducing new ideas, and to provide sufficient opportunities to reinforce those keys ideas considered most important through a wide range of contexts, but to teach less breadth of material. However, such a reduced curriculum should still include both macroscopic and submicroscopic concepts, and the standard forms of vocabulary and symbolic representation for those concepts that are taught.

What research into the psychology of learning and related topics suggests is not that we need to avoid going into the triangle when teaching the subject requires us to, but that we need to be aware of the importance of:

(a) Limiting the amount of new information being presented at any one time;

(b) Helping students relate new teaching to existing learning;

(c) Reinforcing new learning over long enough timescales (e.g. weeks and months) to support the natural processes by which learning is consolidated to become better integrated and more robust (so strengthening connections between concepts and supporting economic ‘chunking’);

(d) Modelling the ways in which chemists operate with and between the two domains of conceptual knowledge (macroscopic descriptions and categories; theoretical submicroscopic models) using the symbolic language of the subject as the means to readily represent and communicate these concepts; but

(e) Offering sufficient scaffolding to support students in gradually learning to operate within and across the domains in the way experts can.

So, for example, there will need to be times in teaching when the focus is on subsets of the macroscopic concepts, and how these are formally represented; and there will need to be times when the focus is on aspects of the submicroscopic models, and the different ways these are formally represented. There will also be times when it is vital to shift between the macroscopic and submicroscopic domains to build up the explanations of the subject, using the standard forms of representation to communicate the ideas (de Jong and Taber, forthcoming). However, ventures into the triangle should be about relating previously taught material, and should be modelled carefully by the teacher before students are asked to lead expeditions there; and such explorations should initially be undertaken with carefully structured support. The aim, after all is not to avoid students being in the triangle, but to make sure that whilst there they can appreciate what teachers like Johnstone already recognise as “a beautiful, integrated view of chemistry” (2009, p. v).

References

1. Alvarez P. and Squire L. R., (1994), Memory consolidation and the medial temporal lobe: a simple network model. [Neurobiology], Proc. Natl. Acad. Sci. U. S. A., 91, 7041–7045.
2. Ausubel D. P., (1968), Educational Psychology: A Cognitive View, New York: Holt, Rinehart & Winston.
3. Ausubel D. P., (2000), The Acquisition and Retention of Knowledge: A Cognitive View, Dordrecht: Kluwer Academic Publishers.
4. Baddeley A., (2003), Working memory: looking back and looking forward. Nat. Rev. Neurosci., 4(10), 829–839.
5. Ben-Zvi R., Bat-Sheva E. and Silberstein J., (1986), Is an atom of copper malleable? J. Chem. Educ.,63(1), 64–66.
6. Brook A., Briggs H. and Driver R., (1984), Aspects of secondary students' understanding of the particulate nature of matter, Leeds: Centre for Studies in Science and Mathematics Education, University of Leeds.
7. Bruner J. S., (1987), The transactional self, in Bruner J. and Haste H. (ed.), Making Sense: The Child's Construction of the World, London: Routledge, pp. 81–96.
8. Cooper J., (2007), Cognitive Dissonance: Fifty Years of a Classic Theory, London: Sage.
9. Cowan N., Chen Z. and Rouder J. N., (2004), Constant Capacity in an Immediate Serial-Recall Task: A Logical Sequel to Miller (1956), Psych. Sci., 15(9), 634–640.
10. de Jong O. and Taber K. S., (forthcoming), Teaching and learning the many faces of chemistry, in Lederman, N. (ed.), Handbook of Research in Science Education, vol. 2, New York: Routledge.
11. De Ribaupierre A., Fagot D. and Lecerf T., (2011), Working Memory Capacity and its Role in Cognitive Development: Are Age Differences Driven by the Same Processes Across the Lifespan? in Barrouillet P. and Gaillard V. (ed.), Cognitive Development and Working Memory: A Dialogue between Neo-Piagetian Theories and Cognitive Approaches, Hove, East Sussex: Psychology Press.
12. Ericsson K. A., Chase W. G. and Faloon S., (1980), Acquisition of a Memory Skill, Science, 208(4448), 1181–1182.
13. Gabel D. L., (1993), Use of the particle nature of matter in developing conceptual understanding, J. Chem. Educ., 70(3), 193.
14. Gilbert J. K. and Treagust D. F., (2009a), Introduction: macro, submicro and symbolic representations and the relationship between them: key models in chemical education, in Gilbert J. K. and Treagust D. F. (ed.), Multiple Representations in Chemical Education, Dordecht: Springer, pp. 1–8.
15. Gilbert J. K. and Treagust D. F., (ed.), (2009b), Multiple Representations in Chemical Education, Dordrecht: Springer.
16. Grosholz E. R. and Hoffman R., (2000), How symbolic and iconic languages bridge the two worlds of the chemist: a case study from contemporary bioorganic chemistry, in Bhushan N. and Rosenfeld S. (ed.), Of Minds and Molecules: New Philosophical Perspectives on Chemistry, Oxford: Oxford University Press, pp. 230–247.
17. Harrison A. G. and Treagust D. F., (1996), Secondary students' mental models of atoms and molecules: implications for teaching chemistry, Sci. Educ., 80(5), 509–534.
18. Harrison A. G. and Treagust D. F., (2002), The particulate nature of matter: challenges in understanding the submicroscopic world, in Gilbert J. K., de Jong O., Justi R., Treagust D. F. and Van Driel J. H. (ed.), Chemical Education: Towards Research-based Practice,Dordrecht: Kluwer Academic Publishers, pp. 189–212.
19. Jaber L. Z. and BouJaoude S., (2011), A Macro-Micro-Symbolic Teaching to Promote Relational Understanding of Chemical Reactions, Int. J. Sci. Educ., 1–26.
20. Johnson P. M., (1998), Progression in children's understanding of a ‘basic’ particle theory: a longitudinal study, Int. J. Sci. Educ.,20(4), 393–412.
21. Johnson P. M., (2005), The development of children's concept of a substance: a longitudinal study of interaction between curriculum and learning, Res. Sci. Educ.,35(1), 41–61.
22. Johnson P. M., (2012), Introducing Particle Theory, in Taber K. S. (ed.), Teaching Secondary Chemistry, 2nd edn, Association for Science Education/John Murray, pp. 49–73.
23. Johnstone A. H., (1982), Macro- and microchemsitry. [Notes and correspondence], Sch. Sci. Rev., 64(227), 377–379.
24. Johnstone A. H., (1989), Some messages for teachers and examiners: an information processing model, Assessment of Chemistry in Schools, vol. Research in Assessment VII, London: Royal Society of Chemistry Education Division, pp. 23–39.
25. Johnstone A. H., (1991), Why is science difficult to learn? Things are seldom what they seem, J. Comput. Assist. Lear., 7, 75–83.
26. Johnstone A. H., (2000a), Chemical Education Research: Where from Here? Univ. Chem. Educ., 4(1), 34–38.
27. Johnstone A. H., (2000b), Teaching of chemistry – logical or psychological? Chem. Educ.: Res. Pract. Eur., 1(1), 9–15.
28. Johnstone A. H., (2009), Foreword, in Gilbert J. K. and Treagust D. F. (ed.), Multiple Representations in Chemical Education, Dordecht: Springer, pp. v–vi.
29. Kouider S. and Dehaene S., (2007), Levels of processing during non-conscious perception: a critical review of visual masking, in Driver J., Haggard P. and Shallice T. (ed.), Mental Processses in the Human Brain, Oxford: Oxford University Press, pp. 155–185.
30. Leach J. and Scott P., (2002), Designing and evaluating science teaching sequences: an approach drawing upon the concept of learning demand and a social constructivist perspective on learning. Stud. Sci. Educ.,38, 115–142.
31. Lorenzo M. G., Farre A. S. and Rossi A. M., (2010), Teachers' discursive practices in a first organic chemistry course, in Çakmakci G. and Taşar M. F. (ed.), Contemporary Science Education Research: Scientific Literacy and Social Aspects of Science, Ankara, Turkey: Pegem Akademi, pp. 13–22.
32. Mathy F. and Feldman J., (2012), What's magic about magic numbers? Chunking and data compression in short-term memory, Cognition, 122(3), 346–362.
33. Mercer N., Dawes L., Wegerif R. and Sams C., (2004), Reasoning as a scientist: ways of helping children to use language to learn science, Brit. Educ. Res. J., 30(3), 359–377.
34. Miller G. A., (1968), The magical number seven, plus or minus two: some limits on our capacity for processing information, The Psychology of Communication: Seven Essays, Harmondsworth: Penguin, pp. 21–50.
35. Mortimer E. F. and Scott P. H., (2003), Meaning Making in Secondary Science Classrooms, Maidenhead: Open University Press.
36. Osborne R. J. and Wittrock M. C., (1983), Learning science: a generative process, Sci. Educ.,67(4), 489–508.
37. Osborne R. J. and Wittrock M. C., (1985), The generative learning model and its implications for science education, Stud. Sci. Educ., 12, 59–87.
38. Parkin A. J., (1987), Memory & Amnesia: An Introduction, Oxford: Basil Blackwell.
39. Piaget J., (1970/1972), The Principles of Genetic Epistemology (W. Mays, Trans.), London: Routledge & Kegan Paul.
40. Popper K. R., (1979), Objective Knowledge: An Evolutionary Approach, revised edn, Oxford: Oxford University Press.
41. Shayer M. and Adey P., (1981), Towards a Science of Science Teaching: Cognitive Development and Curriculum Demand, Oxford: Heinemann Educational Books.
42. Shore B. M. and Dover A. C., (2004), Metacognition, intelligence and giftedness, in Sternberg R. J. (ed.), Definitions and Conceptions of Giftedness, Thousand Oaks, California: Corwin Press, pp. 39–45.
43. Smardon R., (2009), Sociocultural and cultural-historical frameworks for science education, in Roth W.-M. and Tobin K. (ed.), The World of Science Education: Handbook of Research in North America, Rotterdam, The Netherlands: Sense Publishers, pp. 15–25.
44. Staarman J. K. and Mercer N., (2010), The guided construction of knowledge: talk between teachers and students, in Littleton K., Wood C. and Staarman J. K. (ed.), International Handbook of Research of Psychology in Education, Bingley: Emerald, pp. 75–104.
45. Sweller J., (2007), Evolutionary biology and educational psychology, in Carlson J. S. and Levin J. R. (ed.), Educating the Evolved Mind: Conceptual Foundations for an Evolutionary Educational Psychology, Charlotte, North Carolina: Information Age Publishing, pp. 165–175.
46. Taber K. S., (2001), Building the structural concepts of chemistry: some considerations from educational research, Chem. Educ.: Res. Pract. Eur., 2(2), 123–158.
47. Taber K. S., (2002), Chemical Misconceptions – Prevention, Diagnosis and Cure: Theoretical Background, vol. 1, London: Royal Society of Chemistry.
48. Taber K. S., (2003), Lost without trace or not brought to mind? – a case study of remembering and forgetting of college science, Chem. Educ. Res. Pract., 4(3), 249–277.
49. Taber K. S., (2005), Learning quanta: barriers to stimulating transitions in student understanding of orbital ideas, Sci. Educ.,89(1), 94–116.
50. Taber K. S., (2009a), Learning at the symbolic level, in Gilbert J. K. and Treagust D. F. (ed.), Multiple Representations in Chemical Education, Dordrecht: Springer, pp. 75–108.
51. Taber K. S., (2009b), Progressing Science Education: Constructing the Scientific Research Programme into the Contingent Nature of Learning Science, Dordrecht: Springer.
52. Taber K. S., (2010), Straw men and false dichotomies: overcoming philosophical confusion in chemical education, J. Chem. Educ., 87(5), 552–558.
53. Taber K. S., (2011), Constructivism as educational theory: contingency in learning, and optimally guided instruction, in Hassaskhah J. (ed.), Educational Theory, New York: Nova, pp. 39–61. Available from https://camtools.cam.ac.uk/wiki/eclipse/Constructivism.html.
54. Taber K. S., (2012), Key concepts in chemistry, in Taber K. S. (ed.), Teaching Secondary Chemistry, 2nd edn, London: Hodder Education, pp. 1–47.
55. Taber K. S., (forthcoming). Modelling learners and learning in science education: developing representations of concepts, conceptual structure and conceptual change to inform teaching and research.
56. Taber K. S. and Bricheno P. A., (2009), Coordinating Procedural and Conceptual Knowledge to Make Sense of Word Equations: Understanding the Complexity of a ‘Simple’ Completion Task at the Learner's Resolution, Int. J. Sci. Educ., 31(15), 2021–2055.
57. Taber K. S. and Tan K. C. D., (2011), The insidious nature of ‘hard core’ alternative conceptions: implications for the constructivist research programme of patterns in high school students' and pre-service teachers' thinking about ionisation energy, Int. J. Sci. Educ.,33(2), 259–297.
58. Talanquer V., (2011), Macro, submicro, and symbolic: the many faces of the chemistry “triplet”, Int. J. Sci. Educ.,33(2), 179–195.
59. Thagard P., (1992), Conceptual Revolutions, Oxford: Princeton University Press.
60. Vygotsky L. S., (1978), Mind in Society: The Development of Higher Psychological Processes, Cambridge, Massachusetts: Harvard University Press.
61. Walker M. P. and Stickgold R., (2004), Sleep-Dependent Learning and Memory Consolidation, Neuron,44(1), 121–133.
62. Wood D., (1988), How Children Think and Learn: The Social Contexts of Cognitive Development, Oxford: Blackwell.

---