Correlation of nanoscale organizations of polymer and nanocrystals in polymer/inorganic nanocrystal bulk heterojunction hybrid solar cells: insights from multiscale molecular simulations†
Cheng-Kuang
Lee
a,
Chun-Wei
Pao
*a and
Chun-Wei
Chen
b
aResearch Center for Applied Sciences, Academia Sinica, 128 Sec. 2 Academia Rd., Taipei 11529, Taiwan. E-mail: cwpao@gate.sinica.edu.tw
bDepartment of Materials Science and Engineering, National Taiwan University, Taipei, Taiwan
First published on 13th November 2012
Abstract
A comprehensive insight into the correlations of the nanoscale organizations of polymer and nanocrystals in polymer/inorganic nanocrystal bulk heterojunction (BHJ) hybrid solar cells is the key toward nanomorphology control for improving device performance. In this study, we investigated the organizations of both the polymer and nanocrystals in polymer/inorganic nanocrystal hybrid solar cells by performing multiscale molecular simulations of P3HT:TiO2 nanocrystal BHJs incorporating nanocrystals with two different dimensionalities, namely, zero-dimensional nanoparticles (NPs), and one-dimensional nanorods (NRs). We reveal that nanocrystal dimensionality has significant impacts on the polymer/nanocrystal organizations for polymer/inorganic nanocrystal hybrid blends. One-dimensional nanocrystals, such as TiO2 NRs, can effectively enhance the polymer degree of crystallinity as a result of preferential polymer chain alignment along the axial dimension of the NRs, thereby promoting hole transport; in addition, the elongated, anisotropic NRs significantly reduce the probability of electron hopping, and maintain a high specific interfacial area for efficient exciton dissociation. Therefore, the present study demonstrates the possibility of the nanoscale morphology control of polymer/inorganic nanocrystal BHJ hybrid blends via tuning the nanocrystal shapes, which is potentially helpful for developing next-generation polymer/inorganic nanocrystal hybrid electronic devices such as solar cells or thin film transistors.
Broader contextPolymer/inorganic nanocrystal bulk heterojunction (BHJ) hybrid solar cells are one of the promising renewable energy sources due to their low production cost, mechanical flexibility, and lightweight compared with their pure inorganic counterparts. One primary feature of polymer/inorganic nanocrystal BHJ hybrid cells is the tunability of the nanocrystal shapes/sizes. By synthesizing nanocrystals in different shapes [e.g., nanoparticles (NPs), nanorods (NRs), and nanotetrapods] with controllable sizes, the nanocrystal electronic properties can be manipulated to optimize device performance. Nanocrystal shapes/sizes have significant impacts on the polymer/nanocrystal organizations in the BHJ layer, which is critical for the solar cell performance. However, the correlations of polymer and nanocrystal organizations in polymer/inorganic nanocrystal BHJ hybrid cells are still unknown since their introduction in 2002. In this work, we developed a multiscale molecular simulation model to investigate polymer/nanocrystal organizations and morphological properties (e.g., specific interfacial area) in P3HT/TiO2 NP/NR blends. Our simulation results indicate that anisotropic NRs can effectively promote polymer crystallinity and eliminate inter-nanocrystal junctions, thereby promoting hole and electron transport. Therefore, the present study provides comprehensive insights into the correlations of polymer/nanocrystal organizations in polymer/inorganic nanocrystal hybrid solar cells, which is potentially helpful for nanomorphology control in next-generation polymer/inorganic nanocrystal solar cells or thin film transistors. |
1 Introduction
Polymer/inorganic nanocrystal hybrid solar cells have drawn considerable attention as one of the promising renewable energy sources.1–14 The photoactive layers in polymer/inorganic nanocrystal hybrid solar cells comprise interpenetrating networks of electron donor and acceptor phases. The electron donor materials are usually semiconducting conjugated polymers [e.g., regioregular poly(3-hexylthiophene) (P3HT), see Fig. 1a], whereas the electron acceptor materials are usually semiconducting inorganic nanocrystals (e.g., CdSe, ZnO, PbS, TiO2). These hybrid solar cells have several advantageous features over their pure inorganic counterparts: lower production costs through solution processing, greater mechanical flexibility, lighter weight, and additional versatility provided by the ability to control the shapes and sizes of the inorganic nanocrystals.9,10,13 Inorganic nanocrystals can be synthesized in a number of forms with controllable sizes, including nanoparticles (NPs), nanorods (NRs), or nanotetrapods;11–16 the nature of these nanostructural materials can significantly impact (i) the organization of the electron donor and acceptor materials and (ii) the electronic properties of the electron acceptor materials, potentially improving the efficiency of the polymer/inorganic hybrid solar cells.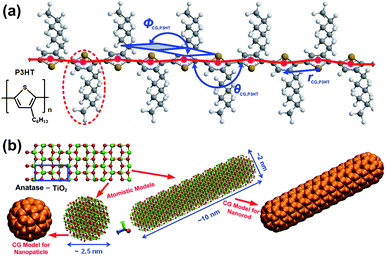 | ||
| Fig. 1 (a) Atomistic structure of a P3HT chain and the CG model employed herein. Red beads represent CG particles of P3HT; the red-dashed line highlights the P3HT repeat unit; all CG intramolecular degrees of freedom (CG bond length, rCG,P3HT; CG bond angle, θCG,P3HT; CG dihedral angle, φCG,P3HT) are displayed in blue. (b) Upper left panel: atomistic structure of anatase TiO2; the blue box highlights the anatase unit cell. Lower left panel: atomistic structure and corresponding CG model of a TiO2 NP; lower right panel: atomistic structure and corresponding CG model of a TiO2 NR. | ||
The nanoscale organization of polymers and inorganic nanocrystals in a polymer/inorganic hybrid cell has a critical effect on device performance. When the photoactive layer absorbs incident photons, excitons are generated within the polymer domains; these excitons diffuse toward the polymer/nanocrystal interface and dissociate into free electrons and holes, which are transported to their corresponding electrodes to generate the photocurrent. In polymer/inorganic nanocrystal hybrid solar cells, the donor–acceptor morphological organizations are critically correlated with the nanocrystal shapes (e.g., NP, NR or nanotetrapod); hence, a comprehensive insight into the correlations of polymer/nanocrystals organizations is critical for morphology control to boost device performance. However, experimental characterization of the polymer/nanocrystal organization of polymer/inorganic hybrid cells is never trivial. Recently, electron tomography experiments have revealed the three-dimensional (3D) structures of various organized inorganic nanocrystal phases (ZnO nanocrystals; CdSe NPs and NRs; TiO2 NPs and NRs) in hybrid polymer/inorganic hybrid cells.14–16 Nevertheless, little information exists regarding the correlation between a nanocrystal's shape and its polymer/nanocrystal organization. Moreover, the general morphological criteria determining the optimal blending ratios in polymer/inorganic hybrid cells, regardless of nanocrystal shape or elemental composition, remain unclear.
In this study, we revealed the correlations of nanoscale organizations of both the polymers and inorganic nanocrystals in polymer/inorganic hybrid cells by performing a series of multiscale, coarse-grained (CG; mesoscale) molecular simulations of the annealing processes of P3HT:TiO2 nanocrystal hybrid blends with two TiO2 nanocrystal dimensionalities: namely, zero-dimensional nanoparticles (NPs), and one-dimensional nanorods (NRs). With the aid of CGMD computational experiments, we were able to simulate a system size around 60 × 60 × 60 nm3, which are compatible with experiments and are well-beyond those that can be achieved by conventional atomistic molecular simulations. Our simulations indicated that a nanocrystal's shape has a significant impact on polymer/nanocrystal organization. Relative to zero-dimensional nanocrystals (i.e., NPs), one-dimensional nanocrystals (i.e., NRs) can enhance the polymer's degree of crystallinity through preferential alignment of the polymer along the NRs' axial directions, thereby promoting hole transport; furthermore, because they are longer in one dimension, NRs can effectively minimize electron hopping events between neighboring NRs to promote electron transport, while retaining a sufficiently small rod diameter to maintain a large specific interfacial area for efficient exciton dissociation. Finally, we found that, regardless of the nanocrystal's shape, polymer/inorganic hybrid cells incorporating favorably organized blends (i.e., blends with optimal performance) must have a high specific interfacial area to maximize exciton dissociation and almost identical electron donor–acceptor percolation probabilities to balance electron and hole transport—similar to those of polymer/fullerene blends. Our present study therefore provides comprehensive insights into the correlation between polymer/nanocrystal organization and nanocrystal shape for polymer/inorganic nanocrystal hybrid blends, potentially helpful for developing novel nanostructural materials of next-generation polymer/inorganic nanocrystal hybrid solar cells or thin film transistors.
2 Models and methods
The atomistic structures of P3HT and anatase TiO2 NP/NR, and their corresponding CG models are depicted in Fig. 1. For the P3HT component, each P3HT repeat unit (region enclosed inside the red dashed line in Fig. 1a) was mapped into a CG bead (colored red in Fig. 1a) centered at the thiophene ring. In general, there are two approaches for deriving the CG force field from atomistic simulations of smaller system of interest, namely, energy- and structural-based approaches. In the energy-based CG approach, the CG force field is targeted to reproduce thermodynamic properties such as energies or free energies.17,18 On the other hand, the structural-based CG scheme is targeted to reproduce structural properties such as radial distribution function (RDF), CG bond length, CG bond angle, and dihedral angles of the CG degrees of freedom.19–30 For the CG model of P3HT, because the conformations of the P3HT chains are critical for investigating polymer organizations, the CG force fields between the CG particles of P3HT were obtained by employing the structural-based CG scheme.19–30 It has been demonstrated that there exists a unique pair function by imposing the same RDF.31 Hence, such a scheme has been demonstrated to be the safest approach for developing CG models of colloids32,33 or water molecules.34 The optimized potential parameters are compiled in Table S1 (ESI).† Detailed procedures for the fitting of the intra- and intermolecular CG potential of P3HT employed in the present study can be found elsewhere.29 The CG force field of P3HT fitted can successfully reproduce the persistence length of P3HT,29 guaranteeing that the chain conformations and associated structural features would be captured well in subsequent CGMD simulations.For constructing CG models of TiO2 nanocrystals, a different approach was employed. TiO2 NPs and NRs with given sizes were mapped into spherical or cylindrical (with hemispherical caps in both ends) clusters comprising CG beads, see the clusters of orange beads in the lower left and right panels of Fig. 1b, and in the insets of Fig. S1 in the ESI.† It must be stressed that we did not coarse-grain one TiO2 nanocrystal into a single large CG particle (e.g., coarse-graining one TiO2 NR into single ellipsoid). Since nanocrystals are rigid, in the present study, only inter-nanocrystal interactions between CG beads (i.e., interactions between CG beads belonging to different NPs/NRs) were taken into account in fitting the CG force fields. The inter-nanocrystal CG force field between the CG beads was fitted into Lennard-Jones form, such that the resultant potential energy between two NPs (NRs) from the multisite inter-nanocrystal interaction of CG beads can reproduce the potential energy surface computed from AMD calculations. The diameter of the TiO2 NPs was chosen to be 2.5 nm; the rod diameter and aspect ratio for the TiO2 NRs were set at 2.0 nm and 5, respectively. These sizes for both the NPs and NRs are comparable with those tested experimentally.14 The potential energy surfaces between two TiO2 NPs and NRs from AMD calculations are displayed in Fig. S1a and b–e (ESI),† respectively. The fluctuations in the potential energy between the NPs/NRs, due to TiO2 crystal orientations (see error bars in Fig. S1†), and the TiO2 NR stacking types (e.g., side-by-side, end-to-end, cross and T-shape; inset to Fig. S1b–e†), were also taken into account. The CG force fields between the CG beads of the TiO2 NPs and NRs were then fitted to reproduce the potential energy surfaces in Fig. S1† through simplex optimization35,36 (see blue lines in Fig. S1†). The optimized CG Lennard-Jones parameters for the NPs and NRs are compiled in Table S1 (ESI).† Note that there is no orientation-dependent terms in the CG force field of TiO2 NRs, because we did not coarse-grain a NR into a single ellipsoid, and the NR orientation dependences were encapsulated into the simple Lennard-Jones-type CG force field between CG beads that takes potential energy surfaces of the four NR stacking types listed above into account. The CG pair potential between P3HT and TiO2 CG beads was obtained using a mixing rule, due to the compatible CG particle sizes. To examine the reliability of the CG potential between P3HT and TiO2 CG particles, two separate simulations were performed to compare the RDFs of P3HT monomers surrounding a TiO2 NP (see insets to Fig. S2, ESI†) from the CG model potential and AMD simulations. The RDF determined by the CG potential for P3HT monomers surrounding TiO2 NPs was in excellent agreement with that from AMD simulations (Fig. S2, ESI†). Subsequent CGMD simulations of P3HT:TiO2 blends employed the MD package DL_POLY_4 (ref. 37) using the Nosé–Hoover thermostat and barostat. The system temperature and pressure were set at 423 K and 1 atm; a large time step (5–10 fs) was used in the CG simulations (cf. 1–2 fs in AMD), and all the boundaries were periodic.
3 Results and discussions
Three-dimensional morphologies of the polymer and nanocrystals
Fig. 2a displays the 3D morphologies of P3HT:TiO2 NP (upper panel) and NR (lower panel) blends prepared at a blending ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 after CG molecular dynamics (CGMD) simulation of the thermal annealing at 423 K for 20 ns; Fig. S3 (ESI)† presents the morphologies obtained at other blending ratios. We observe the formation of interpenetrating networks between the polymer and nanocrystal phases, a critical feature for polymer/inorganic nanocrystal hybrid cells if they are to generate a photocurrent. Fig. 2b and c display the organization of the polymer (Fig. 2b) and nanocrystal (Fig. 2c) units in P3HT:TiO2 NP (upper panel) and NR (lower panel) blends prepared at a blending ratio of 1
1 after CG molecular dynamics (CGMD) simulation of the thermal annealing at 423 K for 20 ns; Fig. S3 (ESI)† presents the morphologies obtained at other blending ratios. We observe the formation of interpenetrating networks between the polymer and nanocrystal phases, a critical feature for polymer/inorganic nanocrystal hybrid cells if they are to generate a photocurrent. Fig. 2b and c display the organization of the polymer (Fig. 2b) and nanocrystal (Fig. 2c) units in P3HT:TiO2 NP (upper panel) and NR (lower panel) blends prepared at a blending ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In Fig. 2b, the self-alignment of polymer chains is evident for both the P3HT:TiO2 NP and NR blends. For mesoscale simulations, such polymer self-alignment can be viewed as polymer crystallization. Close examination of Fig. 2b reveals that the self-alignment (i.e., the degree of crystallinity) of the polymer units in the P3HT:TiO2 NR blend was greater than that in the P3HT:TiO2 NP blend. Hence, our simulations indicate that the nanocrystal's shape can have a significant impact on the polymer's organization. Fig. 2c displays the organization of the TiO2 NPs (upper panel) and NRs (lower panel); we observe nanocrystal aggregation and the existence of percolation pathways through the simulation cells in both NP and NR blends. Notably, the nanocrystal organization determined from our CGMD simulations resemble those from electron tomography experiments of polymer/TiO2, polymer/CdSe and polymer/ZnO nanocrystal hybrid cells;14–16 therefore, the nanocrystal organization revealed in the present study appears to be generic for all nanocrystals in polymer/inorganic nanocrystal hybrid cells.
1. In Fig. 2b, the self-alignment of polymer chains is evident for both the P3HT:TiO2 NP and NR blends. For mesoscale simulations, such polymer self-alignment can be viewed as polymer crystallization. Close examination of Fig. 2b reveals that the self-alignment (i.e., the degree of crystallinity) of the polymer units in the P3HT:TiO2 NR blend was greater than that in the P3HT:TiO2 NP blend. Hence, our simulations indicate that the nanocrystal's shape can have a significant impact on the polymer's organization. Fig. 2c displays the organization of the TiO2 NPs (upper panel) and NRs (lower panel); we observe nanocrystal aggregation and the existence of percolation pathways through the simulation cells in both NP and NR blends. Notably, the nanocrystal organization determined from our CGMD simulations resemble those from electron tomography experiments of polymer/TiO2, polymer/CdSe and polymer/ZnO nanocrystal hybrid cells;14–16 therefore, the nanocrystal organization revealed in the present study appears to be generic for all nanocrystals in polymer/inorganic nanocrystal hybrid cells.
 | ||
Fig. 2 (a) 3D Morphologies of P3HT:TiO2 NP (upper panel) and NR (lower panel) blends; P3HT chains and nanocrystals are colored red and blue, respectively. Organization of (b) P3HT chains and (c) nanocrystals in P3HT:TiO2 NP (upper panel) and NR (lower panel) blends with blending ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. 1. | ||
Nanocrystal shapes and polymer crystallinity
To quantitatively analyze the polymer organization in P3HT:TiO2 nanocrystal hybrid cells, we employed a spatial-discretization (SD) scheme that we had developed earlier for studying polymer/fullerene blends.29,30 In this scheme, the entire simulation cell was discretized into cubes (or “pixels”) having sizes (0.7 nm) comparable with those of the CG particles of P3HT and TiO2. Fig. S4 (ESI)† displays the simulation cell after SD processing. Next, we coarsed several P3HT “pixels” displayed in Fig. S4† into one sub-domain and computed the local orientational order parameter Sj for P3HT monomers within the jth sub-domain, using the equation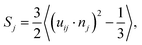 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; we found that the degree of crystallinity of the P3HT:TiO2 NR blend was substantially higher than that of the P3HT:TiO2 NP blend. Therefore, our study reveals that the nanocrystal's shape can significantly affect the polymer's organization; with suitable design of the nanocrystal's shape and size, it should be possible to enhance the degree of crystallinity of the polymer phase, thereby improving hole transport.
1; we found that the degree of crystallinity of the P3HT:TiO2 NR blend was substantially higher than that of the P3HT:TiO2 NP blend. Therefore, our study reveals that the nanocrystal's shape can significantly affect the polymer's organization; with suitable design of the nanocrystal's shape and size, it should be possible to enhance the degree of crystallinity of the polymer phase, thereby improving hole transport.
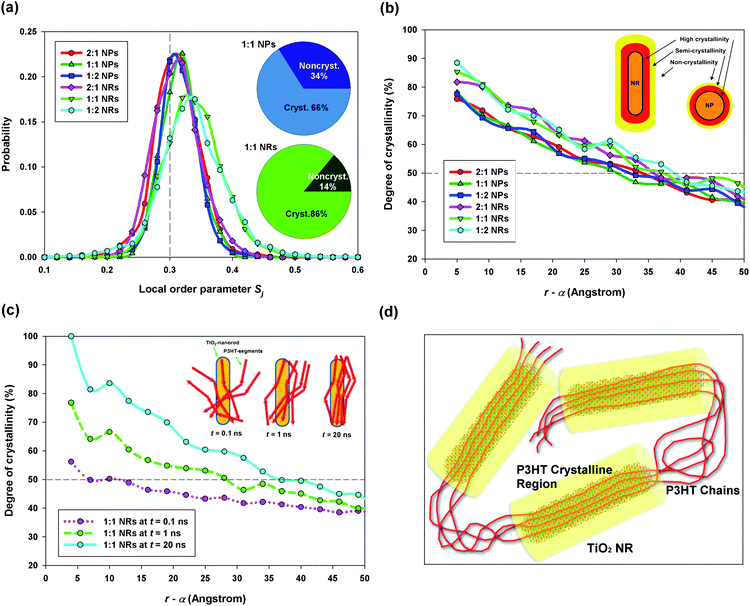 | ||
Fig. 3 (a) Probability distributions of the local order parameter Sj for the P3HT:TiO2 NP/NR blends; inset: degrees of crystallinity of the P3HT:TiO2 NP (upper panel) and P3HT:TiO2 NR (lower panel) blends prepared at blending ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. (b) Radial distributions of the degrees of crystallinity of P3HT near TiO2 NPs and NRs; α: radius of TiO2 NP or NR. (c) Time lapse of the distribution of the degree of axial alignment of P3HT chains with a TiO2 NR. (d) Schematic depiction of NR-assisted polymer crystallization. 1. (b) Radial distributions of the degrees of crystallinity of P3HT near TiO2 NPs and NRs; α: radius of TiO2 NP or NR. (c) Time lapse of the distribution of the degree of axial alignment of P3HT chains with a TiO2 NR. (d) Schematic depiction of NR-assisted polymer crystallization. | ||
Next, we computed the radial distribution of the degree of crystallinity of P3HT—that is, the degree of crystallinity of P3HT within a shell (spherical for NP; cylindrical for NR) between r and r + Δr, where r is the distance from the TiO2 NP/NR center and Δr is the thickness of the shell (here, we set Δr at 5 Å). Fig. 3b displays the radial distributions of the degree of crystallinity of P3HT for both TiO2 NPs and NRs. Note that in the horizontal axis of Fig. 3b and c, we used r − α instead of r, where α denotes the radius of NP/NR. Hence, r − α refers to the distance from the NP/NR surface. It is clear that P3HT chains tend to crystallize close to the nanocrystal surface, with the degrees of crystallinity of the polymer in the P3HT:TiO2 NR blends being generally higher than those in the P3HT:TiO2 NP blends. Such a distribution of polymer crystallinity can be explained by considering heterogeneous nucleation—namely, the polymer–nanocrystal interface providing heterogeneous nucleation sites for polymer crystallization.
We attribute the higher degrees of crystallinity of P3HT in P3HT:TiO2 NR blends to the alignment of P3HT chains along the axial direction of the NRs. For verification, we defined the radial NR axial orientational order parameter σk(r) for P3HT chains as
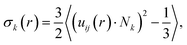 | (2) |
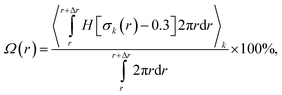 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 P3HT:TiO2 NR blend. Clearly, as the annealing process continued, Ω(r) became increasingly large—particularly in the region near the NR surface. The inset of Fig. 3c provides a schematic representation of this phenomenon, with the polymer units beginning to align themselves with the axial direction of the NRs. Similar phenomena are unlikely for NPs because of their spherical symmetry. Furthermore, by comparing Ω(r), at a t value of 20 ns (blue line in Fig. 3c), with the radial distribution of the degree of crystallinity of P3HT (Fig. 3b, also computed at t = 20 ns), we find that the crystallization of P3HT was correlated directly to the alignment of polymer chains along the NR's axial direction. Fig. 3d presents a schematic representation of the roles played by the TiO2 NRs during the organization of the P3HT polymer units: here, the NRs serve as “templates” for P3HT crystallization. The P3HT chains close to the NR surface tended to align along the NR axial direction; therefore, highly crystallized regions (cylindrical volume highlighted in yellow in Fig. 3d) of P3HT were formed surrounding the NRs, with the P3HT chains aligned along the NR axis. A recent experimental study has revealed P3HT chain alignment with TiO2 rod axis;39 therefore, our observations are in excellent agreement with recent experiments. Hence, by selecting a one-dimensional, anisotropic nanostructural material (e.g., a nanowire or NR), having a suitable size, as the electron acceptor material, the polymer's degree of crystallinity can be enhanced substantially, thereby improving the hole mobility of the polymer/inorganic nanocrystal hybrid cell.
1 P3HT:TiO2 NR blend. Clearly, as the annealing process continued, Ω(r) became increasingly large—particularly in the region near the NR surface. The inset of Fig. 3c provides a schematic representation of this phenomenon, with the polymer units beginning to align themselves with the axial direction of the NRs. Similar phenomena are unlikely for NPs because of their spherical symmetry. Furthermore, by comparing Ω(r), at a t value of 20 ns (blue line in Fig. 3c), with the radial distribution of the degree of crystallinity of P3HT (Fig. 3b, also computed at t = 20 ns), we find that the crystallization of P3HT was correlated directly to the alignment of polymer chains along the NR's axial direction. Fig. 3d presents a schematic representation of the roles played by the TiO2 NRs during the organization of the P3HT polymer units: here, the NRs serve as “templates” for P3HT crystallization. The P3HT chains close to the NR surface tended to align along the NR axial direction; therefore, highly crystallized regions (cylindrical volume highlighted in yellow in Fig. 3d) of P3HT were formed surrounding the NRs, with the P3HT chains aligned along the NR axis. A recent experimental study has revealed P3HT chain alignment with TiO2 rod axis;39 therefore, our observations are in excellent agreement with recent experiments. Hence, by selecting a one-dimensional, anisotropic nanostructural material (e.g., a nanowire or NR), having a suitable size, as the electron acceptor material, the polymer's degree of crystallinity can be enhanced substantially, thereby improving the hole mobility of the polymer/inorganic nanocrystal hybrid cell.
Nanocrystal shape and nanocrystal organization
The organization of nanocrystals has a critical effect on electron transport after exciton dissociation and subsequent charge separation at the polymer–nanocrystal interface. The bottleneck for electron transport within the nanocrystal phase is electron hopping between neighboring nanocrystals; therefore, the number of hopping events required for electron transport within a nanocrystal domain is positively correlated with the electron mobility within the nanocrystal phase. Hence, we can use the number of inter-nanocrystal junctions per nanocrystal domain to estimate the number of hopping events required for electron transport. The number of inter-nanocrystal junctions per domain readily correlates with the number of nanocrystals per domain, which can be estimated by dividing the total number of nanocrystals by the number of nanocrystal domains. Fig. 4a displays a time lapse of the number of TiO2 NP/NR domains obtained at different P3HT:TiO2 blending ratios. We observe that all of the blends reached equilibrium after 20 ns of annealing simulation. Aggregation of the TiO2 NPs and NRs was evident because the number of NP/NR domains underwent a significant decrease during the annealing process. At the beginning of each of our simulations, none of the TiO2 NPs/NRs were in contact; therefore, the number of TiO2 NP/NR domains at t = 0 ns was equal to the total number of TiO2 NPs/NRs in the blends. Therefore, we could estimate the average number of nanocrystals per nanocrystal domain at the end of each simulation. At a blending ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, Fig. 4a reveals that 46.7 and 15.7 TiO2 NPs and NRs, respectively, were present per domain. Therefore, there were many more inter-nanocrystal junctions in the polymer/NP blends than in the polymer/NR blends. As displayed schematically in Fig. 4b, the number of electron hopping events required for electron transport among the NPs was greater than that for the NRs; hence, our study reveals that, due to their long length in one dimension, NRs can effectively minimize the number of electron hopping events required for transporting electrons, thereby promoting electron transport in polymer/inorganic nanocrystal hybrid cells.
1, Fig. 4a reveals that 46.7 and 15.7 TiO2 NPs and NRs, respectively, were present per domain. Therefore, there were many more inter-nanocrystal junctions in the polymer/NP blends than in the polymer/NR blends. As displayed schematically in Fig. 4b, the number of electron hopping events required for electron transport among the NPs was greater than that for the NRs; hence, our study reveals that, due to their long length in one dimension, NRs can effectively minimize the number of electron hopping events required for transporting electrons, thereby promoting electron transport in polymer/inorganic nanocrystal hybrid cells.
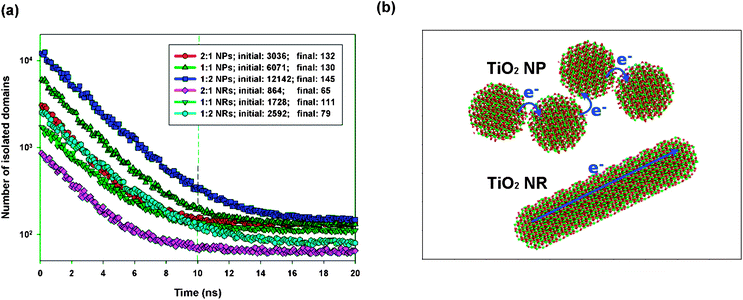 | ||
| Fig. 4 (a) Time lapse of the number of NP/NR domains. (b) Schematic representation of electron transport in NP (upper panel) and NR (lower panel) domains. | ||
Domain characteristic width and specific interfacial area
Our simulations have revealed that polymer/NR blends have superior polymer crystallinity and fewer inter-nanocrystal junctions than those of polymer/NP blends; as a result, we would predict that electron and hole transport in polymer/NR blends should be superior to that in polymer/NP blends. In addition to polymer/nanocrystal organizations and their implication in charge carrier transport, mesoscale, morphological properties correlated with domain sizes and donor–acceptor interfacial area are also critical for charge carrier transport, exciton dissociation, and subsequent photocurrent generation in polymer/nanocrystal hybrid cells. Recent device-oriented, theoretical studies have indicated that large domain size leads to high charge mobilities,40 high current density, and low exciton dissociation efficiencies.41 However, the initial configurations for these mesoscale theoretical calculations were not derived from experiments or from direct molecular simulations. Hence, based on the morphologies directly obtained from CGMD simulations, we wished to investigate the effects of nanocrystal shape on the morphological properties that are correlated with exciton dissociation rates and charge separation probabilities—namely, (i) the characteristic length-scale that excitons must travel in the polymer phase to reach the polymer–nanocrystal interface and (ii) the specific interfacial area of the polymer–nanocrystal interface. The characteristic length-scale for exciton diffusion can be evaluated by computing the characteristic pathway width (w) of polymer/nanocrystal phases through autocorrelation length (ACR) analysis of the polymer phase.42 The details of the ACR analysis employed in the present study are provided in the ESI.†
Fig. 5a displays the characteristic widths w of both the P3HT polymer and the TiO2 nanocrystals phases at different blending ratios and various nanocrystal shapes. We observe that the values of wP3HT in the P3HT:TiO2 NR blends were always larger than those in the P3HT:TiO2 NP blends. Therefore, the chance of charge recombination in P3HT:TiO2 NR blends was greater than that in NP blends. We note, however, that the maximum value of wP3HT in the NR blend was 21 nm (blending ratio: 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1); therefore, the distance one exciton must travel to meet the nearest polymer–nanocrystal interface was approximately 11 nm—within the typical diffusion length of an exciton in P3HT. In addition, we also found that the values of wTiO2 in P3HT:TiO2 NR blends were larger than those in P3HT:TiO2 NP blends; hence, the microstructures in the NR blends were, in general, coarser than those in NP blends.
1); therefore, the distance one exciton must travel to meet the nearest polymer–nanocrystal interface was approximately 11 nm—within the typical diffusion length of an exciton in P3HT. In addition, we also found that the values of wTiO2 in P3HT:TiO2 NR blends were larger than those in P3HT:TiO2 NP blends; hence, the microstructures in the NR blends were, in general, coarser than those in NP blends.
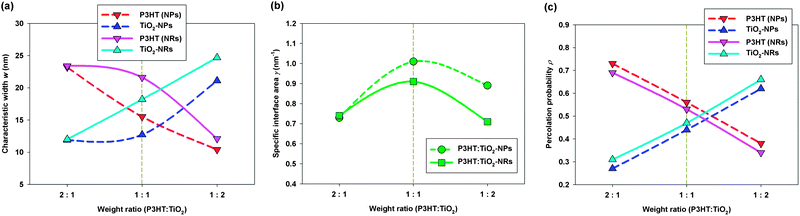 | ||
| Fig. 5 Morphological properties of P3HT:TiO2 NP/NR blends at various blending ratios, determined from the SD scheme: (a) characteristic width w; (b) specific interfacial area γ; (c) percolation probability ρ. The optimal blending ratios for P3HT:TiO2 NP/NR blends, determined experimentally,14 are highlighted with gold dashed lines. | ||
Next, we examined the specific interfacial areas (γ) of the polymer/nanocrystal interfaces. Fig. 5b displays the values of γ plotted with respect to the blending ratio and the nanocrystal's shape. We found that the specific interfacial areas of the P3HT:TiO2 NP blends were, in general, greater than those in the NR blends, suggesting that the microstructures in the P3HT:TiO2 NR blends are “coarser” than those in the P3HT:TiO2 NP blends—in agreement with our characteristic width analyses. Because NRs are long in one dimension and rigid, they cannot form NR domains with domain shapes that meander, such as those of NPs with similar diameters, as displayed schematically in Fig. 4b. Hence, our results indicate that the anisotropy of NRs leads to less meandering domains and coarser polymer/nanocrystal microstructures in comparison with those obtained with NPs. Therefore, we reveal that for similar particle/rod diameters, polymer/NP blends should have slightly superior exciton dissociation and charge separation rates, and lower charge carrier mobilities than those of polymer/NR blends; these observations are in good agreement with recent photocarrier dynamics experiments.14
Based on our analyses, we believe that, when used as electron acceptor materials in polymer/inorganic nanocrystal hybrid cells, one-dimensional nanocrystals, such as NRs, have several advantages over zero-dimensional nanocrystals, such as NPs. The long cylindrical shape of a NR can effectively promote polymer crystallinity and, thereby, facilitate hole transport. In addition, because the specific interfacial area is inversely proportional to the rod diameter, NRs can minimize electron hopping events between neighboring NRs by increasing the rod length, thereby promoting electron transport, while maintaining a rod diameter sufficiently small to maintain a high specific interfacial area for efficient exciton dissociation. For zero-dimensional nanocrystals, such as NPs, the specific interfacial area is inversely proportional to the particle diameter; therefore, it is impossible to increase the particle size (to minimize the number of inter-nanocrystal junctions) while maintaining a high specific interfacial area. For example, to eliminate the NP inter-nanocrystal junctions displayed schematically in Fig. 4b, the particle diameter should be four times larger; this change will, however, result in the specific interfacial area of the NP blend becoming four times smaller. On the other hand, by using the NRs displayed in Fig. 4b, it should be possible to eliminate electron hopping while maintaining a high specific interfacial area. Hence, relative to zero-dimensional NPs, one-dimensional NRs provide a better balance between electron transport and exciton dissociation by promoting polymer crystallinity and minimizing the number of inter-nanocrystal junctions, while maintaining a reasonably high specific interfacial area.
Optimal polymer/nanocrystal blending ratios
We have found a correlation between the morphological properties and the donor–acceptor blending ratio. Fig. 5b reveal that, regardless of the nanocrystal's shape, the blending ratio with a maximum specific interfacial area (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) overlaps with the optimal blending ratio found experimentally. Because the specific interfacial area correlates positively with the degrees of exciton dissociation and charge separation, our results indicate that, for polymer/inorganic nanocrystal hybrid cells, blends with the optimal blending ratio must have a maximum specific interfacial area to facilitate the generation of free electrons and holes. It must be noted that electron–hole recombination also takes place at donor–acceptor interface;43 therefore, large specific interfacial area also increases the charge carrier recombination probability. Since our simulation results show that blends with the highest specific interfacial area correspond to the blending ratio giving the optimal device performance, it is highly likely that charge carrier generation prevails charge carrier recombination. Hence, a mesoscale charge carrier transport simulation such as random walk numerical simulation (RWNS)44 based on the morphologies generated from CGMD in the present study would be helpful in clarifying the complicated interplay between charge carrier generation/recombination.
1) overlaps with the optimal blending ratio found experimentally. Because the specific interfacial area correlates positively with the degrees of exciton dissociation and charge separation, our results indicate that, for polymer/inorganic nanocrystal hybrid cells, blends with the optimal blending ratio must have a maximum specific interfacial area to facilitate the generation of free electrons and holes. It must be noted that electron–hole recombination also takes place at donor–acceptor interface;43 therefore, large specific interfacial area also increases the charge carrier recombination probability. Since our simulation results show that blends with the highest specific interfacial area correspond to the blending ratio giving the optimal device performance, it is highly likely that charge carrier generation prevails charge carrier recombination. Hence, a mesoscale charge carrier transport simulation such as random walk numerical simulation (RWNS)44 based on the morphologies generated from CGMD in the present study would be helpful in clarifying the complicated interplay between charge carrier generation/recombination.
In addition to specific interfacial area, percolation pathways for the electron donor–acceptor phases are also necessary for subsequent electron–hole transport to electrodes. To quantify the percolation quality of each phase, we defined the percolation probability ρ as the volume fraction of each phase that could percolate through the simulation cell. Fig. 5c plots the percolation probabilities ρ of the P3HT and TiO2 nanocrystal phases with respect to the blending ratio and the nanocrystal's shape. We observed that the value of ρP3HT decreased significantly upon increasing the TiO2 blending ratio, indicating that more isolated P3HT domains existed and poorer hole transport occurred at higher TiO2 blending ratios. On the other hand, increasing the P3HT blending ratio led to more isolated TiO2 domains and poorer electron transport. Fig. 5c reveals that the values of ρP3HT and ρTiO2 were most similar at the optimal blending ratio reported from previous experiments (i.e., a P3HT:TiO2 blending ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). This result can be explained by considering the balance between charge carrier trapping and transport: at blending ratios that lead to high values of ρP3HT (ρTiO2) and low values of ρTiO2 (ρP3HT), despite improved hole (electron) transport, the electron (hole) transport would be hindered as a result of the existence of numerous isolated TiO2 (P3HT) domains. Therefore, our study reveals that, for polymer/inorganic nanocrystal hybrid cells, regardless of the nanocrystal's shape, blends featuring the optimal blending ratio must have the maximum specific interfacial areas and the most-similar donor–acceptor percolation probabilities; these criteria are similar to those of the polymer/fullerene blends that we had investigated previously.29,30
1). This result can be explained by considering the balance between charge carrier trapping and transport: at blending ratios that lead to high values of ρP3HT (ρTiO2) and low values of ρTiO2 (ρP3HT), despite improved hole (electron) transport, the electron (hole) transport would be hindered as a result of the existence of numerous isolated TiO2 (P3HT) domains. Therefore, our study reveals that, for polymer/inorganic nanocrystal hybrid cells, regardless of the nanocrystal's shape, blends featuring the optimal blending ratio must have the maximum specific interfacial areas and the most-similar donor–acceptor percolation probabilities; these criteria are similar to those of the polymer/fullerene blends that we had investigated previously.29,30
4 Conclusion
Based on structural properties and potential energy surfaces determined from AMD simulations of smaller systems, we have constructed CG models for P3HT:TiO2 nanocrystal hybrid blends featuring nanocrystals with two types of shapes: NPs and NRs. With such a CG model, we could simulate the thermal annealing processes of blends at various P3HT:TiO2 nanocrystal blending ratios, with system sizes comparable with those found experimentally. We investigated the effect of the nanocrystal shape on the polymer/nanocrystal organization and polymer–nanocrystal interfaces—and, therefore, on hole–electron transport and exciton dissociation/charge separation, respectively. Our results indicate that one-dimensional nanocrystals, such as NRs, can promote polymer crystallinity as a result of preferential polymer alignment along the NR axis, thereby enhancing hole transport. Hence, the present study reveals the possibility of morphology control by fine-tuning nanocrystal shapes. In addition, the one-dimensional features of NRs make it possible to minimize the number of inter-nanocrystal junctions to promote electron transport, while retaining a reasonably high specific interfacial area for efficient exciton dissociation. Finally, we determined the morphological criteria influencing the optimal blending ratios in polymer/inorganic hybrid cells—namely, the highest specific interfacial area to maximize exciton dissociation and the most-similar donor–acceptor percolation probabilities to balance electron–hole transport. This study demonstrates that multiscale molecular simulations and subsequent morphological evaluations can provide comprehensive insight into the mesoscale morphologies of polymer/inorganic blends—features that are difficult to characterize experimentally—and, therefore, it has the potential to aid the development of more-efficient polymer/inorganic nanocrystal hybrid cells.Acknowledgements
We thank for the Research Center for Applied Science, Academia Sinica, and the National Science Council of Taiwan (project no. NSC 99-2112-M-001-004-MY3) for financial support and the National Center for High Performance Computing for computational support.Notes and references
- J. Liu, T. Tanaka, K. Sivula, A. P. Alivisatos and J. M. J. Fréchet, J. Am. Chem. Soc., 2004, 126, 6550 CrossRef CAS.
- Y. Liu, S. R. Scully, M. D. McGehee, J. Liu, C. K. Luscombe, J. M. J. Fréchet, S. E. Shaheen and D. S. Ginley, J. Phys. Chem. B, 2006, 110, 3257 CrossRef CAS.
- I. Gur, N. A. Fromer, C. P. Chen, A. G. Kanaras and A. P. Alivisatos, Nano Lett., 2007, 7, 409 CrossRef CAS.
- C. Goh, S. R. Scully and M. D. McGehee, J. Appl. Phys., 2007, 101, 114503 CrossRef.
- C. Y. Liu, Z. C. Holman and U. R. Kortshagen, Nano Lett., 2009, 9, 449 CrossRef CAS.
- B. Kippelen and J.-L. Brédas, Energy Environ. Sci., 2009, 2, 251 CAS.
- C. M. Rodd and R. Agarwal, Nano Lett., 2011, 11, 3460 CrossRef CAS.
- D. Herrmann, S. Niesar, C. Scharsich, A. Köhler, M. Stutzmann and E. Riedle, J. Am. Chem. Soc., 2011, 133, 18220 CrossRef CAS.
- K. M. Coakley, Y. Liu, M. D. McGehee, K. L. Frindell and G. D. Stucky, Adv. Funct. Mater., 2003, 13, 301 CrossRef CAS.
- I. Gur, N. A. Fromer and A. P. Alivisatos, J. Phys. Chem. B, 2006, 110, 25543 CrossRef CAS.
- Y. Y. Lin, T. H. Chu, S. S. Li, C. H. Chuang, C. H. Chang, W. F. Su, C. P. Chang, M. W. Chu and C. W. Chen, J. Am. Chem. Soc., 2009, 131, 3644 CrossRef CAS.
- S. Dayal, M. O. Reese, A. J. Ferguson, D. S. Ginley, G. Rumbles and N. Kopidakis, Adv. Funct. Mater., 2010, 20, 2629 CrossRef CAS.
- W. U. Huynh, J. J. Dittmer and A. P. Alivisatos, Science, 2002, 295, 2425 CrossRef CAS.
- S. S. Li, C. P. Chang, C. C. Lin, Y. Y. Lin, C. H. Chang, J. R. Yang, M. W. Chu and C. W. Chen, J. Am. Chem. Soc., 2011, 133, 11614 CrossRef CAS.
- J. C. Hindson, Z. Saghi, J.-C. Hernandez-Garrido, P. A. Midgley and N. C. Greenham, Nano Lett., 2011, 11, 904 CrossRef CAS.
- S. D. Oosterhout, M. M. Wienk, S. S. van Bavel, R. Thiedmann, L. J. A. Koster, J. Gilot, J. Loos, V. Schmidt and R. A. J. Janssen, Nat. Mater., 2009, 8, 818 CrossRef CAS.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812 CrossRef CAS.
- L. Monticelli, S. K. Kandasamy, X. Periole, R. G. Larson, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2008, 4, 819 CrossRef CAS.
- W. Tschöp, K. Kremer, J. Batoulis, T. Bürger and O. Hahn, Acta Polym., 1998, 49, 61 CrossRef.
- D. Reith, H. Meyer and F. Müller-Plathe, Macromolecules, 2001, 34, 2335 CrossRef CAS.
- F. Müller-Plathe, ChemPhysChem, 2002, 3, 754 CrossRef.
- E. S. Boek, J. T. Padding, W. K. den Otter and W. J. Briels, J. Phys. Chem. B, 2005, 109, 19851 CrossRef CAS.
- P. Carbone, F. Negri and F. Müller-Plathe, Macromolecules, 2007, 40, 7044 CrossRef CAS.
- W. G. Noid, J. W. Chu, G. S. Ayton, V. Krishna, S. Izvekov, G. A. Voth, A. Das and H. C. Andersen, J. Chem. Phys., 2008, 128, 244114 CrossRef CAS.
- P. Carbone, H. A. K. Varzaneh, X. Chen and F. Müller-Plathe, J. Chem. Phys., 2008, 128, 064904 CrossRef.
- C. Peter and K. Kremer, Soft Matter, 2009, 5, 4357 RSC.
- D. M. Huang, R. Faller, K. Do and A. J. Moulé, J. Chem. Theory Comput., 2010, 6, 526 CrossRef CAS.
- C. K. Lee, C. C. Hua and S. A. Chen, Macromolecules, 2011, 44, 320 CrossRef CAS.
- C. K. Lee, C. W. Pao and C. W. Chu, Energy Environ. Sci., 2011, 4, 4124 CAS.
- C. K. Lee and C. W. Pao, J. Phys. Chem. C, 2012, 116, 12455 CAS.
- R. L. Henderson, Phys. Lett. A, 1974, 49, 197 CrossRef.
- L. Belloni, J. Phys.: Condens. Matter, 2000, 12, 549 CrossRef.
- J. A. Anta and S. Lago, J. Chem. Phys., 2002, 116, 10514 CrossRef CAS.
- M. E. Johnson, T. Head-Gordon and A. A. Louis, J. Chem. Phys., 2007, 126, 144509 CrossRef.
- C. K. Lee, C. C. Hua and S. A. Chen, J. Chem. Phys., 2010, 133, 064902 CrossRef.
- C. K. Lee and C. C. Hua, J. Chem. Phys., 2010, 132, 224904 CrossRef.
- I. T. Todorov and W. Smith, The DL_POLY_4 User Manual, STFC Daresbury Laboratory, Daresbury, 2011 Search PubMed.
- P. J. Collings and M. Hird, Introduction to Liquid Crystals, Taylor & Francis, Bristol, 1997 Search PubMed.
- Z. Sun, J. Li, C. Liu, S. Yang and F. Yan, Adv. Mater., 2011, 23, 3648 CrossRef CAS.
- L. J. A. Koster, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205318 CrossRef.
- B. P. Lyons, N. Clarke and C. Groves, Energy Environ. Sci., 2012, 5, 7657 CAS.
- J. S. Moon, J. K. Lee, S. Cho, J. Byun and A. J. Heeger, Nano Lett., 2009, 9, 230 CrossRef CAS.
- J. Bisquert and G. Garcia-Belmonte, J. Phys. Chem. Lett., 2011, 2, 1950 CrossRef CAS.
- J. P. Gonzalez-Vazquez, V. Morales-Flórez and J. A. Anta, J. Phys. Chem. Lett., 2012, 3, 386 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2ee23372j |
| This journal is © The Royal Society of Chemistry 2013 |
