Phase stability, electrochemical stability and ionic conductivity of the Li10±1MP2X12 (M = Ge, Si, Sn, Al or P, and X = O, S or Se) family of superionic conductors†
Shyue Ping
Ong
a,
Yifei
Mo
a,
William Davidson
Richards
a,
Lincoln
Miara
b,
Hyo Sug
Lee
b and
Gerbrand
Ceder
*a
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, 77 Massachusetts Ave, Cambridge, MA 02139, USA. E-mail: gceder@mit.edu
bSamsung Advanced Institute of Technology, 1 Cambridge Center, Suite 702, Cambridge, MA 02142, USA
First published on 2nd October 2012
Abstract
We present an investigation of the phase stability, electrochemical stability and Li+ conductivity of the Li10±1MP2X12 (M = Ge, Si, Sn, Al or P, and X = O, S or Se) family of superionic conductors using first principles calculations. The Li10GeP2S12 (LGPS) superionic conductor has the highest Li+ conductivity reported to date, with excellent electrochemical performance demonstrated in a Li-ion rechargeable battery. Our results show that isovalent cation substitutions of Ge4+ have a small effect on the relevant intrinsic properties, with Li10SiP2S12 and Li10SnP2S12 having similar phase stability, electrochemical stability and Li+ conductivity as LGPS. Aliovalent cation substitutions (M = Al or P) with compensating changes in the Li+ concentration also have a small effect on the Li+ conductivity in this structure. Anion substitutions, however, have a much larger effect on these properties. The oxygen-substituted Li10MP2O12 compounds are predicted not to be stable (with equilibrium decomposition energies >90 meV per atom) and have much lower Li+ conductivities than their sulfide counterparts. The selenium-substituted Li10MP2Se12 compounds, on the other hand, show a marginal improvement in conductivity, but at the expense of reduced electrochemical stability. We also studied the effect of lattice parameter changes on the Li+ conductivity and found the same asymmetry in behavior between increases and decreases in the lattice parameters, i.e., decreases in the lattice parameters lower the Li+ conductivity significantly, while increases in the lattice parameters increase the Li+ conductivity only marginally. Based on these results, we conclude that the size of the S2− is near optimal for Li+ conduction in this structural framework.
Broader contextSolid lithium superionic conductors exhibit good safety and stability, and are promising to replace organic liquid electrolytes in lithium-ion batteries. The current state-of-the-art Li10GeP2S12 superionic conductor has the highest conductivity ever achieved among the solid lithium electrolytes of 12 mS cm−1 at room temperature and excellent electrochemical performance. In this work, we attempt to address two key limitations of Li10GeP2S12, namely the high cost of germanium and its air and moisture sensitive sulfide-based chemistry, by studying the phase stability, electrochemical stability and Li+ conductivity of the Li10±1MP2X12 family of superionic conductors (M = Ge, Si, Sn, Al or P, and X = O, S or Se) using first principles calculations. We find that the first limitation can be addressed by substituting relatively cheap silicon or tin for germanium in Li10GeP2S12, with limited impact on stability and conductivity. However, the second limitation cannot be easily addressed by substituting oxide-based chemistry for sulfide-based chemistry; Li10MP2O12 compounds are predicted to be significantly less stable and have lower conductivity than their sulfide counterparts. We also quantify the effect of ion substitutions, lattice parameter changes and Li concentrations on various electrochemical properties, which provides a useful insight into the optimization of LGPS and other similar materials. |
Introduction
The continued drive for high performance lithium-ion batteries has imposed stricter requirements on the electrolyte materials.1 Solid electrolytes comprising lithium superionic conductor materials exhibit good safety and stability, and are promising to replace current organic liquid electrolytes.2–5 However, one major limitation in the application of Li-ion conductors is that their typical conductivity is less than 10−4 S cm−1 at room temperature.In September 2011, Kamaya et al. reported a new Li superionic conductor Li10GeP2S12 (LGPS), which has the highest conductivity ever achieved among the solid lithium electrolytes of 12 mS cm−1 at room temperature (comparable conductivity with liquid electrolytes), and outstanding electrochemical performance in Li-ion batteries.6 The high conductivity in LGPS is attributed to the fast diffusion of Li+ in its crystal structural framework (see Fig. 1), which consists of (Ge0.5P0.5)S4 tetrahedra, PS4 tetrahedra, LiS6 octahedra, and LiS4 tetrahedra. Kamaya et al. proposed that diffusion in LGPS occurs along one-dimensional (1D) pathways along the c-axis.6 The authors also proposed that Li atoms in LiS4 tetrahedra enable fast diffusion along the c-direction, while Li atoms in LiS6 octahedra are not active for diffusion. This hypothetical diffusion mechanism in LGPS has been inferred from the large anisotropic thermal factors and the Li disorder in the 1D channels.
Earlier, we investigated the phase stability, electrochemical stability and Li+ conductivity of LGPS using first principles techniques.7 We find that LGPS is a metastable phase in the calculated Li–Ge–P–S phase diagram. We also find that LGPS is not stable against reduction by lithium at low voltage or extraction of Li with decomposition at high voltage. Together with the calculated band gap of 3.6 eV, these predictions suggest that the observed electrochemical window of >5 V for this material is likely the result of a passivation phenomenon, where either Li2S or P2S5 is formed as a decomposition product. Furthermore, while ab initio molecular dynamics (MD) simulations confirm fast Li+ diffusion in the 1D diffusion channel along the c-direction, they also predict two additional diffusion pathways in the a–b plane. Though diffusion in the a–b plane is not as facile as in the c-direction, it nonetheless contributes to the overall performance of the material. A later work by Adams and Prasada Rao8 using classical MD simulations with a force field based on Morse-type interactions derived from bond valence parameters similarly found weakly anisotropic diffusion in LGPS. In practice, diffusion along more than one dimension is necessary to obtain Li transport over reasonable distances.9
Despite its ground-breaking Li+ conductivity and excellent electrochemical performance, LGPS still suffers from two significant obstacles to its adoption as a solid-electrolyte material. First, there is a practical matter of the use of relatively rare and expensive germanium in LGPS, which would limit large-scale application of the material. Second, sulfide-based compounds tend to be air and moisture sensitive, which could pose problems for cost-effective synthesis and application. These limitations of LGPS motivate us to look for other compounds in the same structural framework that can achieve a better balance between electrochemical performance, cost and other properties.
In this work, we investigate the phase stability, electrochemical stability and Li+ conductivity of the Li10±1MP2X12 (LMPX) family of superionic conductors, where M = Ge, Si, Sn, Al or P, and X = O, S or Se, using first principles calculations. We seek to elucidate the effect of cation and anion substitutions on these three key properties. We include aliovalent cation substitutions to study the effect of the Li+ concentration on Li+ conductivity. We also study the effect of lattice parameters on Li+ conductivity in the LGPS structural framework.
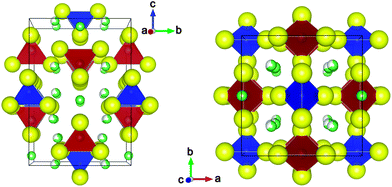 | ||
| Fig. 1 Crystal structure of Li10GeP2S12. Large yellow atoms: S; small green atoms: fully occupied Li sites; small green-white atoms: partially occupied Li sites; red tetrahedra: (Ge0.5P0.5)S4; and blue tetrahedra: PS4. | ||
Methods
All calculations in this work were performed using the Vienna Ab initio Simulation Package (VASP)10 within the projector augmented-wave approach.11 Given the vastly different requirements of the various techniques used in this paper, we have carefully selected the appropriate functionals and methods for each technique based on accuracy and computational cost considerations, as outlined in the following sections.Phase stability
The phase stability of the various LMPX structures was investigated by constructing the relevant Li–M–P–X computational phase diagrams.12,13 To ensure a good coverage of the phase space, we not only included all known Li–M–P–X compounds in the Inorganic Crystal Structure Database,14 but also included structures derived from the following sources:(1) All LixPySz compounds compiled by Holzwarth et al.15
(2) All possible inter-substitutions of existing Li–M–X and Li–P–X compounds. For example, the Li–P–O phase space is generally more well-studied than the Li–P–S and Li–P–Se phase space. In fact, some of the LixPySz compounds compiled by Holzwarth et al.15 have been obtained by substituting O for S in LixPyOz compounds. We adopted a similar strategy to ensure a good coverage of all the investigated phase spaces, e.g., we performed O for Se and S for Se substitutions to obtain possible Li–P–Se and Li–M–Se phases.
All total energy calculations for phase stability analysis were performed using the Perdew–Burke–Ernzerhof (PBE) generalized-gradient approximation (GGA)16 functional. A k-point density of at least 500/(number of atoms in the unit cell) was used for all computations. All calculations were spin-polarized.
As the refined LGPS structure (P42/nmc) has partial occupancies on Li sites as well as Ge/P sites (see Fig. 1),6 we ordered the arrangement of Li, Ge, and P atoms in LGPS using an electrostatic energy criterion17 using the Python Materials Genomics (pymatgen) analysis code.18 All ions were assigned “idealized” charges based on their valence states, i.e., +1 for Li, +4 for Ge, +5 for P and −2 for S. We then selected 30 structures with the lowest electrostatic energy and relaxed them using density functional theory (DFT). It should be noted that the structure that minimizes the electrostatic energy is not the lowest energy structure based on DFT calculations. While the lowest electrostatic energy ordered structure still has a tetragonal P42/mc space group, the lowest DFT energy structure has a P1 space group with a unit cell that is slightly distorted from the tetragonal cell (see the ESI† for details). The DFT energy of the relaxed P1 structure is approximately 10 meV per atom lower than the DFT energy of the structure that minimizes the electrostatic energy for all the LMPX compounds investigated. Henceforth, we will use the DFT ground state structure of LGPS for the remainder of our analyses. We note that while it is possible that there exist orderings (either for a single unit cell or at larger super cell sizes) that could have lower DFT energies, they are unlikely to be significantly lower in energy. Furthermore, the comparison of phase stability is carried out between materials with similar orderings, and we expect relative phase stability to be well characterized even if the exact lowest energy ordering is not obtained. At temperatures of interest (e.g., room-temperature), the Li+ sites are likely to be disordered, and hence, the structure would have higher symmetry.
All derived isovalent LMPX structures are based on M for Ge and X for S substitution of the DFT ground state structure. For aliovalently substituted structures (Al3+ or P5+ for Ge4+ with corresponding changes in the Li+ concentration), we performed a similar electrostatic ordering of the structure and then performed DFT calculations on the lowest electrostatic energy structure only, i.e., we did not perform DFT calculations on multiple possible orderings, given the significant computational time involved. Only the sulfide versions of the Al and P structures are investigated in this work. Please see the ESI† for details on the relaxed structures.
Electrochemical stability
We assessed the electrochemical stability of the LMPX compounds using two approaches:(1) Intrinsic stability against inert electrodes. We assessed the intrinsic stability of the LMPX solid electrolyte with respect to inert electrodes by calculating the band gap of the material.19 As standard semi-local DFT is known to severely underestimate band gaps, the density of states (DOS) of all LMPX compounds were calculated using the Heyd–Scuseria–Ernzerhof (HSE) screened hybrid functional,20,21 which has been tested to give relatively accurate band gaps for a wide range of materials.22,23 Owing to the relatively high computational expense of HSE over PBE, non-spin-polarized calculations were performed. The bandgap itself is not an exact measure of the electrochemical stability on inert electrodes as its alignment with respect to an external reference potential is not known. It can, however, be considered as an upper bound for the electrochemical window.
(2) Chemical stability against electrodes. We also investigated the chemical stability of the LMPX solid electrolytes against typical electrode materials used in lithium-ion batteries. We constructed the lithium grand potential Li–M–P–X phase diagrams using the method outlined by Ong et al.12,13 Lithium grand potential phase diagrams represent the phase equilibria of a Li–M–P–X system that is open to lithium, which is relevant when the LMPX solid electrolyte is in contact with a reservoir or sink of lithium, as is the case in a lithium battery. The voltage in a battery is the negative of the Li chemical potential. By studying the phase evolution of the Li10±1MP2X12 composition with respect to changing lithium chemical potential (μLi), we can determine the equilibrium phases at μ0Li corresponding to the bulk metallic lithium (anode) and (μ0Li − 5) eV corresponding to a 5 V charged cathode. The equilibrium phases provide insight into how sensitive the Li10±1MP2X12 composition is to lithium insertion or extraction at high and low voltages and whether the phases formed would affect lithium conductivity. We should note that this analysis pertains to only one possible reaction path with the electrodes, i.e., the exchange of Li between the electrolyte and the electrode. In the case of the cathode, other possible reactions involving non-Li species in the cathode material were not investigated.
Li+ diffusivity and conductivity
We investigated the Li+ diffusivity and conductivity in the LMPX materials using ab initio molecular dynamics (AIMD) simulations. The AIMD simulations were performed using the PBE GGA functional.16 To keep the computational cost at a reasonable level, smaller plane wave energy cut-offs of 400 eV, 280 eV and 270 eV were chosen as for oxides, sulfides, and selenides, respectively. A minimal Γ-centered 1 × 1 × 1 k-point grid was used, and all calculations were non-spin-polarized.The AIMD simulations were performed on one unit cell of LMPX. We performed convergence tests on a 2 × 2 × 1 supercell of the original LGPS structure and found that a single unit cell is sufficient to obtain converged diffusivity and conductivity numbers. The volume of the unit cell and the initial position of atoms were obtained from the fully relaxed cells in the phase stability calculations. The integration of Newton's equation is based on the Verlet algorithm implemented in VASP. The time step of molecular dynamics was chosen to be 2 fs. The procedure of the AIMD simulations is as follows:
1. At the start of the MD simulations, the LMPX samples are assigned an initial temperature of 100 K according to a Boltzmann distribution.
2. The samples are then heated up to the desired temperature (600 to 1200 K) by velocity scaling over 1000 time steps (2 ps), and then equilibrated at the equilibrium temperature for 5000 time steps (10 ps) in the NVT ensemble with a constant volume and with a Nosé–Hoover thermostat.24,25
3. The MD simulations for diffusion are then performed for 40 ps to 400 ps in the NVT ensemble until the diffusion coefficient is converged. We exclude data points where melting or breaking of M–X bonds is observed.
The diffusion coefficient is defined as the mean square displacement over time:
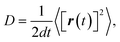 | (1) |
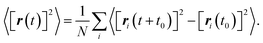 | (2) |
The average mean square displacement is an average over N of all Li ions and is an ensemble average over time t0. Therefore, the calculated diffusion coefficient D is the self-diffusion of Li+ ions rather than the combined diffusion of the center of the mass of all Li+ ions. It is known that these two definitions of diffusion coefficients become equivalent if there is no cross-correlation between displacement ri(t) of different particles at different times.26 The value of D is obtained by performing a linear fitting to the relationship of average mean square displacement versus 2dt.
Results
Stability and relaxed structural parameters
Table 1 shows the thermodynamic phase equilibria determined for a Li10±1MP2X12 (M = Ge, Si, Sn, Al or P and X = O, S or Se) composition in the Li–M–P–X quaternary phase diagram, as well as the calculated equilibrium decomposition energies (rightmost column). The calculated equilibrium decomposition energy Edecomp is a measure of the stability of a material and is defined as the negative of the reaction energy per atom for the Li10±1MP2X12 compound to decompose to the predicted thermodynamic equilibrium mixture of stable phases for that composition. Stable materials have an Edecomp of 0, and the higher the Edecomp, the less likely a structure would be stable. All stable phases in the Li–M–P–X systems investigated are tabulated in the ESI.†All Li10±1MP2X12 compounds are found to be thermodynamically unstable in our calculations. From Table 1, we may identify several clear trends in the stability of the various cation/anion-substituted Li10MP2X12 structures. In general, we find the oxides to be highly unstable in this structure, with Edecomp > 90 meV per atom. The sulfide and selenide structures have somewhat similar stability of less than 25 meV per atom, which are sufficiently small that these compounds can be easily stabilized by entropic effects or created as metastable phases. With the exception of the aliovalently substituted Li11AlP2S12, the cation does not seem to significantly affect the stability of the Li10±1MP2X12 structure. It may be observed that for the oxides and sulfides in general, the equilibrium phases comprise Li4MX4 + Li3PX4. The only exception is Li10SnP2O12 for which Li4SnO4 is unstable versus Li8SnO6 and Li2SnO3. For the selenides, the equilibrium breakdown also contains Li4MSe4, but Li3PSe4 is unstable against a combination of Li4P2Se6 + Li2Se + Se. Li4P2Se6 is a Se-substituted version of the known Li4P2S6 compound.27 We also note that the synthesis of Li4SnS4 (isostructural with Li4GeS4) has only been reported recently28 and is indeed predicted to be stable by our calculations.
Table 2 shows the relaxed structural parameters for the Li10MP2X12 compounds investigated. We may observe that the unit cell volumes of Li10MP2O12 compounds are around 53–55% smaller than the corresponding Li10MP2S12 compounds, while the Li10MP2Se12 compounds have unit cell volumes that are around 16–19% larger than the corresponding Li10MP2S12 compounds. A significant proportion of the differences in volume is accounted for by the differences in the anionic radii. The ionic radii of O2−, S2− and Se2− are 126, 170 and 184 pm respectively,29 which gives 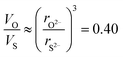 and
and 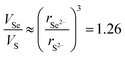 .
.
We also performed a topological analysis of the relaxed Li10MP2X12 compounds using the open source Zeo++ software.30,31 For all materials, we removed all Li in the structure and then calculated the largest free sphere that can pass through the structural framework formed by the remaining cations and anions, which is designated as the “channel size” in Table 2. As we can see, the oxide structures tend to have channel sizes that are around 20% smaller compared to the sulfides, while the selenides have channel sizes that are around 7% larger. We may also observe that the cation M has a relatively small effect on the size of the channels.
| Cation (M) | Anion (X) | Phase equilibria at Li10±1MP2X12 composition | E decomp (meV per atom) |
|---|---|---|---|
| Si | O | Li4SiO4 + 2Li3PO4 | 92 |
| Ge | O | Li4GeO4 + 2Li3PO4 | 96 |
| Sn | O | 0.33Li8SnO6 + 0.67Li2SnO3 + 2Li3PO4 | 97 |
| Si | S | Li4SiS4 + 2Li3PS4 | 19 |
| Ge | S | Li4GeS4 + 2Li3PS4 | 25 |
| Sn | S | Li4SnS4 + 2Li3PS4 | 25 |
| Al | S | Li5AlS4 + 2Li3PS4 | 60 |
| P | S | 3Li3PS4 | 22 |
| Si | Se | Li4SiSe4 + Li4P2Se6 + Li2Se + Se | 16 |
| Ge | Se | Li4GeSe4 + Li4P2Se6 + Li2Se + Se | 16 |
| Sn | Se | Li4SnSe4 + Li4P2Se6 + Li2Se + Se | 19 |
| Cation (M) | Anion (X) | a (Å) | b (Å) | c (Å) | α (°) | β (°) | γ (°) | Volume (Å3) | Channel size (Å) |
|---|---|---|---|---|---|---|---|---|---|
| Si | O | 6.985 | 6.990 | 10.649 | 90.86 | 89.70 | 89.88 | 520 | 1.43 |
| Ge | O | 7.151 | 6.976 | 10.709 | 90.47 | 89.66 | 89.81 | 534 | 1.46 |
| Sn | O | 7.499 | 6.821 | 10.966 | 89.70 | 90.12 | 89.35 | 561 | 1.50 |
| Si | S | 8.566 | 8.848 | 12.920 | 91.90 | 90.65 | 90.31 | 979 | 1.84 |
| Ge | S | 8.561 | 8.847 | 12.929 | 91.97 | 90.63 | 90.24 | 979 | 1.84 |
| Sn | S | 8.666 | 8.950 | 13.133 | 91.97 | 90.58 | 90.08 | 1018 | 1.86 |
| Al | S | 8.722 | 8.567 | 13.662 | 90.69 | 89.19 | 89.47 | 1021 | 1.92 |
| P | S | 8.817 | 8.817 | 12.660 | 90.00 | 90.00 | 89.78 | 984 | 1.87 |
| Si | Se | 9.040 | 9.381 | 13.630 | 91.89 | 90.74 | 90.35 | 1155 | 1.97 |
| Ge | Se | 9.054 | 9.400 | 13.690 | 91.96 | 90.72 | 90.31 | 1164 | 1.96 |
| Sn | Se | 9.084 | 9.434 | 13.797 | 92.09 | 90.70 | 90.17 | 1181 | 1.97 |
Bandgaps
To evaluate the intrinsic redox stability of the various LMPX compounds, we calculated the density of states (DOS) of all LMPX compounds using the HSE screened hybrid functional. Given that the calculated DOS of all LMPX compounds show similar trends regardless of the cation M, only the calculated DOS for Li10GeP2X12 for X = O, S and Se are shown in Fig. 2. We may make the observation that the O-substituted LMPO materials have a larger bandgap than the LMPS materials, which in turn have a larger bandgap than the Se-substituted LMPSe materials. Furthermore, we also find that both the valence band maximum and the conduction band minimum are dominated by anion states, regardless of the anion chemistry.The bandgap of a material provides an upper limit on its electrochemical window.19 The DOS results predict that the O-substituted LMPO materials are expected to have greater intrinsic redox stability than the LMPS compounds, while the Se-substituted compounds are expected to have a lower intrinsic redox stability. This trend can be attributed to the increase in the energy levels of the valence p-orbitals of the anionic species as we move down the periodic table.
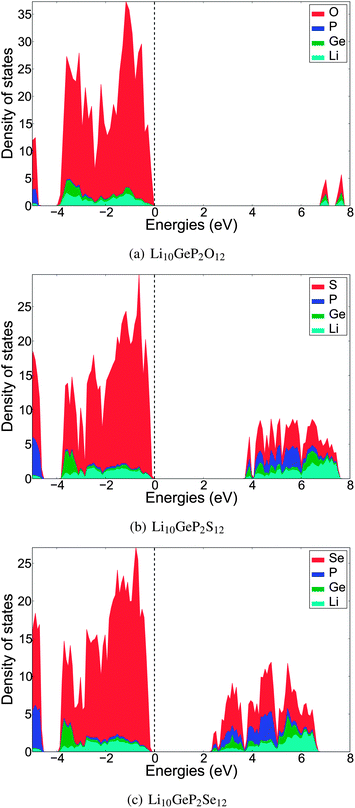 | ||
| Fig. 2 Calculated density of states for Li10GeP2X12 for X = (a) O, (b) S and (c) Se using the HSE screened hybrid functional. | ||
Chemical stability with electrodes
Chemical compatibility between the electrode and the electrolyte is important to prevent capacity degradation and impedance growth. In principle, the electrode material can react with the electrolyte through all of its components, though the reactivity with Li is most critical, as it is, by definition, a mobile species. On the anode side, the chemical potential of Li is very high, and the electrolyte can undergo reduction with Li uptake. The cathode, on the other hand, is strongly oxidizing and can break down the solid electrolyte by extraction of Li.To investigate the chemical compatibility of LMPX electrolytes under extreme conditions of Li chemical potential, we constructed the lithium grand potential phase diagrams for the Li–M–P–X systems and evaluated the phase equilibria at two extremes for the lithium chemical potential (μLi): the bulk Li metal chemical potential μ0Li corresponding to a Li metal anode and μ0Li − 5 eV corresponding to a charged high-voltage (5 V) cathode.
On the anode, the predicted phase equilibria generally comprise Li2X, Li3P and a LixMy alloy. We expect these to have relatively good Li+ conductivity.32,33 Hence, while the solid electrolyte is not stable against metallic Li, it is possible to form a conductive solid electrolyte interphase (SEI). However, the presence of metallic products in the decomposition is worrisome and may lead to thickening of this interphase with time.
On the cathode, however, the phase equilibria are highly dependent on the anion type. The phase equilibria for the oxides at μ0Li − 5 eV generally comprise MxPyOz and O2 gas. This decomposition is likely to lead to significant problems for the long term stability of the electrolyte. For S and Se, the cathodic phase equilibria comprise P2S5 and PSe respectively, which may form potentially good glassy ionic conductors and may be passivating (Table 3).33
| Cation (M) | Anion (X) | Equilibrium phases at cathode, μLi = μ0Li − 5 eV | Equilibrium phases at anode, μLi = μ0Li |
|---|---|---|---|
| Ge | O | GeP2O7, O2 | Li15Ge4, Li2O, Li3P |
| Si | O | SiP2O7, O2 | Li21Si5, Li2O, Li3P |
| Sn | O | SnP2O7, O2 | Li17Sn4, Li2O, Li3P |
| Ge | S | GeS2, P2S5, S | Li15Ge4, Li2S, Li3P |
| Si | S | SiS2, P2S5, S | Li21Si5, Li2S, Li3P |
| Sn | S | SnPS3, P2S5, S | Li17Sn4, Li2S, Li3P |
| Al | S | AlPS4, P2S5, S | Li3Al2, Li2S, Li3P |
| P | S | P2S5, S | Li2S, Li3P |
| Ge | Se | Ge4Se9, PSe, Se | Li15Ge4, Li2Se, Li3P |
| Si | Se | SiSe2, PSe, Se | Li21Si5, Li2Se, Li3P |
| Sn | Se | SnPSe3, PSe, Se | Li17Sn4, Li2Se, Li3P |
Li+ diffusivity and conductivity
To elucidate the factors affecting Li+ diffusivity in the LGPS structural framework, we performed ab initio molecular dynamics (AIMD) simulations of various substituted LMPX compounds. Both cation and anion substitutions were investigated. For cation substitutions, we investigated both isovalent as well as aliovalent substitutions with charge neutrality maintained via changes in the Li+ concentration.Effect of cation substitutions and Li+ concentration
Fig. 3(a) shows the calculated diffusivities of the isovalent-substituted LMPS structures, where M = Si or Sn. The data for LGPS are included as well for comparison. We may observe that in general, isovalent cation substitutions have a relatively small effect on diffusivity in this structure. The activation energy and Li+ conductivity at 300 K for all Li10MP2S12 materials are the same within the error of our simulations, as shown in Table 4.To explore the effect of Li+ carrier concentration on the diffusivity, we also performed aliovalent cation substitutions, i.e., P5+ or Al3+ for Ge4+ to form Li9P3S12 or Li11AlP2S12 respectively. While it can be seen from Fig. 3(b) that aliovalent cation substitutions have a slightly larger effect on the diffusivity than isovalent substitution, the calculated data in Table 4 show that the activation barriers and Li+ conductivities of Li9P3S12 and Li11AlP2S12 are not significantly different from LGPS based on a t-statistic test, which suggests that the effect of carrier concentration and cation substitution is small around the Li+ concentration of LGPS. The slightly higher Li+ conductivity and lower activation barrier for Li11AlP2S12 compared to LGPS may be partially accounted for by the larger channel size in this material (Table 2).
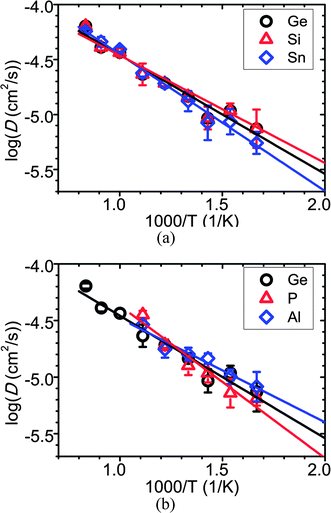 | ||
| Fig. 3 Effect of (a) isovalent (Si4+ and Sn4+) and (b) aliovalent (P5+ and Al3+) cation substitutions on diffusivity in the LGPS structure. Data points at 1000 K, 1100 K, and 1200 K are excluded for Li11AlP2S12 and Li9P3S12 due to melting or breaking of Al–S/P–S bonds in the MD simulations. | ||
| Compound | E a (eV) | Conductivity (mS cm−1) |
|---|---|---|
| Li10GeP2S12 | 0.21 ± 0.04 | 13 |
| Li10SiP2S12 | 0.20 ± 0.03 | 23 |
| Li10SnP2S12 | 0.24 ± 0.03 | 6 |
| Li9P3S12 | 0.26 ± 0.09 | 4 |
| Li11AlP2S12 | 0.18 ± 0.06 | 33 |
| Li10GeP2O12 | 0.36 ± 0.05 | 0.03 |
| Li10GeP2Se12 | 0.19 ± 0.04 | 24 |
Effect of anion substitutions
The calculated diffusivity of Li10GeP2X12 with anion S, O, or Se is shown in Fig. 4. Unlike the case of cation substitutions, we find that anion substitutions in general have a significant effect on Li+ diffusivity in the LGPX structure. Li+ diffusivity is significantly slower in Li10GeP2O12 than in Li10GeP2S12. The calculated activation energy of Li+ diffusion for Li10GeP2O12 of 0.36 eV is also significantly higher than the 0.21 eV of LGPS. As a result, the Li+ conductivity at 300 K is only 0.03 mS cm−1 for Li10GeP2O12, which is three orders of magnitude lower than LGPS. This decrease in Li conductivity is consistent with the general observations that sulfides tend to be much better Li-ion conductors than oxides,3,34–36 due to the greater size and polarizability of the sulfide anion. A Voronoi analysis of the channel sizes in the LMPX structures (see Table 2) also finds significantly reduced channel sizes in the oxides compared to the sulfides, which could contribute to the observed higher activation energies for oxides.Based on the comparison between Li10GeP2O12 and LGPS, one may expect that Li10GeP2Se12 has even better diffusivity than LGPS. However, our AIMD simulations show that the Li diffusivity of Li10GeP2Se12 does not improve significantly compared to LGPS. The activation energies for Li10GeP2Se12 and LGPS are the same within the error bar (Table 4). This result suggests that there is a critical diffusion channel size, beyond which Li+ diffusivity does not improve significantly.
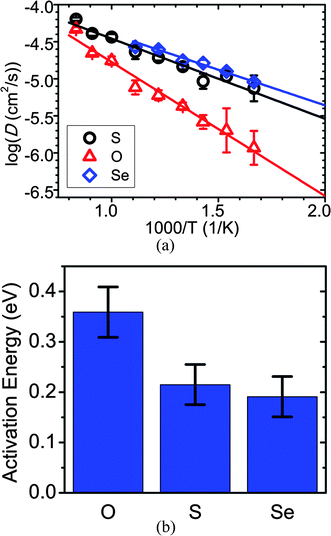 | ||
| Fig. 4 The (a) diffusivities and (b) activation energies of anion-substituted Li10GeP2X12 (X = O, S, and Se). Data points for diffusivity at 1000 K, 1100 K, and 1200 K for Li10GeP2Se12 have been excluded due to melting in the MD simulations. | ||
Effect of lattice parameter changes
To investigate the effect of lattice parameter changes on diffusivity in the LGPS structure, we performed AIMD simulations on isotropically scaled LGPS structures for six different scaling factors, ranging from −4% to +4%. Our simulation results (Fig. 5 and Table 5) show that changes in lattice parameters have a significant effect on the Li+ diffusivity. As the lattice parameters are decreased by 1%, 2%, or 4%, the activation energy increases to 0.28 eV, 0.47 eV and 0.59 eV, respectively. The Li+ conductivity at room temperature drops by an order of magnitude when the lattice parameters are decreased by 1%, and by more than six orders of magnitude when the lattice parameters are decreased by more than 2%.On the other hand, when the lattice parameters are increased, we observe a relatively small improvement in the Li+ diffusivity. Again, this result suggests that the Li diffusion channels in LGPS are already at a somewhat “optimal” size, and further increases in lattice parameters, be it via substitution with a larger anion or by artificially increasing the lattice parameters, have a small effect on the Li+ diffusivity.
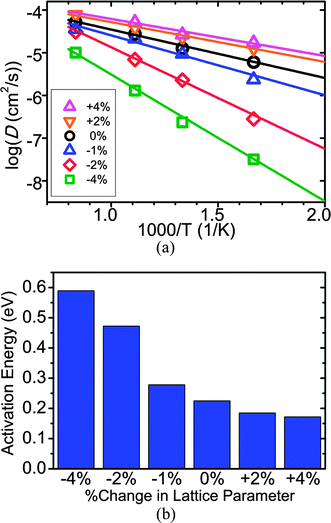 | ||
| Fig. 5 The (a) diffusivities and (b) activation energies of Li10GeP2S12 with different percentage changes in the lattice parameters. | ||
| % Change of lattice parameter | E a (eV) | Conductivity (mS cm−1) |
|---|---|---|
| −4% | 0.59 | 4.6 × 10−8 |
| −2% | 0.47 | 4.8 × 10−6 |
| −1% | 0.28 | 1.7 |
| 0% | 0.23 | 13 |
| +2% | 0.19 | 44 |
| +4% | 0.17 | 75 |
Discussion
Li10GeP2S12 (LGPS) has an unusually high Li-ion conductivity, but the use of Ge as a rare and expensive element, and the sulfide anion chemistry make it an unlikely candidate for large-scale application in Li-ion batteries. We investigated the factors influencing stability and diffusivity in the Li10GeP2S12 structure by performing cation and anion substitutions to obtain Li10±1MP2X12 compounds. In general, we find that cation substitutions have relatively small effects on stability and diffusivity in this structure, while anion substitutions have a much greater effect.Oxides are easier to handle than sulfides, but our results indicate that there is little hope for an oxide version of LGPS. We find that while all Li10MP2X12 (M = Ge, Si, or Sn and X = O, S or Se) compounds are thermodynamically somewhat unstable, the oxides are predicted to be highly unstable with Edecomp in excess of 90 meV per atom. The high decomposition energies suggest that an oxide version of the LGPS structure is unlikely to be synthesizable. This may be due to the high stability of Li3PO4, which competes for stability with Li10MP2O12 as can be seen from Table 1. Our results further indicate that there would be other problematic issues with Li10MP2O12 electrolytes. We find that the oxygen-substituted Li10GeP2O12 compound has much lower diffusivity (two orders of magnitude) than the LGPS compound, making it considerably less interesting than LGPS. This decrease in diffusivity is most likely due to the much smaller anion radius and polarizability of the oxide anion compared to the sulfide anion; similar observations have been made on the difference in conductivity between the LISICON and thio-LISICON conductors.35 Finally, our phase stability calculations predict that in contact with cathodes, Li10MP2O12 compounds may undergo Li loss accompanied by the release of O2 gas, which may prove highly problematic for the long term stability of the electrolyte.
Substituting Se for S only increases the conductivity by a small amount. This is consistent with our investigation of the effect of the lattice parameter on the diffusivity in the LGPS structure: while a decrease in lattice parameters results in significantly lower diffusivity and higher activation barriers, increases in lattice parameters result only in marginally higher diffusivity and marginally lower activation barriers. These observations suggest that the LGPS compound already has somewhat the “ideal” channel size for Li+ diffusivity in this particular structural framework.
The good news is that cation substitutions of Ge seem to have a very little effect on the performance and stability of LGPS. Neither its Li+ conductivity nor its anodic and cathodic stabilities are significantly affected. This result may have been expected, given that the interactions between the cations M and Li+ ions are screened by the S2− anions surrounding the cations. Somewhat surprisingly, we find that aliovalent cation substitutions, with corresponding changes in the Li+ concentration, also have a relatively small effect on the Li+ conductivity in the LGPS structure. This is unlike the significant changes in Li+ conductivity (orders of magnitude) observed in other Li-ion conductors (e.g., lithium lanthanum titanates and NASICON-type materials) with changes in the Li+ concentration.2,3 We believe that this is because the Li10MP2X12 composition already has partial occupancies and most of the Li+ ions are mobile in this structure. Given these data, it seems surprising that so far, no other versions of this compound, other than with Ge, have been reported in the literature.
Finally, a comparison between the DOS in Fig. 2 and the anodic and cathodic decomposition reactions in Table 3 indicates the dangers of assessing the electrochemical stability of potential electrolyte materials based on the intrinsic redox stability alone; chemical compatibility of the electrolyte with electrode materials is an equally important, if not more important, consideration. In terms of redox stability, the HSE-calculated DOS suggest that the oxides would have much better intrinsic redox stability than sulfides and selenides. But while sulfides and selenides form solid reaction products against the cathode and anode, our calculations predict the release of O2 gas when Li10MP2O12 is in contact with a high voltage cathode, which would be detrimental for stable battery operation.
Conclusions
In conclusion, our investigation of substituted Li10±1MP2X12 compounds was motivated by the need to address two key limitations of the LGPS superionic conductor, namely the high cost of germanium, and the air and moisture sensitivity of a sulfide-based chemistry.Our results show that the first limitation may be addressed by substituting relatively cheap silicon or tin for germanium in this structure. Isovalent cation substitutions have a small effect on the similar phase stability, electrochemical stability and diffusivity in these structures, with similar phase stability, electrochemical stability and Li+ conductivity predicted for Li12SiP2S12 and Li12SnP2S12 as for LGPS. Aliovalent cation substitutions (M = Al or P) with corresponding changes in the Li+ concentration also seem to have a small effect on the Li+ conductivity.
However, the second limitation cannot be addressed by a simple substitution of oxide-based chemistry for sulfide-based chemistry. The oxygen-substituted Li10MP2O12 compounds generally have much worse phase stabilities (with equilibrium decomposition energies >90 meV), better intrinsic electrochemical stabilities and much lower Li+ conductivity than their sulfide counterparts. The selenium-substituted Li10MP2Se12 compounds show the opposite trend from the oxide materials, but the magnitude of the increase in Li+ conductivity is much smaller than the decrease in conductivity observed for the oxides. In addition, we also studied the effect of lattice parameter changes on Li+ conductivity in this material and found the same asymmetry in behavior between increases and decreases in the lattice parameters, i.e., decreases in the lattice parameters lower the Li+ conductivity significantly, while increases in the lattice parameters increase the Li+ conductivity only marginally. Based on these results, we conclude that the size of the S2− is near the ideal size for Li+ conduction in this structural framework.
Acknowledgements
We would like to thank the Samsung Advanced Institute of Technology for their funding support for this research. This research also used computational resources from TeraGrid resources provided by Pittsburgh Supercomputing Center and resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U. S. Department of Energy under Contract No. DE-AC02-05CH11231.References
- M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS
.
- S. Stramare, V. Thangadurai and W. Weppner, Chem. Mater., 2003, 15, 3974–3990 CrossRef CAS
.
- P. Knauth, Solid State Ionics, 2009, 180, 911–916 CrossRef CAS
.
- E. Quartarone and P. Mustarelli, Chem. Soc. Rev., 2011, 40, 2525–2540 RSC
.
- C. Galven, J.-l. Fourquet, M.-P. Crosnier-Lopez and F. Le Berre, Chem. Mater., 2011, 23, 1892–1900 CrossRef CAS
.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. mater., 2011, 10, 682–686 CrossRef CAS
.
- Y. Mo, S. P. Ong and G. Ceder, Chem. Mater., 2012, 24, 15–17 CrossRef CAS
.
- S. Adams and R. Prasada Rao, J. Mater. Chem., 2012, 22, 7687 RSC
.
- R. Malik, D. Burch, M. Bazant and G. Ceder, Nano lett., 2010, 10, 4123–4127 CrossRef CAS
.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS
.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef
.
- S. P. Ong, L. Wang, B. Kang and G. Ceder, Chem. Mater., 2008, 20, 1798–1807 CrossRef CAS
.
- S. P. Ong, A. Jain, G. Hautier, B. Kang and G. Ceder, Electrochem. Commun., 2010, 12, 427–430 CrossRef CAS
.
- G. Bergerhoff, R. Hundt, R. Sievers and I. D. Brown, J. Chem. Inf. Model., 1983, 23, 66–69 CrossRef CAS
.
- N. Holzwarth, N. Lepley and Y. a. Du, J. Power Sources, 2011, 196, 6870–6876 CrossRef CAS
.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982 CrossRef CAS
.
- P. P. Ewald, Ann. Phys., 1921, 64, 253–287 CrossRef
.
- S. P. Ong, W. D. Richard, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, 2012, submitted.
- S. P. Ong, O. Andreussi, Y. Wu, N. Marzari and G. Ceder, Chem. Mater., 2011, 23, 2979–2986 CrossRef CAS
.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS
.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef
.
- J. Heyd and G. E. Scuseria, J. Chem. Phys., 2004, 121, 1187–1192 CrossRef CAS
.
- T. M. Henderson, J. Paier and G. E. Scuseria, Phys. Status Solidi B, 2011, 248, 767–774 CrossRef CAS
.
- W. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef
.
- S. NoseÌĄ, J. Chem. Phys., 1984, 81, 511 CrossRef
.
- R. Gomer, Rep. Prog. Phys., 1990, 53, 917–1002 CrossRef CAS
.
- R. Mercier, J. Malugani, B. Fahys, J. Douglade and G. Robert, J. Solid State Chem., 1982, 162, 151–162 CrossRef
.
- T. Kaib, S. Haddadpour, M. Kapitein, P. Bron, C. S. Der, H. Eckert, B. Roling and S. Dehnen, Chem. Mater., 2012, 8, 2–10 Search PubMed
.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef
.
- R. L. Martin, B. Smit and M. Haranczyk, J. Chem. Inf. Model., 2012, 52, 308–318 CrossRef CAS
.
- T. F. Willems, C. H. Rycroft, M. Kazi, J. C. Meza and M. Haranczyk, Microporous Mesoporous Mater., 2012, 149, 134–141 CrossRef CAS
.
- G. Nazri, Solid State Ionics, 1989, 34, 97–102 CrossRef CAS
.
- F. Mizuno, a. Hayashi, K. Tadanaga and M. Tatsumisago, Adv Mater., 2005, 17, 918–921 CrossRef CAS
.
- B. T. Ahn and R. A. Huggins, Mater. Res. Bull., 1989, 24, 889–897 CrossRef CAS
.
- R. Kanno, T. Hata, Y. Kawamoto and M. Irie, Solid State Ionics, 2000, 130, 97–104 CrossRef CAS
.
- R. Kanno and M. Murayama, J. Electrochem. Soc., 2001, 148, A742 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c2ee23355j |
| This journal is © The Royal Society of Chemistry 2013 |
