¹¹B and ²³Na solid-state NMR and density functional theory studies of electric field gradients at boron sites in ulexite

Abstract

Nuclear magnetic resonance (NMR) parameters of ¹¹B in borates and borosilicates, unlike those of many other nuclei such as ²⁹Si and ²⁷Al, vary only over limited ranges and have been thought to be insensitive to local structural environments. High-resolution NMR spectroscopy at high (14 T) and ultrahigh (21 T) fields yield precise ¹¹B and ²³Na NMR parameters for ulexite, which contains the pentaborate polyanion ([B₅O₆(OH)₆]³⁻) as the fundamental building block (FBB). These NMR parameters are compared with ab initio theoretical calculations as implemented in WIEN2K, including optimization of the ulexite structure, determination of the electric field gradients (EFG) and consequently the nuclear quadrupole interaction (QI) parameters at the five distinct B sites, and calculations of the density of states (DOS). These calculations show that the magnitudes and signs of the EFG for ^[3]B and ^[4]B are determined by multiple factors, including the electron distributions in the B 2p_z orbitals and their interactions with Ca-3p/O-2s orbitals. Most importantly, the calculated B 2p_z orbitals at all B sites in ulexite are predominantly affected by the atoms within the fundamental building block, resulting in the insensitivity of the ¹¹B QI parameters to the weak interunit interactions among FBB. Calculations with the water molecules removed from the ulexite structure provide further support for the strong intraunit interactions in FBB as a cause for the poor sensitivity of ¹¹B NMR parameters to local structural environments, including hydrogen bonding, in borates.

---

1. Introduction

Ulexite (NaCa[B₅O₆(OH)₆]·5H₂O) is a common hydrated calcium and sodium borate of economic significance in boron deposits and saline lake sediments.¹ The fundamental building block (FBB) in ulexite is the pentaborate polyanion ([B₅O₆(OH)₆]³⁻) with five distinct boron sites: three four-coordinate (^[4]B) and two three-coordinate (^[3]B) species, in the form of two hexagonal soroborate rings connected via oxygen atoms (Fig. 1). The isolated FBB in ulexite is cross-linked by chains of hydrated Na- and Ca-coordination polyhedra via hydrogen bonds.¹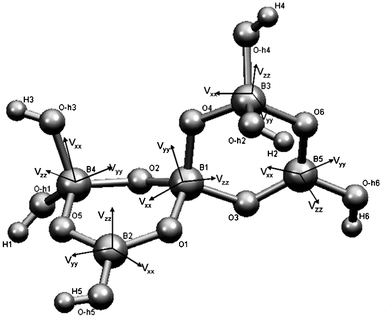

Fig. 1 Fundamental building block of ulexite, with boron EFG tensor orientations.

Solid-state nuclear magnetic resonance (NMR) is a powerful technique for probing subtle structural differences and disorder in minerals and other materials.^2,3 For example, ²⁹Si (i.e., chemical shift) and ²⁷Al (i.e., chemical shift and nuclear quadrupolar coupling) NMR parameters have long been used as highly sensitive tools in identifying local structural environments in silicates. ¹¹B NMR parameters in both borates and borosilicates, however, generally show limited variations. The moderate quadrupolar broadening of trigonal boron requires moderate field strengths and magic-angle spinning in order to achieve clear spectral differentiation between ^[4]B and ^[3]B. Hence, ¹¹B MAS NMR studies are often limited in their ability to identify secondary structural information. The chemical shift of ^[4]B has been shown to be sensitive to changes in the second coordination sphere in crystalline borosilicates^4,5 and borophosphates.⁶ Furthermore, the ability of ¹¹B to probe the presence of ^[4]B in disordered minerals has enabled the identification of local structural details that are not available from other techniques such as X-ray diffraction.^4,5 Due to these advances in NMR analysis, as well as progress in quantum mechanical theoretical calculations, interest in ¹¹B NMR for local structural characteristics in borates has been rekindled.⁷

¹¹B (and ²³Na) has a nuclear spin quantum number I = 3/2, and therefore possesses an electric quadrupole moment which interacts with the electric-field gradient (EFG) generated by its surroundings to give rise to quadrupole effects described by the quadrupole coupling constant (C_Q) and the asymmetry parameter (η). These nuclear quadrupole interaction (QI) parameters can be investigated by using several spectroscopic methods, including NMR, to provide detailed information about the local structural environments of nuclei. This is due to the EFG being highly sensitive to the electronic charge distribution at the nucleus and its surroundings. Specifically, the QI parameters are related to the principal elements of the EFG tensor at the site as (Slichter 1992):⁸

C_Q = eV_zzQ/h (1)

η = |V_xx − V_yy|/V_zz (2)

where V_zz, V_yy and V_xx are the EFG components in the principal axis system (PAS) and fulfil the condition |V_zz| ≥ |V_yy| ≥ |V_xx|, e is the electron charge, h is Planck's constant, and Q is the quadrupole moment. The recommended quadrupole moment of 0.0409 × 10⁻²⁸ m² for the bare boron atom was determined from multiconfigurational Hartree–Fock calculations of the EFG, derived from the hyperfine structure of B(²p), combined with the experimental nuclear quadrupole coupling constant obtained from atomic-beam magnetic resonance measurements.⁶ The quadrupole moment for ²³Na is 0.0102 × 10⁻²⁸ m².⁹

In addition to spectroscopic experiments, ab initio theoretical calculations have gained popularity for quantitatively predicting the EFG of nuclei in crystalline solids.^10,6 For example, Full Potential Linear Augmented Plane Wave (FP LAPW) modeling has been widely used for theoretical calculations and the prediction of electronic and other properties, including EFG, for solids with periodic boundary conditions.^11–17 For this full-potential and all-electron method, the electronic potential in the unit cell is partitioned into non-overlapping atom-centered spheres and an interstitial area between the spheres (Muffin-Tin partition), no approximation to either the potential or charge density is made, and the exchange and correlation effects are treated in the density functional theory (DFT) using the generalized gradient approximation (GGA). A linear combination of the products of radial functions and spherical harmonics is then used inside the atomic spheres and a plane wave expansion is used in the interstitial area as the basis sets.¹⁵ Finally, the Kohn–Sham equations¹⁶ and thus the crystal wavefunctions are solved by a linear variation of LAPW, and thus the electronic structure can be obtained. These calculations are implemented in the computer package WIEN2k.^18–22 FP LAPW calculations have proven to be very sensitive to atomic positions,^6,23,24 because small differences in structural data exert significant effects on the calculated EFG values.

In this contribution, aspects of the electronic structure of ulexite such as the origin of the EFG, the anisotropy of the electron density distribution, the p-orbital occupation and charge transfer at the B sites, have been investigated by ab initio density of states (DOS) calculations combined with high-resolution ¹¹B and ²³Na MAS NMR spectroscopy at high (14 T) and ultrahigh (21 T) fields. These theoretical results shed new light on the interpretation of ¹¹B and ²³Na NMR parameters in borates, especially possible causes for the insensitivity of ¹¹B QI parameters to local structural environment. Together, the experimental and theoretical values suggest a refinement to the hydrogen positions in ulexite obtained from X-ray diffraction.

2. Experiments and theoretical calculations

2.1. Material and characterization

A ulexite sample from Tibet was provided by Prof. Mianping Zheng of the Chinese Academy of Geological Sciences. Small crystals of ulexite in this sample were visually separated and ground into a fine powder using an agate mortar and pestle. The identity of this sample was verified by powder X-ray diffraction (PXRD) analysis, using a PANalytical X'Pert Pro Bragg–Brentano X-ray diffractometer. Analytical conditions included the Bragg–Brentano geometry, a Cu Kα radiation source (λ = 0.15418 nm), an X'Celerator detector, and a Ni-filter diffracted beam. Data were acquired at room temperature with a 2θ range of 10° to 110° at an increment of 0.017° and 305.5 seconds per step. The PXRD pattern confirms that ulexite is the dominant phase in this sample.

2.2. Nuclear magnetic resonance

All NMR spectra were regulated at 298 K using variable-temperature cooling gas to account for frictional heating. The magic angle was adjusted by optimizing the ²³Na linewidths of the satellite transition spinning sideband manifold of NaNO₃. Ulexite was packed into a 3.2 mm (outer diameter, 22 μL fill volume) zirconia oxide rotor (sample size of 35 mg).

2.2.1. 14 T. ¹¹B and ²³Na MAS NMR spectra were acquired using a Varian ^UNITYInova 600 (14.1 T) spectrometer equipped with a 3.2 mm double-resonance Varian-Chemagnetics probe (H/F-X). ¹¹B MAS NMR data were acquired using a Bloch-delay pulse sequence (ν_rf = 79 kHz) with a 0.2 μs excitation pulse (∼7° tip angle) at the nuclear Larmor frequency of 192.4 MHz and a recycle delay of 5 seconds. ²³Na MAS NMR data were acquired by Bloch decay (ν_rf = 71 kHz) using a 10° tip angle and a recycle delay of 2 seconds. Experimental spectra were acquired using 64 and 1024 co-added transients, and spinning frequencies of 16 and 4 kHz, for ¹¹B and ²³Na respectively.

¹¹B NMR spectra were referenced with respect to BF₃–Et₂O (0.00 ppm) using 0.1 M boric acid (H₃BO₃) at +19.6 ppm as a secondary standard and ²³Na NMR spectra were referenced to 1 M NaCl at 0 ppm. Due to the large proportion of protons in the minerals, all spectra were acquired with and without ¹H decoupling (ν_rf = 80 kHz) to investigate the effects of heteronuclear dipolar coupling. Spectral simulations were done within the VNMRj software environment (Varian, Inc.) using STARS.²⁵

2.2.2. 21 T. ¹¹B MAS NMR data were collected on a Bruker Avance II 900 spectrometer (21.1 T) using a 4 mm double-resonance Bruker probe and a Bloch-decay pulse sequence (∼10° tip angle), with a recycle delay of 10 seconds, 256 co-added transients and a spinning frequency of 18 kHz. Spectral simulations were performed using WSOLIDS.²⁶

2.3. DFT calculations

FP LAPW calculations were done using the WIEN2k software package. The atomic coordinates of ulexite from the XRD study of Ghose et al.¹ were taken as the input data. The following atomic-sphere radii (RMT), given in atomic unit (a.u.), were used so that the calculations ran with the highest efficiency without core charge leakage occurring: H (0.5), B (1.3), O (1.6), Na (2.2) and Ca (2.3). The core electron states were separated from the valence states at −6.0 Ry. Calculations were performed at a plane-wave cut-off defined by min(RMT) × max(K_n) of 2.5 where K_n is the k vector; such a cut-off value corresponds to approximate 10 000 plane waves for the mineral. In all calculations, the irreducible Brillouin Zone was sampled on shifted tetrahedral meshes at 32 k-points, which is expected to achieve a good convergence for insulators. Angular momentum components up to l = 12 were included for the wavefunctions inside the atomic spheres. The self-consistent calculations were run in a non-spin-polarized mode and the convergent conditions of the self-consistent cycles were set at 5 × 10⁻⁵ Ry. The optimization employed the experimental XRD fractional atomic coordinates as starting values and kept the unit cell parameters unchanged. Using a definition of the incremental interval, the atomic coordinates were optimized by reducing the forces acting on atoms to less than 1 mRy per a.u. The DFT structure optimizations typically required 16 steps. Optimization for both the unit cell parameters and atomic coordinates was also carried out by keeping the a : b : c ratio constant but changing the unit cell volume from 12% to −10% in steps of 2%, and then optimizing the atomic coordinates in each of the new structures created. In addition, “computer experiments” involving the removal of one or more water molecules from the ulexite structure (i.e., dehydrating) were made to investigate the effects of the H₂O molecules on EFGs at ¹¹B and ²³Na. All of the WIEN2k calculations were performed on a multi-node cluster of computers (16 nodes with a total of 256 cores) at the Shanghai Super Computer Center (SSC) with the Quad-Core AMD Opteron™ Processor 2350 at 2 GHz and 1024 G RAM.

3. Results and discussion

3.1. MAS NMR spectra

The ¹¹B MAS NMR spectra (14.1 and 21.1 T) of ulexite are displayed in Fig. 2. Although there are three crystallographically distinct ^[4]B sites in the structure of ulexite, only a single broad resonance centered at 1 ppm is observed in both the 14.1 and 21.1 T spectra, due to the similar structural environments and the small chemical shift range for ^[4]B in borates.^27–29 Nevertheless, the 21.1 T ¹¹B NMR spectrum does have a hint of asymmetry in the ^[4]B peak (Fig. 2a), possibly because of the greater chemical shift dispersion at the higher field. The full-width at half-maximum (FWHM) of the ^[4]B peak is almost identical at the two fields due to the negligible second-order quadrupole effect (SOQE) in the pseudotetrahedral environment. Fast MAS and high-power proton decoupling eliminate homo- and heteronuclear dipolar effects, respectively, bringing us to the limit of the MAS NMR spectral resolution at the ^[4]B sites.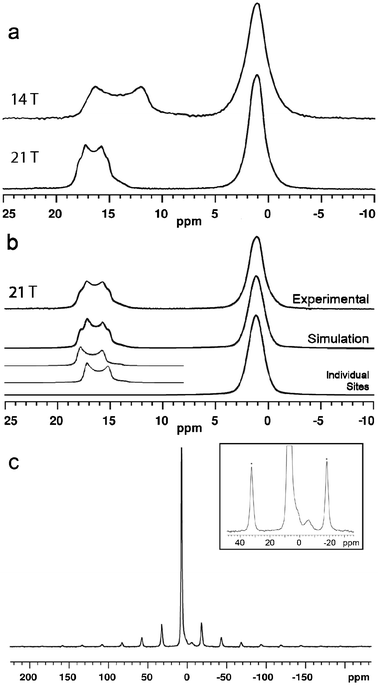

Fig. 2 (a) ¹¹B MAS NMR spectra of ulexite at 14.1 T and 21.1 T; (b) lineshape fitted to the 21.1 T data; (c) ²³Na MAS NMR (14.1 T) spectrum of ulexite. Inset is a 10× increase in vertical scale illustrating a small impurity resonance at −6 ppm (spinning sidebands are identified by asterisks).

The 21.1 T spectrum has a narrower central-transition lineshape with more obvious edges for the two ^[3]B sites (from 11 to 18 ppm) than its 14.1 T counterpart.³⁰ This increased resolution is attributable to the nearly twofold reduction in the SOQE at high field, allowing us to resolve the overlapping of two typical second-order quadrupolar lineshapes (Fig. 2b). The NMR parameters from simulations of the spectra are given in Table 1.

Table 1 Experimental and calculated NMR results using WIEN2k for ulexite (uncertainties for the experimental parameters are listed in parentheses)

	Experimental			Theoretical calculation
				WIEN2k^a		WIEN2k^b		WIEN2k^c
	δiso, ppm (0.1)	CQ, MHz (0.01)	η (0.05)	CQ, MHz	η	CQ, MHz		CQ, MHz	η
a Calculated results from the XRD structure^1 using WIEN2k.b Calculated results from the structure with all atoms optimized using WIEN2k.c Calculated results from the structure with lattice parameters and all atoms optimized using WIEN2k; the optimized unit cell parameters are: a = 8.8015 Å; b = 12.8488 Å and c = 6.6670 Å.d Average value of three ^[4]B sites; the uncertainty in η is 0.15.
^[3]B(2)	18.0	2.57	0.15	2.41	0.18	2.43	0.09	2.49	0.05
^[3]B(5)	18.9	2.51	0.08	2.43	0.08	2.42	0.04	2.49	0.09
^[4]B(1)	1.2^d	0.42^d	0.42^d	−0.40	0.41	−0.37	0.36	−0.38	0.38
^[4]B(3)				−0.46	0.92	−0.49	0.99	−0.52	0.98
^[4]B(4)				−0.38	0.38	0.44	0.48	0.45	0.53
^23Na	7.1	0.07	n.d.	1.33	0.54	1.21	0.84	1.20, 1.12	0.83, 0.80

---

The highly symmetrical octahedral sodium site in ulexite gives a narrow ²³Na MAS NMR resonance at 7.1 ppm. A low intensity broad resonance at −6 ppm is interpreted as arising from an impurity (Fig. 2c) that may be a sodium borate such as Na₂O·4B₂O₃ (ref. 31) or Na₂B₄O₅(OH)₄·nH₂O,³² although neither was detected in the PXRD pattern. The estimated abundance of this impurity phase at ∼3% would not be expected to exert a significant impact on the ¹¹B spectrum of ulexite. The narrow Gaussian-like central transition (CT) lineshape ²³Na resonance at 7.1 ppm indicates a small C_Q. Slow spinning MAS experiments performed to determine C_Q from the spinning sideband manifold of the satellite transitions yielded a value of 70(5) kHz (Fig. 2c), which deviates from theoretical calculations (Table 1). Bonhomme et al.³³ suggested that discrepancies between calculated and experimental data may indicate the presence of local motions such as exchange, reorientation, vibration, libration or even hopping of Na⁺ and its coordinated water molecules. In ulexite, such motions may result in partial averaging of the quadrupolar interaction. The small QI of ²³Na in ulexite corresponds to a second-order quadrupolar shift of about 2 Hz and allows the center of gravity shift at 7.1 ppm (Fig. 2b) to be taken as the isotropic chemical shift.

3.2. DFT structural optimization

Our DFT structural optimizations resulted in the forces acting on each of the atoms in ulexite to decrease from the average values of 737 mRy per a.u. (and a maximum of 2031 mRy per a.u.) to only 1 mRy per a.u. Fig. 3 shows that the calculated total energy is the lowest, when the volume of the unit cell is reduced by 6% from the original X-ray structure.¹ This volume reduction is at least partially attributable to the fact that theoretical calculations are done at 0 K, whereas the XRD data¹ were obtained at room temperature.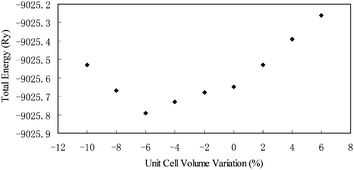

Fig. 3 Structural energy (Ry) as a function of cell volume change (%) for ulexite.

The optimized fractional atomic coordinates as well as the original XRD data for ulexite¹ are listed in Table 2. The changes in the coordinates of the 16 H atoms in ulexite after structural optimizations are more dramatic than those of the O, B and Na atoms, with the maximum change of 21.2% for the z-coordinate of H14 (Table 3). The positions of the B, Na and O atoms in ulexite are almost unchanged (less than 1%). The non-hydrogen bond distances from XRD and optimized structures are compared in Table 3. The largest deviation in the bond distance is Ca–O4 at 0.0309 Å (Table 3). The deviations of the B–O bond lengths after DFT optimizations are less than 0.02 Å for both BO₄ and BO₃ sites, and the average B–O bond distances in the optimized structure are systematically ∼0.01 Å longer than those from the XRD experiment.

Table 2 Optimized fractional atomic coordinates (without unit cell optimized) for ulexite from WIEN2k with XRD results in parentheses^a

Atom	x/a	y/b	z/c
a The XRD atomic coordinates and lattice constants (a = 8.816 Å, b = 12.870 Å, c = 6.678 Å, α = 90.36°, β = 109.05°, γ = 104.98°) are from the single-crystal XRD study.^1
Ca	0.14156 (0.14220)	0.02682 (0.02560)	0.30524 (0.30420)
Na	0.47668 (0.47740)	0.50068 (0.50150)	0.24579 (0.24380)
B1	0.05057 (0.05060)	0.19935 (0.20020)	0.66895 (0.66850)
B2	0.34849 (0.34640)	0.27096 (0.27000)	0.89703 (0.89950)
B3	0.81188 (−0.18910)	0.22321 (0.22400)	0.79072 (0.78210)
B4	0.23618 (0.23440)	0.07225 (0.07370)	0.78240 (0.78340)
B5	0.82416 (−0.17370)	0.26976 (0.26970)	0.43090 (0.42760)
O1	0.19892 (0.19850)	0.29018 (0.28900)	0.78804 (0.79290)
O2	0.10127 (0.10240)	0.10501 (0.10660)	0.62128 (0.62080)
O3	0.96816 (−0.02890)	0.23995 (0.24240)	0.46610 (0.46640)
O4	0.93876 (−0.06500)	0.16820 (0.16770)	0.79426 (0.78400)
O5	0.37402 (0.37010)	0.16922 (0.16920)	0.90955 (0.91120)
O6	0.73701 (−0.25910)	0.25795 (0.26020)	0.57186 (0.56670)
O7(O–H1)	0.29934 (0.29920)	0.00727 (0.00850)	0.66385 (0.66830)
O8(O–H2)	0.88579 (−0.11320)	0.32412 (0.32280)	0.94502 (0.93690)
O9(O–H3)	0.15931 (0.15800)	0.00593 (0.00680)	0.92705 (0.92650)
O10(O–H4)	0.68436 (−0.31830)	0.14404 (0.14690)	0.84859 (0.83610)
O11(O–H5)	0.47997 (0.47760)	0.36197 (0.35970)	0.00086 (0.00250)
O12(O–H6)	0.76293 (−0.23830)	0.31835 (0.31300)	0.24661 (0.24050)
O13(OW1)	0.76293 (0.14620)	0.21313 (0.21060)	0.22885 (0.22400)
O14(OW2)	0.43141 (0.42930)	0.09921 (0.10210)	0.32561 (0.33020)
O15(OW3)	0.46921 (0.47070)	0.35928 (0.35860)	0.48395 (0.48700)
O16(OW4)	0.19068 (0.19250)	0.48437 (0.47940)	0.17752 (0.18500)
O17(OW5)	0.22980 (0.22520)	0.47635 (0.47650)	0.59758 (0.61070)
H1	0.42163 (0.39700)	0.02061 (0.02200)	0.71112 (0.69800)
H2	0.85061 (−0.13400)	0.38829 (0.37300)	0.88012 (0.87800)
H3	0.21449 (0.19300)	0.94672 (−0.04500)	0.97341 (0.97500)
H4	0.60401 (−0.37900)	0.17417 (0.16900)	0.88662 (0.87200)
H5	0.58017 (0.55500)	0.33975 (0.34200)	0.09282 (0.07800)
H6	0.82294 (−0.18900)	0.31652 (0.31300)	0.13468 (0.14700)
H7	0.07813 (0.08600)	0.23168 (0.23000)	0.30097 (0.28500)
H8	0.09030 (0.09200)	0.21046 (0.21800)	0.07266 (0.08800)
H9	0.43203 (0.43900)	0.12977 (0.12700)	0.18872 (0.22900)
H10	0.53472 (0.51300)	0.14385 (0.13400)	0.43536 (0.41800)
H11	0.36440 (0.39200)	0.30451 (0.31600)	0.39629 (0.42100)
H12	0.55898 (0.55500)	0.32183 (0.33500)	0.51004 (0.51300)
H13	0.09937 (0.12000)	0.42131 (0.43100)	0.08909 (0.11300)
H14	0.18880 (0.19200)	0.47575 (0.47300)	0.32732 (0.29400)
H15	0.19470 (0.20200)	0.40843 (0.42200)	0.66474 (0.66400)
H16	0.20400 (0.19100)	0.53662 (0.52100)	0.66187 (0.66200)

---

Table 3 Comparison of non-hydrogen bond distances (Å) in ulexite from structures of XRD and optimized using WIEN2k

Bonds	WIEN2k	XRD
Ca–O(14)	2.4402	2.4142
Ca–O(7)	2.3969	2.4173
Ca–O(4)	2.4483	2.4174
Ca–O(13)	2.4369	2.4376
Ca–O(9)	2.5195	2.5123
Ca–O(2)	2.4986	2.5151
Ca–O(2)	2.5539	2.5719
Ca–O(9)	2.5973	2.5844
Mean	2.4865	2.4838
Na–O(16)	2.3631	2.3514
Na–O(15)	2.3839	2.3832
Na–O(17)	2.3896	2.4183
Na–O(11)	2.4255	2.4277
Na–O(15)	2.4268	2.4632
Na–O(11)	2.4659	2.4800
Mean	2.4091	2.4206
B1–O(4)	1.4732	1.4510
B1–O(2)	1.4638	1.4614
B1–O(3)	1.4830	1.4820
B1–O(1)	1.4929	1.4856
Mean	1.4782	1.47
B3–O(10)	1.4657	1.4493
B3–O(4)	1.4647	1.4571
B3–O(8)	1.5100	1.4918
B3–O(6)	1.5175	1.4982
Mean	1.4895	1.4741
B4–O(7)	1.4676	1.4655
B4–O(2)	1.4765	1.4657
B4–O(5)	1.5114	1.4935
B4–O(9)	1.5029	1.4963
Mean	1.4896	1.4802
B2–O(1)	1.3691	1.3520
B2–O(5)	1.3840	1.3651
B2–O(11)	1.3999	1.3871
Mean	1.3843	1.3680
B5–O(3)	1.3689	1.3555
B5–O(6)	1.3837	1.3620
B5–O(12)	1.3958	1.3800
Mean	1.3828	1.3658

---

The atomic coordinates that changed most after DFT optimizations are the H atoms (Table 4). This is attributable to the large uncertainty in the location of H atoms by XRD due to the non-spherical electron density and the small diffraction coefficient of the H atom.^6,34–36 Other contributing factors may be the dynamic or static disorder of H atoms in the crystal structure, which cause XRD to give only average H positions, especially those in the water molecules. The inaccuracy of H positions from XRD is shown by the significantly shorter O–H bond distances from XRD data than those determined by neutron diffraction techniques.^33,35 The optimized O–H distances in ulexite (Table 4) in this study are in agreement with values reported by neutron diffraction of borates.^37,38,6 The structural optimization for ulexite leads to systematically longer donor (D)–H distances by ∼0.2 Å (with the largest variation of 0.3131 Å between OW1–H7), and the donor–acceptor (A) distances are shorter by 0.04 Å (with the largest variation of 0.1029 Å between OW4 and O–H2) (Table 4). This is similar to the optimization of borate dimorphs, kurnakovite and inderite.²⁴ These results suggest that the water molecules in ulexite exert a greater influence on the structure than suggested by previous XRD data. It is noteworthy that the calculated D–A and D–H values from the two structural optimization methods (i.e., with and without changing the unit cell parameters) are very close, differing only by less than 0.03 Å.

Table 4 Comparison of hydrogen bond distances (Å) in ulexite from optimized structure by WIEN2k with original XRD structure in parentheses

Hydrogen bond			Distance
Donor	H	Acceptor	D–A	D–H	H–A
O12(O–H6)	H6	O8(O–H2)	2.5732 (2.5949)	1.0504 (0.8694)	1.5343 (1.7325)
O13(OW1)	H7	O3	2.6991 (2.6684)	1.0131 (0.8475)	1.7071 (1.8442)
O17(OW5)	H15	O1	2.7119 (2.6999)	1.0079 (0.7981)	1.7374 (1.9184)
O11(O–H5)	H5	O12(O–H6)	2.7002 (2.7115)	1.0093 (0.7931)	1.6959 (1.9244)
O16(OW4)	H14	O17(OW5)	2.7187 (2.7637)	1.0124 (0.7344)	1.7209 (2.0368)
O17(OW5)	H16	O12(O–H6)	2.811 (2.8407)	0.9946 (0.8310)	1.8785 (2.1229)
O14(OW2)	H9	O5	2.8528 (2.8561)	0.9988 (0.7701)	1.8758 (2.1240)
O8(O–H2)	H2	O16(OW4)	2.7790 (2.8647)	1.0080 (0.7894)	1.7859 (2.1039)
O13(OW1)	H8	O4	2.8580 (2.8779)	1.0050 (0.8964)	1.8781 (2.0352)
O15(OW3)	H12	O6	2.8835 (2.8813)	0.9993 (0.8413)	1.8854 (2.0439)
O16(OW4)	H13	O8(O–H2)	2.7790 (2.8819)	1.0009 (0.7858)	1.9029 (2.1142)
O14(OW2)	H10	O6	2.8913 (2.9015)	0.9929 (0.7841)	1.9329 (2.1567)
O9(O–H3)	H3	O10(O–H4)	2.8158 (2.9061)	1.0048 (0.8297)	1.8530 (2.0956)
O15(OW3)	H11	O13(OW1)	2.8876 (2.9594)	0.9994 (0.7596)	1.8923 (2.2054)
O10(O–H4)	H4	O5	2.9904 (3.0307)	0.9882 (0.7657)	2.0674 (2.3113)
O7(O–H1)	H1	O14(OW2)	2.9824 (3.0824)	0.9865 (0.7896)	2.3135 (2.5259)
O7(O–H1)	H1	O10(O–H4)	3.2085 (3.1942)	0.9865 (0.7896)	2.3289 (2.4736)

---

3.3. DFT calculations of QI parameters

The calculated C_Q and η values at the ^[3]B and ^[3]B sites from the XRD and optimized structures of ulexite are also listed in Table 1. Thermal vibrations do not alter the calculated EFG values significantly; especially for sp-hybridized atoms, such effects are expected to be negligible.³⁹ However, if the atomic positions are not determined accurately, agreement between theoretical and experimental EFGs (particularly for η) is not expected.⁴⁰ Table 1 shows that the C_Q parameters for the ^[3]B sites calculated from the optimized structures are in better agreement with the experimental values than those from the XRD structure. Usually the ¹¹B C_Q and η change little with geometric distortion,^41,27,28 therefore, the slightly better agreements between the experimental C_Q values for the ^[3]B sites and those calculated from the optimized structure are significant. The calculated average ¹¹B C_Q values of 0.43 MHz and 0.41 MHz for the ^[4]B sites with and without structural optimization, respectively, are both in agreement with the experimental value of 0.42 MHz. The η values at the ^[4]B sites are poorly constrained by theoretical calculations owing to the very small and similar EFG tensor components (see eqn (2)).

Table 5 shows the calculated EFG results from the “dehydrated” ulexite structures with different numbers of water molecules removed. The calculated C_Q values for both Na and Ca sites that coordinate directly with water molecules are changed not only in amplitude (up to ∼3 times) but also in sign. On the other hand, the calculated C_Q values for the ^[3]B sites decrease by <0.1 MHz (i.e., B(2), 2.51 to 2.42 MHz; B(5), 2.50 to 2.47 MHz) after the removal of all five water molecules. Similarly, the calculated C_Q values for the ^[4]B sites increase only marginally (Table 5). These results demonstrate that the H₂O molecules and hydrogen bonds in ulexite do not exert a significant influence on the EFG at the B sites.

Table 5 The calculated C_Q (MHz) and η values for ulexite with different numbers of H₂O molecules

	Ca		Na		^[4]B(1)		^[3]B(2)		^[4]B(3)		^[4]B(4)		^[3]B(5)
Water^a	CQ	η	CQ	η	CQ	η	CQ	η	CQ	η	CQ	η	CQ	η
a Index of water molecule removed in the calculation.
None	1.35	0.52	1.18	0.85	−0.37	0.39	2.51	0.08	−0.51	0.98	0.45	0.50	2.50	0.05
1	3.35	0.41	−1.54	0.76	−0.32	0.84	2.49	0.13	0.52	0.98	0.44	0.58	2.50	0.12
4	1.35	0.52	2.42	0.45	−0.36	0.34	2.51	0.11	0.52	0.99	0.46	0.49	2.50	0.05
3	1.42	0.56	−4.78	0.37	−0.43	0.51	2.50	0.12	−0.51	0.71	0.51	0.42	2.51	0.11
3, 2	3.66	0.25	−4.76	0.37	−0.36	0.48	2.48	0.11	−0.39	0.63	0.31	0.55	2.48	0.15
1, 5	3.38	0.40	2.16	0.79	−0.28	0.60	2.47	0.22	−0.56	0.90	0.44	0.61	2.48	0.13
1, 5, 2	−3.91	0.46	2.16	0.79	−0.25	0.85	2.47	0.19	−0.43	0.86	−0.24	0.93	2.47	0.08
1, 5, 2, 3	−3.79	0.42	2.82	0.45	0.29	0.81	2.45	0.23	−0.40	0.74	0.29	0.85	2.49	0.08
1, 5, 2, 4	−3.91	0.47	5.49	0.31	0.25	0.96	2.45	0.22	0.42	0.99	−0.25	0.99	2.46	0.09
1, 2, 3, 4, 5	−3.79	0.43	−2.62	0.59	0.32	0.65	2.42	0.28	−0.38	0.83	0.32	0.79	2.47	0.09

---

The EFG at the B atoms in borates results mainly from the anisotropy and distortion of the valence electron distribution, therefore, even slightly different occupations in the p_x, p_y and p_z orbitals due to polarization effects and chemical bonding with neighboring atoms are expected to have a significant effect on EFG.^42,6 The non-cubic oxygen atom environment surrounding the B sites and B sp³/sp² hybridizations lead to different occupations in p_x, p_y and p_z orbitals, thus causing anisotropic B-2p charge distribution around the B nucleus. The degree of such anisotropy of the p electron density, which is proportional to V_zz, can be described by eqn (3):⁴²

Δn_p = ½(p_x + p_y) − p_z (3)

and the sign for V_zz (thus the sign for C_Q) is also determined by this equation. The calculated Δn_p values for the ^[4]B(1), ^[3]B(2), ^[4]B(3), ^[4]B(4) and ^[3]B(5) sites in ulexite are 0.00485, 0.1119, 0.00078, −0.00115 and 0.0538, respectively. The large Δn_p values correspond to the ^[3]B sites, and the calculated Δn_p values can qualitatively explain the signs as well as the magnitudes of C_Q for ^[3]B and ^[4]B in ulexite. Similarly, the calculated Δn_p value of 0.0005 for ^[6]Na in ulexite corresponds well to its small experimental C_Q value (Fig. 2b and Table 1). In comparison with ^[4]B sites, the large positive C_Q values of the ^[3]B sites are due to deficiency in the negative charge in p_z relative to the σ-bonding p_x and p_y orbitals. As the B p_z orbital is not full (eqn (3)) it gives rise to weak B p_z π bonding.

Theoretical calculations also provide information about the orientation of the EFG tensors at the B sites, which can assist in structural interpretations of experimental QI parameters that are not available from powder NMR spectra.⁶ The orientations of the EFG tensor elements at each B site in the pentaborate FBB are illustrated by Fig. 1. The unique EFG element V_zz at the two BO₃ sites (^[3]B(2) and ^[3]B(5)) is approximately perpendicular to the trigonal plane. Such an orientation of V_zz and values close to 0 for η, which are common for all BO₃ units, are caused by sp² hybridization.⁶ Fig. 1 also shows that V_xx and V_yy at the ^[3]B sites lie between the B–O bonds in the BO₃ plane.

Hansen et al.⁶ noted that interpretation of the EFG tensor orientation for the BO₄ sites is less straightforward, because the three tensor elements are often oriented between the B–O bonds of the BO₄ tetrahedra due to the character of sp³ hybridization at the ^[4]B sites (Fig. 1). The calculated V_zz at ^[4]B(3) in ulexite is approximately parallel to the shortest B–O bond (1.449 Å) and has a negative sign for C_Q, indicating that p_z with the highest electron density distribution is along this bond. Similarly, the smallest EFG component, V_xx, corresponds to the longest B–O bond (1.496 Å) at the ^[4]B(4). The EFG tensor components for ^[4]B(1), where the four B–O bond distances are similar, do not coincide with any of the B–O bonds.

The calculated total charge inside the spheres around B atoms at the ^[4]B sites in ulexite is ∼2.88 eV, in comparison with 2.99 eV at the ^[3]B sites, and the calculated valence densities at the former are ∼0.2 eV higher than those at the latter. The larger total charges at the ^[3]B sites may be caused by their shorter B–O bonds, such that more charge from neighboring O enters the B atomic sphere through B–O bonding. The shorter B–O bond distances for ^[3]B also leads to stronger antibonding and thus more unoccupied orbitals, less interstitial charge and lower valence density around the ^[3]B atomic sphere.

The B atoms in each pentaborate FBB in ulexite are closely linked, resulting in stronger intraunit interactions within an FBB than interunit interactions between FBBs. In particular, the B 2p_z orbital is oriented toward open space without any neighboring atoms. This orientation is obviously responsible for the insensitivity of the B 2p_z orbital (and C_Q) at the ^[3]B sites to neighboring atoms and local structural environments in general. The same is true for the B p_z orbitals and the C_Q values at the ^[4]B sites, which always point to atoms within the FBB.

3.4. DOS calculations of EFG contributions

To further examine the insensitivity of EFG at the B sites as well as the reasons for the large differences between QI parameters for ^[3]B and ^[4]B in ulexite, the sources contributing to EFG have been investigated through theoretical analysis of DOS and the electronic charge distribution. Our DOS calculations show the energy windows that may contribute to EFG: −∞ up to −3.6 (core), −3.6 to −3.5 (Na-2s), −2.8 to −2.6 (Ca-3s), −1.5 to −1.45 (Na-2p), −1.45 to −1.1 (Ca-3p and O-2s), −0.7 to −0.45 (roughly B-2s), −0.45 to Fermi energy (E_F) (B-2p, interacting with Na-3s, Ca-4s, O-2p and H-1s). The calculated peaks of Na-2s and Na-2p, Ca-3s are narrow, but the Ca-3p peak is much broader owing to strong hybridization between Ca-3p and O-2s. O-2s does not interact significantly with Na-2s, Na-2p or Ca-3s.

After projecting the EFG at all different energy windows into the same principal axis system, the EFG contributions from different energy windows are obtained and are summarized in Table 6. These data clearly show that there are no EFG contributions to the B sites from the three deepest states (Na-2s, Na-2p and Ca-3s). Therefore, contributions from the energy window below −1.46 Ry can be ignored. The interesting region starts only from −1.46 to −1.1 Ry (i.e., Ca-3p/O-2s), and the most important energy window contributing to EFG at the B sites ranges from −1.1 Ry to the E_F of 0.033 Ry, which is a strongly broadened band containing all valence electrons such as B-2s, B-2p, Na-3s, Ca-3p, Ca-4s, O-2p and H-1s (Fig. 4a–d).

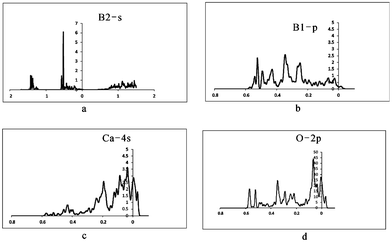Fig. 4 Calculated DOS maps for the atoms in ulexite. (a) DOS from B2 s orbital; (b) DOS from B1 p orbital; (c) DOS from Ca 4s orbital; (d) DOS from O 2p orbital.

Table 6 EFG contributions from different energy windows projected into the same PAS for the five B sites in ulexite

Energy window	^[4]B(1)			^[3]B(2)			^[4]B(3)			^[4]B(4)			^[3]B(5)
	Vxx	Vyy	Vzz	Vxx	Vyy	Vzz	Vxx	Vyy	Vzz	Vxx	Vyy	Vzz	Vxx	Vyy	Vzz
−12, −1.46	0.000	0.000	0.000	0.002	0.000	0.005	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
−1.46, −1.1	−0.13	−0.00	0.139	−0.79	−0.52	1.318	−0.15	−0.05	0.201	−0.10	−0.00	0.103	−0.79	−0.54	1.330
−1.1, −0.45	0.353	−0.38	0.036	−0.27	−0.68	0.953	0.522	−0.16	−0.36	0.159	0.060	−0.22	−1.16	0.042	1.124
−0.45, EF	−0.59	0.472	0.123	−0.74	−0.22	0.970	−0.90	0.168	0.735	−0.43	−0.09	0.530	0.169	−0.96	0.789
Sum	−0.37	0.073	0.298	−1.80	−1.44	3.247	−0.53	−0.04	0.573	−0.38	−0.03	0.413	−1.78	−1.46	3.245

---

Table 6 also shows that the magnitude of the EFG contributions from the energy windows mentioned above to the ^[3]B sites is several times larger than that to ^[4]B. The contributions to EFG at ^[4]B from different states have opposite signs which results in a small total EFG. This is different from ^[3]B where the signs of the individual contributions are the same, resulting in a large total EFG (Table 6). Another notable difference between ^[4]B and ^[3]B is that the Ca-3p/O-2s region contributes little to the EFG at ^[4]B but makes an important contribution at ^[3]B (Table 6). This non-zero contribution from Ca-3p/O-2s is surprising because there is no B orbital involved in this band. This contribution may arise from the indirect interaction between the Ca–O bond and B ‘in the way’: one or more of such bond configurations lead to non-spherical electron distributions and thus a significant EFG contribution to ^[3]B. Clearly, the small EFG at the ^[4]B sites (B(1), B(3), B(4)) relative to those at the ^[3]B sites (B(2) and B(5)) in ulexite are caused by multiple factors.

It is also interesting to note that there are differences between the total EFG calculated and the EFG inside the Muffin-Tin sphere at the B sites (Tables 1 and 6). These differences may be caused by the ‘lattice’ contribution (i.e., from outside the Muffin-Tin spheres). It is not surprising that the ‘lattice’ contribution to EFG is large for B, because the lighter the element, the larger the lattice EFG contribution.¹⁹ Table 6 also suggests that interaction between B-2s and O-2p (Fig. 4a and d) distorts B-2s (−0.6 to −0.5 Ry) from spherical symmetry, thus resulting in further anisotropic local electronic distribution and another source of contribution to EFG, i.e., both p–p and s–p contributions.

4. Conclusions

High resolution solid-state NMR experiments at 14 and 21 T provide accurate ¹¹B and ²³Na NMR parameters for the pentaborate mineral ulexite. The ulexite structure has been optimized using DFT calculations, resulting in better agreement with experimental ¹¹B QI parameters. More reasonable H–O bond distances indicate stronger hydrogen bonds than suggested by a previous XRD study. DFT calculations are used to determine the orientations of the EFG tensors at the B sites in ulexite.

The EFG is shown to arise from the anisotropic electron distribution around the B nucleus. This anisotropic electron distribution and the variation in charge density inside the B atomic spheres at ^[3]B and ^[4]B are related to the differing B–O bond distances. The strong intraunit interactions within each FBB compared with interunit interactions between FBBs is a major reason for the small variation in EFG at different B sites in borates, i.e., the insensitivity of C_Q and η at the B sites in borates to local structural environments. DOS calculations show that the EFGs at the B sites in ulexite arise mainly from the valence states (B 2s and 2p, Ca 4s, Na 3s, O 2p) and that the lattice EFG contribution is also significant, however, the EFG contributions at ^[3]B and ^[4]B sites are different. Combining high-resolution NMR experiments with theoretical modeling is a powerful tool for probing the subtle geometric and electronic structural characters for borates.

Acknowledgements

The authors are very grateful to Dr. Stefaan Cottenier for insightful discussions and instructions for EFG analysis. B. Z. received a research grant of the “One Hundred People Plan” provided by Chinese Academy of Geological Sciences for this study. Funding was also provided by the Canada Foundation for Innovation, Natural Sciences and Engineering Research Council of Canada (Discovery Grant (S. K., B. L. S.); PGSD3 (V. K. M.)) and the Government of Manitoba. Y. Y. acknowledges financial support from NSFC grant no. 20804016. The authors would like to thank Mr. S. Giesbrecht and Mr. B. Greer for helpful discussions, and Dr. Victor V. Terskikh for assistance at the ultrahigh-field NMR facility. Access to the 900 MHz NMR spectrometer was provided by the National Ultrahigh-Field NMR Facility for Solids (Ottawa, Canada), a national research facility funded by the Canada Foundation for Innovation, the Ontario Innovation Trust, Recherche Quebec, the National Research Council Canada, and Bruker BioSpin and managed by the University of Ottawa (www.nmr900.ca). The Natural Sciences and Engineering Research Council of Canada (NSERC) is acknowledged for a Major Resources Support grant.

References

1. S. Ghose, C. Wan and J. R. Clark, Am. Mineral., 1978, 63, 160–171.
2. G. D. Enright, V. V. Terskikh, D. H. Brouwer and J. A. Ripmeester, Cryst. Growth Des., 2007, 7, 1406–1410.
3. R. K. Harris, S. Cadars, L. Emsley, J. R. Yates, C. J. Pickard, R. K. R. Jetti and U. J. Griesser, Phys. Chem. Chem. Phys., 2007, 9, 360–368.
4. A. J. Lussier, P. M. Aguiar, V. K. Michaelis, S. Kroeker, S. Herwig, Y. Abou and F. C. Hawthorne, Mineral. Mag., 2008, 72, 747–761.
5. A. J. Lussier, P. M. Aguiar, V. K. Michaelis, S. Kroeker and F. C. Hawthorne, Am. Mineral., 2009, 94, 785–792.
6. M. R. Hansen, G. K. Madsen, H. J. Jakobsen and J. Skibsted, J. Phys. Chem. A, 2005, A109, 1989–1997.
7. O. L. G. Alderman, D. Iuga, A. P. Howes, K. J. Pike, D. Holland and R. Dupree, Phys. Chem. Chem. Phys., 2013, 15, 8208–8221.
8. C. P. Slichter, Springer-Verlag, Principles of Magnetic Resonance, Berlin, 1992.
9. P. Pyykkö, Mol. Phys., 2001, 99, 1617–1629.
10. H. M. Petrilli, P. E. Blöchl, P. Blaha and K. Schwarz, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, B57, 14690–697.
11. B. Winkler, P. Blaha and K. Schwarz, Am. Mineral., 1996, 81, 545–549.
12. P. L. Bryant, C. R. Harwell, K. Wu and F. R. Fronczek, J. Phys. Chem., 1999, 103, 5246–5252.
13. B. L. Sherriff and B. Zhou, Can. Mineral., 2004, 42, 1027–1035.
14. B. Zhou and B. L. Sherriff, Am. Mineral., 2004, 89, 377–381.
15. S. Cottenier, WIEN2k-Textbook, Instituut voor Kern-en Stralingsfysica, K. U. Leuven, Belgium, 2002.
16. W. Kohn and L. J. Sham, Phys. Rev., 2005, 140(4A), 1133–1138.
17. V. K. Michaelis and S. Kroeker, J. Phys. Chem. C, 2010, 114(49), 21736–21744.
18. P. Blaha, K. Schwarz and P. Herzig, Phys. Rev. Lett., 1985, 54, 1192–1195.
19. P. Blaha, K. Schwarz and P. H. Dederichs, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, B37, 2792–2796.
20. P. Blaha, K. Schwarz and P. Sorantin, Comput. Phys. Commun., 1990, 59, 39–415.
21. P. Blaha, D. J. Singh, P. I. Sorantin and K. Schwarz, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, B46, 1321–1325.
22. P. Blaha, K. Schwarz, G. K. Madsen, D. Kvasnicka and J. Luitz, WIEN2k, ISBN 3-9501031-1-2, Technische Universität, Wien, 2001.
23. B. Zhou, T. Giavani, H. Bildsøe, J. Skibsted and H. Jakobsen, Chem. Phys. Lett., 2005, 402, 133–137.
24. B. Zhou, V. K. Michaelis, Y.-M. Pan, Y.-Y. Yao, K. T. Tait, B. C. Hyde, J. E. C. Wren, B. L. Sherriff and S. Kroeker, Am. Mineral., 2012, 97, 1858–1865.
25. J. Skibsted, N. Nielsen, H. Bildsøe and H. Jakobsen, J. Magn. Reson., 1991, 95, 117–132.
26. K. Eichele, WSolids1, version 1.20.21, Universität Tübingen, 2013.
27. G. L. Turner, K. A. Smith, R. J. Kirkpatrick and E. Oldfield, J. Magn. Reson., 1986, 67, 544–550.
28. S. Kroeker and J. F. Stebbins, Inorg. Chem., 2001, 40, 6239–6246.
29. D. Müller, A. R. Grimmer, U. Timper, G. Heller and M. Shakibaie-Moghadam, Z. Anorg. Allg. Chem., 1993, 619, 1262–1268.
30. S. R. Giesbrecht, V. K. Michaelis, B. Zhou, B. L. Sherriff and S. Kroeker, Annual Report of the Canadian National Ultrahigh-Field Facility for Solids, 2010–11, pp. 48–49.
31. A. M. George, S. Sen and J. F. Stebbins, Solid State Nucl. Magn. Reson., 1997, 10, 9–17.
32. B. Zhou, V. K. Michaelis, S. R. Giesbrecht, S. Kroeker, B. L. Sherriff, Z. Sun, Y.-Y. Yao and Y.-M. Pan, Phys. Chem. Miner., 2012, 39, 373–383.
33. C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azaïs, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 112, 5733–5779.
34. P. C. Burns and F. C. Hawthorne, Can. Mineral., 1993, 31, 297–304.
35. P. C. Burns and F. C. Hawthorne, Can. Mineral., 1994, 32, 885–894.
36. W. Sun, Y.-X. Huang, Z. Li, Y.-M. Pan and J.-X. Mi, Can. Mineral., 2011, 49, 823–834.
37. H. A. Levy and G. C. Lisensky, Acta Crystallogr., Sect. B: Struct. Sci., 1978, 34, 3502–3510.
38. N. Perchiazzi, A. F. Gualtieri, S. Merlino and A. R. Kampf, Am. Mineral., 2004, 89, 767–776.
39. D. Torumba, K. Parlinski, M. Rots and S. Cottenier, Phys. Rev., 2006, B74, 144304.
40. M. Body, G. Silly, C. Legein, J.-Y. Buzare, F. Calvayrac and P. Blaha, Chem. Phys. Lett., 2006, 424, 321–326.
41. P. Bray, J. Edwards, J. O'Keefe, V. Ross and I. Tatsuzaki, J. Phys. Chem., 1961, 35, 435–442.
42. M. Iglesias, K. Schwarz, P. Blaha and D. Baldomir, Phys. Chem. Miner., 2001, 28, 67–75.

---

Footnote

† Current address: Francis Bitter Magnet Laboratory and Department of Chemistry, Massachusetts Institute of Technology, Cambridge, MA 02139 USA.

---