Conformational analysis via calculations and NMR spectroscopy for isomers of the mono(imino)pyridine ligand, 2-{(2,6-Me₂-C₆H₃)NC(i-Pr)}C₅H₄N

Abstract

Sterically hindered (imino)pyridine 2-{(2,6-Me₂-C₆H₃)NC(i-Pr)}C₅H₄N (1) was synthesized via addition of isolated imidoyl chloride to an in situ lithiated pyridine. Room temperature 1-D and 2-D NMR spectroscopy reveals two rapidly equilibrating isomers in solution. Interconversion of these two isomers was verified by 2D-EXSY NMR spectroscopy. Calculations at the B3LYP and MP2 levels of theory reveal four relevant isomers, with two atropisomers of E geometry (1-E_A and 1-E_B) and two atropisomers of Z geometry (1-Z_A and 1-Z_B). A simple carbon–carbon bond rotation to alter the orientation of the isopropyl group provides a fifth, related conformer, 1-Z_B′, that is the most stable species at the MP2 level. The transition states for E/Z isomerization and the isomerization pathways between atropisomers have been characterized. Comparison of experimental and ab initio NMR chemical shifts in combination with NOE analysis suggests that isomers 1-E_B and 1-Z_B/1-Z_B′ are the dominant species in our solution phase NMR studies. Our understanding of the isomerization behavior of 1 will help inform the future design of readily complexed, sterically hindered mono(imine) and bis(imine) ligands.

---

Introduction

For mono(imino)pyridine¹ and bis(imino)pyridine ligands,^2,3E/Z isomerization is an important, yet often overlooked, issue. For complexation to a metal, the E- or E,E-isomeric form is required for bidentate or tridentate coordination, respectively. In prior work, we postulated that the unique pseudo C_s-symmetric Z,Z isomeric form of bis(imino)pyridine A (Fig. 1) resists isomerization to the E,E isomer, and thus, formation of the desired tridentate Fe(II) complex was not realized (Fig. 1).⁴ A pseudo C₂-symmetric Z,Z isomeric form is revealed by others using X-ray crystallography for a bis(imino)pyrimidine ligand, B,⁵ and two bis(imino)pyridine ligands, C⁶ and D⁷ (Fig. 1); all three ligands readily adopt an E,E isomeric form upon complexation with Fe(II). ¹H NMR analysis of B⁵ is described and a minimum of two isomers are identified in solution at room temperature. Limited attention is devoted to NMR analysis of bis(imino)pyridine ligands C⁶ and D.⁷ Laine et al.⁸ suggest that mono(imino)pyridine E (Fig. 1) exists as a mixture of E and Z isomers in solution based on the ¹H NMR spectrum at room temperature; this ligand is readily complexed using NiBr₂(DME). In contrast, mono(imino)pyridine F (Fig. 1) exists as solely one isomer in the solid state (Z isomer, as evidenced by X-ray crystallography) and in solution (¹H NMR spectroscopy at room temperature), and no complexation attempts were reported.⁹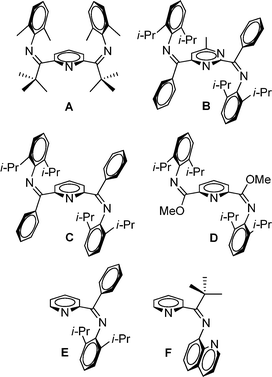

Fig. 1 Previously reported bis(imino)pyridine (A,⁴C,⁶ and D⁶), bis(imino)pyrimidine (B⁵), and mono(imino)pyridine ligands (E⁸ and F⁹) with evidence for the existence of the Z,Z- or Z-isomer, respectively.

The two limiting mechanisms of E/Z isomerization for imines are inversion at nitrogen (lateral shift) or rotation about the C=N double bond.^10–12 For N-aryl imines, inversion at nitrogen is the generally accepted mechanism.¹³ Identification of both the E and Z isomers for N-aryl imines has been made by X-ray crystallography¹⁴ and by ¹H NMR spectroscopy, with NOE experiments used to assist with conformational assignments,¹⁵ and variable temperature NMR used to measure the free energies of activation for the E/Z isomerization.^15,16 Calculations suggest that C=N rotation would have a free energy of activation that is twice the magnitude of that for inversion at nitrogen, with the latter typically falling in a range from 12–29 kcal mol⁻¹.^{16,17and cited references}

For select imines, atropisomerism¹⁸ is invoked in combination with E/Z isomerism with experimental evidence derived from NMR spectroscopy¹⁶ and X-ray crystallography.¹⁴ In other cases, atropisomerism is not invoked, presumably since no experimental evidence exists to suggest its relevance.^15,17,19 Atropisomerism was implied by Small and Brookhart²⁰ and Cámpora et al.²¹ for free asymmetric bis(imino)pyridine ligands and for select corresponding Fe(II) complexes; ¹³C NMR spectroscopy provided evidence of hindered rotation about the imino N-aryl C bonds. It is notable that these authors do not invoke E/Z isomerization as an explanation for the fluxional behavior observed by NMR spectroscopy; presumably, the primary alkyl substituents on the imino carbon positions (methyl^20,21 or butyl²¹) render the E,E-isomer energetically favorable. This is in contrast to studies by Orrell et al. where a symmetric bis(imino)pyridine ligand serves a bidentate ligand for Pd(II) or Pt(II),²² Re(I)^23,24 and Pt(IV),²⁵ and E/Z isomerization of the non-coordinated imine arm is invoked in combination with atropisomerism (again, with methyl substituents on the imino carbon positions). Finally, an account from 1987 with the closest structural similarity to our work describes theoretical identification of two atropisomers of the E-isomer of mono(imino)pyridine 2-(HN=CH)C₅H₄N.²⁶

Herein, we describe the preparation and conformational analysis of the sterically hindered mono(imino)pyridine, 2-{(2,6-Me₂-C₆H₃)NC(i-Pr)}C₅H₄N (1). For 1, our calculations reveal two atropisomers of E geometry and two atropisomers of Z geometry that are energetically viable. We have obtained experimental evidence of facile isomerization via 1-D and 2-D NMR spectroscopy. Importantly, ligand 1 is readily complexed with Ni(II) (vide infra), providing further support for E/Z isomerization. We believe our studies will help direct future development of sterically hindered bidentate and tridentate ligands containing the imine functionality.

Results and discussion

Synthesis of 2-{(2,6-Me₂-C₆H₃)NC(i-Pr)}C₅H₄N

Amide 2 was prepared by combination of isobutyryl chloride with 2,6-dimethylaniline and stoichiometric triethylamine (Scheme 1, step (i)) and it was isolated as a white crystalline solid. Our characterization data was consistent with that of prior accounts of the preparation of 2.²⁷ Next, imidoyl chloride 3 was generated by treatment of a toluene solution of amide 2 with phosphorus pentachloride (Scheme 1, step (ii)) following the general procedure reported by Cunico and Pandey.²⁸ Purification of imidoyl chloride 3 is critical for subsequent steps in the reaction sequence, and Kügelrohr distillation proved to be an optimal method for removal of the POCl₃ byproduct. Compound 3 was isolated as a colorless oil. Lithiation of 2-bromopyridine at −78 °C followed by treatment with imidoyl chloride, 3, afforded the desired mono(imino)pyridine 1 upon slow warming to 22 °C (Scheme 1, steps (iii) and (iv)). Flash silica gel column chromatography is the preferred purification method in order to isolate 1 as a yellow oil. The C=N infrared stretching frequency of 1651 cm⁻¹ for 1 is consistent with our structural assignment.

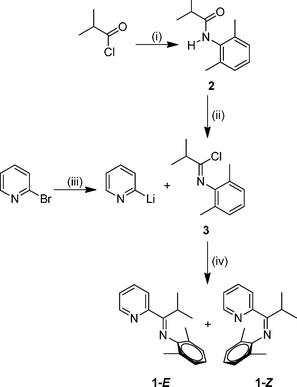Scheme 1 Reagents and conditions: (i) 2,6-dimethylaniline, NEt₃, CH₂Cl₂, reflux, 1 h ; (ii) PCl₅, toluene, 22 °C, 15 h ; (iii) n-BuLi, CH₂Cl₂, −78 °C, 15 min ; (iv) −78–22 °C, 21 h.

NMR analysis of 2-{(2,6-Me₂-C₆H₃)NC(i-Pr)}C₅H₄N

Initial investigation of 1via¹H NMR spectroscopy at 20 °C in methylene chloride-d₂ solvent revealed two unequal sets of broad resonances, consistent with fluxional behavior for 1. The isopropyl methine position is particularly diagnostic, with two broad singlets appearing at 3.54 and 2.76 ppm, respectively. Low temperature ¹H NMR spectra were acquired to provide further evidence of the fluxional behavior; indeed, spectra acquired at −40 °C and −60 °C displayed two unequal sets of sharp resonances; the latter temperature was used for primary structural assignments for 1. Fig. 2 gives an atom labeling scheme for ¹H NMR assignments of 1, and Fig. 3 shows the upfield ¹H NMR spectral region at 20 °C, −40 °C, and −60 °C (stacked plot).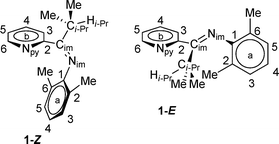

Fig. 2 Compound 1 atom labeling scheme.

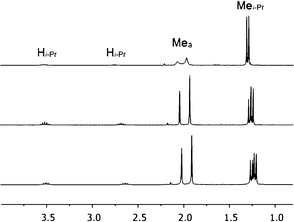Fig. 3 Upfield region of ¹H NMR spectra of 1 at 20 °C (top), −40 °C (middle), and −60 °C (bottom), respectively, in methylene chloride-d₂ solvent.

Assignments of 1 at low temperature were simplified due to general weak coupling giving “first order” resonances. The 6-position of the pyridine ring (H_6b) was the starting point for the assignment, because this position has a smaller ortho coupling to the 5-position (H_5b) than the other ortho couplings in the pyridine ring.²⁹ A gCOSY plot was especially useful for resolving the partial overlap of the minor isomer H_5b and major isomer H_4b protons (see ESI†). Final confirmation used an EXSY plot at 20 °C where each site pair for the two isomers gave an exchange crosspeak on the 2D map. A listing of ¹H NMR chemical shift assignments and coupling constants at −60 °C is provided in Table 1, and the −40 °C and 20 °C ¹H NMR spectral data are present in the ESI.†

Table 1 ¹H NMR chemical shifts and coupling constants in methylene chloride-d₂ solvent for major and minor isomers of 1 at −60 °C

δ (ppm)	Major isomer	Minor isomer	J (Hz)	Major isomer	Minor isomer
H3,5-a	6.86	7.05	H3a, H4a	7.59	7.38
H4a	6.75	6.90	H3b, H4b	8.01	7.89
Mea	1.91	2.02	H3b, H5b	1.16	1.00
H3b	6.67	8.04	H3b, H6b	0.98	0.85
H4b	7.39	7.81	H4b, H5b	7.59	7.76
H5b	7.17	7.36	H4b, H6b	1.75	1.76
H6b	8.57	8.60	H5b, H6b	4.80	4.94
Hi-Pr	3.51	2.64	Hi-Pr, Mei-Pr	6.81	7.00
Mei-Pr	1.22	1.26	—	—	—

---

For a given proton of 1, the chemical shift difference between the major and minor isomer at −60 °C is generally small (< 0.20 ppm), with three notable exceptions: H_i-Pr (0.87 ppm), H_3b (1.37 ppm) and H_4b (0.42 ppm). The magnitudes of these chemical shift differences are maintained across the range of temperatures examined.

In an attempt to rationalize the chemical shift differences for H_i-Pr, H_3b and H_4b for the major versus minor isomer of 1, NOE experiments were carried out at −60 °C using a degassed methylene chloride-d₂ solution of 1. A 2D-NOESY pulse sequence was used, and NOE peaks were observed as negative cross peaks found on the two-dimensional map. The only apparent through-space NOE signal was observed for the Me_a–H_3b interaction for the major isomer, as shown in Fig. 4. One may consider the normalized volume integral data to support this through-space interaction. If the major isomer Me_a–H_3,5-a volume integral is set to 100, the minor isomer Me_a–H_3,5-a normalized volume integral has a value of 94 and the major isomer Me_a–H_3b normalized volume integral has a value of 49. Thus, qualitatively the two “a”-ring methyl groups (Me_a) must make a close approach to the pyridine proton, H_3b, in the major isomer.

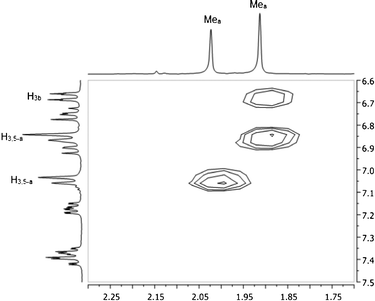Fig. 4 NOESY map of 1 at −60 °C in methylene chloride-d₂.

The involvement of H_3b in this through-space interaction is notable, since this is one of the three protons with highly disparate chemical shift behavior for the major and minor isomers of 1. The structural implications of these results will be discussed in context with our computational analysis.

To determine the temperature dependence of the rate of exchange for the major and minor isomers of 1, we used dynamic NMR techniques. ¹H NMR spectra were collected in methylene chloride-d₂ solvent over a range of temperatures from 0 °C (273 K) to 30 °C (303 K). Line shape analysis was carried out by using the commercially available program WINDNMR. Line broadening of the Me_a signals was modelled, and both k and ΔG‡ were calculated over the range of temperatures following the methods described in the recent microreview by Mazzanti and coworkers.³⁰ At 10 °C, the value of k is 10.9 ± 0.1 s⁻¹, corresponding to a ΔG‡ value of 15.3 ± 0.1 kcal mol⁻¹. An isomer ratio of 1.42 : 1 (major : minor) was found at this temperature. Our experimental isomerization barrier is in line with a computed isomerization barrier, as described in the next section.

Identification of low energy conformers of 1via computational analysis

In an attempt to further understand the fluxional behavior of 1 in solution, we turned to computational analysis to identify energetically viable structures for 1. In addition, we sought to map out the process for interconversion (exchange) of the two isomers observed by NMR spectroscopy. Four distinct structural forms of 1 have been characterized at the B3LYP and MP2 levels of theory. Two structures (1-E_A and 1-Z_A in Fig. 5) have the nitrogen atoms in an approximate syn configuration with respect to the C_im–C_2b bond while the other two structures (1-E_B and 1-Z_B in Fig. 6) have an approximate anti configuration. These four structures have stereoisomeric relationships that relate the structural forms: geometric isomerism (1-E_Aversus1-Z_A, and 1-E_Bversus1-Z_B) and atropisomerism (1-E_Aversus1-E_B, and 1-Z_Aversus1-Z_B). Structure 1-E_A resembles the orientation of the ligand when it is bound to a metal (i.e., the nitrogen atom lone pairs oriented to favor bidentate ligand coordination), such as the observed structure when ligand 1 is coordinated to Ni(II).‡ Structure 1-Z_A was derived by using inversion at nitrogen to generate the geometric isomer of 1-E_A. Structure 1-E_B resembles the X-ray crystal structure of the free (imino)pyridine unit when the imino carbon has a substituent of limited steric bulk, such as methyl.³¹ Finally, structures similar to 1-Z_B have appeared in the literature on a limited basis; compound F (Fig. 1) and 2-{(2,6-Me₂-C₆H₃)NC(t-Bu)}-6-Br-C₅H₃N⁴ are two known (imino)-pyridine examples with available crystallographic data.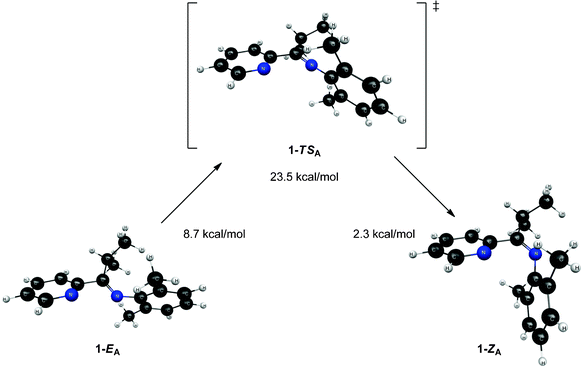

Fig. 5 Structures and relative energies associated with the isomerization pathway between 1-E_A and 1-Z_A. Geometries are optimized at the B3LYP/6-31G* level of theory and energies are determined using single point MP2/6-311+G** calculations. The relative energies are referenced to 1-Z_B.

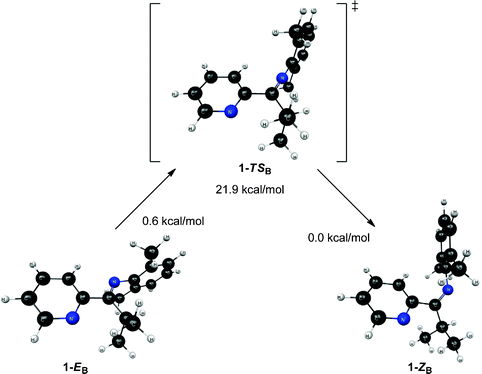Fig. 6 Structures and relative energies associated with the isomerization pathway between 1-E_B and 1-Z_B. Geometries are optimized at the B3LYP/6-31G* level of theory and energies are determined using single point MP2/6-311+G** calculations. The relative energies are referenced to 1-Z_B.

Though 1-E_A resembles the structure of the ligand when it is complexed to a metal, it is the highest energy equilibrium structure presented (see Fig. 5). It is connected to its geometric isomer, 1-Z_A, through a transition state (1-TS_A) that corresponds to inversion at the imine nitrogen, as shown in Fig. 5. This inversion mechanism is consistent with other reports for the interconversion of geometric isomers of N-aryl substituted imines.¹³ While the 2,6-dimethylphenyl moiety (“a” ring, Fig. 2) changes orientation drastically between 1-E_A and 1-Z_A, the N_im–C_im–C_2b–N_py dihedral angle changes little between structures (39.7° in 1-Z_A and 38.0° in 1-E_A). The most interesting features of transition state 1-TS_A involve three atoms: C_im, N_im, and C_1a. The angle between these atoms is nearly linear (175.3°), which is expected since the transition between 1-Z_A and 1-E_A is described as an inversion at N_im. Both the C_im–N_im and C_1a–N_im bonds (see Table 2) are significantly shorter (between 0.03 and 0.06 Å) in 1-TS_A than in either 1-E_A or 1-Z_A.

Table 2 Geometrical parameters of 1-E_A, 1-Z_A, and 1-TS_A determined at the B3LYP/6-31G* level of theory. Bond lengths are in Angstroms

	1-EA	1-ZA	1-TSA
C1a–Nim	1.405	1.414	1.350
Nim–Cim	1.275	1.276	1.248
Cim–C2b	1.511	1.506	1.521
C2b–Npy	1.345	1.344	1.345

---

Unlike structures 1-E_A and 1-Z_A, structures 1-E_B and 1-Z_B exhibit a significant change in the N_im–C_im–C_2b–N_py dihedral angle (see Fig. 6). The atoms are nearly planar in 1-E_B (∠N_im–C_im–C_2b–N_py = 175.8°) while they deviate significantly from planarity in 1-Z_B (∠N_im–C_im–C_2b–N_py = −138.8°). The transition state (1-TS_B) connecting 1-E_B and 1-Z_B resembles 1-E_B in terms of the aforementioned dihedral (∠N_im–C_im–C_2b–N_py = −174.7°), but differs from both 1-E_B and 1-Z_B in terms of the bonds involving the same atoms (see Table 3). The trends are similar to those observed in 1-TS_A, where both bonds involving N_im in 1-TS_B are significantly shorter (between 0.03 and 0.06 Å) than those in either intermediate structure (either 1-E_B or 1-Z_B). Intrinsic reaction coordinate (IRC) calculations suggest the transition from 1-E_B to 1-Z_B corresponds to inversion at N_im and a subsequent rotation around the C_im–C_2b bond.

Table 3 Geometrical parameters of 1-E_B, 1-Z_B, and 1-TS_B determined at the B3LYP/6-31G* level of theory. Bond lengths are in Angstroms

	1-EB	1-ZB	1-TSB
C1a–Nim	1.411	1.411	1.350
Nim–Cim	1.283	1.281	1.253
Cim–C2b	1.506	1.509	1.516
C2b–Npy	1.345	1.346	1.344

---

The relative energies of the structures at the MP2/6-311+G** level of theory (all referenced to the 1-Z_B form) are shown in Fig. 5 and Fig. 6. Structures 1-E_B and 1-Z_B are the lowest energy structures and are nearly identical in energy (a difference of 0.6 kcal mol⁻¹), with the barrier to their interconversion being between 21–22 kcal mol⁻¹. Fig. 7 shows a fifth structure (1-Z_B′) that is the lowest energy structure related to these imines. It corresponds to a rotation around the C_im–C_i-Pr bond, with H_i-Pr pointed towards N_py (see Fig. 2 for atom labelling). While this structure is closely related to 1-Z_B and is probably in equilibrium with 1-Z_B, its structure has an important property that helps in the identification of the isomers observed in NMR experiments. We will represent an equilibrium mixture of 1-Z_B and 1-Z_B′ as 1-Z_B/1-Z_B′.

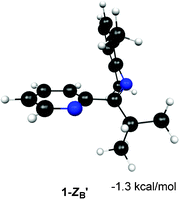Fig. 7 Structure and relative energy of 1-Z_B′. Geometry is optimized at the B3LYP/6-31G* level of theory and the relative energy is determined using single point MP2/6-311+G** calculations. The relative energy is referenced to 1-Z_B.

The computed barrier to interconversion of 1-E_B and 1-Z_B/1-Z_B′ (21–22 kcal mol⁻¹) shows reasonable agreement with the experimentally derived barrier of 15.3 kcal mol⁻¹. It is relevant that the computed barrier is derived from gas-phase calculations and the experimental barrier is derived from NMR spectra acquired in methylene chloride-d₂ solvent—this may account for some of the discrepancy in values.

The interconversion of atropisomers (1-E_Aversus1-E_B, and 1-Z_Aversus1-Z_B) was also probed. These relationships are defined as atropisomerism due to hindered rotation about the C_im–C_2b single bond. It is anticipated that the energy required for interconversion of these atropisomers would be much lower than that required for interconversion of geometric isomers (passing through transition states 1-TS_A and 1-TS_B, respectively). This is indeed the case, where constrained optimization calculations reveal a minimal barrier to interconversion of 1-Z_A and 1-Z_B. Further, the high-energy 1-E_A structure readily converts to the lower energy 1-E_B structure without surpassing a measurable barrier. Vibrational energy considerations render 1-E_A as a structure with more transition state character as opposed to that of a discrete intermediate. Despite this distinction, the 1-E_A/1-E_B interconversion remains relevant for complexation to a metal.

Ab initio ¹H NMR chemical shift determinations

As discussed above, variable temperature ¹H NMR experiments indicate that two isomers of 1 are present in solution. While four structural forms have been presented to this point, it appears that only three of them (1-Z_A, 1-E_B, 1-Z_B/1-Z_B′) are possible candidates based on energy considerations. We have used ab initio NMR chemical shift calculations in an attempt to determine which two of these structural forms correspond to the isomers prevalent in solution. The usefulness of ab initio NMR chemical shifts in structural characterization is generally limited by two factors. First, most of the shift differences between the same protons on different stereoisomers are expected to be relatively small. While ¹H NMR chemical shifts are more generally sensitive to changes in spatial orientation (as compared to ¹³C NMR shifts), the observed chemical shifts for 1 fall in a fairly typical, narrow range (1.2–8.6 ppm), such that even small errors in ab initio¹H NMR shifts could limit their usefulness. The reliability of ¹H NMR calculations is the second limiting factor. ¹H NMR chemical shifts from ab initio calculations can be very sensitive to both basis set and level of theory.^{32,33and cited references} Thus, meaningful comparisons can only be made for shifts that differ significantly from one structural form to another.

Fortunately, two such instances were observed for 1. The experimental ¹H NMR chemical shift for H_3b differs significantly between the two isomers (a 1.4 ppm difference at −60 °C, see Table 1), with the proton in the minor isomer having the downfield chemical shift. Structure 1-E_B has a much larger chemical shift for H_3b (> 1.1 ppm downfield) than all other energetically viable structures (Table 4), suggesting it corresponds to the minor isomer. While the pattern of shifts observed for the other pyridine protons appears to corroborate this conclusion, the differences between shifts between the major and minor isomers is not large enough to make the computational results meaningful (including H_4b, which experimentally has a 0.42 ppm difference in chemical shift upon comparison of the major and minor isomers). However, the shift difference observed for H_i-Pr is relatively large (a 0.87 ppm difference at −60 °C), making a comparison between computational and experimental results more conclusive. The minor isomer has the upfield H_i-Pr chemical shift, which is also the case for 1-E_B, thus corroborating that 1-E_B is the minor isomer.

Table 4 Theoretical ¹H NMR shifts (ppm) for protons used to identify structural forms of 1 determined at the B3LYP/6-31G* level of theory

	H3b	H4b	H5b	H6b	Hi-Pr
1-ZB	6.72	7.14	6.90	8.62	3.22
1-ZB′	6.86	7.15	6.93	8.66	4.33
1-ZA	7.34	7.48	6.85	8.32	3.05
1-EB	8.51	7.56	7.04	8.61	2.72

---

The most downfield predicted chemical shift for H_i-Pr is observed for the most stable species at the MP2 level, 1-Z_B′. While this value seems too large compared to the experimental value observed for the major isomer (3.51 ppm at −60 °C), the actual value of the shift is likely a weighted average of the shifts for 1-Z_B (3.22 ppm) and 1-Z_B′ (4.33 ppm) since they are related through a simple rotation around the C_im–C_i-Pr bond and the structures are relatively close in energy (0.6 kcal mol⁻¹ difference).

Discussion of NOE analysis of 1 and proposed assignment of isomers observed in solution

While the ab initio¹H NMR chemical shifts appear to assign 1-E_B as the minor isomer and 1-Z_B/1-Z_B′ as the major isomer, further support is needed to definitively rule out structure 1-Z_A as a candidate for the major isomer. Hence, NOE experiments were used to confirm the assignment of 1-Z_B/1-Z_B′ as the major isomer. The protons of Me_a (attached to the “a” ring, Fig. 2) show a large NOE interaction with the protons on the adjacent carbon of the “a” ring (H_3a/H_5a) for both the major and minor isomers (see Fig. 4). DFT calculations show that the closest approach between these protons is approximately 2.33 Å; thus, this distance was used as an internal reference for distances for which NOE interactions between protons could be expected for our system. Through-space, the Me_a protons show a significant NOE interaction with H_3b in the major isomer; no such interaction is observed for the minor isomer (see Fig. 4). Only structures 1-E_B, 1-Z_B, and 1-Z_B′ have these Me_a protons in proximity to H_3b based on DFT calculations, so the major isomer is not likely to be 1-E_A or 1-Z_A. The Me_a protons in 1-E_B are much farther from H_3b (3.61 Å, DFT) than in either 1-Z_B (2.49 Å, DFT) or 1-Z_B′ (2.57 Å, DFT). The distances in 1-Z_B and 1-Z_B′ are close to the internal reference (2.33 Å, DFT), corroborating the assignment of the major isomer to 1-Z_B/1-Z_B′.

Conclusions

Sterically hindered (imino)pyridine 2-{(2,6-Me₂-C₆H₃)NC(i-Pr)}C₅H₄N (1) was synthesized and a series of studies (computational analysis, ab initio NMR chemical shift determination, and NOE experiments) were used to fully understand the fluxional behavior for 1 observed by NMR spectroscopy. We have identified the major and minor isomers of 1 as geometric isomers 1-Z_B/1-Z_B′ and 1-E_B, respectively. Since the 1-E_A structure approximates the ligand conformer adopted upon complexation to a metal, we propose the following pathway for complexation of 1: conversion of major isomer 1-Z_B/1-Z_B′ to minor isomer 1-E_Bvia transition state 1-TS_B and subsequent conversion of 1-E_B to its atropisomer 1-E_Avia rotation about the C_im–C_2b bond (with a negligible barrier). The successful complexation of 1 with Ni(II)‡ suggests that the barrier to geometric isomerism is readily surpassed under our reaction conditions. Our methods for isomeric analysis of (imino)pyridine 1 will be used to identify new sterically hindered ligands with energetically viable pathways for isomerization and subsequent complexation. This is an ongoing area of investigation in our laboratories.

Experimental section

General considerations

All chemical reactions were carried out under an atmosphere of argon using standard Schlenk techniques³⁴ unless otherwise noted. Argon gas was purified by passage over Drierite™. All chemicals were purchased from Aldrich and used as received unless otherwise noted. Benzene-d₆ and methylene chloride-d₂ were purchased from Cambridge Isotope Laboratories and dried over molecular sieves (8–12 mesh, 4 Å, activated) before use. A MBraun Manual Solvent Purification System (MB-SPS) was used to obtain the following anhydrous solvents: toluene, pentane, and dichloromethane; solvents were submitted to three freeze–pump–thaw cycles before use.³⁵ Molecular sieves (8–12 mesh, 4 Å) were purchased from J. T. Baker and activated before use. Silica gel used for flash chromatography³⁶ was purchased from Aldrich (200–425 mesh). n-BuLi was purchased from Aldrich as a 1.6 M solution in hexanes (Sure/Seal bottle™) and titrated before use.³⁷ Before use, 2-bromopyridine was distilled.³⁸N-(2,6-dimethylphenyl)isobutyramide (2) was prepared via the method of N-(2,6-dimethyl-phenyl)-2,2-dimethyl-propionamide as described previously,⁴ and the characterization data was consistent with literature reports.²⁷

NMR spectra were recorded on a Varian Mercury 300 Plus spectrometer at 300 MHz (¹H) and 75 MHz (¹³C) at temperatures over a 210–300 K range, depending on the purpose of the given experiment. All chemical shifts were referenced relative to the NMR solvent (either residual protio or ¹³C signals for the solvent peak(s)). Temperature calibrations were performed using the standard methanol sample and software provided by Varian (now Agilent). gCOSY and NOESY 2D-NMR were obtained using standard Varian (now Agilent) pulse sequences. NOESY relative distance 2D-NMR plots were obtained using the NOESY sequence on degassed samples at −40 °C and −60 °C with 1.2 s mixing times. EXSY 2D-NMR plots were obtained using the NOESY sequence with 100 to 200 ms mixing times on un-degassed samples, typically at 20–30 °C. The following abbreviations are used for NMR splitting patterns: cd (complex doublet), ct (complex triplet), cm (complex multiplet) and br s (broad singlet). Infrared spectra were recorded using a Perkin-Elmer Spectrum One FTIR System; samples were prepared by placing the compounds on a diamond attenuated total reflectance (ATR) plate in either solid or liquid form. Elemental analyses were performed at Atlantic Microlab, Inc. in Norcross, Georgia, USA.

Preparation of N-(2,6-dimethyl-phenyl)isobutyramide (2)

N-(2,6-dimethylphenyl)isobutyramide (2) was prepared via the method of N-(2,6-dimethyl-phenyl)-2,2-dimethyl-propionamide as described previously.⁴ A solution of 2,6-dimethylaniline (12.4 mL, 100 mmol, 1.0 equiv) and triethylamine (14.0 mL, 100 mmol, 1.0 equiv) was prepared using dichloromethane (160 mL) in a 500 mL round bottom flask, equipped with addition funnel. In a separate 250 mL round bottom flask, isobutyryl chloride (10.5 mL, 100 mmol, 1.0 equiv) was dissolved in dichloromethane (40 mL). The latter solution was added to the former solution using slow, dropwise addition via the addition funnel. The reaction mixture was heated to reflux for 1 h, cooled to 22 °C and then extracted with water (2 × 70 mL). The organic phase was dried over magnesium sulfate, subjected to filtration, and the filtrate concentrated in vacuo to yield compound 2 as a white solid (18.2 g, 94.9% yield). Found: C, 74.7; H, 9.0; N, 7.2. Calc. for C₁₅H₁₇NO: C, 74.7; H, 9.0; N, 7.3%. ν_max(ATR)/cm⁻¹: 1656 (C=O). ¹H NMR (benzene-d₆, 22 °C): δ 6.94 (3H, m, Ar), 5.71 (1H, br s, N–H), 2.06 (6H, s, CH₃), 2.03 (1H, septet, J = 7.2 Hz, CH(CH₃)₂), 1.07 (6H, d, J = 7.2 Hz, CH(CH₃)₂). ¹³C{¹H} NMR (benzene-d₆, 22 °C): δ 174.3 (C=O), 135.8, 134.9, 128.2, 127.1, 35.5, 19.9, 18.4. Characterization data is consistent with prior findings.²⁷

Preparation of N-(2,6-dimethyl-phenyl)-isobutyrimidoyl chloride (3)

Under a positive pressure of argon, phosphorus pentachloride (5.68 g, 27.0 mmol, 1.0 equiv) was slowly added to a pale-orange colored slurry of 2 (5.74 g, 30.0 mmol, 1.1 equiv) in anhydrous toluene (63 mL). The hydrogen chloride gaseous by-product was bubbled through a sodium hydroxide solution. The reaction mixture was stirred for 20 h at 22 °C. Next, atmospheric pressure distillation was used to remove toluene and the POCl₃ by-product, followed by Kügelrohr distillation at 105 °C and 1.5 Torr to collect the desired product as a colorless oil (4.75 g, 79.6% yield). Found: C, 67.7; H, 7.7; N, 6.6. Calc. for C₁₂H₁₇ClN: C, 68.7; H, 7.7; N, 6.7%. ν_max(ATR)/cm⁻¹: 1698 (C=N). ¹H NMR (benzene-d₆, 22 °C): δ 6.97 (3H, m, Ar), 2.69 (1H, septet, J = 7.2 Hz, CH(CH₃)₂), 2.05 (6H, s, CH₃), 1.14 (6H, d, J = 7.2 Hz, CH(CH₃)₂).

Preparation of 2,6-dimethyl-N-(2-methyl-1-(pyridin-2-yl)propylidene)aniline (1)

A 250 mL Schlenk flask was charged with 2-bromopyridine (0.46 mL, 4.76 mmol, 1.0 equiv) and anhydrous dichloromethane (100 mL), then cooled to −78 °C using a dry ice–acetone bath. This solution was treated with 1.6 M n-butyllithium in hexanes (3.48 mL, 5.22 mmol, 1.1 equiv). The resulting orange solution was stirred at −78 °C for 15 min. Meanwhile, a 100 mL Schlenk flask was charged with 3 (1.00 g, 4.76 mmol, 1.0 equiv) and anhydrous dichloromethane (10 mL). This solution of 3 was added to the reaction flask via cannula transfer to yield a yellow-orange solution. The 100 mL Schlenk flask was washed with anhydrous dichloromethane (2 mL), and this wash was also transferred to the reaction flask via cannula transfer. Stirring of the reaction mixture continued at −78 °C and the cold bath was left intact to warm to 22 °C over the course of 21 h. At this point, a yellow-orange slurry was present. Solvent was removed in vacuo, anhydrous pentane (100 mL) was added, and the resulting slurry was filtered through a fine porosity glass filter. The concentrated filtrate was dissolved in 1.0% methanol–dichloromethane (v/v) and subjected to flash silica gel column chromatography using 1.0% methanol–dichloromethane (v/v) as eluent. Combined fractions were dried in vacuo to yield a yellow oil (0.94 g, 78.5% yield). Found: C, 80.5; H, 8.0; N, 11.1. Calc. for C₁₇H₂₀N₂: C, 80.9; H, 8.0; N, 11.1%. ν_max(ATR)/cm⁻¹: 1651 (C=N). ¹H NMR (methylene chloride-d₂, −60 °C, major isomer): δ 8.57 (1H, ddd, J = 4.80 Hz, 1.75 Hz, 0.98 Hz, H_6b), 7.39 (1H, m, ddd, J = 8.01 Hz, 7.59 Hz, 1.75 Hz, H_4b), 7.17 (1H, ddd, J = 7.59 Hz, 4.80 Hz, 1.16 Hz, H_5b), 6.86 (2H, d, J = 7.59 Hz, H_3,5-a), 6.75 (1H, t, J = 7.59 Hz, H_4a), 6.67 (1H, ddd, J = 8.01 Hz, 1.16 Hz, 0.98 Hz, H_3b), 3.51 (1H, septet, J = 6.81 Hz, H_i-Pr), 1.91 (6H, s, Me_a), 1.22 (6H, d, J = 6.81 Hz, Me_i-Pr). ¹H NMR (methylene chloride-d₂, −60 °C, minor isomer): δ 8.60 (1H, ddd, J = 4.94 Hz, 1.76 Hz, 0.85 Hz, H_6b), 8.04 (1H, m, ddd, J = 7.89 Hz, 7.38 Hz, 0.85 Hz, H_3b), 7.81 (1H, ddd, J = 7.89 Hz, 7.76 Hz, 1.76 Hz, H_4b), 7.36 (1H, ddd, J = 7.76 Hz, 4.94 Hz, 1.00 Hz, H_5b), 7.05 (2H, d, J = 7.38 Hz, H_3,5-a), 6.90 (1H, t, J = 7.38 Hz, H_4a), 2.64 (1H, septet, J = 7.00 Hz, H_i-Pr), 2.02 (6H, s, Me_a), 1.26 (6H, d, J = 7.00 Hz, Me_i-Pr). See Fig. 2 for an atom labeling scheme for compound 1 and see the ESI† for additional ¹H NMR data of 1 in methylene chloride-d₂ at −40 °C and 20 °C, respectively.

Computational methods

All geometrical structures and energies were calculated using GAMESS.³⁹ Geometries were optimized at the B3LYP/6-31G* level of theory with the maximum gradient tolerance set to 0.001 Hartree/Bohr. Frequency calculations were performed at all stationary points using numerical differentiation of analytic energy gradients. Central differences were used in all frequency calculations. Transition states were connected to their respective minima by intrinsic reaction coordinate (IRC) calculations using the second-order Gonzalez–Schlegel algorithm.⁴⁰ All parameters in the IRC calculations were GAMESS default values. Relative energies reported in this work were determined by performing single point MP2/6-311+G** energy calculations at the B3LYP/6-31G* optimized geometries. Relative energies in this work were not zero-point energy (ZPE) corrected. NMR chemical shifts were calculated at the B3LYP/6-31G* level of theory using Spartan08.⁴¹

Acknowledgements

Acknowledgement is made to Villanova University for the support of this research. We thank Rachel L. Hardie for assisting in the development of the synthetic protocols reported herein.

References

1. C. Bianchini, G. Giambastiani, L. Luconi and A. Meli, Coord. Chem. Rev., 2010, 254, 431.
2. V. C. Gibson, C. Redshaw and G. A. Solan, Chem. Rev., 2007, 107, 1745–1776.
3. Q. Knijnenburg, S. Gambarotta and P. H. M. Budzelaar, Dalton Trans., 2006, 5442–5448.
4. J. E. Steves, M. D. Kennedy, K. P. Chiang, W. S. Kassel, W. G. Dougherty, T. J. Dudley and D. L. Zubris, Dalton Trans., 2009, 1214.
5. G. J. P. Britovsek, V. C. Gibson, O. D. Hoarau, S. K. Spitzmesser, A. J. P. White and D. J. Williams, Inorg. Chem., 2003, 42, 3454.
6. N. Kleigrewe, W. Steffen, T. Blömker, G. Kehr, R. Fröhlich, B. Wibbeling, G. Erker, J.-C. Wasilke, G. Wu and G. C. Bazan, J. Am. Chem. Soc., 2005, 127, 13955.
7. T. M. Smit, A. K. Tomov, V. C. Gibson, A. J. P. White and D. J. Williams, Inorg. Chem., 2004, 43, 6511.
8. T. V. Laine, U. Piironen, K. Lappalainen, M. Klinga, E. Aitola and M. Leskela, J. Organomet. Chem., 2000, 606, 112.
9. C. Rangheard, D. Proriol, H. Olivier-Bourbigou and P. Braunstein, Dalton Trans., 2009, 770.
10. J. B. Lambert, Y. Takeuchi, Acyclic organonitrogen stereodynamics, VCH Publishers, New York, NY, 1992.
11. R. Knorr, Chem. Ber., 1980, 113, 2441.
12. S. Patai, The chemistry of the carbon-nitrogen double bond, Interscience Publishers, London, NY, 1970.
13. R. Knorr, J. Ruhdorfer, J. Mehlstaubl, P. Bohrer and D. S. Stephenson, Chem. Ber., 1993, 126, 747.
14. J. H. Matthews, I. C. Paul and D. Y. Curtin, J. Chem. Soc., Perkin Trans. 2, 1991, 113.
15. L. Strekowski, M. T. Cegla, D. B. Harden and S. B. Kong, J. Org. Chem., 1989, 54, 2464.
16. A. Guerra and L. Lunazzi, J. Org. Chem., 1995, 60, 7959.
17. C. Garino, S. Ghiani, R. Gobetto, C. Nervi, L. Salassa, G. Croce, M. Milanesio, E. Rosenberg and J. B. A. Ross, Eur. J. Inorg. Chem., 2006, 2885.
18. E. L. Eliel, S. H. Wilen, L. N. Mander, Stereochemistry of organic compounds, Wiley, New York, 1994.
19. C. R. Kowol, R. Berger, R. Eichinger, A. Roller, M. A. Jakupec, P. P. Schmidt, V. B. Arion and B. K. Keppler, J. Med. Chem., 2007, 50, 1254.
20. B. L. Small and M. Brookhart, Macromolecules, 1999, 32, 2120.
21. J. Cámpora, M. A. Cartes, A. Rodriguez-Delgado, A.M. Naz, P. Palma and C. M. Perez, Inorg. Chem., 2009, 48, 3679.
22. K. G. Orrell, A. G. Osborne, V. Sik and M. W. da Silva, J. Organomet. Chem., 1997, 530, 235.
23. K. G. Orrell, A. G. Osborne, V. Sik, M. W. da Silva, M. B. Hursthouse, D. E. Hibbs, K. M. A. Malik and N. G. Vassilev, J. Organomet. Chem., 1997, 538, 171.
24. J. Granifo, S. J. Bird, K. G. Orrell, A. G. Osborne and V. Sik, Inorg. Chim. Acta, 1999, 295, 56.
25. K. G. Orrell, A. G. Osborne, V. Sik, M. W. da Silva, M. B. Hursthouse, D. E. Hibbs, K. M. A. Malik and N. G. Vassilev, J. Organomet. Chem., 1998, 555, 35.
26. B. Crociani and G. Granozzi, Inorg. Chim. Acta, 1987, 132, 197.
27. B. T. Gowda, K. M. Usha and K. Jyothi, Z. Naturforsch. A, 2004, 59, 69.
28. R. F. Cunico and R. K. Pandey, J. Org. Chem., 2005, 70, 5344.
29. S. Castella, C. Sun and R. Kostelni, J. Chem. Phys., 1967, 46, 327.
30. D. Casarini, L. Lunazzi and A. Mazzanti, Eur. J. Org. Chem., 2010, 2035.
31. K. Nienkemper, V. V. Kotov, G. Kehr, G. Erker and R. Frohlich, Eur. J. Inorg. Chem., 2006, 366.
32. T. Helgaker, M. Jaszunski and K. Ruud, Chem. Rev., 1999, 99, 293.
33. G. Bifulco, P. Dambruoso, L. Gomez-Paloma and R. Riccio, Chem. Rev., 2007, 107, 3744.
34. D. F. Shriver, M. A. Drezdzon, The manipulation of air-sensitive compounds, Wiley, New York, 2nd edn, 1986.
35. A. B. Pangborn, M. A. Giardello, R. H. Grubbs, R. K. Rosen and F. J. Timmers, Organometallics, 1996, 15, 1518.
36. W. C. Still, M. Kahn and A. Mitra, J. Org. Chem., 1978, 43, 2923.
37. W. G. Kofro and L. M. Baclawski, J. Org. Chem., 1976, 41, 1879.
38. W. L. F. Armarego, D. D. Perrin, Purification of laboratory chemicals, Butterworth Heinemann, Oxford, Boston, 4th edn, 1996.
39. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347.
40. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154.
41. Spartan'08, Wavefunction Inc., Irvine, CA, USA. Except for molecular mechanics and semi-empirical models, the calculation methods used in Spartan have been documented in: Y. Shao, L. F. Molnar, Y. Jung, J. Kussmann, C. Ochsenfeld, S. T. Brown, A. T. B. Gilbert, L. V. Slipchenko, S. V. Levchenko, D. P. O'Neill, R. A. DiStasio Jr., R. C. Lochan, T. Wang, G. J. O. Beran, N. A. Besley, J. M. Herbert, C. Y. Lin, T. Van Voorhis, S. H. Chien, A. Sodt, R. P. Steele, V. A. Rassolov, P. E. Maslen, P. P. Korambath, R. D. Adamson, B. Austin, J. Baker, E. F. C. Byrd, H. Daschel, R. J. Doerksen, A. Dreuw, B. D. Dunietz, A. D. Dutoi, T. R. Furlani, S. R. Gwaltney, A. Heyden, S. Hirata, C.-P. Hsu, G. Kedziora, R. Z. Khallilulin, P. Klunzinger, A. M. Lee, M. S. Lee, W. Z. Liang, I. Lotan, N. Nair, B. Peters, E. I. Proynov, P. A. Pieniazek, Y. M. Rhee, J. Ritchie, E. Rosta, C. D. Sherrill, A. C. Simmonette, J. E. Subotnik, H. L. Woodcock III, W. Zhang, A. T. Bell, A. K. Chakraborty, D. M. Chipman, F. J. Keil, A. Warshel, W. J. Hehre, H. F. Schaefer, J. Kong, A. I. Krylov, P. M. W. Gill and M. Head-Gordon , Phys. Chem. Chem. Phys., 2006, 8, 3172.

---

Footnotes

† Electronic Supplementary Information (ESI) available: NMR spectral characterization data for 1. Cartesian coordinates (in Angstroms) and absolute energies for all structures reported. CIF file for the Ni(II) complex‡ of ligand 1. See DOI: 10.1039/c2ra20688a/

‡ Single crystals of ([2-{(2,6-Me₂-C₆H₃)NC(i-Pr)}C₅H₄N]NiBr₂)₂ were obtained from slow evaporation of an anhydrous dichloromethane solution at 22 °C. A single crystal was mounted using Paratone oil onto a glass fiber and transferred to the cold gas stream of the diffractometer. Crystal data. C₁₇H₂₀Br₂N₂Ni, M = 470.88, monoclinic, a = 12.1735(8), b = 10.4451(7), c = 14.3322(9) Å, α = 90, β = 100.5480(10), γ = 90°, U = 1793.3(2) ų, T = 100 K, space group P2(1)/n, Z = 4, 17630 reflections measured, 6803 unique (R_int = 0.0362) which were used in all calculations. The final wR(F₂) was 0.0606 (all data). CCDC reference number 840092.

---