 Open Access Article
Open Access ArticleCosmic dust in the earth's atmosphere†
John M. C.
Plane
*
School of Chemistry, University of Leeds, Woodhouse Lane, Leeds LS2 9JT, U.K. E-mail: j.m.c.plane@leeds.ac.uk; Fax: 44 113 343 6401; Tel: 44 113 343 8044
First published on 7th June 2012
Abstract
This review discusses the magnitude of the cosmic dust input into the earth's atmosphere, and the resulting impacts from around 100 km to the earth's surface. Zodiacal cloud observations and measurements made with a spaceborne dust detector indicate a daily mass input of interplanetary dust particles ranging from 100 to 300 tonnes, which is in agreement with the accumulation rates of cosmic-enriched elements (Ir, Pt, Os and super-paramagnetic Fe) in polar ice cores and deep-sea sediments. In contrast, measurements in the middle atmosphere – by radar, lidar, high-flying aircraft and satellite remote sensing – indicate that the input is between 5 and 50 tonnes per day. There are two reasons why this huge discrepancy matters. First, if the upper range of estimates is correct, then vertical transport in the middle atmosphere must be considerably faster than generally believed; whereas if the lower range is correct, then our understanding of dust evolution in the solar system, and transport from the middle atmosphere to the surface, will need substantial revision. Second, cosmic dust particles enter the atmosphere at high speeds and undergo significant ablation. The resulting metals injected into the atmosphere are involved in a diverse range of phenomena, including: the formation of layers of metal atoms and ions; the nucleation of noctilucent clouds, which are a sensitive marker of climate change; impacts on stratospheric aerosols and O3 chemistry, which need to be considered against the background of a cooling stratosphere and geo-engineering plans to increase sulphate aerosol; and fertilization of the ocean with bio-available Fe, which has potential climate feedbacks.
 John M. C. Plane | Following his PhD in physical chemistry at Cambridge University (1983), John Plane was a Research Fellow at St. John's College and then Associate Professor at the Rosenstiel School of Marine and Atmospheric Science (University of Miami, Florida). He moved to the University of East Anglia (1991), becoming Professor of Environmental Science in 1999. Since 2006 he has been Professor of Atmospheric Chemistry at the University of Leeds. |
Introduction
The solar system is full of dust: if all the dust in the inner solar system (i.e. between the sun and Jupiter) were compressed together it would form a moon 25 km in diameter.1 The main sources of dust are collisions between asteroids (the asteroid belt lies between the orbits of Mars and Jupiter), and the sublimation of comets (which are balls of dust-laden ice) as they approach the sun on their orbits through the solar system.2,3 Fresh dust trails produced by comets which crossed the earth's orbit recently (within the last 100 years or so) are the origin of meteor showers such as the Perseids and Leonids.4 Dust particles from long-decayed cometary trails and the asteroid belt give rise to a continuous input of sporadic meteoroids, which provides a much greater mass flux on average than meteor showers.2,3This review addresses an apparently simple question: what is the magnitude of the cosmic dust input to the earth's atmosphere? Table 1 shows that even very recent estimates of the Interplanetary Dust Particle (IDP) input vary from 5 to 270 t d−1 (tonnes per day). Zodiacal cloud observations and spaceborne dust detection (dark blue shading in Table 1) indicate a daily input of 100–300 t d−1, which is mostly in agreement with the accumulation rates of cosmic elements in polar ice cores and deep-sea sediments (grey shading). In contrast, measurements in the middle atmosphere (light blue shading) – by radar, lidar, high-flying aircraft and satellite remote sensing – indicate that the input is only 5–50 tonnes.

|
There are two reasons why this matters. First, if the upper range of estimates is correct, then vertical transport in the middle atmosphere must be considerably faster than is generally thought to be the case, so that meteoritic material is removed more rapidly from the atmosphere in order to sustain a higher rate of injection; whereas if the lower range is correct, then our understanding of dust evolution in the solar system, and transport mechanisms from the middle atmosphere to the earth's surface, will need substantial revision. Second, cosmic dust particles enter the atmosphere at high speeds (11–72 km s−1) and in most cases completely ablate.5 The resulting metals injected into the atmosphere are involved in a diverse range of impacts, including the formation of layers of metal atoms and ions,6 nucleation of noctilucent clouds,7 effects on stratospheric aerosols and O3 chemistry, and fertilization of the ocean with bio-available Fe.8 These impacts of meteoric ablation obviously depend on the magnitude of the IDP input.
Although the actual measurements in Table 1 appear to be sound, their interpretation to yield the estimated IDP input is potentially compromised by significant uncertainties (final column of Table 1) which are discussed in detail below. The enormous range of values in Table 1 implies a fundamental lack of understanding in at least some parts of the system. In fact, the range is so large that even if the true input is in the “middle” (∼20–50 t d−1), significant reassessment of many of these processes will be required.
In this review, the different ways of estimating the IDP input and assessing its impact are grouped into five Science Topics (STs), illustrated in Fig. 1. Moving downwards from the top of the atmosphere, these topics are: the source of IDPs in the inner solar system and the process of meteoric ablation (ST1); the layers of metal atoms and ions which result from ablation (ST2); the formation of meteoric smoke particles and their role as ice nuclei in the mesosphere (ST3); the impacts of meteoric smoke on aerosols and O3 chemistry in the stratosphere (ST4); and the deposition of smoke to the earth's surface (ST5). Fig. 1 illustrates the relationship between these STs. Each ST (grey shaded box) contains phenomena in the Earth System (red boxes) which provide an estimate of the IDP input through relevant observations (blue boxes). Note that a list of acronyms appears at the end of the review.
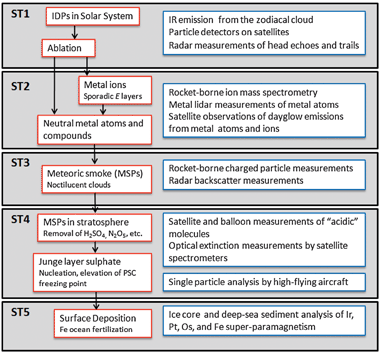 | ||
| Fig. 1 Structure of the review material, grouped into five Science Topics. Each topic (grey shaded box) contains phenomena in the Earth System (red boxes) which provide an estimate of the IDP input through relevant observations (blue boxes). | ||
ST1. IDPs in the solar system and meteoric ablation
Zodiacal light is the very faint diffuse glow caused by sunlight scattering off the zodiacal cloud. This cloud consists of IDPs concentrated close to the ecliptic (i.e., the plane containing the sun and orbits of the planets). A recent Zodiacal Cloud Model (ZCM)1 starts with the orbital properties of comets and asteroids and then follows the dynamical evolution of dust particles after ejection from these sources. The model is constrained by observations of the zodiacal cloud in the infrared at 25 μm, made by the Infrared Astronomical Satellite (IRAS). The ZCM predicts that 85–95% of the dust in the inner solar system comes from Jupiter family comets, which are comets with short orbital periods (typically 20 years) and an aphelion close to the orbit of Jupiter. The remaining dust comes from the asteroid belt and Halley family and Oort cloud comets. Most of the dust, which drifts into the inner solar system under the influence of Poynting-Robertson drag (solar photon pressure, which causes the orbital velocities of IDPs with a radius larger than ∼1 μm to decelerate), has a mass in the range 1–10 μg and provides a continuous input of sporadic meteoroids. The model predicts that these IDPs should enter the terrestrial atmosphere from a near-prograde orbit with a mean speed of ∼14 km s−1, producing a global mass input around 270 t d−1, the highest estimate in Table 1.The input flux of meteoroids into the atmosphere is so uncertain because no single technique can observe particles over the mass range from about 10−12 to 1 g which make up the bulk of the incoming material.3Fig. 2 shows that the particle mass can vary by 30 orders of magnitude, although the largest contribution of mass entering the atmosphere on a daily basis comes from particles around 10 μg. Assuming a meteoroid density of ∼2.8 g cm−3, these particles will have a diameter of ∼200 μm. There is a population of huge impactors with masses greater than 1010 g which make a significant contribution, but only on a geological timescale! Any single measurement technique will only sample a subset of this size distribution. For instance, optical camera networks which observe visible meteors detect particles larger than about 1 mg in mass, or 1 mm in radius. Larger particles (approaching 1 g in mass) are much rarer, so that counting statistics on a time scale of months start to matter.
![Mass influx (per decade of mass) plotted against particle mass [data taken from Flynn21].](/image/article/2012/CS/c2cs35132c/c2cs35132c-f2.gif) | ||
| Fig. 2 Mass influx (per decade of mass) plotted against particle mass [data taken from Flynn21]. | ||
Meteor radars measure particles with masses between about 10−9 and 10−3 g, and therefore cover the most important mass range (Fig. 2). Meteor radar data was used to produce a much-quoted estimate of 44 t d−1 for the global input, although this involved artificially increasing the size distribution to match visual meteor observations.11 The evaporating atoms, particularly metals, ionize through hyperthermal collisions with air molecules.5 This creates a trail of electrons behind the meteoroid, which can be detected by radar. The mass and speed of the meteoroid then have to be estimated indirectly.22 Furthermore, the wavelength of the radar only samples a subset of the mass/velocity/altitude distribution of the meteoroids, so that some extrapolation is required to estimate the total mass input.11
In the past two decades, high-powered large aperture (HPLA) radars, such as the Arecibo Observatory and the EISCAT radars in the Arctic, have been able to detect by incoherent scatter the meteor head echo (i.e. the ball of plasma around the ablating particle as it descends through the atmosphere). This enables measurements of the direction of origin, velocity, deceleration and (indirectly) mass to be made.10,23–25 While initially the mean entry velocity seemed to be significantly higher, around 40–50 km s−1, than the velocity measured with conventional meteor radars, it has now been realised that there is a sampling bias towards high-speed meteors.26 Conventional meteor radars do not efficiently detect meteors which occur at higher altitudes (>100 km), because of the rapid diffusion of the ionized trails. Since faster meteors generally occur at higher altitudes, distributions measured by meteor radars are biased towards the lower speeds. In fact, it has now been shown27 that HPLA radars observe the same population of meteors as observed by meteor radars, and in addition detect a population of faster meteors that ablate at altitudes where trails are not efficiently detected. However, the magnitude of the head echo still depends on the meteoroid mass and velocity, and each HPLA radar is sensitive to a particular mass range.27 This implies that the velocity distribution of the smallest particles measured by an HPLA radar will be biased towards faster speeds: small and slow particles will not have sufficient kinetic energy to ablate, and hence will not produce sufficient electrons to be detected. The average entry speeds are now thought to be between 25 and 30 km s−1.28 It should be noted that particles which originate within the solar system must have entry velocities that range from 11.5 km s−1 for a particle in the same prograde orbit as the Earth (i.e. orbiting in the same direction), to 72 km s−1 for a particle in a retrograde orbit.2
The population of IDPs smaller than 10−9 g can only be measured by impact detectors on satellites. An important estimate of the IDP input was provided by the Long Duration Exposure Facility (LDEF), an orbital impact detector placed on a spacecraft for several years, which yielded an estimate of 110 t d−1.9 However, the LDEF experiment measured crater size, which was treated as a proxy for particle kinetic energy. Hence, the particle velocity distribution had to be assumed in order to determine the mass distribution. If the average velocity is higher (see above) than the value of only 18 km s−1 that was employed in the LDEF analysis, then the corresponding mass distribution would be shifted down by more than an order of magnitude.10
Because of their very high entry velocities, meteoroids undergo rapid frictional heating by collision with air molecules. If the particles reach melting point (∼1800 K), their constituent minerals will then rapidly vaporize – the process termed meteoric ablation. Ablation tends to occur where the atmospheric pressure is around 1 μbar. In the case of the Earth, the peak ablation rate is around 90 km, compared with 80 km on Mars, 115 km on Venus, and 500 km on Titan.29 The physical chemistry of ablation has been treated in detail by several investigators.30–32 The problem becomes manageable for particles smaller than about 250 μm in radius, because heat conductivity through the particle is then fast enough for the particle to be treated as isothermal.30 Assuming a density of 2.8 g cm−3 (typical of an ordinary chondrite), a 250 μm meteoroid has a mass of 180 μg (which, as Fig. 2 shows, is larger than the bulk of the IDP mass input).
The frictional heating of the meteoroid by collisions with air molecules is balanced by radiative loss and the consumption of heat energy through temperature increase, melting and vaporization.5 In order to calculate these terms, parameters such as the meteoroid shape, density, and composition are needed. The question of composition has been discussed in detail recently.33,34 There is some uncertainty here because of the great variability in composition of different types of meteorites.33 Furthermore, it may be that the composition of the meteoroids that ablate in the upper atmosphere is different from that of the meteorites that have survived transit through the atmosphere.33 Nevertheless, the current assumption is that most IDPs have the composition of ordinary chondrites, which is essentially olivine (FeMgSiO4). The elemental abundances of the major metallic constituents relative to Si (1.0) are then: Mg (1.07), Fe (0.90), Al (0.085), Ca (0.061), Na (0.057) and Ni (0.049).35
If the particle is roughly spherical (which should be the case once it has melted), then the energy balance equation is given by:36
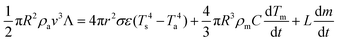 | (I) |
The deceleration of the meteoroid is given by
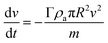 | (II) |
Inspection of eqn (I) shows that for very small particles the heat capacity term will be much smaller than the radiative loss term, in which case the meteoroid will not become hot enough to ablate. This is the case for all particles smaller than 10−12 g. A 10−10 g particle must enter the atmosphere at over 40 km s−1 in order for its temperature to exceed 1800 K, the temperature at which volatile elements such as Na begin to evaporate rapidly. All meteoroids larger than 10−7 g should reach this ablation temperature.5
Interpreting radar measurements requires a model to predict the evaporation rate and subsequent ionization rate of the elemental constituents during ablation. The most recent example is the Chemical Ablation Model (CABMOD),5 which treats the physics and chemistry of ablation by including sputtering by inelastic collisions with air molecules before the meteoroid melts, evaporation of atoms and oxides from the molten particle, and impact ionization of the ablated fragments by hyperthermal collisions with air molecules. Evaporation is based on the assumption of thermodynamic equilibrium within the molten meteoroid and between the particle and the surrounding vapour phase. The thermodynamics are provided by the well-established MAGMA code,37 which is based on a fractionation model used by planetary scientists to account for mass loss from the planet Mercury. The loss rate of each element is then calculated by applying Langmuir evaporation, which assumes that the rate of evaporation into a vacuum is equal to the rate of evaporation needed to balance the rate of uptake of a species i in a closed system. The rate of mass release of species i with molecular weight μi is given by the Herz–Knudsen equation:
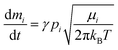 | (III) |
Fig. 3 illustrates the elemental injection profiles calculated by CABMOD for a meteoroid entering the atmosphere with the most likely mass and velocity according to LDEF.5 The mass loss which occurs above 105 km, when the particle has not yet melted (Tm < 1800 K), is due to sputtering. Note that CABMOD predicts differential ablation, i.e. the most volatile elements – Na and K – ablate first, followed by the main constituents Fe, Mg and Si, and finally the most refractory elements such as Ca. CABMOD has been used successfully to model the variation of meteor head echoes with height, using measurements made at the Arecibo Observatory.38 However, there are two important caveats. First, much of the thermodynamic data in MAGMA has to be extrapolated to temperatures above 2000 K from measurements below 1700 K.37 Second, Langmuir evaporation represents an upper limit to the evaporation rate, since evaporation into a vacuum can be significantly slower than into a vapour at equilibrium (because diffusion from the bulk into the surface film can become rate-determining). For instance, the evaporation coefficient from a molten silicate into vacuum can be much less than 1 for elements such as Fe (0.25) and Ca (0.06),39 which affects the height in the atmosphere where these elements ablate (and also the heating rate of the meteoroid).
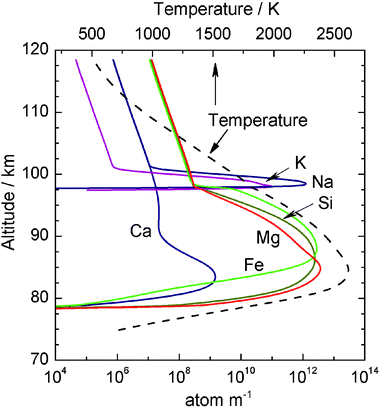 | ||
| Fig. 3 Elemental ablation profiles for a 5 μg meteoroid entering at 20 km s−1, as predicted by the Chemical Ablation Model (CABMOD). The particle temperature is shown on the top abscissa. | ||
Further work is need to remove these uncertainties in chemical ablation models, so that they can be used to correct for biases in the meteor mass/velocity distribution measured by radars.26 One important reason for doing this is to refine the ZCM described above, by constraining the predicted IDP orbits and velocities by using radar data. An initial attempt in this direction was published very recently, showing that the IDP input could be reduced to only 41 t d−1 by changing the initial orbital characteristics of IDPs ejected by Jupiter family comets.40
ST2. metallic neutral and ion layers
Ablation produces layers of neutral metal atoms, such as Fe, Mg and Na, which peak between 85 and 95 km in the terrestrial atmosphere.6 Several of these layers – Na, K, Li, Ca, Ca+ and Fe – can be observed using ground-based resonance lidars, where the transmitter is tuned to a strongly allowed optical transition (e.g. the Na(2P3/2–2S1/2) transition at 589.0 nm).41 Observations can be made continuously over a complete diurnal cycle, provided an astronomical quality telescope and narrow band optical filter are employed for daytime measurements.42 One constraint is that the optical transition must be at wavelengths greater than about 300 nm; otherwise, strong absorption by the Hartley band of O3 in the stratospheric ozone layer prevents optical transmission between the ground and the mesosphere, which rules out observations of important metallic species such as Mg, Mg+ and Fe+.Lidar observations can be made with extremely good time and height resolution (typically 60 s and 40 m, respectively, for the Na layer), so that the metal layers can be used as tracers of atmospheric motions such as tides and gravity waves.43 In the case of Na, K and Fe, a narrow line-width laser can be used in the lidar transmitter to measure temperature and wind profiles in the upper mesosphere.42,44,45 This is achieved by scanning the laser across the resonance line to measure the degree of Doppler broadening, and hence the local temperature. By employing a laser with a tuning accuracy and frequency stability of at least 50 MHz, the temperature can be measured with an error of ∼2 K. The wind along the line-of-sight of the lidar can be determined from the net Doppler shift of the resonance line, typically with an error of less than 3 m s−1. By pointing the lidar sequentially in both zenith and off-zenith directions, the wind can then be resolved into the zonal, merional and even vertical components. Another way to measure the temperature is to use a two-colour lidar to measure simultaneously the relative populations of the 5D4 and 5D3 spin–orbit multiplets of ground-state Fe, from which the temperature can be derived assuming Boltzmann equilibrium.46
Metal resonance lidars are thus an extremely important tool for studying the chemistry and physics of the mesosphere/lower thermosphere (MLT), which is largely inaccessible to direct measurements. High altitude aircraft and research balloons reach altitudes of about 22 and 45 km, respectively, whereas satellites cannot operate below 150 km without atmospheric drag causing rapid re-entry. The only way to sample the MLT in situ is via rocket-borne payloads. However, because the payload traverses the MLT region at a velocity typically in excess of 1 km s−1, the instruments must have a rapid time response.47 There have been a number of measurements of the concentrations of positive metallic ions made by rocket-borne mass spectrometry.48,49 These flights have been motivated to establish whether there is a link between meteor showers and the abundance of metallic ions (there does not appear to be a significant correlation49), and the role of metallic ions in forming sporadic E layers and noctilucent clouds48 (see ST3).
Metallic ions such as Mg+ and Fe+ have also been observed by resonant scattering of sunlight, using spectrometers on space vehicles.50 More recently, satellite observations have also been made of the neutral Na and Mg layers.51–53 The vertical resolution achievable with limb-scanning spectrometers on satellites is only about 2 km (cf. the lidar vertical resolution of 40 m), but satellites in polar sun-synchronous orbits provide near-global coverage. Fig. 4 illustrates the Na column abundance (i.e. the concentration of the Na layer integrated over height), as a function of latitude and season. The satellite data-set51 has been supplemented with ground-based lidar data during the polar winter when the Na layer is not solar-illuminated. Fig. 4 illustrates that there is very little seasonal variation at low latitudes (less than a factor of 2), but the winter/summer ratio increases to nearly an order of magnitude at high latitudes. The primary reason for the large summertime depletion at high latitudes is the very low temperature during the summer because of the adiabatic cooling of upwelling air.6 A secondary reason is the efficient removal of metallic species on noctilucent cloud particles (see ST3).54,55
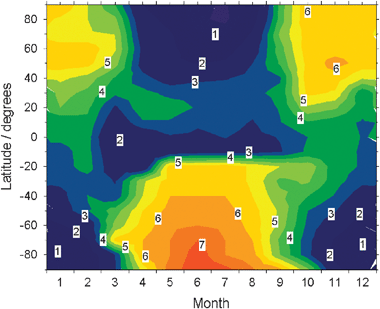 | ||
| Fig. 4 Column abundance of the Na layer (units: 109 atom cm−2) as a function of latitude and month. | ||
Understanding the characteristic features of the metallic layers in the upper atmosphere has required studying the reaction kinetics of neutral and ionized metallic species with atmospheric constituents such as O3, O2, O and H. Over the past 30 years, the two classical techniques of flash photolysis and the fast flow tube have provided a great deal of kinetic data on the pertinent reactions of the meteoric metals Fe, Mg, Na, Ca and K.6,41,56 The results have been used to construct atmospheric models which successfully explain the metal layers above 80 km.6,12,13,41,57Fig. 5 illustrates the author's current model of iron chemistry in the upper atmosphere. The rate coefficients for the reactions depicted with black arrows have all been measured. Above 95 km, Fe+ ions are produced by charge transfer with the lower E region ions NO+ and O2+. Neutralisation of Fe+ then occurs via reaction with O3 to form FeO+, or recombination with O2 to form FeO2+, producing molecular ions which can then undergo dissociative recombination (DR) with electrons to generate Fe (red arrows in Fig. 4).
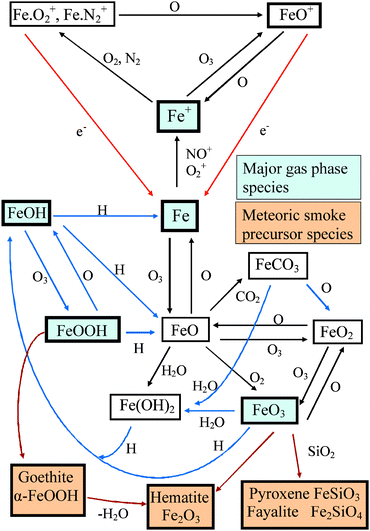 | ||
| Fig. 5 Fe chemistry in the MLT. Black arrows: reactions with measured rate coefficients; red, blue, brown arrows indicate reactions which need laboratory study (see text). | ||
Metallic ions, particularly Fe+ and Mg+, are the major constituents of sporadic E layers, thin layers of concentrated plasma which occur in the lower thermosphere (95–130 km).48,49 Sporadic E layers are important for radio communications, both enabling over-the-horizon radio propagation and attenuating ground-to-space communications. The chemical lifetimes (against neutralisation) of these metallic ions are controlled by the ion-molecule chemistry illustrated for the case of Fe+ in Fig. 5. This shows that once molecular ions such as FeO+ or FeO2+ form, there is a competition between DR and conversion back to Fe+ by reactions with atomic O, which effectively slows down neutralisation. When a sporadic E layer descends below 100 km, the concentration of atomic O decreases markedly in relation to O3,O2 and N2.6 Thus, molecular ions form more quickly and are converted back to Fe+ more slowly. The combined effect is to reduce the lifetime of Fe+ from days above 100 km, to only minutes at 90 km.58
Recently, low-lying sporadic ion layers have been observed, using radio occultation from spacecraft, to occur around 90 km on Mars,59,60 120 km on Venus61 and 550 km on Titan.62 The CO2 atmospheres of Mars and Venus pose a particular challenge to the existence of metallic ions, because they should form CO2-clusters very rapidly and undergo DR. In fact, it turns out that sporadic layers in the Martian atmosphere are most likely Mg+ rather than Fe+, following a recent laboratory study63 which showed that atomic O reacts much more rapidly with molecular Mg-containing ions to form Mg+, compared with their Fe-containing analogues. This very effectively slows down the neutralisation of Mg+ in a CO2-rich atmosphere. Titan is interesting because ablation occurs over a much greater altitude range, as a result of its small atmospheric scale height.29 An important reason for carrying out comparative studies with these other atmospheres is that this provides a self-consistency check of the meteor input functions produced from the ZCM throughout the solar system.
Below 85 km in the terrestrial atmosphere, Fig. 5 shows that atomic Fe is oxidised in a series of reactions involving O3, O2, CO2 and H2O to form FeO3, Fe(OH)2 and FeOH.64 The latter may also be oxidized by O3 to form FeOOH (which is the building block of the mineral goethite). The reaction kinetics (blue arrows in Fig. 5) and photochemistry of species such as FeOH, FeOOH, FeO3 with H need to be studied experimentally, because they are key to understanding how quickly the metal reservoir species are permanently removed. This is thought to happen through the polymerisation of these compounds together with SiO2 vapour in the mesosphere over several days (brown arrows in Fig. 5), forming nanometre-sized meteoric smoke particles (MSPs) which provide a permanent sink for gas-phase metallic compounds (see ST3).65
The chemistry in Fig. 5 was recently incorporated into a 1-D model of the MLT to study the behavior of the Fe layer over Rothera (Antarctica), where a Fe lidar had been operated for two years.13Fig. 6 (upper panel) illustrates the observed seasonal variation of the layer height profile. As in the case of Na layer (Fig. 4), the minimum occurs during the summer months when the MLT is cold and noctilucent clouds are present. The maximum in the Fe layer occurs in late autumn rather than mid-winter, because the MLT temperature and the meteor input function both maximize then.13 The lower panel of Fig. 6 shows that the model is able to capture this seasonal variation, as well as the correct height of the peak of the layer.
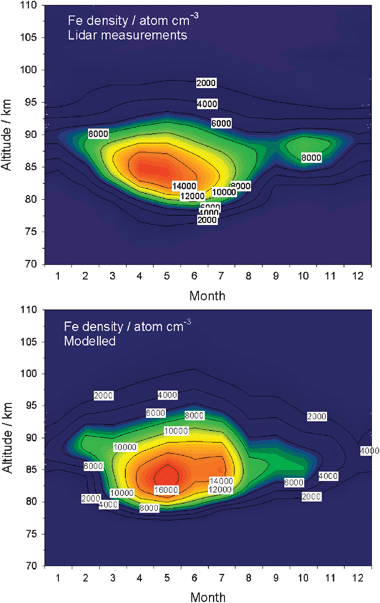 | ||
| Fig. 6 Seasonal variation of the Fe layer vertical profile at Rothera (Antarctica). Top panel: lidar measurements. Bottom panel: model simulation with an Fe injection rate equivalent to an IDP input of 6 t d−1.13 | ||
Strikingly, an IDP input of only 6 t d−1 was required for the model to produce the observed absolute Fe concentration. However, this depends crucially on the rate of vertical transport of the ablated Fe through the MLT to below 80 km, where it is presumed to be permanently removed as MSPs. A previous modelling study of the Na layer12 showed that the size of the IDP input required to model the observed atomic Na layer correlates roughly linearly with the vertical eddy diffusion coefficient (Kzz). Since Kzz is itself a poorly known parameterisation of vertical transport, measurements of metal atom concentrations do not directly constrain the IDP input rate.
Four components of vertical transport in the MLT have been identified recently.66 These are: the residual mean circulation (downwards in winter, reverse in summer); turbulent (eddy) diffusion, produced by breaking gravity waves; downwards dynamical transport caused by dissipating gravity waves; and chemical transport, where wave action and irreversible chemical loss at a lower altitude (e.g. to form MSPs) produces a net flux. A high performance metal resonance lidar has been used to measure the Na atom density and vertical wind profiles simultaneously; the average of their product yields the vertical Na atom flux as a function of height.66 The annual-average downward Na flux measured at the Starfire Optical Range (New Mexico) corresponds to an IDP input of about 24 t d−1. Interestingly, this input is ∼4 times higher than that needed for the 1-D simulation in Fig. 6, which only includes vertical transport by eddy diffusion.13 Dynamical and chemical transport appear to be much more important than turbulent transport, so that until these transport mechanisms are included in models it will not be possible to use the measured metal atom concentrations to constrain the IDP input (or at least the ablated input) reliably. Unfortunately, both dynamical and chemical transport are driven by relatively short period/wavelength gravity waves which cannot yet be resolved explicitly in general circulation models.
Nevertheless, the relative concentrations of the different meteoric metal atoms provide valuable information. Now that the relevant ion-molecule and neutral reactions of Na-, Fe-, Mg- and Ca-containing species have been studied in detail in the laboratory,6,12,56,64,67–71 the atmospheric chemistries of these metals can be reasonably well quantified in a model. This means that more robust conclusions can be drawn regarding the relative meteoric ablation rates of Na, Fe, Mg and Ca that are required to reproduce lidar measurements of the metals. In the case of Na and Fe, modelling a set of lidar observations of both metals at South Pole showed that the Fe ablation rate, relative to that of Na, needed to be reduced by a factor of ∼4.72 That is, the Fe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na ablation rates need to be ∼4
Na ablation rates need to be ∼4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, compared to their chondritic ratios of 15
1, compared to their chondritic ratios of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The Mg ablation rate needs to be decreased relative to that of Na by a factor of ∼5, while Ca ablation rate needs to be decreased by a factor of ∼40.57 These relative ablation factors therefore increase as the element becomes more refractory. As discussed in ST1, significant differential ablation will occur if most of the incoming IDs are small and/or slow, i.e. in close to prograde orbits. Alternatively, the evaporation coefficients39 for the refractory elements in the Herz–Knudsen equation (eqn (III)) could be much less than unity.
1. The Mg ablation rate needs to be decreased relative to that of Na by a factor of ∼5, while Ca ablation rate needs to be decreased by a factor of ∼40.57 These relative ablation factors therefore increase as the element becomes more refractory. As discussed in ST1, significant differential ablation will occur if most of the incoming IDs are small and/or slow, i.e. in close to prograde orbits. Alternatively, the evaporation coefficients39 for the refractory elements in the Herz–Knudsen equation (eqn (III)) could be much less than unity.
However, this creates a potential difficulty. If there is a population of meteoroids that lose all their volatile elements (Na and K), but do not then ablate completely, this implies that the particles must have melted (diffusion of Na and K through the solid particles would be too slow to allow them to escape into the gas phase). If a particle of mass greater than 10−9 g survives atmospheric entry, then it should sediment rapidly to the earth's surface (within a day). Hence, there should be a fairly homogeneous scattering of once-molten IDPs at the surface. These particles are termed cosmic spherules, and can be identified in polar ice because they are close to perfectly spherical and glassy, having melted during atmospheric entry.
The accretion rate of cosmic spherules has been measured by retrieving them from the bottom of an ice chamber used for a drinking water tank at the Scott–Amundsen base at South Pole.73 The flux and size distribution of 50–700 μm diameter particles, corresponding to particles in the mass range from 0.2 to 500 μg, were used in the study. This mass range covers the bulk of IDP particles (Fig. 2), so these cosmic spherules should provide a useful measure of the bulk of IDPs which underwent partial ablation. Furthermore, because the spherules sediment rapidly through the atmosphere, they are not subject to atmospheric circulation, as in the case of the much smaller MSPs (see ST 5). Thus, the flux measured at South Pole should be a good measure of the flux of unablated IDP material. This flux corresponds to a global input of 7.4 ± 0.9 t d−1.73
If the average meteoroid entry velocity peaks around 25 km s−1 based on radar measurements (see ST 1), then about 90% of the incoming mass should ablate.5,73 This would imply that the total IDP input was around 74 t d−1. However, that would not explain why a fraction of only ∼0.25 of the incoming Fe and Mg ablated relative to Na. Since these are the major meteoric constituents, the implication would be that the total IDP input is only around 7.4/(1–0.25) = 10 t d−1. That in turn would imply that the average entry velocity is less than 15 km s−1i.e., most of the IDPs are in a prograde orbit, in accord with the ZCM.1
ST3. Formation and impact of MSPs in the upper mesosphere
A measurement of the size distribution (or volume density) of MSPs in the middle mesosphere should provide another constraint on the IDP input. MSPs can be measured directly above 70 km by rocket-borne particle detectors.74–76 However, these detectors measure only those particles that are charged. Thus, the total MSP concentration is obtained by dividing the measured number by the estimated fraction of charged particles in the plasma. Because the plasma density in the D region is in the region of 100–1000 cm−3, similar to the number density of MSPs, the modelled fraction of MSPs which are charged is sensitive to a number of poorly known parameters (e.g. electron-particle attachment rates, positive ion-charged particle recombination rates).74 In order to improve this situation, a new particle detector has recently been flown which contains a pulsed VUV lamp to photo-detach electrons from negatively charged particles (the ECOMA instrument).77 Importantly, instruments of this type could potentially measure the MSP volume density (the number of electrons on an MSP should scale with its volume), rather than the number density, once photo-detachment rates from MSP analogues have been measured in the laboratory.77 The total MSP volume density could then be related to the IDP input. It is worth noting that the MSP number density and size have also been estimated by analysing the backscatter signals from HPLA radars,78 although this is a less direct technique.An important reason for studying MSPs in the mesosphere is their relation to noctilucent clouds (NLCs). These clouds were first reported in 1885, and have been growing brighter and spreading to lower latitudes through much of the last century, so that they appear to be a clear signal of climate change.79 NLCs occur between 80 and 86 km, at high latitudes in the summer where the temperature falls below 150 K and H2O vapour, which is present at mixing ratios of only a few parts per million, is then able to form ice particles spontaneously.7 An important uncertainty in NLC research is the nature of the nuclei on which the ice particles grow. Understanding this is important because changes to the dominant meridional circulation in the mesosphere (which is driven by gravity waves from the lower atmosphere6) may alter the supply of nuclei, which would then affect both the occurrence frequency and brightness of the clouds. Furthermore, the increasingly consistent estimates of ice cloud particle numbers obtained from lidar, radar and satellite observations7 can be linked back to the MSP number density and hence to the IDP input.
Electronic structure calculations have recently been used to demonstrate that the smallest MSPs which should act as ice nuclei are the metal silicate molecules FeSiO3 and MgSiO3.80 This is because MgSiO3 and FeSiO3 have extremely large electric dipole moments of 12.2 and 9.5 Debye, respectively, so that H2O molecules bind to them with large negative free energies. The hydration thermodynamics indicate that ice nucleation should occur at a temperature around 140 K for a H2O mixing ratio of 4 ppm, typical of the polar summer mesosphere where NLCs form.
ST4. MSPs in the lower mesosphere, stratosphere and upper troposphere
Below 80 km, ultrafine particles (diameter <10 nm) do not sediment rapidly. Instead, whole atmosphere circulation models predict that MSPs should be swept to the winter pole by the mean meridional circulation in the mesosphere before downward transport within the polar vortex to the lower stratosphere.81–83 Indeed, recent airborne measurements have revealed a 3-fold increase of the meteoritic content of stratospheric sulphate aerosol inside the winter Arctic vortex.84 During the months which MSPs spend in the mesosphere and upper stratosphere, the particles are likely to grow by agglomerative coagulation, which can be very rapid because of the long-range magnetic dipole forces between the Fe-containing particles.85 Models predict that the particles could grow to around 40 nm in radius by the time they reach the middle stratosphere around 30 km.81,82An important constraint on the IDP input is the optical extinction caused by MSPs between about 40 and 75 km. It has recently become possible to measure these small extinctions (as low as 10−8 km−1), using a visible/near-IR spectrometer on the Aeronomy of Ice in the Mesosphere (AIM) satellite.15 Extinction measurements indicate that the MSP composition is probably olivine (Mg2xFe2−2xSiO4, x = 0.4). However, the refractive indices used for this study were for bulk crystalline minerals, whereas MSPs are nm-size (and likely amorphous) particles; very small particles often have quite different refractive indices.86 The particles are also likely to be chemically weathered by H2O and H2SO4 during the months they spend descending into the stratosphere; this will probably lead to hydroxide and sulphate groups on the particle surfaces which again may change their optical properties significantly. Measured refractive index data on realistic particles are needed to relate the observed atmospheric extinctions to the MSP volume densities, and hence through a general circulation model to the IDP input.
Metal-rich MSPs should readily remove acidic species (e.g. H2SO4, HCl, HNO3) from the gas phase. This may explain the unexpected decrease of H2SO4 measured by mass spectrometry on balloons in the upper stratosphere.87–89 Indeed, a recent study83 using the UK Met Office's Unified Model has shown that the observed removal of H2SO4 could be explained if the uptake coefficient of H2SO4 on MSPs is greater than 10−2 (for an IDP input of around 20 t d−1). If the uptake coefficient of H2SO4 on MSP analogue particles could be determined in the future, this type of modelling exercise could be reversed to obtain the volumetric surface area of MSPs in the upper stratosphere, and hence the IDP input.
Airborne flights of an aerosol mass spectrometer in the mid-latitude lower stratosphere have shown that sulphate particles contain ∼0.75 wt% and ∼0.2 wt% of meteoric Fe and Mg, respectively.14 These fractions are even higher inside the winter polar vortices.84 A recent laboratory study83 showed that amorphous Fe-Mg-silicate particles dissolve in concentrated H2SO4 solutions at temperatures down to 230 K (typical lower stratospheric temperatures) on a time scale of less than a week. In fact, the very high concentrations of Fe and Mg measured by the airborne mass spectrometer14 imply that these metals are mostly in the form of solid sulphate particles in the droplets. Solid particles can act as efficient heterogeneous nuclei; this may explain an earlier laboratory study90 which found that concentrated binary H2SO4-H2O solutions containing FeSO4 and MgSO4 freeze to form sulphuric acid tetrahydrate (SAT) between 12 and 20 K higher than supercooled pure solutions.
Explaining nitric acid trihydrate (NAT) formation from the tertiary HNO3-H2SO4-H2O system in the winter polar stratosphere has been a long-standing problem. Homogeneous nucleation of NAT is too slow to account for observed NAT particles in the polar vortex,91 and MSPs have therefore been proposed as likely heterogeneous nuclei.92 Although experiments have been performed with silica particles93 and ground-up meteorites,94 neither of these surrogates is representative of the amorphous, fractal-like nature of MSPs,65,85 so that the nucleating ability of realistic MSP analogues should be investigated.
MSPs could therefore modify the O3 depletion in the lower stratosphere resulting from chlorine activation on PSCs and de-nitrification.92 A detailed understanding of interactions between MSPs and stratospheric aerosols will be important for accurate predictions as the stratosphere cools over the next century.95 Also, in the context of proposed geo-engineering plans to increase the sulphate aerosol by pumping SO2 into the stratosphere (in order to increase the amount of solar radiation scattered directly back to space, thus counteract greenhouse gas-driven warming in the troposphere),96 a quantitative assessment should be made of the possible effects caused by meteoric debris.
ST5. deposition to the surface
The IDP input has been estimated from the accumulation of several different elements – Ir, Pt and super-paramagnetic Fe – in ice cores.16–18,97,98 The deposition flux is determined by measuring the concentration of the element in the ice sample, and using the snow accumulation rate to obtain the flux. Ir, Pt and Fe also occur in terrestrial dust, so the terrestrial signal has to be carefully removed. In the case of Ir and Pt, these elements are highly enriched in cosmic dust compared with crustal dust.18,98 This enrichment occurs because they are both siderophile elements, so that Ir and Pt present in the original solar nebula from which the Earth formed are now mostly dissolved in the molten iron core rather than in crustal rocks. Super-paramagnetic Fe occurs in Fe-rich particles trapped in the ice. Meteoric smoke particles are much smaller than terrestrial dust, so the MSPs can be selectively observed by cooling the ice sample to 77 K and then allowing it to warm. The MSPs (which are estimated to have radii between 3 and 9 nm 97) become mobile in the ice lattice at temperatures just above 100 K, and their paramagnetism measured. Terrestrial dust exhibits its paramagnetism at much higher temperatures (>200 K).16–17,97 Measurements in ice cores in central Greenland,17,18 and Vostok in the Eastern Antarctic highlands,16 reveal a consistent picture: the deposition rate in Greenland is ∼10 times higher than at Vostok, and the Greenland estimate of the IDP input is at the high end of the range in Table 1 (175–224 t d−1). Similarly, the measured accumulation of Ir20 and Os19 in ocean-floor sediments indicates that the meteoric influx is around 240 t d−1.How can these very high fluxes be reconciled with the estimates from within the atmosphere, which seem to be consistent with a flux of less than 50 t d−1 (Table 1)? Interpreting the ice core flux measurements requires understanding the transport of MSPs into the troposphere, and their subsequent deposition mechanisms. For instance, in the study18 of Ir/Pt in the Greenland ice core it was postulated that MSPs descended from the mesosphere into the troposphere within the winter polar vortex, causing a localised concentration of MSPs at polar latitudes and hence the high deposition flux. However, a recent study83 of MSP transport using the Unified Model indicates that once MSPs reach the lower stratosphere in either polar vortex, they mostly enter the troposphere through mid-latitude tropopause folding. Dry deposition should then be reasonably uniform (within a factor of 2) over the entire earth's surface.
There are two problems with a uniform distribution of MSP deposition. First, it implies that the IDP flux really is much greater than 200 t d−1. Second, it does not explain why the deposition in Greenland is so much higher than Eastern Antarctica. The answer to the second point is that the snowfall rate in central Greenland is about 7 times greater than the Antarctic interior, implying that wet deposition is a more important removal mechanism for MSPs than dry deposition.97 Assuming that this is the case, the deposition map in Fig. 7 was generated by simply multiplying the precipitation rate by the MSP concentration in the lowest layer of the Unified Model, and then scaling to the Greenland ice core flux. Inspection of the figure shows that the deposition flux in central Greenland is about 7 times larger than in eastern Antarctica, in agreement with the measurements. However, the global IDP input is only reduced to 210 t d−1, so this serious discrepancy with the atmospheric estimates in Table 1 remains.
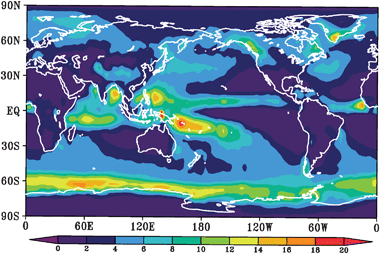 | ||
| Fig. 7 Annual-averaged flux of MSPs to the earth's surface by wet deposition predicted by the Unified Model (Units: 10−11 g cm−2 d−1). Plot provided by S. Dhomse (University of Leeds). | ||
Fig. 7 shows that the model predicts a large MSP deposition flux into the Southern Ocean around the coastal shelf of Antarctica (particularly in the Pacific sector), where the supply of bio-available iron to phytoplankton is limited.8 The estimated input from the Unified Model is ∼3 μmol Fe m−2 y−1, compared with an Aeolian dust input of ∼30 μmol Fe m−2 y−1.99 However, unlike continental mineral dust which has a low solubility (estimates vary from <1 to 10%), the MSP Fe should be in the form of highly soluble Fe2SO4 after processing in the stratospheric sulphate layer (see ST4 above). Thus, the input of bio-available Fe from IDPs is likely to at least as large as (and perhaps an order of magnitude greater than) the Aeolian dust input. This could have significant climate implications because phytoplankton both draw down CO2 and produce dimethyl sulphide, which evades into the atmosphere and contributes to the formation of ultra-fine aerosol which may grow large enough to act as cloud condensation nuclei.100
Conclusions
The magnitude of the IDP input is uncertain by at least a factor of 10. This review has examined some of the different ways which can be used to determine this input, ranging from a solar system dust model to deposition at the Earth's surface. In each case, key uncertainties have been identified and future courses of action suggested to address them. To summarize, estimates of the IDP input fall into three ranges:• 5–10 t d−1: this range is supported by: models of the metal layers in the MLT (although these models only include vertical transport by eddy diffusion); and the micrometeorite flux if the average entry velocity <15 km s−1, which then also explains the differential ablation of Ca and Fe relative to Na.
• 20–50 t d−1: this range is supported by: the micrometeorite flux if the average entry velocity >20 km s−1 (although then differential ablation is limited); MSP optical extinction in the middle atmosphere; the meteoritic content of stratospheric sulphate particles; and probably by MLT models if dynamical and chemical transport terms are included.
• 100–300 t d−1: this range is supported by spaceborne IDP detection (the LDEF experiment), and by the ZCM, although in both cases the estimates are reduced into the middle range if constrained by meteor radar measurements of entry velocity; the high range is also supported by surface deposition measurements, though there is uncertainty concerning transport into the troposphere and deposition mechanisms.
Finally, it is worth emphasising two points. First, the ablation of cosmic dust plays a number of significant roles throughout the atmosphere from the thermosphere to the surface, and some of these may be even more important if the IDP input is close to the upper end of current estimates. Second, even if the IDP input is close to the lower end of the range, this indicates that there are important gaps in understanding the evolution of dust in the solar system, and the transport processes coupling the different regions of the atmosphere.
Acronyms
| CABMOD | Chemical Ablation Model |
| DR | dissociative recombination (with electrons) |
| HPLA | high performance large aperture (radar) |
| IDP | interplanetary dust particle |
| LDEF | Long Duration Exposure Facility |
| MIF | meteoric input function |
| MLT | mesosphere/lower thermosphere |
| MSP | meteoric smoke particle |
| NAT | nitric acid trihydrate |
| NLC | noctilucent cloud |
| PSC | polar stratospheric cloud |
| SAT | sulphuric acid tetrahydrate |
| ST | Science Topic |
| UM | Unified Model |
| ZCM | Zodiacal Cloud Model. |
Acknowledgements
This study was supported by project number 291332 (CODITA – Cosmic Dust in the Terrestrial Atmosphere) from the European Research Council. The author thanks Dr Sandip Dhomse and Professor Martyn Chipperfield for providing unpublished data from the Unified Model.Notes and references
- D. Nesvorny, P. Jenniskens, H. F. Levison, W. F. Bottke, D. Vokrouhlicky and M. Gounelle, Astrophys. J., 2009, 713, 816–836 Search PubMed.
- I. P. Williams, in Meteors in the earth's atmosphere, ed. E. Murad and I. P. WIlliams, Cambridge University Press, Cambridge, 2002, pp. 2–32 Search PubMed.
- Z. Ceplecha, J. Borovicka, W. G. Elford, D. O. Revelle, R. L. Hawkes, V. Porubcan and M. Simek, Space Sci. Rev., 1998, 84, 327–471 CrossRef CAS.
- P. Jenniskens, Earth Planets Space, 1998, 50, 555–567 CAS.
- T. Vondrak, J. M. C. Plane, S. Broadley and D. Janches, Atmos. Chem. Phys., 2008, 8, 7015–7031 CrossRef CAS.
- J. M. C. Plane, Chem. Rev., 2003, 103, 4963–4984 CrossRef CAS.
- M. Rapp and G. E. Thomas, J. Atmos. Sol.–Terr. Phys., 2006, 68, 715–744 CrossRef.
- K. S. Johnson, Global Biogeochem. Cycles, 2001, 15, 61–63 CrossRef CAS.
- S. G. Love and D. E. Brownlee, Science, 1993, 262, 550–553 CAS.
- J. D. Mathews, D. Janches, D. D. Meisel and Q. H. Zhou, Geophys. Res. Lett., 2001, 28, 1929–1932 CrossRef.
- D. W. Hughes, in Cosmic Dust, ed. J. A. M. McDonnell, Wiley, London, 1978, pp. 123–185 Search PubMed.
- J. M. C. Plane, Atmos. Chem. Phys., 2004, 4, 627–638 CrossRef CAS.
- C. S. Gardner, X. Z. Chu, P. J. Espy, J. M. C. Plane, D. R. Marsh and D. Janches, J. Geophys. Res., 2011, 116, D02304 CrossRef.
- D. J. Cziczo, D. S. Thomson and D. M. Murphy, Science, 2001, 291, 1772–1775 CrossRef CAS.
- M. E. Hervig, L. L. Gordley, L. E. Deaver, D. E. Siskind, M. H. Stevens, J. M. Russell, S. M. Bailey, L. Megner and C. G. Bardeen, Geophys. Res. Lett., 2009, 36, L18805 CrossRef.
- L. Lanci, D. V. Kent and P. E. Biscaye, Geophys. Res. Lett., 2007, 34, L10803 CrossRef.
- L. Lanci and D. V. Kent, Geophys. Res. Lett., 2006, 33, L13308 CrossRef.
- P. Gabrielli, C. Barbante, J. M. C. Plane, A. Varga, S. Hong, G. Cozzi, V. Gaspari, F. A. M. Planchon, W. Cairns, C. Ferrari, P. Crutzen, P. Cescon and C. F. Boutron, Nature, 2004, 432, 1011–1014 CrossRef CAS.
- B. Peucker-Ehrenbrink, Geochim. Cosmochim. Acta, 1996, 60, 3187–3196 CrossRef CAS.
- J. T. Wasson and F. T. Kyte, Geophys. Res. Lett., 1987, 14, 779–783 CrossRef.
- G. J. Flynn, in Meteors in the earth's atmosphere, ed. E. Murad and I. P. WIlliams, Cambridge University Press, Cambridge, 2002 Search PubMed.
- W. J. Baggaley, in Meteors in the earth's atmosphere, ed. E. Murad and I. P. Williams, Cambridge University Press, Cambridge, 2002, pp. 123–148 Search PubMed.
- D. Janches, J. D. Mathews, D. D. Meisel and Q. H. Zhou, Icarus, 2000, 145, 53–63 CrossRef.
- A. Pellinen-Wannberg and G. Wannberg, J. Geophys. Res., 1994, 99, 11379–11390 CrossRef.
- S. Close, S. Hunt, M. Minardi and F. McKeen, Radio Sci., 2000, 35, 1233–1240 CrossRef.
- S. Close, P. Brown, M. Campbell-Brown, M. Oppenheim and P. Colestock, Icarus, 2007, 186, 547–556 CrossRef.
- D. Janches, S. Close and J. T. Fentzke, Icarus, 2008, 193, 105–111 CrossRef.
- D. Janches, C. J. Heinselman, J. L. Chau, A. Chandran and R. Woodman, J. Geophys. Res., 2006, 111, A07317 CrossRef.
- J. G. Molina-Cuberos, J. J. Lopez-Moreno and F. Arnold, Space Sci. Rev., 2008, 137, 175–191 CrossRef CAS.
- S. G. Love and D. E. Brownlee, Icarus, 1991, 89, 26–43 CrossRef.
- O. Kalashnikova, M. Horanyi, G. E. Thomas and O. B. Toon, Geophys. Res. Lett., 2000, 27, 3293–3296 CrossRef CAS.
- D. M. Hunten, R. P. Turco and O. B. Toon, J. Atmos. Sci., 1980, 37, 1342–1357 CrossRef CAS.
- F. J. M. Rietmeijer, Meteorit. Planet. Sci., 2000, 35, 1025–1042 CrossRef CAS.
- F. J. M. Rietmeijer, in Meteors in the earth's atmosphere, ed. E. Murad and I. P. Williams, Cambridge University Press, Cambridge, 2002, pp. 215–245 Search PubMed.
- E. Anders and M. Ebihara, Geochim. Cosmochim. Acta, 1982, 46, 2363–2380 CrossRef CAS.
- J. Jones and T. R. Kaiser, Mon. Not. R. Astr. Soc., 1966, 133, 411–420 Search PubMed.
- J. B. Fegley and A. G. W. Cameron, Earth Planet. Sci. Lett., 1987, 82, 207–222 CrossRef.
- D. Janches, L. P. Dyrud, S. L. Broadley and J. M. C. Plane, Geophys. Res. Lett., 2009, 36, L06101 CrossRef.
- C. Alexander, Meteorit. Planet. Sci., 2002, 37, 245–256 CrossRef CAS.
- D. Nesvorny, D. Janches, D. Vokrouhlicky, P. Pokorny, W. F. Bottke and P. Jenniskens, Astrophys. J., 2011, 743, 129 CrossRef.
- J. M. C. Plane, Int. Rev. Phys. Chem., 1991, 10, 55–106 CrossRef CAS.
- R. J. States and C. S. Gardner, J. Atmos. Sci., 2000, 57, 66–77 CrossRef.
- C. S. Gardner and M. J. Taylor, J. Geophys. Res., 1998, 103, 6427–6437 CrossRef.
- V. Eska, J. Hoffner and U. von Zahn, J. Geophys. Res., 1998, 103, 29207–29214 CrossRef CAS.
- F. J. Lübken, J. Höffner, T. P. Viehl, B. Kaifler and R. J. Morris, Geophys. Res. Lett., 2011, 38, L24806 CrossRef.
- X. Z. Chu, W. L. Pan, G. C. Papen, C. S. Gardner and J. A. Gelbwachs, Appl. Opt., 2002, 41, 4400–4410 CrossRef.
- B. R. Clemesha, D. M. Simonich, H. Takahashi, S. M. L. Melo and J. M. C. Plane, J. Geophys. Res., 1995, 100, 18909–18916 CrossRef.
- E. Kopp, J. Geophys. Res., 1997, 102, 9667–9674 CrossRef CAS.
- J. M. Grebowsky and A. C. Aikin, in Meteors in the earth's atmosphere, ed. E. Murad and I. P. Williams, Cambridge University Press, Cambridge, 2002, pp. 189–214 Search PubMed.
- J. A. Gardner, E. Murad, R. A. Viereck, D. J. Knecht, C. P. Pike and A. L. Broadfoot, Adv. Space Res., 1998, 21, 867–870 CrossRef CAS.
- Z. Y. Fan, J. M. C. Plane, J. Gumbel, J. Stegman and E. J. Llewellyn, Atmos. Chem. Phys., 2007, 7, 4107–4115 CrossRef CAS.
- J. Correira, A. C. Aikin, J. M. Grebowsky, W. D. Pesnell and J. P. Burrows, Geophys. Res. Lett., 2008, 35, L06103 CrossRef.
- M. Scharringhausen, A. C. Aikin, J. P. Burrows and M. Sinnhuber, J. Geophys. Res., 2008, 113, D13303 CrossRef.
- J. M. C. Plane, B. J. Murray, X. Z. Chu and C. S. Gardner, Science, 2004, 304, 426–428 CrossRef CAS.
- S. Raizada, M. Rapp, F. J. Lübken, J. Höffner, M. Zecha and J. M. C. Plane, J. Geophys. Res., 2007, 112, D08307 CrossRef.
- J. M. C. Plane, in Meteors in the earth's atmosphere, ed. E. Murad and I. P. Williams, Cambridge University Press, Cambridge, 2002, pp. 289–309 Search PubMed.
- M. Gerding, M. Alpers, U. von Zahn, R. J. Rollason and J. M. C. Plane, J. Geophys. Res., 2000, 105, 27131–27146 CrossRef CAS.
- K. R. S. Woodcock, T. Vondrak, S. R. Meech and J. M. C. Plane, Phys. Chem. Chem. Phys., 2006, 8, 1812–1821 RSC.
- M. Pätzold, S. Tellman, B. Häusler, D. Hinson, R. Schaa and G. L. Tyler, Science, 2005, 310, 837–839 CrossRef.
- P. Withers, M. Mendillo, D. P. Hinson and K. Cahoy, J. Geophys. Res., 2008, 113, A12314 CrossRef.
- M. Pätzold, S. Tellmann, B. Häusler, M. K. Bird, G. L. Tyler, A. A. Christou and P. Withers, Geophys. Res. Lett., 2009, 36, L05203 CrossRef.
- A. J. Kliore, A. F. Nagy, E. A. Marouf, R. G. French, F. M. Flasar, N. J. Rappaport, A. Anabttawi, S. W. Asmar, D. S. Kahann, E. Barbinis, G. L. Goltz, D. U. Fleischman and D. J. Rochblatt, J. Geophys. Res., 2008, 113, A09317 CrossRef.
- C. L. Whalley and J. M. C. Plane, Faraday Discuss., 2010, 147, 349–368 RSC.
- D. E. Self and J. M. C. Plane, Phys. Chem. Chem. Phys., 2003, 5, 1407–1418 RSC.
- R. W. Saunders and J. M. C. Plane, Icarus, 2011, 212, 373–382 CrossRef CAS.
- C. S. Gardner and A. Z. Liu, J. Geophys. Res., 2010, 115, D20302 CrossRef.
- S. L. Broadley and J. M. C. Plane, Phys. Chem. Chem. Phys., 2010, 12, 9095–9107 RSC.
- S. L. Broadley, T. Vondrak and J. M. C. Plane, Phys. Chem. Chem. Phys., 2007, 9, 4357–4369 RSC.
- S. L. Broadley, T. Vondrak, T. G. Wright and J. M. C. Plane, Phys. Chem. Chem. Phys., 2008, 10, 5287–5298 RSC.
- C. L. Whalley, J. C. Gomez Martin, T. G. Wright and J. M. C. Plane, Phys. Chem. Chem. Phys., 2011, 13, 6352–6364 RSC.
- J. M. C. Plane and C. L. Whalley, J. Phys. Chem. A, 2012 DOI:10.1021/jp211526h.
- C. S. Gardner, J. M. C. Plane, W. L. Pan, T. Vondrak, B. J. Murray and X. Z. Chu, J. Geophys. Res., 2005, 110, D1030210 CrossRef.
- S. Taylor, J. H. Lever and R. P. Harvey, Nature, 1998, 392, 899–903 CrossRef CAS.
- M. Rapp, I. Strelnikova and J. Gumbel, Adv. Space Res., 2007, 40, 809–817 CrossRef.
- K. A. Lynch, L. J. Gelinas, M. C. Kelley, R. L. Collins, M. Widholm, D. Rau, E. MacDonald, Y. Liu, J. Ulwick and P. Mace, J. Geophys. Res., 2005, 110, A03302 CrossRef.
- L. J. Gelinas, K. A. Lynch, M. C. Kelley, R. L. Collins, M. Widholm, E. MacDonald, J. Ulwick and P. Mace, J. Geophys. Res., 2005, 110, A01310 CrossRef.
- M. Rapp, I. Strelnikova, B. Strelnikov, P. Hoffmann, M. Friedrich, J. Gumbel, L. Megner, U. P. Hoppe, S. Robertson, S. Knappmiller, M. Wolff and D. R. Marsh, J. Geophys. Res., 2010, 115, D00I16 CrossRef.
- J. T. Fentzke, D. Janches, I. Strelnikova and M. Rapp, J. Atmos. Sol.–Terr. Phys., 2009, 71, 1982–1991 CrossRef CAS.
- E. P. Shettle, M. T. DeLand, G. E. Thomas and J. J. Olivero, Geophys. Res. Lett., 2009, 36, L02803 CrossRef.
- J. M. C. Plane, J. Atmos. Sol.–Terr. Phys., 2011, 73, 2192–2200 CrossRef CAS.
- C. G. Bardeen, O. B. Toon, E. J. Jensen, D. R. Marsh and V. L. Harvey, J. Geophys. Res., 2008, 113, D17202 CrossRef.
- L. Megner, D. E. Siskind, M. Rapp and J. Gumbel, J. Geophys. Res., 2008, 113, D03202 CrossRef.
- R. W. Saunders, S. Dhomse, W. S. Tian, M. P. Chipperfield and J. M. C. Plane, Atmos. Chem. Phys., 2012, 12, 4387–4398 CrossRef.
- J. Curtius, R. Weigel, H. J. Vossing, H. Wernli, A. Werner, C. M. Volk, P. Konopka, M. Krebsbach, C. Schiller, A. Roiger, H. Schlager, V. Dreiling and S. Borrmann, Atmos. Chem. Phys., 2005, 5, 3053–3069 CrossRef CAS.
- R. W. Saunders and J. M. C. Plane, J. Atmos. Sol.–Terr. Phys., 2006, 68, 2182–2202 CrossRef.
- D. R. Huffman, Adv. Phys., 1977, 26, 129–230 CrossRef CAS.
- M. J. Mills, O. B. Toon, V. Vaida, P. E. Hintze, H. G. Kjaergaard, D. P. Schofield and T. W. Robinson, J. Geophys. Res., 2005, 110, D08201 CrossRef.
- E. Arijs, D. Nevejans, J. Ingels and P. Frederick, J. Geophys. Res., 1985, 90, 5891–5896 CrossRef CAS.
- F. Arnold, R. Fabian and W. Joos, Geophys. Res. Lett., 1981, 8, 293–296 CrossRef CAS.
- M. E. Wise, S. D. Brooks, R. M. Garland, D. J. Cziczo, S. T. Martin and M. A. Tolbert, J. Geophys. Res., 2003, 108, 4434 CrossRef.
- D. A. Knopf, J. Phys. Chem. A, 2006, 110, 5745–5750 CrossRef CAS.
- C. Voigt, H. Schlager, B. P. Luo, A. D. Dornbrack, A. Roiger, P. Stock, J. Curtius, H. Vossing, S. Borrmann, S. Davies, P. Konopka, C. Schiller, G. Shur and T. Peter, Atmos. Chem. Phys., 2005, 5, 1371–1380 CrossRef CAS.
- A. Bogdan, M. J. Molina, M. Kulmala, A. R. MacKenzie and A. Laaksonen, J. Geophys. Res., 2003, 108, 4302 CrossRef.
- U. M. Biermann, T. Presper, T. Koop, J. Mossinger, P. J. Crutzen and T. Peter, Geophys. Res. Lett., 1996, 23, 1693–1696 CrossRef CAS.
- Scientific Assessment of Ozone Depletion: 2010, WMO/UNEP, Geneva, 2011.
- S. Tilmes, R. Muller and R. Salawitch, Science, 2008, 320, 1201–1204 CrossRef CAS.
- L. Lanci, B. Delmonte, D. V. Kent, V. Maggi, P. E. Biscaye and J. R. Petit, Quat. Sci. Rev., 2012, 33, 20–31 CrossRef.
- P. Gabrielli, J. M. C. Plane, C. F. Boutron, S. M. Hong, G. Cozzi, P. Cescon, C. Ferrari, P. J. Crutzen, J. R. Petit, V. Y. Lipenkov and C. Barbante, Earth Planet. Sci. Lett., 2006, 250, 459–469 CrossRef CAS.
- C. Lancelot, A. de Montety, H. Goosse, S. Becquevort, V. Schoemann, B. Pasquer and M. Vancoppenolle, Biogeosciences, 2009, 6, 2861–2878 CrossRef CAS.
- A. J. Watson, D. C. E. Bakker, A. J. Ridgwell, P. W. Boyd and C. S. Law, Nature, 2000, 407, 730–733 CrossRef CAS.
Footnote |
| † Part of the atmospheric chemistry themed issue. |
| This journal is © The Royal Society of Chemistry 2012 |
