Glutathione: mechanism and kinetics of its non-enzymatic defense action against free radicals
Annia
Galano
*a and
J. Raúl
Alvarez-Idaboy
*ab
aDepartamento de Química. Universidad Autónoma Metropolitana-Iztapalapa, San Rafael Atlixco 186, Col. Vicentina. Iztapalapa, C. P. 09340, México D. F. México. E-mail: agal@xanum.uam.mx; jidaboy@unam.mx
bFacultad de Química, Departamento de Física y Química Teórica, Universidad Nacional Autónoma de México, México, DF 04510, México
First published on 25th October 2011
Abstract
Glutathione, which is the most abundant cytosolic thiol, plays important roles in the non-enzymatic antioxidant defence system. Its free radical scavenging activity towards radicals of different nature (·OH, ·OOH, ·OCH3, ·OOCH3, ·OOCHCH2 and ·OOCCl3) have been studied in aqueous solution, using the Density Functional Theory. It was found that the rate constants range from 2.02 × 104 M−1s−1 to diffusion limit (7.68 × 109 M−1s−1). Therefore it can be stated that glutathione is an excellent free radical scavenger, able of efficiently scavenging a wide variety of free radicals. It reacts exclusively by H transfer, and with the exception of its reaction with ·OH there is only one important channel of reaction, yielding to the S-centered radical. For the reaction with ·OH, on the other hand, a wide product distribution is expected, which explains the formation of C-centered radicals experimentally observed. Glutathione was found to be exceptionally good as a OOH radical scavenger, comparable to 2-propenesulfenic acid. This has been explained based on the strong H bonding interactions found in the transition states, which involves the carboxylate moiety. Therefore this might have implications for other biological systems where this group is present.
Introduction
Glutathione (GSH) is a tripeptide formed by the amino acidsL-glutamate, L-cysteine and L-glycine (Glu-Cys-Gly). It is the most abundant cytosolic thiol with concentrations ranging ∼0.1–10 mM, and plays important roles in the non-enzymatic antioxidant defence and cell signaling systems.1–7GSH is also an essential cofactor to glutathione peroxidases and glutathione S-transferases for detoxifying non-radical oxidants.4 However, in this work we will focus only on the non-enzymatic free radical scavenging activity of GSH.This particular activity has interested the scientific community for over four decades. As early as 1977, Quintiliani et al.8 proposed that H transfer from GSH to carbon radicals appears to be the most likely, non-enzymatic, mechanism of protection of glutathione. This conclusion was in agreement with what had been previously proposed by Adams.9 Shortly after, Sjoberg, et al.10 proposed for the ·OH + GSH reaction that in addition to the sulfur-centered radical formed by electron transfer or H abstraction from glytathione, at least one carbon-centered radical is formed in a pH dependent way. They also proposed that the non-sulfur H abstraction take place from the γcarbon, or from the amino group on the glutamyl moiety. These findings are in line with those reported by Eriksen et al.,11 who found that the OH-induced oxidation of glutathione produce the sulfur-centered radical and two reducing radicals. They suggested that the mechanism involved in the formation of these species is based on pH-dependent conformational changes of GSH, followed by the ·OH addition to the cysteine sulfur, or H abstraction from the α carbon. Abedinzadeh et al.12 also found that OH-induced oxidation of glutathione in neutral aqueous solution produces not only the sulphur-centered radical but at least one other alkyl radical.
Grierson et al. proposed that the thyl radical rapidly decay in aqueous solution by intramolecular rearrangement reactions into non-sulfur centered radicals, which were identified by EPR as the α-amino radical at the glutamyl residue of GSH.13 An intramolecular hydrogen abstraction mechanism for the transformation of thiyl radical to α-amino carbon-centered radical was also postulated by Zhao et al.14 Very recently Hofstetter et al.15 used the UV absorbance signatures of α and β centered radicals and concluded that the equilibrium ratio of S-centered: β-centered: α-centered radicals is, approximately, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
Regarding kinetics, there are previous reports on the rate constants (k) of the GSH reactions with ·OH and ·OCH3 free radicals. Quintiliani et al.8 reported that a value of 1.3 × 1010 M−1s−1 for rate constant of the GSH + ·OH reaction, at pH = 5.5. Eriksen and Fransson11 estimated that the rate constant of this reaction is 1.4 × 1010 and 4.4 × 1010 M−1s−1, at pH = 7.8 and 10.6, respectively. More recently, Mezyk16 reported a lower value for the same reaction, 3.48 × 109 M−1s−1. For the GSH + ·OCH3 reaction, on the other hand, only one value of k has been reported so far. It was estimated by Baker et al.17 and reported to be 9 × 108 M−1s−1, at pH = 8.4.
According to the above mentioned data, there seems to be a general agreement that the reaction of GSH + OH yield not only the sulfur centered radical but also other products. However there are different suggestions regarding which are these products and their proportion. On the other hand, there is no information on such mechanistic aspects for the reactions of GSH with other radicals. Therefore it is the main aim of this work to investigate in detail the reactions of GSH with free radicals of different nature. To that purpose we have studied H transfer and single electron transfer from GSH to ·OH, ·OOH, ·OCH3, ·OOCH3, ·OOCHCH2 and ·OOCCl3. Providing estimations of the branching ratios, and of the relative populations of the formed products, is also a goal of the present work. In addition there is very scarce data regarding the rate constants of the reactions of GSH with free radicals other than ·OH. Thus, kinetic data are also provided, for the first time, for some of these reactions. The calculated rate constants have been compared to the available experimental data to test the reliability of the presented results. The good agreement achieved validates the presented calculations.
Computational details
Geometry optimizations and frequency calculations have been carried out using the M05-2X functional18 and the 6-311+G(d,p) basis set. The M05-2X functional has been recommended for kinetic calculations by their developers,18 and it has been also successfully used by independent authors to that purpose.19–28 Geometry optimizations and frequency calculations have been carried out in solution, using the SMD continuum model29 and water as a solvent. Unrestricted calculations were used for open shell systems and local minima and transition states were identified by the number of imaginary frequencies (NIMAG = 0 or 1, respectively). In the case of the transition states it was verified that the imaginary frequency corresponds to the expected motion along the reaction coordinate, by Intrinsic Coordinate calculations (IRC). All the electronic calculations were performed with Gaussian 09 package of programs.30 Thermodynamic corrections at 298 K were included in the calculation of relative energies. We have not corrected interaction energies for basis set superposition errors (BSSE) because it has been demonstrated that counterpoise corrections overcorrect the BSSE31 and worsens the results.32,33The Gibbs free energies of reaction (ΔG) and the reaction barriers, in terms of Gibbs free energies (ΔG≠) have been calculated as the relative energies of the products and transition states, respectively, with respect to the isolated reactants. The thermodynamic corrections were directly obtained from the calculations in solution, i.e. the variations in G were computed using the Gibbs free energies of the different species in solution.
The solvent cage effects have been included according to the corrections proposed by Okuno,34 taking into account the free volume theory.35 These corrections are in good agreement with those independently obtained by Ardura et al.36 and have been successfully used by other authors.37–42 They are necessary to avoid over-penalizing entropy losses in solution.
The rate constants (k) were calculated using Conventional Transition State Theory (TST)43–45 and 1 M standard state. Reaction path degeneracies and tunneling corrections have been taken into account. The tunneling corrections defined as the Boltzmann average of the ratio of the quantum and the classical probabilities were calculated using the Zero Curvature Tunneling corrections (ZCT).46
Some of the calculated rate constants (k) are close to the diffusion-limit. Accordingly, the apparent rate constant (kapp) cannot be directly obtained from TST calculations. In the present work the Collins–Kimball theory is used to that purpose:47
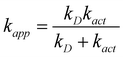 | (1) |
| kD = 4πRDABNA | (2) |
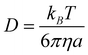 | (3) |
The branching ratios of the different reaction channels, which represent the percent of their contribution to the overall free radical scavenging activity of GSH, have been calculated as:
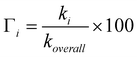 | (4) |
The electronic spectra have been computed using the time dependent density functional theory (TD-DFT), based on vertical excitations involving the 3 lowest lying excited states.
Results and discussion
The first pKa of GSH is 3.59,51 therefore at physiological pH (7.4) the concentration of its protonated form is negligible. Accordingly in the present work we will only consider the anionic form of GHS (GS−). However, there are three possible tautomers of GS− (Fig. 1) and consequently, all of them have been modeled to estimate their relative abundance. According to the calculated Gibbs free energy in aqueous solution, T1 is the lowest in energy. It was found that both T2 and T3 are more than 5 and 9 kcal mol−1 higher in energy than T1. Their relative populations have been estimated, using the Maxwell–Boltzman distribution, and it was found that more than 99% of GS− correspond to T1. Therefore, this is the only tautomer of GS− that is considered in the present work. These results are in agreement with a previous conformational study of glutathione in aqueous solution, reported by Lampela et al.52 Moreover, since a full conformational study of T1 escapes the purpose of the present work, we have used the conformer identified as the most stable in ref. 52.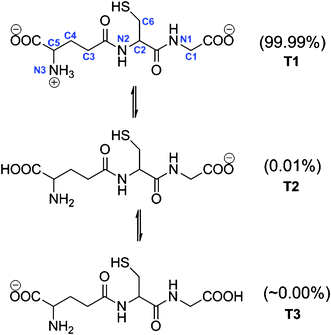 | ||
| Fig. 1 Tautomers of the anionic form of GSH and site numbers. | ||
The mechanisms considered in this work are the single electron transfer (SET) and the H transfer (HT):
Single electron transfer (SET):
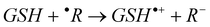 | (5) |
Hydrogen transfer (HT):
 | (6) |
They have been found to play important role in free radical scavenging processes.53–58 The latter has been studied including all the possible reaction sites, which have been numbered as shown in Fig. 1. The Gibbs free energies of reaction (ΔG) are reported in Table 1. As these values show, the single electron transfer process was found to be endergonic for all the studied free radicals. Therefore this mechanism has been ruled out for the free radical scavenging activity of glutathione, under physiological conditions. The values of ΔG are about 20 kcal mol−1 or higher, which is significantly above of the inaccuracy of the performed calculations. Therefore the conclusion that the SET mechanism does not contribute to the overall antioxidant activity of glutathione is reliable.
| R1 | R2 | R3 | R4 | R5 | R6 | |
|---|---|---|---|---|---|---|
| SET | 18.56 | 35.92 | 42.13 | 43.96 | 37.35 | 21.54 |
| C1 | −35.02 | −19.70 | −2.00 | −0.37 | −1.58 | −9.11 |
| C2 | −35.18 | −19.86 | −2.16 | −0.53 | −1.74 | −9.27 |
| C3 | −30.10 | −14.78 | 2.93 | 4.55 | 3.35 | −4.18 |
| C4 | −24.41 | −9.09 | 8.61 | 10.24 | 9.03 | 1.50 |
| C5 | −26.87 | −11.56 | 6.15 | 7.77 | 6.57 | −0.96 |
| C6 | −28.50 | −13.19 | 4.52 | 6.14 | 4.94 | −2.59 |
| N1 | −11.17 | 4.15 | 21.85 | 23.48 | 22.27 | 14.74 |
| N2 | −10.96 | 4.36 | 22.06 | 23.69 | 22.48 | 14.95 |
| N3 | −1.85 | 13.46 | 31.17 | 32.79 | 31.59 | 24.06 |
| S | −38.21 | −22.89 | −5.19 | −3.56 | −4.77 | −12.30 |
The thermochemical viability of the H transfer reactions was found to be highly influenced by the nature of the reacting radical. For the reaction of GS− with the hydroxyl radical all the HT channels of reaction were found to be exergonic. For the GS− + ·OCH3 reaction, the H transfer from S and C sites are predicted to have negative ΔG values, while the HT processes from N sites were found to be endergonic. The reactions involving ·OOH, ·OOCH3, and ·OOCHCH2 radicals were found to be feasible only when the H transfer takes place from sites S, C1, and C2. The GS− + ·OOCCl3 reaction was found to be viable, from a thermochemical point of view, for H transfers from sites S, C1, C2, C3, C5 and C6. These results are in line with chemical intuition and in agreement with previous studies. ·OH is the most electrophilic59 and reactive of the oxygen-centered radicals, with a half-life of ∼10−9 s.60 Compared to ·OH, peroxyl radicals (ROO) are less reactive species capable of diffusing to remote cellular locations.61 Their half-lives are of the order of seconds62 and their electrophilicity is significantly lower than that of ·OH.59 However, if R is a more electron-accepting group, for example R = −CCl3, the ROO radicals significantly increase their reactivity towards organic molecules.63Alkoxyl radicals are significantly more reactive than ROO radicals, provided that R is the same in both species,64–68 while they are less reactive than ·OH.64–68 In fact this intermediate activity has lead to the proposal that they are ideal candidates to test the efficiency of antioxidants.64,69–71
For all the studied reactions the largest exergonicity corresponds to the H transfer from the sulfur atom, the smallest exergonicities are those involving N sites, and the ΔG values of the H transfers from C sites are inbetween. H transfers from N sites were found to be endergonic for the reactions of glutathione with all the studied radicals, but ·OH; and in this particular case the corresponding ΔG values are significantly less negative than those involving HT from S and C sites (more than 20 kcal mol−1). Therefore, the contributions of N sites of reaction to the overall scavenging activity of glutathione are proposed to be negligible.
For the kinetic study we have not included the channels of reaction described above as endergonic because even if they take place at a significant rate, they would be reversible and therefore the formed products will not be observed. Using the same reasoning the HT from N sites were also excluded. However, it should be noticed that they might still represent significant channels if their products rapidly react further. This would be particularly important if these subsequent stages are sufficiently exergonic to provide a driving force, and if their barriers of reactions are low.
The fully optimized geometries of the transition states (TS) are shown in Fig. 2 to 7. All the transition states involving the OH radical (Fig. 2) present H bond like interactions between the H atom in the radical and one of the O atoms in GS−. The shortest interaction distance corresponds to the TS associated with H transfer from the S site. This structural feature is expected to lower the reaction barrier. For the reactions of GS− with ·OCH3 (Fig. 3), ·OOCH3 (Fig. 5), ·OOCHCH2 (Fig. 6), and ·OOCCl3 (Fig. 7) such interactions are not possible. However they are also present in the TSs corresponding to the GS− + ·OOH reaction (Fig. 4). In this case the shortest interaction distance also corresponds to the TS associated with H transfer from the S site.
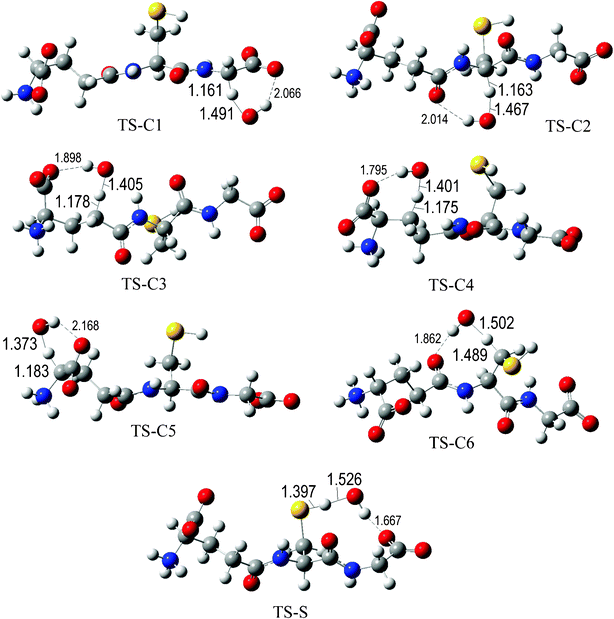 | ||
| Fig. 2 Transition states involved in the GS− + ·OH reaction. | ||
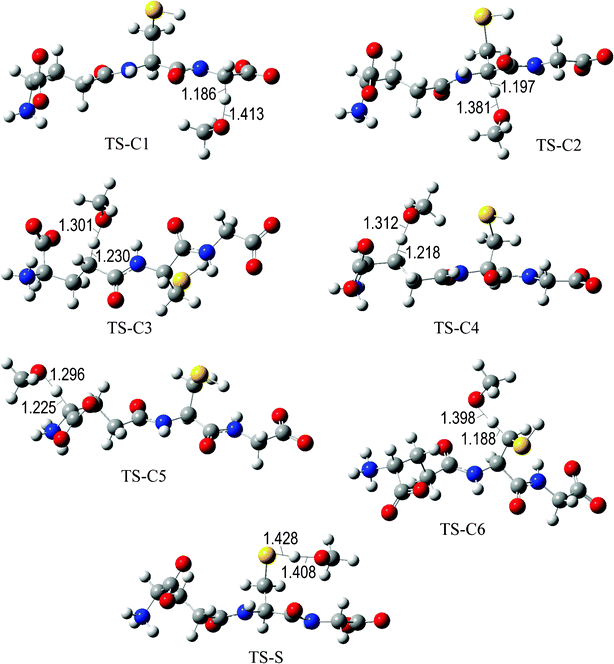 | ||
| Fig. 3 Transition states involved in the GS− + ·OCH3 reaction. | ||
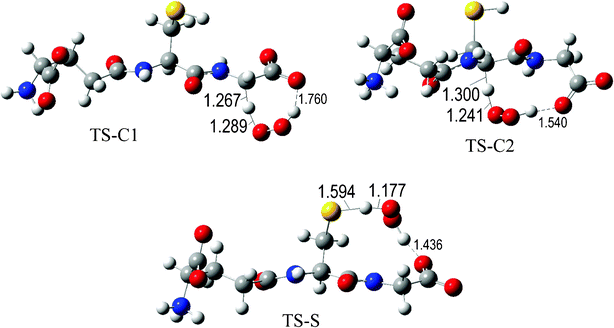 | ||
| Fig. 4 Transition states involved in the GS− + ·OOH reaction. | ||
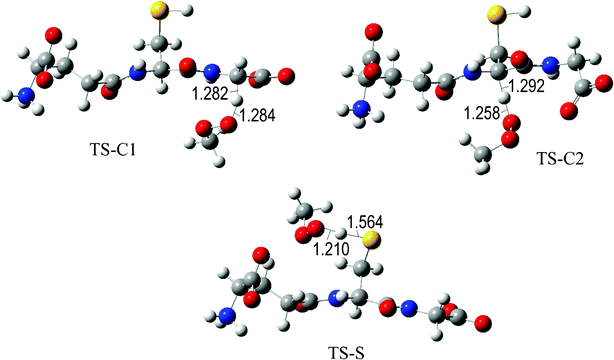 | ||
| Fig. 5 Transition states involved in the GS− + ·OOCH3 reaction. | ||
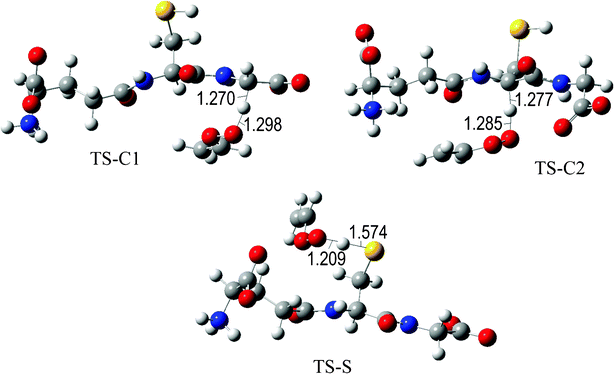 | ||
| Fig. 6 Transition states involved in the GS− + ·OOCHCH2 reaction. | ||
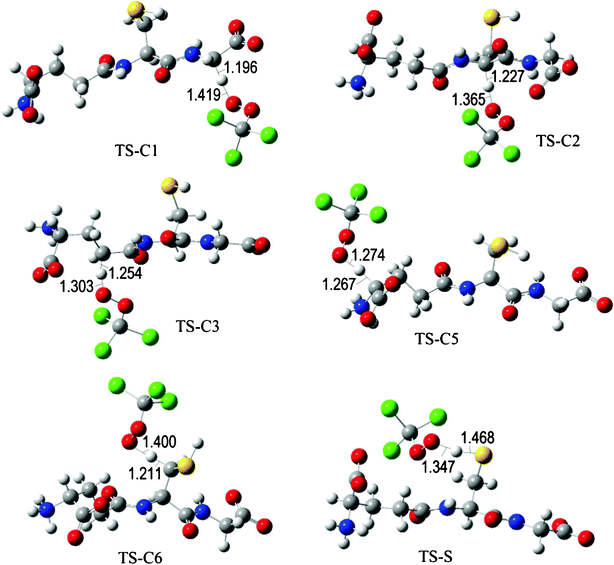 | ||
| Fig. 7 Transition states involved in the GS− + ·OOCCl3 reaction. | ||
The values of the reaction barriers, in terms of Gibbs free energies (ΔG≠) are reported in Table 2. The ΔG≠ values of the reaction paths corresponding to the reaction of GS− with the hydroxyl radical are systematically lower than those involving the other studied radicals, as expected based on their relative reactivity. Regarding the reaction sites, the barriers associated with H transfer from the S sites were found to be the lowest ones, regardless of the reacting free radical. This indicates that this should be the most reactive site of glutathione, through the H transfer mechanism. This is in agreement with the experimental evidences. Moreover, for the GS− + ·OH reaction the H transfer from the S site was found to be barrier-less, indicating that this reaction is diffusion-controlled.
| R1 | R2 | R3 | R4 | R5 | R6 | |
|---|---|---|---|---|---|---|
| C1 | 3.41 | 9.33 | 18.56 | 18.73 | 16.63 | 13.82 |
| C2 | 3.27 | 10.57 | 14.94 | 21.09 | 18.65 | 15.20 |
| C3 | 3.56 | 12.73 | 16.51 | |||
| C4 | 2.51 | 12.79 | ||||
| C5 | 5.62 | 13.27 | 21.05 | |||
| C6 | 3.31 | 11.35 | 14.22 | |||
| S | 0.00 | 5.15 | 8.60 | 13.30 | 12.37 | 11.48 |
The rate constants (k) calculated for all channels of reaction, as well as the overall rate coefficients (koverall) are reported in Table 3. The branching ratios, which represent the percent of the contributions of the different channels of reaction to the overall reactivity of GS−, are reported in Table 4. The calculated overall rate coefficients lead to the following order of glutathione's reactivity towards the studied radicals ·OH > ·OCH3 > ·OOH > ·OOCCl3 > ·OOCHCH2 > ·OOCH3. The unexpected increased reactivity of ·OOH, with respect to the chlorinated peroxyl radical, is explained by the relatively strong H bond interactions present in the transition states.
| R1 | R2 | R3 | R4 | R5 | R6 | |
|---|---|---|---|---|---|---|
| a ref. 8. b ref. 11. c ref. 16. d ref. 17. | ||||||
| C1 | 1.13E + 09 | 1.33E + 07 | 6.15E + 01 | 1.17E + 01 | 2.76E + 02 | 1.07E + 04 |
| C2 | 1.11E + 09 | 1.10E + 06 | 4.35E + 03 | 8.29E-01 | 1.39E + 01 | 8.68E + 02 |
| C3 | 1.12E + 09 | 1.23E + 05 | 5.04E + 02 | |||
| C4 | 1.16E + 09 | 1.01E + 05 | ||||
| C5 | 8.62E + 08 | 3.89E + 04 | 2.86E-01 | |||
| C6 | 1.14E + 09 | 6.71E + 05 | 1.60E + 03 | |||
| S | 1.16E + 09 | 5.74E + 08 | 2.69E + 07 | 2.02E + 04 | 2.91E + 05 | 3.58E + 05 |
| Overall | 7.68E+09 | 5.89E + 08 | 2.69E + 07 | 2.02E + 04 | 2.92E + 05 | 3.72E + 05 |
| Exp. | 1.3E + 10a | 9E + 08d | ||||
| 1.4E + 10b | ||||||
| 4.4E + 10b | ||||||
| 3.48E + 09c |
| R1 | R2 | R3 | R4 | R5 | R6 | |
|---|---|---|---|---|---|---|
| C1 | 14.73 | 2.26 | 0.00 | 0.06 | 0.09 | 2.87 |
| C2 | 14.48 | 0.19 | 0.02 | ∼0 | ∼0 | 0.23 |
| C3 | 14.59 | 0.02 | 0.14 | |||
| C4 | 15.05 | 0.02 | ||||
| C5 | 11.22 | 0.01 | ∼0 | |||
| C6 | 14.78 | 0.11 | 0.43 | |||
| S | 15.15 | 97.39 | 99.98 | 99.94 | 99.90 | 96.33 |
The values of the overall rate coefficients reported in Table 3 indicate that the efficiency of glutathione as OOH radical scavenger is higher than those of carotenes (∼105–106 M−1s−1)53 and allicin (∼8 × 103 M−1s−1),54 much higher than those of melatonin (∼2 × 101 M−1s−1),63 and caffeine (∼3 × 101 M−1s−1);64 and similar to that of 2-Propenesulfenic acid (∼2.6 ×107 M−1s−1).54 It is important to notice that this exceptional reactivity is not only because of the presence of the S-H moiety but also because of the strong H bond that is formed in the transition state with COO− that lowers the reaction barrier. This kind of interaction is not possible for the usually more reactive ·OOCCl3 and other peroxyl radicals. The OCH3 radical reacts only 21 times faster than OOH with GS−, thus it can be concluded that GS− is an exceptional, and specific, OOH scavenger. The COO−group is very common in biological media, for example in lipids and other sulfur containing antioxidants. Therefore our finding for GS− could have implications for other systems with this characteristic.
Due to the relative low reactivity of peroxyl radicals (R4, R5), compared to other oxygenated radicals like ·OH, the efficiency for scavenging this particular kind of radicals is an excellent criterion to compared the antioxidant activity of different compounds. Therefore it can be stated that glutathione is an excellent free radical scavenger due to its versatility, i.e. its capability of efficiently scavenging a wide variety of free radicals. It should be noticed that the compounds mentioned above all react with OH at diffusion-limited rates. However, it has been proposed that this radical can react with almost any molecule in the vicinity of where it is generated.72 Accordingly, the reactivity towards OH is not the best criterion to characterize the efficiency of antioxidants.71 On the other hand, usually the most abundant kinetic data concerning the free radical scavenging activity of chemical compounds involves their reaction with ·OH. Thus, they can be used to validate the reliability of the calculations. This comparison has been made (Table 3) and an excellent agreement has been achieved with the experimental available data. The calculated overall rate coefficient for the GS− + ·OH reaction is in between those obtained from experimental techniques, and closest to the most recent value.16 In the particular case of glutathione there is also one experimental value reported for the rate coefficient of the reaction with ·OCH3. Our calculations also correctly reproduce this value; the calculated koverall is only 1.5 times lower than the experimental one. The agreement between the calculated and the experimental rates coefficients supports the reliability of the results presented in this work for the first time.
With the exception of the H transfer from C5, all the channels of the GS− + ·OH reaction were found to be diffusion-controlled; and for the C5 channel the rate constant is very close to this limit. Accordingly the OH radical reacts with glutathione in a non-specific way leading to a widespread distribution of C centered radicals, in addition to the S centered one (Table 4). This is in line with the discussion on the OH reactivity presented above. On the other hand the reactions of glutathione with all the other studied radicals lead to the formation of only one main product, that arising from H transfer from the S site. This particular channel was found to contribute to the overall reactivity of glutathione towards ·OCH3, ·OOH, ·OOCCl3, ·OOCHCH2, and ·OOCH3 by more than 96%. Accordingly the contributions of the other H transfer channels can be considered negligible. Therefore the formation of C centered radicals seems to be exclusively present for the reaction with the most reactive oxygenated radical, the ·OH.
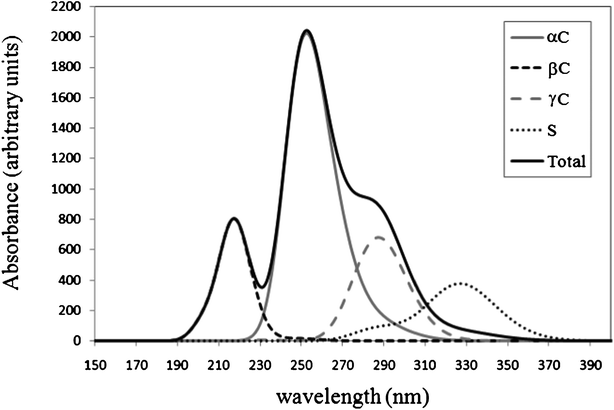
The UV-Vis spectra of the products of the GS− + ·OH reaction have been computed. They are shown in Fig. 8, together with the total spectrum, which be the one intended to reproduce the observed one. The latter was obtained using the additivity of absorbance and the relative abundance of the formed products, according to their branching ratios. It has been established that the spectrum of the radical formed from H transfer from the S site has a maximum at ∼330 nm.8,11,12,15,16 The value obtained from the calculated spectrum is 1.2 times larger than that. Therefore all the calculated data has been scaled, using this factor.
The radicals formed at sites C1, C2, and C5, which correspond to α amino sites, were found to have the maximum absorption at 250, 263, and 266 nm, respectively. The combined band associated with αC radicals is predicted to have its maximum at 254 nm. This value is in agreement with those previously observed by other authors (250–260 nm,73 235–270 nm,74 280 nm,13 and 260 nm15). The radicals formed at sites C4 and C6, which correspond to β sites, show λmax equal to 203 and 215 nm; and the band associated with βC radicals is predicted to have its maximum at 219 nm. This value is also in agreement with previous assignments. Neta et al.73 proposed that βC radicals have lower λmax than αC radicals with values < 240 nm. This value is also in line with the assignment by Hofstetter et al.15 To our best knowledge there are no previous assignments for the UV-vis spectrum of the γC-centered radical of glutathione. According to our results we propose that for this particular radical λmax ≈ 290 nm.
Conclusions
The free radical scavenging activity of glutathione has been studied in aqueous solution. Its reactions with a set of radicals of different nature (·OH, ·OOH, ·OCH3, ·OOCH3, ·OOCHCH2 and ·OOCCl3) have been modeled. It was found that the order of glutathione's reactivity towards the studied radicals is: ·OH > ·OCH3 > ·OOH > ·OOCCl3 > ·OOCHCH2 > ·OOCH3. The rate constants range from 2.02 × 104M−1s−1 to diffusion limit (7.68 × 109M−1s−1). Therefore it can be stated that glutathione is an excellent free radical scavenger, able of efficiently scavenging a wide variety of free radicals.Glutathione reacts exclusively by H transfer, and with the exception of its reaction with OH there is only one important channel of reaction, yielding to the S-centered radical. For the reaction with ·OH, on the other hand, a wide product distribution is expected, which explain the formation of C-centered radicals experimentally observed. The UV-vis spectra of the products is provided, and in agreement with the available experimental data.
The efficiency of glutathione as OOH radical scavenger was found to be higher than those of carotenes and allicin, much higher than those of melatonin and caffeine, and similar to that of 2-propenesulfenic acid. This exceptional reactivity towards ·OOH has been explained based on the strong H bonding interactions found in the transition states, which involves the carboxylate moiety. Therefore this might have implications for other biological systems where this group is present.
Acknowledgements
We gratefully acknowledge the Laboratorio de Visualización y Cómputo Paralelo at Universidad Autónoma Metropolitana-Iztapalapa and Dirección General de Cómputo y de Tecnologías de Información y Comunicación (DGCTIC) at Universidad Nacional Autónoma de México. This work is a result of the FONCICYT 545 Mexico-EU ‘‘RMAYS’’ network, Project No. 94666.References
- A. Meister and M. E. Anderson, Annu. Rev. Biochem., 1983, 52, 711 CrossRef CAS.
- A. Meister and J. Biol, Chem., 1988, 263, 17205 CAS.
- A. Corazza, I. Harvey and P. J. Sadler, Eur. J. Biochem., 1996, 236, 697 CAS.
- J. D. Hayes and L. I. McLellan, Free Radical Res., 1999, 31, 273 CrossRef CAS.
- H. Sies, Free Radical Biol. Med., 1999, 27, 916 CrossRef CAS.
- G. Wu, Y.-Z. Fang, S. Yang, J. R. Lupton and N. D. Turner, J. Nutr., 2004, 134, 489 CAS.
- K. Ehrlich, S. Viirlaid, R. Mahlapuu, K. Saar, T. Kullisaar, M. Zilmer, U. Langel and U. Soomets, Free Radical Res., 2007, 41, 779 CrossRef CAS.
- M. Quintiliani, R. Badiello, M. Tamba, A. Esfandi and G. Gorin, Int. J. Radiat. Biol., 1977, 32, 195 CrossRef CAS.
- G. E. Adams, Advances in Radiation Research, 1972Vol. 3, ed. M. Burton and J . L. Magee, New York : Wiley-Intersciencep. 126 Search PubMed.
- L. Sjoberg, T. E. Eriksen and L. Revesz, Radiat. Res., 1982, 89, 255 CrossRef CAS.
- T. E. Eriksen and G. Fransson, J. Chem. Soc., Perkin Trans. 2, 1988, 1117 RSC.
- Z. Abedinzadeh, M. Gardes-Albert and C. Ferradini, Radiat. Phys. Chem., 1992, 40, 551 CrossRef CAS.
- L. Grierson, K. Hildenbrand and E. Bothe, Int. J. Radiat. Biol., 1992, 62, 265 CrossRef CAS.
- R. Zhao, J. Lind, G. Merbnyi and T. E. Eriksen, J. Am. Chem. Soc., 1994, 116, 12010 CrossRef CAS.
- D. Hofstetter, T. Nauser and W. H. Koppenol, Chem. Res. Toxicol., 2010, 23, 1596 CrossRef CAS.
- S. P. Mezyk, J. Phys. Chem., 1996, 100, 8861 CrossRef CAS.
- M. Z. Baker, R. Badzello, M. Tamba, M. Quintiliani and G. Gorin, Int. J. Radiat. Biol., 1982, 41, 595 CrossRef CAS.
- Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364 CrossRef.
- C. Zavala-Oseguera, J. R. Alvarez-Idaboy, G. Merino and A. Galano, J. Phys. Chem. A, 2009, 113, 13913 CrossRef CAS.
- E. Velez, J. Quijano, R. Notario, E. Pabón, J. Murillo, J. Leal, E. Zapata and G. Alarcón, J. Phys. Org. Chem., 2009, 22, 971 CrossRef CAS.
- A. Vega-Rodriguez and J. R. Alvarez-Idaboy, Phys. Chem. Chem. Phys., 2009, 11, 7649 RSC.
- A. Galano and J. R. Alvarez-Idaboy, Org. Lett., 2009, 11, 5114 CrossRef CAS.
- G. Black and J. M. Simmie, J. Comput. Chem., 2010, 31, 1236 CAS.
- T. Furuncuoglu, I. Ugur, I. Degirmenci and V. Aviyente, Macromolecules, 2010, 43, 1823 CrossRef CAS.
- A. Galano, N. A. Macías-Ruvalcaba, O. N. M. Campos and J. Pedraza-Chaverri, J. Phys. Chem. B, 2010, 114, 6625 CrossRef CAS.
- A. Perez-Gonzalez and A. Galano, J. Phys. Chem. B, 2011, 115, 1306 CrossRef CAS.
- T. Gao, J. M. Andino and J. R. Alvarez-Idaboy, Phys. Chem. Chem. Phys., 2010, 12, 9830 RSC.
- A. Galano, Theor. Chem. Acc., 2011, 130, 51 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS.
- Gaussian 09, Revision A.02 M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford CT, 2009.
- A. Galano and J. R. Alvarez-Idaboy, J. Comput. Chem., 2006, 27, 1203 CrossRef CAS.
- J. R. Alvarez-Idaboy and A. Galano, Theor. Chem. Acc., 2010, 126, 75 CrossRef CAS.
- H. G. Wallnoefer, T. Fox, K. R. Liedl and C. S. Tautermann, Phys. Chem. Chem. Phys., 2010, 12, 14941 RSC.
- Y. Okuno, Chem.–Eur. J., 1997, 3, 212 CrossRef CAS.
- S. W. Benson, The Foundations of Chemical Kinetics, Krieger, FL, 1982 Search PubMed.
- D. Ardura, R. Lopez and T. L. Sordo, J. Phys. Chem. B, 2005, 109, 23618 CrossRef CAS.
- J. R. Alvarez-Idaboy, L. Reyes and J. Cruz, Org. Lett., 2006, 8, 1763 CrossRef CAS.
- J. R. Alvarez-Idaboy, L. Reyes and N. Mora-Diez, Org. Biomol. Chem., 2007, 5, 3682 CAS.
- A. Galano, J. Phys. Chem. A, 2007, 111, 1677 CrossRef CAS.
- A. Galano, J. Phys. Chem. C, 2008, 112, 8922 CAS.
- A. Galano and A. Cruz-Torres, Org. Biomol. Chem., 2008, 6, 732 CAS.
- A. Galano and M. Francisco-Márquez, Chem. Phys., 2008, 345, 87 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1935, 3, 107 CrossRef CAS.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1935, 31, 875 RSC.
- D. G. Truhlar, W. L. Hase and J. T. Hynes, J. Phys. Chem., 1983, 87, 2664 CrossRef CAS.
- D. G. Truhlar and A. Kuppermann, J. Am. Chem. Soc., 1971, 93, 1840 CrossRef.
- F. C. Collins and G. E. Kimball, J. Colloid Sci., 1949, 4, 425 CrossRef CAS.
- M. Smoluchowski, Z. Phys. Chem., 1917, 92, 129 Search PubMed.
- D. G. Truhlar, J. Chem. Educ., 1985, 62, 104 CrossRef CAS.
- (a) A. Einstein, Ann. Phys. (Leipzig), 1905, 17, 549 CAS; (b) G. G. Stokes, Mathematical and Physical Papers, Cambridge University Press, Cambridge, 1903, Vol. 3 (esp. Sect.) Search PubMed.
- J. Bjerrum, G. Schwarzenbach and L. G. Sillen, Stability Constants, Chemical Society, London, 1958 Search PubMed.
- O. Lampela, A. H. Juffer and A. Rauk, J. Phys. Chem. A, 2003, 107, 9208 CrossRef CAS.
- A. Galano and M. Francisco-Márquez, J. Phys. Chem. B, 2009, 113, 11338 CrossRef CAS.
- A. Galano and M. Francisco-Márquez, J. Phys. Chem. B, 2009, 113, 16077 CrossRef CAS.
- M. Belcastro, T. Marino, N. Russo and M. Toscano, Theor. Chem. Acc., 2006, 115, 361 CrossRef CAS.
- M. Leopoldini, N. Russo, S. Chiodo and M. Toscano, J. Agric. Food Chem., 2006, 54, 6343 CrossRef CAS.
- M. Leopoldini, F. Rondinelli, N. Russo and M. Toscano, J. Agric. Food Chem., 2010, 58, 8862 CrossRef CAS.
- M. Leopoldini, N. Russo and M. Toscano, Food Chem., 2011, 125, 288 CrossRef CAS.
- W. A. Pryor, Free Radical Biol. Med., 1988, 4, 219 CrossRef CAS.
- I. G. Draganic, and Z. D. Draganic, The Radiation Chemistry of Water, Academic Press, New York, 1971 Search PubMed.
- L. J. Marnett, Carcinogenesis, 1987, 8, 1365 CrossRef CAS.
- W. A. Pryor, Annu. Rev. Physiol., 1986, 48, 657 CrossRef CAS.
- A. Galano, Phys. Chem. Chem. Phys., 2011, 13, 7147 Search PubMed.
- J. R. Leon-Carmona and A. Galano, J. Phys. Chem. B, 2011, 115, 4538 CrossRef CAS.
- A. Galano, J. Phys. Chem. B, 2007, 111, 12898 CrossRef CAS.
- A. Martinez, R. Vargas and A. Galano, J. Phys. Chem. B, 2009, 113, 12113 CrossRef CAS.
- A. Martinez, R. Vargas and A. Galano, Theor. Chem. Acc., 2010, 127, 595 CrossRef CAS.
- A. Martinez and A. Galano, J. Phys. Chem. C, 2010, 114, 8184 CAS.
- A. Galano, R. Alvarez-Diduk, M. T. Ramírez-Silva, G. Alarcon-Angeles and A. Rojas-Hernández, Chem. Phys., 2009, 363, 13 CrossRef CAS.
- M. Francisco-Marquez, A. Galano and A. Martinez, J. Phys. Chem. C, 2010, 114, 6363 CAS.
- A. Galano, D. X. Tan and R. J. Reiter, J. Pineal Res., 2011, 51, 1 CrossRef CAS.
- R. C. Rose and A. M. Bode, FASEB J, 1993, 7, 1135 CAS.
- P. Neta, M. Simic and E. Hayon, J. Phys. Chem., 1970, 74, 1214 CrossRef CAS.
- E. Hayon, T. Ibata, N. N. Lichtin and M. Simic, J. Am. Chem. Soc., 1970, 92, 3898 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2011 |