On the role of mercury in the non-covalent stabilisation of consecutive U–HgII–U metal-mediated nucleic acid base pairs: metallophilic attraction enters the world of nucleic acids†
Ladislav
Benda
a,
Michal
Straka
*a,
Yoshiyuki
Tanaka
b and
Vladimír
Sychrovský
*a
aInstitute of Organic Chemistry and Biochemistry, Academy of Sciences of the Czech Republic, Flemingovo nám. 2, 16610 Praha 6, Czech Republic. E-mail: straka@uochb.cas.cz; vladimir.sychrovsky@uochb.cas.cz; Fax: +420 220 183 578; Tel: +420 220 183 234
bDivision of Pharmaceutical Chemistry, Tohoku University, Aobayama, Aoba-ku, Sendai, Miyagi 980-8578, Japan
First published on 3rd November 2010
Abstract
Metal atoms with a closed-shell electronic structure and positive charge as for example the AuI, PtII, AgI, TlI or HgII atoms do not in some compounds repel each other due to the so-called metallophilic attraction (P. Pyykkö, Chem. Rev., 1997, 97, 597–636). Here we highlight the role of the HgII⋯HgII metallophilic attraction between the consecutive metal-mediated mismatched base pairs of nucleic acids. Usually, the base stacking dominates the non-covalent interactions between steps of native nucleic acids. In the presence of metal-mediated base pairs these non-covalent interactions are enriched by the metal–base interactions and the metallophilic attraction. The two interactions arising due to the metal linkage of the mismatches were found in this study to have a stabilizing effect on nucleic acid structure. The calculated data are consistent with recent experimental observations. The stabilization due to the metallophilic attraction seems to be a generally important concept for the nucleic acids containing heavy metals with short contacts.
The complexes of nucleic acids (NAs) with metals are promising materials for nanotechnology with tuneable properties depending on the metal and its coordination. The molecular devices developed so far include among others NA sensors,1,2 electric transport materials3,4 or artificial NAs.5–11 The functional materials targeting mercury as a pollutant with high toxicity utilise the unique coordination properties of mercury.12,13 The high specificity of the mercury binding to thymine-rich single-strand NAs allowed the design of fluorescent sensors.14
The coordination of mercury in the Watson–Crick edge of the thymine base, i.e. the substitution of imine hydrogen at nitrogen N3 by HgII (Fig. 1), actually makes possible the formation of T–HgII–T base pairs inside double-stranded DNA.15–17 A recent Raman spectroscopy study characterised the T–HgII–T linkage as covalent–ionic.18 It was further proved that the double-stranded DNA containing T–HgII–T base pairs is substantially more stable than that containing only mismatched T–T base pairs and that the metal links are formed reversibly after temperature denaturation.16,17,19
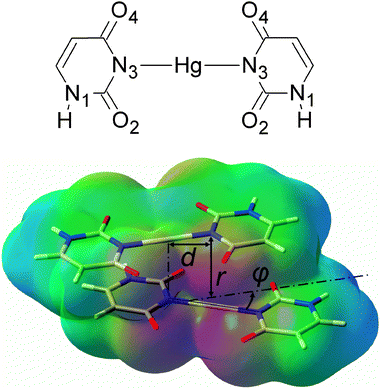 | ||
| Fig. 1 A chemical diagram of the U–HgII–U base pair (top) and a view of the U–HgII–U·U–HgII–U dimer with the electrostatic potential depicted (red = −0.1 a.u., green = 0 a.u., blue = 0.1 a.u.). The parameter d was 0 or 2.006 Å (the length of the N3–HgII bond), angle φ was 0°, 30° or 90°. | ||
One factor enhancing the stability of the metal–DNA with T–HgII–T base pairs is clear: HgII provides a strong covalent–ionic linkage18 of the mismatched T–T base pairs. However, non-covalent interactions between the consecutive base pairs also contribute to the stability: the Coulomb and base–base dispersion interactions known for native NAs20 are enriched by the interactions of HgII with the base(s) of the neighbouring base-pair steps. Furthermore, the metal links can appear consecutively (Fig. 1) as was experimentally evidenced for the DNA containing multiple T–HgII–T steps16,17 as well as for the double-stranded RNA containing multiple U–HgII–U steps.21 In such a situation, the HgII atoms may mutually interact. The effect of the HgII⋯HgII interaction on the stability of the molecular structure has so far been omitted in the context of NAs. Recently, Johannsen et al. discussed the role of analogous AgI⋯AgI interactions in silver-containing DNA.22 Miyachi et al. have suggested that the HgII⋯HgII interaction has an effect on the UV absorption spectra of the T–HgII–T·T–HgII–T dimer.23 The topic of this work is to highlight the role of non-covalent interactions between the consecutive HgII-mediated base pairs including the HgII⋯HgII interaction.
The interaction between metal atoms/ions with a closed-shell electronic structure, such as AuI, PtII, AgI, TlI or HgII, commonly called metallophilic attraction (MA), was shown in a number of experimental and theoretical studies.24–26 Experimentally, the MA is manifested mainly in short non-covalent M⋯M contacts in crystal structures. The MA phenomenon is seemingly in contradiction with the usual expectation that the positively charged ions repel each other. The origin of MA has been ascribed to the London dispersion forces including their ionic terms amplified by the relativistic effects in heavy elements.24 The calculated MA in dimers of HgII with different ligands ranged from −1 to −3 kcal mol−1 for the HgII⋯HgII contacts within 3.2 to 4 Å which were experimentally observed in crystals (see ref. 25 and references therein). The base-pair separation in the most common forms of the NA double-helix structures is about 2.6–3.7 Å.27 Thus, it can be anticipated that the HgII⋯HgII interactions will have a stabilising effect in metal–NAs.
We studied the effect of the non-covalent interactions on the stability of metal–NAs for the dimer of mismatched uracil–uracil (U–U) base pairs linked by HgII (U–HgII–U·U–HgII–U). The resolution of identity Møller–Plesset second-order perturbation theory (RI-MP228,29) method as implemented in the TURBOMOLE 5.10 program package30 and the def2-TZVP basis set31 (Hg, O, C, N, H) with the corresponding effective core potential for mercury (MWB-6032) were used throughout this study. All complexes in this study were built from three molecules whose geometries were optimized at the RI-MP2/def2-TZVP level of theory: the uracil base (U), the U–HgII–U base pair, and the H–HgII–H molecule. In all calculations for dimers, the monomers were kept rigid and only their separation r, mutual rotation φ, and displacement d were varied as shown in Fig. 1. The interaction energies were corrected for the basis-set superposition error (BSSE).
MP2 is an established and well-tested computational method for obtaining the energy of MA.33 It is also known to overestimate the van der Waals interactions.33 Therefore, we also used the spin-component-scaled variant of the MP2 method (SCS-MP234) developed to correct this MP2 deficiency. The benchmark CCSD(T) method was not affordable for a system as large as the U–HgII–U·U–HgII–U dimer and the empirically adjusted DFT-D approaches have not been properly tested for the complexes containing heavy elements like HgII.
The attraction of the U–HgII–U base pairs increases with their mutual rotation (φ = 0°, 30° and 90°) owing to the enhancement of the Coulomb attraction (Fig. 2 and Fig. S1 (ESI†)). Similarly, the Coulomb attraction increases when the base pairs are displaced (d = 2.006 Å) because the HgII appears closer to the negatively charged nitrogen N3 and oxygen atoms of the carbonyl groups. The rotated and displaced geometries of the metal–base pairs are therefore energetically favoured. This spatial arrangement can be also seen in the crystals of thymidine–HgII (CSD ID MTYMHG1035 and DOJSAW36). In order to gain further insight into the spatial arrangement of the HgII-mediated T–T base pairs, we fully optimised the geometry of an experimentally known complex18 consisting of two T–p-T dinucleoside monophosphates linked with HgII. The resulting mutual base-pair rotation was φ ≈ 50° (ESI†). In all three of the above-mentioned structures, the HgII⋯HgII distances were found to be near 3.5 Å, which is in the range of the attractive HgII⋯HgII interactions (cf. above).
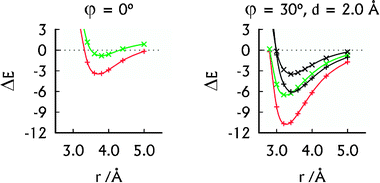 | ||
| Fig. 2 The MP2 interaction energies (in kcal mol−1) of the U–HgII–U·U–HgII–U (red, +) and U–U·U–U (green, ×) dimers in their parallel arrangement (left) and A-RNA-like arrangement (right). The SCS-MP2 interaction energies (right) of the U–HgII–U·U–HgII–U (black, +) and U–U·U–U (black, ×) dimers were added for comparison. | ||
The spatial arrangement of the U–HgII–U·U–HgII–U dimer with the displaced base pairs rotated by 30° is close to that of the base pairs in A-RNA.27 Its interaction energy of −10.7 kcal mol−1 (Fig. 2) falls between the interaction energy of the U–U·U–U dimer, which was −6.5 kcal mol−1 (Fig. 2) and the interaction energies of the canonical base-pair steps, ranging from −14.0 to −19.2 kcal mol−1 (MP2/aug-cc-pVTZ calculations37). Thus the non-covalent interactions arising because of HgII bring the stability of the HgII-mediated base pairs closer to that of the canonical base pairs. As expected, the SCS-MP2 method provided smaller interaction energies of the U–HgII–U·U–HgII–U and U–U·U–U dimers (Fig. 2). We note that all of the HgII⋯HgII distances at the calculated interaction energy minima in the U–HgII–U·U–HgII–U dimer (3.2–3.8 Å; see Fig. 2 and ESI†) lie in the range of the MA contacts.
The non-covalent interactions in the U–HgII–U·U–HgII–U dimer can be virtually separated into the ‘native’ U⋯U interactions, the HgII⋯U interactions, and the HgII⋯HgII metallophilic attraction. The overall stabilisation energy arising from HgII consisting of the HgII⋯U and HgII⋯HgII contributions was calculated as a difference of the U–HgII–U·U–HgII–U and U–U·U–U interaction energies (Fig. 3). The energy of the HgII⋯HgII metallophilic attraction was obtained using two alternative approaches (Scheme 1). These decompositions are not strictly exact as the calculations employed dimers with different ligands of HgII (–U, –H) and U (–HgII, –H) and the distributions of the electron density in such complexes are not exactly equivalent. Furthermore, energies of the MA were calculated as differences of relatively large numbers. The qualitative picture for the HgII⋯HgII attraction was, however, obtained, and the two employed schemes provided practically the same results (Fig. 3).
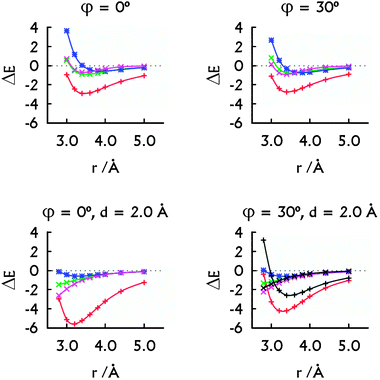 | ||
| Fig. 3 The decomposition of the MP2 interaction energies: the metal–metal plus metal–base contribution arising from HgII (red, +), the HgII⋯HgII interaction energy calculated with Scheme 1A (green, ×) and with Scheme 1B (magenta, ×). The interaction energy in the H–HgII–H·H–HgII–H dimer (blue, *). The decomposition of the SCS-MP2 interaction energies (bottom right): the contribution arising from HgII (black, +) and the HgII⋯HgII interaction energy calculated with Scheme 1B (black, ×). All energies are in kcal mol−1. Note that the HgII⋯HgII contacts correspond to r only when d = 0.0 Å. | ||
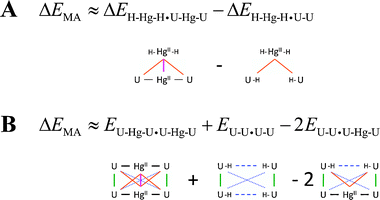 | ||
| Scheme 1 The decomposition schemes for obtaining the energy of the metallophilic attraction ΔEMA. (A) The ΔEMA (magenta) was obtained by subtracting the metal–base (orange) components of the interaction energy in the H–HgII–H·U–HgII–U hetero-dimer. (B) The ΔEMA (solid magenta) was calculated from the U–HgII–U·U–HgII–U total electronic energy by subtracting the energy contributions for the metal–base covalent–ionic (solid black), base–base stacking (solid green), base–base distant non-covalent (dotted blue), base–base mismatch (dashed blue) and metal–base non-covalent (solid orange) interactions. | ||
The overall stabilising effect of HgII in the U–HgII–U·U–HgII–U dimer depends on the mutual orientation of the base pairs (Fig. 3). The sum of the HgII⋯U interaction energies dominates over the HgII⋯HgII metallophilic attraction. Nevertheless, the MA was present for all the orientations of the U–HgII–U base pairs (Fig. 3) and was of similar magnitude (−0.7 to −1.1 kcal mol−1) as in the H–HgII–H·H–HgII–H dimer. Interestingly, the SCS-MP2 and MP2 methods provided similar MA energies (Fig. 3, bottom right). Thus, the HgII⋯HgII metallophilicity stabilises the metal–NA steps as seen from the energy decomposition and also from the short optimal distances between the mercury atoms.
In more detail, the total stabilisation due to HgII (the U⋯HgII plus HgII⋯HgII interactions) in the U–HgII–U·U–HgII–U dimer amounted −2.6 kcal mol−1 at MP2 level, i.e. ∼75% of the total interaction energy when the metal-mediated base pairs adopted parallel arrangement (Fig. 2 and 3, r = rHg⋯Hg = 3.8 Å). When the spatial arrangement of the base pairs was closer to that in A-form of NAs, the sum of U⋯HgII and HgII⋯HgII interactions accounted for −4.2 or −2.6 kcal mol−1 at MP2 or SCS-MP2 levels (Fig. 3, r = 3.4 Å, rHg⋯Hg ∼ 3.9 Å).
Is the HgII⋯HgII interaction in our model a stand-alone case or are there more examples of the MA in metallated NAs? Indeed, the concept might be rather general. Possible short HgII⋯HgII contacts can indicate stabilising role of the MA in mercurated RNA duplex.21 During the course of this work, Johannsen et al. published a structure of DNA containing three consecutive imidazole–AgI–imidazole base pairs with AgI⋯AgI contacts within 3.9–4.0 Å.22 The strongest metallophilic interactions occur in the AuI⋯AuI systems, however, we have not found any example of gold-mediated NAs in the literature.
In summary, we have shown that the experimentally observed consecutive HgII-mediated base pairs are stabilised by the non-covalent metal–base interaction and the HgII⋯HgII metallophilic attraction. It seems that the general concept of metallophilic attraction has not yet been explored fully in the world of nucleic acid. Considering the richness of the metallophilic-attraction-driven structures in the solid state, we foresee its important role in the future design of metal-containing nucleic acids and molecular wires.
Acknowledgements
The project was supported by the Czech Science Foundation, projects no. P203/09/2037, P205/10/0228, and the Academy of Sciences of the Czech Republic, project no. Z04 055 905. M.S. acknowledges European Reintegration Grant no. 230955. V.S. and Y.T. acknowledge Human Frontiers Science Organization's Young Investigator Grant.Notes and references
- E. M. Nolan and S. J. Lippard, Chem. Rev., 2008, 108, 3443–3480 CrossRef CAS.
- J. W. Liu, Z. H. Cao and Y. Lu, Chem. Rev., 2009, 109, 1948–1998 CrossRef CAS.
- A. A. Voityuk, J. Phys. Chem. B, 2006, 110, 21010–21013 CrossRef CAS.
- S.-P. Liu, S. H. Weisbrod, Z. Tang, A. Marx, E. Scheer and A. Erbe, Angew. Chem., Int. Ed., 2010, 49, 3313–3316 CAS.
- K. Tanaka and M. Shionoya, J. Org. Chem., 1999, 64, 5002–5003 CrossRef CAS.
- E. Meggers, P. L. Holland, W. B. Tolman, F. E. Romesberg and P. G. Schultz, J. Am. Chem. Soc., 2000, 122, 10714–10715 CrossRef CAS.
- H. Weizman and Y. Tor, J. Am. Chem. Soc., 2001, 123, 3375–3376 CrossRef CAS.
- H. A. Wagenknecht, Angew. Chem., Int. Ed., 2003, 42, 3204–3206 CrossRef CAS.
- G. H. Clever, C. Kaul and T. Carell, Angew. Chem., Int. Ed., 2007, 46, 6226–6236 CrossRef CAS.
- J. Müller, Eur. J. Inorg. Chem., 2008, 3749–3763 CrossRef.
- G. H. Clever and M. Shionoya, Coord. Chem. Rev., 2010, 254, 2391–2402 CrossRef CAS.
- J. S. Lee, M. S. Han and C. A. Mirkin, Angew. Chem., Int. Ed., 2007, 46, 4093–4096 CrossRef CAS.
- M. Hollenstein, C. Hipolito, C. Lam, D. Dietrich and D. M. Perrin, Angew. Chem., Int. Ed., 2008, 47, 4346–4350 CrossRef CAS.
- A. Ono and H. Togashi, Angew. Chem., Int. Ed., 2004, 43, 4300–4302 CrossRef CAS.
- S. Katz, Biochim. Biophys. Acta, 1963, 68, 240–253 CAS.
- Y. Miyake, H. Togashi, M. Tashiro, H. Yamaguchi, S. Oda, M. Kudo, Y. Tanaka, Y. Kondo, R. Sawa, T. Fujimoto, T. Machinami and A. Ono, J. Am. Chem. Soc., 2006, 128, 2172–2173 CrossRef CAS.
- Y. Tanaka, S. Oda, H. Yamaguchi, Y. Kondo, C. Kojima and A. Ono, J. Am. Chem. Soc., 2007, 129, 244–245 CrossRef CAS.
- T. Uchiyama, T. Miura, H. Takeuchi, M. Kudo, T. Komuro, T. Kawamura, Y. Tanaka, Y. Kondo, L. Benda, V. Sychrovský, P. Bouř, I. Okamoto and A. Ono, unpublished data.
- Y. Tanaka and A. Ono, Dalton Trans., 2008, 4965–4974 RSC.
- J. Šponer, P. Jurečka and P. Hobza, in Computational studies of RNA and DNA, ed. J. Šponer and F. Lankaš, Springer, 2006, vol. 2, p. 636 Search PubMed.
- S. Johannsen, S. Paulus, N. Dupre, J. Muller and R. K. O. Sigel, J. Inorg. Biochem., 2008, 102, 1141–1151 CrossRef CAS.
- S. Johannsen, N. Megger, D. Bohme, R. K. O. Sigel and J. Muller, Nat. Chem., 2010, 2, 229–234 CrossRef CAS.
- H. Miyachi, T. Matsui, Y. Shigeta and K. Hirao, Phys. Chem. Chem. Phys., 2010, 12, 909–917 RSC.
- P. Pyykkö, Chem. Rev., 1997, 97, 597–636 CrossRef.
- P. Pyykkö and M. Straka, Phys. Chem. Chem. Phys., 2000, 2, 2489–2493 RSC.
- H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2008, 37, 1931–1951 RSC.
- W. Saenger, Principles of Nucleic Acid Structure, Springer-Verlag, 1984 Search PubMed.
- F. Weigend and M. Haser, Theor. Chem. Acc., 1997, 97, 331–340 CrossRef CAS.
- F. Weigend, M. Haser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
- R. Ahlrichs, M. Bar, M. Haser, H. Horn and C. Kolmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- U. Haussermann, M. Dolg, H. Stoll, H. Preuss, P. Schwerdtfeger and R. M. Pitzer, Mol. Phys., 1993, 78, 1211–1224.
- P. Pyykkö, N. Runeberg and F. Mendizabal, Chem.–Eur. J., 1997, 3, 1451–1457 CrossRef CAS.
- S. Grimme, J. Chem. Phys., 2003, 118, 9095–9102 CrossRef CAS.
- L. D. Kosturko, C. Folzer and R. F. Stewart, Biochemistry, 1974, 13, 3949–3952 CrossRef CAS.
- F. Guay and A. L. Beauchamp, Can. J. Chem., 1985, 63, 3456–3463 CrossRef CAS.
- J. Šponer, P. Jurečka, I. Marchan, F. J. Luque, M. Orozco and P. Hobza, Chem.–Eur. J., 2006, 12, 2854–2865 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Computational details, molecular geometries, and U–HgII–U·U–HgII–U dimer interaction energy profiles. See DOI: 10.1039/c0cp01534b |
| This journal is © the Owner Societies 2011 |
