Vertex-, face-, point-, Schläfli-, and Delaney-symbols in nets, polyhedra and tilings: recommended terminology

Abstract

We review the various kinds of symbols used to characterize the topology of vertices in 3-periodic nets, tiles and polyhedra, and symbols for tilings, making a recommendation for uniform nomenclature where there is some confusion and misapplication of terminology.

---

V. A. Blatov

Vladislav A. Blatov was born in 1965 in Samara (former Kuibyshev), Russia. He graduated from Samara State University (1987) and got degrees of Candidate (1991) and Doctor in Chemistry (1998) from the Institute of General and Inorganic Chemistry (Moscow). He has been Full Professor at SSU Chemistry Department since 1998. His research and educational interests concern geometrical and topological methods in crystal chemistry and their computer implementation in the program package TOPOS developed since 1989.

M. O'Keeffe

Michael O'Keeffe was born in Bury St Edmunds, UK in 1934 and attended the University of Bristol (BSc 1954, PhD 1958, DSc 1976). He is Regents' Professor of Chemistry at Arizona State University where he has been since 1963. His research has ranged over many areas of solid state chemistry. Recent efforts have been devoted particularly to development of the theory of periodic nets and tilings and its application to materials synthesis by design.

D. M. Proserpio

Davide M. Proserpio was born in Italy in 1962. In 1986 he got the “Laurea” in Chemistry at the University of Pavia. In the next five years he was active in the field of applied theoretical chemistry under the supervision of Carlo Mealli (CNR Florence, Italy) and Roald Hoffmann (Cornell University, USA). Since 1991 he has been at the DCSSI of the University of Milano and Associate Professor since 2003 with special interests in topological crystal chemistry: interpenetration, polycatenation and polythreading of nets.

---

The recent explosion of interest in periodic nets and tilings as applied to the description of the topology of materials such as coordination polymers/networks and metal–organic frameworks (MOFs)¹ points to the need for clarification and agreement on the definition and terminology for certain commonly-used topological indices. Since the early work on coordination networks it has been evident there was need for a common terminology and software to examine the architectures observed and compared with the inorganic anologues (if any)² and many cases of wrong assignment of topology appeared in the literature (for example the confusion between NbO and CdSO₄ related topologies).³ For recent applications derived from the geometrical study of periodic nets,⁴ see the reticular chemistry approach⁵ and many references reported in ref. 1.

In this highlight we review the various kinds of symbols used to characterize the topology of vertices in 3-periodic nets, tiles and polyhedra, and symbols for tilings. We make a recommendation for uniform nomenclature in this area wherever there is some confusion and misapplication of terminology. Some of the symbols in question rely on the identification of cycles and rings in the net so we first recall definitions in this area.⁶

An elementary cycle of a graph (net) is a sequence of vertices 1,2,3,…,n,1 of the graph such that (1,2), (2,3)…(n,1) are edges, and no vertex other than the beginning and ending one occurs more than once in the sequence.

The sum of two cycles is the set of edges (and their vertices) contained in just one or the other, but not both, cycles. A straightforward generalization is to the sum of a number of cycles as the set of all edges that occur only an odd number of times in the set of cycles.

A ring is a cycle that is not the sum of two smaller cycles. Rings have also been called fundamental circuits.⁷

A strong ring is not the sum of any number of smaller cycles and is necessarily also a ring.⁸ See Fig. 1 for some examples from the graph of a cube.

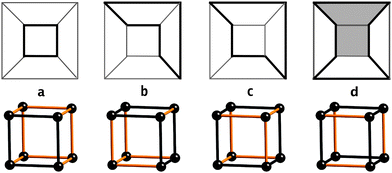Fig. 1 Cycles, rings and strong rings in a cube shown on top as heavy lines on a Schlegel diagram and below as black edges. (a) a 4-cycle that is a strong ring, (b) a 6-cycle that is the sum of two 4-cycles and hence not a ring, (c) a 6-cycle that is the sum of three smaller cycles but not of two and is therefore a ring (but not a strong ring), (d) an 8-cycle that is the sum of two smaller cycles – a 6-cycle (shaded) and a 4-cycle and hence not a ring.

It is appropriate to start with Schläfli symbols which have a long history in mathematics.⁹ These are of the form {p,q,r…} and a symbol with n entries refers to a tiling of an n-dimensional space. {p} refers to tiling a 1-sphere (a circle) with line segments and is a regular polygon with p sides. {p,q} refers to a pattern in which q {p}'s meet at each vertex. Examples are the five Platonic solids: tetrahedron {3,3}, cube {4,3}, octahedron {3,4}, icosahedron {3,5} and dodecahedron {5,3}, which in this context are tilings of the 2-sphere. {6,3} refers to tiling the plane with hexagons in the familiar honeycomb pattern and {4,4} is the plane tiling by squares. A symbol such as {10,3} refers to tiling the hyperbolic plane by decagons.

A Schläfli symbol {p,q,r} refers to a tiling of 3-D space in which r {p,q}'s meet at an edge. The familiar tiling of 3-D space with cubes has Schläfli symbol {4,3,4}, and {4,3,3} is the hypercube—a tiling of the 3-sphere which requires four dimensions for an embedding in Euclidean space just as a cube (tiling of the 2-sphere) requires 3-dimensions for an embedding in Euclidean space. {4,3,3,4} is a tiling of 4-D Euclidean space by hypercubes; and so it goes.

A flag of a tiling of n-dimensional space is an assembly of contiguous 1, 2…n-dimensional components. Thus a flag of a 2-D tiling is the combination of a polygon, an edge of that polygon, and a vertex of that edge; for a 3-D tiling a flag is a polyhedron, a face of that polyhedron, an edge of that face, and a vertex of that edge (Fig. 2). If all flags of a tiling are related by symmetry (flag transitive), the tiling is said to be regular. Note that flag transitivity implies vertex-, edge- etc. transitivity. The Schläfli symbol as here described refers only to regular tilings; for other tilings a Delaney symbol (“extended Schläfli symbol”) is needed as discussed below.

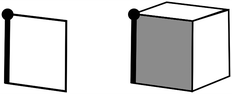Fig. 2 Left, a flag of a 2-D tiling (a contiguous polygon, edge and vertex). Right a flag of a 3-D tiling (a contiguous polyhedron, polygon, edge and vertex).

For vertices in polyhedra and 2-periodic tilings it is common to use a vertex symbol (sometimes also referred to as vertex type or vertex configuration) to describe the local topology of a vertex.¹⁰ This denotes in cyclic order the size of the polygons meeting at a vertex and for an Archimedean polyhedron or plane tiling (one with one kind of vertex) is of the form A.B.C….Thus the vertices of a cuboctahedron are 3.4.3.4 and those of a truncated tetrahedron are 3.6² (short for 3.6.6). Note that adherence to cyclic order is necessary to distinguish the nets of the 2-periodic tilings 3³.4² and 3².4.3.4 (Fig. 3). Note also that subject to the constraint of cyclic order, smallest faces come first (3.4.3.4 not 4.3.4.3). In this symbolism the vertices of a cube are 4³. This notation, with obvious extensions to structures with more than kind of vertex—thus a square pyramid is (3⁴)(3².4)₄ giving also the ratio of different vertices—is almost universally used in crystal chemistry, but unfortunately in some influential books called Schläfli symbols.¹¹ A vertex symbol does not always describe a unique structure; thus there are two distinct polyhedra with vertex symbol 3.4³ (Fig 4).^10c

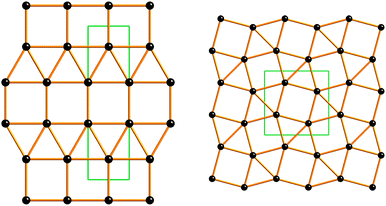Fig. 3 Two 2-periodic nets of tilings by triangles and squares 3³.4² (left cem) and 3².4.3.4 (right tts).

Fig. 4 Left: a rhombicuboctahedron rco with all vertices related by symmetry (symmetry O_h) and with vertex symbol 3.4³ Right: a second polyhedron (symmetry D_4d) with two kinds of vertex, but both having symbol 3.4³. Both polyhedra also have the same face symbol [3⁸.4¹⁸].

O'Keeffe and Hyde¹² point out that the faces of a polyhedron or 2-periodic tiling are rings, and not necessarily shortest cycles. Consider, for example, the plane tiling 4.6.12 (Fig. 5). At the angle containing the 12-sided face there is a shorter 8-cycle that is the sum of a 4-cycle and a 6-cycle. Likewise in the polyhedron 4.6.10 (truncated icosidodecahedron tid) at the angle containing the 10-ring there is again a shorter 8-cycle.

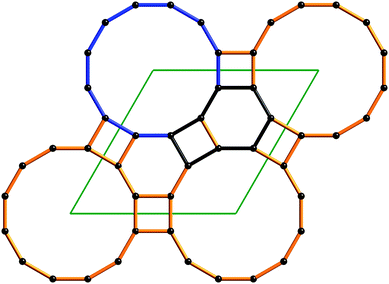Fig. 5 Part of the vertex-transitive 2-periodic tiling fxt with vertex symbol 4.6.12. At an angle containing a 12-ring (blue) a shorter 8-cycle is indicated in black.

But the faces of polyhedra may not be strong rings—consider for example the base quadrangle of a square pyramid which is the sum of four 3-rings (corresponding to the four triangular faces). So the numbers in vertex symbols refer to shortest rings, which in some instances may not be shortest cycles or strong rings—this is important in what follows.

We turn now to our main concern, 3-periodic nets. Wells¹³ in his pioneering work placed special emphasis on uniform nets (which, unwisely we believe, he also called Platonic). In these the shortest cycle (necessarily also a strong ring in this case) at each angle at a vertex is of the same length. For a 3-coordinated net there are 3 angles at a vertex and for a net of this type, in which the shortest cycles at the angles are all of length p, Wells used the symbol (p,3). This was a unfortunate as these symbols have been confused with Schläfli symbols, although Wells himself appears not to have used that term. We emphasize that the Schläfli symbol {10,3} refers to tiling of the hyperbolic plane in which three 10-gons meet at each vertex. The Wells symbol (10,3) refers to a 3-periodic net in which the shortest ring at each angle of the net is a 10-ring. There are several nets known of this type; the one Wells called (10,3)-a has fifteen 10-rings meeting at a vertex as Wells was well aware.

For other than uniform nets Wells used a symbol, that he called a point symbol, which has superficial resemblance to a vertex symbol, but is really rather different. First we note that for an n-coordinated vertex in a 3-D net there are n(n-1)/2 angles and the shortest cycle at each angle was identified. The point symbol then was of the form A^a.B^b… indicating that there are a angles with shortest cycles that are A-cycles, b angles with shortest cycles that are B-cycles, etc. with A < B, < … and a + b +… = n(n-1)/2. So net (10,3)-a has point symbol 10³.

Unfortunately point symbols also became called Schläfli symbols in important papers by Smith¹⁴ although in later work he called them circuit symbols¹⁵ and finally vertex symbols.¹⁶ The description of point symbols as Schläfli symbols has been misused in about 300 articles from RSC and ACS journals since year 2000 (searching the words “Schläfli symbol” as text search from the web pages of the two chemical societies) and persists in recent comprehensive accounts^17–19 and tutorial reviews.²⁰

Smith¹⁴ did remark that instead of using point symbols (which, as we have seen, he called Schläfli symbols) it would be better to use symbols involving shortest rings but did not implement that suggestion. O'Keeffe²¹ appears to be the first to implement Smith's suggestion and he defined a symbol using shortest rings, which he called “fundamental circuits” as in some earlier practice.⁷ This symbol was unfortunately called an “extended Schläfli symbol”, or “long Schläfli symbol”²¹ although later a vertex symbol.²² These symbols (described next) are also called vertex symbols in the zeolite framework type²³ and RCSR²⁴ databases and we recommend that that name be adopted.

The vertex symbol devised by O'Keeffe was an attempt to extend the vertex symbol as used for 2-D structures to 3-D ones; hence the use of shortest rings rather than either shortest cycles or strong rings to be consistent with the usage for 2-dimensions. For 3-coordinated vertices with three angles it is of the form A_a.B_b.C_c indicating that there are a shortest rings that are A-rings at the first angle, b shortest rings that are B-rings at the next angle, etc. Thus Wells' net (10,3)-a has vertex symbol 10₅.10₅.10₅. To avoid subscripts and superscripts in the computer output of programs like TOPOS²⁵ this net has point symbol expressed as {10^3} and vertex symbol as [10(5).10(5).10(5)]. If there is only one shortest ring the subscript is suppressed.

In the case of 4-coordinated nets with six angles it was proposed²¹ to group the angles in three pairs of opposite angles (those without a common edge). One advantage of this is that then the vertex symbol gives also the information embedded in loop configuration (a graphic symbol commonly used in the description of zeolite net topology).^22,23 Subject to this pairing the symbol is written in lexicographic order (smallest numbers first). This is illustrated (Fig. 6) for a vertex of the net sod (the symbol is the RCSR symbol²⁴), zeolite code²³SOD. Here the vertex symbol is 4.4.6.6.6.6; notice that the first two 4's indicate that the 4-rings are contained in opposite angles. In this case the rings are also shortest cycles so the point symbol is 4².6⁴. Sometimes there is no ring contained in an angle and this is indicated by “*”. For example, for the important cds net the vertex symbol is 6.6.6.6.6₂.*. However there are always shortest cycles and the point symbol for this net is 6⁵.8. The net of the feldspar framework, RCSR symbol fel, has two kinds of vertex, both with point symbol 4².6³.8; here the vertex symbols are 4.6.4.6.8₂.10₁₀ and 4.6₂.4.8.6.6₂. Notice that we can immediately see that the 4-rings share edges.

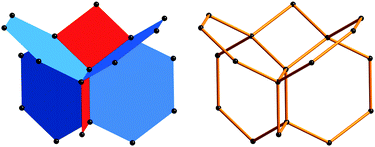Fig. 6 Two views of the rings meeting at a vertex in the sod net.

For higher coordination, no simple grouping of angles is possible and the vertex symbol is such that the smaller rings come first, with angles with the same ring size sorted so that smaller subscripts come first. Thus for the 6-coordinated net with RCSR symbol pcu-m the vertex symbol is 3.3.3.3.4.4.4.8₂.8₂.8₃.9₂.9₃.9₄.9₅.9₆.

Why should we use both point symbols and vertex symbols when vertex symbols are more informative and more in accord with long practice? The answer is, at least in part, that vertex symbols become very cumbersome for nets of high coordination numbers and we suggest they not be used, at least not in a printed form (they can be useful in electronic databases), when coordination numbers exceed 6. The current record for a MOF is 24-coordinated in a structure based on the rht topology.²⁶ The net is 24,3-coordinated and it would take quite a few lines of text to write down the vertex symbol for the 24-coordinated vertex which has 24 × 23/2 = 276 angles. However the point symbol for the net is very compact: (4³)₈(4⁷².6¹³².8⁷²). A second difficulty with vertex symbols is that they can be tricky to compute for some nets. The problem is that there may be no ring at some angles and one does not know a priori the maximum size of cycle to use for testing for the presence of a ring, and a large maximum can lead to very long computing times. On the other hand point symbols, such as the one given above for rht, are computed essentially “instantly” with a program such as TOPOS.²⁵

For polyhedra and tiles (which may be generalized polyhedra or cages) it is generally more informative to use a face symbol which is of the form [A^a.B^b…] indicating that there are a faces that are A-rings, b faces that are B-rings, etc. We suggest using the brackets to avoid possible confusion with point symbols. Most nets admit a natural tiling²⁷ which may consist of tilings by several kinds of tile; here one can give a signature (as reported by the program 3dt²⁸ and TOPOS²⁵) that gives the ratio of numbers of tiles. Thus for tilings by tetrahedra and octahedra in which the tiles are in the ratio 2 : 1 the signature may be written [3⁴]₂[3⁸]. Because of the inconvenience of having subscripts and superscripts in computer output, 3dt and TOPOS would write this as 2[3^4] + [3^8].

If we want a symbol to describe tilings in general in the same way as the Schläfli symbol describes regular tilings, there is an extended Schläfli symbol available named a Delaney symbol by its inventor Andreas Dress, but also known as a Delaney–Dress symbol or just a D-symbol.²⁹ In generating a D-symbol, tiles are first dissected into chambers. In two dimensions a chamber is a triangle with vertices at the center of a tile, at the center of an edge of that tile, and at a vertex on that edge. In three dimensions a chamber is a tetrahedron with vertices at the center of a tile, at the center of a face of that tile, at the center of an edge of that face, and at a vertex of that edge. Fig. 7 illustrates a tile of the diamond (dia) net dissected into chambers. The D-symbol specifies how these chambers are inter-connected. The details of deriving and interpreting D-symbols would take us too far afield here. We remark however that their power in systematically enumerating tilings, and hence the nets they carry, has been amply demonstrated.²⁹ 2-D D-symbols are used extensively by Conway et al.³⁰ (who call them extended Schläfli symbols) and by Ramsden et al.³¹ The number of different kinds of chamber in a tiling is called the complexity by 3dt and reported as D-size by RCSR; this is in fact the same as the flag transitivity i.e. the number of non-equivalent flags. The only 3-D tiling with D-size equal to 1 is the regular tiling by cubes {4,3,4}.

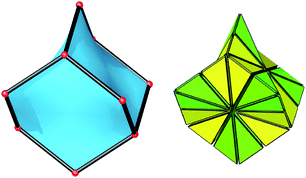Fig. 7 A tile of the diamond structure (left) dissected into chambers (right).

In conclusion we remark that with the signs of awakening interest of mathematicians in periodic graphs,³² it is important to use terminology that is as far as possible consistent with long-established mathematical usage. In particular we should reserve the term “Schläfli symbol” to its mathematical sense, and refer to the symbols for local topology of vertices in 3-periodic nets as “point symbols” (using shortest cycles) and “vertex symbols” (using shortest rings) as appropriate. Fig. 8 summarizes these recommendations; note particularly the difference between Schläfli, point, and vertex symbol for pcu.

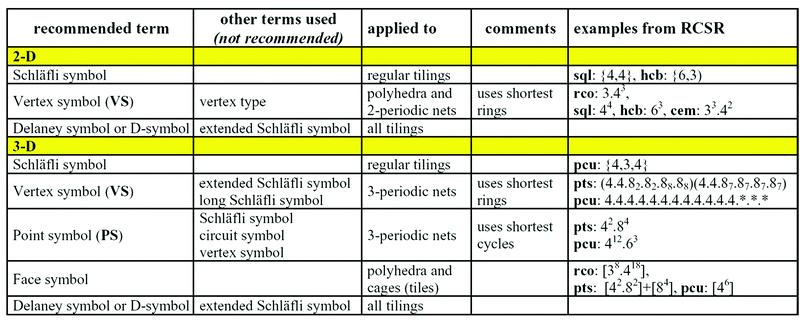Fig. 8 Recommended definitions and use of topological indices

Acknowledgements

Work on nets and tilings at ASU is supported by the U.S. National Science Foundation (grant number DMR 0804828). V.A.B. thanks Cariplo Foundation & Landau Network - Centro Volta (Como - Italy).

References

1. See for example the Metal–Organic Frameworks themed issue 5 of 2009 of Chem. Soc. Rev., guest editors J. R. Long and O. M. Yaghi.
2. (a) M. O'Keeffe, M. Eddaoudi, H. Li, T. Reineke and O. M. Yaghi, J. Solid State Chem., 2000, 152, 3–20; (b) M. Schindler, F. C. Hawthorne and W. H. Baur, Acta Crystallogr., Sect. B: Struct. Sci., 1999, B55, 811–829; (c) U. Müller, Angew. Chem., Int. Ed., 2000, 39, 502–504; (d) R. Robson, J. Chem. Soc., Dalton Trans., 2000, 3735–3744.
3. L. Carlucci, G. Ciani, P. Macchi and D. M. Proserpio, Chem. Commun., 1998, 1837–1838.
4. O. Delgado-Friedrichs, M. D. Foster, M. O'Keeffe, D. M. Proserpio, M. M. J Treacy and O. M. Yaghi, J. Solid State Chem., 2005, 178, 2533–2554.
5. (a) O. M. Yaghi, M. O'Keeffe, M. Eddaoudi, H. K. Chae, J. Kim and N. W. Ockwig, Nature, 2003, 423, 705–714; (b) N. W. Ockwig, O. Delgado-Friedrichs, M. O'Keeffe and O. M. Yaghi, Acc. Chem. Res., 2005, 38, 176–182.
6. O. Delgado-Friedrichs and M. O'Keeffe, J. Solid State Chem., 2005, 178, 2480–2485.
7. (a) C. S. Marians and L. W. Hobbs, J. Non-Cryst. Solids, 1990, 124, 242–253; (b) L. Stixrude and M. S. T. Bukowinski, Am. Mineral., 1990, 75, 104–111.
8. R. Goetzke and H. -J. Klein, J. Non-Cryst. Solids, 1991, 127, 215–220.
9. (a) H. S. M. Coxeter, Regular Polytopes 3rd edn, Dover Publications, New York. 1973; (b) H. S. M. Coxeter, The Beauty of Geometry. Dover Publications, New York. 1999 (reprint of Twelve Geometric Essays, Southern Illinois University Press, Carbondale, IL. 1968).
10. (a) H. M. Cundy and A. P. Rollett, Mathematical Models 2nd edn, Clarendon Press, Oxford, 1961; (b) R. Williams, The geometrical foundation of natural structuresDover Publications, New York. 1979; (c) P. R. Cromwell, Polyhedra, Cambridge University Press, 1997.
11. W. B. Pearson, The Crystal Chemistry and Physics of Metals and Alloys, Wiley, New York, 1972.
12. M. O'Keeffe and B. G. Hyde, Crystal Structures I: Patterns and Symmetry, Mineral. Soc. Am, Washington D.C. 1996.
13. (a) A. F. Wells, Acta Crystallogr., 1954, 7, 535–544; (b) A. F. Wells, Three-Dimensional Nets and Polyhedra. Wiley, New York, 1977.
14. (a) J. V. Smith, Am. Mineral., 1977, 62, 703–709; (b) J. V. Smith, Am. Mineral., 1978, 63, 960–969.
15. (a) J. V. Smith, Am. Mineral., 1979, 64, 551–562; (b) J. V. Smith, Chem. Rev., 1988, 88, 149–182.
16. J. V. Smith, Tetrahedral Frameworks of Zeolites, Clathrates and Related Materials, Landolt-Börnstein New Series IV/14 Subvolume A, Springer, 2000.
17. L. Carlucci, G. Ciani and D. M. Proserpio, in Making Crystals by Design: Methods, Techniques and Applications, ed. D. Braga and F. Grepioni, Wiley-VCH, Weinheim, 2007, Ch. 1.3Networks, Topology and Entanglements, pp. 58–85.
18. L. Öhrström and K. Larsson, Molecular Based Materials: The Structural Network Approach, Elsevier, Amsterdam, 2005.
19. S. R. Batten, S. M. Neville, D. R. Turner, Coordination Polymers: Design, Analysis and Application, Royal Society of Chemistry, Cambridge, 2009.
20. S. Natarajan and P. Mahata, Chem. Soc. Rev., 2009 10.1039/b815106g , Advance Article.
21. M. O'Keeffe, Z. Kristallogr., 1991, 196, 21–37.
22. M. O'Keeffe and S. T. Hyde, Zeolites, 1997, 19, 370–374.
23. Ch. Baerlocher, W. N. Meier and D. H. OlsonAtlas of Zeolite Framework Types, 5th revised edition, Elsevier, Amsterdam, ( 2001). Data available on line at http://www.iza-structure.org/databases/.
24. M. O'Keeffe, M. A. Peskov, S. J. Ramsden and O. M. Yaghi, Acc. Chem. Res., 2008, 30, 1782–1789 See also http://rcsr.anu.edu.au/. RCSR database gives a name also to selected layers and polyhedra.
25. V. A. Blatov, IUCr CompComm Newsletter, 2006, 7, 4–38 TOPOS is available at http://www.topos.ssu.samara.ru.
26. F. Nouar, J. F. Eubank, T. Bousket, L. Wojtas, M. J. Zaworotko and M. Eddaoudi, J. Am. Chem. Soc., 2008, 130, 1833–1835.
27. V. A. Blatov, O. Delgado-Friedrichs, M. O'Keeffe and D. M. Proserpio, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2007, 63, 418–425.
28. O. Delgado-Friedrichs, The Gavrog Project. http://www.gavrog.org/.
29. (a) O. Delgado-Friedrichs, A. W. S. Dress, D. H. Huson, J. Klinowsky and A. L. Mackay, Nature, 1999, 400, 644–647; (b) O. Delgado-Friedrichs and M. O'Keeffe, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2007, 63, 344–347 . These papers give further references to D-symbols and their applications..
30. J. H. Conway, H. Burgiel and C. Goodman-Strauss, The Symmetries of Things, ed. A. K. Peters, Wellesley, MA, 2008.
31. S. J. Ramsden, V. Robbins and S. T. Hyde, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2009, 65, 81–108.
32. S. T. Hyde, M. O'Keeffe and D. M. Proserpio, Angew. Chem., Int. Ed., 2008, 47, 7996–8000.

---