Design of ternary alkaline-earth metal Sn(II) oxides with potential good p-type conductivity

Abstract

Oxides with good p-type conductivity have been long sought after to achieve high performance all-oxide optoelectronic devices. Divalent Sn(II) based oxides are promising candidates because of their rather dispersive upper valence bands caused by the Sn-5s/O-2p anti-bonding hybridization. There are so far few known Sn(II) oxides being p-type conductive suitable for device applications. Here, we present via first-principles global optimization structure searches a material design study for a hitherto unexplored Sn(II)-based system, ternary alkaline-earth metal Sn(II) oxides in the stoichiometry of MSn₂O₃ (M = Mg, Ca, Sr, Ba). We identify two stable compounds of SrSn₂O₃ and BaSn₂O₃, which can be stabilized by Sn-rich conditions in phase stability diagrams. Their structures follow the Zintl behaviour and consist of basic structural motifs of SnO₃ tetrahedra. Unexpectedly they show distinct electronic properties with band gaps ranging from 1.90 (BaSn₂O₃) to 3.15 (SrSn₂O₃) eV, and hole effective masses ranging from 0.87 (BaSn₂O₃) to above 6.0 (SrSn₂O₃) m₀. Further exploration of metastable phases indicates a wide tunability of electronic properties controlled by the details of the bonding between the basic structural motifs. This suggests further exploration of alkaline-earth metal Sn(II) oxides for potential applications requiring good p-type conductivity such as transparent conductors and photovoltaic absorbers.

---

1 Introduction

Metal oxides promise to be an important class of optoelectronic semiconductors owing to their robust environmental stabilities, earth-abundance, low-cost processing, etc.¹ Depending on specific band gaps, oxides can be applied in various devices such as emitters and detectors in blue and ultraviolet spectral region,² photocatalysts,³ transparent conductors,⁴ photovoltaic absorbers,⁵etc. The most significant factor hindering further development of the oxides based optoelectronic devices is their generally low p-type conductivity. Taking transparent conducting oxides (TCO) as examples, the industry standard n-type TCO, Sn-doped indium oxide, has a conductivity of at least 1000 S cm⁻¹, whereas the best p-type TCO, Mg-doped CuCrO₂ in delafossite, only exhibits a one-order lower conductivity of 220 S cm⁻¹.⁶

Design principles for achieving p-type conductivity in oxides

The low p-type conductivity in oxides originates predominately from the localized O-2p orbital dominated upper valence bands (VBs) at relatively deep binding energies. This results in low hole mobility and difficulty in finding suitable dopants to form shallow acceptor levels and create enough hole carriers.⁷ One strategy to overcome this issue is to take advantage of coupling/hybridization between the O-2p orbital and other orbitals. This can enhance dispersion of VBs and simultaneously raise their binding energies. The performance of the CuAlO₂, a recognized good p-type TCO, is related to this design principle, i.e., the hybridization between O-2p and Cu-3d (in d¹⁰ configuration) states.⁸ In addition to the strategy of the p–d coupling, one may also make use of the s–p coupling between lone-pair M-s (in s² configuration) orbital of some heavy metalloids of M in low-valence state (for instance Tl(I), Sn/Pb(II), Bi(III), etc.) and O-2p orbitals.^9,10 The fact that s-orbitals are generally more delocalized than d-orbitals means that the s–p coupling scenario may basically lead to more dispersive VBs, and thus is more effective in rendering oxides p-type conductive. Meanwhile, since the d¹⁰ and s² orbitals are filled, their derived VBs (by hybridizing with O-2p) are anti-bonding states. The anti-bonding feature of VBs usually causes defect tolerant behavior,^11,12i.e., bond breaking associated with the formation of defect states will produce but shallow rather than deep acceptor levels in the mid-gap region. This greatly facilitates p-type doping, giving rise to required ambipolar conductivity in photovoltaic materials of chalcopyrites¹³ and hybrid halide perovskites.¹⁴ Besides these efforts on utilizing the hybridization between cationic states and O-2p, introduction of anionic (e.g., chalcogen) states to couple with O-2p has also been considered;^15,16 however the actual VBs usually derive from the introduced anions, rather than the mixtures with O-2p.¹⁷

Sn(II) based oxides as promising p-type conducting materials

Sn(II) oxides with s–p coupling in VBs are therefore of interest, both in view of the design rules as above, and because Sn is an abundant, non-toxic element suitable for practical device applications. Binary Sn monoxide (SnO) has been demonstrated to have good p-type conductivity^18–20 up to 300 S cm⁻¹,²¹ and was proposed as candidate p-type TCO^21–23 and to realize ambipolar oxide devices.^24,25 The outstanding p-type conducting behaviors are associated with its dispersive VBs, consisting of mixtures of anti-bonding Sn-5s/O-2p states and Sn-5p_z states.^26–28 It has a small indirect band gap of 0.7 eV (and a direct gap of 2.7 eV), but suffers from a highly anisotropic effective mass of holes owing to its layered structure and issues with stability. Alloying SnO with other isoelectronic oxides to reduce its direct gap (to visible spectral region) has been suggested to render it efficient photovoltaic absorber.²⁹ Ternary oxides containing Sn(II) have been less studied. The known materials of oxostannates, e.g., A₂Sn₂O₃ (A = Na, K, Rb and Cs),^30,31 having rather low calculated hole effective mass and band gaps of 2.4–2.7 eV, were recently proposed as promising p-type TCO.¹⁰ However, the compounds containing alkali metals are prone to hydrolysis on exposure to air,³⁰ and are meanwhile may not be fully compatible with semiconductor based devices. Finding alternative ternary Sn(II) oxides that may offer good p-type conductivity is thus of current interest.

Here we investigate crystal structures and phase stability of hitherto unexplored ternary Sn(II) oxides containing alkaline-earth metals, i.e., MSn₂O₃ with M = Mg, Ca, Sr, Ba, with first-principles particle swarm optimization structure search calculations.^32,33 The most challenging issue associated with this class of materials is whether they are thermodynamically stable relative to the strongly competing Sn(IV) compounds such as ternary perovskites of Ca/Mg/Sr/BaSnO₃. We find while the less electropositive cations of Mg and Ca do not lead to stable compounds, the more electropositive cations of Sr and Ba stabilize ternary Sn(II) oxides against decomposing into competing phases under Sn-rich conditions. The identified stable phases of SrSn₂O₃ and BaSn₂O₃ show remarkably different electronic properties. BaSn₂O₃ has highly dispersive VBs with a low hole effective mass comparable to that of electron, leading to an expectation of both high electron and high hole mobility for ambipolar conduction. This work offers useful guidance to further exploration of ternary alkaline-earth metal Sn(II) oxides for applications requiring good p-type conductivity such as p-type TCO and photovoltaic absorbers.

2 Computational methods

Stable crystal structures of MSn₂O₃ are searched by first principles DFT energetic calculations guided by an in-house developed Crystal structure AnaLYsis by Particle Swarm Optimization (CALYPSO) methodology.^32,33 The key feature of our structure search method is its capability of rapidly identifying ground-state and metastable structures of materials with the only knowledge of chemical composition through intelligent exploration of the potential energy landscape. The algorithm details and its successful application in a variety of functional material systems have been discussed elsewhere.^34–37 We perform structure searches with 1, 2 and 4 formulas of MSn₂O₃ in the unit cell. For each search, the population size of each generation is chosen as 30 and around 50 generations are carried out (see Fig. 1) to guarantee convergence of the search. That is, ∼1500 structures are explored for each search calculation.

Fig. 1 Energies of explored structures as the function of generation for the structure search of BaSn₂O₃. The RGB color coding represents the deviation of coordination number of Sn(n) from 3 (|n − 3|). The lowest-energy structures of all the generations are connected with a solid line.

The underlying DFT calculations are performed with the projector-augmented wave (PAW) method³⁸ as implemented in the VASP code.³⁹ The 4d¹⁰5s²5p² (Sn), 2s²2p⁴ (O), 3s² (Mg), 3p⁶4s² (Ca), 4s²4p⁶5s² (Sr), 5s²5p⁶6s² (Ba) shells are treated as valence electrons of PAW pseudopotentials. The Perdew–Burke–Ernzerhof generalized gradient approximation (GGA)⁴⁰ is chosen as exchange–correlation functional. We employ medium quality computational parameters to evaluate relative energies of explored structures and accelerate structure searches. Then the low-lying energy structures are further optimized with more accurate computational parameters, e.g., kinetic energy cutoff of 520 eV and k-point meshes with grid spacing of 2π × 0.037 Å⁻¹. These settings ensure convergence of total energies at the level of less than 1 meV per atom. The hybrid functional (HSE06)^41,42 is used in band structure calculations to properly consider self-interaction correction and get correct band gaps. The average effective mass tensor that relates directly to carrier's electrical conductivity, is calculated based on the DFT-GGA rendered eigenvalues at more dense k-points grid of 2π × 0.016 Å⁻¹ through the semiclassical Boltzmann transport theory.⁴³ This takes into account effects of non-parabolicity and anisotropy of bands, multiple minima and multiple bands, etc. on carrier transport. The unified carrier concentration of 1.0 × 10¹⁸ cm⁻³ and room temperature of 300 K are chosen for such calculations. The phonon dispersions of predicted stable SrSn₂O₃ and BaSn₂O₃ phases are calculated by the supercell finite difference method as implemented in the PHONOPY code.⁴⁴ The absorption coefficients are evaluated via calculating the imaginary part of the dielectric tensor, i.e., through the sum over occupied and unoccupied bands of the dipole matrix elements, neglecting local field effects.⁴⁵

3 Results and discussion

Ground-state structures and their thermodynamic stabilities

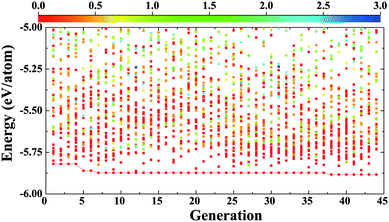
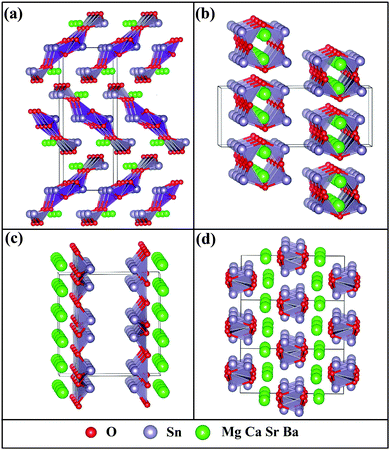
We begin with the identification of stable compounds based on extensive structure searches. Fig. 1 depicts an evolution of typical structure search (for BaSn₂O₃) with generation. One sees that more energetically favorable structures continually emerge with generation and the lowest-energy structure appears at the 38th generation. The overwhelming majority of low-lying energy structures are found to contain Sn coordinated by three O atoms (in red). This resembles that of A₂Sn₂O₃ (A = Na, K, Rb and Cs),^30,31 but is distinct from that of the litharge SnO where Sn is four-fold coordinated by O. The changes in local chemical bondings between Sn and O cause deviation of electronic structure in ternary Sn(II) oxides from that in binary SnO (see below).

The lowest-energy structures of MSn₂O₃ identified from structure searches are shown in Fig. 2 and their explicit structural information is listed in Table 1. The basic motif forming this class of materials is the SnO₃ tetrahedron in which Sn is 3-fold coordinated by O as mentioned. The exceptional feature of MgSn₂O₃ is that it contains SnO₄ pentahedron as well (Fig. 2a). The SnO₃/SnO₄ polyhedra connect with each other by sharing vertexes or edges in different manners for different materials, e.g., in planar sheets for MgSn₂O₃ and SrSn₂O₃, and in spiral chains for CaSn₂O₃ and BaSn₂O₃. These form framework of materials. The role of alkaline-earth metals is to donate electrons and stabilize lattices via Madelung potential. Therefore in general these compounds belong to the category of Zintl phase materials.⁴⁶ The averaged Sn–O bond lengths of four compounds are 2.22 (MgSn₂O₃), 2.13 (CaSn₂O₃), 2.16 (SrSn₂O₃), and 2.12 (BaSn₂O₃) Å, respectively. Considering the usual overestimation of lattice constants by the DFT-GGA method, the actual bond lengths should be smaller than that in SnO (2.22 Å).

Fig. 2 The lowest-energy structures of MgSn₂O₃ (a), CaSn₂O₃ (b), SrSn₂O₃ (c) and BaSn₂O₃ (d) identified by structure searches. In (a), the pentahedrons formed by Sn atoms coordinated by four O are highlighted in purple.

Table 1 Structural data of the lowest-energy structures of MSn₂O₃ (M = Mg, Ca, Sr, Ba) identified from structure searches

Material	Lattice parameters (Å)	Wyckoff positions	Atoms	x	y	z
Space group
MgSn2O3	a = 6.4662	4c	Mg	0.2190	0.7500	0.8319
Pnma	b = 3.6456		Sn1	0.7695	0.7500	0.0042
	c = 16.7450		Sn2	0.1382	0.2500	0.6676
			O1	0.5853	0.7500	0.5530
			O2	0.0407	0.7500	0.7340
			O3	0.3212	0.2500	0.8641
CaSn2O3	a = 5.8286	4c	Ca	0.2323	0.7500	0.4627
Pnma	b = 14.5058	8d	Sn	0.7284	0.3923	0.0011
	c = 5.5208	8d	O1	0.0023	0.1466	0.7807
		4c	O2	0.3289	0.7500	0.8737
SrSn2O3	a = 5.7666	4d	Sr	0.7500	0.0000	0.8795
Pcca	b = 9.9340	8f	Sn	0.6335	0.7194	0.5929
	c = 10.2191	8f	O1	0.9297	0.8387	0.5453
		4c	O2	0.0000	0.1569	0.7500
BaSn2O3	a = 5.7512	4e	Ba	0.0000	0.7371	0.2500
C2/c	b = 11.0753	8f	Sn	0.7494	0.0734	0.0058
	c = 9.9113	4d	O1	0.0000	0.1277	0.2500
	β = 124.331°	8f	O2	0.3615	0.1079	0.9789

---

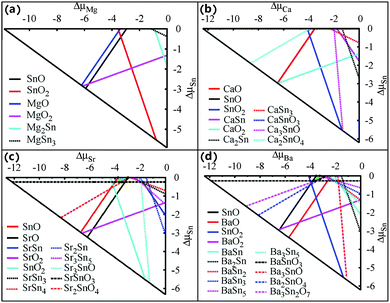
In actual crystal growth, the thermodynamic equilibrium condition requires a stable MSn₂O₃ compound to meet the following three criteria:

Δμ_M + 2Δμ_Sn + 3Δμ_O = ΔH_f (MSn₂O₃), (1)

Δμ_i ≤ 0, (i = M, Sn, O), (2)

n_jΔμ_M + m_jΔμ_Sn + q_jΔμ_O ≤ ΔH_f (M_njSn_mjO_qj), j = 1,…,t, (3)

where Δμ_i = μ_i − μ⁰_i is the deviation of actual chemical potential of the atomic species i during growth (μ_i) from that of bulk elemental solid or gas phase (μ⁰_i), ΔH_f is heat of formation, and M_njSn_mjO_qj represent all the known j competing phases. The eqn (1) is for equilibrium growth, eqn (2) is to prevent precipitation to elemental phases of atomic species, and eqn (3) is to ensure MSn₂O₃ stable against the formation of competing phases. To accurately evaluate ΔH_f, the fitted elemental-phase reference energies⁴⁷ (i.e., μ⁰_i) are used to improve the error cancellation when calculating the energy differences between the compound and its elemental constituents. Fig. 3 shows two-dimensional phase stability diagrams with two independent quantities of Δμ_M and Δμ_Sn as variables. For each case, all the competing phases of binary and ternary compounds are considered. As clearly seen, while no stable region exists for MgSn₂O₃ and CaSn₂O₃, SrSn₂O₃ and BaSn₂O₃ exhibit visible stability under Sn-rich conditions (i.e., Δμ_Sn close to zero). As expected the strongest competitions come from binary SnO and ternary Sn(IV) compounds, which provide limitation to broadening of the stable regions of Sr/BaSn₂O₃. In addition to the thermodynamic stability with respect to competing phases, we have also examined lattice dynamical stability of SrSn₂O₃ and BaSn₂O₃. Fig. 4 shows their phonon dispersion curves. Absence of any imaginary phonon mode in the whole Brillouin zone clearly reflects their lattice stabilities at ambient condition. These results indicate that by deliberately controlling chemical potentials of reactants, single-phases of Sr/BaSn₂O₃ can be experimentally grown.

Fig. 3 Phase stability diagrams of MgSn₂O₃ (a), CaSn₂O₃ (b), SrSn₂O₃ (c) and BaSn₂O₃ (d), respectively. In each case, each line represent a known competing phase; the stable region of MSn₂O₃ is indicated in green if there is.

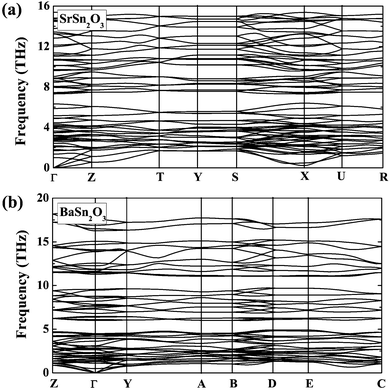Fig. 4 Calculated phonon dispersion curves of (a) SrSn₂O₃ in the ground-state Pcca structure and (b) BaSn₂O₃ in the ground-state C2/c structure.

Electronic properties of stable compounds: SrSn₂O₃ and BaSn₂O₃

Fig. 5 shows calculated band gaps and average effective masses for the predicted lowest-energy structures of MSn₂O₃. All the compounds show indirect band gaps, along with larger direct gaps above 2 eV. For the stable compounds of SrSn₂O₃ and BaSn₂O₃, the direct gaps are 3.31 and 2.37 eV, respectively. The direct gap of SrSn₂O₃ is higher than those of SnO⁴⁸ and K₂Sn₂O₃,¹⁰ making it transparent for entire range of visible spectrum. Turning to the effective masses, both MgSn₂O₃ and BaSn₂O₃ show low effective masses of holes (m_h*), 0.78 and 0.87m₀, respectively, comparable to those of electrons. The low m_h* values are comparable to those of Na/K₂Sn₂O₃ and other p-type TCO candidates proposed in ref. 10. This is, however, not the case for SrSn₂O₃, which exhibits an unexpected heavy m_h* (above 6.0m₀) originating from its generally quite dispersionless VBs (as discussed below). Table 2 shows calculated electrical conductivities (σ) at the selected hole carrier concentration (n) for p-type SrSn₂O₃ and BaSn₂O₃, compared with the experimental values of typical p-type materials, CuAlO₂⁸ and SnO.²¹ For these calculations, the assumed same n and carrier relaxation time (τ) as those of SnO are adopted. The τ of SnO is evaluated with the experimental σ and our calculated σ/τ through the Boltzmann transport theory in the constant τ approximation.⁴³ As seen, the theoretical σ of SrSn₂O₃ (96 S cm⁻¹) and BaSn₂O₃ (450 S cm⁻¹) are much higher than that of CuAlO₂ (0.095 S cm⁻¹, at the lower n), and comparable to the value (300 S cm⁻¹) of SnO. BaSn₂O₃ with the lighter m_h* exhibits even higher σ than that of SnO.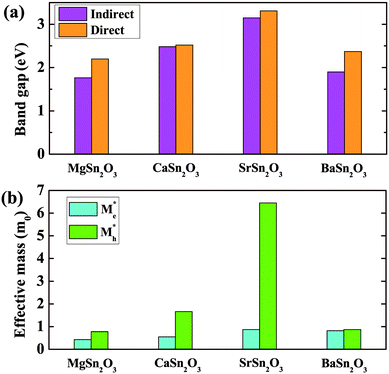

Fig. 5 Calculated (indirect/direct) band gaps (a) and average effective masses of electrons (m_e*) and holes (m_h*) (b) of the predicted lowest-energy structures of MSn₂O₃ (M = Mg, Ca, Sr, Ba).

Table 2 Calculated electrical conductivities (σ) at the selected hole carrier concentration (n) for p-type SrSn₂O₃ and BaSn₂O₃, compared with the experimental values of typical p-type materials, CuAlO₂ ⁸ and SnO ²¹

Material	n (cm^−3)	σ (S cm^−1)
CuAlO2 ^8	1.30 × 10^17	0.95 × 10^−1
SnO ^21	2.00 × 10^20	3.00 × 10^2
SrSn2O3	2.00 × 10^20	0.96 × 10^2
BaSn2O3	2.00 × 10^20	4.50 × 10^2

---

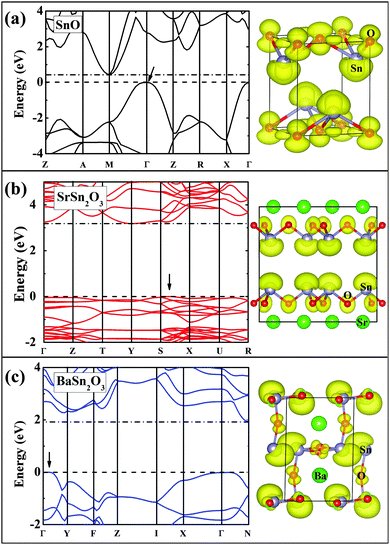
Fig. 6 and 7 show band structures and atomic orbital-projected density of states (DOS) for two stable compounds, SrSn₂O₃ (in red) and BaSn₂O₃ (in blue), compared with those of SnO (in black). The crystal orbital overlap population (COOP) results⁴⁹ for bonding-type analysis are shown in Fig. S1 (ESI†). The electronic structure of SnO is calculated at experimental structural parameters, giving a slightly lower band gap of 0.44 eV than the experimental 0.7 eV;⁴⁸ the remaining features are well consistent with previous calculations.^26–28 One clearly observes that the band gaps of ternary compounds are significantly widened relative to binary SnO. Similar trends were found in the compounds with the p–d hybridization dominating VBs, e.g., from Cu₂O⁵⁰ to CuAlO₂.⁸

Fig. 6 Calculated band structures of (a) SnO, (b) SrSn₂O₃ and (c) BaSn₂O₃, respectively. Decomposed charge density for the VB maximum (indicated by red arrow) of each material is shown as right panel.

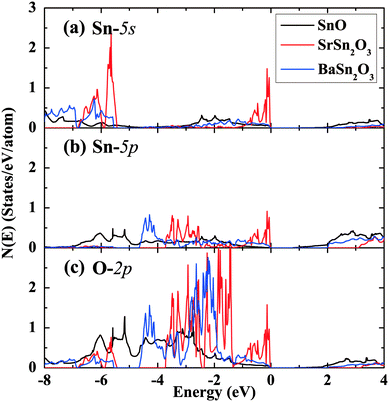Fig. 7 Projected density of states of SnO, SrSn₂O₃ and BaSn₂O₃ onto the atomic orbitals of (a) Sn-5s, (b) Sn-5p, and (c) O-2p, respectively. The VB maximum is set to energy zero.

For BaSn₂O₃, the dispersion of VBs is quite high, resembling that of SnO. This is responsible for its low m_h* as mentioned, and originates from the strong hybridization between Sn-5s and O-2p states in the region of −4 to 0 eV (Fig. 7). The anti-bonding feature of such hybridization is unambiguously indicated in the COOP results (with positive n(e) representing bonding and negative n(e) representing anti-bonding, see ESI,† Fig. S1a). In addition to the Sn-5s states, there appear substantial Sn-5p states in VBs (−4.7 to 0 eV in Fig. 7b), forming bonding states with O-2p orbitals. The decomposed charge density at the VB maximum shows an asymmetric distribution around each Sn atom with a “lobe” pointing to interstitial region. The involvement of the nominally unoccupied Sn-5p orbitals of Sn(II) in the VBs is essential to produce such an anisotropic charge distribution and contribute to stabilization of the structure.^26,28 These electronic structure features are closely similar to those of SnO, though BaSn₂O₃ has one less coordination number of Sn.

By considering the usually similar properties of Ba and Sr oxides and the common motif of SnO₃ tetrahedron making up Sr/BaSn₂O₃, one may suppose that SrSn₂O₃ will show similar electronic properties. However, in fact, SrSn₂O₃ shows rather flat VBs (Fig. 6b) with a remarkably heavy m_h*. This is reflected in its decomposed charge density at VB maximum (right panel of Fig. 6b) where the charge is relatively symmetrically localized around Sn and O atoms. In contrast to the case of BaSn₂O₃ where the anti-bonding hybridization between Sn-5s and O-2p is spread over the energy rang of −4 to 0 eV, the Sn-5s/O-2p anti-bonding states are mainly located within a narrow energy range of −1 to 0 eV (Fig. 7 and Fig. S1a(ESI†)). Additionally in the same energy range there exists bonding hybridization between Sn-5p and O-2p states (Fig. S1b(ESI†)). These two types of hybridizing states with strong localization cause the remarkably heavy VBs and a sharp DOS peak at VB edges of SrSn₂O₃. Such a large difference between chemically similar compounds is unusual, but does occur in some systems including Sn⁴⁺ ternary oxides with perovskite based structures.^51–53

Wide tunability of optoelectronic properties in metastable materials

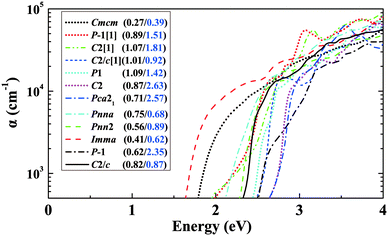
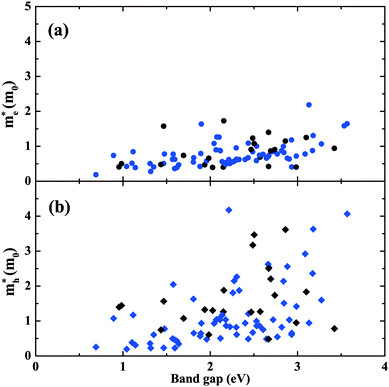
In addition to the lowest-energy ground-state structure, our structure searches have also identified metastable structures. These structures represent local minima of the potential energy landscape. If they are not so high in energy, there is the possibility that they could be stabilized under some particular conditions. It is also of interest to study the metastable structures to access the extent to which properties are likely to be tunable. Also, exploration of the metastable structures can provide understanding of structure–property relationships. Focusing on BaSn₂O₃, we first choose 11 low-lying metastable structures that can survive in the phase stability diagram of Fig. 3d, i.e., their energies are low enough to render the stable green region existing. The maximum difference in energy between them and the ground-state C2/c structure is 47 meV per atom. Their detailed structure information is listed in Table S1(ESI†). The results of their absorption spectra, as well as m_e* and m_h* are shown in Fig. 8, compared with those of the ground-state structure (solid line). One observes that the absorption thresholds of them span a wide energy range of more than 1 eV. Besides the ground-state structure, five of them (e.g., Imma, Pnn2, Pnna, C2/c[1] and Cmcm) show low m_h* below 1.0m₀; the remaining ones have medium-low m_h* between 1.0 and 3.0m₀. The C2 and Pca2₁ structures with rather high thresholds of ∼2.7 eV (just above the blue part of the visible spectrum) may be used as potential p-type TCOs depending on the exact optical window of interest. The particularly interesting case is the Imma structure, which is only 11 meV per atom higher in energy than the ground-state, starts absorbing visible light from a low threshold of ∼1.6 eV. Also, it has simultaneously low m_e* (0.41m₀) and low m_h* (0.62m₀) favourable for ambipolar conductivity. Therefore it would be potentially good photovoltaic absorber if it can be made.

Fig. 8 Calculated absorption spectra of selected metastable BaSn₂O₃ compounds identified from structure searches (see text). The result of the ground-state C2/c structure is shown for comparison (in solid line). The values following space groups of materials are their m_e* and m_h* (highlighted in blue), respectively.

We then take into account more metastable structures with energies of no more than 0.2 eV per atom higher than the ground-state structure. Fig. 9 shows mapping these structures onto the variables of m_e*/m_h* and band gap. Most of the structures are made up of SnO₃ tetrahedra with 3-fold coordinated Sn (in blue), consistent with Fig. 1. In spite of containing the common SnO₃ tetrahedra, their electronic properties exhibit a wide range of changes, e.g., band gap from 0.5 to 3.5 eV, m_h* from ∼0 to 4.0m₀. This implies the specific manner in which the SnO₃ tetrahedra connect with each other plays an important role in determining materials properties. From Fig. 9a, one can see a general trend that the larger band gap, the higher m_e*. This trend is in accord with the discipline derived from the k·p theory for conventional semiconductors.⁵⁴ Turning to m_h*, the data seems rather scattered without clear trend. For the structures with the smaller band gaps (<2 eV), their m_h* are also lower (<2m₀), and only the wide-gap (>2 eV) structures have chances to own high m_h*.

Fig. 9 Distribution map of the metastable compounds of BaSn₂O₃ with energies of no more than 0.2 eV per atom higher than the ground-state C2/c structure, onto the variables of m_e* vs. band gaps (a) and m_h* vs. band gaps (b) respectively. The data in blue represent the structures with Sn 3-fold coordinated by O.

4 Summary and further discussion

With the aim of designing new-type oxides with the s–p hybridization in valence bands for achieving good p-type conductivity, we explore crystal structures and phase stability of ternary alkaline-earth metal Sn(II) oxides by using first-principles global optimization structure search calculations. We identify two stable compounds, SrSn₂O₃ in the Pcca structure and BaSn₂O₃ in the C2/c structure, exhibiting both lattice dynamical stabilities and thermodynamic stabilities with respect to competing phases. BaSn₂O₃ shows a moderate band gap of 1.90 eV (with a direct gap of 2.37 eV), and quite dispersive valence bands with a low hole effective mass of 0.87m₀. This originates mainly from the anti-bonding hybridization between Sn-5s and O-2p states in valence bands, resembling that of litharge SnO. In contrast, SrSn₂O₃ have a wide band gap of 3.15 eV, and unexpected flat valence bands with a very heavy hole effective mass of above 6.0m₀. Further analysis of low-lying metastable phases indicate that this class of materials show a wide range of change in electronic properties with respect to specific connection manners of the basic structural motifs of SnO₃ tetrahedra. The remarkable differences in properties of the two newly identified stable compounds, BaSn₂O₃ and SrSn₂O₃ and the fact that this class of materials span ranges of applications requiring p-type conductivity such as transparent conductors and solar absorbers, suggests experimental investigation of these compounds as well as searches for quaternary Sn(II) oxide compounds and alloys with related compositions.

The family of ternary Sn(II) oxides containing alkaline/alkaline-earth metals follows Zintl behavior in that the cationic metals act only by providing electrons and supporting the lattices, and the structural framework is made up of connected SnO₃ tetrahedra. The electronic properties of materials are to a large extent determined by the Sn–O framework. In this sense these materials can be viewed as stuffed, though very heavily distorted, SnO (e.g., with the change of Sn coordination number from 4 to 3). The breaking of ideal layered structure of SnO increases isotropy of transport-related properties. The tetrahedra connecting with each other within the Sn–O framework facilitates carriers band transport. The stabilization of Sr/BaSn₂O₃ in the system can also be rationalized based on this Zintl concept. Compared with Mg/Ca, Sr and Ba have the lower electronegativities, 0.95 and 0.89 by Pauling scale, respectively, which are comparable to those of Na (0.93) and K (0.82). Such more electropositive cations correspond to the more complete charge transfer from cation sites to the Sn–O framework. The sufficient amount of electrons available for Sn–O bonding in the framework prevents Sn from being oxidized to Sn(IV) and thus stabilizes Sn(II) compounds. This underlines the important role of the electronegativity of metals in stabilizing relevant ternary or quaternary Sn(II) oxides. Furthermore the existence of alkaline-earth metals with +2 valence in the system is greatly beneficial to p-type doping, since partial substitution of alkaline-earth metals with alkali metals is a well established doping routine, as demonstrated for instance in Fe-based superconductor of Ba_1−xK_xFe₂As₂.⁵⁵ The possibility of existence of compensating intrinsic defects (i.e., hole killers) such as the Sn interstitial and oxygen vacancy^56,57 should be considered in the context of doping studies if these compounds are successfully synthesized.

Acknowledgements

The work at Jilin Univ. is supported by the funding of National Natural Science Foundation of China under Grant No. 11274136 and 11534003, 2012 Changjiang Scholar of Ministry of Education and the Postdoctoral Science Foundation of China under grant 2013M541283. L. Z. acknowledges funding support from the Recruitment Program of Global Youth Experts in China. D. J. S. is supported by the U.S. Department of Energy, Basic Energy Sciences through the computational synthesis of materials software project. M.-H. D. was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. Part of calculations was performed in the high performance computing center of Jilin University.

References

1. P. Kofstad, Nonstoichiometry, diffusion, and electrical conductivity in binary metal oxides, Wiley, New York, 1972.
2. M. E. Levinshtein, S. L. Rumyantsev and M. S. Shur, Properties of Advanced Semiconductor Materials: GaN, AIN, InN, BN, SiC, SiGe, Wiley, New York, 2001.
3. X. Chen, S. Shen, L. Guo and S. S. Mao, Chem. Rev., 2010, 110, 6503–6570.
4. D. S. Ginley and C. Bright, Mater. Res. Bull., 2000, 25, 15–18.
5. S. Ruhle, A. Y. Anderson, H.-N. Barad, B. Kupfer, Y. Bouhadana, E. Rosh-Hodesh and A. Zaban, J. Phys. Chem. Lett., 2012, 3, 3755–3764.
6. R. Nagarajan, A. D. Draeseke, A. W. Sleight and J. Tate, J. Appl. Phys., 2001, 89, 8022–8025.
7. S. Zhang, S.-H. Wei and A. Zunger, J. Appl. Phys., 1998, 83, 3192–3196.
8. H. Kawazoe, M. Yasukawa, H. Hyodo, M. Kurita, H. Yanagi and H. Hosono, Nature, 1997, 389, 939–942.
9. A. Walsh, D. J. Payne, R. G. Egdell and G. W. Watson, Chem. Soc. Rev., 2011, 40, 4455–4463.
10. G. Hautier, A. Miglio, G. Ceder, G.-M. Rignanese and X. Gonze, Nat. Commun., 2013, 4, 2292.
11. S. B. Zhang, S.-H. Wei, A. Zunger and H. Katayama-Yoshida, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 9642–9656.
12. R. E. Brandt, V. Stevanović, D. S. Ginley and T. Buonassisi, MRS Commun., 2015, 5, 265–275.
13. R. Herberholz, V. Nadenau, U. Rühle, C. Köble, H. Schock and B. Dimmler, Sol. Energy Mater. Sol. Cells, 1997, 49, 227–237.
14. M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643–647.
15. H. Hiramatsu, K. Ueda, H. Ohta, M. Hirano, T. Kamiya and H. Hosono, Appl. Phys. Lett., 2003, 82, 1048.
16. K. Ueda, H. Hiramatsu, H. Ohta, M. Hirano, T. Kamiya and H. Hosono, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 155305.
17. D. O. Scanlon, J. Buckeridge, C. R. A. Catlow and G. W. Watson, J. Mater. Chem. C, 2014, 2, 3429–3438.
18. Y. Ogo, H. Hiramatsu, K. Nomura, H. Yanagi, T. Kamiya, M. Hirano and H. Hosono, Appl. Phys. Lett., 2008, 93, 2113.
19. Y. Ogo, H. Hiramatsu, K. Nomura, H. Yanagi, T. Kamiya, M. Kimura, M. Hirano and H. Hosono, Phys. Status Solidi B, 2009, 206, 2187–2191.
20. D. Granato, J. Caraveo-Frescas, H. Alshareef and U. Schwingenschlögl, Appl. Phys. Lett., 2013, 102, 212105.
21. A. Behrendt, C. Friedenberger, T. Gahlmann, S. Trost, T. Becker, K. Zilberberg, A. Polywka, P. Görrn and T. Riedl, Adv. Mater., 2015, 27, 5961–5967.
22. E. Fortunato, R. Barros, P. Barquinha, V. Figueiredo, S.-H. K. Park, C.-S. Hwang and R. Martins, Appl. Phys. Lett., 2010, 97, 052105.
23. J. A. Caraveo-Frescas, P. K. Nayak, H. A. Al-Jawhari, D. B. Granato, U. SchwingenschloÌĹgl and H. N. Alshareef, ACS Nano, 2013, 7, 5160–5167.
24. K. Nomura, T. Kamiya and H. Hosono, Adv. Mater., 2011, 23, 3431–3434.
25. H. Hosono, Y. Ogo, H. Yanagi and T. Kamiya, Electrochem. Solid-State Lett., 2011, 14, H13–H16.
26. G. W. Watson, J. Chem. Phys., 2001, 114, 758–763.
27. J.-M. Raulot, G. Baldinozzi, R. Seshadri and P. Cortona, Solid State Sci., 2002, 4, 467–474.
28. A. Walsh and G. W. Watson, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235114.
29. H. Peng, A. Zakutayev and S. Lany, 2015, arXiv:1504.01168.
30. R. M. Braun and R. Hoppe, Angew. Chem., Int. Ed. Engl., 1978, 17, 449–450.
31. R. M. Braun and R. Hoppe, Z. Naturforsch., B: J. Chem. Sci., 1982, 37, 688–694.
32. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
33. Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070.
34. Z. Zhao, B. Xu, X.-F. Zhou, L.-M. Wang, B. Wen, J. He, Z. Liu, H.-T. Wang and Y. Tian, Phys. Rev. Lett., 2011, 107, 215502.
35. X. Zhang, Y. Wang, J. Lv, C. Zhu, Q. Li, M. Zhang, Q. Li and Y. Ma, J. Chem. Phys., 2013, 138, 114101.
36. M. Zhang, H. Liu, Q. Li, B. Gao, Y. Wang, H. Li, C. Chen and Y. Ma, Phys. Rev. Lett., 2015, 114, 015502.
37. Q. Wang, B. Xu, J. Sun, H. Liu, Z. Zhao, D. Yu, C. Fan and J. He, J. Am. Chem. Soc., 2014, 136, 9826–9829.
38. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
39. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
40. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
41. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
42. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
43. G. K. H. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71.
44. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
45. M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112.
46. T. F. Fässler, Zintl Phases: Principles and Recent Developments, Springer, Berlin, Heidelberg, New York, 2011, vol. 139.
47. V. Stevanović, S. Lany, X. Zhang and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115104.
48. R. Sivaramasubramaniam, M. R. Muhamad and S. Radhakrishna, Phys. Status Solidi B, 1993, 136, 215–222.
49. R. Hoffman, Solids and Surfaces, Wiley-VCH, New York, 1988, p. 42.
50. E. Ruiz, S. Alvarez, P. Alemany and R. A. Evarestov, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 7189–7196.
51. X. Fan, W. Zheng, X. Chen and D. J. Singh, PLoS One, 2014, 9, e91423.
52. D. J. Singh, Q. Xu and K. P. Ong, Appl. Phys. Lett., 2014, 104, 011910.
53. Y. Li, L. Zhang, Y. Ma and D. J. Singh, APL Mater., 2015, 3, 011102.
54. S. Adachi, Physical properties of III-V semiconductor compounds, John Wiley & Sons, New York, 1992.
55. M. Rotter, M. Tegel and D. Johrendt, Phys. Rev. Lett., 2008, 101, 107006.
56. A. Togo, F. Oba, I. Tanaka and K. Tatsumi, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 195128.
57. J. P. Allen, D. O. Scanlon, L. F. Piper and G. W. Watson, J. Mater. Chem. C, 2013, 1, 8194–8208.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6tc00996d

---