Surface tension and a self-consistent theory of soft composite solids with elastic inclusions

Abstract

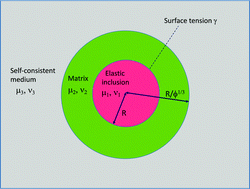
The importance of surface tension effects is being recognized in the context of soft composite solids, where they are found to significantly affect the mechanical properties, such as the elastic response to an external stress. It has recently been discovered that Eshelby's inclusion theory breaks down when the inclusion size approaches the elastocapillary length L ≡ γ/E, where γ is the inclusion/host surface tension and E is the host Young's modulus. Extending our recent results for liquid inclusions, here we model the elastic behavior of a non-dilute distribution of isotropic elastic spherical inclusions in a soft isotropic elastic matrix, subject to a prescribed infinitesimal far-field loading. Within our framework, the composite stiffness is uniquely determined by the elastocapillary length L, the spherical inclusion radius R, and the stiffness contrast parameter C, which is the ratio of the inclusion to the matrix stiffness. We compare the results with those from the case of liquid inclusions, and we derive an analytical expression for elastic cloaking of the composite by the inclusions. Remarkably, we find that the composite stiffness is influenced significantly by surface tension even for inclusions two orders of magnitude more stiff than the host matrix. Finally, we show how to simultaneously determine the surface tension and the inclusion stiffness using two independent constraints provided by global and local measurements.