Soft modes and strain redistribution in continuous models of amorphous plasticity: the Eshelby paradigm, and beyond?

Abstract

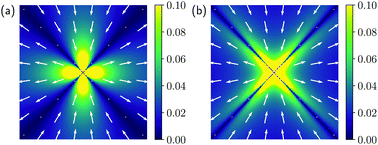
The deformation of disordered solids relies on swift and localised rearrangements of particles. The inspection of soft vibrational modes can help predict the locations of these rearrangements, while the strain that they actually redistribute mediates collective effects. Here, we study soft modes and strain redistribution in a two-dimensional continuous mesoscopic model based on a Ginzburg–Landau free energy for perfect solids, supplemented with a plastic disorder potential that accounts for shear softening and rearrangements. Regardless of the disorder strength, our numerical simulations show soft modes that are always sharply peaked at the softest point of the material (unlike what happens for the depinning of an elastic interface). Contrary to widespread views, the deformation halo around this peak does not always have a quadrupolar (Eshelby-like) shape. Instead, for finite and narrowly-distributed disorder, it looks like a fracture, with a strain field that concentrates along some easy directions. These findings are rationalised with analytical calculations in the case where the plastic disorder is confined to a point-like ‘impurity’. In this case, we unveil a continuous family of elastic propagators, which are identical for the soft modes and for the equilibrium configurations. This family interpolates between the standard quadrupolar propagator and the fracture-like one as the anisotropy of the elastic medium is increased. Therefore, we expect to see a fracture-like propagator when extended regions on the brink of failure have already softened along the shear direction and thus rendered the material anisotropic, but not failed yet. We speculate that this might be the case in carefully aged glasses just before macroscopic failure.