Valence, loop formation and universality in self-assembling patchy particles
Abstract
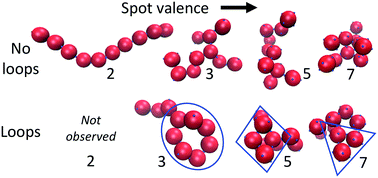
Patchy particles have emerged as an attractive model to mimic phase separation and self-assembly of globular proteins solutions, colloidal patchy particles, and molecular fluids where directional interactions are operative. In our previous work, we extensively explored the coupling of directional and isotropic interactions on both the phase separation and self-assembly in a system of patchy particles with five spots. Here, we extend this work to consider different patch valences and isotropic interaction strengths with an emphasis on self-assembly. Although the location of self-assembly transition lines in the temperature–density plane depend on a number of parameters, we find universal behavior of cluster size that is dependent only on the probability of a spot being bound, the patch valence, and the density. Using these principles, we quantify both the mass distribution and the shape for all clusters, as well as clusters containing loops. Following the logical implications of these results, combined with a simplified version of a mean-field theory that incorporates Flory–Stockmayer theory, we find a universal curve for the temperature dependence of cluster mass and a universal curve for the fraction of clusters that contain loops. As the curves are dependent on the particle valence, such results provide a method for parameterizing patchy particle models using experimental data.


 Please wait while we load your content...
Please wait while we load your content...