Optimized monotonic convex pair potentials stabilize low-coordinated crystals

Abstract

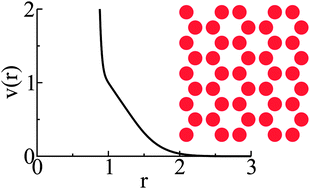
We have previously used inverse statistical-mechanical methods to optimize isotropic pair interactions with multiple extrema to yield low-coordinated crystal classical ground states (e.g., honeycomb and diamond structures) in d-dimensional Euclidean space ^d. Here we demonstrate the counterintuitive result that no extrema are required to produce such low-coordinated classical ground states. Specifically, we show that monotonic convex pair potentials can be optimized to yield classical ground states that are the square and honeycomb crystals in ² over a non-zero number density range. Such interactions may be feasible to achieve experimentally using colloids and polymers.