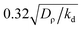Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Pattern formation in chemically interacting active rotors with self-propulsion†
Benno
Liebchen
*a,
Michael E.
Cates
b and
Davide
Marenduzzo
a
aSUPA, School of Physics and Astronomy, University of Edinburgh, Edinburgh EH9 3FD, UK. E-mail: Benno.Liebchen@staffmail.ed.ac.uk
bDAMTP, Centre for Mathematical Sciences, University of Cambridge, Cambridge CB3 0WA, UK
First published on 8th August 2016
Abstract
We demonstrate that active rotations in chemically signalling particles, such as autochemotactic E. coli close to walls, create a route for pattern formation based on a nonlinear yet deterministic instability mechanism. For slow rotations, we find a transient persistence of the uniform state, followed by a sudden formation of clusters contingent on locking of the average propulsion direction by chemotaxis. These clusters coarsen, which results in phase separation into a dense and a dilute region. Faster rotations arrest phase separation leading to a global travelling wave of rotors with synchronized roto-translational motion. Our results elucidate the physics resulting from the competition of two generic paradigms in active matter, chemotaxis and active rotations, and show that the latter provides a tool to design programmable self-assembly of active matter, for example to control coarsening.
Various self-propelled microorganisms, like the bacterium E. coli1–3 or the slime mold Dictyostelium disoideum (Dicty)4 can adapt their motion in response to gradients of chemicals which they produce themselves (Fig. 1a). Such a chemical ‘signalling’ can induce spontaneous aggregation through a positive feedback (Fig. 1b): an initial positive chemical density fluctuation attracts microorganisms, which produce further chemicals; this amplifies the initial fluctuation supporting the recruitment of further microorganisms, which eventually condense into a macroscopic cluster coexisting with a dilute microbial bath (Fig. 1b). Quantified by the Keller–Segel (KS) model in the 1970s,5,6 this signalling-route to phase separation now serves as a prototypical example for self-organization in nonequilibrium.7 It is crucial for the life cycle of Dicty;4 it is also one possible mechanism to explain pattern formation in bacterial colonies within agar,1,2 alongside an alternative explanation based on arrested motility induced phase separation.8
Currently, the KS instability is attracting renewed attention in active synthetic Janus colloids. These particles catalyse reactions within a chemical bath, yielding gradients which drive self-propulsion via diffusiophoresis or a similar mechanism. Importantly, other colloids may feel rotational torques caused by the same long-ranged gradients and respond to them by adapting their swimming direction, thereby providing a synthetic analog of chemotactic signalling.9–11 The same KS equations can therefore be transferred from the microbiological world to phoretic colloids.10,12–14 Here, either the KS instability, or instabilities based on chemorepulsion15 may help explain the still elusive dynamic clustering observed in experiments.10,16,17
In all these cases chemotactic instability relies on the ability of weak chemical fluctuations around the uniform density to align microswimmers up (or down) chemical gradients. However, under many circumstances microswimmers vary their swimming direction autonomously of chemical cues: this occurs, e.g., for bacteria swimming clockwise close to a glass wall,18 or anti-clockwise near an oil–water interface19 (see ESI† for a discussion on parameters). Synthetic examples of active signalling rotors with self-propulsion (sometimes called ‘circle swimmers’) may be realised with L-shaped phoretic swimmers,20,21 or with active particles with dipole moments16,22,23 which will track the rotation of applied external fields16,24 and can interact via self-produced phoretic fields.16
We should expect that, close to uniform states, finite active torques as caused by intrinsic rotations will generally outcompete chemotactic torques which are proportional to the chemical gradient, when it comes to determining swimming direction: hence, they might generically lead to a breakdown of the linear KS instability. Does this rule out the possibility of phase separation and patterning in signalling rotors? This could have profound consequences for systems like thin (bio)films of chemotactic bacteria25 or actuated phoretic particles.
Here, we propose a generic model to study active signalling rotors. As a key result we find that even weak active rotations suppress the linear KS instability. However, we identify an instability mechanism which is distinct from the KS mechanism and creates a nonlinear, but deterministic, route to pattern formation.
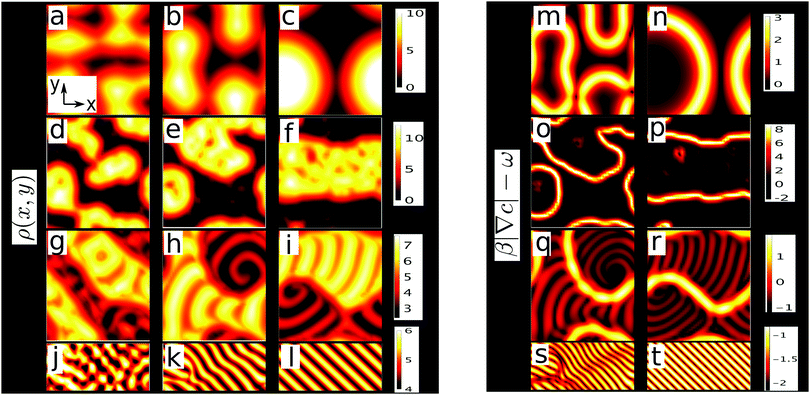
For small rotation frequency, this route generates macroscopic phase separation: a fraction of the rotors condenses into a dense phase, separated from a dilute gas by a quasi-stationary interface where chemotaxis suppresses rotations and ‘locks’ the average swimming direction onto the upward density gradient. Away from the interfaces, rotations persist in both phases and lead to dynamic patterns, such as spots or moving stripes and spirals (Fig. 2h and i) This combination of phase separation with pattern formation within both phases represents a novel type of hierarchical structure formation. When increasing the rotation frequency above a certain threshold, strikingly, the growing clusters do not coarsen any more but form a global pattern of travelling stripes with self-limiting size, suggesting that active rotations can be used to control coarsening in suspensions of self-propelled particles (Fig. 2l).
We describe active particles which self-propel with velocity v0 and rotate with frequencies ωi > 0 at a coarse grained level in two-dimensions. A smooth ρ(x,t) represents the active particle density and p(x,t) is the local average of the unit vector describing the direction of self-propulsion. We focus on polarized rotors with identical frequencies, which applies to synthetic colloidal rotors locked to a rotating field, but also to bacterial rotors where short-ranged alignment interactions can synchronize the individual rotations locally (see ESI† and final paragraph). Thus, in absence of signalling, p rotates with a collective frequency ω. Generally however, our rotors produce signalling molecules with a local rate k0ρ; hence p also responds, via chemotaxis, to gradients of the resulting chemical field c(x,t), which is degraded with a rate kd (compare ref. 5 and 26). This yields a competition of intrinsic active rotations and chemotactic alignment which determines the behaviour of the signalling rotors at large scales. Allowing for finite diffusion of the chemical and colloidal density fields with coefficients Dc and Dρ, we describe signalling rotors phenomenologically by:
![[small rho, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a6.gif) = −v0∇·(ρp) + Dρ∇2ρ + K∇2ρ3 = −v0∇·(ρp) + Dρ∇2ρ + K∇2ρ3 | (1) |
![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) = ω + β = ω + β![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) × ∇c; p = (cos × ∇c; p = (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ, sin ϕ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ)T ϕ)T | (2) |
| ċ = k0ρ − kdc + Dc∇2c + ε(c0 − c)3. | (3) |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) c = Dc/Dρ which measures the ratio of chemical and colloidal/bacterial diffusion, both mainly affecting length scales here, these parameters determine the linear behaviour of the present model. The two remaining parameters κ = Kkd2v02/(Dρk02β2) and ε = εv02/(kdβ2) control non-linear effects. We choose experimentally sensible values for these parameters (ESI†) and introduce the dimensionless number Δ = ωv0/(ρ0k0β) as a measure of the relative importance of active rotations (circular swimming) and chemotaxis (biased swimming up chemical gradients) as our key control parameter.
c = Dc/Dρ which measures the ratio of chemical and colloidal/bacterial diffusion, both mainly affecting length scales here, these parameters determine the linear behaviour of the present model. The two remaining parameters κ = Kkd2v02/(Dρk02β2) and ε = εv02/(kdβ2) control non-linear effects. We choose experimentally sensible values for these parameters (ESI†) and introduce the dimensionless number Δ = ωv0/(ρ0k0β) as a measure of the relative importance of active rotations (circular swimming) and chemotaxis (biased swimming up chemical gradients) as our key control parameter.
We now explore the competition of active rotations and chemotaxis by solving eqn (1)–(3) for different Δ on a square lattice with Lx × Ly grid points and periodic boundary conditions using finite difference methods. As an initial state, we choose a small and random perturbation of the spatially uniform and coherently rotating state (ρ,ϕ,c) = (ρ0,ωt,(k0/kd)ρ0) which solves eqn (1)–(3). In absence of rotations (Δ = 0) we observe clusters growing out of the uniform state (Fig. 2a), which colocalise with chemical density maxima and coarsen at long times (Fig. 2b), yielding one dense macroscopic cluster coexisting with a dilute gas (Fig. 2c). Here, instability of the uniform state is expected due to the positive feedback loop of particle aggregation and chemical production we discussed in the introduction and in ref. 15.
For Δ = 5 × 10−3 this picture changes dramatically. Now the uniform state persists for a certain duration (see Videos 1 and 2 in ESI†): we call this the initial lag regime. Then, almost suddenly, fluctuations ‘awake’ and grow to create clusters (Fig. 2d). These clusters coarsen into a relatively dense phase separated from a dilute rotor gas (Fig. 2f) by a slowly-moving interface where rotations are suppressed and particles swim, on average, up the chemical gradient (Video 2, ESI†). Away from the interface, all colloids perform a ‘stop-and-go’ rotation, which is associated with dynamic short-lived density dips and peaks (white spots and red dips in yellow region in Fig. 2e and f). Choosing stronger rotations (Δ = 0.024) we observe a similar suppression of rotations at the interfaces, but within both phases stripe and spiral patterns form (Fig. 2g–i and Video 2, ESI†).
For Δ = 0.044 complexity suddenly breaks down: after a long initial lag regime and an intermediate regime where short-lived dynamic clusters continuously emerge and decay, we find a travelling wave made of straight parallel stripes (Fig. 2k and l, Video 4, ESI†) with self-limiting wavelength. This sudden emergence of a length scale upon increasing Δ allows control of coarsening via active rotations. The length scale of the stripe pattern which decreases as ω increases and thus can be also controlled.
Rotation-locking transition
To understand the origin of cluster growth for Δ > 0 and the related suppression of rotations at the cluster interfaces, we recast eqn (2) as![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) = ω + β|∇c|sin(ϕ + δ); δ = arg(−∂xc + i∂yc) = ω + β|∇c|sin(ϕ + δ); δ = arg(−∂xc + i∂yc) | (4) |
Locking instability
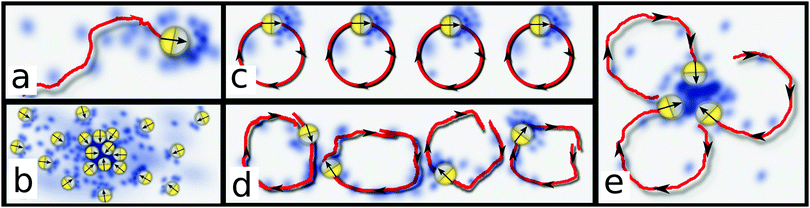
Since the locking mechanism stabilizes clusters, we expect an instability mechanism allowing for the growth of these clusters out of the uniform state. We now resolve this in detail. Working in the adiabatic limit where p responds fast to changes of c, eqn (1)–(3) simplify significantly. If ω = 0, they resemble the Keller–Segel model (ESI†), which leads to phase separation through a long wavelength linear instability – essentially this is the positive feedback described in the Introduction. In sharp contrast, we show in the ESI† that active rotations generically suppress linear instability of the uniform phase in eqn (1)–(3). Physically, this is in line with the intuitive expectation that small chemical gradients caused by fluctuations around the uniform state are too weak to fix the orientations of active rotors and cannot promote a linear instability. As a result, the KS instability is ineffective for active signalling rotors.This raises the question why we could still observe cluster growth in our simulations. The answer is that chemotaxis can abduct the rotors into the nonlinear regime before they complete a full rotation, and this in turn can lead to a nonlinear instability. To understand the underlying physical mechanism, let us reconsider our coherently rotating uniform initial state, where all rotors are in phase (Fig. 1c). While ρ, c remain approximately uniform in the course of the early-stage dynamics, weak fluctuations of c continuously dephase the orientation field p due to chemotaxis (Fig. 1d). Once the rotors are sufficiently out of phase, they can form, temporarily, aster-like ‘seed’ configurations (Fig. 1e), where all particles in the vicinity of a positive fluctuation of c swim up the chemical gradient. This configuration promotes, temporarily, a growth of the fluctuation via the standard KS feedback loop. If this growth generates a chemical gradient surpassing the locking-threshold (β|∇c| > ω) before the seed decays, then p remains locked in its vicinity – leading to a stable cluster as just discussed.35 Hence, we call our nonlinear instability the ‘locking instability’. Whether the locking instability is effective or not in practice is a matter of competing timescales, between the instantaneous growth rate of chemical gradients and ω – the former needs to dominate to create locking. Video 5 in the ESI† shows the early stage dynamics of c and p, reflecting that c and its gradients can indeed grow beyond the locking threshold on timescales where p rotates only slightly.
Breakdown of locking
Locking gets increasingly difficult as Δ increases and eventually breaks down, quite suddenly, at Δ ≈ 0.027 (for parameters as in Fig. 2); beyond this, stable clusters are no longer possible. Specifically, as Δ increases (i) steeper interfaces are needed to satisfy the locking criterion and (ii) active rotations increasingly dominate the equilibrium between chemotaxis and rotations which leads to a steering of the locked p away from its ‘ideal’ orientation up the gradient. This in turn reduces the advective flux up the density gradient leading to shallower interfaces (see ESI† and Videos 2 and 3). Unlike for linear (supercritical) instabilities an instability criterion is ill-defined here, and the breakdown of locking depends on an implicit balance between steepness of interfaces and locking orientation of p far away from the uniform state. Likewise, when comparing the locking instability to nucleation in systems approaching thermal equilibrium, which is also nonlinear and requires a seed configuration, we find again important differences. Crucially, for example, our clusters require steep interfaces to survive, and a dense cluster with shallow interfaces would quickly decay; in contrast, for near-equilibrium systems, once a dense seed has nucleated it will grow, however shallow its interfaces may be.Active rotations arrest coarsening
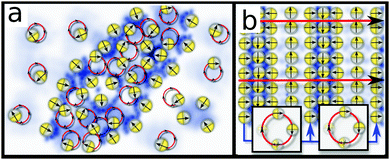
For large Δ, where rotations are too strong to allow locking, we observed a long period where small and short lived clusters dynamically emerge and decay on timescales ∼2π/ω. These clusters emerge from seeds which promote a growth of ρ and c which is too slow to surpass the locking threshold and hence slows down the rotation of p only temporarily. Strikingly, however, this dynamic clustering does not proceed forever, and eventually some clusters merge (due to diffusion and short ranged repulsions which penalize large interfaces) and synchronise their rotations and translations to form coherent waves (see Video 4 in ESI†). Specifically, within clusters, the relative phases (frequencies) of adjacent rotors change continuously until the system eventually reaches a steady state. Here such a steady state is possible in the form of a stripy pattern (Fig. 2l), which moves precisely by one spatial period during one rotational cycle of p. In a frame comoving with the pattern, p is then fixed (Fig. 3b) and the pattern, a periodic non-uniform state, is an attractor for the dynamics of the system. Hence, merging and approaching this steady state represents a second route allowing short lived clusters to avoid decay.This process of forming short lived clusters which prevent their decay by merging and moving into a collective direction (spontaneous symmetry breaking) constitutes a second nonlinear instability mechanism of the uniform state that is independent of the locking mechanism. In contrast with the latter, this mechanism works at all frequencies, but is comparatively slow since it involves the coordination of several clusters. Hence this second route to structure formation in signalling rotors is particularly relevant in parameter regimes where the locking mechanism is ineffective, i.e., for large ω, but applies similarly to the moving stripes formed within the dense and the dilute phase in Fig. 2g–i.
As its most remarkable feature and contrasting the locking instability, this route to pattern formation introduces a length scale in steady state. Within a large region of parameter space, this length scale increases approximately as v0/ω. Hence, for synthetic rotors this length scale can be tuned via the frequency of an applied rotating field. We emphasize that this length scale is determined purely dynamically and cannot be calculated via the standard tools for linear (supercritical) instabilities like amplitude equations.32
Non-identical frequencies
We finally discuss signalling rotors with non-identical frequencies (e.g., a population of bacteria close to a wall). In absence of alignment effects these rotors quickly dephase and destroy the local polar order. However, hydrodynamic33 or steric alignment interactions can ‘synchronize’ individual rotations. Assuming, e.g., short ranged polar alignment interactions with alignment rate (g/rc2)sin(θj − θi) between particles i, j (polar coordinates) if their distance |ri − rj| is smaller than a cutoff radius rc and ignoring chemotaxis (which supports alignment), the local orientation of a rotor follows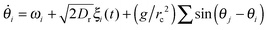 | (5) |
In conclusion, although even weak active rotations linearly stabilise the uniform phase in ensembles of auto-chemotactic particles, they generate a nonlinear route to structure formation. This route creates novel patterns including hierarchically organized states combining phase separation and pattern formation. It also allows for features which would be impossible to achieve in linear instability scenarios, such as a delayed onset of patterning whose lag time can be programmed via the initial conditions. More generally, we showed that rotations provide a versatile new tool to design self-assembly and collective behaviour of active matter, for example to control coarsening.
Acknowledgements
BL gratefully acknowledges funding by a Marie Skłodowska Curie Intra European Fellowship (G.A. no. 654908) within Horizon 2020. MEC holds a Royal Society Research Professorship. Work funded in part by EPSRC EP/J007404/1.References
- E. O. Budrene and H. C. Berg, Nature, 1991, 349, 630 CrossRef CAS PubMed.
- E. O. Budrene and H. C. Berg, Nature, 1995, 376, 49 CrossRef CAS PubMed.
- N. Mittal, E. O. Budrene, M. P. Brenner and A. Van Oudenaarden, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 13259 CrossRef CAS PubMed.
- G. Gerisch, Annu. Rev. Physiol., 1982, 44, 535 CrossRef CAS PubMed.
- E. F. Keller and L. A. Segel, J. Theor. Biol., 1970, 26, 399 CrossRef CAS PubMed.
- E. F. Keller and L. A. Segel, J. Theor. Biol., 1971, 30, 225 CrossRef CAS PubMed.
- H. Haken, The Science of Structure: Synergetics, Van Nostrand Reinhold Company, 1984 Search PubMed.
- M. E. Cates, D. Marenduzzo, I. Pagonabarraga and J. Tailleur, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11715 CrossRef CAS PubMed.
- Y. Hong, N. M. K. Blackman, N. D. Kopp, A. Sen and D. Velegol, Phys. Rev. Lett., 2007, 99, 178103 CrossRef PubMed.
- I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2012, 108, 268303 CrossRef CAS PubMed.
- S. Saha, R. Golestanian and S. Ramaswamy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062316 CrossRef PubMed.
- J. Taktikos, V. Zaburdaev and H. Stark, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 051901 CrossRef PubMed.
- M. Meyer, L. Schimansky-Geier and P. Romanczuk, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022711 CrossRef PubMed.
- O. Pohl and H. Stark, Phys. Rev. Lett., 2014, 112, 238303 CrossRef PubMed.
- B. Liebchen, D. Marenduzzo, I. Pagonabarraga and M. E. Cates, Phys. Rev. Lett., 2015, 115, 258301 CrossRef PubMed.
- J. Palacci, S. Sacanna, A. P. Steinberg, D. J. Pine and P. M. Chaikin, Science, 2013, 339, 936 CrossRef CAS PubMed.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef PubMed.
- E. Lauga, W. R. DiLuzio, G. M. Whitesides and H. a. Stone, Biophys. J., 2006, 90, 400 CrossRef CAS PubMed.
- R. Di Leonardo, D. Dell'Arciprete, L. Angelani and V. Iebba, Phys. Rev. Lett., 2011, 106, 038101 CrossRef CAS PubMed.
- F. Kümmel, B. ten Hagen, R. Wittkowski, I. Buttinoni, R. Eichhorn, G. Volpe, H. Löwen and C. Bechinger, Phys. Rev. Lett., 2013, 110, 198302 CrossRef PubMed.
- M. Wykes, J. Palacci, T. Adachi, L. Ristroph, X. Yhong, M. Ward, J. Zhang and M. Shelley, 2015, arXiv:1509.06330v1 [cond-mat.soft].
- L. Baraban, D. Makarov, O. G. Schmidt, G. Cuniberti, P. Leiderer and A. Erbe, Nanoscale, 2013, 5, 1332 RSC.
- L. Baraban, R. Streubel, D. Makarov, L. Han, D. Karnaushenko, O. G. Schmidt and G. Cuniberti, ACS Nano, 2013, 7, 1360 CrossRef CAS PubMed.
- N. H. P. Nguyen, D. Klotsa, M. Engel and S. C. Glotzer, Phys. Rev. Lett., 2014, 112, 075701 CrossRef PubMed.
- H. C. Berg and L. Turner, Biophys. J., 1990, 58, 919 CrossRef CAS PubMed.
- J. Murray, Mathematical Biology. II: Spatial Models and Biomedical Applications, Springer-Verlag Berlin, 2003 Search PubMed.
- While we chose a cubic interaction term in analogy with the ϕ4 theory, a quadratic interaction term ∝∇2ρ2 with appropriately increased coefficient does not change our results. Similarly, replacing the cubic reaction term by e.g. a quadratic, sign-changing term ∝ (c0 − c)|c0 − c| has very little bearing on our results. (A quadratic, non sign-changing term ∝ (c0 − c)2 would lead to a blowup of fluctuations rather than to their saturation).
- E. Bertin, M. Droz and G. Grégoire, J. Phys. A: Math. Theor., 2009, 42, 445001 CrossRef.
- R. Adler, Proc. IRE, 1946, 34, 351 CrossRef.
- A. Pikovsky, M. Rosenblum and J. Kurths, Synchronization: A Universal Concept in Nonlinear Sciences, Cambridge University Press, 2003 Search PubMed.
- T. Erneux and P. Glorieux, Laser Dynamics, Cambridge University Press, 2010 Search PubMed.
- P. C. Hohenberg and M. C. Cross, Rev. Mod. Phys., 1993, 65, 851 CrossRef.
- R. Golestanian, J. M. Yeomans and N. Uchida, Soft Matter, 2011, 7, 3074 RSC.
- J. A. Acebrón, L. L. Bonilla, C. J. P. Vicente, F. Ritort and R. Spigler, Rev. Mod. Phys., 2005, 77, 137 CrossRef.
- Note that in contrast to asters, 'anti-asters' with p pointing outwards from a center where ρ, c show minima, suffer from the fact that both ρ, c cannot decay below zero. This limits the maximal possible steepness of chemical gradients to values which are typically insufficient to generate locking.
- J. Ito and K. Kaneko, Phys. Rev. Lett., 2001, 88, 028701 CrossRef PubMed.
- F. Peruani, E. M. Nicola and L. G. Morelli, New J. Phys., 2010, 12, 093029 CrossRef.
- K. Uriu, S. Ares, A. C. Oates and L. G. Morelli, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 032911 CrossRef.
- R. Grossmann, F. Peruani and M. Bär, Phys. Rev. E, 2016, 93, 040102 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm01162d |
| This journal is © The Royal Society of Chemistry 2016 |