Structures, stability and hydrogen bonding in inositol conformers

Abstract

Various ab initio calculations using the density-functional (DFT), the second order Möller–Plesset perturbation (MP2) and self-consistent reaction field (SCRF) theories were performed on thirteen theoretically possible inositol stereoisomers. Gas phase calculations reveal that the myo- and neo-isomers of inositol (bearing one and two axial hydroxyl groups, respectively) are marginally more stable (by 0.5 kcal mol⁻¹) than the all equatorially substituted scyllo-inositol. The calculations when done in different polar solvents show that the scyllo-inositol becomes the most stable inositol isomer, a fact attributed to weaker intramolecular hydrogen bonds. The individual hydrogen bond energy in all the isomers of inositol was also estimated using the molecular tailoring approach (MTA). The calculated hydrogen bond energies in these isomers are in excellent agreement with reported O–H⋯O hydrogen bond distances and ν_O–H stretching frequencies. The estimated H-bond energy values suggest that the order of the intramolecular hydrogen bond strength follows: axial–axial > equatorial–axial > axial–equatorial > equatorial–equatorial hydrogen bonds. The intramolecular hydrogen bonds in the scyllo isomer are much weaker than those in other conformers, thus making this isomer more stable in polar solvents.

---

Introduction

Inositol is a sixfold alcohol of cyclohexane. The most abundant derivatives of inositol include its methyl esters and phosphate esters. Inositol derivatives function as intracellular signal transduction molecules^1–4 and thus play important roles in various biological activities.^5–8 Amino or substituted amino derivatives of inositol also occur in many antibiotics.^9–10 Inositol derivatives are extensively used in the treatment of panic disorders,¹¹ polycystic ovary syndrome (PCOS),¹² cancer,¹³ metabolic syndrome¹⁴etc. Inositols serve as a building block for the synthesis of natural products^15–21 and molecular crystals with unusual properties.^22–23 “Insoamino acids” are a new class of inositol derivatives composed of inositol and β- or γ-amino acids, used for the construction of peptide nanotubes with hydrophobic cavities.^24–25

The maximum number of stereoisomers for a molecule with more than one stereogenic centres is given by the 2ⁿ rule (where, n = number of stereogenic centers), which in the case of inositol should be sixty four (2⁶). The symmetry inherent in inositol, as it is a cyclic six membered ring, reduces the possible distinct stereoisomers to sixteen. Of these six are made of three enantiomeric pairs while the rest are meso compounds leading to only thirteen theoretically possible isomers of inositol as enantiomeric pairs (i.e., dl(4e/2a), allo(3e/3a) and 1,2eq(2a/4e)) have identical energies (Fig. 1). A survey of the literature reveals that all previous theoretical studies consider only eight stereoisomers, ignoring the more axially substituted inositols.^26–28 The conformational study of inositols is thus important as they provide a simple model system for investigating conformational effects in other substituted cyclohexane systems.^29–30 Important theoretical studies were mostly performed on phosphate derivatives of myo-inositol. Other than that, NMR analysis of the O-methyl-inositol isomer,²⁸ crystal structure for myo-³¹ and epi-³² inositols, and vibrational spectral study of all inositols³³ were also reported. Ab initio calculations on scyllo, myo, dl, epi and neo isomers of inositols have already been reported, which show that myo- and neo-inositols are much lower in energy as compared to scyllo-inositol.²⁷

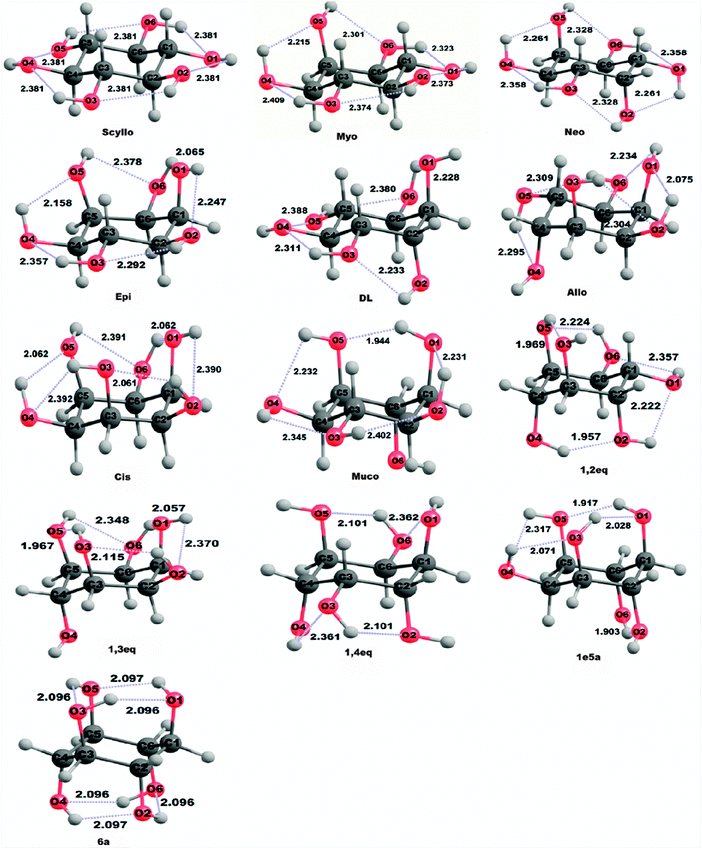
Fig. 1 The thirteen possible inositol isomers, e and eq stand for equatorial and a stands for axial hydroxyl groups.

In this work, we investigate the structures and the relative stability of all thirteen possible inositol isomers by employing DFT and MP2 levels of theory. The effect of solvent on the relative stability of these conformers is also discussed. Importantly, we show here that the intramolecular O–H⋯O hydrogen bonding patterns and the strength of these interactions in terms of the hydrogen bond (H-bond) energy calculated by the molecular tailoring based approach (MTA),^34–39 in these inositol conformers, make scyllo-inositol more stable in polar media.

Computational methods

The geometries of all theoretically possible thirteen stereoisomers of inositol were constructed and optimized considering the concerted intramolecular hydrogen bonding arrangement of the hydroxyl groups at the second order Möller–Plesset perturbation (MP2) level^40–41 employing the 6-311+G(d,p)^42–43 basis sets. During optimization of the geometries, no symmetry was imposed. Frequency calculations were performed to characterize the optimized structures as true minima (no imaginary frequency found). In order to evaluate the changes in energy of inositol isomers in solvent media, we also carried out the single point calculations in various solvents at the B3LYP^44–46 density functional theory (DFT) and the 6-311+G(d,p) basis set using the polarizable continuum model (PCM)^47–51 method. Intramolecular hydrogen bond energies in inositol isomers were obtained using the molecular tailoring approach (MTA).^34–39 All quantum chemical calculations mentioned above were carried out using the GAUSSIAN 09 program package.⁵²

Results and discussion

Geometry of inositol isomers

Fig. 2 presents the MP2/6-311+G(d,p) optimized structures of thirteen inositol isomers. As seen in Fig. 2, the hydroxyl groups in these isomers were oriented to maximize internal hydrogen bonding which is retained in these final optimized structures. Individual C–C bond lengths in all these optimized structures do not show any systematic variation, see Table 1. The C–C bond distances are in general shorter than those in cyclohexane optimized at the MP2/6-311+G(d,p) level of theory. This may be due to the substitution by electronegative hydroxyl groups as predicted by the Bent's rule,^53–54 (electron withdrawing substituents tend to reduce the covalent radius of carbon). In general, it is observed that the average C–C bond length increases as the number of axial hydroxyl groups increases from 6e to 6a inositol isomers, see Table 2 for the axial (ax) and equatorial (eq) orientations of hydroxyl groups in these inositol conformers. This increment in bond lengths can be accounted on the basis of the size of the hydrogen bonded ring in inositols. In general, a five membered H-bonded ring is more strained than a six membered ring. For example, in inositols up to 3e/3a isomers, hydrogen bonding between hydroxyl groups mainly leads to the formation of five membered H-bonded rings making them more strained thus resulting in shortened bond lengths (cf.Table 1 and Fig. 2). From 2e/4a to 6a isomers, the number of six membered H-bonded rings increases from two to six because of the increase in the number of axial–axial hydrogen bonds, which makes the cyclohexane ring slightly pucker away from the normal chair form resulting in lengthening of C–C bond lengths.

Fig. 2 The MP2/6-311+G(d,p) optimized structures for all thirteen inositol conformers.

Table 1 Average C–C bond lengths of inositol isomers calculated at the MP2/6-311+g(d,p) level of theory. e and eq stand for equatorial and a stands for axial hydroxyl groups

Inositol isomers	Average C–C bond length (in Å)
scyllo(6e)	1.518
myo(5e/1a)	1.520
neo(4e/2a)	1.522
epi(4e/2a)	1.524
dl(4e/2a)	1.521
muco(3e/3a)	1.525
allo(3e/3a)	1.525
cis(3e/3a)	1.528
1,3eq(2e/4a)	1.529
1,2eq(2e/4a)	1.529
1,4eq(2e/4a)	1.528
1e/5a	1.533
6a	1.533

---

Table 2 The axial (ax) and the equatorial (eq) orientation of hydroxyl groups in 13 inositol isomers

Conformers	O^1H	O^2H	O^3H	O^4H	O^5H	O^6H
scyllo(6e)	eq	eq	eq	eq	eq	eq
myo(5e/1a)	eq	eq	eq	eq	ax	eq
neo(4e/2a)	eq	ax	eq	eq	ax	eq
epi(4e/2a)	ax	eq	eq	eq	ax	eq
dl(4e/2a)	ax	ax	eq	eq	eq	eq
allo(3e/3a)	ax	eq	ax	ax	eq	eq
cis(3e/3a)	ax	eq	ax	eq	ax	eq
muco(3e/3a)	ax	eq	eq	eq	ax	ax
1,2eq(2e/4a)	eq	ax	ax	ax	ax	eq
1,3eq(2e/4a)	ax	eq	ax	ax	ax	eq
1,4eq(2e/4a)	ax	ax	eq	ax	ax	eq
1e/5a	ax	ax	ax	eq	ax	ax
6a	ax	ax	ax	ax	ax	ax

---

In inositols, the CCC angle values do not show any dependence on the position of hydroxyl groups (cf.Table 3). The average CCC angle in scyllo inositol is smaller compared to other inositol isomers by 0.3 to 3.0°. The above results indicate the small degree of planarity in all isomers except scyllo inositol (in consideration of planar cyclohexane rings whose CCC angles are 120°). Whereas, the orientation of hydroxyl groups in inositols shows correlation with the values of OCC angles. Inositol isomers show a wide range of adjoining OCC angles varying from 0.4 to 6.1°, depending upon the orientation of two –OH groups on adjacent carbons and the strength of intramolecular hydrogen bonding among them. An OCC angle on the same side of the OC bond as a hydroxyl group is about 4.4 to 5.2° larger than that on the opposite side in scyllo, myo and neo isomers. The intramolecular hydrogen bonding is likely to be the reason for the deviation of OCC angles from the regular tetrahedral angle of 109.5°, analogous to that observed in 1,2-ethanediol.^55–56 The average C–C–C–C (ring torsion) angles in all inositol isomers range between 1.2 and 9.3° and are smaller than that observed for scyllo-inositol, see Table S1 (ESI‡). The above results are consistent with the CCC angles showing slightly planar cyclohexane rings in all isomers other than scyllo inositol. Thus, the flattening of ring torsion angles, differences in C–O bond lengths and CCC angles in all inositol isomers are in accordance with stereorepulsion involving axial OH group(s).

Table 3 The C–C–C bond angles (in degree) in the various MP2/6-311+G(d,p) optimized inositol isomers

Angles	6e	5e/1a	4e/2a			3e/3a			2e/4a			1e/5a	6a
	scyllo	myo	neo	epi	dl	allo	cis	muco	1,2eq	1,3eq	1,4eq
C5C6C1	110.4	111.5	111.3	110.3	111.0	112.2	114.7	111.0	111.2	111.4	114.5	112.4	112.0
C6C1C2	110.4	110.4	111.7	111.9	111.8	114.9	112.2	112.1	111.9	112.0	112.3	111.9	112.0
C1C2C3	110.4	109.5	110.6	115.1	111.6	111.8	114.7	111.4	112.2	111.4	112.4	112.0	112.0
C2C3C4	110.4	110.6	111.3	111.9	111.3	111.6	112.2	110.9	111.2	113.9	114.5	111.1	112.0
C3C4C5	110.4	111.3	111.7	111.1	110.1	110.5	114.7	111.3	111.7	113.1	112.3	112.9	112.0
C4C5C6	110.4	111.2	110.6	109.8	109.9	111.0	112.2	110.9	111.5	113.9	112.4	115.0	112.0
Average	110.4	110.7	111.2	111.7	110.9	112.0	113.4	111.2	111.6	112.6	113.0	112.5	112.0

---

It is seen that on going from 6e scyllo to 6a isomers of inositol, the orientation of the –OH groups varies considerably, see Fig. 2. For instance, in the scyllo, myo, neo, epi, dl, and cis isomers, the orientation of –OH groups is in the clockwise direction, that is, it forms a network of OH(1) → OH(2) → OH(3) → OH(4) → OH(5) → OH(6) → OH(1) hydrogen bonds. However, in the dl isomer, the H-bond network starts from the OH(2) group and there is no H-bond between OH(1) and OH(2) hydroxyl groups due to their axial and adjacent positions. In the allo isomer, hydroxyl groups are oriented in the counterclockwise direction forming OH(3) → OH(2) → OH(1) → OH(6) → OH(5) → OH(4) network of H-bond. The orientation of –OH groups is in a counterclockwise direction in the muco isomer, in the sequence of OH(1) → OH(5) → OH(4) → OH(3) → OH(2) → OH(1), with OH(6) and OH(1) groups at axial positions. In 1,2eq isomer, –OH groups are in a counterclockwise direction in the sequence OH(4) → OH(2) → OH(1) → OH(6) → OH(5) → OH(3) with OH(1) and OH(6) hydroxyl groups occupying the equatorial positions. 1,3eq isomer have OH(1) → OH(2) → OH(3) → OH(5) → OH(6) → OH(1) H-bond network with clockwise direction of –OH groups, where OH(1), OH(3), OH(4) and OH(5) groups are at axial positions. The 1,4eq isomer forms two short OH(1) → OH(6) → OH(5) and OH(4) → OH(3) → OH(2) H-bond networks in a counter-clockwise direction, where OH(1), OH(2), OH(4) and OH(5) groups are at axial positions. The isomers 1e/5a and 6a show the orientation of –OH groups in the clockwise direction. In the 1e/5a isomer, OH(1) → OH(5) → OH(4) → OH(3) → OH(1) H-bond network contains all –OH groups at axial positions except OH(4). Also, the OH(6) → OH(1) axial–axial H-bond is present in the 1e/5a isomer. Two H-bond networks OH(1) → OH(5) → OH(3) → OH(1) and OH(2) → OH(6) → OH(4) → OH(2) are present in the 6a isomer with all –OH groups at axial positions.

The presence of intramolecular hydrogen bonding in inositols is supported by various studies like H¹ NMR, infrared spectra, study of 1,3,5-trideoxy-1,3,5-tris(dimethylamino)-cis inositol (TDCI),⁵⁷ NMR dynamics study of chair–chair interconversion of cis-inositol.⁵⁸ In order to understand the differences in the intramolecular hydrogen bonds between these inositol isomers, we discussed here the intramolecular O–H⋯O H-bond distances in these inositol isomers; see Table 4 and Fig. 2 for details. As seen in Table 4, the OH⋯O hydrogen bond distances are in the range of 1.9 to 2.4 Å in these inositol isomers. The OH⋯O distances in the hydrogen bond involving two equatorial hydroxyl groups are found to be about 2.2 to 2.4 Å and 1.9 to 2.3 Å for those involving axial –OH groups. This indicates that the intramolecular hydrogen bond involving axial hydroxyl groups is stronger than that involving equatorial hydroxyl groups. Thus, the axial hydroxyl group actually provides a stabilizing effect, which may be the reason for the lower internal energies obtained for certain inositol isomers as compared to scyllo-inositol. The order of strength of intramolecular hydrogen bonding follows: O_axial–H⋯O_axial > O_equatorial–H⋯O_axial > O_axial–H⋯O_equatorial > O_equatorial–H⋯O_equatorial.

Table 4 The intramolecular O–H⋯O H-bond distances (in Angstrom) in the MP2/6-311+G(d,p) optimized inositol conformers

	scyllo	myo	neo	epi	dl	allo	cis	muco	1,2eq	1,3eq	1,4eq	1e/5a	6a
O1H⋯O2	2.381	2.373	2.261	2.247	—	2.075	2.390	2.231	2.222	2.370	—	—	—
O2H⋯O3	2.381	2.374	2.328	2.292	2.233	2.304	2.061	2.402	—	2.115	2.101	—	2.096
O3H⋯O4	2.381	2.409	2.358	2.357	2.311	—	2.392	2.345	—	—	2.361	2.071	—
O4H⋯O5	2.381	2.215	2.261	2.158	2.388	2.295	2.062	2.232	—	—	—	2.317	2.096
O5H⋯O6	2.381	2.301	2.328	2.378	2.380	2.309	2.391	—	2.224	2.348	2.101	—	—
O6H⋯O1	2.381	2.323	2.358	2.065	2.228	2.234	2.062	—	2.357	2.057	2.362	—	—
O4H⋯O6	—	—	—	—	—	—	—	—	—	—	—	—	—
O5H⋯O3	—	—	—	—	—	—	—	—	1.969	1.967	—	—	—
O2H⋯O4	—	—	—	—	—	—	—	—	1.957	—	—	—	—
O5H⋯O1	—	—	—	—	—	—	—	1.944	—	—	—	1.917	2.096
O3H⋯O1	—	—	—	—	—	—	—	—	—	—	—	2.028	—
O6H⋯O2	—	—	—	—	—	—	—	—	—	—	—	1.903	2.096
O1H⋯O4	—	—	—	—	—	—	—	—	—	—	—	—	2.096
O3H⋯O6	—	—	—	—	—	—	—	—	—	—	—	—	2.096

---

In Table 5 the unscaled O–H stretching frequencies calculated at the MP2/6-311+G(d,p) level are listed. The unscaled O–H frequencies lie between 3882 and 3729 cm⁻¹. In these inositols, the –OH groups that are not involved in H-bonding are seen to show a high stretching frequency; for instance, the O¹H group of the dl(4e/2a) conformer has the highest O–H stretching frequency of 3882 cm⁻¹. The average O–H stretching frequency of the –OH groups forming an O–H⋯O hydrogen bond between the equatorial hydroxyl groups is about 3849 cm⁻¹. The O–H stretching frequency decreases further when OH groups are involved in either equatorial–axial or axial–equatorial hydrogen bonded interactions (∼3800 cm⁻¹). A further decrease in O–H stretching frequency up to 3729 cm⁻¹ is observed when the hydroxyl group involved in the axial–axial hydrogen bonds. This decrease in frequency (red shift) is in agreement with the shortening of O–H⋯O distances on moving from equatorial–equatorial to axial–axial O–H⋯O H-bonds.

Table 5 The unscaled O–H stretching frequency (cm⁻¹) in the MP2/6-311+G(d,p) optimized inositol conformers

Conformers	O^1H	O^2H	O^3H	O^4H	O^5H	O^6H
scyllo(6e)	3849.5	3849.5	3849.7	3849.9	3849.9	3849.9
myo(5e/1a)	3849.6	3849.8	3842.0	3817.9	3839.4	3841.1
neo(4e/2a)	3821.0	3840.9	3833.2	3820.9	3840.8	3832.9
epi(4e/2a)	3834.4	3839.2	3837.2	3810.1	3802.6	3808.6
dl(4e/2a)	3882.6	3822.9	3840.7	3851.2	3839.7	3818.7
allo(3e/3a)	3832.6	3806.0	3848.2	3881.6	3821.3	3828.6
cis(3e/3a)	3859.8	3797.9	3860.6	3798.4	3860.0	3798.1
muco(3e/3a)	3735.3	3795.5	3838.1	3843.8	3812.6	3877.0
1,2eq(2e/4a)	3827.0	3805.9	3866.0	3768.6	3786.8	3790.1
1,3eq(2e/4a)	3849.0	3772.5	3729.2	3878.3	3841.6	3806.7
1,4eq(2e/4a)	3857.3	3877.3	3808.6	3857.0	3877.4	3808.8
1e/5a	3739.9	3868.8	3765.9	3777.0	3836.7	3790.3
6a	3794.8	3771.3	3794.6	3791.9	3772.0	3791.7

---

Thus, from the above discussion about the H-bond distances and O–H stretching frequencies, it is conjectured that stronger O–H⋯O hydrogen bonds are formed when there are more axial–axial O–H⋯O interactions. Besides this, the axial–equatorial O–H⋯O bonds also emerge to be stronger than the equatorial–equatorial ones. The above gas phase observations regarding the strength of hydrogen bonds in inositol isomers is supported by various reports present in the literature.^59,60

Relative stability of the inositol isomers

The absolute energy of the scyllo isomer and the relative energies of all inositol isomers with respect to the scyllo isomer, calculated at MP2 and B3LYP levels employing 6-311+G(d,p) basis sets, are reported in Table 6. In general, it is believed that in the case of substituted cyclohexanes, there is a large steric strain if a substituent is present at the axial position due to butane gauche interactions than when it is present at the equatorial position. Thus, axial substitution makes the molecule generally less stable (or higher energy) than an equatorially substituted molecule. But, here the trend in energies obtained at the MP2/6-311+G(d,p) level reveals that neo-inositol (with 2 axial hydroxyl groups) is most stable followed by myo-inositol (with 1 axial hydroxyl group) and then by scyllo-inositol (with all 6 equatorial hydroxyl groups). However, the energy difference in these conformers is very marginal (∼0.5 kcal mol⁻¹). There may be other reasons (such as strong intramolecular hydrogen bonding due to axial –OH groups) that may provide the slightly higher stability of two and one axial –OH groups containing inositols (–neo and –myo) over all equatorial –OH groups containing scyllo-inositol. Thus, the above discussed generalization works in these inositol isomers as well with exceptions of –neo and –myo isomers. These results calculated at the MP2 level are similar to those calculated at the B3LYP level, except that the myo isomer becomes less stable than scyllo at the B3LYP level (cf.Table 6).

Table 6 The computed absolute energies of scyllo-isomers (in Hatree) and that of other isomers of inositols (in kcal mol⁻¹) relative to scyllo-inositol in gas and solvent phases at various levels of theory and employing 6-311+G(d,p) basis sets

Method	6e	5e/1a	4e/2a			3e/3a			2e/4a			1e/5a	6a
	scyllo	myo	neo	epi	dl	allo	cis	muco	1,2eq	1,3eq	1,4eq
MP2(gas)	−685.69545	−0.54	−0.36	2.52	5.62	4.47	9.80	1.26	2.80	5.28	11.30	7.21	11.40
B3LYP(gas)	−687.42282	0.01	−0.38	3.01	6.45	5.27	9.81	2.26	3.60	6.00	11.50	7.34	11.70
B3LYP(water)	−687.45997	0.32	1.42	4.50	16.51	4.70	9.74	2.57	4.86	6.49	6.73	9.53	19.35
B3LYP(DMSO)	−687.45667	0.95	0.86	4.53	14.56	4.64	8.57	2.71	4.47	6.11	7.07	8.93	17.18
B3LYP(ethanol)	−687.45596	0.90	1.22	4.06	14.39	3.60	9.21	2.45	4.40	6.21	7.34	9.05	17.02

---

Free energies

Calculation using MP2/6-311+G** molecular structures of the corresponding free energies (at 298.15 K) of inositols was also performed. Table 7 presents various thermodynamic quantities including zero-point vibrational energy (ZPE), thermal energy (E) and entropy contributions. The trend in ZPE reveals that the all equatorially substituted scyllo (6e) inositol is more stable relative to other isomers. However, other isomers are favoured over scyllo-inositol when the entropy is considered. All inositol isomers show stability over the scyllo-inositol except the 1,4eq isomer, in terms of the thermal energies. But, if we consider overall energies by inclusion of electronic energies along with thermal energies, then, it shows only myo (with 1 –OH group) and neo (with 2 –OH groups) inositols to be more relatively stable than scyllo-inositol. In the case of free energies of inositols, the scyllo-isomer shows stability over all other isomers. The thermodynamic quantities of inositol at the B3LYP level in the gas phase and free energies of all isomers relative to –scyllo isomer in various solvents are also listed in ESI‡ as Tables S2 and S3, respectively.

Table 7 Thermodynamic quantities^a of inositols relative to the scyllo isomer

Quantities	5e/1a	4e/2a			3e/3a			2e/4a			1e/5a	6a
	myo	neo	epi	dl	allo	cis	muco	1,2eq	1,3eq	1,4eq
a Calculated at 298.15 K using the MP2/6-311+G** method, in kcal mol^−1. b For scyllo, ZPE = 125.65 kcal mol^−1. c Sum of rotational, translational, and thermal vibrational energies (excluding ZPE). For scyllo, Et = 7.68 kcal mol^−1. d For scyllo, TS = 31.45 kcal mol^−1. e For scyllo, G = 102.47 kcal mol^−1.
ΔZPE^b	0.40	0.80	0.55	0.41	0.54	0.30	0.85	1.13	0.78	0.09	0.94	0.46
ΔE^c	−0.16	−0.31	−0.24	−0.15	−0.21	−0.11	−0.35	−0.51	−0.33	0.002	−0.44	−0.13
−TΔS^d	−0.39	−0.72	−0.58	−0.37	−0.52	−0.30	−0.84	−1.23	−0.83	0.06	−1.11	−0.36
ΔG^e	0.61	1.18	0.88	0.62	0.84	0.46	1.33	1.84	1.27	0.02	1.59	0.68

---

Solvent effects on the relative stabilities of inositols

Gas phase calculations of inositols show that certain axial inositols (neo- and myo-inositols in the case of the MP2 level and neo-inositol in the case of the B3LYP level) are more stable than all equatorial scyllo-inositol because of presence of a more favorable intramolecular hydrogen bonding in the former. But, in the presence of solvent, competition with intermolecular hydrogen bonding could alter the strength of intramolecular hydrogen bonding, which in turn could depend on the polarity of the solvents. In nonpolar solvents, intramolecular hydrogen bonding is likely to dominate but, in polar solvents, competition from intermolecular hydrogen bonding could be more favorable. A study of the solvent effect on the closely related glucose molecule shows that aqueous solution favors all equatorially substituted β-isomer over the α-isomer.⁵⁹ Studies on other similar carbohydrates, which are related to the inositol structure, also show significant differences in gas and condensed phases.⁶⁰ Thus, we performed calculations in the presence of various solvents using the self-consistent reaction field (SCRF) with the polarizable continuum method (PCM) at the B3LYP level of theory.

PCM calculations suggest the all equatorially substituted scyllo-inositol as the most stable inositol as compared to other isomers especially, –myo and –neo inositols, in all 3 polar solvents (water, DMSO, ethanol), see Table 6 for details. This may be attributed to favorable intermolecular solute–solvent interaction present in –scyllo relative to other axial –OH groups containing inositols, where the intramolecular hydrogen bonding is expected to be more dominant. Also, the hydroxyls in the all equatorial scyllo-inositol are better positioned to form intermolecular hydrogen bonds, supported by the study of solvent effects on the closely related glucose molecule.⁵⁹

The comparison of energy of these isomers in the gas phase and solvents obtained by the B3LYP method shows that the overall energy gets lowered in condensed phases. Thus, the presence of polar solvent stabilizes all isomers of inositols more than when they are present in vacuum. Also, the scyllo-inositol becomes most stable in all polar solvents because of favorable intermolecular solute–solvent interaction.

Strength of intramolecular O–H⋯O hydrogen bonds in inositol isomers

As discussed earlier, the hydroxyl groups in inositol are involved in the formation of the network of intramolecular OH⋯O H-bonds. Here, we discuss the energy of each individual hydrogen bond and the effect of the cooperative networking on their strength estimated by the molecular tailoring approach proposed in the recent past.^34,61–64 The estimated hydrogen bond energy of each individual hydrogen bond in the presence of the cooperative H-bonded network at the MP2 level is reported in Table 8. In this table, the individual hydrogen bonds are labelled based on the hydroxyl groups involved and the exact directionality is not considered. For example, the hydrogen bond between O¹H and O²H in the allo isomer is labelled as O¹H⋯O² in Table 8 although it should have been O²H⋯O¹ as per Fig. 2. As seen in Table 8, the estimated hydrogen bond energies are in the range of 1.9 to 3.9 kcal mol⁻¹ suggesting that the variable strengths of hydrogen bonds are found in these inositol isomers. As one moves across Table 8, the H-bond strength increases; in other words, the hydrogen bonds in inositol isomers involving more equatorial groups are relatively much weaker. In general, the estimated hydrogen bond energy follows: O_axial–H⋯O_axial > O_equtorial–H⋯O_axial > O_axial–H⋯O_equatorial > O_equatorial–H⋯O_equatorial. Thus the estimated hydrogen bond energies are in agreement with the previously discussed H-bond strength based on hydrogen bond distances and vibrational frequency. For instance, the average hydrogen bond energy of one H-bond in the scyllo isomer is about 2.2 kcal mol⁻¹ as compared to the 6a isomer wherein the average hydrogen bond energy is the largest (3.02 kcal mol⁻¹). There are certain exceptions to this average hydrogen bond energy; there are hydrogen bonds in some of these isomers wherein the H-bond energy is smaller than the scyllo isomer and larger than those in the 6a isomer despite the fact that the number of hydroxyl groups are less in equatorial and axial positions with respect to scyllo and 6a isomers, respectively. For instance, the strength of some of the hydrogen bonds in myo (O⁴H⋯O⁵), neo (O¹H⋯O² and O⁴H⋯O⁵) etc. is smaller than that in the scyllo isomer despite the less number of equatorial groups in myo, neo, dl and allo isomers. Also the hydrogen bond strength in muco (O⁵H⋯O¹), 1,3eq (O²H⋯O³,O⁵H⋯O³) and 1e/5a (O³H⋯O⁴, O⁵H⋯O¹) is larger than the average hydrogen bond energy in the 6a(6axial groups) isomer despite the lesser number of axial groups in muco, 1,3eq and 1e/5a. There is one major exception to the above discussed trend in H-bond energies which is 1,4eq isomer. In the 1,4eq isomer, the hydrogen bond energy is much smaller (1.7 to 1.9 kcal mol⁻¹) than that of the scyllo isomer despite four axial hydroxyl groups in 1,4eq inositol. The reason for this weaker strength of hydrogen bonds in the 1,4eq conformer is clear if one looks at the structure of this isomer (see Fig. 2). As seen in 1,4eq isomers, despite the four axial groups, there are in total four hydrogen bonds which involve two equatorial⋯axial and two axial⋯equatorial interactions. Thus the smaller hydrogen bond energy in the 1,4eq isomer may be attributed to weaker axial⋯equatorial (or equatorial⋯axial) interaction than those in axial⋯axial interaction in the 6a isomer. However, as discussed earlier, axial⋯equatorial (or equatorial⋯axial) are in general stronger than equatorial–equatorial interaction thus we expect the hydrogen bond strength in the 1,4eq isomer to be stronger than those in the scyllo isomer. The reason for the weaker hydrogen bond strength in 1,4eq and other isomers of inositol than in the scyllo isomer may be attributed to loss of cooperativity due to networking of hydrogen bonds in 1,4eq as will be discussed in the next section.

Table 8 Intramolecular O–H⋯O hydrogen bond energy for individual hydrogen bonds in the presence of the OH⋯O hydrogen bond network in various inositol isomers calculated at the MP2/6-311+G(d,p) level of theory

	scyllo	myo	neo	epi	dl	allo	cis	muco	1,2eq	1,3eq	1,4eq	1e/5a	6a
O1H⋯O2	−2.19	−2.17	−1.80	−2.85	—	−1.90	−2.33	−2.91	−3.03	−2.58	—	—	—
O2H⋯O3	−2.19	−2.13	−2.62	−2.24	−2.76	−3.43	−2.13	−2.49	—	−3.49	−1.92	—	−3.02
O3H⋯O4	−2.19	−2.56	−2.64	−2.72	−2.27	—	−2.32	−2.03	—	—	−1.67	−3.49	—
O4H⋯O5	−2.19	−1.90	−1.80	−2.03	−1.98	−1.87	−2.13	−2.82	—	—	—	−2.50	−3.02
O5H⋯O6	−2.19	−2.71	−2.62	−2.45	−2.56	−2.67	−2.33	—	−3.00	−1.98	−1.92	—	—
O6H⋯O1	−2.19	−2.96	−2.64	−2.05	−2.03	−2.89	−2.13	—	−2.61	−1.69	−1.67	—	—
O4H⋯O6	—	—	—	—	—	—	—	—	—	—	—	—	—
O5H⋯O3	—	—	—	—	—	—	—	—	−3.01	−3.36	—	—	—
O2H⋯O4	—	—	—	—	—	—	—	—	−3.16	—	—	—	—
O5H⋯O1	—	—	—	—	—	—	—	−3.84	—	—	—	−3.66	−3.02
O3H⋯O1	—	—	—	—	—	—	—	—	—	—	—	−2.44	—
O6H⋯O2	—	—	—	—	—	—	—	—	—	—	—	−3.03	−3.02
O1H⋯O4	—	—	—	—	—	—	—	—	—	—	—	—	−3.02
O3H⋯O6	—	—	—	—	—	—	—	—	—	—	—	—	−3.02
Sum	−13.14	−14.43	−14.13	−14.35	−11.61	−12.76	−13.37	−14.09	−14.80	−13.10	−7.18	−15.13	−18.12

---

The effect of cooperativity on the strength of the intramolecular O–H⋯O hydrogen bonds in inositol isomers

In general, it is accepted fact that the strength of individual hydrogen bond is enhanced due to presence of an interconnected network of hydrogen bonds. The phenomenon is well known as the cooperativity effect in Chemistry and Biology. In this work, we quantified this effect on the strength of individual hydrogen bonds by estimating their energy by isolating such bonds from the network keeping the overall geometry the same as that in the presence of a cooperative network. We have applied this methodology in the recent past for various systems of interest. For details of the general methodology for estimation of hydrogen energy and cooperative contribution see ref. 34 and 61–64. In Table 9, we present the intramolecular OH⋯O hydrogen bond energy of the individual H-bond in the absence of a cooperative network of hydrogen bonds at the MP2 level. The difference between the sum of H-bond energy in the presence of a cooperative network (cf.Table 8) and in the absence of a cooperative network of H-bonds is also presented in Table 9 as the total cooperative contribution. As seen in Table 9, the hydrogen bond energy estimated in the absence of a cooperative network of H-bonds is smaller than the respective ones in the presence of a network. In general the cooperative contribution is indeed substantial (2 to 5 kcal mol⁻¹) in these inositol isomers and is seen to be increased across Table 9 apart from some exceptions which are discussed separately. This increase in the cooperative contributions seems to depend on two factors (a) the number of hydrogen bonds in the network and (b) the strength of each of these bonds. As discussed in previous sections, the equatorial–equatorial hydrogen bonds are weaker than the equatorial–axial (or axial–equatorial) and the axial–axial hydrogen bonds are strongest. In the case of the scyllo isomer, there is a pleasant symmetric network of hydrogen bonds, the cooperative contribution is although substantial but is not large enough as compared to other isomers. This may be attributed to the weaker equatorial–equatorial (six) H-bonds (evident from the H-bond energy in Table 8) in this isomer. The cooperativity contribution is seen to increase in the myo isomer and may be attributed to stronger equatorial–axial and axial–equatorial interaction. The cooperative contribution in neo and epi isomers is similar to that in the scyllo isomer and may be due to some of the weak hydrogen bond in the network. In dl and allo isomers, there are only five H-bonds in the network and hence the cooperative contribution is smaller than that in scyllo, myo, neo and epi isomers. The cooperative contribution is substantially large (5 kcal mol⁻¹) in the cis isomer and may be attributed to nice alternate three axial–equatorial and three equatorial–axial (total six) H-bonds in the network. In muco, 1,2eq and 1,3eq isomers, although there are stronger axial–axial H-bonds in the network, it is expected that an increase in the cooperative contribution is compensated by much weaker equatorial–equatorial hydrogen bond/s in the networks. More importantly, there are only five H-bonds in the network and the total contribution is smaller in these isomers. The cooperative contribution is almost null (0.1 kcal mol⁻¹) in the 1,4eq isomer is apparently due to the absolutely no networking (only two hydrogen bonds in the network) of the H-bonds as discussed in the previous section. This is the reason that although there are equatorial–axial and axial–equatorial H-bonds in the 1,4eq isomer, the estimated H-bond energies are smallest in this isomer. The cooperative contribution is highest (5.4 kcal mol⁻¹) in the 6a isomer wherein there are stronger axial–axial H-bonds (3 above and 3 below the cyclohexane ring).

Table 9 Intramolecular O–H⋯O hydrogen bond energy for individual hydrogen bond in the absence of the OH⋯O hydrogen bond network various inositol isomers calculated at the MP2/6-311+G(d,p) level of theory

	scyllo	myo	neo	epi	dl	allo	cis	muco	1,2eq	1,3eq	1,4eq	1e/5a	6a
O1H⋯O2	−1.73	−1.66	−1.46	−2.22	—	−1.42	−1.98	−2.40	−2.57	−2.01	—	—	—
O2H⋯O3	−1.73	−1.61	−2.20	−1.68	−2.54	−2.09	−1.82	−2.02	—	−2.76	−1.90	—	−2.12
O3H⋯O4	−1.73	−2.23	−2.40	−2.27	−1.78	—	−1.97	−1.50	—	—	−1.64	−2.78	—
O4H⋯O5	−1.73	−1.55	−1.46	−1.70	−1.41	−1.79	−1.82	−2.35	—	—	—	−2.10	−2.12
O5H⋯O6	−1.73	−2.23	−1.63	−2.14	−2.20	−2.37	−1.15	—	−2.48	−1.85	−1.90	—	—
O6H⋯O1	−1.73	−1.83	−2.40	−1.59	−1.95	−2.24	−1.81	—	−2.21	−1.41	−1.64	—	—
O4H⋯O6	—	—	—	—	—	—	—	—	—	—	—	—	—
O5H⋯O3	—	—	—	—	—	—	—	—	−3.01	−2.81	—	—	—
O2H⋯O4	—	—	—	—	—	—	—	—	−2.61	—	—	—	—
O5H⋯O1	—	—	—	—	—	—	—	−3.20	—	—	—	—	−2.12
O3H⋯O1	—	—	—	—	—	—	—	—	—	—	—	−2.47	—
O6H⋯O2	—	—	—	—	—	—	—	—	—	—	—	−1.57	−2.12
O1H⋯O4	—	—	—	—	—	—	—	—	—	—	—	−3.03	−2.12
O3H⋯O6	—	—	—	—	—	—	—	—	—	—	—	—	−2.12
Sum	−10.38	−11.11	−11.56	−11.60	−9.86	−9.91	−10.54	−11.47	−12.88	−10.83	−7.07	−11.95	−12.75
Cooperativity	−2.76	−3.34	−2.57	−2.75	−1.75	−2.85	−5.12	−2.63	−1.92	−2.28	−0.10	−3.17	−5.37

---

In summary, the intramolecular hydrogen bond strengths in all the inositol isomers studied in the present work are substantially enhanced or altered due to the interconnected networking of H-bonds. In general, the strength of stronger (axial–axial) hydrogen bonds is enhanced substantially than the weaker equatorial–equatorial bonds. Furthermore the total cooperativity contributions depend on the number and strength of individual H-bonds in the network.

Conclusions

In the present work, the geometries of all the thirteen theoretical possible conformers of isomers of inositol are explored at the correlated MP2 level of theory for the first time. Earlier studies in the literature report only some of the lower energy conformers and ignored the conformers with axial orientation of hydroxyl groups. We studied the relative stability of these conformers in both gas as well as solvent phases. It is seen that in the gas phase, the conformers –neo and –myo with two axial hydroxyl groups are marginally stable (by 0.5 and 0.3 kcal mol⁻¹) compared to that with all equatorial hydroxyl groups (scyllo-inositol). The gas phase stability of the conformers with increase in number of axial hydroxyl groups decreases substantially. For instance, the 6a conformer (six axial hydroxyl groups) is destabilized by 11.5 kcal mol⁻¹ than the scyllo conformer (six equatorial hydroxyl groups).

These gas phase results are also seen to be consistent with those in the solvent phase. The scyllo isomer becomes the most stable and the 6a isomer is the least stable in solvents. The hydroxyl groups in these inositol isomers are involved in the formation of a network of intramolecular OH⋯O hydrogen bonds. In general, it follows that the OH⋯O hydrogen bond distances are longer when two hydroxyl groups involved in the formation of hydrogen bonds are in equatorial positions. The hydrogen bond distances with hydroxyl groups with axial–equatorial or equatorial–axial orientations are generally shorter than those with equatorial–equatorial orientations and are longer than those observed for axial–axial orientations. These geometrical parameters suggest that the strength of hydrogen bonds in these inositol isomers follows: O_axial–H⋯O_axial > O_equtorial–H⋯O_axial > O_axial–H⋯O_equatorial > O_equatorial–H⋯O_equatorial. This trend in hydrogen bond strength is reflected in the corresponding O–H stretching frequencies. For instance, the hydroxyl groups that are not involved in formation of hydrogen bonds have the highest O–H stretching frequency. The O–H stretching frequency decreases (red shift) substantially when OH groups are involved in the formation of stronger hydrogen bonds. The decrease in frequency (red shift) is in agreement with the shortening of OH⋯O distances on moving from equatorial–equatorial to axial–axial O–H⋯O hydrogen bonds. In order to get further insight into the strengths of these hydrogen bonds, we quantified the individual bond strengths and the effect of formation of the cooperative network on the hydrogen bond strengths in all inositol isomers. For this purpose, the hydrogen bond energies were estimated in the presence and absence of cooperative networking using the molecular tailoring approach. The estimated hydrogen bond energy in the presence of a cooperative network of hydrogen bonds is in the range of 2.2 to 3.8 kcal mol⁻¹. The estimated hydrogen bond energies are in qualitative agreement with the above discussed trend in their bond strength based on bond distances and vibrational frequency. The estimated cooperative contribution is substantial (2 to 5 kcal mol⁻¹) in most of these inositol isomers and is seen to increase as we go from isomers with more equatorial hydroxyl groups to isomers with more axial hydroxyl groups. This increase in the cooperative contributions seems to depend on two factors (a) the number of hydrogen bonds in the network and (b) the strength of each of these bonds. In general, it is seen that the strength of hydrogen bonds increases substantially due to cooperative interaction when hydroxyl groups are involved in the formation of stronger axial–axial H-bonds.

We also wish to attribute the highest stability of the scyllo isomer in the solvent to weaker intramolecular OH⋯O hydrogen bonds between equatorial hydroxyl groups, which in turn, may facilitate favourable intermolecular interaction. This stability correlates well with the natural abundance in inositol isomers. In contrast, the inositol isomers with axial hydroxyl groups are involved in the formation of relatively strong H-bonds (for example, 6a isomer) and hence are less stable due to overpowering steric factors in the gas phase and unfavourable intermolecular interaction in the solvent phase. It is indeed of great importance to understand this competition between the intermolecular and intramolecular interactions which effectively governs the relative stability of these inositol isomers in the solvent phase. We hope that such a study would provide insights into the physicochemical properties of these important biological systems.

Acknowledgements

NS is thankful to the Indian Institute of Technology Kanpur (IITK), for a senior research fellowship. VS is thankful to the Dr Harisingh Gour University for research fellowship. MMD is thankful to University Grant Commission for the initial start-up grant (No. F. 30-56/2014/BSR).

References

1. M. J. Berridge, Nature, 1993, 361, 315.
2. S. B. Shears, Biochem. J., 1989, 260, 313.
3. A. Toker and L. C. Cantley, Nature, 1997, 387, 673.
4. R. F. Irvine and M. J. Schell, Nat. Rev. Mol. Cell Biol., 2001, 2, 327.
5. A. Toker, Cell. Mol. Life Sci., 2002, 59, 761.
6. B. Vanhaesebroek, S. Leevers, K. Ahmadi, J. Timms, R. Katso, P. C. Drisscoll, R. Woscholski, P. J. Parker and M. D. Waterfield, Annu. Rev. Biochem., 2001, 70, 535.
7. S. B. Shears, Biochim. Biophys. Acta, 1998, 1436, 49.
8. A. L. Frank and P. N. M. Pushpalatha, Plant Sci., 2000, 150, 1.
9. S. Umezawa, Advances in Carbohydrate Chemistry and Biochemistry, Academic Press, New York, 1974.
10. J. D. Dutcher, Advances in Carbohydrate Chemistry, Academic Press, New York, 1963.
11. B. Jonathan, L. Joseph, F. Mendel, A. Alex, L. Daniel and R. H. Belmaker, Am. J. Psychiatry, 1995, 152, 1084.
12. A. D. Genazzani and S. Aprati, Gynecol. Endocrinol., 2012, 28, 969.
13. I. Vucenik and A. M. Shamsuddin, J. Nutr., 2003, 133, 3778S.
14. D. Giordano, F. Corrado, A. Santamaria, S. Quattrone, B. Pintaudi, A. D. Benedetto and R. D'Anna, Menopause, 2011, 18, 102.
15. B. Tse and Y. Kishi, J. Am. Chem. Soc., 1993, 115, 7892.
16. D. R. Gauthier and S. L. Bender, Tetrahedron Lett., 1996, 37, 13.
17. N. Chida and S. Ogawa, Chem. Commun., 1997, 807.
18. S. Tomatus, T. S. Sayaka, Y. Iwao, K. Yoshiaki, Y. Kazue and C. Noritaka, J. Org. Chem., 2002, 67, 2874.
19. S. Ken-ichi, A. Shoji, S. Naoki, O. Tadatsugu, K. Tomokazu, S. Hirotsugu and Y. Juji, J. Org. Chem., 2005, 70, 7496.
20. L. Min, W. Anmei and Z. Peijie, Tetrahedron Lett., 2006, 47, 3707–3710.
21. C. J. Rajendra and S. S. Mysore, Tetrahedron, 2011, 67, 7963.
22. T. Steiner, W. Hinrichs, W. Saenger and R. Gigg, Acta Crystallogr., Sect. B: Struct. Sci., 1993, 49, 708.
23. C. Murali, M. S. Shashidhar, R. G. Gonnade and M. M. Bhadbhade, Chem. – Eur. J., 2009, 15, 261.
24. P. Sarah, K. K. Gabriele, D. L. Matthew and E. L. Simon, Chem. Commun., 2011, 47, 4799.
25. M. Amorin, L. Castedo and J. R. Granja, J. Am. Chem. Soc., 2003, 125, 2844.
26. K. S. Vijayalakshmi and V. S. R. Rao, Proc. Indian Acad. Sci., 1973, 77, 83–91.
27. L. Congxin, S. E. Carl, R. S. Terry and T. H. Arnold, J. Am. Chem. Soc., 1994, 116, 3904.
28. V. D. A. Mauro, R. C. C. Mara, V. D. A. Joao, P. A. A. Cleber, F. D. S. Hélio and W. B. D. Almeida, Magn. Reson. Chem., 2012, 50, 608.
29. W. Pigman and D. Horton, Carbohydrates, Academic Press, New York, 1972.
30. E. L. Eliel, N. L. Allinger, S. J. Angyal and G. A. Morrison, Conformational Analysis, Interscience, New York, 1965.
31. T. R. Lomer, A. Miller and C. A. Beevers, Acta Crystallogr., 1963, 16, 264.
32. G. A. Jeffrey and S. H. Kim, Carbohydr. Res., 1970, 15, 310.
33. R. M. Williams and R. H. Atalla, J. Phys. Chem., 1984, 88, 508.
34. M. M. Deshmukh, S. R. Gadre and L. J. Bartolotti, J. Phys. Chem. A, 2006, 110, 12519.
35. K. Babu, V. Ganesh, S. R. Gadre and N. E. Ghermani, Theor. Chem. Acc., 2004, 111, 255.
36. S. R. Gadre, K. Babu and V. Ganesh, in Proceedings of NRB Seminar, ed. S. N. Maheshwari, Viva Books, New Delhi, 2005.
37. S. R. Gadre and V. Ganesh, J. Theor. Comput. Chem., 2006, 5, 835.
38. S. R. Gadre, R. N. Shirsat and A. C. Limaye, J. Phys. Chem., 1994, 98, 9165.
39. V. Ganesh, R. K. Dongare, P. Balanarayan and S. R. Gadre, J. Chem. Phys., 2006, 125, 104109/1.
40. K. Ishimura, P. Pulay and S. A. Nagase, J. Comput. Chem., 2006, 27, 407.
41. K. Ishimura, P. Pulay and S. Nagase, J. Comput. Chem., 2007, 28, 2034.
42. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294.
43. W. J. Hehre, L. Radom, P. V. R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, Wiley, New York, 1986.
44. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
45. K. Kim and K. D. Jordan, J. Phys. Chem., 1994, 98, 10089.
46. C. Lee, W. Yang and R. G. Parr, Phys. Rev., 1988, B37, 785.
47. S. Miertus, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117.
48. C. Maurizio, B. Vincenzo, C. Roberto and T. Jacopo, Chem. Phys. Lett., 1996, 255, 327.
49. V. Barone, M. Cossi, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3210.
50. M. T. Cances, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032.
51. V. Barone, M. Cossi and J. Tomasi, Comput. Chem., 1998, 19, 404.
52. M. J. Frisch, et al., Gaussian Inc., PA, Pittsburgh, 2003; M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford, CT, 2010.
53. H. A. Bent, J. Chem. Phys., 1960, 33, 1258.
54. H. A. Bent, Chem. Rev., 1961, 61, 275.
55. P. I. Nagy, W. J. Dunn, G. Alagona and C. Ghio, J. Am. Chem. Soc., 1991, 113, 6719.
56. M. A. Murcko and R. A. Dipaola, J. Am. Chem. Soc., 1992, 114, 10010.
57. K. Hegetschweiler, I. Emi, W. Schneider and H. Schmalle, Helv. Chim. Acta, 1990, 73, 97.
58. K. Dhl and L. Huang, Carbohydr. Res., 1991, 215, 351.
59. S. Ha, J. Gao, B. Tidor, J. W. Brady and M. Karplus, J. Am. Chem. Soc., 1991, 113, 1553.
60. D. French and J. W. Brady, Computer Modeling of Carbohydrate Molecules, ACS Symposium Series No. 430, American Chemical Society, Washington, DC, 1990.
61. M. M. Deshmukh, L. J. Bartolotti and S. R. Gadre, J. Phys. Chem. A, 2008, 112, 312.
62. M. M. Deshmukh and S. R. Gadre, J. Phys. Chem. A, 2009, 113, 7927.
63. M. M. Deshmukh, L. J. Bartolotti and S. R. Gadre, J. Comput. Chem., 2011, 32, 2996.
64. J. K. Khedkar, M. M. Deshmukh, L. J. Bartolotti, S. R. Gadre and S. P. Gejji, J. Phys. Chem. A, 2012, 116, 3739.

---

Footnotes

† Authors wish to dedicate this work to Professor Shridhar R. Gadre on his 65th birthday.

‡ Electronic supplementary information (ESI) available: The C–C–C–C ring torsion angle is reported in Table S1. See DOI: 10.1039/c5cp02690c

---