Estimating chemical reactivity and cross-influence from collective chemical knowledge†
Siowling
Soh
a,
Yanhu
Wei
b,
Bartlomiej
Kowalczyk
b,
Chris M.
Gothard
b,
Bilge
Baytekin
b,
Nosheen
Gothard
b and
Bartosz A.
Grzybowski
*ab
aDepartment of Chemical and Biological Engineering, Northwestern University, 2145 Sheridan Road, Evanston, IL 60208. E-mail: grzybor@northwestern.edu
bDepartment of Chemistry, Northwestern University, 2145 Sheridan Road, Evanston, IL 60208
First published on 23rd February 2012
Abstract
Although modern chemical databases store a great wealth of structural and reactivity data, this vast “universe” of chemical information has not yet been systematically analyzed. Here, we use computers to derive from the entire body of organic-chemical knowledge the indices that estimate the reactivity and cross influence of functional groups. The major premise of our approach is that in sufficiently large and diverse collections of reactions (as the entire “history” of organic chemistry is), the frequencies with which transformations of certain groups occur, reflect their reactivities. Illustrative examples spanning several classes of reactions demonstrate that our knowledge-based indices capture the well-known reactivity trends. A free-access software is also developed with which other trends can be analyzed for various combinations of functional groups.
Introduction
In synthetic practice, reactivity estimates are largely based on the chemist's experience, often helped by the information stored in textbooks, journal articles, or chemical databases. While for specific individual groups such estimates are usually straightforward and sufficient, the mutual influence of one chemical functionality on another is inherently harder to quantify, even with the help of empirical trends (e.g., Hammett1 or Taft2 equations, structure–activity relationships3) or computational methods.4–7 Save for rather select examples, a priori predictions of whether the presence of group B makes group A in the same molecule more or less reactive can be a non-trivial question. It is this question we address in the present paper using the so-called knowledge-based statistical approach.Recently, we have shown that accurate reactivity indices for specific individual groups involved in various classes of reactions can be derived from the existing body of chemical knowledge8,9—namely, from the statistics of reactions reported in literature from the times of Lavoisier to the present and nowadays stored in chemical databases such as Beilstein/Reaxys, The Chemical Thesaurus, or Current Chemical Reactions. The premise of this knowledge-based approach has been that in sufficiently large, diverse and unbiased collections of reactions—as the entire “history” of organic chemistry certainly is8,10–12—the numbers of transformations in which specific functional groups have reacted should reflect the reactivity of these groups. In other words, with adequate reaction statistics, synthetic “popularity” is proportional to chemical reactivity. In ref. 9, we validated this approach against experimental data (notably, Hammett constants) for several classes of reactions including formation of diazo-compounds, Stille cross-coupling, Heck and/or Suzuki type couplings, and more. With hindsight, the fact that admittedly simple reaction counting yielded accurate estimates of reactivity is, perhaps, not that surprising. After all, every successful chemical reaction reported in the literature is an outcome of an experiment in chemical reactivity, kinetics, and thermodynamics. What our approach quantifies is, in essence, the fact that more kinetically and/or thermodynamically favorable reactions have higher chances of being carried out successfully than those that are less favored. While such conclusion would be premature when considering only few select reactions, large reaction sets “average over” specific conditions (solvents, temperature, etc.) and if the comparisons are made for specific groups, it is the inherent reactivities and cross-reactivities that our statistical method yields.
In the present paper, we extend this statistical approach to attack a problem that is significantly more challenging than determining the reactivities of individual groups—specifically, our objective is, to back-track from all known synthetic knowledge (cf.Fig. 1a) the measures that quantify mutual influence of organic functionalities present in the same molecule. Based on the counts of database-stored chemical reactions, we derive conditional probabilities of certain groups being present in a molecule and reacting – these probabilities then lead to indices, ηAB, that quantify cross-influence (activating vs. deactivating) for arbitrary pairs of chemical functionalities in different mutual arrangements (e.g., directly connected or separated within a molecule). The reactivity trends the ηAB, indices predict are congruent with common chemical intuition for several well studied classes of reactions. In addition to the illustrative examples discussed in the paper, a β-version software—which we call ChemGPS for Chemical Group Predictor Software—that calculates the ηAB indices for user-specified group pairs is made freely available through our group web page (http://www.dysa.northwestern.edu/ChemGPS). Our work aims to supplement “intuitive”/subjective cross-influence/reactivity measures with ones that are based on the entire, collective knowledge of several generations of chemists. It is the first time in the history of chemistry that this knowledge can be analyzed and quantified en masse with the help of modern computers.
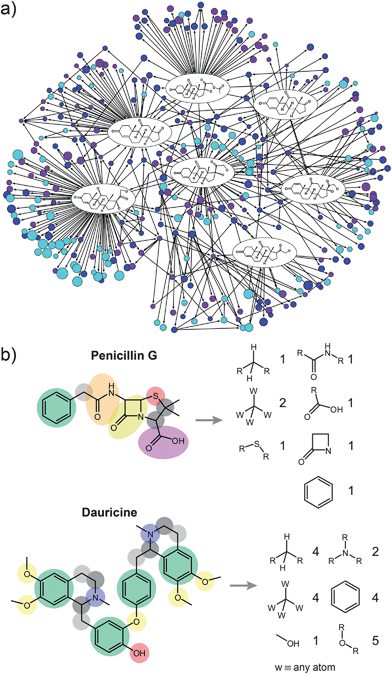 | ||
| Fig. 1 (a) A small (∼300 nodes) sub-network of organic chemistry centered around cortisone. Individual nodes represent the molecules, arrows represent reactions. The entire “universe” of known organic reactions is more than 25,000 times larger than the sub-network shown here. Yet, the wealth of structural and reactivity information stored in this repository created collectively by generations of chemists8,9,11,12 has not been systematically explored. Of course, to make predictions beyond simple network connectivity, the individual nodes of the network must be analyzed in structural detail. In the present work, all nodes/molecules are decomposed into functional groups as illustrated in (b) for Penicillin G (top) and Dauricine (bottom). The numbers on the right correspond to the occurrences of each functional group in the molecule. The algorithm for decomposition will be published separately; most important 322 groups are listed in the Supplementary Information†, Section 1. | ||
Methods
Our analyses are based on all organic reactions reported in the chemical literature since 1779 and stored in chemical databases (especially, Beilstein). Pruning the raw dataset (see ref. 8,9,11,12) to remove catalysts, solvents, substances that do not participate in reactions, duplicate reactions, and reactions which lack either reactants or products (that is, “half reactions”) leaves ca. 7 million reactions and ca. 7 million substances on which further analyses are based. Unlike in our previous studies of the “Network of Chemistry”8,9,11,12 where the molecules were simply dot-like nodes of the network, the present work requires the knowledge of molecular structural details, and thus necessitates dividing all molecules into functional groups. Given the size of the dataset, this procedure had to be automated. Accordingly, we have developed an efficient pattern-recognition algorithm that partitions each molecule unambiguously into functional groups taken from a list of 322 common chemical functionalities (Fig. 1b and also Supplementary Information†, SI, Section 1). Division of the entire dataset of 7 million molecules took several days on a 425-node computer cluster; subsequent analyses of the already-divided molecules took only minutes on a standard desktop computer.Results and discussion
Reactivity indices of individual groups
The estimation of cross influence of functional groups has two steps. First, we use the previously described popularity-vs.-reactivity measure9 to estimate the “baseline”/inherent reactivity of an individual group, say A, irrespective of the presence of any other specific groups in the same molecule. Briefly, a search is performed to identify all NAtot reactions in which the substrate molecules contain group A; within this set, the number of reactions in which A changes into some other functional group is determined and denoted as NA (Fig. 2a). Given a large and unbiased reaction pool, NA then reflects/estimates9 the inherent propensity of A to react – casting in the form of probabilities, the reactivity index can then be defined as RA = NA/NAtot, and its value ranges from 0 to 1 (the higher the value of RA, the more reactive group A is). As discussed in detail in our previous work,9 this simple measure (reminiscent of the so-called knowledge-based potentials of proteins13) correlates well with frontier orbital populations or Hammett σ and ρ parameters for a range of reactions, and its fidelity is relatively high even for datasets comprising as few as tens of reactions (which is much smaller than the sets we analyze here; see ref. 14 and SI†, Section 2). Several reactivity trends based on statistically significant RA values are illustrated in Fig. 2b—these trends are in good agreement with what can be considered a chemical “common sense”. For instance, Trend 1 illustrates that reactivity of an acetyl group increases with increasing electrophilic ability of the carbonyl carbon (influenced by the electron withdrawing, donating, and/or resonance effects of various substituents shown). In Trend 2, the familiar reactivity of halides is based on two factors: (i) the strength of the carbon–halogen covalent bond, and (ii) the stability of halide ion leaving group. Trend 3 captures the well-known reactivity ordering alkynes > alkenes > aromatic rings. For all trends, the RA's are determined with high accuracy since the sample sizes, NAtot, are large (on the order of 105–106 reactions). This is reflected by the 95% confidence interval values, CIA, being very small (the smaller these values, the smaller the uncertainties in RA's; see also footnote14).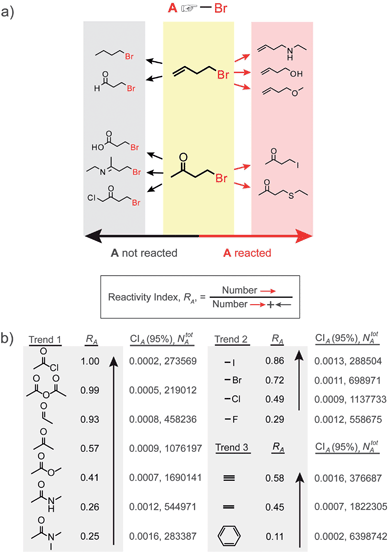 | ||
| Fig. 2 Reactivity of individual functional groups. (a) Scheme illustrating the calculation of the reactivity index, RA, defined as the fraction of reactions, in which group A reacts. In this case, RA = 5/10 = 0.5. (b) Three examples of calculated RA trends, which are consistent with common chemical knowledge. The sizes of the reaction sets, NAtot, and the 95% confidence intervals, CIA, are indicated for each RA. | ||
Cross-influence indices
Following a similar logic, a reactivity index for A can now be defined that takes into account the presence of some other group B in the molecule. In this case, the reactivity measure has a meaning of conditional probability, RAB = NAB/NABtot, where NABtot denotes the total number of reactions in which the substrate molecules contain both A and B groups, and NAB denotes the subset of these reactions, in which group A changes (Fig. 3a).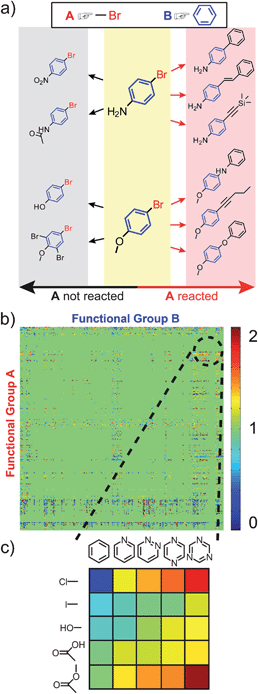 | ||
| Fig. 3 The cross-influence of functional groups A and B. (a) Shows a scheme for calculating the reactivity index, RAB, when both A and B, are present. In this case, RAB = 6/10 = 0.6. The cross-influence index is then, ηAB = RAB/RA, where ηAB > 1 indicates that B increases the reactivity of A, while ηAB < 1 indicates that B decreases it. (b) Table of ηAB for all 322 × 322 functional groups, where A and B are directly connected. The values of ηAB are color-coded as illustrated in the scale on the right. A magnified view of the table's fragment is shown in (c). In this specific example, ηAB generally increases “to the right,” with increasing number of nitrogen atoms in the aromatic ring (see main text for discussion). | ||
The key point of our work is then as follows: if RAB > RA, the presence of B renders A more reactive than its inherent/“average” reactivity; in this case, a cross-influence index ηAB = RAB/RA > 1. Conversely, if RAB < RA (or ηAB < 1), B causes A to be less reactive than in the generic case (i.e., when the reactivity of A is determined irrespective of any other groups present on the same molecule). We make three further comments about the cross-influence indices ηAB thus defined: (1) these indices can take into account specific arrangement of the A and B groups within the molecules. In the present work, we focus on examples where A and B are either directly connected or separated by one carbon atom, such that steric or electronic effects of proximal groups are most pronounced (though, of course, the same methodology can be applied to situations where A and B are more distant). (2) For a given arrangement of groups, ηAB indices can be generated rapidly (within seconds on a standard PC) for all possible pairs of functional groups. This procedure generates a cross-influence matrix such as that in Fig. 3b, where the colors correspond to the activating or deactivating effect of B on A. (3) The indices can be calculated within specific classes of reactions; in such a case, NAB values are reaction counts over a particular reaction class only (as discussed later in the text, see Fig. 5).
Specific cross-influence trends
In the remaining portion of the paper, our aim is to validate the ηAB indices by showing that they predict plausible reactivity trends in different sets/classes of reactions. These examples are subjectively chosen such that the results of our analysis can be easily compared and contrasted with common chemical knowledge/intuition. For other combinations of the A/B groups (in fact, 207368 combinations based on 322 groups) and for constructing desired reactivity trends, the reader is invited to use the ChemGPS software posted at http://www.dysa.northwestern.edu/ChemGPS.The first case study is illustrated in Fig. 3c for substituted heterocyclic compounds where the reactivity of the substituents (e.g., A = Cl, I, OH, COOH, COOR) increases with increasing number of nitrogen atoms present on the aromatic ring B (i.e., from left to right in the figure, values of ηAB are color-coded, see figure caption). These results are chemically reasonable, since in the presence of more nitrogen atoms, there is an increasing electron withdrawing effect, causing groups A to be more active in various reactions. For instance, with the increase of the number of nitrogen atoms, hydroxyl and carboxylic acid groups are more easily deprotonated, ester group is more prone to the attack of nucleophilic reagents, and the decrease of electron density around carbon atoms makes aryl chloride or iodide more prone to nucleophilic attack or Pd catalyzed coupling.
Another trend is shown in Fig. 4 where the cross-influence of several synthetically important groups—either directly connected or separated by one carbon atom—is considered. When A is directly connected to B (Fig. 4a), it becomes an easier target for nucleophilic reagents because of two factors: (i) a significant electron withdrawing effect of groups B (here, ketone, carboxylic acid, ester, amide) on A (alkene, ketone, ester) or (ii) electron conjugation of A to B. In both cases, ηAB > 1. Similarly, when A and B are separated by one carbon atom (Fig. 4b), electron withdrawing groups, B (e.g., nitro and ketone), encourage nucleophilic attack, while B = benzene or alkyne can help stabilize the transition states of SN1/SN2 chloride substitution via the conjugation effect. Further examples, this time such that B “deactivates” A (i.e., ηAB < 1), are discussed in the SI†, Section 3.
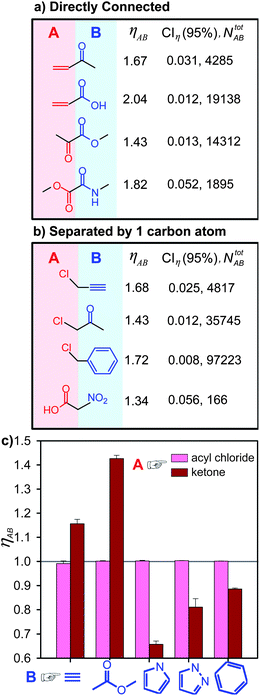 | ||
| Fig. 4 Examples of the cross-influence indices, ηAB, calculated for the case when (a) functional groups A and B are directly connected, and (b) when they are separated by one carbon atom. Owing to the large sample size (NABtot ∼ 103–104), the 95% confidence intervals values, CIη, for ηAB, are small, indicating reliable statistics. (c) The reactivity of inherently highly reactive functional groups (here, A = acyl chloride), does not depend perceptibly on the nature of other groups present in the molecule; in this case, ηAB ∼ 1. In contrast, when A is less inherently reactive (here A = ketone), the nature of B can influence its reactivity to a much higher degree (ηAB's above or below 1). Error bars correspond to CIη. | ||
An interesting situation arises when A is a highly reactive group itself—in this case, one could expect that less reactive groups B would have a marginal effect on the already high reactivity of A. This, indeed, is the case, as illustrated in Fig. 4c where various substituents connected to the highly reactive acyl chloride have minimal effect on its reactivity, so that RAB ∼ RA and ηAB ∼ 1. This is in contrast to a case where A is less reactive (e.g., ketone), and the nature of B influences the values of ηAB perceptibly (also see SI†, Section 4 for further examples).
While the trends discussed above are taken across all possible reaction types, ηAB can be also calculated for specific types of transformations. In such cases, the statistics become more scarce (reaction counts, N's, are smaller) but are still high enough for statistical significance at the 95% confidence levels (see ref. 14). As an illustration, first consider a general trend for the case of A = ester and B = halides (Fig. 5a). As seen, ηAB increases with increasing electronegativity of the halide which, as any chemist knows, renders the carbonyl atom more susceptible toward a nucleophilic attack. This trend is also present—albeit with different values of the ηAB indices—in specific reaction classes such as the hydrolysis of esters (Fig. 5b) or the conversion of esters into amides via a nucleophilic attack (Fig. 5c). These trends are established by narrowing the counts of reactions (NA and NAB) to specific sub-classes of transformations (these narrowed counts are denoted NSA and NSAB such that the reaction-type-specific index ηSAB = (NSAB/NABtot)/(NSA/NAtot).
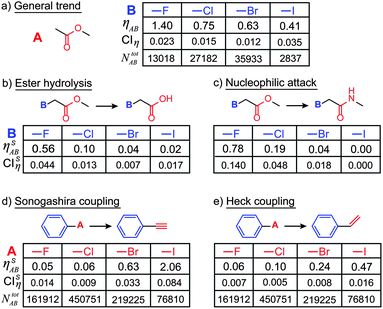 | ||
| Fig. 5 Examples of the cross-influence indices for specific reaction sub-types. (a) Shows the general trend (i.e., for all sub-classes of reactions), where the reactivity index, ηAB, of esters increases with increasing electronegativity of the halide substituents. When specific reactions are considered, the trends are qualitatively similar, but the reaction-specific values of ηSAB are different: (b) ester hydrolysis, (c) conversion of esters into amides via a nucleophilic attack. Note that NABtot is the same for all examples in (a–c). Reactivity indices and trends for two other important and popular reaction classes: (d) the Sonogashira coupling and (e) the Heck coupling. | ||
This methodology is applicable to arbitrary reaction types. For example, in Fig. 5d–e the influence of halides B on the Sonogashira and Heck couplings is quantified. The ηSAB index values for both of these reactions reflect the reactivity of aryl halides (R–I > R–Br > R–Cl > R–F). These results are well known and chemically reasonable because cleavage of aryl halide bonds is involved in both Sonogashira and Heck reactions, and the energies of aryl halide bonds follow a R–I < R–Br < R–Cl < R–F ordering.
The final set of examples in Fig. 6a applies the ηSAB indices to the popular Diels–Alder reactions—importantly, it is chosen to provide some quantitative comparison with available experimental data. It is known that in this reaction, the reactivity of dienes can be enhanced either by n-electron donating substituents (e.g., methoxy) or by bulky substituents such as t-Butyl-ester, trimethylsilyl (TMS) or t-butyl silyloxy (TBS) in whose presence the diene is more prone to assume the s-cis conformation. These effects have been studied systematically by Fowler15 and Sauer16 who quantified the reactivity of dienes in terms of the reaction rate constants. These experimental reactivity measures are listed in the top row of Fig. 6a and are normalized with respect to the rate constant of an unsubstituted diene. For comparison, the bottom row in the same figure gives the ηSAB indices we derived from the reported reaction counts (with A being the diene and B = chloro, bromo, ether, ester, silyl ether)—these indices agree qualitatively with the experimental trends. We note that this particular analysis is relevant to modern synthesis. A classic example here is the wide use of the Danishefsky's diene (Fig. 6b), whose reactivity derives from the synergistic effect of the OMe and TMS substituents. Another interesting example is the Nicolaou's synthesis of a natural product colombiasin A (Fig. 6c; for two more examples, see SI†, Section 5).
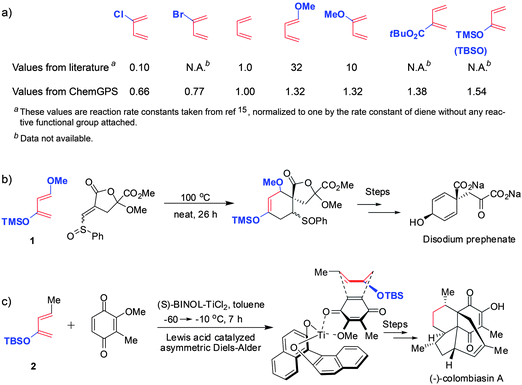 | ||
| Fig. 6 Reactivity of substituted dienes in Diels–Alder reaction. (a) Reactivities measured experimentally (by determining the reaction rate constants15,16 and normalizing to unity for diene without any reactive functional groups attached) and those (ηSAB) estimated by our method. (b,c) Two contemporary synthetic examples in which the diene's reactivity is enhanced by substituents that ChemGPS finds activating: (b) the use of Danishefsky's diene (1) in the total synthesis of disodium prephenate;24 (c) K. C. Nicolaou's synthesis of colombiasin A, where the TBS protecting group is used as a steric tool to favor s-cis conformation of diene (2).25 | ||
Conclusions
The statistical cross-influence indices we described reflect “common chemical knowledge”—and, in some cases, less intuitive but general reactivity relationships17,18—and are based on large numbers of successful experiments in chemical reactivity (which the published reactions are!). As such, these simple indices implicitly reflect the electronic, steric and other effects that are operative in every chemical reaction—albeit, they average these effects over large numbers of specific reactions. We suggest that in addition to the practice of organic synthesis, these reactivity indices can be of use when incorporated into algorithms constructing drug-like molecules from chemical fragments.19–23 In such cases, the reactivity indices can guide fragment “stitching” such as to produce molecules that would not only have high potency of binding towards specific biomolecular targets, but would also be synthetically “makeable”.19,23 We conclude with some broader statements: having assembled a huge body of chemical knowledge, we finally have at our disposal computers powerful enough to analyze it and learn from its entirety. With millions of reactions performed and compounds made, there are likely many reactivity/structural trends buried in the annals of our discipline that are beyond the cognition of any one individual chemist and can be (re)discovered only with the help of computers. In this spirit, the use of interactive tools—like our ChemGPS and other programs similar to it—can help rapidly establish knowledge-based reactivity and structural trends. This philosophy of helping future research with the computational analysis of the already amassed data has been used widely and successfully in disciplines ranging from structural biology and biochemical network analysis to economics and ecology. We feel similar approaches should also be implemented in chemical research.Acknowledgements
This work was supported by the Non-equilibrium Energy Research Center (NERC) which is an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DE-SC0000989.References
- L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96–103 CrossRef CAS
.
- R. W. Taft, J. Am. Chem. Soc., 1952, 74, 3120–3128 CrossRef CAS
.
- C. D. Selassie, R. Garg, S. Kapur, A. Kurup, R. P. Verma, S. B. Mekapati and C. Hansch, Chem. Rev., 2002, 102, 2585–2605 CrossRef CAS
.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1873 CrossRef CAS
.
- P. A. Bash, L. L. Ho, A. D. MacKerell, D. Levine and P. Hallstrom, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 3698–3703 CrossRef CAS
.
- M. Haran, J. R. Engstrom and P. Clancy, J. Am. Chem. Soc., 2006, 128, 836–847 CrossRef CAS
.
- Influence of specific functional groups on molecular reactivity can be examined through advanced quantum mechanical calculations, such as the Density Functional Theory (DFT) or from more traditional ab initio calculations. These methods, however, typically involve approximations which may render results prone to error and are computationally costly (see A. J. Cohen, P. Mori-Sanchez and W. T. Yang, Science, 2008, 321, 792–794 CrossRef CAS
).
- B. A. Grzybowski, K. J. M. Bishop, B. Kowalczyk and C. E. Wilmer, Nat. Chem., 2009, 1, 31–36 CrossRef CAS
.
- B. Kowalczyk, K. J. M. Bishop, S. K. Smoukov and B. A. Grzybowski, J. Phys. Org. Chem., 2009, 22, 897–902 CrossRef CAS
.
-
C. Schorlemmer, The Rise and Development of Organic Chemistry, Macmillan and Co., New York, 1894 Search PubMed
.
- M. Fialkowski, K. J. M. Bishop, V. A. Chubukov, C. J. Campbell and B. A. Grzybowski, Angew. Chem., Int. Ed., 2005, 44, 7263–7269 CrossRef CAS
.
- K. J. M. Bishop, R. Klajn and B. A. Grzybowski, Angew. Chem., Int. Ed., 2006, 45, 5348–5354 CrossRef CAS
.
- Conceptually similar, knowledge-based measures have been used and validated in protein science and rational drug design. In these approaches, the numbers/probabilities of contacts between certain amino acids or specific atoms are first derived from large protein-structure databases, and are then related to the energies of these contacts, typically via Boltzmann-like statistics. For discussion, see
(a) B. A. Grzybowski, A. V. Ishchenko, J. Shimada and E. I. Shakhnovich, Acc. Chem. Res., 2002, 35, 261–269 CrossRef CAS
; (b) P. D. Thomas and K. A. Dill, J. Mol. Biol., 1996, 257, 457–469 CrossRef CAS
.
- For the derivation of CI indices, see in the present study, the statistical reliability of the indices is quantified in terms of confidence intervals, CIs, at the 95% level, or in other words, the intervals which include the “true” value of the indices with a 95% probability. The narrower the confidence interval is, the closer the estimated reactivity index to its “true” value and the higher its statistical reliability. SI†, Section 2.
- D. Craig, J. J. Shipman and R. B. Fowler, J. Am. Chem. Soc., 1961, 83, 2885–2891 CrossRef CAS
.
- J. Sauer, D. Lang and A. Mielert, Angew. Chem., Int. Ed. Engl., 1962, 1, 268–269 CrossRef
.
- K. W. Moore, A. Pechen, X. J. Feng, J. Dominy, V. Beltrani and H. Rabitz, Chem. Sci., 2011, 2, 417–424 RSC
.
- K. W. Moore, A. Pechen, X. J. Feng, J. Dominy, V. J. Beltrani and H. Rabitz, Phys. Chem. Chem. Phys., 2011, 13, 10048–10070 RSC
.
- P. S. Kutchukian, D. Lou and E. I. Shakhnovich, J. Chem. Inf. Model., 2009, 49, 1630–1642 CrossRef CAS
.
- R. S. Bohacek, C. McMartin and W. C. Guida, Med. Res. Rev., 1996, 16, 3–50 CrossRef CAS
.
- R. S. Bohacek and C. McMartin, J. Am. Chem. Soc., 1994, 116, 5560–5571 CrossRef CAS
.
- H. J. Bohm, J. Comput.-Aided Mol. Des., 1992, 6, 61–78 CrossRef CAS
.
- H. J. Bohm, J. Comput.-Aided Mol. Des., 1996, 10, 265–272 CrossRef CAS
.
- S. Danishefsky, M. Hirama, N. Fritsch and J. Clardy, J. Am. Chem. Soc., 1979, 101, 7013–7018 CrossRef CAS
.
- K. C. Nicolaou, G. Vassilikogiannakis, W. Magerlein and R. Kranich, Angew. Chem., Int. Ed., 2001, 40, 2482–2486 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: the list of 322 functional groups, calculation of the indices' confidence intervals and more chemical trends/examples. See DOI: 10.1039/c2sc00011c |
| This journal is © The Royal Society of Chemistry 2012 |
