Negative ion photoelectron spectroscopy confirms the prediction that D_3h carbon trioxide (CO₃) has a singlet ground state

Abstract

The CO₃ radical anion (CO₃˙⁻) has been formed by electrospraying carbonate dianion (CO₃²⁻) into the gas phase. The negative ion photoelectron (NIPE) spectrum of CO₃˙⁻ shows that, unlike the isoelectronic trimethylenemethane [C(CH₂)₃], D_3h carbon trioxide (CO₃) has a singlet ground state. From the NIPE spectrum, the electron affinity of D_3h singlet CO₃ was, for the first time, directly determined to be EA = 4.06 ± 0.03 eV, and the energy difference between the D_3h singlet and the lowest triplet was measured as ΔE_ST = − 17.8 ± 0.9 kcal mol⁻¹. B3LYP, CCSD(T), and CASPT2 calculations all find that the two lowest triplet states of CO₃ are very close in energy, a prediction that is confirmed by the relative intensities of the bands in the NIPE spectrum of CO₃˙⁻. The 560 cm⁻¹ vibrational progression, seen in the low energy region of the triplet band, enables the identification of the lowest, Jahn–Teller-distorted, triplet state as ³A₁, in which both unpaired electrons reside in σ MOs, rather than ³A₂, in which one unpaired electron occupies the b₂ σ MO, and the other occupies the b₁ π MO.

---

Introduction

Carbon trioxide, CO₃, is an unusual molecule with a long history. In 1962 CO₃ was proposed by Katakis and Taube to be an intermediate in photoreaction of O₃ with CO₂.¹ Four years later, CO₃ was again postulated as a reactive intermediate, this time in the photoreaction of CO₂ with itself.²

Experimental confirmation of the existence of CO₃ was obtained by IR spectroscopy on the matrix-isolated molecule, first by Moll, Clutter and Thompson in 1966,³ and subsequently by Weissberger, Breckenridge and Taube in 1967 (ref. 4) and by Jacox and Milligan in 1971.⁵ These experiments favored a C_2v structure for CO₃, containing a three-membered O–C–O ring and a carbonyl group. Nevertheless, a higher energy, D_3h isomer was detected by Kaiser and coworkers in 2006.⁶ Very recently, the C_2v and D_3h isomers were reported by Sivaraman and coworkers to coexist in ion-irradiated CO₂ ice.⁷

A number of theoretical studies from the 1960s to 1980s investigated the structure of CO₃, mainly focusing on relative stabilities of the cyclic C_2v structure, the acyclic C_s structure, and the linear C_∞v structure.⁸ These INDO, EH, SCF, and MP2 calculations all found that the C_2v isomer is the lowest in energy.⁹

Nevertheless, in 1987 CISD calculations by Mulder and coworkers found the D_3h structure to be lower in energy than the C_2v structure.¹⁰ However, subsequent calculations at higher levels of theory agree that the ground state of CO₃ possesses a C_2v structure, which is computed to be 1.8–6.4 kcal mol⁻¹ lower in energy than the D_3h isomer.¹¹ A small barrier of 4.0–8.6 kcal mol⁻¹ is calculated for the isomerization from the C_2v to D_3h structure.^11b,e,12 The computational finding of separate C_2v and D_3h minima, with the former lower in energy than the latter, is, of course, consistent with the results of the experiments on matrix-isolated CO₃.^3–7

The singlet-triplet energy difference (ΔE_ST) in CO₃ has also been computed. ΔE_ST between the ¹A₁ singlet ground state and the ³A₁ triplet state at their C_2v equilibrium geometries was calculated by fourth-order MBPT calculations to be −20.5 kcal mol⁻¹.^11a (The negative sign indicates that the singlet is lower in energy than the triplet). Similar values were obtained by QCISD(T) calculations.^11b,g The ΔE_ST of CO₃ between the ¹A₁ singlet state and a different triplet state (³B₂) was computed to be −22.5 kcal mol⁻¹ at the MRCI+Q(16,13)/6-311+G(3df)//CASSCF(16,13)/6-311G(d) level of theory.¹²

Also of interest have been the roles of CO₃ in the quenching of the singlet excited state of oxygen atom (¹D) by CO₂ and in the ¹⁸O enrichment in CO₂ in the atmospheres of Earth and Mars.¹³ Singlet and triplet potential energy surfaces for the reaction of O with CO₂ have both been calculated.^9,11b,14

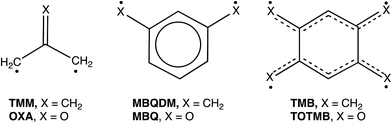
Our own interest in CO₃ comes from the fact that it is the n = 3 member of the isoelectronic series of C(CH₂)_3−nO_n diradicals, for which n = 0 is trimethylenemethane (TMM) and n = 1 is oxyallyl (OXA). Negative ion photoelectron spectroscopy (NIPES) has shown that the substitution of the oxygen in OXA for one CH₂ group in TMM changes ΔE_ST by 17.5 kcal mol⁻¹, from ΔE_ST = 16.2 kcal mol⁻¹ for the triplet ground state of TMM¹⁵ to ΔE_ST = −1.3 kcal mol⁻¹ for the singlet ground state of OXA.¹⁶

However, the substitution of oxygen for CH₂ does not always have such a large effect on ΔE_ST in diradicals. For example, NIPES has shown that substitution of the oxygens in meta-benzoquinone (MBQ) for both CH₂ groups in meta-benzoquino-dimethane (MBQDM) changes ΔE_ST by only 0.6 kcal mol⁻¹, from ΔE_ST = 9.6 kcal mol⁻¹ in MBQDM¹⁷ to ΔE_ST = 9.0 kcal mol⁻¹ in MBQ.¹⁸ Substituting the oxygens in 1,2,4,5-tetraoxatetramethylenebenzene (TOTMB) for the four methylene groups in tetramethylenebenzene (TMB) has been predicted actually to destabilize the singlet, relative to the triplet, decreasing ΔE_ST by 2.7 kcal mol, from a calculated value of ΔE_ST = −6.2 kcal mol⁻¹ in TMB to a value of ΔE_ST = −3.5 kcal mol⁻¹, both calculated for and subsequently found by NIPES in TOTMB.¹⁹

As mentioned above, calculations have predicted a singlet ground state with C_2v geometry for CO₃, with ΔE_ST values ranging from −18.3 kcal mol⁻¹ (ref. 11b) to −22.5 kcal mol⁻¹.¹² However, an experimental measurement of ΔE_ST in CO₃ has not been published.

Similarly, the electron affinity (EA) of CO₃ has been computed, with the best values ranging from EA = 3.84 eV to EA = 4.08 eV.²⁰ However, the EA of CO₃ has not been directly measured. With one exception,²¹ the experimental estimates are in the range EA = 1.8–3.5 eV,²² far below the best calculated values.²⁰

In order to obtain accurate experimental values for both EA and ΔE_ST in CO₃, we sought to obtain the NIPE spectrum of CO₃˙⁻. Herein we report this spectrum and assign the peaks in it with the help of DFT and ab initio calculations. The NIPE spectrum and our analysis of it lead to values of EA = 4.06 ± 0.03 eV, and ΔE_ST = −17.8 ± 0.9 kcal mol⁻¹ between the D_3h¹A^′₁ state and the Jahn–Teller distorted ³E′ state.

Experimental methodology

The NIPES experiments were performed with an apparatus that consisted of an electrospray ionization source, a cryogenic ion trap, and a magnetic-bottle time-of-flight (TOF) photoelectron spectrometer.²³ Electrospraying an aqueous methanolic solution of Na₂CO₃ into a vacuum afforded generation of a weak CO₃˙⁻ radical anion beam, although HCO₃⁻ was always the dominant anion formed.²⁴ The anions generated were guided by quadrupole ion guides into an ion trap, where they were accumulated and cooled by collisions with cold buffer gas, before being transferred into the extraction zone of a TOF mass spectrometer.

The CO₃˙⁻ radical anions were carefully mass selected, and decelerated before being photodetached with a laser beam of 193 nm (6.424 eV) from an ArF laser in the photodetachment zone. The laser was operated at a 20 Hz repetition rate with the ion beam off at alternating laser shots, to enable shot-to-shot background subtraction to be carried out. Photoelectrons were collected at ∼100% efficiency with the magnetic bottle and analyzed in a 5.2 m long electron flight tube.

The TOF photoelectron spectra were converted into electron kinetic energy spectra by calibration with the known NIPE spectra of I⁻ and Cu(CN)₂⁻. The electron binding energies, given in the spectrum in Fig. 1 were obtained by subtracting the electron kinetic energies from the detachment photon energy.

Fig. 1 The 20 K NIPE spectrum of CO₃˙⁻ at 193 nm (6.424 eV). The intensity of the low binding energy band X is ca. one sixth of the high binding energy band A. The inset in blue is the X band enlarged by a factor of 6. The spectrum yields values of EA = 4.06 ± 0.03 eV, and ΔE_ST = −0.77 ± 0.04 eV = −17.8 ± 0.9 kcal mol⁻¹.

The best instrumental resolution was 20 meV full width at half maximum for 1 eV kinetic energy electrons, as demonstrated in the I⁻ spectrum after a maximum deceleration. However, due to the weak mass intensity and light mass of CO₃˙⁻, the NIPE spectra of CO₃˙⁻ were obtained under compromised conditions with 4% energy resolution, i.e., 40 meV for 1 eV kinetic energy electrons.

Computational methodology

In order to help analyze the NIPE spectrum of CO₃˙⁻, three different types of electronic structure calculations were performed – B3LYP DFT calculations,²⁵ CCSD(T) coupled cluster calculations,²⁶ and (16/13)CASPT2 calculations.²⁷ In the CASPT2 calculations second-order perturbation theory was used to add the effects of dynamic electron correlation²⁸ to a (16/13)CASSCF wavefunction. The (16/13)CASSCF active space consisted of all the configurations that can be generated by distributing four valence electrons from carbon and four from each of the three oxygens among 13 MOs. The MOs were those formed from the σ and π 2p lone-pair AOs on each oxygen in CO₃, the three C–O bonding and three C–O antibonding σ orbitals, and the 2p–π AO on carbon.

All of the calculations were performed using the aug-cc-pVTZ basis set.²⁹ The B3LYP and CCSD(T) calculations and vibrational analyses at these two levels of theory were carried out using the Gaussian09 suite of programs.³⁰ The CASSCF and CASPT2 calculations were performed with MOLCAS.³¹ The program ezSpectrum³² was used to compute the Franck–Condon factors³³ that were necessary in order to simulate the vibrational progressions in the NIPE spectrum of CO₃˙⁻.

Results and discussion

The NIPE spectrum of CO₃˙⁻

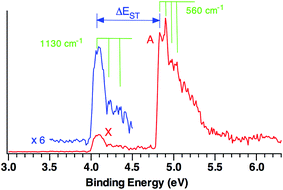
Fig. 1 shows the 20 K NIPE spectrum of CO₃˙⁻ at 193 nm. A weak band, X, peaked at electron binding energy (EBE) of ∼4.1 eV, and a strong band A, peaked at EBE of ∼4.9 eV, are observed in the spectrum. The intensity of the X band is ca. one sixth of the A band.

For statistical reasons, formation of a triplet state is a factor of three more probable than formation of a singlet state; so triplet states invariably give the most intense peaks in NIPE spectra.³⁴ Thus, the NIPE spectrum of CO₃˙⁻ indicates that the ground state of CO₃ is a singlet and that the lowest excited state is a triplet. However, the factor of about six difference between the intensities of the X and A bands in the NIPE spectrum in Fig. 1 suggests that CO₃ has two triplet states with very similar energies and that both can be formed in the photodetachment of an electron from CO₃˙⁻.

From the rising edge of the X band, we estimate the adiabatic detachment energy (ADE) of CO₃˙⁻ (or, equivalently, the electron affinity, EA of CO₃) to be 4.06 ± 0.03 eV. The EA of CO₃ has been the subject of many previous experimental studies;²² but our NIPES value is considerably larger than all but one of these experimental estimates.²¹ However, our value of EA = 4.06 ± 0.03 eV is within experimental error of the value of EA = 4.08 eV, calculated at the CCSD(T)/aug-cc-pVTZ level by Cappa and Elrod in 2001.²⁰

The experimental singlet–triplet gap of CO₃, ΔE_ST, is defined as the difference between the EBE of the X band (EBE = 4.06 ± 0.03 eV) and the EBE of the first resolved peak in the A band (EBE = 4.83 ± 0.03 eV). Therefore, ΔE_ST = −0.77 ± 0.04 eV = −17.8 ± 0.9 kcal mol⁻¹ is obtained from the NIPE spectrum in Fig. 1.

Vibrational structure can be discerned in both the X and A bands. The ground state X band shows a vibrational progression with a frequency of 1130 cm⁻¹. This frequency is high enough that it is likely to belong to a C–O stretching, rather than to an O–C–O bending mode.

The vibrational mode that appears to be excited in the A band transition has a frequency of 560 cm⁻¹. Its low frequency makes it much more likely to be due to an O–C–O bending mode than to a C–O stretching mode.

The electronic structure of CO₃ – qualitative considerations

Understanding the NIPE spectrum of CO₃˙⁻ requires understanding the electronic structure of CO₃. As already noted, D_3hTMM and D_3h CO₃ are isoelectronic. Therefore, like D_3hTMM, D_3h CO₃ might have been expected to have a triplet ground state. However, as discussed in the previous section, the NIPE spectrum of CO₃˙⁻ shows that the ground state of D_3h CO₃ is a singlet and that ΔE_ST = −17.8 ± 0.9 kcal mol⁻¹.

The reason that TMM has a triplet ground state is that in D_3hTMM two electrons occupy two degenerate, e′′, π MOs. The MOs are non-disjoint;³⁵ therefore, as expected from Hund's rule,³⁶ the triplet is the electronic state of lowest energy.¹⁶

However, the C–H bonds in D_3hTMM are replaced by σ lone pairs of electrons on the three oxygens of CO₃. As shown in Fig. 2, the a^′₂ combination of oxygen lone pair orbitals is antibonding between all three oxygens. Therefore, in the lowest electronic state of D_3h CO₃, the a^′₂ MO is left empty.

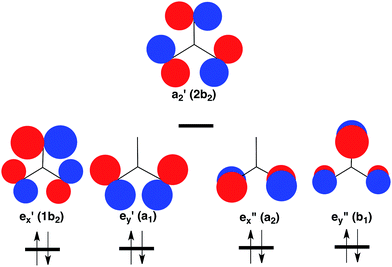Fig. 2 Schematic depiction of the three σ and two π lone-pair MOs of highest energy that are localized on the three oxygens in CO₃. Symmetries of these MOs are given at D_3h and (C_2v) geometries. Of these MOs, a^′₂ is highest in energy, because it contains antibonding σ interactions between all three oxygens. Therefore, a^′₂ is left empty and the degenerate pairs of e′ and e′′ MOs are each doubly occupied in the closed-shell singlet ground state of CO₃.³⁷ The orbital occupancy in this ¹A^′₁ state is indicated at the bottom of Fig. 2.

The pair of electrons that occupy the a^′₂ C–H bonding MO in D_3hTMM reside in one of the pair of e′′ π MOs in D_3h CO₃. Consequently, a total of four electrons occupy the e′′, π MOs in D_3h CO₃, and four more electrons occupy the degenerate pair of e′, σ MOs. This is the reason why the lowest electronic state of D_3h CO₃ is a closed-shell singlet.

In the CO₃˙⁻ radical anion one electron occupies the a^′₂ MO. In the low energy triplet states of neutral CO₃ one electron in the closed-shell, singlet, ground state is excited into this MO. However, whether the electron that occupies the a^′₂ MO in the triplet comes from one of the e′ σ MOs or one of the e′′ π MOs in the singlet is not obvious. The question of the relative energies of the resulting ³E′ and ³E′′ states of CO₃ has been addressed by the calculations that are described in a later section of this paper.

Computational results for the lowest singlet state of CO₃

The results of our B3LYP, CCSD(T), and CASPT2 calculations on CO₃˙⁻ and CO₃ are summarized in Table 1. All of these calculations find that in the lowest electronic state of the radical anion the unpaired electron occupies the a^′₂ MO, so that CO₃˙⁻ maintains D_3h symmetry.³⁸ The B3LYP and CASPT2 calculations find that the D_3h singlet state is also an energy minimum.

Table 1 Calculated B3LYP,²⁵ CCSD(T),²⁶ and CASPT2 (ref. 27) energies (kcal mol⁻¹) of the ground state of CO₃˙⁻ and of the low-lying electronic states of CO₃, relative to the D_3h¹A^′₁ state of CO₃. Calculations were carried out with the aug-cc-pVTZ basis set.²⁹ Electronic states and orbital occupancies after Jahn–Teller distortions to C_2v symmetry of the two components of ³E′ and ³E′′ states are given in parentheses, and the energies after the Jahn–Teller distortions are indicated by arrows

Electronic state	B3LYP	CCSD(T)	CASPT2
a Previous calculations at this level of theory obtained −4.08 eV for the EA of CO3.^20 b Artifactual symmetry breaking^39–41 results in this state having two imaginary frequencies for distortions that lead to three equivalent C2v minima. These minima have CCSD(T) energies that are 0.9 kcal mol^−1 lower than that of the D3h singlet state. c One of three transition structures that connect the D3h singlet to one of the three C2v structures that are the global minima on the potential energy surface for the lowest singlet state of CO3.
^2A^′2 of CO3˙^−	−116.4 (−5.05 eV)	−95.4 (−4.13 eV)^a	−93.9 (−4.07 eV)
^1A^′1 (D3h minimum)	0	0^b	0
^1A1 (C2v TS)^c	0.6	1.5	6.6
^1A1 (C2v minimum containing an O–C–O ring)	−13.4	−5.5	−2.2
^3E^′x (^3B2 = |…a1^α2b2^α>)	−1.0 → −4.2	19.1 → 16.3	24.8 → 21.0
^3E^′y (^3A1 = |…1b2^α2b2^α>)	−1.0 → −3.6	18.6 → 15.5	23.7 → 20.8
^3E^′′x (^3A2 = |…b1^α2b2^α>)	1.0 → −1.0	19.5 → 17.8	20.1 → 19.8
^3E^′′y (^3B1 = |…a2^α2b2^α>)	−0.6 → −0.7	19.5 → 19.2	20.2 → 19.3
^3A^′2 (^3B2 = |…b1^αa2^α>)	11.7	28.4	35.9

---

However, the CCSD(T) calculations find that the D_3h geometry of the ¹A^′₁ state has two imaginary frequencies of 472i cm⁻¹. These correspond to a degenerate pair of e′ vibrations that lead to a trio of slightly distorted structures with C_2v symmetry (not to be confused with the cyclic C_2v structure with an O–C–O ring and a carbonyl group). The three equivalent C_2v structures are 0.9 kcal mol⁻¹ lower in energy than the D_3h structure at the CCSD(T)/aug-cc-pVTZ level of theory.

When the basis set is expanded to aug-cc-pVQZ, the energy difference between the D_3h and C_2v structures drops to only 0.3 kcal mol⁻¹. Since the B3LYP and the CASPT2 calculations both find the D_3h structure to be an energy minimum, we believe that the small geometry distortions to structures with C_2v symmetry in the CCSD(T) calculations are due to artifactual symmetry breaking in the CCSD(T) wave function for the ¹A^′₁ state at D_3h geometries.^39–41

If the lowest electronic states of CO₃˙⁻ and CO₃ both have D_3h symmetry, it is possible to assign the vibrational progression in the X band of the NIPE spectrum in Fig. 1 to a symmetrical C–O stretching mode. Only vibrational modes that preserve those symmetry elements that the electronic states of the radical ion and the neutral molecule have in common are seen in NIPE spectra. Therefore, the vibrational progression with a frequency of 1130 cm⁻¹ that is seen in the X band in Fig. 1 must belong to the a^′₁ vibration of D_3h CO₃.

On going from the CO₃˙⁻ radical anion to neutral CO₃ the C–O bond lengths are calculated to shorten by 0.013 Å (CASPT2), 0.015 Å [CCSD(T)], and 0.023 Å (UB3LYP). Consequently, the calculated Franck–Condon factors predict that an a^′₁ C–O bond stretching vibrational progression should be seen in the X band in Fig. 1. The calculated harmonic frequencies for the a^′₁ C–O stretching vibration are 1083 cm⁻¹ (CASPT2), 1090 cm⁻¹ [CCSD(T)] and 1140 cm⁻¹ (B3LYP). The B3LYP value differs by only 10 cm⁻¹ from the experimental value of 1130 cm⁻¹.

Since the 1130 cm⁻¹, a^′₁, C–O bond stretching mode is totally symmetric, it would not have been seen in the IR spectrum of D_3h CO₃ in matrix isolation. The observed, asymmetric (e′), C–O bond-stretching frequency was reported to be 1165 cm⁻¹.⁶

As shown in Table 1, and, in agreement with the results of previous calculations¹¹ and experiments,^3–7 B3LYP, CCSD(T), and CASPT2 all find that there is a C_2v singlet energy minimum, containing an O–C–O ring, that is lower in energy than the D_3h singlet. Not unexpectedly, the barrier height that is calculated for ring closure increases as the calculated exothermicity of this reaction decreases.

Because the D_3h → C_2v ring closure reaction requires mixing of the filled e′ MOs in Fig. 2 with the empty a^′₂ MO, ring closure is computed to involve passage over a barrier. This orbital mixing, which occurs on an e′ distortion from D_3h to C_2v symmetry, may be regarded as a second-order Jahn–Teller effect.⁴²

For example, at C_2v geometries e^′_x and a^′₂ both have b₂ symmetry and so can be mixed by an e_y distortion from D_3h symmetry. From inspection of the MOs in Fig. 2, one can deduce that this mixing reduces the contribution of the AOs on the two oxygens between which O–O bond formation occurs and thus makes the resulting b₂ MO much less antibonding than the e^′_x MO. In fact, the b₂ MO that results from the mixing between e^′_x and a^′₂ MOs becomes the 2p_x lone-pair AO on the carbonyl group of the C_2v singlet energy minimum.

The large change in geometry that occurs on formation of the cyclic singlet CO₃ molecule results in the absence of overlap between its vibrational wave function and the vibrational wave function of the D_3h CO₃˙⁻ radical anion. Consequently, the Franck–Condon factor for the laser-induced transition from D_3h CO₃˙⁻ to the C_2v energy minimum of singlet CO₃ is calculated to be effectively zero. Therefore, the value of EA = 4.06 ± 0.03 eV in the NIPE spectrum corresponds to the energy difference between the D_3h equilibrium geometry of CO₃˙⁻ and the local D_3h energy minimum of neutral singlet CO₃, not the global C_2v energy minimum, of singlet, CO₃.

There are two types of experimental evidence that support this conclusion. The first is that the measured EA is very close to the calculated CCSD(T) and CASPT2 energy differences in Table 1 between the D_3h equilibrium geometry of CO₃˙⁻ and the local D_3h energy minimum of neutral CO₃. Second, as already discussed, the vibrational progression of 1130 cm⁻¹ seen in the X band of the NIPE spectrum in Fig. 1 is in good agreement with that predicted by all three levels of theory for the D_3h local minimum.

Computational results for the lowest triplet state of CO₃

As shown in Table 1, there are two low-lying triplet states in CO₃. They are E′, in which the two unpaired electrons occupy the a^′₂ and e′ σ MOs, and E′′, in which the second unpaired electron occupies the e′′ π MO, instead of the e′ σ MO.

A third triplet, ³A^′₂, which is the ground state of TMM, is calculated to be very high in energy in CO₃. In this state the e^′′_x and e^′′_y π MOs are each singly occupied, and the a′₂ MO is doubly occupied. As shown in Fig. 2, the a^′₂ MO is strongly O–O antibonding; and its double occupancy in ³A^′₂ makes this triplet state much higher in energy than either ³E′ or ³E′′, in both of which the a^′₂ MO is singly occupied.

Whether ³E′ or ³E′′ is lower in energy is not clear from qualitative considerations. As shown in Fig. 2, the e′ MOs are weakly bonding σ MOs; whereas, the e′′ MOs are non-bonding π MOs. On this basis, leaving e′ doubly occupied and having e′′ singly occupied should be favored; so ³E′′ should be lower in energy than ³E′.

On the other hand, two electrons of the same spin cannot simultaneously occupy the same AO. With one electron in the a^′₂ σ MO, having a second electron of the same spin in an e′ σ MO prevents these two electrons from ever appearing on the same atom; whereas, no such prohibition exists if the second unpaired electron occupies an e′′ π MO. Consequently, although maximization of bonding is expected to favor the ³E′′ state, minimization of electron repulsion should favor the ³E′ state. Which effect dominates cannot be predicted from qualitative considerations; so one has to rely on calculations for the prediction of which triplet state, ³E′ and ³E′′, is lower in energy.

Table 1 shows that ³E′ and ³E′′ are, in fact, calculated to be very close in energy. Both degenerate triplet states are expected to undergo first-order Jahn–Teller distortions to C_2v symmetry,⁴³ and the calculated energy differences between the two triplet states at their C_2v equilibrium geometries range between 1 and 3 kcal mol⁻¹.

Interestingly, the results, tabulated in Table 1, reveal that the CCSD(T) and CASPT2 calculations differ as to which triplet state is predicted to be lower in energy. The CCSD(T) calculations predict that the C_2v triplet, formed by exciting an electron from the pair of e′ σ MOs into the a^′₂ σ MO, is lower in energy than the triplet that is formed by exciting an electron from the pair of e′′ π MOs into the a^′₂ MO. B3LYP makes the same prediction as CCSD(T). However, it should be noted that B3LYP erroneously predicts that both triplet states are lower in energy than the D_3h¹A^′₁ state (Table 1).

CCSD(T) and B3LYP both predict that the ³E′ and ³E′′ states have very similar energies at their respective D_3h geometries. However, as would be expected, removing an electron from one of the e′ σ MOs results in a larger Jahn–Teller distortion than removing an electron from one of the e′′ π MOs. B3LYP, CCSD(T), and CASPT2 calculations all find that this is, in fact, the case. The larger energy lowering of the ³E′ state by a first-order Jahn–Teller distortion leads to the prediction by both CCSD(T) and B3LYP that the C_2v distorted ³E′ state is the lowest energy triplet state of CO₃ by 2–3 kcal mol⁻¹.

In contrast to CCSD(T), CASPT2 places ³E′′ well below ³E′ at their respective D_3h geometries. Even though the first-order Jahn–Teller distortion to C_2v symmetry stabilizes ³E′ more than ³E′′, the energetic advantage of ³E′′ over ³E′ at their respective D_3h geometries prevails; and the C_2v distorted ³E′′ (³A₂) state is calculated to be lower in energy than the C_2v distorted ³E′ (³A₁) state by 1–2 kcal mol⁻¹.

Which triplet state is lower in energy, ³E′ (³A₁) or ³E′′ (³A₂)?

Which method, CCSD(T) or CASPT2, gives the correct answer to the question of what is the lowest triplet state of CO₃, ³E′ → ³A₁ or ³E′′ → ³A₂? As described in the following paragraphs, the NIPE spectrum in Fig. 1 indicates that the CCSD(T) prediction is correct; and, although ³A₁ and ³A₂ are very close in energy, ³A₁ is the lower energy of these two triplet states.

This conclusion follows from the vibrational progression seen in the low energy portion of the triplet peak. As already noted, this region of the NIPE spectrum shows a progression of 560 cm⁻¹. This vibrational frequency is too low to be associated with C–O stretching, but is the right size to be due to O–C–O bending. Our calculations indicate that only ³A₁ should show an O–C–O bending progression, so it must be the lower energy of the two closely-spaced triplet states.

The conclusion that only ³A₁ should show an O–C–O bending progression follows from the calculated geometries of ³A₁ and ³A₂ and is supported by our simulations of the vibrations in the peaks due to ³A₁ and ³A₂ in the NIPE spectra of CO₃˙⁻. Table 2 gives the bond lengths and the unique bond angle of the C_2v minima to which CCSD(T) and CASPT2 both predict that ³E′ and ³E′′ distort. It is clear that both the bond lengths and the bond angles of the ³A₁ minima of the distorted ³E′ state deviate significantly from the equality they have at D_3h geometries. However, the bond angles of the ³A₂ minima of the distorted ³E′′ state are calculated to remain much more nearly equal after Jahn–Teller distortions.

Table 2 Optimized bond lengths (Å) and bond angles (degs) at the C_2v geometries of the ³A₁ and ³A₂ states of CO₃, calculated with B3LYP, CCSD(T), and CASPT2, using the aug-cc-pVTZ basis set. O₁ is the unique oxygen, and O₂ and O₃ are the two equivalent oxygens at C_2v geometries

Bond length, or bond angle	B3LYP		CCSD(T)		CASPT2
	^3A1	^3A2	^3A1	^3A2	^3A1	^3A2
R(C–O1)	1.311	1.338	1.321	1.334	1.325	1.315
R(C–O2) = R(C–O3)	1.257	1.245	1.259	1.254	1.259	1.267
O2–C–O3	113.6°	122.0°	113.8°	119.2°	114.2°	119.7°
O1–C–O2 = O1–C–O3	123.2°	119.0°	123.1°	120.4°	122.9°	120.1°

---

The difference between the geometries of the C_2v minima for the two triplet states is a consequence of the difference between the MOs that are occupied in these two states. In the ³A₁ state an electron, which occupies the 1b₂ σ MO in the D_3h¹A^′₁ ground state, is removed and placed in the 2b₂ σ MO. As shown in Fig. 2, this electronic excitation results in the O₁–O₂ and O₁–O₃ σ bonding interactions in the 1b₂ MO being replaced by σ antibonding interactions between all of the oxygens in the 2b₂ MO. Consequently, the O₁–C–O₂ and O₁–C–O₃ bond angles in ³A₁ are calculated to be larger than 120°; so the O₂–C–O₃ bond angle is predicted to be much less than 120° in this state.

In the ³A₂ state an electron, which occupies the b₁ π MO in the D_3h¹A^′₁ ground state, is removed and placed in the 2b₂ σ MO. The antibonding O₁–O₂ and O₁–O₃ π interactions in b₁ are lost, as is the bonding O₂–O₃ π interaction. Consequently, the O₁–C–O₂ and O₁–C–O₃ angles in the ³A₂ state are expected to be less than 120°, and the O₂–C–O₃ angle is expected to be greater than 120°.

These qualitative expectations are fulfilled at the B3LYP level of theory. However, because the 1,3-interactions between the oxygens in ³A₂ involve π, rather than σ AOs, the deviations of the B3LYP bond angles from 120° are about three times smaller in ³A₂ than in ³A₁. In fact, the π interactions in ³A₂ are so small that, in the optimized CCSD(T) and CASPT2 geometries, the deviations of the bond angles from 120° are not only less than 1° but they actually deviate from 120° in the opposite direction from the B3LYP bond angles.

In NIPE spectra progressions are only seen in vibrational modes that affect the geometrical parameters by which an electronic state differs from the radical anion from which the electronic state is formed.³⁴ The calculated O–C–O bond angles in the ³A₁ state of CO₃ differ significantly from those in the D_3h equilibrium geometry of the ²A^′₂ ground state of CO₃˙⁻. Therefore, one would expect to see a long vibrational progression in O–C–O bending in the band for formation of the ³A₁ state of CO₃ in the NIPE spectrum of CO₃˙⁻.

On the other hand, the calculated O–C–O bond angles in the ³A₂ state of CO₃ are very close to those in the D_3h equilibrium geometry of the ²A^′₂ radical anion. Therefore, one would not expect to see a long vibrational progression in O–C–O bending in the band for formation of the ³A₂ state of CO₃ in the NIPE spectrum of CO₃˙⁻. The only long vibrational progression that should appear in the band for formation of the ³A₂ state is one in C–O bond stretch, since the C–O bond lengths in the C_2v equilibrium geometry of ³A₂ in Table 2 differ from those in the D_3h equilibrium geometry of the radical anion.⁴⁴

Fig. 1 shows that a vibrational progression of 560 cm⁻¹ in O–C–O bending is found in the band for formation of the lowest triplet state of CO₃ in the NIPE spectrum of CO₃˙⁻. As discussed above, such a progression is expected to be seen in the ³A₁ state of CO₃, but not in the ³A₂ state. Thus, it follows that the lowest triplet state of CO₃ is the ³A₁ state, in which one unpaired electron resides in the 1b₂ MO and the other resides in the 2b₂ MO.

This qualitative conclusion is supported by both B3LYP and CCSD(T) simulations of the triplet region of the NIPE spectrum of CO₃˙⁻. Using the Franck–Condon factors (FCFs) calculated with ezSpectrum,³²Fig. 3 shows how the NIPE spectrum of CO₃˙⁻ is predicted to appear, based on the results obtained with B3LYP calculations.

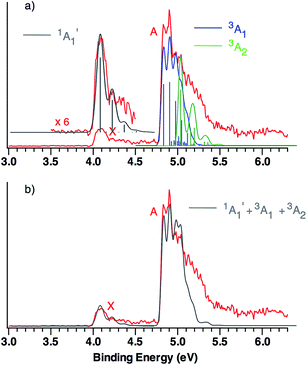Fig. 3 (a) B3LYP/aug-cc-pVTZ calculated vibrational structure in the NIPE spectrum of CO₃˙⁻, superimposed on the experimental NIPE spectrum (red). The positions of the bands in the calculated stick spectrum for ¹A^′₁ (grey), ³A₁ (blue), and ³A₂ (green) have been adjusted, in order to align the 0–0 bands in the calculated spectrum with the 0–0 bands in the observed spectrum. The calculated spectrum, using Gaussian line shapes with, respectively, 100, 60, and 60 meV full widths at half maxima for each stick in ¹A^′₁, ³A₁, and ³A₂, is also shown. (b) The computed NIPE spectrum (grey), calculated from the sum of the convoluted contributions of the singlet and two triplets in Fig. 3a, superimposed on the experimental 193 nm spectrum (red).

The predicted vibrational structure for the triplet region of the NIPE spectrum, based on the results of CCSD(T) calculations, has a very similar appearance to the B3LYP-based simulation in Fig. 3. The CCSD(T) simulations are provided in Fig. S1 and S2 of the ESI† of this manuscript, and the vibrational mode assignments are given in Fig. S1.† Both the B3LYP and CCSD(T) simulations confirm that the vibrational progressions in the triplet region of the experimental NIPE spectrum are dominated by the O–C–O bending mode in ³A₁ and by C–O bond stretch in ³A₂.

Comparison of the simulated spectra for both triplet states with the actual NIPE spectrum suggests aligning the 0–0 band of ³A₂ with the fourth resolved peak (EBE = 5.03 eV) in band A, which leads to the conclusion that the ³A₂ state is 0.20 eV (4.6 kcal mol⁻¹) higher in energy than ³A₁. This ordering of the two triplet states is in accordance with the results of both the B3LYP and CCSD(T) calculations (Table 1). However, an energy difference of 4.6 kcal mol⁻¹ would be about twice the size of the energy differences of, respectively, 2.6 and 2.3 kcal mol⁻¹ that are predicted by these two types of calculations.

An alternative alignment of the 0–0 band of ³A₂ with the third resolved peak (EBE = 4.97 eV) in band A is shown in Fig. S3 of the ESI.† This alignment makes the ³A₂ state only 0.14 eV (3.2 kcal mol⁻¹) higher in energy than ³A₁, which is in better agreement with the energy differences between these two states, computed by both B3LYP and CCSD(T). However, comparison of Fig. S3† with Fig. 3, shows that the alignment in Fig. S3† fits the observed intensities of the peaks in the experimental NIPE spectrum less well than the alignment in Fig. 3.

The simulated vibrational structure for formation of the singlet ground state of CO₃ is also shown in Fig. 3. The simulation reproduces well the observed vibrational progression in the singlet ground state and confirms the conclusion that this progression is due to the symmetric C–O stretching.

The simulations, based on the calculated FCFs, for formation of the singlet and two triplet states of CO₃ from the ²A^′₂ state of CO₃˙⁻, provide a good fit to the experimental NIPE spectrum of CO₃˙⁻ up to 5.1 eV. There appears to be a shoulder at EBE ∼ 5.3 eV in the experimental spectrum, which might be due to formation of the third, low-lying triplet state, ³A^′₂, which is predicted by the CCSD(T) calculations to have EA = 5.37 eV.

The similarity between the calculated and experimental NIPE spectra of CO₃˙⁻ in Fig. 3 provides evidence that our assignments of the peaks in the experimental NIPE spectra are correct and that, as predicted by both B3LYP and CCSD(T), the ³A₁ state of CO₃ is lower in energy than the ³A₂ state.

Conclusions

We report the first NIPE spectrum of CO₃˙⁻. The spectrum shows that, substitution of the three oxygens in CO₃ for the three CH₂ groups in TMM results in a change in the ground state, going from ³A^′₂ and ΔE_ST = 16.2 kcal mol⁻¹ in TMM¹⁵ to ¹A^′₁ and ΔE_ST = −17.8 ± 0.9 kcal mol⁻¹ in CO₃. The NIPE spectrum also provides the first measurement of EA = 4.06 ± 0.03 eV in D_3h CO₃. Qualitative MO analysis and quantitative electronic structure calculations confirm that the ground state of CO₃ is a singlet and reveal which of the two closely-spaced triplet excited states is lower in energy. The CCSD(T) and CASPT2 calculations reproduce the experimental EA and ΔE_ST values of CO₃ rather well.

The combined results of our experiments and calculations contribute fundamental information about the electronic structure of CO₃, a molecule that is not only of interest because it is isoelectronic with both TMM and OXA, but that is also important in both atmospheric chemistry and astrochemistry.^12–14,45

Conflict of interest

The authors declare no competing financial interest.

Acknowledgements

The calculations at UNT were supported by Grant B0027 from the Robert A. Welch Foundation. The NIPES research at PNNL was supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences and Biosciences and was performed at the EMSL, a national scientific user facility sponsored by DOE's Office of Biological and Environmental Research and located at Pacific Northwest National Laboratory, which is a multiprogram national laboratory operated for DOE by Battelle.

Notes and references

1. D. Katakis and H. Taube, J. Chem. Phys., 1962, 36, 416.
2. A.-Y. Ung and H. I. Schiff, Can. J. Chem., 1966, 44, 1981.
3. N. G. Moll, D. R. Clutter and W. E. Thompson, J. Chem. Phys., 1966, 45, 4469.
4. E. Weissberger, W. H. Breckenridge and H. Taube, J. Chem. Phys., 1967, 47, 1764.
5. M. E. Jacox and D. E. Milligan, J. Chem. Phys., 1971, 54, 919.
6. C. S. Jamieson, A. M. Mebel and R. I. Kaiser, ChemPhysChem, 2006, 7, 2508.
7. B. Sivaraman, B. N. R. Sekhar, D. Fulvio, A. Hunniford, B. McCullough, M. E. Palumbo and N. Mason, J. Chem. Phys., 2013, 139, 074706.
8. (a) B. M. Gimarc and T. S. Chou, J. Chem. Phys., 1968, 49, 4043; (b) J. F. Olsen and L. Burnelle, J. Am. Chem. Soc., 1969, 91, 7286; (c) M. Cornille and J. Horsley, Chem. Phys. Lett., 1970, 6, 373; (d) J. R. Sabin and H. Kim, Chem. Phys. Lett., 1971, 11, 593; (e) J. A. Pople, U. Seeger, R. Seeger and P. v. R. Schleyer, J. Comput. Chem., 1980, 1, 199; (f) J. S. Francisco and I. H. Williams, Chem. Phys., 1985, 95, 373.
9. P. LaBonville, R. Kugel and J. R. Ferraro, J. Chem. Phys., 1977, 67, 1477.
10. W. J. van de Guchte, J. P. Zwart and J. J. C. Mulder, J. Mol. Struct.: THEOCHEM, 1987, 152, 213.
11. (a) M. A. Castro, S. Canuto and A. M. Simas, Chem. Phys. Lett., 1991, 177, 98; (b) R. D. J. Froese and J. D. Goddard, J. Phys. Chem., 1993, 97, 7484; (c) T. Kowalczyk and A. I. Krylov, J. Phys. Chem. A, 2007, 111, 8271; (d) Y. Liu, I. B. Bersuker, W. Zou and J. E. Boggs, J. Chem. Theory Comput., 2009, 5, 2679; (e) C. Qin and T.-Y. Soo, J. Mol. Struct.: THEOCHEM, 2009, 897, 32; (f) F. Grein, J. Chem. Phys., 2013, 138, 204305; (g) A. S. Averyanov, Y. G. Khait and Y. V. Puzanov, J. Mol. Struct.: THEOCHEM, 1999, 459, 95.
12. A. M. Mebel, M. Hayashi, V. V. Kislov and S. H. Lin, J. Phys. Chem. A, 2004, 108, 7983.
13. Review: R. I. Kaiser and A. M. Mebel, Chem. Phys. Lett., 2008, 465, 1.
14. C. J. Bennett, C. Jamieson, A. M. Mebel and R. I. Kaiser, Phys. Chem. Chem. Phys., 2004, 6, 735.
15. (a) P. G. Wenthold, J. Hu, R. R. Squires and W. C. Lineberger, J. Am. Chem. Soc., 1996, 118, 475; (b) P. G. Wenthold, J. Hu, R. R. Squires and W. C. Lineberger, J. Am. Soc. Mass Spectrom., 1999, 10, 800.
16. (a) T. Ichino, S. M. Villano, A. J. Gianola, D. J. Goebbert, L. Velarde, A. Sanov, S. J. Blanksby, X. Zhou, D. A. Hrovat, W. T. Borden and W. C. Lineberger, Angew. Chem., Int. Ed., 2009, 48, 8509; (b) T. Ichino, S. M. Villano, A. J. Gianola, D. J. Goebbert, L. Velarde, A. Sanov, S. J. Blanksby, X. Zhou, D. A. Hrovat, W. T. Borden and W. C. Lineberger, J. Phys. Chem. A, 2011, 115, 1634.
17. P. G. Wenthold, J. B. Kim and W. C. Lineberger, J. Am. Chem. Soc., 1997, 119, 1354.
18. (a) Q. Fu, J. Yang and X.-B. Wang, J. Phys. Chem. A, 2011, 115, 3201; (b) B. Chen, D. A. Hrovat, S. H. M. Deng, J. Zhang, X.-B. Wang and W. T. Borden, J. Am. Chem. Soc., 2014, 136, 3589; (c) R. C. Fort Jr, S. J. Getty, D. A. Hrovat, P. M. Lahti and W. T. Borden, J. Am. Chem. Soc., 1992, 114, 7549.
19. D. A. Hrovat, G.-L. Hou, X.-B. Wang and W. T. Borden, J. Am. Chem. Soc., 2015, 137, 9094.
20. C. D. Cappa and M. J. Elrod, Phys. Chem. Chem. Phys., 2001, 3, 2986.
21. R. G. Ewing and M. Waltman, Int. J. Mass Spectrom., 2010, 296, 53.
22. (a) D. E. Hunton, M. Hofmann, T. G. Lindeman and A. W. Castleman Jr, J. Chem. Phys., 1985, 82, 134; (b) J. T. Snodgrass, C. M. Roehl, A. M. van Koppen, W. E. Palke and M. T. Bowers, J. Chem. Phys., 1990, 92, 5935; (c) J. F. Hiller and M. L. Vestal, J. Chem. Phys., 1980, 72, 4713; (d) S. E. Novich, P. Engelking, P. L. Jones, J. H. Futrell and W. C. Lineberger, J. Chem. Phys., 1979, 70, 2652; (e) I. Dotan, J. A. Davidson, G. E. Streit, D. L. Albritton and F. C. Fehsenfeld, J. Chem. Phys., 1977, 67, 2874; (f) S. P. Hong, S. B. Woo and E. M. Helmy, Phys. Rev. A, 1977, 15, 1563; (g) M. L. Vestal and G. H. Mauclaire, J. Chem. Phys., 1977, 67, 3758; (h) T. O. Tiernan and R. L. C. Wu, Adv. Mass Spectrom., 1978, 7, 136.
23. X.-B. Wang and L.-S. Wang, Rev. Sci. Instrum., 2008, 79, 073108.
24. Assuming the last phase to generate CO₃˙⁻ from the Na₂CO₃ aqueous solutions in the electrospray ionization process is nanodroplets of waters containing one CO₃²⁻ solute, then we can estimate the ratio of CO₃²⁻ over HCO₃⁻ is about 0.1% from the known carbonic acid dissociation constants. Because CO₃˙⁻ is derived from autodetachment of CO₃²⁻, a weak intensity of CO₃˙⁻ ion beam is expected.
25. B3LYP is a combination of Becke's 3-parameter hybrid exchange functional ( A. D. Becke, J. Chem. Phys, 1993, 98, 5648 ) with the electron correlation functional of Lee, Yang, and Parr ( C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 ).
26. (a) G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910; (b) K. Raghavachari, G. W. Trucks, J. A. Pople and M. H. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479.
27. K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218.
28. W. T. Borden and E. R. Davidson, Acc. Chem. Res., 1996, 29, 87.
29. (a) T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007; (b) R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6769.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013.
31. K. Andersson, F. Aquilante, M. Barysz, A. Bernhardsson, M. R. A. Blomberg, Y. Carissan, D. L. Cooper, M. Cossi, L. DeVico, N. Ferré, M. P. Fülscher, A. Gaenko, L. Gagliardi, G. Ghigo, C. de Graaf, S. Gusarov, B. A. Hess, D. Hagberg, A. Holt, G. Karlström, R. Lindh, P.-Å. Malmqvist, T. Nakajima, P. Neogrády, J. Olsen, T. Pedersen, M. Pitonak, J. Raab, M. Reiher, B. O. Roos, U. Ryde, B. Schimmelpfennig, M. Schütz, L. Seijo, L. Serrano-Andrés, P. E. M. Siegbahn, J. Stålring, T. Thorsteinsson, V. Veryazov and P.-O. Widmark, MOLCAS version 7, Lund University, Sweden, 2008.
32. V. A. Mozhayskiy and A. I. Krylov, ezSpectrum, version 3.0, see http://iopenshell.usc.edu/downloads.
33. (a) J. Franck, Trans. Faraday Soc., 1926, 21, 536; (b) E. Condon, Phys. Rev., 1926, 28, 1182.
34. Reviews: (a) L. C. Lineberger and W. T. Borden, Phys. Chem. Chem. Phys., 2011, 13, 11792; (b) W. T. Borden, in Fifty Years of the James Flack Norris Award, ed. E. T. Strom and V. Mainz, American Chemical Society, Washington, DC, in press.
35. (a) W. T. Borden and E. R. Davidson, J. Am. Chem. Soc., 1977, 99, 4587; (b) W. T. Borden, in Diradicals, ed. W. T. Borden, Wiley-Interscience, New York, 1982, pp. 1–72.
36. Review: W. Kutzelnigg, Angew. Chem., Int. Ed. Engl., 1996, 35, 573 and references therein.
37. Because the a^′′₂ π lone-pair MO contains bonding interactions between the 2p–π lone-pairs on the oxygens and the 2p–π AO on the carbon, it is considerably lower in energy than the σ and π lone-pair MOs on oxygen that are shown in Fig. 2.
38. As found previously,²⁰ a C_2v structure for CO₃˙⁻ is computed to be higher in energy than the D_3h structure.
39. Review: E. R. Davidson and W. T. Borden, J. Phys. Chem., 1983, 87, 4783.
40. For more recent discussions of artifactual symmetry breaking in D_3h molecules, see (a) W. Eisfeld and K. Morokuma, J. Chem. Phys., 2000, 113, 5587; (b) C. E. Miller and J. W. Francisco, J. Phys. Chem. A, 2001, 105, 1662; (c) Ref. 21 .
41. Artifactual symmetry breaking leads to another phenomenon that can be seen in the results given in Table 1 for the triplet states. At D_3h geometries the E^′_x and E^′_y components of the ³E′ state should have identical energies, as should the E^′′_x and E^′′_y components of the ³E′′ state. The fact that the two components of each degenerate state do not have exactly the same energies in Table 1 can be viewed as a consequence of the fact that, in general, electronic structure codes impose only C_2v symmetry on the MOs used to construct D_3h wave functions. Consequently, a wave function that nominally has E_x symmetry actually contains an A₂ contaminant; and a wave function that nominally has E_y symmetry actually contains an A₁ contaminant. Although the E_x and E_y components of such wavefunctions do have the same energies, the A₂ and A₁ contaminants do not; and this leads to the energy differences at D_3h geometries between the “E_x” and “E_y” states in Table 1.^39a.
42. See, inter alia, (a) U. Öpik and M. H. L. Pryce, Proc. R. Soc. London, Ser. A, 1957, 238, 425; (b) R. F. W. Bader, Can. J. Chem., 1962, 40, 1164; (c) R. G. Pearson, J. Am. Chem. Soc., 1969, 91, 4947; (d) R. G. Pearson, J. Mol. Struct., 1983, 103, 25. For a recent review see: (e) I. B. Bersuker, Chem. Rev., 2013, 113, 1351.
43. H. A. Jahn and E. Teller, Proc. R. Soc. London, Ser. A, 1937, 161, 220.
44. A similar situation occurs in the lowest energy triplet state of (CO)₅, which undergoes a first-order Jahn–Teller distortion from the D_5h geometry of the radical anion. The expected C–C bond stretching progression is, in fact, seen in the NIPE spectrum of (CO)₅˙⁻ in the band for formation of the lowest triplet state of (CO)₅. X. Bao, D. A. Hrovat, W. T. Borden and X.-B. Wang, J. Am. Chem. Soc., 2013, 135, 4291.
45. C. J. Bennett, C. S. Jamieson and R. I. Kaiser, Phys. Chem. Chem. Phys., 2010, 12, 4032.

---

Footnote

† Electronic supplementary information (ESI) available: Optimized geometries, electronic energies, zero-point vibrational energies, and imaginary frequencies for all of the CO₃ electronic states discussed in this manuscript, computed with the aug-cc-pVTZ basis set, using B3LYP, CCSD(T), and (16/13)CASPT2 calculations. Fig. S1 contains the CCSD(T) simulation of the triplet region of the NIPE spectrum of (CO)₃˙⁻ and the assignment of the vibrational progressions in it; Fig. S2 shows the calculated NIPE spectrum, with the lines in the stick spectrum in Fig. S1, convoluted with Gaussians; and Fig. S3 shows how the appearance of the simulation in Fig. 3 is modified by choosing a different value of the energy difference between the 0–0 bands in the two lowest energy triplet states (9 pages). See DOI: 10.1039/c5sc03542b

---